Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking
Abstract
:1. Introduction
2. Multiple Object Tracking Formulation
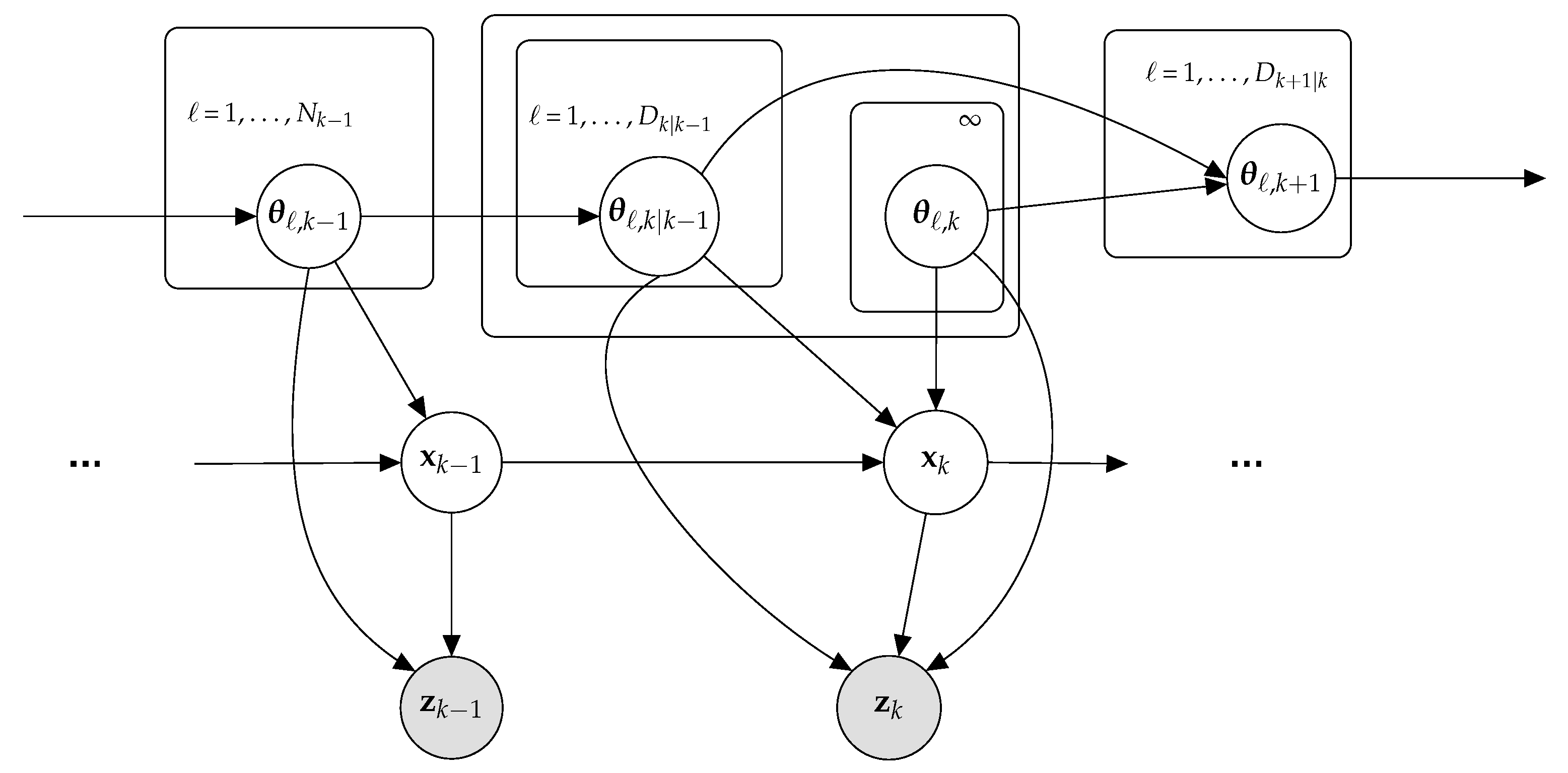
3. Multiple Object Tracking with Dependent Dirichlet Process
3.1. Dependent Dirichlet Process as Prior
3.2. Construction of DDP Prior for State Prediction
- (i)
- Parameters available at the previous time step:At time step , we assume that objects are present in the tracking scene and that there are non-empty (unique) DDP clusters. As unique clusters can include more than one object, multiple objects can be related to the same cluster parameter. We also assume that the following parameters are available at time step .
- –
- Set of object state vectors, =
- –
- Set of DDP cluster parameters for object states, =
- –
- Set of unique DDP cluster parameters,
- –
- Cardinality of lth unique cluster, = , l =
- –
- Cluster label indicator, , l = and set =
- (ii)
- Transitioning between time steps.From time step to time step k, objects may leave the scene or remain (survive) in the scene. We model this transition using an object survival indicator that is drawn from a Bernoulli process whose parameter is the probability of object survival . If = 1, the ℓth object with state remains in the scene with probability ; if = 0, the object leaves the scene with probability . The total number of objects that transitioned is given by = .
| Algorithm 1 Construction of the prior distribution of DDP-STP |
| (i) Available parameters at time step |
| – Object state parameter , ℓ = , set |
| – Cluster parameter , ℓ = , for ℓth object, set |
| – Parameter of unique cluster , l = , set |
| – Cluster label indicator , l = and set |
| – Cardinality of lth unique cluster , l = |
| (ii) Transitioning from time step − to k |
| – Draw object survival indicator ∼, ℓ = |
| – If = 1, the ℓth object survives; if = 0, it leaves the scene |
| – Compute number of transitioned objects = |
| – Denote cardinality of lth cluster, l = , after transitioning by |
| – If ≥ 1, cluster survival indicator = 1; if = 0, = 0 |
| – Compute number of unique clusters to = |
| – Denote cardinality of lth transitioned cluster by , l = |
| – Denote parameter of transitioned cluster by , l = |
| (iii) Current time step k |
| for ℓ = 1 to do |
| if Case 1 (on page 6) then |
| Draw from the prior PDF in (6) with probability in (5) |
| else if Case 2 (on page 6) then |
| Draw from |
| Draw from the prior PDF in (8) with probability in (7) |
| else if Case 3 (on page 7) then |
| Draw following |
| Draw from the PDF in (10) with probability in (9) |
| end if |
| end for |
| Update number of objects using and number of new objects under Case 3 |
| Update lth unique cluster cardinality and parameter |
| return , |
- (iii)
- State prediction at current time step.We identify the cluster parameter for the ℓth object present at time step k following three case scenarios. In Case 1, the ℓth object survived, ℓ = , from a transitioned cluster that is already occupied by at least one of the first transitioned objects. In Case 2, the ℓth object survived, ℓ = , from a cluster not yet transitioned. In Case 3, a new object enters the scene and a new cluster is generated. The prior state PDF obtained in each case is discussed next.
3.3. Learning Measurement Model for State Update
| Algorithm 2 Infinite mixture model for measurement-to-object association |
| Input: , measurements |
| From construction of prior distribution from Algorithm 1 |
| Input: Object state vectors |
| Input: Cluster parameter vectors |
| Input: Cluster label indicators |
| At time k: |
| for m = 1 do |
| Draw from Equation (13) |
| return , induced cluster assignment indicators |
| end for |
| return (number of clusters) and |
| return posterior of , m = |
3.4. DDP-STP Approach Properties
4. Tracking with Dependent Pitman–Yor Process
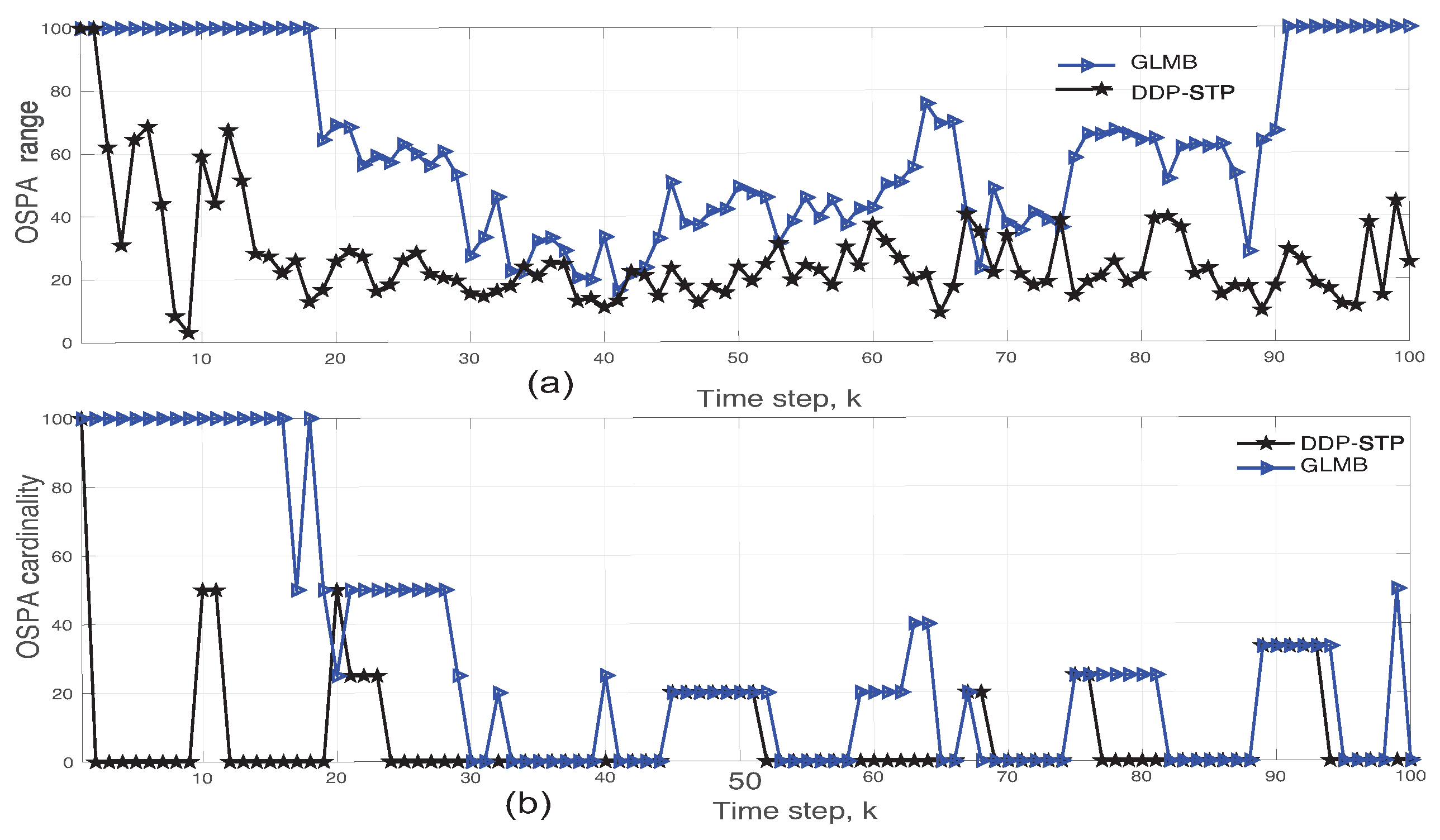
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bar-Shalom, Y.; Li, X.R. Multitarget-Multisensor Tracking: Principles and Techniques; YBs: Storrs, CT, USA, 1995; Volume 19. [Google Scholar]
- Mahler, R.P.S. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Mahler, R. Random Set Theory for Target Tracking and Identification; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef] [Green Version]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Hoang, H.G. An efficient implementation of the generalized labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef] [Green Version]
- Punchihewa, Y.G.; Vo, B.T.; Vo, B.N.; Kim, D.Y. Multiple object tracking in unknown backgrounds with labeled random finite sets. IEEE Trans. Signal Process. 2018, 66, 3040–3055. [Google Scholar] [CrossRef] [Green Version]
- Buonviri, A.; York, M.; LeGrand, K.; Meub, J. Survey of challenges in labeled random finite set distributed multi-sensor multi-object tracking. In Proceedings of the IEEE Aerospace Conference, Sky, MT, USA, 2–9 March 2019; pp. 1–12. [Google Scholar]
- Ferguson, T.S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1973, 1, 209–230. [Google Scholar] [CrossRef]
- Gershman, S.J.; Blei, M. A tutorial on Bayesian nonparametric models. J. Math. Psychol. 2012, 56, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Antoniak, C.E. Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Stat. 1974, 2, 1152–1174. [Google Scholar] [CrossRef]
- Pitman, J.; Yor, M. The two-parameter Poisson-Dirichlet distribution derived from a stable subordinator. Ann. Probab. 1997, 25, 855–900. [Google Scholar] [CrossRef]
- Teh, Y.W. Dirichlet Process. Encyclopedia of Machine Learning. 2010, pp. 280–287. Available online: https://www.stats.ox.ac.uk/teh/research/npbayes/Teh2010a.pdf (accessed on 1 December 2021).
- Topkaya, I.S.; Erdogan, H.; Porikli, F. Detecting and tracking unknown number of objects with Dirichlet process mixture models and Markov random fields. In Proceedings of the International Symposium on Visual Computing, Rethymnon, Greece, 29–31 July 2013; pp. 178–188. [Google Scholar]
- Fox, E.; Sudderth, E.B.; Jordan, M.I.; Willsky, A.S. Bayesian nonparametric inference of switching dynamic linear models. IEEE Trans. Signal Process. 2011, 59, 1569–1585. [Google Scholar] [CrossRef] [Green Version]
- Caron, F.; Davy, M.; Doucet, A. Generalized Pólya urn for time-varying Dirichlet process mixtures. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, Vancouver, BC, Canada, 19–22 July 2007; pp. 33–40. [Google Scholar]
- Caron, F.; Neiswanger, W.; Wood, F.; Doucet, A.; Davy, M. Generalized Pólya urn for time-varying Pitman-Yor processes. J. Mach. Learn. Res. 2017, 18, 1–32. [Google Scholar]
- MacEachern, S.N. Dependent nonparametric processes. In Proceedings of the Bayesian Statistical Science Section; American Statistical Association: Boston, MA, USA, 1999. [Google Scholar]
- MacEachern, S.N. Dependent Dirichlet Processes; Technical Report; Department of Statistics, Ohio State University: Columbus, OH, USA, 2000. [Google Scholar]
- Campbell, T.; Liu, M.; Kulis, B.; How, J.P.; Carin, L. Dynamic clustering via asymptotics of the dependent Dirichlet process mixture. arXiv 2013, arXiv:1305.6659. [Google Scholar]
- Blei, D.M.; Frazier, P.I. Distance dependent Chinese restaurant processes. J. Mach. Learn. Res. 2011, 12, 2461–2488. [Google Scholar]
- Neiswanger, W.; Wood, F.; Xing, E. The dependent Dirichlet process mixture of objects for detection-free tracking and object modeling. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 660–668. [Google Scholar]
- Sethuraman, J. A constructive definition of Dirichlet priors. Stat. Sin. 1994, 4, 639–650. [Google Scholar]
- Aldous, D.J. Exchangeability and related topics. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1985; pp. 1–198. [Google Scholar]
- Moraffah, B.; Papandreou-Suppappola, A. Dependent Dirichlet process modeling and identity learning for multiple object tracking. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 1762–1766. [Google Scholar]
- MacEarchern, S.N. Computational methods for mixture of Dirichlet process models. In Practical Nonparametric and Semiparametric Bayesian Statistics; Springer: New York, NY, USA, 1998; Volume 133. [Google Scholar]
- Moraffah, B. Bayesian Nonparametric Modeling and Inference for Multiple Object Tracking. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2019. [Google Scholar]
- Escobar, M.D.; West, M. Bayesian density estimation and inference using mixtures. J. Am. Stat. Assoc. 1995, 90, 577–588. [Google Scholar] [CrossRef]
- Escobar, M.D. Estimating normal means with a Dirichlet process prior. J. Am. Stat. Assoc. 1994, 89, 268–277. [Google Scholar] [CrossRef]
- Choi, T.; Ramamoorthi, R.V. Remarks on consistency of posterior distributions. IMS Collect. 2008, 3, 170–186. [Google Scholar]
- Teh, Y.W. A hierarchical Bayesian language model based on Pitman-Yor processes. In Proceedings of the 21st International Conference on Computational Linguistics and 44th Annual Meeting of the Association for Computational Linguistics, Sydney, Australia, 17–21 July 2006; pp. 985–992. [Google Scholar]
- Moraffah, B.; Papandreou-Suppappola, A.; Rangaswamy, M. Nonparametric Bayesian methods and the dependent Pitman-Yor process for modeling evolution in multiple object tracking. In Proceedings of the International Conference on Information Fusion, Ottawa, ON, Canada, 2–5 July 2019. [Google Scholar]
- Ristic, B.; Vo, B.N.; Clark, D.; Vo, B.T. A metric for performance evaluation of multi-target tracking algorithms. IEEE Trans. Signal Process. 2011, 59, 3452–3457. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Fortmann, T.E. Tracking and Data Association; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Mahler, R. A clutter-agnostic generalized labeled multi-Bernoulli filter. In Proceedings of the SPIE Signal Processing, Sensor/Information Fusion, and Target Recognition XXVII, Orlando, FL, USA, 16–19 April 2018; Volume 10646. [Google Scholar]
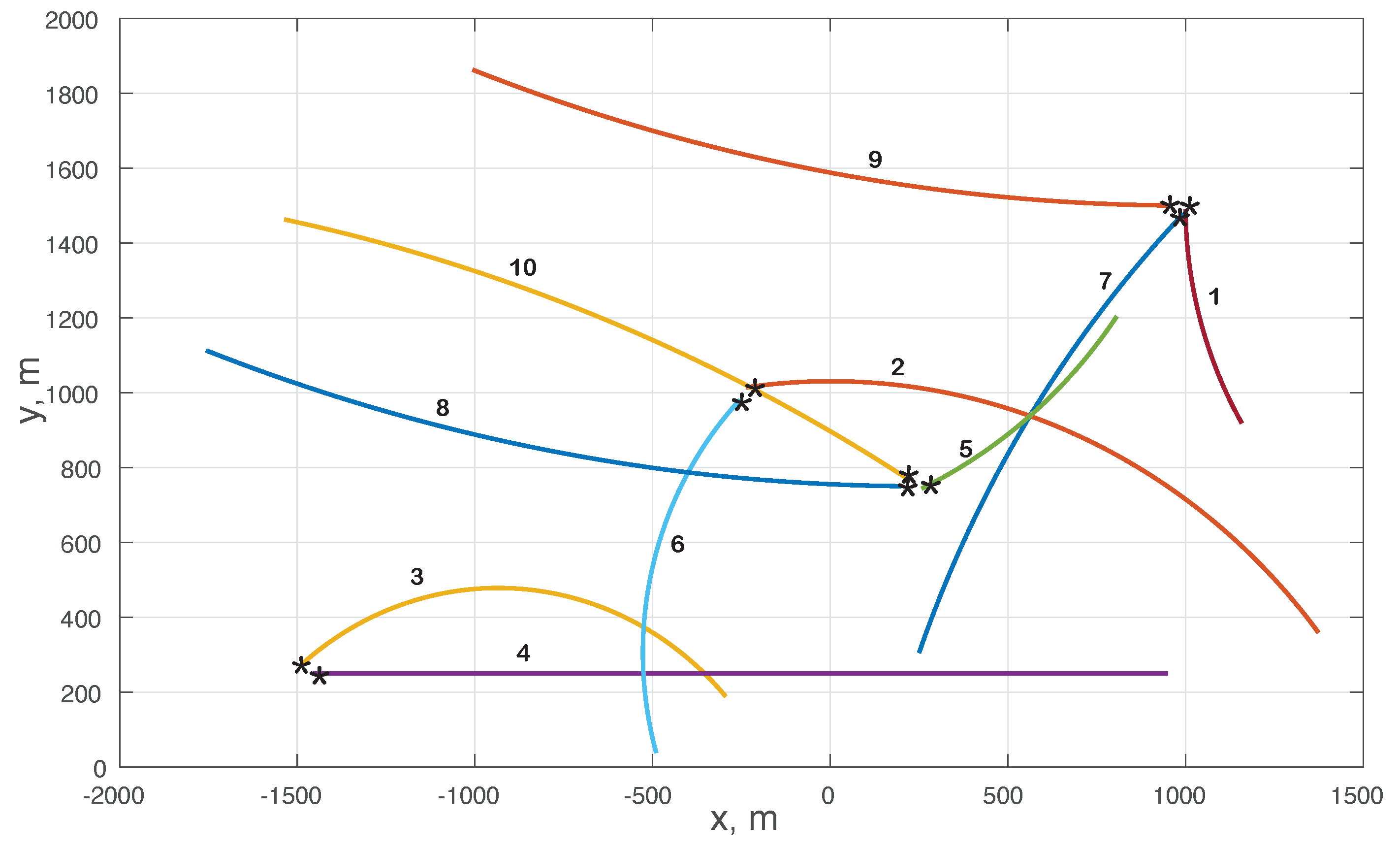

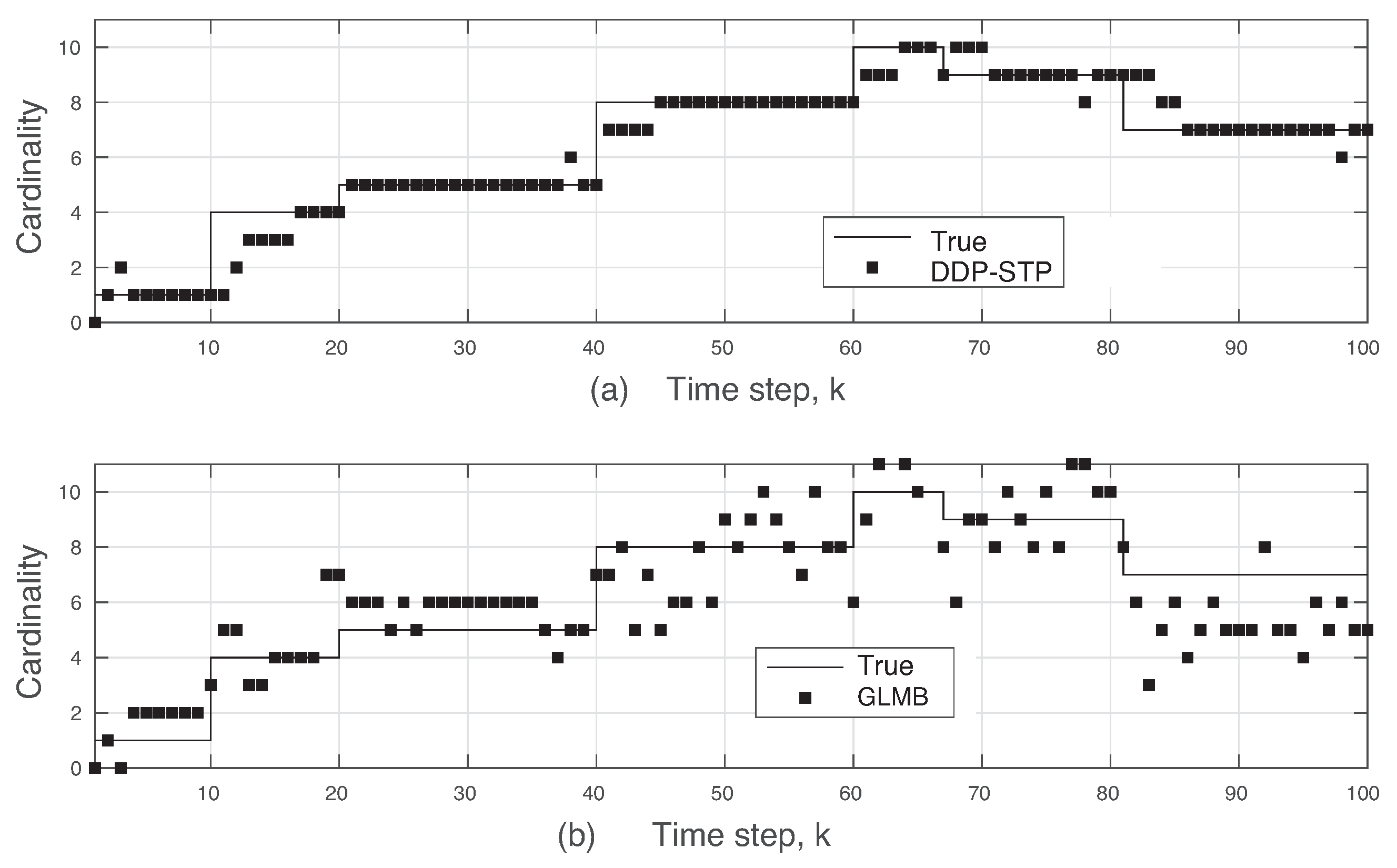

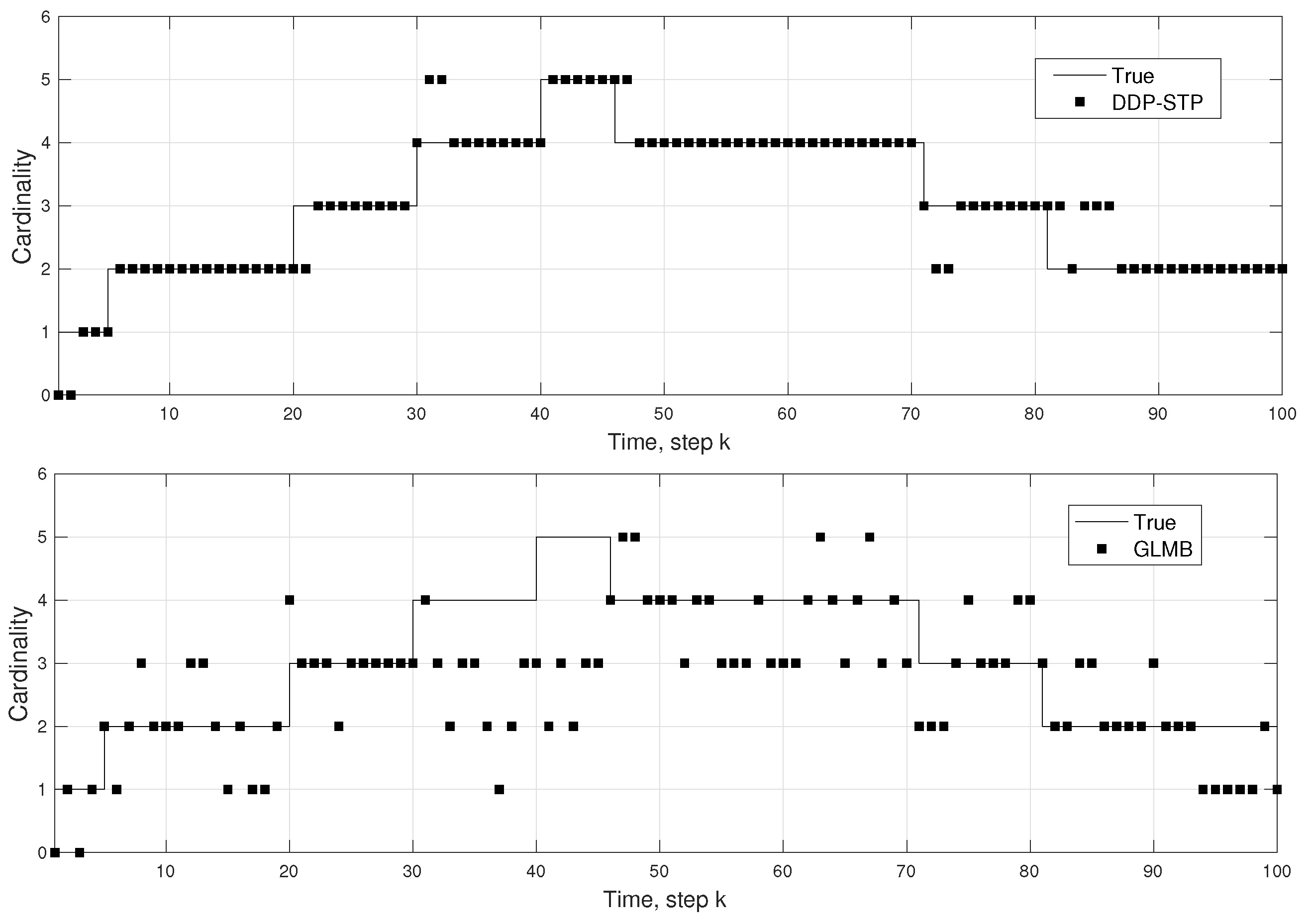




| Object Number ℓ | Time Step k Object Enters | Time Step k Object Leaves | (x,y) m That Object Enters |
|---|---|---|---|
| 1 | 0 | 100 | (1000, 1488) |
| 2 | 10 | 100 | (−245, 1011) |
| 3 | 10 | 100 | (−1500, 260) |
| 4 | 10 | 66 | (−1450, 250) |
| 5 | 20 | 80 | (245, 740) |
| 6 | 40 | 100 | (−256, 980) |
| 7 | 40 | 100 | (950, 1470) |
| 8 | 40 | 80 | (230, 740) |
| 9 | 60 | 100 | (930, 1500) |
| 10 | 60 | 100 | (220, 750) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moraffah, B.; Papandreou-Suppappola, A. Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking. Sensors 2022, 22, 388. https://doi.org/10.3390/s22010388
Moraffah B, Papandreou-Suppappola A. Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking. Sensors. 2022; 22(1):388. https://doi.org/10.3390/s22010388
Chicago/Turabian StyleMoraffah, Bahman, and Antonia Papandreou-Suppappola. 2022. "Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking" Sensors 22, no. 1: 388. https://doi.org/10.3390/s22010388
APA StyleMoraffah, B., & Papandreou-Suppappola, A. (2022). Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking. Sensors, 22(1), 388. https://doi.org/10.3390/s22010388





