Figure 1.
Genetic operators: (a) crossover (b) mutation.
Figure 1.
Genetic operators: (a) crossover (b) mutation.
Figure 2.
High-level crossover operation.
Figure 2.
High-level crossover operation.
Figure 3.
Model structure: (a) equation error model; (b) output error model.
Figure 3.
Model structure: (a) equation error model; (b) output error model.
Figure 4.
Planar model of an overhead crane.
Figure 4.
Planar model of an overhead crane.
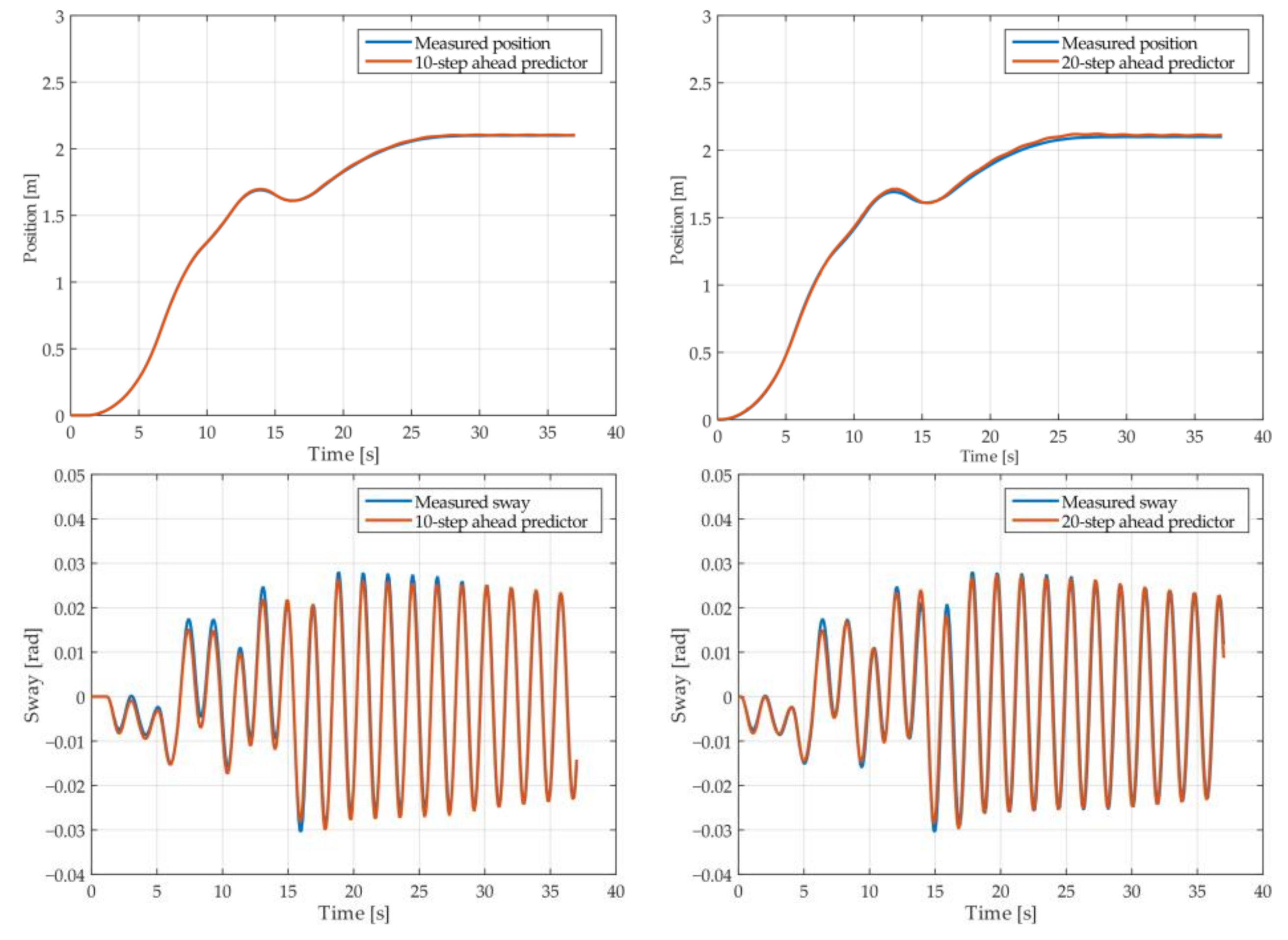
Figure 5.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 0.9 m rope length and 10 kg payload mass.
Figure 5.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 0.9 m rope length and 10 kg payload mass.
Figure 6.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 0.9 m rope length and 40 kg payload mass.
Figure 6.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 0.9 m rope length and 40 kg payload mass.
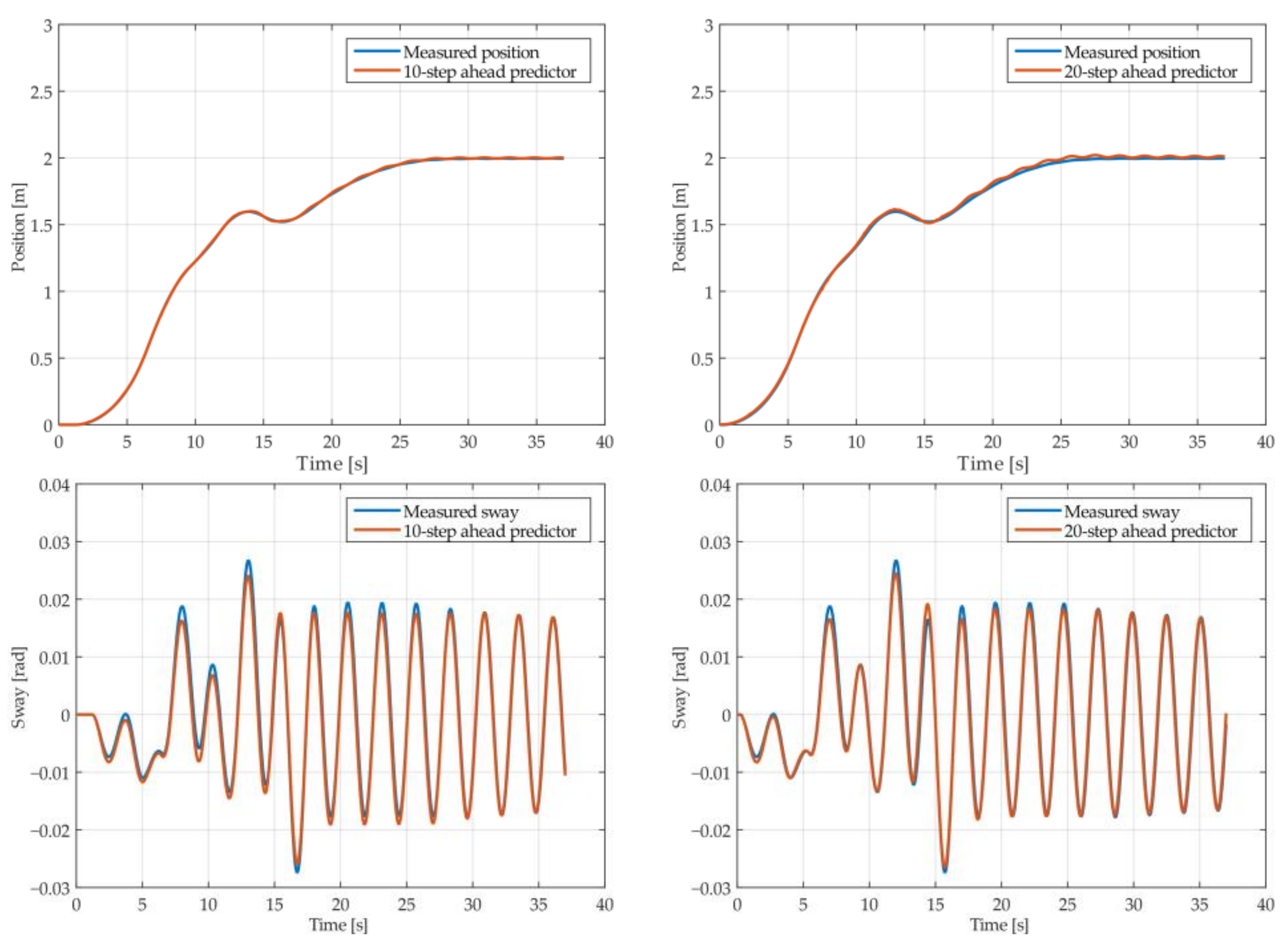
Figure 7.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 1.3 m rope length and 40 kg payload mass.
Figure 7.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 1.3 m rope length and 40 kg payload mass.
Figure 8.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 1.7 m rope length and 10 kg payload mass.
Figure 8.
The 10- and 20-step ahead prediction with the MGGP model of the simulated crane position and payload sway with 1.7 m rope length and 10 kg payload mass.
Figure 9.
The 10- and 20-step ahead prediction with the ARX model of the simulated crane position and payload sway with 0.9 m rope length and 10 kg payload mass.
Figure 9.
The 10- and 20-step ahead prediction with the ARX model of the simulated crane position and payload sway with 0.9 m rope length and 10 kg payload mass.
Figure 10.
The 10- and 20-step ahead prediction with the ARX model of the simulated crane position and payload sway with 1.3 m rope length and 40 kg payload mass.
Figure 10.
The 10- and 20-step ahead prediction with the ARX model of the simulated crane position and payload sway with 1.3 m rope length and 40 kg payload mass.
Figure 11.
The laboratory stand.
Figure 11.
The laboratory stand.
Figure 12.
Excitation input signal (control input), position response and sway response for training data set with rope length of 1.2 m and payload mass of 20 kg.
Figure 12.
Excitation input signal (control input), position response and sway response for training data set with rope length of 1.2 m and payload mass of 20 kg.
Figure 13.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 0.9-meter rope and 10 kg payload mass.
Figure 13.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 0.9-meter rope and 10 kg payload mass.
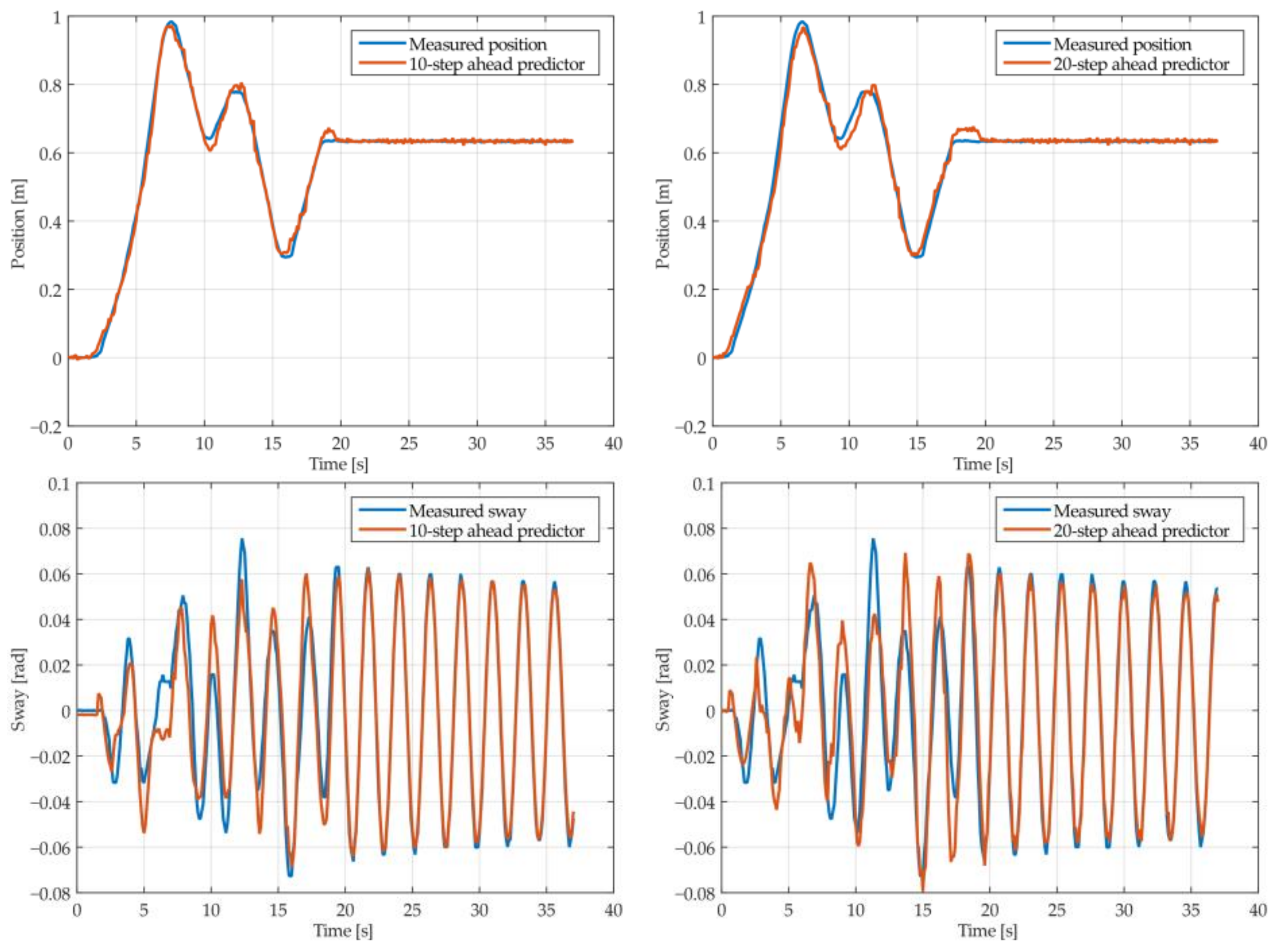
Figure 14.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 0.9-meter rope and 40 kg payload mass.
Figure 14.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 0.9-meter rope and 40 kg payload mass.
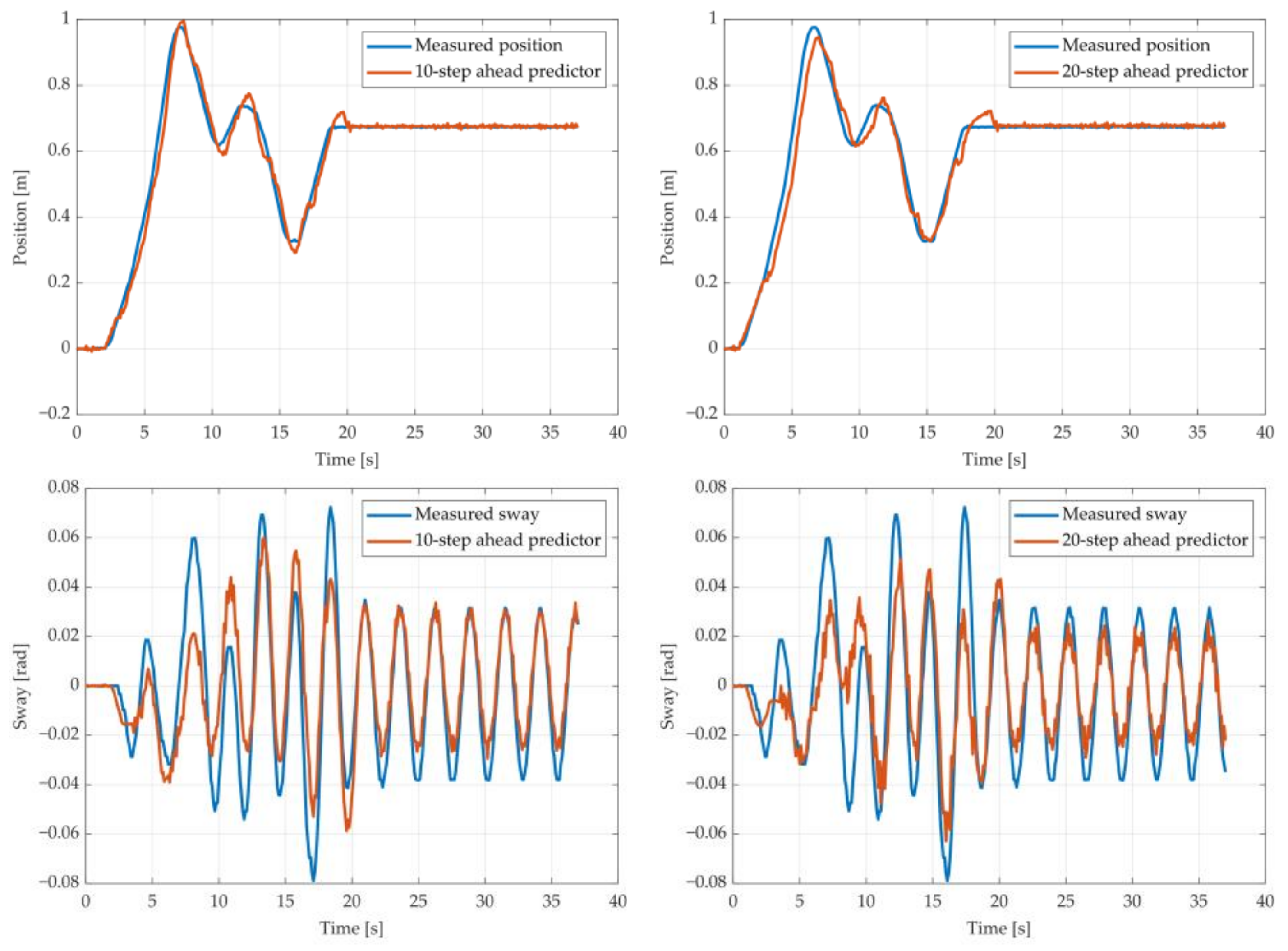
Figure 15.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 1.3-meter rope and 40 kg payload mass.
Figure 15.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 1.3-meter rope and 40 kg payload mass.
Figure 16.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 1.7-meter rope length and 10 kg payload mass.
Figure 16.
The 10- and 20-step ahead prediction with the MGGP model of the experimental crane position and payload sway with 1.7-meter rope length and 10 kg payload mass.
Figure 17.
The 10- and 20-step ahead prediction with the ARX model of the experimental crane position and payload sway with 0.9-meter rope and 10 kg payload mass.
Figure 17.
The 10- and 20-step ahead prediction with the ARX model of the experimental crane position and payload sway with 0.9-meter rope and 10 kg payload mass.
Figure 18.
The 10- and 20-step ahead prediction with the ARX model of the experimental crane position and payload sway with 1.3-meter rope and 40 kg payload mass.
Figure 18.
The 10- and 20-step ahead prediction with the ARX model of the experimental crane position and payload sway with 1.3-meter rope and 40 kg payload mass.
Table 1.
Simulation model parameters.
Table 1.
Simulation model parameters.
| Parameters | Values |
|---|
| M [kg] | 500 |
| m [kg] | 10–50 |
| l [m] | 0.5–3 |
| 4.4 |
| 0.01 |
| 0.05 |
| 0.45 |
Table 2.
Multi-gene genetic programming parameters for simulated data.
Table 2.
Multi-gene genetic programming parameters for simulated data.
| Parameters | Simulation |
|---|
| Population size | 200 |
| Number of generations | 100 |
| Initialization method | PTC2 [31] |
| Max tree depth during initialization | 5 |
| Max number of genes | 8 |
| Terminal set | u(k−1), …, u(k−5), y(k−1), …, y(k−3), m, g, 1/l, ts |
| Non-terminal set | +, −, ×, analytic quotient |
| High level crossover | 0.2 |
| Mutation | 0.14 |
| Tournament size | 8 |
| Prediction horizon | 20 |
Table 3.
Gene weights for the position and sway predictor.
Table 3.
Gene weights for the position and sway predictor.
| Weights | x(k)
| α(k)
|
|---|
| θ1 | −0.9947 | −0.9987 |
| θ2 | 1.9947 | −0.1042 |
| θ3 | −8.1689 × 10−6 | −1.0723 × 10−5 |
| θ4 | 1.3829 × 10−4 | 1.9993 |
| θ5 | 2.6866 × 10−5 | −8.4135 × 10−6 |
| θ6 | −2.9573 × 10−8 | −1.5966 × 10−4 |
Table 4.
Coefficients of the simulation position and sway ARX models.
Table 4.
Coefficients of the simulation position and sway ARX models.
| Coefficients | x(k)
| α(k)
|
|---|
| b1 | 1.0229 × 10−5 | −5.9573 × 10−6 |
| b2 | 9.4147 × 10−6 | −6.1440 × 10−6 |
| a1 | 1.9944 | 1.8967 |
| a2 | −0.9944 | −0.9914 |
Table 5.
Statistics of the identified prediction model of the simulated system.
Table 5.
Statistics of the identified prediction model of the simulated system.
| Output | Parameters | NMSE | R2 |
|---|
| 10-Step Ahead | 20-Step Ahead | 10-Step Ahead | 20-Step Ahead |
|---|
| MGGP | ARX | MGGP | ARX | MGGP | ARX | MGGP | ARX |
|---|
| Position | l = 0.9 m; m = 10 kg | 0.0013 | 0.0028 | 0.0046 | 0.0043 | 0.9999 | 0.9998 | 0.9995 | 0.9996 |
| l = 0.9 m; m = 40 kg | 0.0016 | 0.0028 | 0.0047 | 0.0043 | 0.9999 | 0.9998 | 0.9994 | 0.9996 |
| l = 1.3 m; m = 40 kg | 0.0017 | 0.0029 | 0.0050 | 0.0046 | 0.9999 | 0.9998 | 0.9994 | 0.9995 |
| l = 1.7 m; m = 10 kg | 0.0013 | 0.0028 | 0.0047 | 0.0044 | 0.9999 | 0.9998 | 0.9995 | 0.9996 |
| Sway | l = 0.9 m; m = 10 kg | 0.0578 | 0.2840 | 0.0776 | 0.3823 | 0.9868 | 0.6988 | 0.9762 | 0.4702 |
| l = 0.9 m; m = 40 kg | 0.0577 | 0.3226 | 0.0320 | 0.4466 | 0.9866 | 0.6136 | 0.9958 | 0.2662 |
| l = 1.3 m; m = 40 kg | 0.0572 | 0.1082 | 0.0380 | 0.1562 | 0.9868 | 0.9568 | 0.9941 | 0.9126 |
| l = 1.7 m; m = 10 kg | 0.0618 | 0.2402 | 0.0595 | 0.5006 | 0.9850 | 0.7876 | 0.9862 | 0.0787 |
Table 6.
Multi-gene genetic programming parameters for experimental data.
Table 6.
Multi-gene genetic programming parameters for experimental data.
| Parameters | Simulation |
|---|
| Population size | 200 |
| Number of generations | 100 |
| Initialization method | PTC2 [31] |
| Max tree depth during initialization | 5 |
| Max number of genes | 8 |
| Terminal set | u(k−5), …, u(k−9), y(k−1), …, y(k−3), m, g, 1/l, ts |
| Non-terminal set | +, −, ×, analytic quotient |
| High level crossover | 0.2 |
| Mutation | 0.14 |
| Tournament size | 8 |
| Prediction horizon | 20 |
Table 7.
Gene weights for the position and sway predictor.
Table 7.
Gene weights for the position and sway predictor.
| Weights | x(k)
| α(k)
|
|---|
| θ1 | 0.1025 | −0.0753 |
| θ2 | −0.1025 | 1.4887 |
| θ3 | −1.2238 × 10−4 | −0.5138 |
| θ4 | −0.0062 | 9.0125 × 10−4 |
| θ5 | 1.6469 | 1.0233 × 10−5 |
| θ6 | - | −0.0010 |
Table 8.
Coefficients of the experimental position and sway ARX models.
Table 8.
Coefficients of the experimental position and sway ARX models.
| Coefficients | x(k)
| α(k)
|
|---|
| b1 | 0.0031 | −2.1083 × 10−4 |
| b2 | 0.0423 | 8.2345 × 10−5 |
| a1 | 1.8249 | 1.8980 |
| a2 | −0.8249 | −0.9626 |
Table 9.
Statistics of the identified prediction model of experimental stand.
Table 9.
Statistics of the identified prediction model of experimental stand.
| Output | Parameters | NMSE | R2 |
|---|
| 10-Step Ahead | 20-Step Ahead | 10-Step Ahead | 20-Step Ahead |
|---|
| MGGP | ARX | MGGP | ARX | MGGP | ARX | MGGP | ARX |
|---|
| Position | l = 0.9 m; m = 10 kg | 0.0109 | 0.0214 | 0.0169 | 0.0320 | 0.9964 | 0.9876 | 0.9891 | 0.9662 |
| l = 0.9 m; m = 40 kg | 0.0113 | 0.0229 | 0.0169 | 0.0353 | 0.9962 | 0.9861 | 0.9895 | 0.9600 |
| l = 1.3 m; m = 40 kg | 0.0115 | 0.0218 | 0.0154 | 0.0330 | 0.9959 | 0.9869 | 0.9907 | 0.9634 |
| l = 1.7 m; m = 10 kg | 0.0119 | 0.0235 | 0.0177 | 0.0353 | 0.9959 | 0.9857 | 0.9888 | 0.9615 |
| Sway | l = 0.9 m; m = 10 kg | 0.0799 | 0.2851 | 0.0893 | 0.3898 | 0.9753 | 0.7384 | 0.9640 | 0.5694 |
| l = 0.9 m; m = 40 kg | 0.1450 | 0.3355 | 0.1599 | 0.4245 | 0.9185 | 0.6375 | 0.8771 | 0.4721 |
| l = 1.3 m; m = 40 kg | 0.1722 | 0.3416 | 0.1770 | 0.2925 | 0.8726 | 0.7235 | 0.7911 | 0.6647 |
| l = 1.7 m; m = 10 kg | 0.1911 | 0.3487 | 0.1815 | 0.4868 | 0.8404 | 0.6222 | 0.7561 | 0.3685 |