1. Introduction
Image fusion has been a crucial low-level image processing task for various applications, such as multi-spectrum image fusion [
1,
2], multi-focus image fusion [
3], multi-modal image fusion [
4], and multi-exposure image fusion [
5]. Among these applications, thanks to smartphones’ prevalence with their built-in cameras, multi-exposure image fusion is one of the most common applications. Since most natural scenes have a larger ratio of light to dark than what a single camera shot can capture, a single-shot image usually cannot present details of high dynamic ranges, thus having under- or overexposed parts for the scene. When a camera captures an image, its sensors can only catch a limited luminance range during a specific exposure time, resulting in a so-called low-dynamic-range image. An image taken for short exposure tends to be dark, while it is bright for long exposure, as shown in
Figure 1a. Fusing differently exposed low-dynamic-range (LDR) images to obtain a high-dynamic-range (HDR) image requires extracting well-exposed (highlighted) regions from each LDR image to generate an excellent fused image, which has been very challenging.
Several research works have been performed for Multi-scale Exposure Fusion (MEF) [
6,
7,
8]. In general, it is common to fuse LDR images using a weighted sum, where the weight associated with each input LDR is determined in a pixel-wise fashion [
6,
7,
8]. Mertens et al. [
6] proposed the fusion of images in a multi-scale manner based on pixel contrast, saturation, and well-exposedness to ease content inconsistency issues in the fused results. However, this often yields halo artifacts in its fusion results. In [
7,
8], the authors addressed the artifacts by applying modified guided image filtering to weight maps to eliminate halos around edges.
The abovementioned methods produce good results using a sequence of images exposed in a small interval of different exposure values (EV). Thanks to advanced sensor technology, a camera with Binned Multiplexed Exposure High-Dynamic-Range (BME-HDR) or Spatially Multiplexed Exposure High-Dynamic-Range (SME-HDR) technology can simultaneously capture an image pair with short- and long-exposure image sensors. The captured pair has only a negligible difference, possibly caused by local motion blur between them. The existing MEF methods may not work well with two exposure images, since none of the inputs may have well-exposed contents. In addition, weighted-sum fusion based on well-exposedness may not be able to deal with highlighted regions of a short-exposure image that are darker than dark parts in a long-exposure image, resulting in the method ignoring contents in the short-exposure image. Yang et al. [
9] proposed the production of an intermediate virtual image with a medium exposure based on an image pair with two exposures to help generate better fusion results. Nevertheless, it does not work in situations where highlighted regions of both input LDR images are not well exposed.
In recent years, deep convolutional neural networks (CNNs) have gained tremendous success in low-level image processing works. In MEF, CNN-based methods [
10,
11] can better learn features from input multiple-exposure images and fuse them into a nice image. However, the fused images often lack image details [
12], since spatial information may be lost when features pass through deep layers. Xu et al. [
13] proposed a unified unsupervised image fusion network trained based on the importance and information carried by the two input images to generate fusion results. However, these learning-based methods can only produce a fused image based on the two input images’ interpolation. They cannot deal with cases where both of the input images do not have highlighted regions/contents.
This paper presents a two-exposure fusion framework that generates a more helpful intermediate virtual image for fusion using the proposed Optimized Adaptive Gamma Correction (OAGC). The virtual image has better contrast, saturation, and well-exposedness, and it is not restricted to being an interpolated version of the two input images. Fusing the input images with their virtual image processed by OAGC works well even though both inputs have no well-exposed contents or regions.
Figure 1b shows an example where the proposed framework can still generate a good fusion result for when both of the input images lack highlighted regions (
Figure 1a). Our primary contributions are three-fold:
Our image fusion framework adopting the proposed OAGC can produce better fusion results for two input images with various exposure ratios, even when both of the input images lack well-exposed regions.
The proposed framework with OAGC can also adapt to single-image enhancement.
We conduct an extensive experiment using a public multi-exposure dataset [
14] to demonstrate that the proposed fusion framework performs favorably against the state-of-the-art image fusion methods.
2. Related Work
MEF-based methods produce fusion results using a weighted combination of the input images based on each pixel’s “well-exposedness”. In [
15], fusion weight maps were calculated based on the correlation-based match and salience measures of the input images. With the weight maps, one can fuse the input images into one by using the gradient pyramid.
Mertens et al. [
6] constructed fusion weight maps based on contrast, saturation, and exposedness of the input images. Differently from [
15], the fusion was performed with the Gaussian and Laplacian pyramids. The problem was that using the smoothed weight maps in fusion often causes halo artifacts, especially around the edges. The method proposed in [
7] addressed this issue by applying an edge-preserving filter (weighted guided image filtering [
16]) to fusion weight maps. Kou et al. [
8] further proposed an edge-preserving gradient-domain guided image filter (GGIF) to avoid generating halo artifacts in the fused image. To extract image details, Li et al. [
7] proposed a weighted structure tensor to manipulate details presented in a fused image. In general, MEF-based methods can generate decent fusion results.
General MEF algorithms [
6,
8] that require a sequence of images with different exposure ratios as the inputs may not work with only two input images. Yang et al. [
9] proposed the use of the MEF algorithm for two-exposure-ratio image fusion, where an intermediate virtual image with a medium exposure is generated to help produce a better fusion result. However, the virtual image’s intensity and exposedness are bounded by the two input images, which often fails to work for cases where two images are both underexposed and overexposed. Yang’s method [
9] can only generate both the intermediate and fusion results with approximate medium exposure between its two input images. The problem is that medium exposure between the inputs may still be under- or overexposure. Image fusion will not improve visual quality. We will discuss this issue more in the next section.
In the following paragraphs, we introduce the techniques adopted in the work of Yang et al., including the generation of the virtual image and fusion weights and the multi-scale image fusion. Before continuing, we define several notations that are used here. Let be a color image. We denote as the color channel c, where stand for the red, green, and blue channels. represents the pixel located at , where and . M and N are the image width and height. Let be the luminance component or the grayscale version of . Note that the values of images in this paper are normalized to .
2.1. Quality Measures and Fusion Weight Maps
In HDR imaging, an image taken at a certain exposure may contain underexposed or overexposed regions, which are less informative and should be assigned fewer weights in multi-exposure fusion. The input’s contrast, saturation, and well-exposedness determine a pixel’s weight at
[
6]. The contrast of a pixel, denoted by
, is obtained by applying a
Laplacian filter to a grayscale version of the image:
Let
be the map of the contrast of
; therefore,
where
,
,
, and
are obtained from
,
,
, and
; i.e., shifting
one pixel left, right, up, and down, respectively. The saturation of the pixel, denoted by
, is obtained by computing the standard deviation across the red, green, and blue channels:
where
The well-exposedness of the pixel,
, is defined as:
where
and
. Essentially,
E is a normal distribution centered at
with a standard deviation of
. The maps of saturation and well-exposedness of
can, respectively, be represented as
and
. Next, the weight of the pixel for fusion is computed using:
where
,
, and
can be adjusted to emphasize or ignore one or more measures. Considering a set of
P images
for image fusion, the weight of this pixel in the
image is normalized by the sum of the weights across all the images at the same pixel:
The weight map of the image is represented as .
2.2. Multi-Scale Fusion
In the MEF algorithm [
6], a fusion image,
, is obtained through multi-scale image fusion based on the standard Gaussian and Laplacian pyramids. For each input image
in the set of
, the Laplacian pyramid,
, and the Gaussian pyramid of its weight map,
, in the
level are constructed by applying the Gaussian pyramid generation [
17]. In this level, the overall Laplacian pyramid is collapsed by performing weighted averaging on the Laplacian pyramids from all of the input images in the set:
where ⊙ denotes element-wise multiplication. Finally, the fusion image,
, is reconstructed by collapsing the Laplacian pyramids
.
Applying edge-preserving filtering to preserve edges in the weight maps before averaging the Laplacian pyramids in Equation (
6) can reduce halo artifacts in fused images. In [
9], the GGIF [
18] was adopted to smooth the weight maps
and to preserve the significant change as well. Let
be the square local patch with a radius of
centered at
, and let
be a pixel in the patch. In
, the weight map in the
level of the
image,
, is the linear transform of the luminance component,
:
where
and
are the coefficients and are assumed to be constant in
.
and
can be obtained by minimizing the objective function:
where
is a constant for regularization. The variance of the intensities within this local patch,
, is computed when solving for the coefficients in Equation (
8).
In GGIF, a
local window,
, is applied to the pixels within
for capturing the structure within
by computing the variance within
,
[
18]. This local window makes GGIF a content-adaptive filter; thus, GGIF produces fewer halos and better preserves the edge than the GIF. In GGIF, the regularization term is designed to yield:
where
and
are computed according to the product of
and
(the standard deviations of the pixels within
and
), and
is a constant for regularization. The filter coefficients
and
can solved by minimizing
in Equation (
9).
The fused image
can be obtained by fusing the Laplacian pyramids of the input images taken at different exposures using the weight maps retrieved from the Gaussian pyramids,
. Note that the weight maps are filtered using GGIF, as described in Equation (
9), to preserve edges.
2.3. Virtual Image Generation
In [
9], Yang et al. proposed the modification of two differently exposed images to have the same medium exposure using the intensity mapping function based on the cross-histogram between two images, called the comparagram (Ref. [
19]), and fused them to produce an intermediate virtual image. Let
and
be the two input images and let
and
be the intensity mapping functions (IMFs) that map
to
and
to
. Based on [
19], the IMFs that map the two images to the same exposure, denoted as
and
, are computed as
where
z is a pixel intensity. The two modified images with the same exposure are
,
. The desired virtual image
is computed by fusing
and
using the weighting functions adopted in [
9]. The two-exposure-fusion image in [
9] is obtained by fusing
,
, and
based on the MEF algorithm [
8].
As described previously, Yang’s method often fails to produce a satisfying fusion result when the medium exposure between inputs is still under- or overexposure. The proposed method addresses this issue by improving the contrast, saturation, and well-exposedness for the intermediate virtual image to generate better fusion results under different input conditions.
3. Proposed Method
The algorithm in [
9] can work for two images with a large difference between their exposure ratios. In this case, the intermediate virtual image with medium exposure helps bridge the dynamic range gap between the two inputs. Thus, it can improve the quality of the fusion result. However, if the two inputs’ exposure is under- or overexposure, the generated virtual image would not help fusion. Thus, the quality of the fused image is not improved much.
For example, to fuse
Figure 2a,b, both of which look overexposed, the virtual image
(
Figure 2c) generated by [
9] with medium exposure between the inputs is still overexposed and, thus, not helpful for the fusion result (
Figure 2e). We propose Optimized Adaptive Gamma Correction (OAGC) to enhance the intermediate virtual image to have better contrast, saturation, and well-exposedness (
Figure 2d) so that it can improve the fusion quality and produce a better result (
Figure 2f).
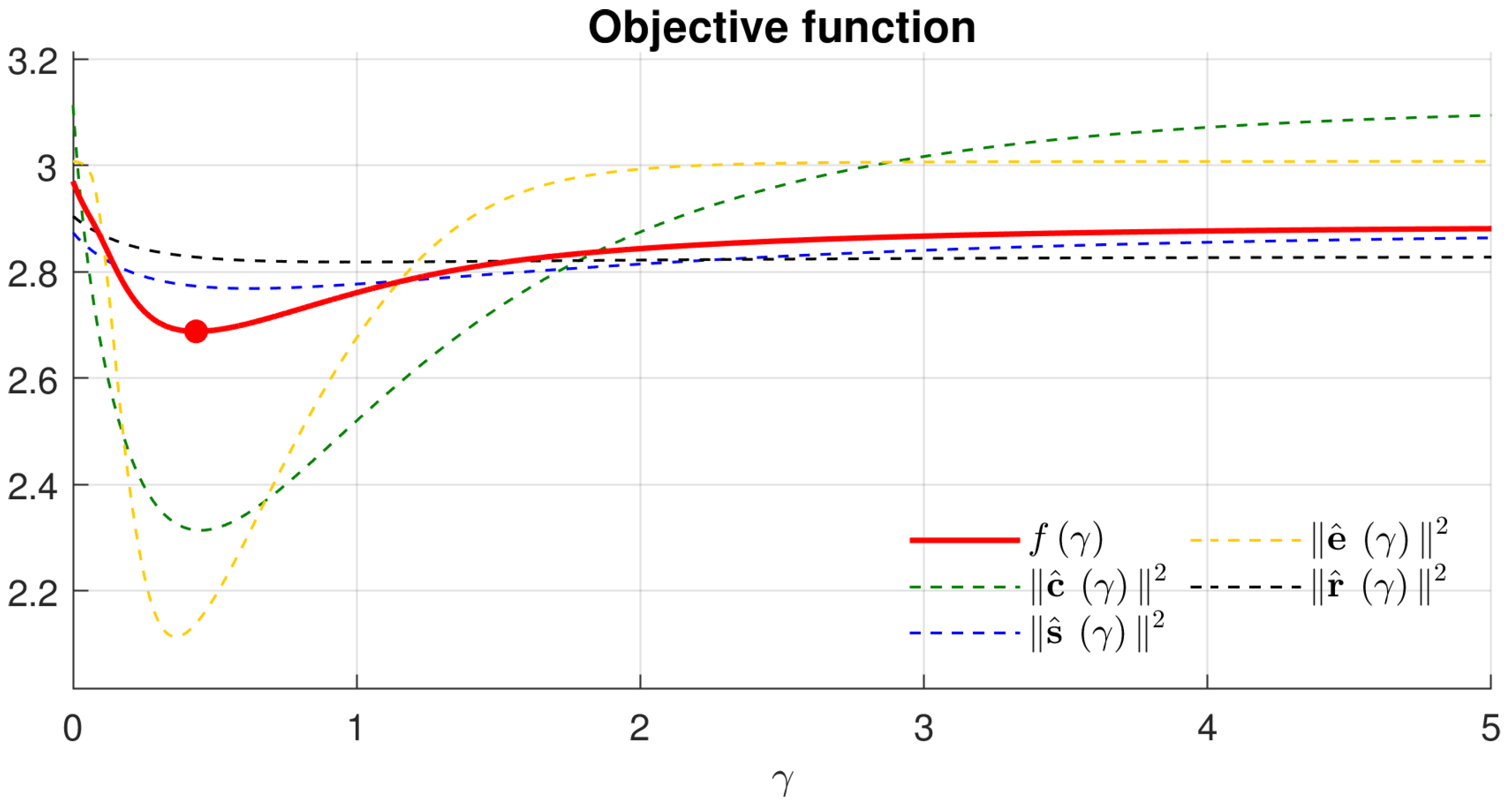
In OAGC, we derive an optimal
based on the input’s contrast, saturation, and well-exposedness by formulating an objective function based on these image quality metrics and apply it to the input image using gamma correction. Let
be the luminance of a pixel. One can gamma-correct the image
to alter its luminance through the power function as follows:
where
is the corrected image,
and
are positive scalars, and
is usually set to 1 [
20]. Here, the notation
in bold represents the entire image, while
stands for the pixel located at
. If
, it stretches the contrast of shadow regions (pixel intensities less than the mid-tone of
), and features in these regions become discernible, whereas if
, it stretches the contrast of bright regions (intensities larger than
), and features in the regions become perceptible. For
, it is linear mapping.
To derive the optimal gamma, we design an objective function as follows:
where
,
,
, and
, where
,
, and
are the maps of quality measures computed based on the gamma-corrected version of the input image, denoted as
. Here, the virtual image
is used as the input, which is
. We set
,
, and
to 4,
, and 1 according to the upper bounds of the corresponding quality measures (contrast, saturation, and well-exposednesse; refer to the
Appendix A for the derivation). The term with
in the objective function prevents the corrected image from deviating the input too much. Hence, minimizing the objective function
is to maximize all three quality measures: the contrast, saturation, and well-exposedness.
,
, and
are the weighting factors for the contributions from different quality measures (independent from
,
, and
in Equation (
4) and are all set to
.
is a small, fixed scalar and is set to
in the present study.
is the vector of 1s,
is the vectorization of a matrix, and
represents the 2-norm of a vector. The regularization term is added to avoid possible color distortion caused by gamma correction.
The optimal gamma,
, which aims to increase contrast, saturation, and well-exposedness simultaneously, can be obtained by minimizing the optimization function
:
Since there is no closed-form solution for Equation (
13), we apply the gradient descent to iteratively approximate it:
where
with
,
,
, and
being the vectorization of
,
,
, and
, as well as
,
, and
being
,
, and
respectively.
with ⊘ being the element-wise division,
and
is the adjustable learning rate.
Figure 3 shows the flowchart of the presented two-exposure image fusion framework, where the two inputs are taken in the same scene at different exposure ratios. The virtual image is first generated using the intensity mapping function [
9]. Next, we solve Equation (
12) to find the optimal gamma value
for the virtual image, which enhances the contrast, saturation, and well-exposedness of
. The final fused image,
, is obtained by applying the MEF algorithm [
8,
9] to the fusion of two input images and
.