A Novel Calibration Method for Gyro-Accelerometer Asynchronous Time in Foot-Mounted Pedestrian Navigation System
Abstract
:1. Introduction
2. The Reference Frame Definitions
3. Gyro-Accelerometer Asynchronous Time
3.1. Error Model of Gyro-Accelerometer Asynchronous Time
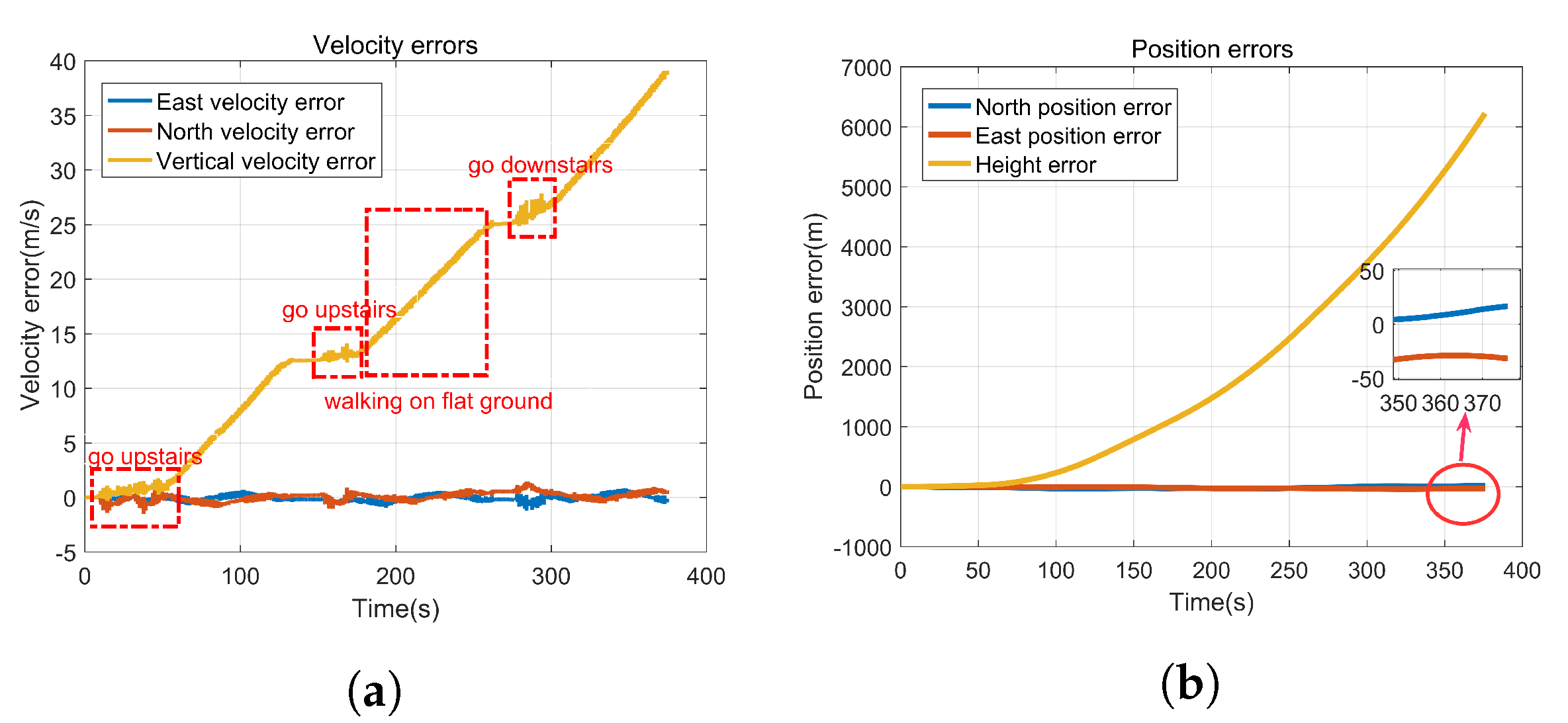
3.2. Effects of Gyro-Accelerometer Asynchronous Time on Pedestrian Navigation
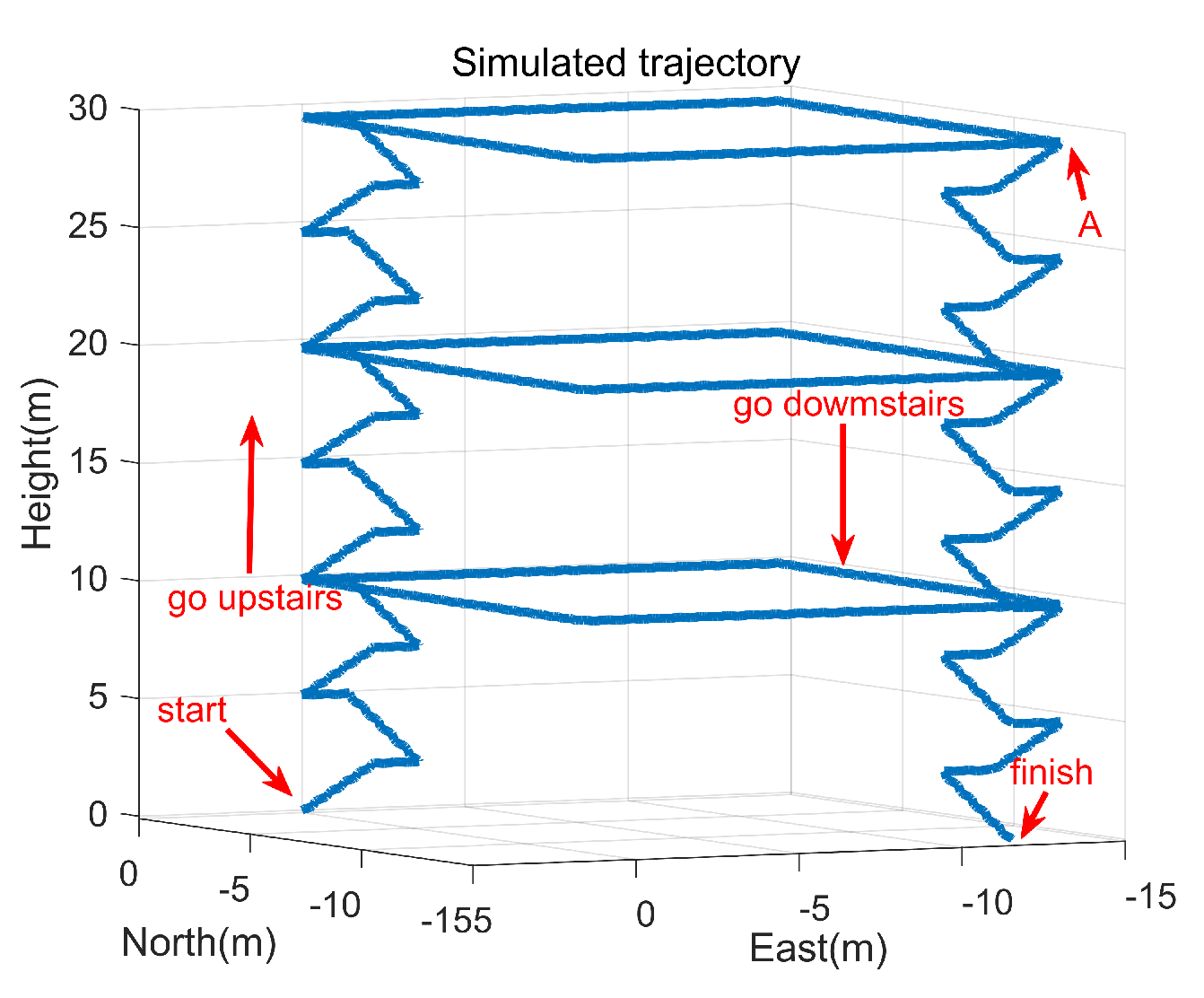
3.3. Simulation
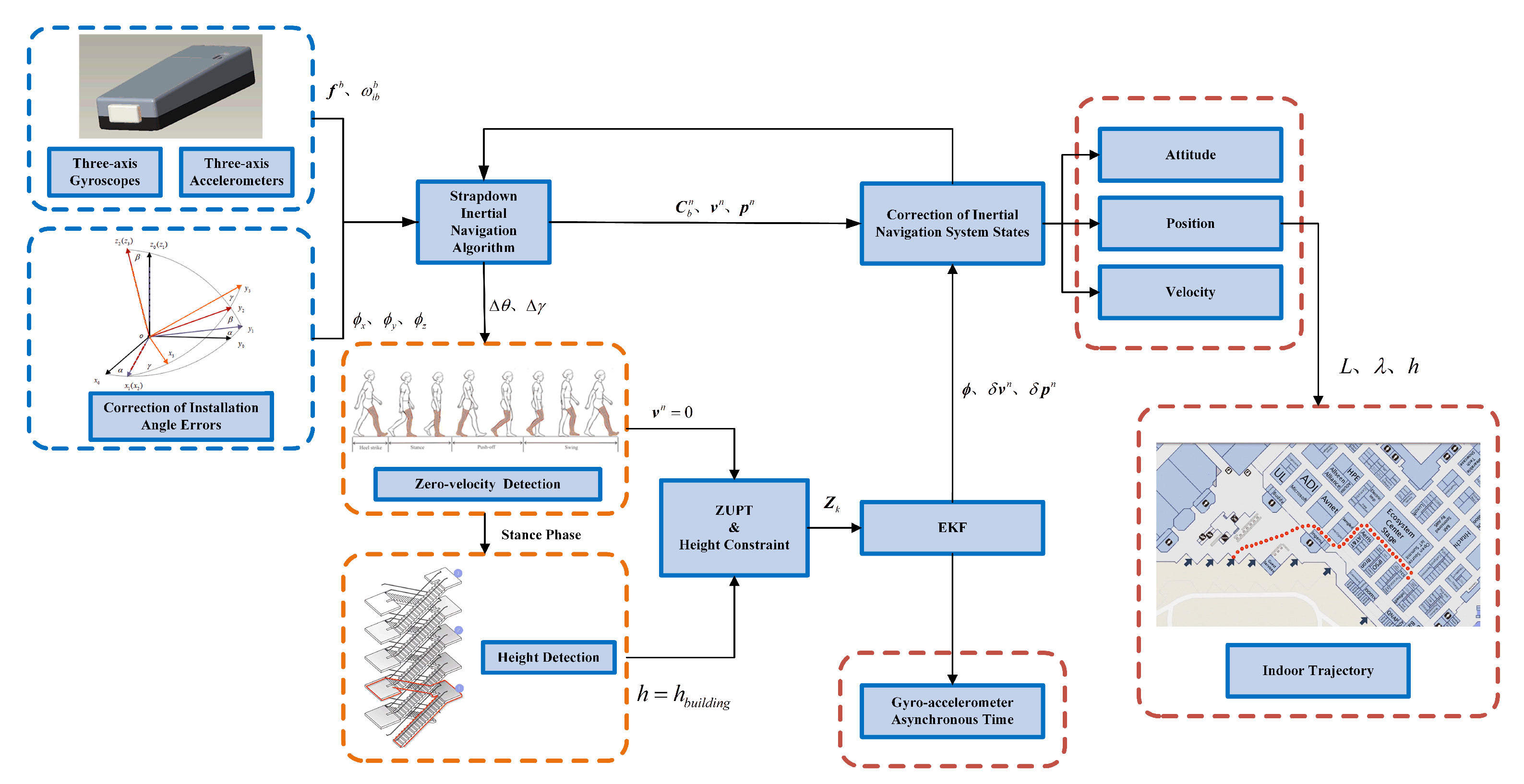
4. A Calibration Method for Gyro-Accelerometer Asynchronous Time
4.1. Error Model of Pedestrian Navigation System Based on Gyro-Accelerometer Asynchronous Time
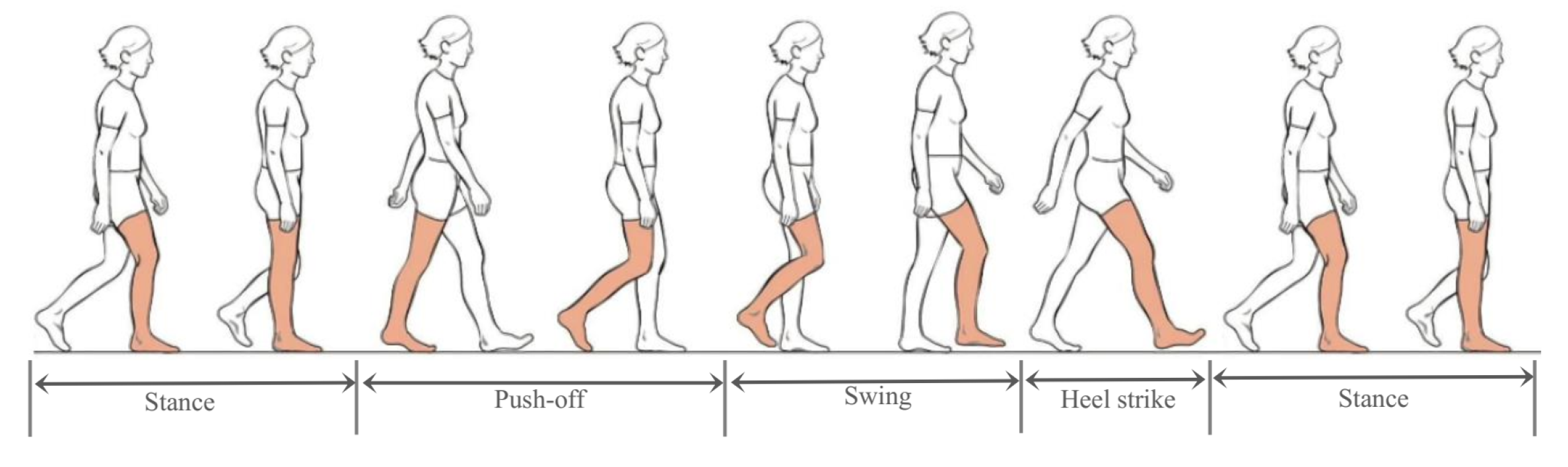
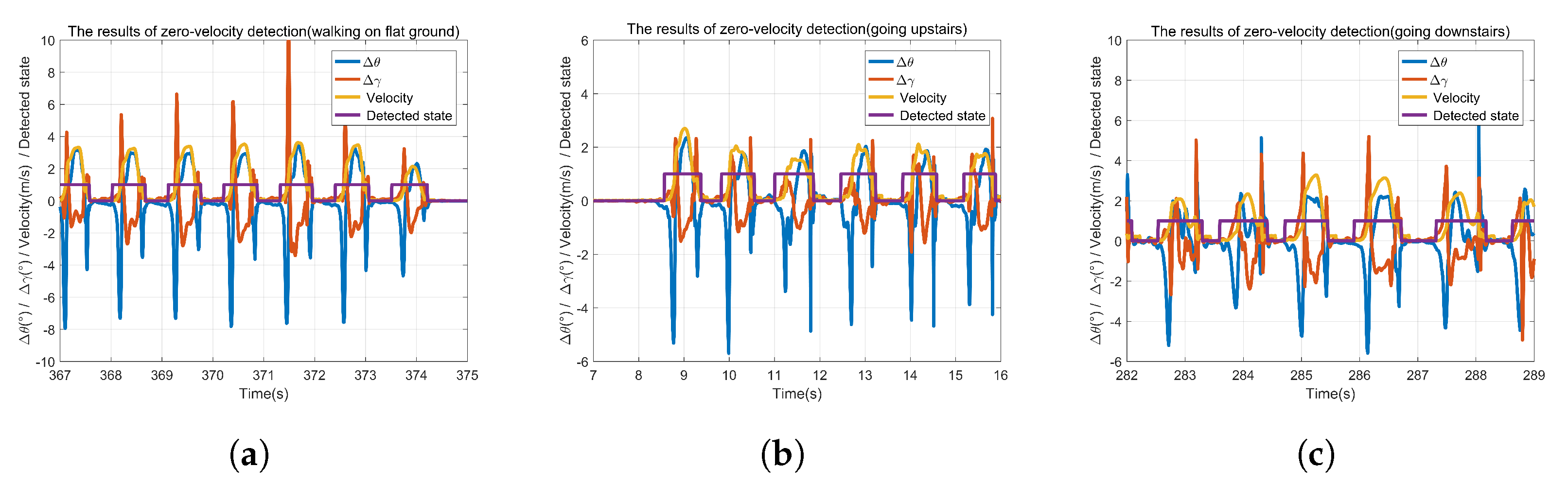
4.2. Zero-Velocity Detection
4.3. Kalman Filter Design
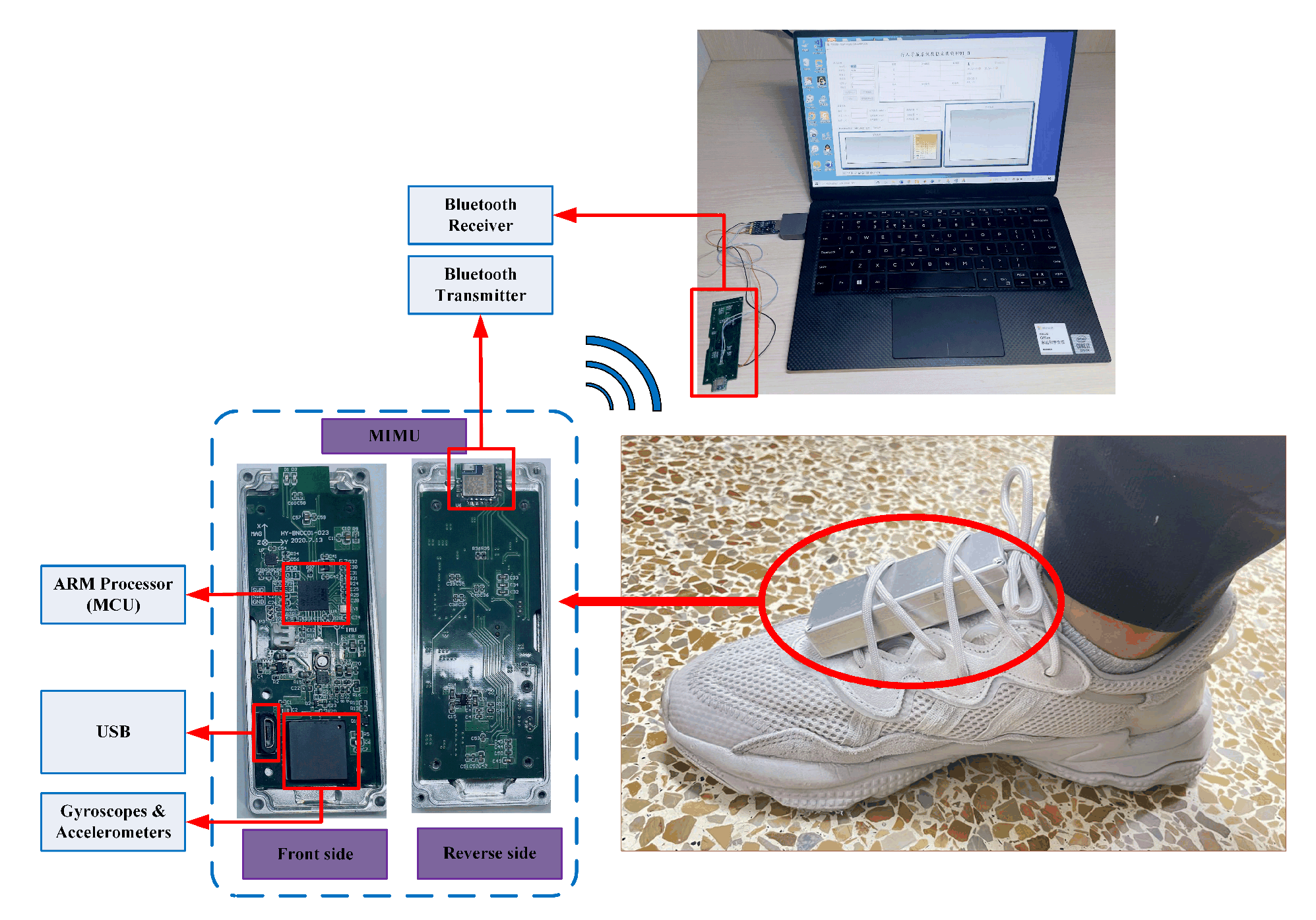
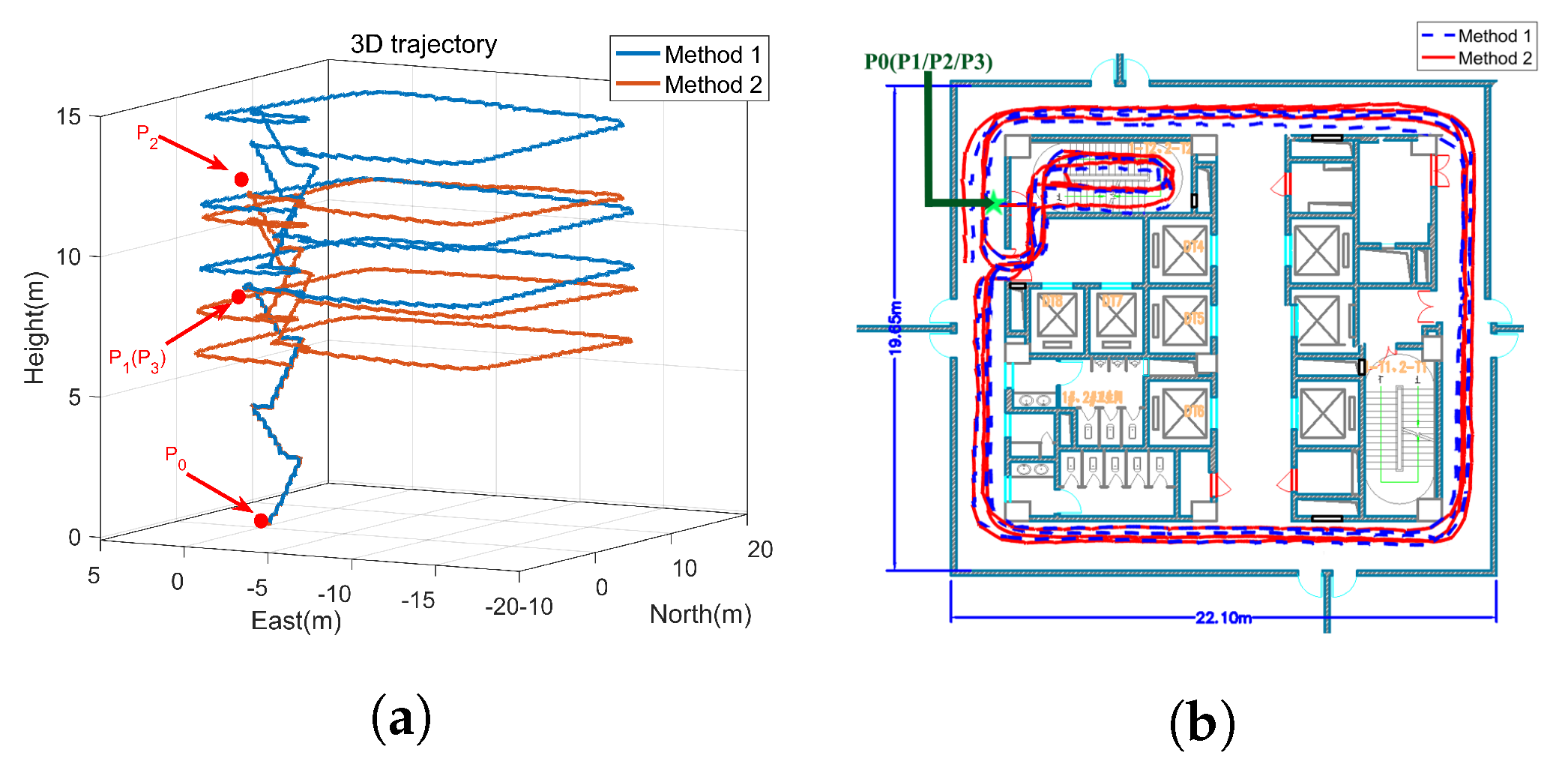
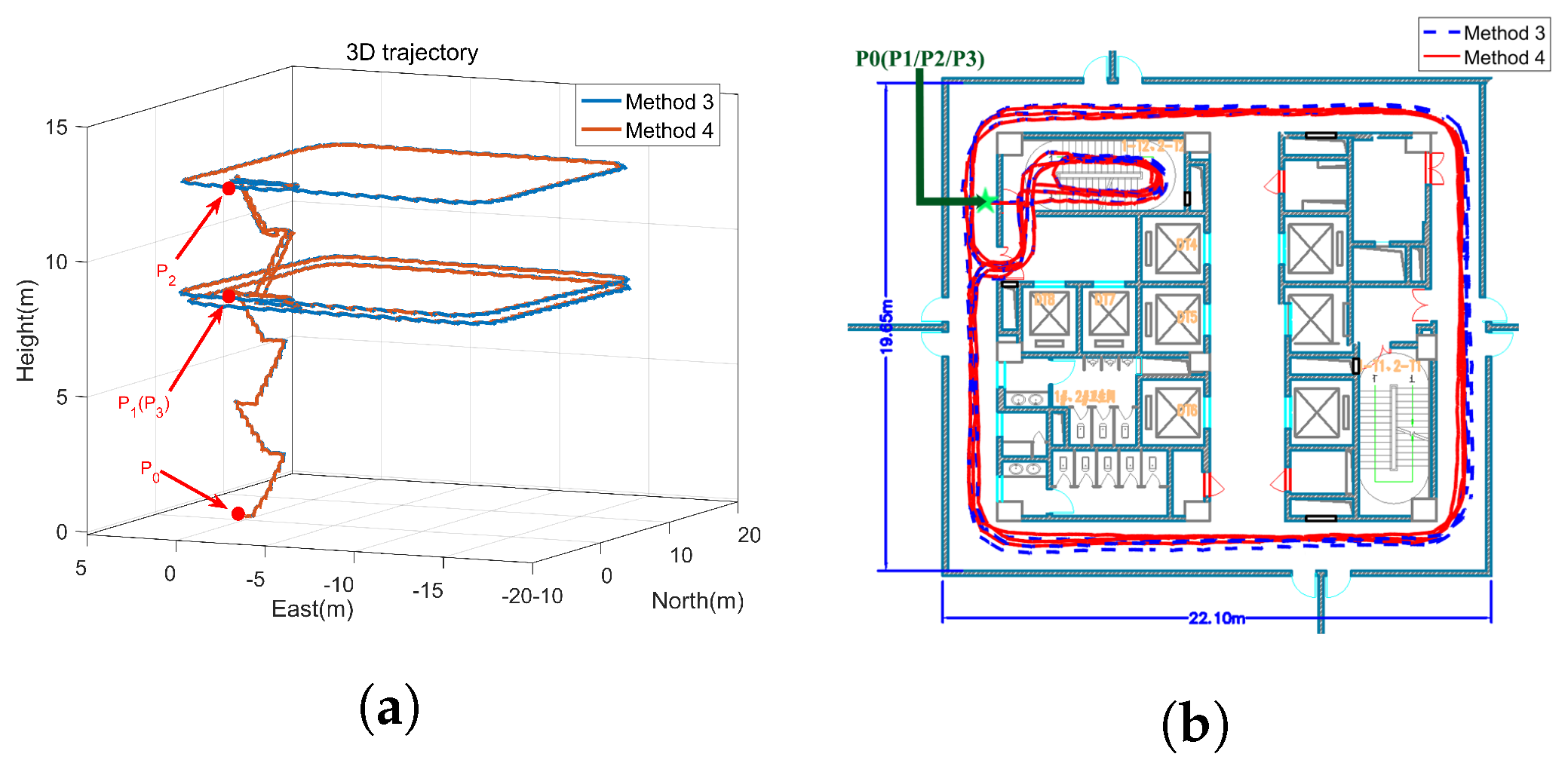
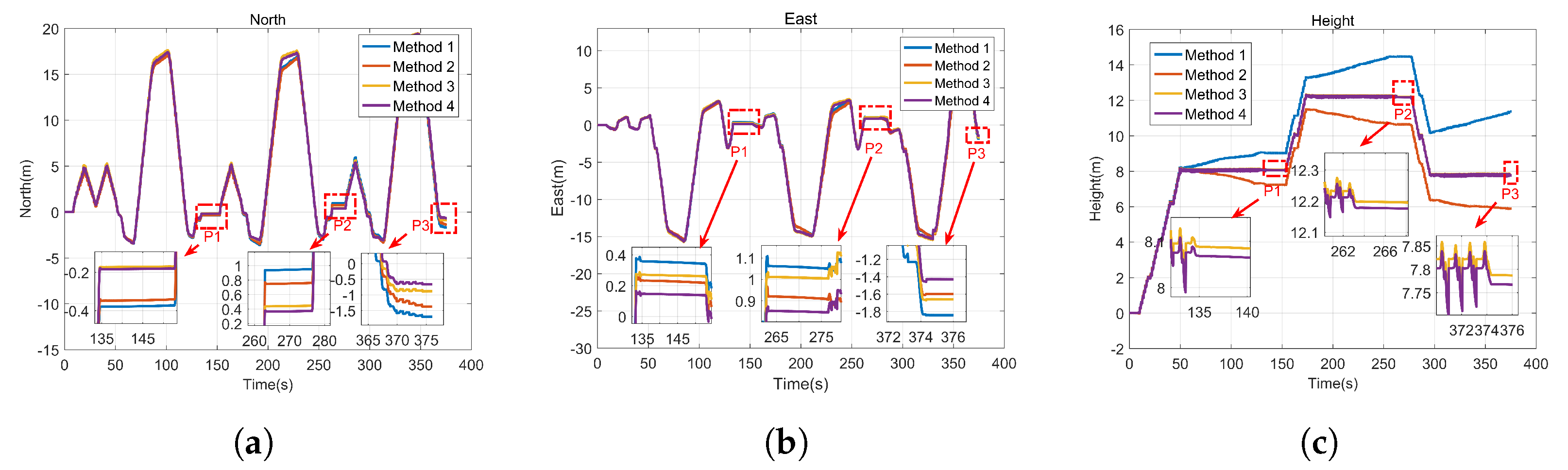
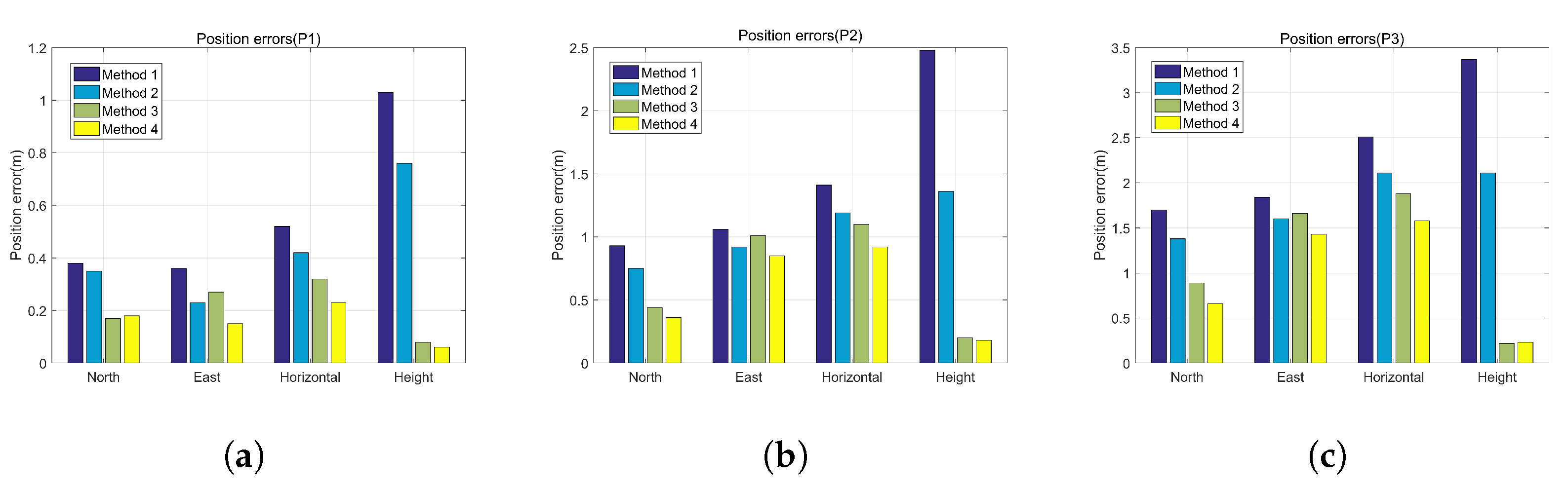
5. Experiments and Analysis
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Li, D.; Gu, Y.; Kamijo, S. Pedestrian positioning in urban environment by integration of PDR and traffic mode detection. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Gu, Y.; Zhou, C.; Wieser, A.; Zhou, Z. Pedestrian positioning using WiFi fingerprints and a foot-mounted inertial sensor. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 91–99. [Google Scholar]
- Mazhar, F.; Khan, M.G.; Sällberg, B. Precise indoor positioning using UWB: A review of methods, algorithms and implementations. Wirel. Pers. Commun. 2017, 97, 4467–4491. [Google Scholar] [CrossRef]
- Zhou, C.; Yuan, J.; Liu, H.; Qiu, J. Bluetooth indoor positioning based on RSSI and Kalman filter. Wirel. Pers. Commun. 2017, 96, 4115–4130. [Google Scholar] [CrossRef]
- Uradzinski, M.; Guo, H.; Liu, X.; Yu, M. Advanced indoor positioning using zigbee wireless technology. Wirel. Pers. Commun. 2017, 97, 6509–6518. [Google Scholar] [CrossRef]
- Yang, C.; Shao, H.R. WiFi-based indoor positioning. IEEE Commun. Mag. 2015, 53, 150–157. [Google Scholar] [CrossRef]
- Ren, M.; Pan, K.; Liu, Y.; Guo, H.; Zhang, X.; Wang, P. A novel pedestrian navigation algorithm for a foot-mounted inertial-sensor-based system. Sensors 2016, 16, 139. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Xiu, C.; Zhang, J.; Yang, D. A novel 3D pedestrian navigation method for a multiple sensors-based foot-mounted inertial system. Sensors 2017, 17, 2695. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Song, Q.; Li, Y.; Ma, M. Foot-mounted pedestrian navigation based on particle filter with an adaptive weight updating strategy. J. Navig. 2015, 68, 23–38. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, H.B.; Du, Q.X.; Tang, S.M. A survey of the research status of pedestrian dead reckoning systems based on inertial sensors. Int. J. Autom. Comput. 2019, 16, 65–83. [Google Scholar] [CrossRef]
- Wang, Y.; Shkel, A.M. Adaptive threshold for zero-velocity detector in ZUPT-aided pedestrian inertial navigation. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Barsocchi, P.; Carbonaro, N.; Cimino, M.G.; La Rosa, D.; Palumbo, F.; Tognetti, A.; Vaglini, G. Detecting User’s Behavior Shift with Sensorized Shoes and Stigmergic Perceptrons. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 265–268. [Google Scholar]
- Skog, I.; Handel, P.; Nilsson, J.O.; Rantakokko, J. Zero-Velocity Detection—An Algorithm Evaluation. IEEE. Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef]
- Skog, I.; Nilsson, J.O.; Händel, P. Evaluation of zero-velocity detectors for foot-mounted inertial navigation systems. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–6. [Google Scholar]
- Nilsson, J.O.; Skog, I.; Händel, P.; Hari, K.V.S. Foot-mounted INS for everybody-an open-source embedded implementation. In Proceedings of the IEEE/ION PLANS 2012, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 140–145. [Google Scholar]
- Ruiz, A.R.J.; Granja, F.S.; Honorato, J.C.P.; Rosas, J.I.G. Accurate Pedestrian Indoor Navigation by Tightly Coupling Foot-Mounted IMU and RFID Measurements. IEEE Trans. Instrum. Meas. 2011, 61, 178–189. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Xiong, Z.; Xu, J.; Xu, L. Research on pedestrian navigation system aided by indoor geomagnetic matching. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 946–1951. [Google Scholar]
- Ji, M.; Xu, X.; Guo, Y. An Adaptive Heading Correction Algorithm for Suppressing Magnetic Interference in Inertial Navigation System. IEEE Trans. Instrum. Meas. 2021, 70, 9513010. [Google Scholar] [CrossRef]
- Borenstein, J.; Ojeda, L.; Kwanmuang, S. Heuristic reduction of gyro drift for personnel tracking systems. J. Navig. 2009, 62, 41–58. [Google Scholar] [CrossRef] [Green Version]
- Abdulrahim, K.; Hide, C.; Moore, T.; Hill, C. Aiding low cost inertial navigation with building heading for pedestrian navigation. J. Navig. 2011, 64, 219–233. [Google Scholar] [CrossRef] [Green Version]
- Tanigawa, M.; Luinge, H.; Schipper, L.; Slycke, P. Drift-free dynamic height sensor using MEMS IMU aided by MEMS pressure sensor. In Proceedings of the 2008 5th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 27 March 2008; pp. 191–196. [Google Scholar]
- Gu, Y.; Ma, M.; Li, Y.H.; Song, Q. Accurate height estimation based on apriori knowledge of buildings. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard-Belfort, France, 28–31 October 2013; pp. 1–7. [Google Scholar]
- Jing, H.; Pinchin, J.; Hill, C.; Moore, T. An adaptive weighting based on modified DOP for collaborative indoor positioning. J. Navig. 2016, 69, 225–245. [Google Scholar] [CrossRef]
- Ding, Y.; Xiong, Z.; Li, W.; Cao, Z.; Wang, Z. Pedestrian navigation system with trinal-IMUs for drastic motions. Sensors 2020, 20, 5570. [Google Scholar] [CrossRef] [PubMed]
- Skog, I.; Nilsson, J.O.; Händel, P.; Nehorai, A. Inertial sensor arrays, maximum likelihood, and cramér–rao bound. IEEE Trans. Signal Process. 2016, 64, 4218–4227. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Zhang, Q.; Peng, H.; Qin, Y. Study on gyro-accelerometer asynchronous time Compensation for Accelerometers in SINS. J. Astronaut. 2013, 34, 1578–1583. [Google Scholar]
- Wen, Z.; Yang, G.; Cai, Q.; Sun, Y. Modeling and Calibration of the Gyro–Accelerometer Asynchronous Time in Dual-Axis RINS. IEEE Trans. Instrum. Meas. 2020, 70, 3503117. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: Berlin/Heidelberg, Germany, 2013; Volume 70, pp. 978–983. [Google Scholar]
- Chandrasekhary, R.S.; Murthy, B.N. Novel two position ground alignment technique for Strapdown Inertial Navigation System. In Proceedings of the 2014 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology, Yogyakarta, Indonesia, 13–14 November 2014; pp. 94–98. [Google Scholar]
- Deng, Z.; Wang, P.; Liu, T.; Cao, Y.; Wang, B. Foot-mounted pedestrian navigation algorithm based on BOR/MINS integrated framework. IEEE Trans. Ind. Electron. 2019, 67, 3980–3989. [Google Scholar] [CrossRef]
- Fang, J.; Sun, H.; Cao, J.; Zhang, X.; Tao, Y. A novel calibration method of magnetic compass based on ellipsoid fitting. IEEE Trans. Instrum. Meas. 2011, 60, 2053–2061. [Google Scholar] [CrossRef]
- Abdulrahim, K.; Hide, C.; Moore, T.; Hill, C. Using constraints for shoe mounted indoor pedestrian navigation. J. Navig. 2012, 65, 15–28. [Google Scholar] [CrossRef]





| - | Pitch | Roll | Yaw |
|---|---|---|---|
| 0 | |||
| 0 |
| Motion | Horizontal Velocity Error | Vertical Velocity Error |
|---|---|---|
| Pitch motion | The errors will cancel each other out in opposite directions | Increase |
| Roll motion | The errors will cancel each other out in opposite directions | Increase |
| Yaw motion | The errors will cancel each other out in opposite directions | Make no difference |
| Walking on flat ground | The errors will cancel each other out when walking on a closed-loop trajectory | Increase |
| Going upstairs | The errors will cancel each other out when walking on a closed-loop trajectory | Increase |
| Going downstairs | The errors will cancel each other out when walking on a closed-loop trajectory | Increase |
| Performance | Gyros | Accelerometers |
|---|---|---|
| In-run stability | /h | 40 ug |
| Random walk | / | 0.06 m/s / |
| Full range | /h | ±40 g |
| Method | Detail |
|---|---|
| Method 1 | ZUPT with gyro-accelerometer asynchronous time ignored |
| Method 2 | ZUPT with gyro-accelerometer asynchronous time considered |
| Method 3 | ZUPT/height constraint with gyro-accelerometer asynchronous time ignored |
| Method 4 | ZUPT/height constraint with gyro-accelerometer asynchronous time considered |
| Errors | Method 1 | Method 2 | Method 3 | Method 4 |
|---|---|---|---|---|
| North position error (m) | 0.38 | 0.35 | 0.17 | 0.18 |
| East position error (m) | 0.36 | 0.23 | 0.27 | 0.15 |
| Horizontal position error (m) | 0.52 | 0.42 | 0.32 | 0.23 |
| Error percentage (%D) | 0.50 | 0.40 | 0.31 | 0.22 |
| Height error (m) | 1.03 | 0.76 | 0.08 | 0.06 |
| Errors | Method 1 | Method 2 | Method 3 | Method 4 |
|---|---|---|---|---|
| North position error (m) | 0.93 | 0.75 | 0.44 | 0.36 |
| East position error (m) | 1.06 | 0.92 | 1.01 | 0.85 |
| Horizontal position error (m) | 1.41 | 1.19 | 1.10 | 0.92 |
| Error percentage (%D) | 0.70 | 0.59 | 0.54 | 0.46 |
| Height error (m) | 2.48 | 1.36 | 0.20 | 0.18 |
| Errors | Method 1 | Method 2 | Method 3 | Method 4 |
|---|---|---|---|---|
| North position error (m) | 1.70 | 1.38 | 0.89 | 0.66 |
| East position error (m) | 1.84 | 1.60 | 1.66 | 1.43 |
| Horizontal position error (m) | 2.51 | 2.11 | 1.88 | 1.58 |
| Error percentage (%D) | 0.84 | 0.70 | 0.64 | 0.53 |
| Height error (m) | 3.37 | 2.11 | 0.22 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Yang, G.; Cai, Q.; Wen, Z.; Zhang, W. A Novel Calibration Method for Gyro-Accelerometer Asynchronous Time in Foot-Mounted Pedestrian Navigation System. Sensors 2022, 22, 209. https://doi.org/10.3390/s22010209
Chen T, Yang G, Cai Q, Wen Z, Zhang W. A Novel Calibration Method for Gyro-Accelerometer Asynchronous Time in Foot-Mounted Pedestrian Navigation System. Sensors. 2022; 22(1):209. https://doi.org/10.3390/s22010209
Chicago/Turabian StyleChen, Tianyu, Gongliu Yang, Qingzhong Cai, Zeyang Wen, and Wenlong Zhang. 2022. "A Novel Calibration Method for Gyro-Accelerometer Asynchronous Time in Foot-Mounted Pedestrian Navigation System" Sensors 22, no. 1: 209. https://doi.org/10.3390/s22010209
APA StyleChen, T., Yang, G., Cai, Q., Wen, Z., & Zhang, W. (2022). A Novel Calibration Method for Gyro-Accelerometer Asynchronous Time in Foot-Mounted Pedestrian Navigation System. Sensors, 22(1), 209. https://doi.org/10.3390/s22010209






