Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression
Abstract
:1. Introduction
2. Related Work
3. Projection Types and Their Description
3.1. Lambert Azimuthal Equal-Area Projection
3.2. Albers Equal-Area Conic Projection
3.3. Cylindrical Projection
3.4. Cylindrical Equal-Area Projection
3.5. Equidistant Cylindrical Projection
3.6. Mercator Projection
3.7. Miller Projection
3.8. Rectilinear Projection
3.9. Pannini Projection
3.10. Stereographic Projection
4. Creation of Panorama Images from Point Clouds and Recreation of Point Clouds
| //create geometry and texture image using 3DTK //get mask as the inverse of the existing pixels from~geometry |
| distanceTransform(mask, distance, labels, CV_DIST_L2, CV_DIST_MASK_PRECISE, CV_DIST_LABEL_PIXEL); |
| //map labels to indices std::vector<cv::Vec2i> label_to_index; |
| //reserve memory for faster push_back label_to_index.reserve(sum(~mask)[0]); |
| for (int row = 0; row < mask.rows; ++row) for (int col = 0; col < mask.cols; ++col) if (mask.at<uchar>(row, col) == 0) //this pixel exist label_to_index.push_back(cv::Vec2i(row, col)); |
| //create ``full’’ image for (int row = 0; row < mask.rows; ++row) { for (int col = 0; col < mask.cols; ++col) { if (mask.at<uchar>(row, col) > 0) { //so this pixel needs to be filled colorImage.at<cv::Vec3b>(row,col)= cv::Vec3b(colorImage.at<cv::Vec3b>(label_to_index[labels.at<int>(row, col)])[0], colorImage.at<cv::Vec3b>(label_to_index[labels.at<int>(row, col)])[1], colorImage.at<cv::Vec3b>(label_to_index[labels.at<int>(row, col)])[2]); } } } |
- normal estimation using CloudCompare version 2.11.1 x64 [46], for the later screened Poisson reconstruction, in “command line” mode. Specific parameters used were: -OCTREE_NORMALS auto -ORIENT PLUS_ZERO -MODEL TRI -ORIENT_NORMS_MST 8 -ORIENT_NORMS_MST 4.
- Surface Reconstruction: Screened Poisson filter using MeshLab 2020.09 [45]: reconstruction depth 11 and other default values.
- Poisson-disk Sampling filter using MeshLab: using the same number of samples as the original point cloud, Monte Carlo OverSampling of 20 and other default values. However, usually somewhat higher number of output points were created.
- Vertex Attribute Transfer filter using MeshLab: using default values.
5. Results
5.1. Objective Measures Used for Point Cloud Performance Comparison
5.2. Point Cloud Compression Using Different Projections—Compression Efficiency
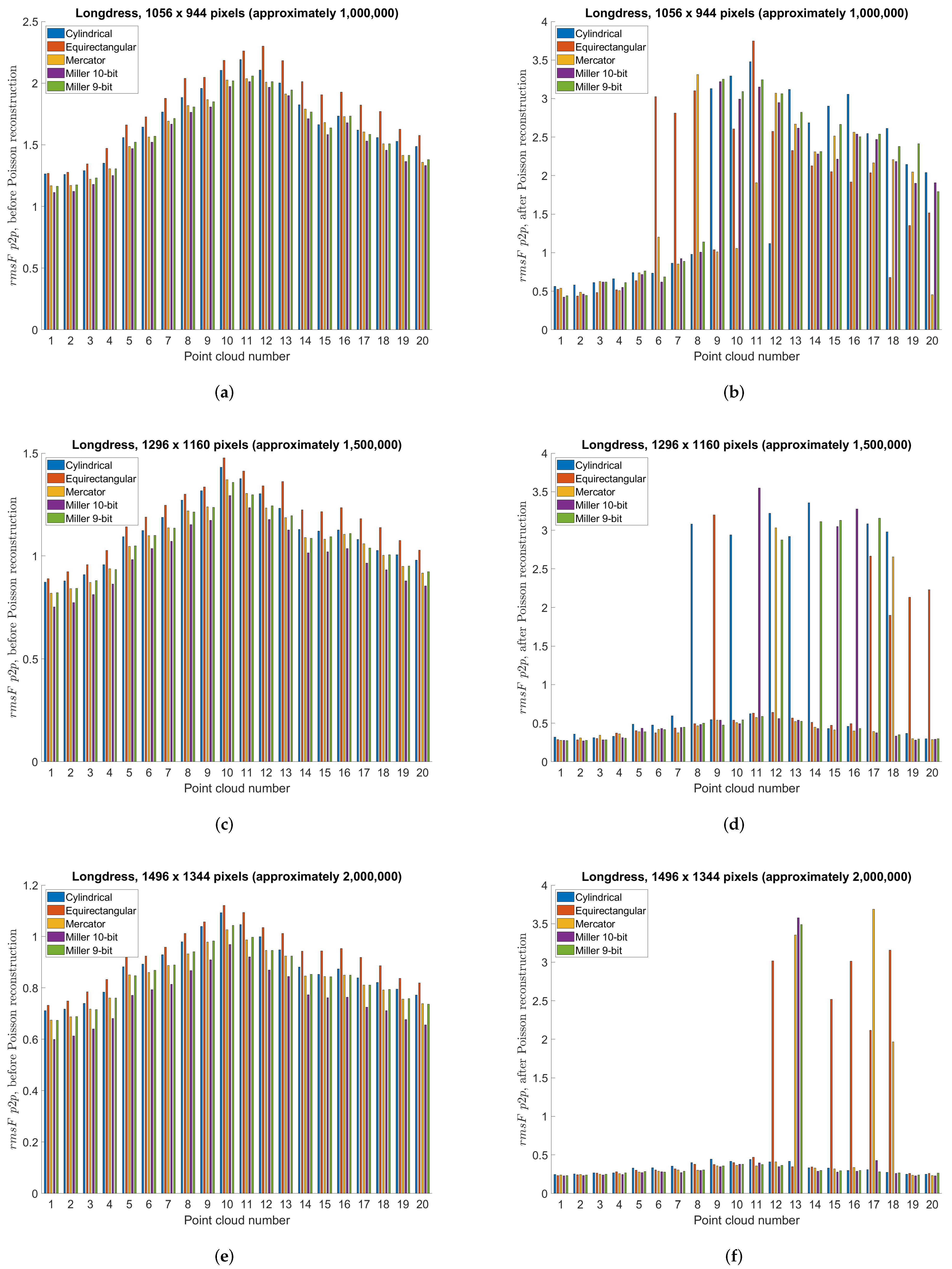
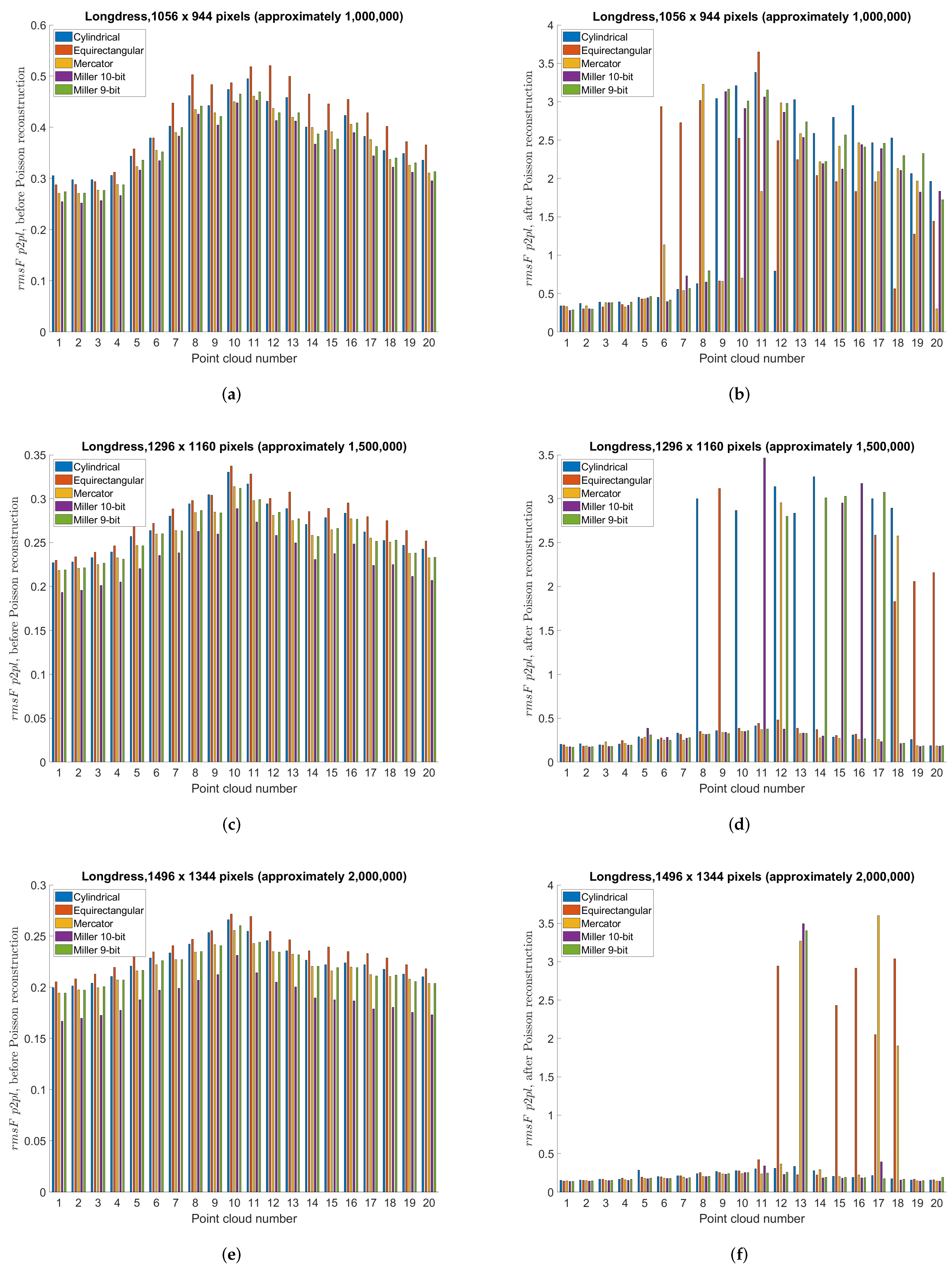
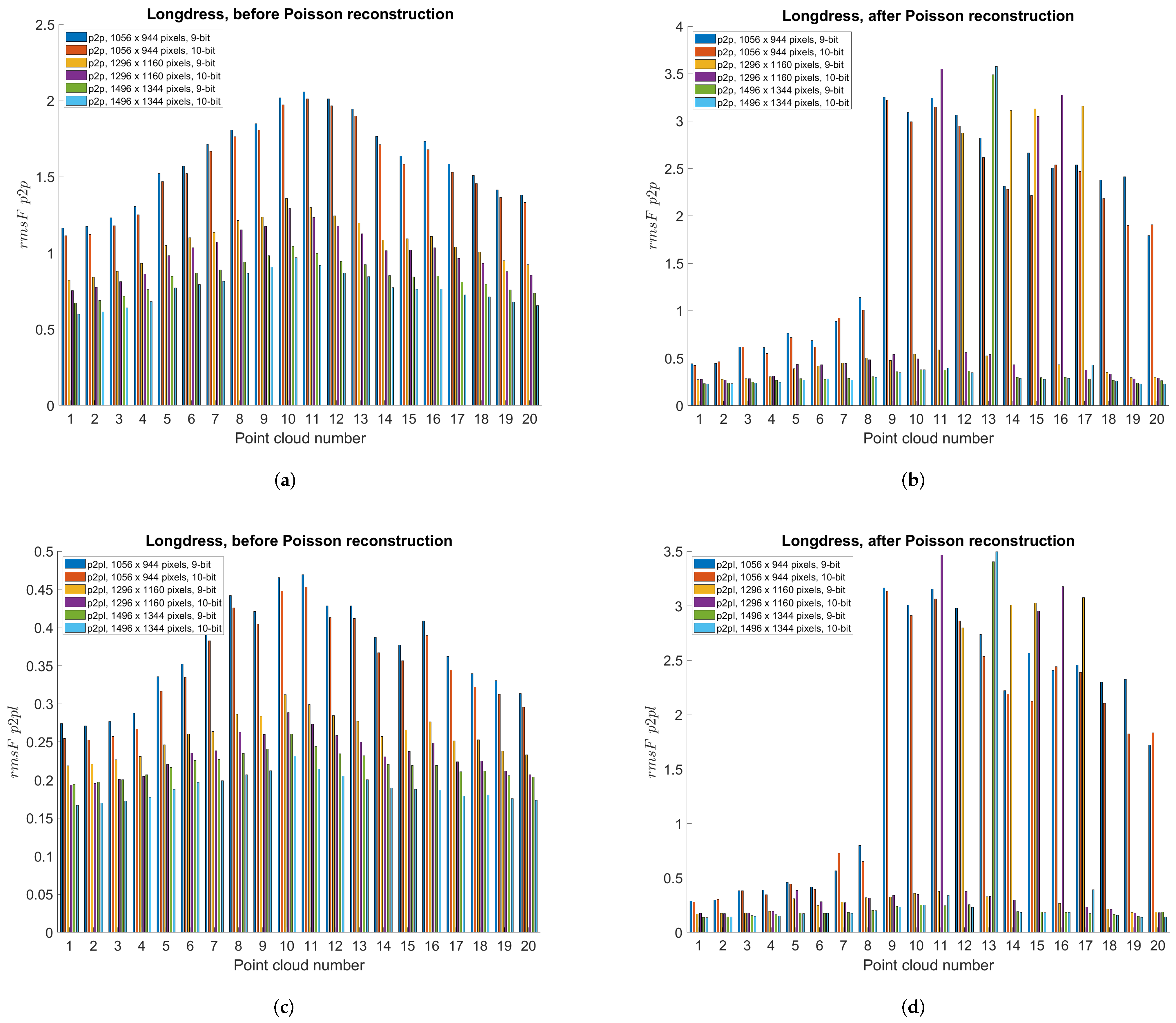
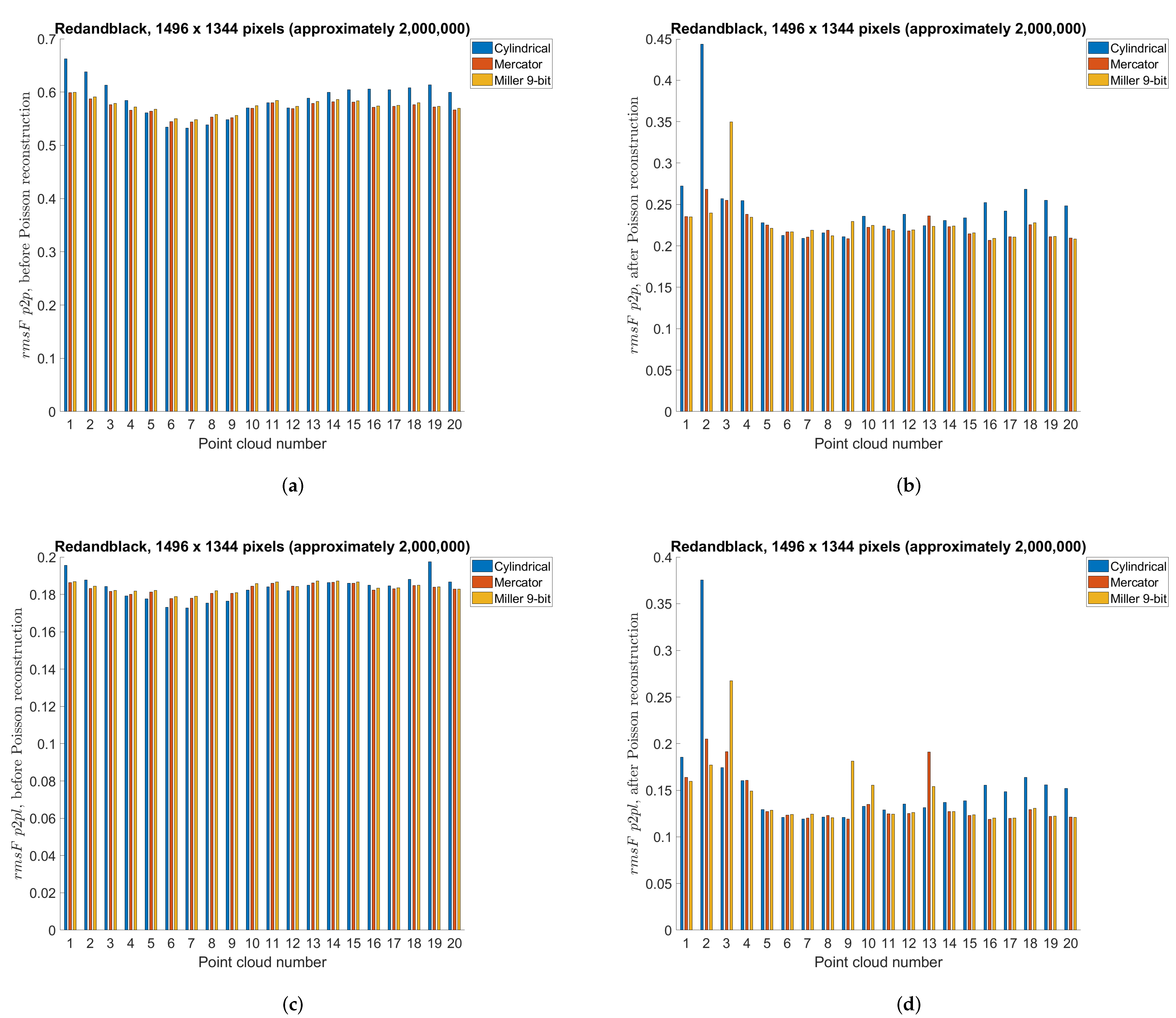
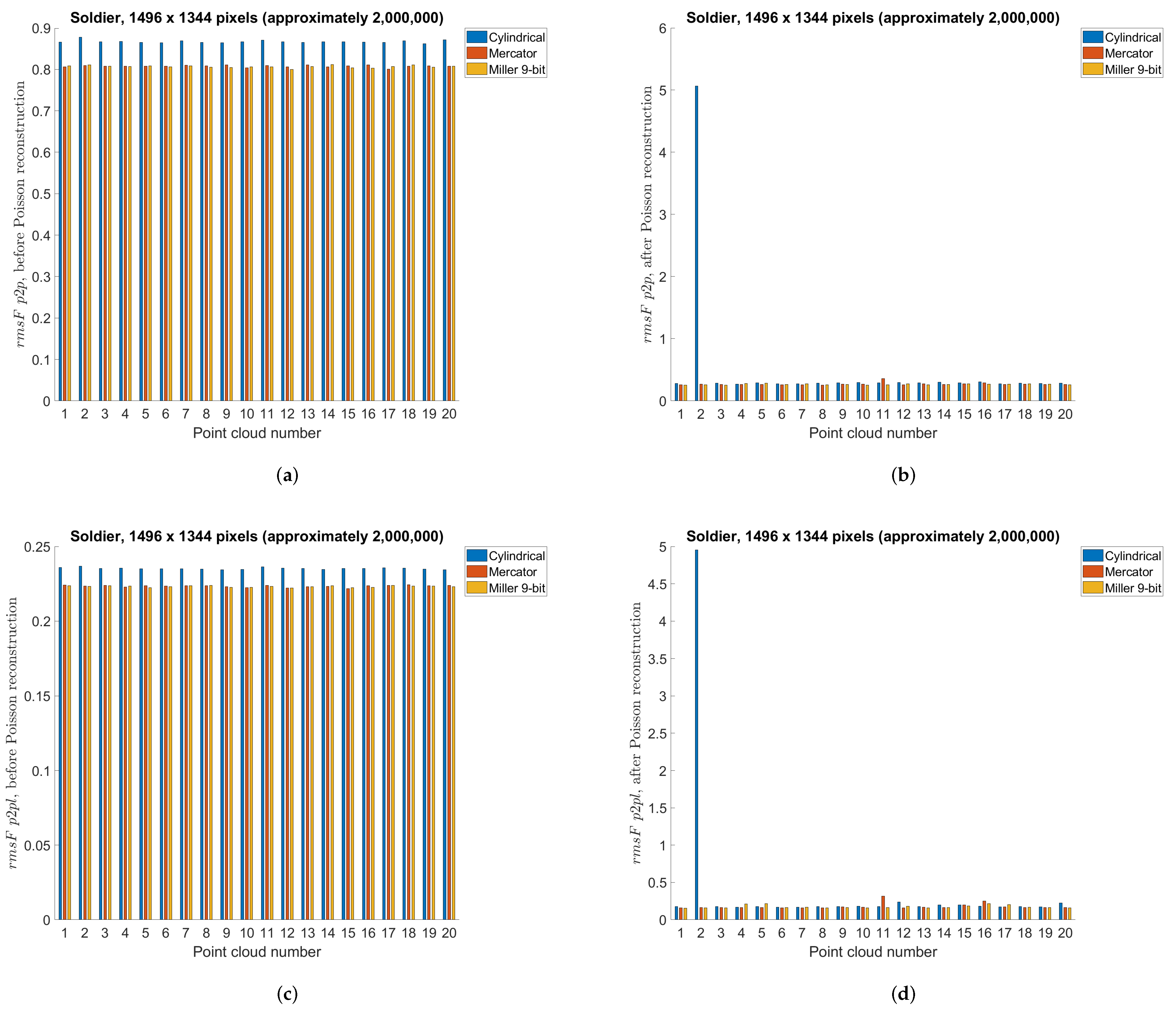
5.3. Point Cloud Compression Using Different Projections—Objective Measures
5.4. Point Cloud Compression—Timing Performance
5.5. Point Cloud Compression Using Different Point Clouds
5.6. Comparison with Octree Reduction from 3DTK Toolkit
5.7. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Astola, P.; da Silva Cruz, L.A.; da Silva, E.A.; Ebrahimi, T.; Freitas, P.G.; Gilles, A.; Oh, K.J.; Pagliari, C.; Pereira, F.; Perra, C.; et al. JPEG Pleno: Standardizing a Coding Framework and Tools for Plenoptic Imaging Modalities. ITU J. ICT Discov. 2020, 3, 1–15. [Google Scholar] [CrossRef]
- Perkis, A.; Timmerer, C.; Baraković, S.; Husić, J.B.; Bech, S.; Bosse, S.; Botev, J.; Brunnström, K.; Cruz, L.; Moor, K.D.; et al. QUALINET White Paper on Definitions of Immersive Media Experience (IMEx). In Proceedings of the European Network on Quality of Experience in Multimedia Systems and Services, 14th QUALINET Meeting, Online, 25 May 2020; pp. 1–15. [Google Scholar]
- Wang, Q.; Tan, Y.; Mei, Z. Computational Methods of Acquisition and Processing of 3D Point Cloud Data for Construction Applications. Arch. Comput. Methods Eng. 2020, 27, 479–499. [Google Scholar] [CrossRef]
- Pereira, F.; da Silva, E.A.; Lafruit, G. Chapter 2—Plenoptic imaging: Representation and processing. In Academic Press Library in Signal Processing; Chellappa, R., Theodoridis, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 75–111. [Google Scholar] [CrossRef]
- van der Hooft, J.; Vega, M.T.; Timmerer, C.; Begen, A.C.; De Turck, F.; Schatz, R. Objective and Subjective QoE Evaluation for Adaptive Point Cloud Streaming. In Proceedings of the 2020 Twelfth International Conference on Quality of Multimedia Experience (QoMEX), Athlone, Ireland, 26–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Han, B.; Liu, Y.; Qian, F. ViVo: Visibility-aware mobile volumetric video streaming. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking, MobiCom 2020, London, UK, 21–25 September 2020; pp. 137–149. [Google Scholar] [CrossRef]
- Dumic, E.; Battisti, F.; Carli, M.; da Silva Cruz, L.A. Point Cloud Visualization Methods: A Study on Subjective Preferences. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2020; pp. 1–5. [Google Scholar]
- Javaheri, A.; Brites, C.; Pereira, F.M.B.; Ascenso, J.M. Point Cloud Rendering after Coding: Impacts on Subjective and Objective Quality. IEEE Trans. Multimed. 2020, 23, 4049–4064. [Google Scholar] [CrossRef]
- Dumic, E.; Bjelopera, A.; Nüchter, A. Projection based dynamic point cloud compression using 3DTK toolkit and H.265/HEVC. In Proceedings of the 2019 2nd International Colloquium on Smart Grid Metrology (SMAGRIMET), Split, Croatia, 9–12 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- da Silva Cruz, L.A.; Dumić, E.; Alexiou, E.; Prazeres, J.; Duarte, R.; Pereira, M.; Pinheiro, A.; Ebrahimi, T. Point cloud quality evaluation: Towards a definition for test conditions. In Proceedings of the 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), Berlin, Germany, 5–7 June 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Elseberg, J.; Borrmann, D.; Nüchter, A. One billion points in the cloud—An octree for efficient processing of 3D laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 76, 76–88. [Google Scholar] [CrossRef]
- Elseberg, J.; Magnenat, S.; Siegwart, R.; Nüchter, A. Comparison of nearest-neighbor-search strategies and implementations for efficient shape registration. J. Softw. Eng. Robot. 2013, 3, 2–12. [Google Scholar] [CrossRef]
- 3DTK—The 3D Toolkit. Available online: http://slam6d.sourceforge.net/ (accessed on 13 September 2021).
- Houshiar, H.; Borrmann, D.; Elseberg, J.; Nüchter, A. Panorama based point cloud reduction and registration. In Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Houshiar, H.; Nüchter, A. 3D point cloud compression using conventional image compression for efficient data transmission. In Proceedings of the 2015 XXV International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 29–31 October 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Mammou, K.; Chou, P.A.; Flynn, D.; Krivokuća, M.; Nakagami, O.; Sugio, T. G-PCC Codec Description v2; Technical Report, ISO/IEC JTC1/SC29/WG11 Input Document N18189; MPEG: Marrakech, MA, USA, 2019. [Google Scholar]
- Zakharchenko, V. V-PCC Codec Description; Technical Report, ISO/IEC JTC1/SC29/WG11 Input Document N18190; MPEG: Marrakech, MA, USA, 2019. [Google Scholar]
- Sullivan, G.J.; Ohm, J.; Han, W.; Wiegand, T. Overview of the High Efficiency Video Coding (HEVC) Standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1649–1668. [Google Scholar] [CrossRef]
- Schwarz, S.; Preda, M.; Baroncini, V.; Budagavi, M.; Cesar, P.; Chou, P.A.; Cohen, R.A.; Krivokuća, M.; Lasserre, S.; Li, Z.; et al. Emerging MPEG Standards for Point Cloud Compression. IEEE J. Emerg. Sel. Top. Circuits Syst. 2019, 9, 133–148. [Google Scholar] [CrossRef] [Green Version]
- Graziosi, D.; Nakagami, O.; Kuma, S.; Zaghetto, A.; Suzuki, T.; Tabatabai, A. An overview of ongoing point cloud compression standardization activities: Video-based (V-PCC) and geometry-based (G-PCC). APSIPA Trans. Signal Inf. Process. 2020, 9, e13. [Google Scholar] [CrossRef] [Green Version]
- Alexiou, E.; Viola, I.; Borges, T.M.; Fonseca, T.A.; de Queiroz, R.L.; Ebrahimi, T. A comprehensive study of the rate-distortion performance in MPEG point cloud compression. APSIPA Trans. Signal Inf. Process. 2019, 8, 27. Available online: https://www.epfl.ch/labs/mmspg/quality-assessment-for-point-cloud-compression/ (accessed on 13 September 2021). [CrossRef] [Green Version]
- Perry, S.; Cong, H.P.; da Silva Cruz, L.A.; Prazeres, J.; Pereira, M.; Pinheiro, A.; Dumic, E.; Alexiou, E.; Ebrahimi, T. Quality Evaluation of Static Point Clouds Encoded Using MPEG Codecs. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 3428–3432. [Google Scholar] [CrossRef]
- Alexiou, E.; Tung, K.; Ebrahimi, T. Towards neural network approaches for point cloud compression. In Proceedings Volume 11510, Applications of Digital Image Processing XLIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; p. 1151008. [Google Scholar] [CrossRef]
- Mekuria, R.; Blom, K.; Cesar, P. Design, Implementation, and Evaluation of a Point Cloud Codec for Tele-Immersive Video. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 828–842. [Google Scholar] [CrossRef] [Green Version]
- Quach, M.; Valenzise, G.; Dufaux, F. Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing, ICIP 2019, Taipei, Taiwan, 22–25 September 2019; pp. 4320–4324. [Google Scholar] [CrossRef] [Green Version]
- Loop, C.; Cai, Q.; Escolano, S.O.; Chou, P. Microsoft Voxelized Upper Bodies—A Voxelized Point Cloud Dataset; Technical Report, ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) Input Document m38673/M72012. 2016. Available online: http://plenodb.jpeg.org/pc/microsoft/ (accessed on 13 September 2021).
- Quach, M.; Valenzise, G.; Dufaux, F. Improved Deep Point Cloud Geometry Compression. In Proceedings of the 2020 IEEE 22nd International Workshop on Multimedia Signal Processing (MMSP), Tampere, Finland, 21–24 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.; Liu, H.; Ma, Z. Lossy Point Cloud Geometry Compression via End-to-End Learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4909–4923. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Ma, Z. Multiscale Point Cloud Geometry Compression. In Proceedings of the 2021 Data Compression Conference (DCC), Virtual, 23–26 March 2021; pp. 73–82. [Google Scholar] [CrossRef]
- Guarda, A.F.R.; Rodrigues, N.M.M.; Pereira, F. Point Cloud Coding: Adopting a Deep Learning-based Approach. In Proceedings of the 2019 Picture Coding Symposium (PCS), Ningbo, China, 12–15 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Guarda, A.F.R.; Rodrigues, N.M.M.; Pereira, F. Deep Learning-based Point Cloud Geometry Coding with Resolution Scalability. In Proceedings of the 2020 IEEE 22nd International Workshop on Multimedia Signal Processing (MMSP), Tampere, Finland, 21–24 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Guarda, A.F.R.; Rodrigues, N.M.M.; Pereira, F. Adaptive Deep Learning-Based Point Cloud Geometry Coding. IEEE J. Sel. Top. Signal Process. 2021, 15, 415–430. [Google Scholar] [CrossRef]
- Milani, S. ADAE: Adversarial Distributed Source Autoencoder For Point Cloud Compression. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3078–3082. [Google Scholar] [CrossRef]
- Lazzarotto, D.; Alexiou, E.; Ebrahimi, T. On Block Prediction For Learning-Based Point Cloud Compression. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3378–3382. [Google Scholar] [CrossRef]
- Yan, W.; Shao, Y.; Liu, S.; Li, T.H.; Li, Z.; Li, G. Deep AutoEncoder-based Lossy Geometry Compression for Point Clouds. arXiv 2019, arXiv:1905.03691. Available online: https://arxiv.org/abs/1905.03691 (accessed on 13 September 2021).
- Huang, T.; Liu, Y. 3D Point Cloud Geometry Compression on Deep Learning. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 890–898. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Learning-Based Lossless Compression of 3D Point Cloud Geometry. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4220–4224. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Multiscale deep context modeling for lossless point cloud geometry compression. In Proceedings of the 2021 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Shenzhen, China, 5–9 July 2021. [Google Scholar] [CrossRef]
- Que, Z.; Lu, G.; Xu, D. VoxelContext-Net: An Octree based Framework for Point Cloud Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2021, Virtual, 19–25 June 2021; pp. 6042–6051. [Google Scholar]
- Lazzarotto, D.; Ebrahimi, T. Learning residual coding for point clouds. In Applications of Digital Image Processing XLIV; Tescher, A.G., Ebrahimi, T., Eds.; International Society for Optics and Photonics: Washington, DC, USA, 2021; Volume 11842, pp. 223–235. [Google Scholar] [CrossRef]
- Weisstein, E.W. Map Projection. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/topics/MapProjections.html (accessed on 16 April 2021).
- Houshiar, H. Documentation and Mapping with 3D Point Cloud Processing. Ph.D. Thesis, University of Würzburg, Würzburg, Germany, 2017. [Google Scholar] [CrossRef]
- d’Eon, E.; Harrison, B.; Myers, T.; Chou, P.A. 8i Voxelized Full Bodies—A Voxelized Point Cloud Dataset; Technical Report, ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) Input Document WG11M40059/WG1M74006. 2017. Available online: https://jpeg.org/plenodb/pc/8ilabs/ (accessed on 13 September 2021).
- Lab, Visual Computing, MeshLab. Available online: http://www.meshlab.net/ (accessed on 13 September 2021).
- CloudCompare—3D Point Cloud and Mesh Processing Software—Open Source Project. Available online: http://www.cloudcompare.org (accessed on 6 February 2019).
- FFmpeg Team. FFmpeg. Available online: https://www.ffmpeg.org/download.html (accessed on 2 May 2021).
- Weisstein, E.W. Voronoi Diagram. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/VoronoiDiagram.html (accessed on 6 November 2021).
- Dumic, E. Scripts for Dynamic Point Cloud Compression. Available online: http://msl.unin.hr/ (accessed on 8 November 2021).
- Dumic, E.; da Silva Cruz, L.A. Point Cloud Coding Solutions, Subjective Assessment and Objective Measures: A Case Study. Symmetry 2020, 12, 1955. [Google Scholar] [CrossRef]
- Tian, D.; Ochimizu, H.; Feng, C.; Cohen, R.; Vetro, A. Geometric distortion metrics for point cloud compression. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3460–3464. [Google Scholar] [CrossRef]
- Grieger, B. Quincuncial adaptive closed Kohonen (QuACK) map for the irregularly shaped comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2019, 630, A1. [Google Scholar] [CrossRef] [Green Version]

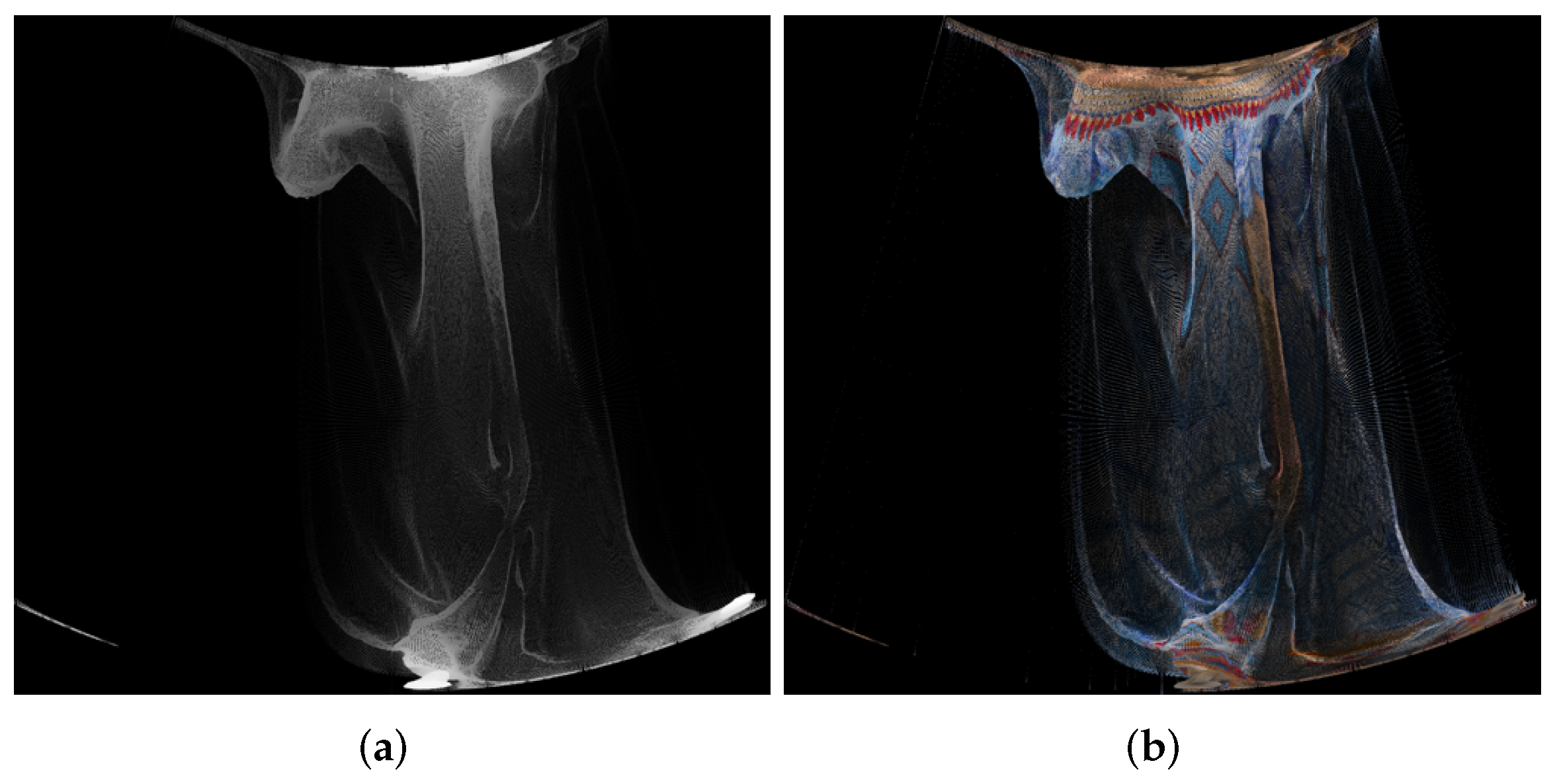
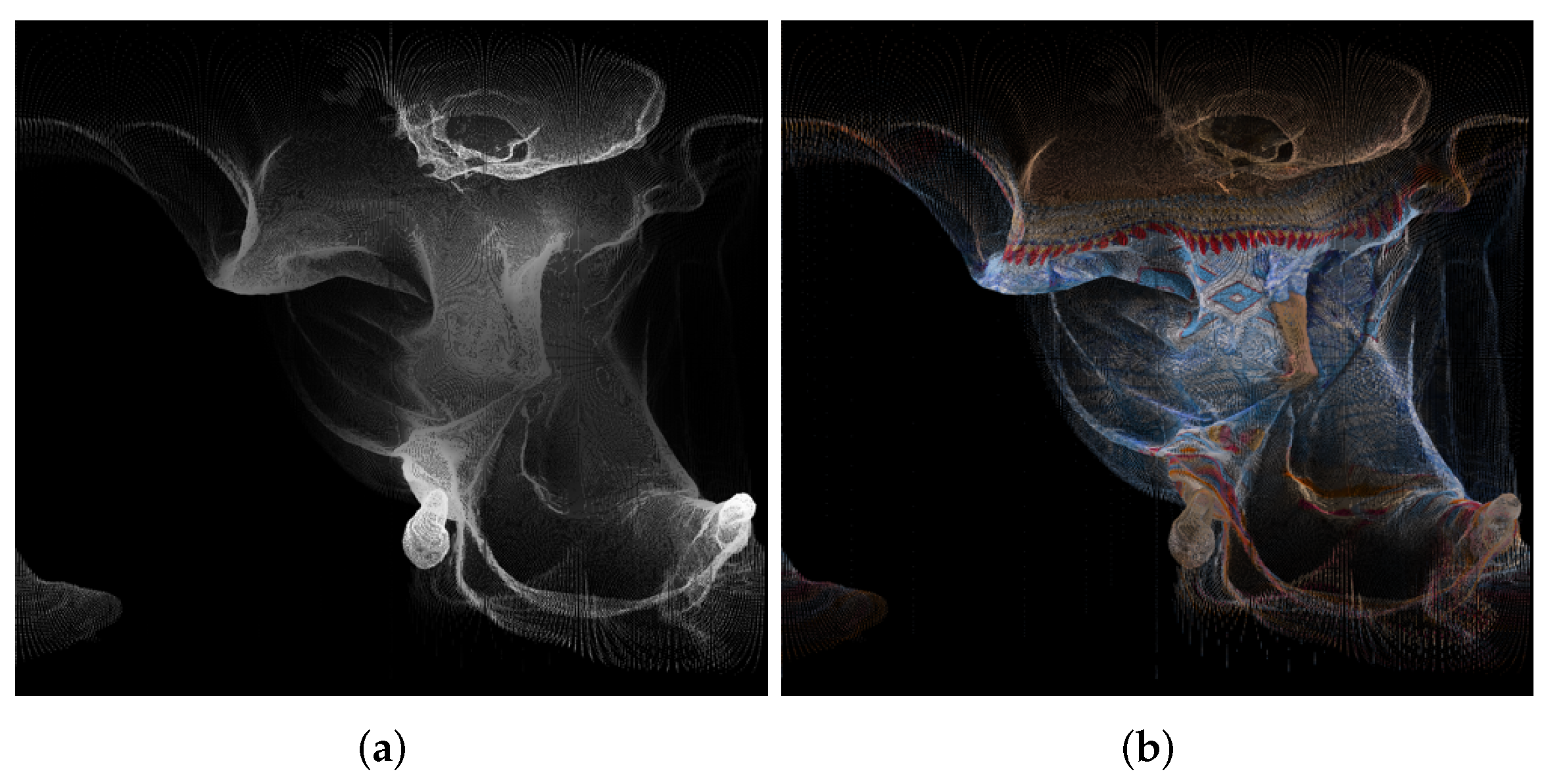
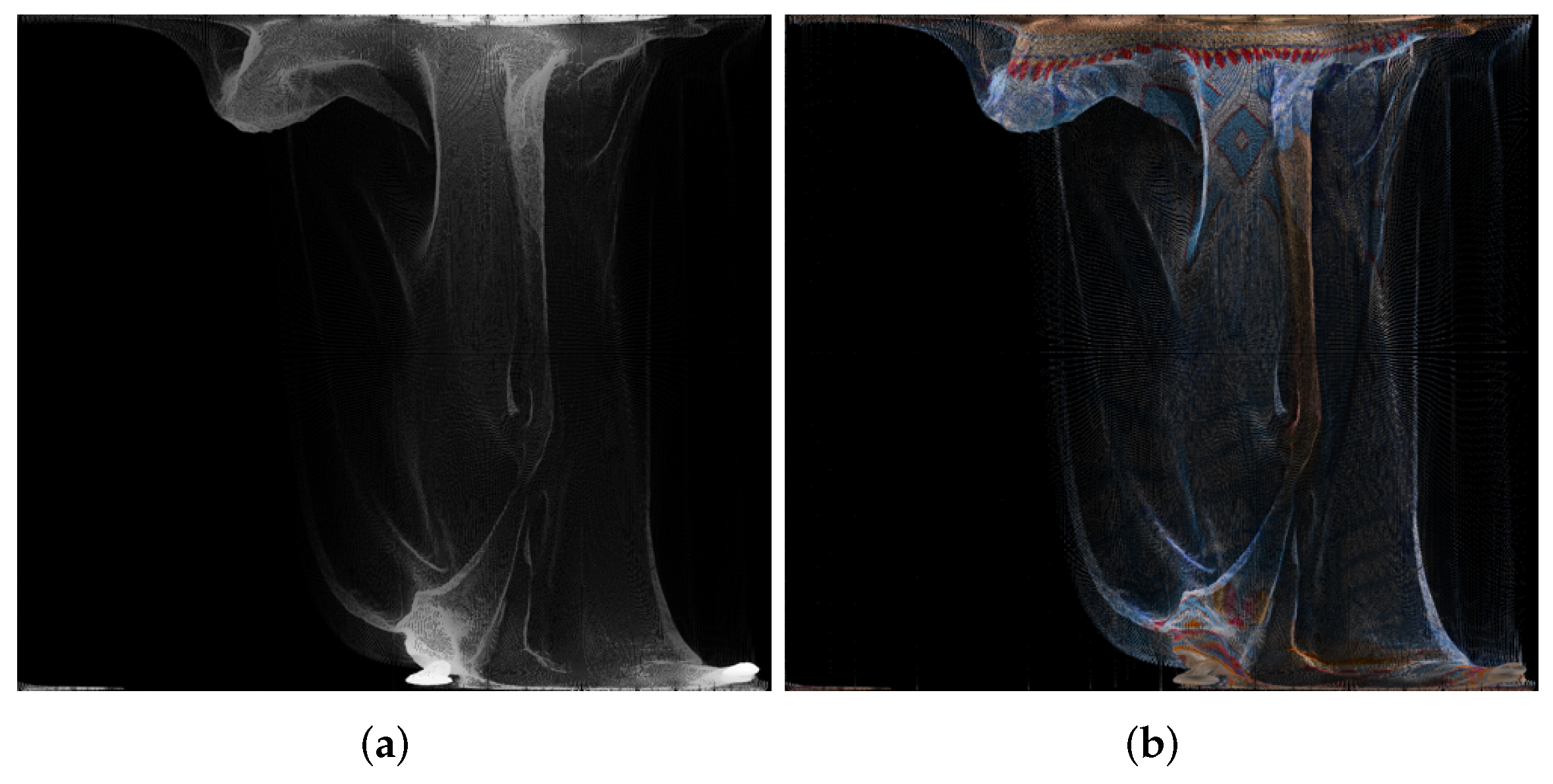
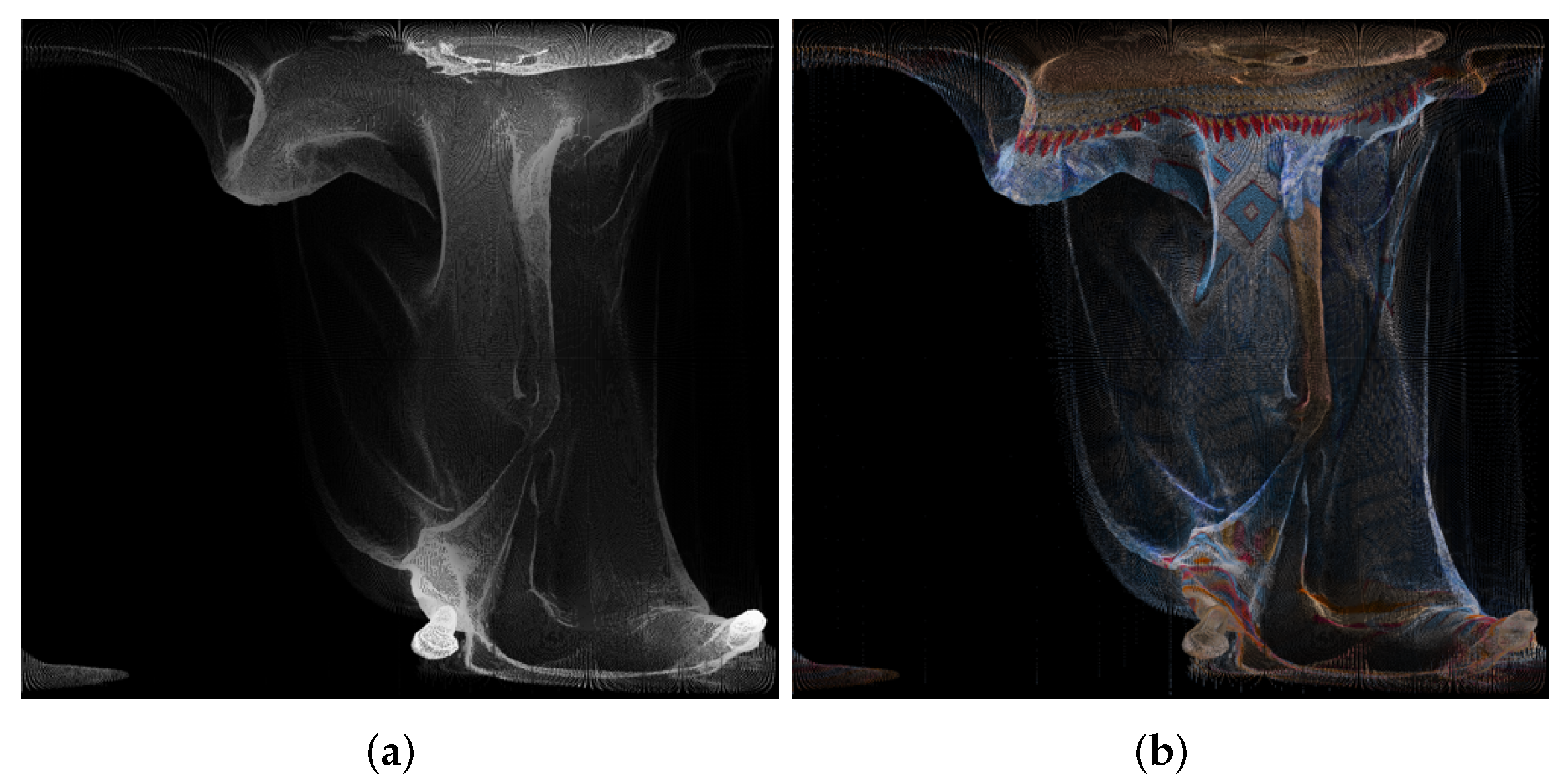
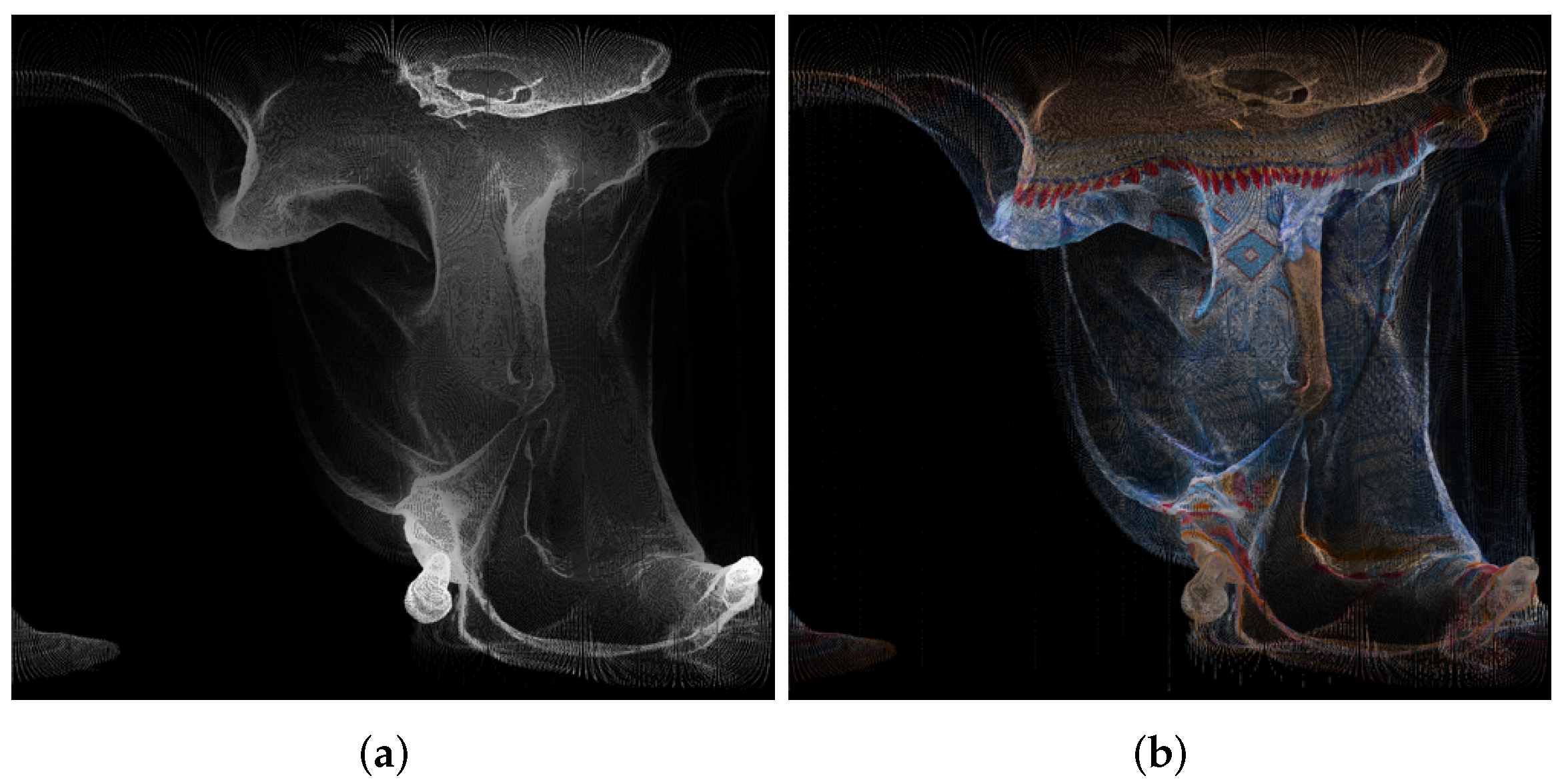

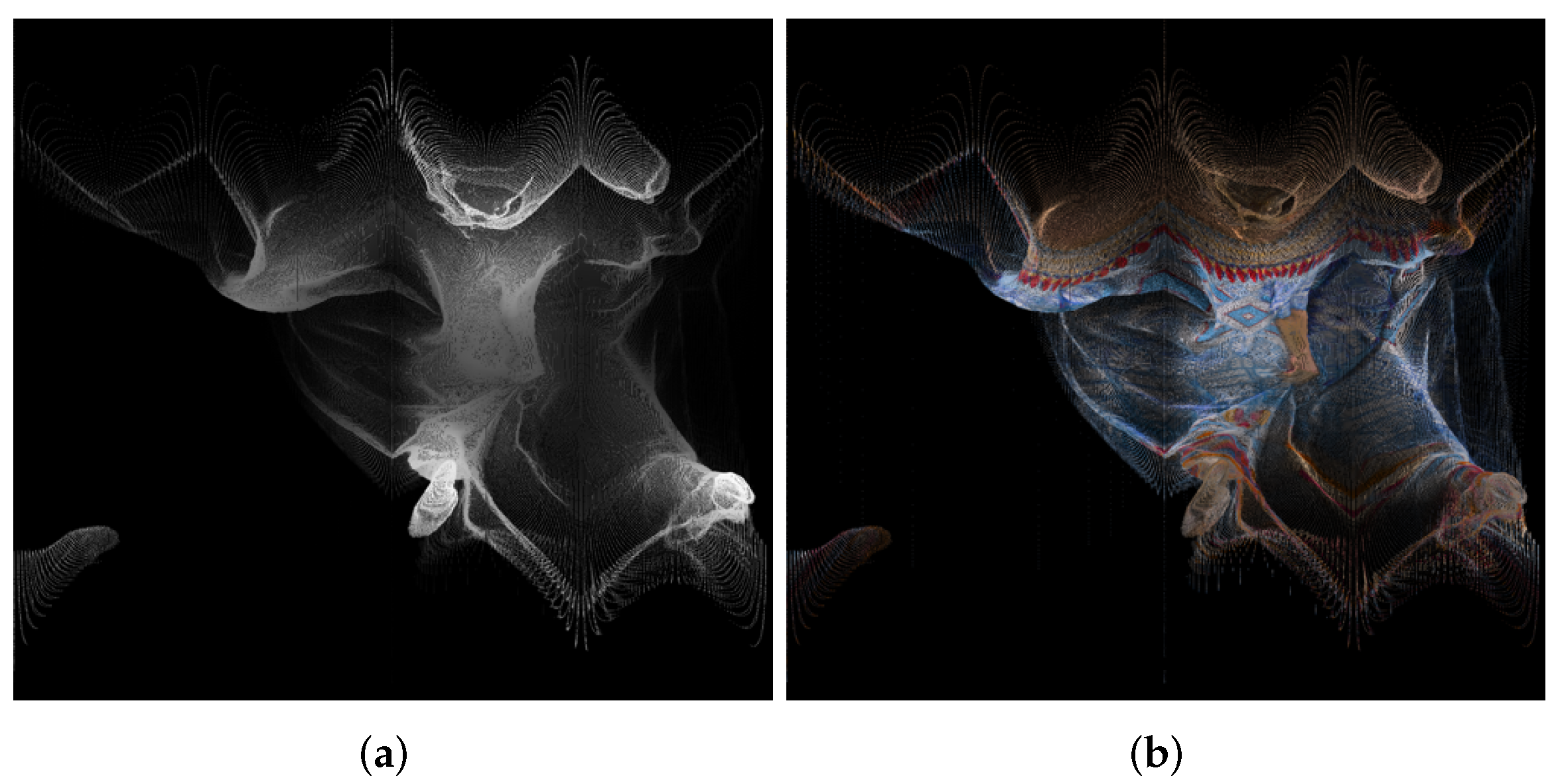
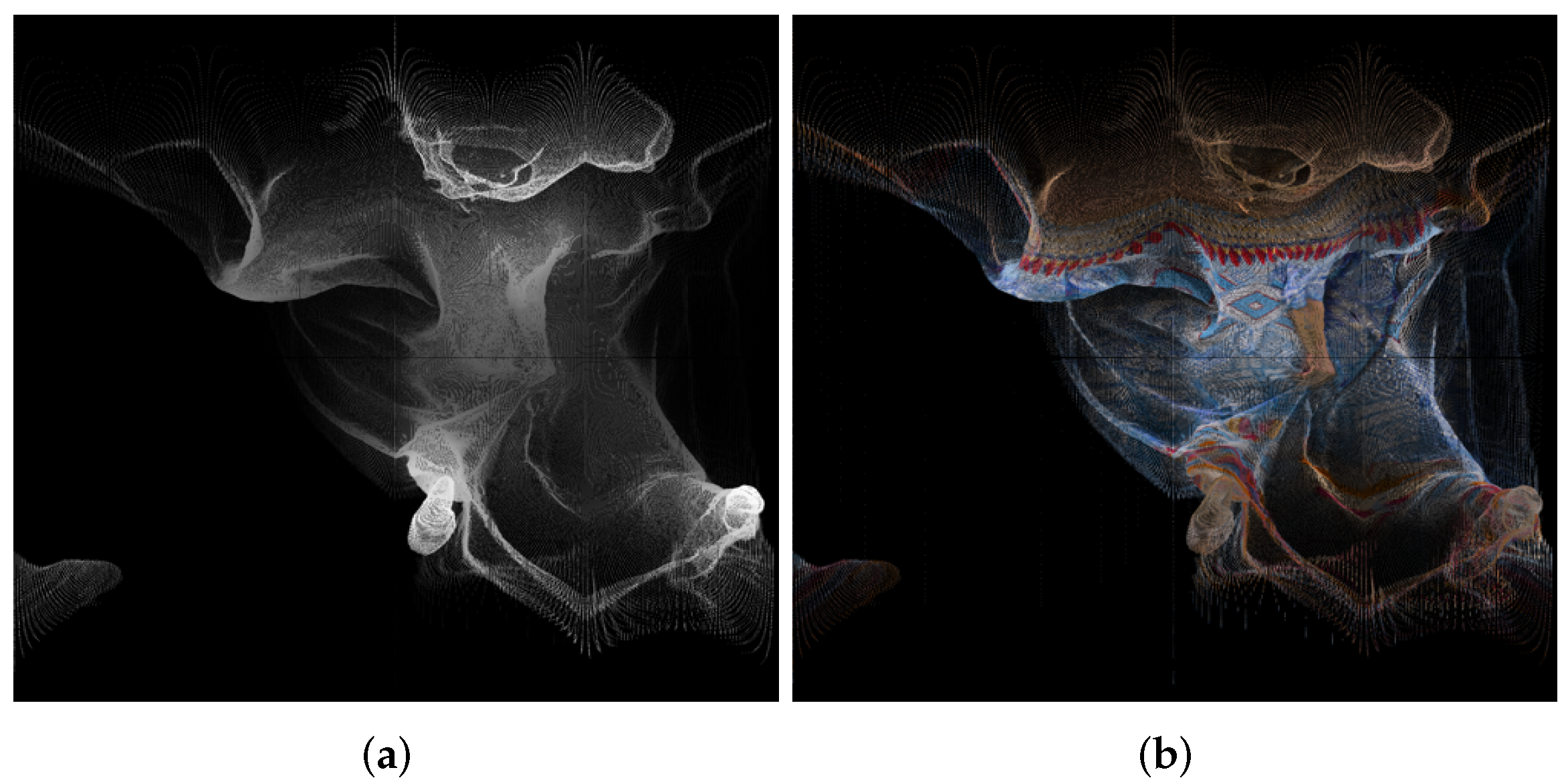
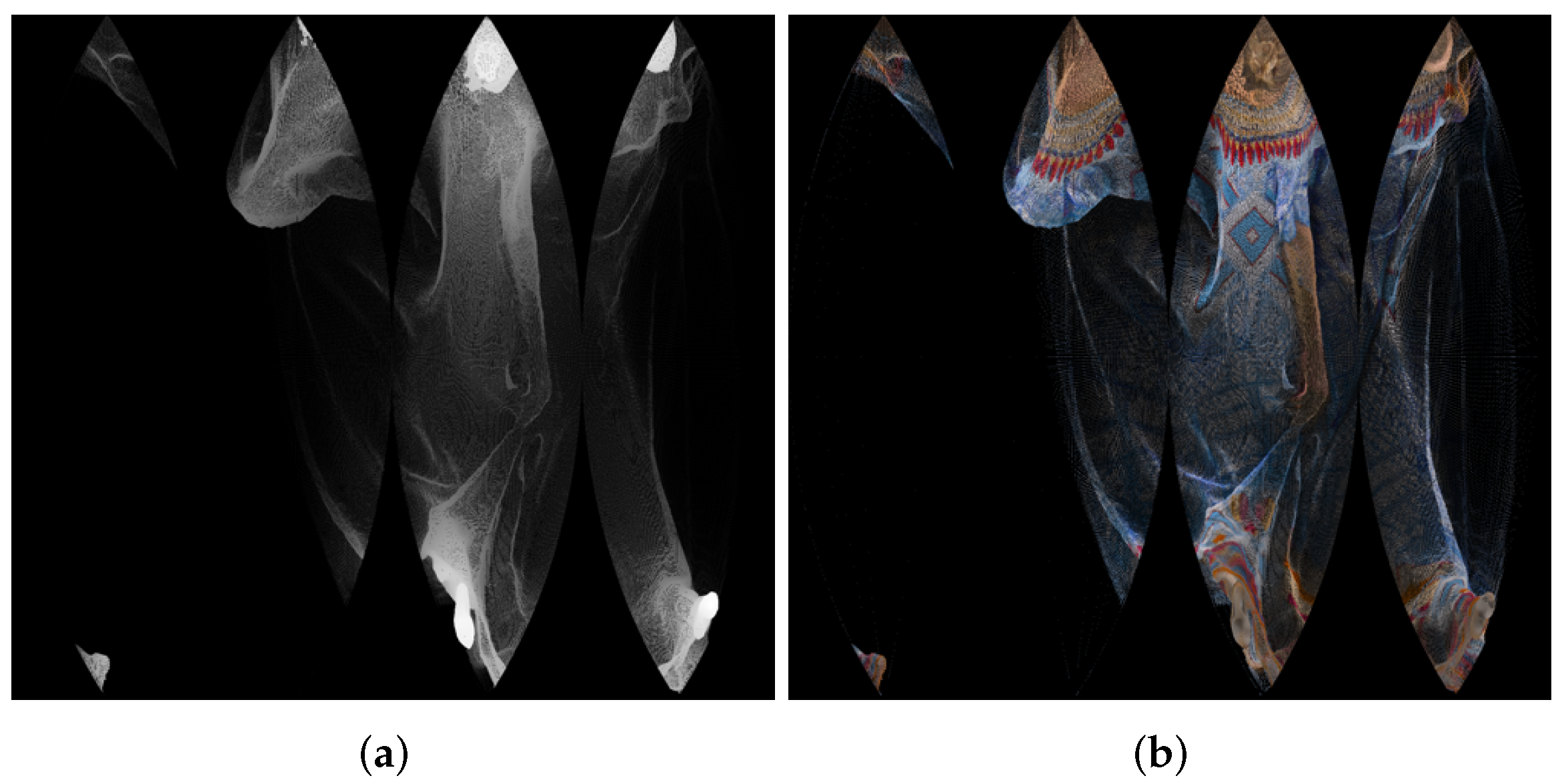
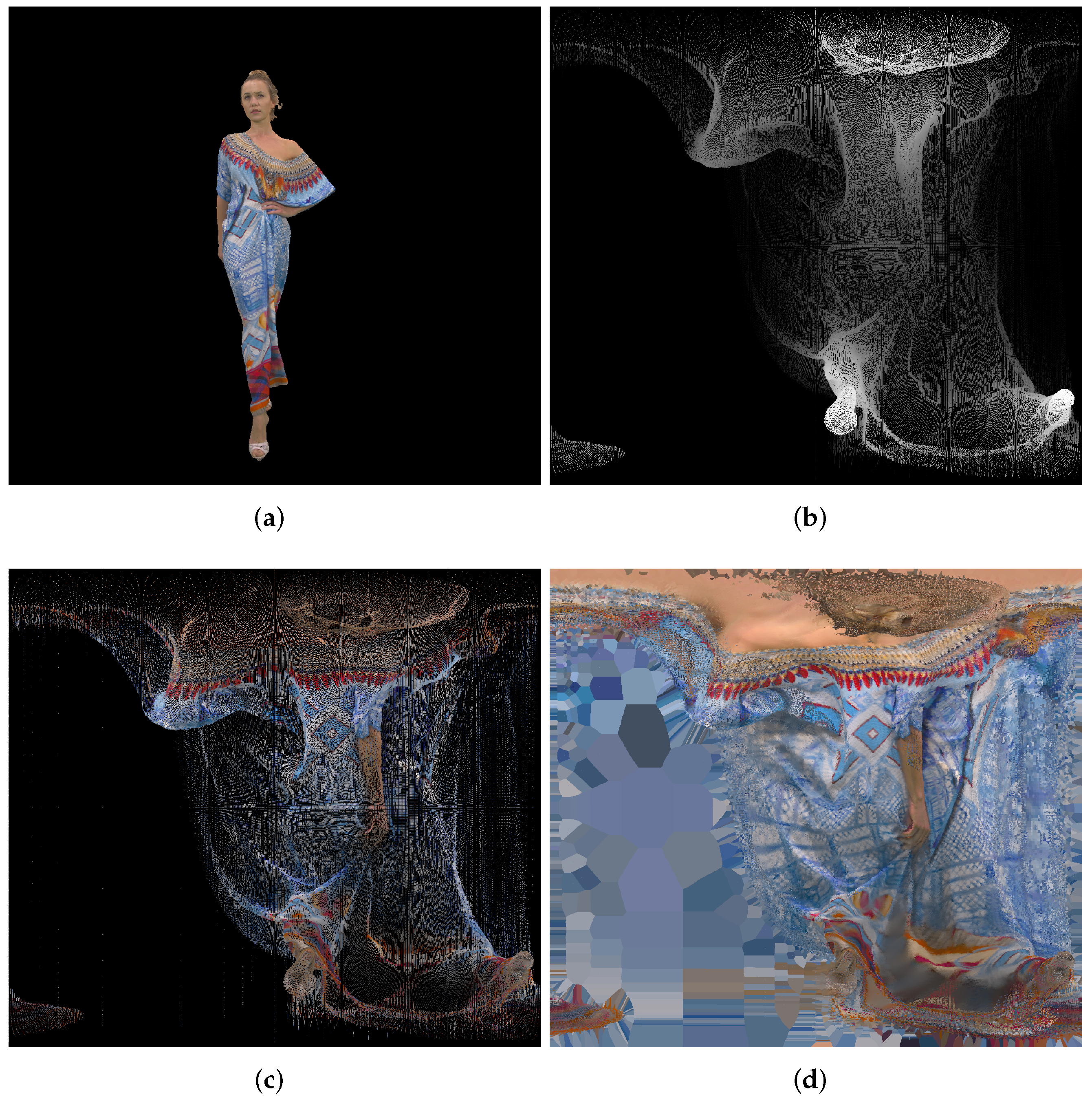




| 1056 × 944 Pixels (Approximately 1,000,000) | Azimuthal | Conic | Cylindrical | Equalareacylindrical | Equirectangular | Mercator | Miller 10-Bit | Miller 9-Bit | Pannini | Rectilinear | Stereographic |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Compressed color average bits per input point (bpp): | 2.2018 | 2.4025 | 3.0207 | 2.7203 | 2.8726 | 2.9612 | 2.9618 | 2.9618 | 2.826 | 2.63 | 2.3026 |
| Compressed range average bits per input point (bpp): | 3.0784 | 2.8992 | 3.4701 | 3.6785 | 4.074 | 3.9306 | 4.7362 | 3.9652 | 3.1382 | 2.7561 | 3.0313 |
| Compressed range+color average bits per input point (bpp): | 5.2803 | 5.3016 | 6.4908 | 6.3987 | 6.9467 | 6.8918 | 7.698 | 6.927 | 5.9642 | 5.386 | 5.3339 |
| Input average bits per input point (binary format) (bpp): | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 |
| Ratio (input bpp)/(compressed bpp) * 100% | 4.4001 | 4.418 | 5.409 | 5.3322 | 5.7888 | 5.7431 | 6.4149 | 5.7724 | 4.9701 | 4.4883 | 4.4448 |
| Compressed video color (Mbps): | 52.514 | 57.2993 | 72.0449 | 64.8792 | 68.5135 | 70.626 | 70.6387 | 70.6387 | 67.3999 | 62.7257 | 54.9167 |
| Compressed video range (Mbps): | 73.4217 | 69.146 | 82.7638 | 87.7325 | 97.1667 | 93.7467 | 112.9608 | 94.5713 | 74.8475 | 65.7331 | 72.2982 |
| Compressed video range+color (Mbps): | 125.9357 | 126.4452 | 154.8087 | 152.6117 | 165.6802 | 164.3727 | 183.5995 | 165.2101 | 142.2474 | 128.4588 | 127.2149 |
| Input point cloud (binary format) (Mbps): | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 |
| Ratio (input Mbps)/(compressed Mbps) * 100% | 4.4001 | 4.4180 | 5.4090 | 5.3322 | 5.7888 | 5.7431 | 6.4149 | 5.7724 | 4.9701 | 4.4883 | 4.4448 |
| 1296 × 1160 Pixels (Approximately 1,500,000) | Azimuthal | Conic | Cylindrical | Equalareacylindrical | Equirectangular | Mercator | Miller 10-Bit | Miller 9-Bit | Pannini | Rectilinear | Stereographic |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Compressed color average bits per input point (bpp): | 3.2534 | 3.4712 | 4.3975 | 3.9488 | 4.2032 | 4.4046 | 4.3085 | 4.3085 | 4.1135 | 3.8306 | 3.4746 |
| Compressed range average bits per input point (bpp): | 4.4431 | 4.1957 | 4.7533 | 5.1534 | 5.7746 | 5.5972 | 6.6708 | 5.6485 | 4.3288 | 3.8173 | 4.5586 |
| Compressed range+color average bits per input point (bpp): | 7.6965 | 7.6669 | 9.1508 | 9.1022 | 9.9778 | 10.0018 | 10.9793 | 9.957 | 8.4423 | 7.6479 | 8.0332 |
| Input average bits per input point (binary format) (bpp): | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 |
| Ratio (input bpp)/(compressed bpp) * 100% | 6.4136 | 6.389 | 7.6255 | 7.585 | 8.3147 | 8.3347 | 9.1493 | 8.2974 | 7.0352 | 6.3732 | 6.6942 |
| Compressed video color (Mbps): | 77.5949 | 82.7901 | 104.881 | 94.18 | 100.2465 | 105.0509 | 102.7599 | 102.7599 | 98.109 | 91.36 | 82.8696 |
| Compressed video range (Mbps): | 105.9685 | 100.0686 | 113.3672 | 122.9091 | 137.726 | 133.4953 | 159.1008 | 134.7181 | 103.2435 | 91.0447 | 108.7247 |
| Compressed video range+color (Mbps): | 183.5634 | 182.8587 | 218.2482 | 217.0891 | 237.9725 | 238.5462 | 261.8607 | 237.4779 | 201.3525 | 182.4047 | 191.5943 |
| Input point cloud (binary format) (Mbps): | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 |
| Ratio (input Mbps)/(compressed Mbps) * 100% | 6.4136 | 6.3890 | 7.6255 | 7.5850 | 8.3147 | 8.3347 | 9.1493 | 8.2974 | 7.0352 | 6.3732 | 6.6942 |
| 1496 ×1344 Pixels (Approximately 2,000,000) | Azimuthal | Conic | Cylindrical | Equalareacylindrical | Equirectangular | Mercator | Miller 10-Bit | Miller 9-Bit | Pannini | Rectilinear | Stereographic |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Compressed color average bits per input point (bpp): | 4.2758 | 4.5804 | 5.6975 | 5.1732 | 5.5685 | 5.675 | 5.669 | 5.669 | 5.3434 | 4.9298 | 4.6411 |
| Compressed range average bits per input point (bpp): | 5.5811 | 5.3118 | 5.8544 | 6.3141 | 7.1576 | 6.9908 | 8.2718 | 7.0543 | 5.348 | 4.7428 | 5.8841 |
| Compressed range+color average bits per input point (bpp): | 9.8569 | 9.8922 | 11.5519 | 11.4873 | 12.7261 | 12.6657 | 13.9409 | 12.7233 | 10.6913 | 9.6726 | 10.5252 |
| Input average bits per input point (binary format) (bpp): | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 | 120.0017 |
| Ratio (input bpp)/(compressed bpp) * 100% | 8.2139 | 8.2434 | 9.6265 | 9.5726 | 10.6049 | 10.5546 | 11.6172 | 10.6026 | 8.9093 | 8.0604 | 8.7709 |
| Compressed video color (Mbps): | 101.9793 | 109.2427 | 135.8868 | 123.3824 | 132.8104 | 135.3498 | 135.2079 | 135.2079 | 127.4406 | 117.5775 | 110.6906 |
| Compressed video range (Mbps): | 133.1103 | 126.6887 | 139.6304 | 150.594 | 170.7107 | 166.7318 | 197.286 | 168.2461 | 127.5504 | 113.1165 | 140.3382 |
| Compressed video range+color (Mbps): | 235.0896 | 235.9314 | 275.5172 | 273.9764 | 303.5211 | 302.0816 | 332.4939 | 303.454 | 254.991 | 230.6941 | 251.0288 |
| Input point cloud (binary format) (Mbps): | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 | 2862.0774 |
| Ratio (input Mbps)/(compressed Mbps) * 100% | 8.2139 | 8.2434 | 9.6265 | 9.5726 | 10.6049 | 10.5546 | 11.6172 | 10.6026 | 8.9093 | 8.0604 | 8.7709 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 4.3569 | 58.5848 | −5.7881 | 1.1374 | 64.4248 | 5.8920 | 795,010 | 260,522 | 32.7697 |
| Conic | 3.8489 | 59.1248 | −4.7080 | 1.0048 | 64.9778 | 6.9979 | 795,010 | 250,454 | 31.5033 |
| Cylindrical | 1.6901 | 62.7506 | 2.5435 | 0.3878 | 69.1378 | 15.3180 | 795,010 | 318,703 | 40.0879 |
| Equalareacylindrical | 3.2290 | 59.8909 | −3.1758 | 0.7819 | 66.0874 | 9.2171 | 795,010 | 283,737 | 35.6897 |
| Equirectangular | 1.8139 | 62.4501 | 1.9426 | 0.4156 | 68.8628 | 14.7679 | 795,010 | 333,865 | 41.9951 |
| Mercator | 1.6177 | 62.9459 | 2.9342 | 0.3677 | 69.3777 | 15.7978 | 795,010 | 344,682 | 43.3557 |
| Miller 10-bit | 1.5704 | 63.0796 | 3.2017 | 0.3505 | 69.5962 | 16.2347 | 795,010 | 345,223 | 43.4237 |
| Miller 9-bit | 1.6200 | 62.9388 | 2.9200 | 0.3686 | 69.3682 | 15.7787 | 795,010 | 345,223 | 43.4237 |
| Pannini | 1.7741 | 62.5377 | 2.1177 | 0.4092 | 68.9031 | 14.8485 | 795,010 | 291,890 | 36.7153 |
| Rectilinear | 1.9423 | 62.1427 | 1.3278 | 0.4655 | 68.3559 | 13.7542 | 795,010 | 260,368 | 32.7503 |
| Stereographic | 3.6261 | 59.3823 | −4.1930 | 0.8135 | 65.9116 | 8.8655 | 795,010 | 283,551 | 35.6663 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 3.4281 | 59.6300 | −3.6976 | 0.8209 | 65.8651 | 8.7725 | 795,010 | 313,372 | 39.4174 |
| Conic | 3.0146 | 60.1911 | −2.5754 | 0.7793 | 66.0917 | 9.2258 | 795,010 | 300,309 | 37.7742 |
| Cylindrical | 1.1212 | 64.5158 | 6.0740 | 0.2697 | 70.6845 | 18.4113 | 795,010 | 389,681 | 49.0159 |
| Equalareacylindrical | 2.4257 | 61.1371 | −0.6835 | 0.5808 | 67.3735 | 11.7893 | 795,010 | 329,721 | 41.4738 |
| Equirectangular | 1.1851 | 64.2722 | 5.5868 | 0.2797 | 70.5251 | 18.0925 | 795,010 | 390,058 | 49.0633 |
| Mercator | 1.0756 | 64.6961 | 6.4347 | 0.2590 | 70.8577 | 18.7578 | 795,010 | 406,907 | 51.1826 |
| Miller 10-bit | 1.0077 | 64.9852 | 7.0127 | 0.2333 | 71.3168 | 19.6760 | 795,010 | 406,868 | 51.1777 |
| Miller 9-bit | 1.0758 | 64.6942 | 6.4308 | 0.2593 | 70.8521 | 18.7466 | 795,010 | 406,868 | 51.1777 |
| Pannini | 1.1853 | 64.2675 | 5.5774 | 0.2849 | 70.4427 | 17.9277 | 795,010 | 359,861 | 45.2650 |
| Rectilinear | 1.3303 | 63.7622 | 4.5667 | 0.3185 | 69.9618 | 16.9659 | 795,010 | 324,548 | 40.8231 |
| Stereographic | 2.5708 | 60.8974 | −1.1628 | 0.5539 | 67.6207 | 12.2838 | 795,010 | 343,921 | 43.2600 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 2.4840 | 61.0363 | −0.8851 | 0.5858 | 67.3331 | 11.7085 | 795,010 | 351,469 | 44.2094 |
| Conic | 2.4327 | 61.1258 | −0.7061 | 0.6254 | 67.0423 | 11.1270 | 795,010 | 334,183 | 42.0351 |
| Cylindrical | 0.8799 | 65.5575 | 8.1574 | 0.2266 | 71.4296 | 19.9015 | 795,010 | 441,458 | 55.5286 |
| Equalareacylindrical | 1.8918 | 62.2127 | 1.4677 | 0.4537 | 68.4265 | 13.8954 | 795,010 | 361,188 | 45.4319 |
| Equirectangular | 0.9269 | 65.3283 | 7.6989 | 0.2354 | 71.2633 | 19.5689 | 795,010 | 428,221 | 53.8636 |
| Mercator | 0.8436 | 65.7380 | 8.5184 | 0.2199 | 71.5590 | 20.1603 | 795,010 | 449,793 | 56.5770 |
| Miller 10-bit | 0.7681 | 66.1541 | 9.3506 | 0.1907 | 72.1825 | 21.4073 | 795,010 | 449,260 | 56.5100 |
| Miller 9-bit | 0.8462 | 65.7263 | 8.4950 | 0.2203 | 71.5502 | 20.1427 | 795,010 | 449,260 | 56.5100 |
| Pannini | 0.9405 | 65.2639 | 7.5701 | 0.2402 | 71.1749 | 19.3922 | 795,010 | 410,965 | 51.6931 |
| Rectilinear | 1.0556 | 64.7615 | 6.5653 | 0.2653 | 70.7451 | 18.5326 | 795,010 | 374,173 | 47.0652 |
| Stereographic | 1.8777 | 62.2770 | 1.5964 | 0.4012 | 69.0208 | 15.0840 | 795,010 | 386,019 | 48.5552 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 3.9483 | 59.2665 | −4.4246 | 3.7950 | 59.4562 | −4.0451 | 795,010 | 1,153,609 | 145.1062 |
| Conic | 3.6778 | 60.0292 | −2.8992 | 3.4638 | 60.3884 | −2.1809 | 795,010 | 1,153,016 | 145.0316 |
| Cylindrical | 1.8932 | 63.1058 | 3.2539 | 1.7200 | 64.0822 | 5.2069 | 795,010 | 1,155,024 | 145.2842 |
| Equalareacylindrical | 3.6355 | 59.5268 | −3.9040 | 3.5119 | 59.6839 | −3.5898 | 795,010 | 1,153,801 | 145.1304 |
| Equirectangular | 1.7756 | 63.3958 | 3.8340 | 1.6544 | 64.0645 | 5.1714 | 795,010 | 1,154,894 | 145.2679 |
| Mercator | 1.6122 | 63.7848 | 4.6119 | 1.4535 | 64.7498 | 6.5421 | 795,010 | 1,154,705 | 145.2441 |
| Miller 10-bit | 1.7871 | 63.3660 | 3.7744 | 1.6477 | 64.1868 | 5.4161 | 795,010 | 1,156,485 | 145.4680 |
| Miller 9-bit | 1.8834 | 63.1429 | 3.3282 | 1.7325 | 64.0029 | 5.0481 | 795,010 | 1,155,006 | 145.2819 |
| Pannini | 2.1112 | 62.6956 | 2.4336 | 1.9620 | 63.4910 | 4.0243 | 795,010 | 1,155,073 | 145.2904 |
| Rectilinear | 2.0828 | 62.6544 | 2.3512 | 1.9141 | 63.4887 | 4.0197 | 795,010 | 1,154,906 | 145.2694 |
| Stereographic | 3.5426 | 59.6347 | −3.6883 | 3.4265 | 59.7821 | −3.3934 | 795,010 | 1,155,261 | 145.3140 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 3.4226 | 59.8245 | −3.3087 | 3.2923 | 60.0029 | −2.9519 | 795,010 | 1,153,402 | 145.0802 |
| Conic | 3.0916 | 60.6366 | −1.6844 | 2.9537 | 60.8878 | −1.1820 | 795,010 | 1,152,742 | 144.9972 |
| Cylindrical | 1.3590 | 65.7201 | 8.4825 | 1.2248 | 67.0806 | 11.2035 | 795,010 | 1,154,542 | 145.2236 |
| Equalareacylindrical | 3.3320 | 60.1398 | −2.6780 | 3.2203 | 60.3042 | −2.3493 | 795,010 | 1,153,681 | 145.1153 |
| Equirectangular | 0.9471 | 66.7002 | 10.4428 | 0.8230 | 67.9619 | 12.9661 | 795,010 | 1,154,483 | 145.2162 |
| Mercator | 0.6504 | 68.1203 | 13.2829 | 0.5124 | 69.8651 | 16.7726 | 795,010 | 1,154,466 | 145.2140 |
| Miller 10-bit | 0.8328 | 67.7035 | 12.4494 | 0.7035 | 69.2895 | 15.6213 | 795,010 | 1,156,160 | 145.4271 |
| Miller 9-bit | 0.9335 | 67.2952 | 11.6327 | 0.8016 | 68.8654 | 14.7731 | 795,010 | 1,154,383 | 145.2036 |
| Pannini | 1.1857 | 65.9413 | 8.9250 | 1.0427 | 67.3226 | 11.6876 | 795,010 | 1,154,553 | 145.2250 |
| Rectilinear | 1.3954 | 64.9695 | 6.9813 | 1.2327 | 66.2226 | 9.4875 | 795,010 | 1,154,607 | 145.2318 |
| Stereographic | 2.4495 | 61.1509 | −0.6558 | 2.3639 | 61.3091 | −0.3394 | 795,010 | 1,155,021 | 145.2838 |
| Average Input Points | Average Output Points | Output/Input | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Azimuthal | 3.5851 | 59.9790 | −2.9997 | 3.4530 | 60.1616 | −2.6345 | 795,010 | 1,153,094 | 145.0414 |
| Conic | 4.0596 | 59.8137 | −3.3304 | 3.9061 | 60.0175 | −2.9226 | 795,010 | 1,152,734 | 144.9962 |
| Cylindrical | 0.3314 | 69.8545 | 16.7514 | 0.2215 | 71.6639 | 20.3702 | 795,010 | 1,154,352 | 145.1997 |
| Equalareacylindrical | 3.1122 | 60.9044 | −1.1489 | 3.0077 | 61.0880 | −0.7816 | 795,010 | 1,153,599 | 145.1050 |
| Equirectangular | 0.9305 | 67.6623 | 12.3669 | 0.8296 | 69.0639 | 15.1701 | 795,010 | 1,154,520 | 145.2208 |
| Mercator | 0.7053 | 68.7747 | 14.5918 | 0.6102 | 70.3353 | 17.7129 | 795,010 | 1,154,439 | 145.2106 |
| Miller 10-bit | 0.4555 | 69.8594 | 16.7611 | 0.3619 | 71.5899 | 20.2221 | 795,010 | 1,156,008 | 145.4080 |
| Miller 9-bit | 0.4522 | 69.8166 | 16.6757 | 0.3492 | 71.6585 | 20.3594 | 795,010 | 1,154,324 | 145.1962 |
| Pannini | 0.5384 | 68.7913 | 14.6249 | 0.4139 | 70.5697 | 18.1817 | 795,010 | 1,154,358 | 145.2004 |
| Rectilinear | 1.2472 | 66.2188 | 9.4800 | 1.1264 | 67.5502 | 12.1428 | 795,010 | 1,154,410 | 145.2070 |
| Stereographic | 2.8045 | 61.1347 | −0.6883 | 2.6960 | 61.3675 | −0.2226 | 795,010 | 1,155,019 | 145.2836 |
| Timing Performance | Seconds per Point Cloud | Seconds per 20 Point Clouds |
|---|---|---|
| Point cloud to panorama: | 1.9030 | 38.0603 |
| Compression (texture): | - | 117.3344 |
| Decompression (texture): | - | 2.0918 |
| Compression (geometry): | - | 0.9477 |
| Decompression (geometry): | - | 1.2366 |
| Panorama to point cloud: | 4.9350 | 98.6991 |
| Normal calculation (CloudCompare): | 6.2539 | 125.0783 |
| Poisson reconstruction and upsampling (MeshLab): | 97.0496 | 1941.0 |
| Longdress, R = 1 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 230,014 | 427,083 | 575,585 | 698,867 | 761,164 | 793,732 | 794,969 | 795,009 |
| Average size of .oct file, bytes: | 3,684,335 | 6,837,436 | 9,213,473 | 11,185,991 | 12,182,742 | 12,703,824 | 12,723,616 | 12,724,261 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 37.0746 | 68.8035 | 92.7130 | 112.5620 | 122.5921 | 127.8356 | 128.0348 | 128.0413 |
| : | 0.7755 | 0.4700 | 0.2766 | 0.1209 | 0.0426 | 0.0016 | 0.0001 | 0.0000 |
| : | 66.0727 | 68.2475 | 70.5507 | 74.1436 | 78.6783 | 92.9780 | 108.5374 | Inf |
| : | 9.1877 | 13.5374 | 18.1437 | 25.3295 | 34.3989 | 62.9984 | 94.1172 | Inf |
| : | 0.2547 | 0.1700 | 0.1012 | 0.0499 | 0.0178 | 0.0007 | 0.0000 | 0.0000 |
| : | 70.9081 | 72.6655 | 74.9173 | 77.9851 | 82.4677 | 96.4049 | 112.7170 | Inf |
| : | 18.8587 | 22.3734 | 26.8770 | 33.0126 | 41.9778 | 69.8522 | 102.4764 | Inf |
| Longdress, R = 2 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 60,161 | 116,599 | 170,613 | 222,186 | 270,673 | 317,488 | 362,572 | 406,039 |
| Average size of .oct file, bytes: | 966,646 | 1,869,673 | 2,733,914 | 3,559,090 | 4,334,882 | 5,083,923 | 5,805,268 | 6,500,740 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 9.7271 | 18.8141 | 27.5107 | 35.8143 | 43.6209 | 51.1583 | 58.4171 | 65.4154 |
| : | 1.5428 | 1.1679 | 0.9701 | 0.8358 | 0.7339 | 0.6492 | 0.5757 | 0.5099 |
| : | 63.0855 | 64.2946 | 65.1006 | 65.7477 | 66.3126 | 66.8453 | 67.3669 | 67.8937 |
| : | 3.2134 | 5.6316 | 7.2437 | 8.5378 | 9.6676 | 10.7330 | 11.7762 | 12.8298 |
| : | 0.3484 | 0.3121 | 0.2846 | 0.2599 | 0.2369 | 0.2152 | 0.1945 | 0.1748 |
| : | 69.5486 | 70.0257 | 70.4259 | 70.8213 | 71.2238 | 71.6410 | 72.0803 | 72.5437 |
| : | 16.1395 | 17.0939 | 17.8941 | 18.6850 | 19.4899 | 20.3244 | 21.2030 | 22.1299 |
| Redandblack, R = 1 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 211,582 | 389,317 | 517,726 | 620,888 | 672,157 | 699,481 | 701,144 | 701,234 |
| Average size of .oct file, bytes: | 3,389,106 | 6,232,878 | 8,287,429 | 9,938,021 | 10,758,325 | 11,195,502 | 11,222,110 | 11,223,546 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 34.1038 | 62.7200 | 83.3945 | 100.0040 | 108.2585 | 112.6577 | 112.9255 | 112.9399 |
| Symmetric rmsF p2p: | 0.7591 | 0.4515 | 0.2622 | 0.1146 | 0.0415 | 0.0025 | 0.0001 | 0.0000 |
| Symmetric PSNR_1 p2p: | 66.1656 | 68.4226 | 70.7825 | 74.3788 | 78.7935 | 90.9982 | 103.9500 | Inf |
| Symmetric PSNR_2 p2p: | 10.4646 | 14.9786 | 19.6983 | 26.8910 | 35.7204 | 60.1298 | 86.0333 | Inf |
| Symmetric rmsF p2pl: | 0.2497 | 0.1630 | 0.0955 | 0.0472 | 0.0173 | 0.0011 | 0.0000 | 0.0000 |
| Symmetric PSNR_1 p2pl: | 70.9956 | 72.8476 | 75.1677 | 78.2340 | 82.5916 | 94.4710 | 108.0630 | Inf |
| Symmetric PSNR_2 p2pl: | 20.1246 | 23.8286 | 28.4687 | 34.6014 | 43.3166 | 67.0754 | 94.2595 | Inf |
| Redandblack, R = 2 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 55,189 | 106,830 | 156,077 | 202,877 | 246,949 | 289,386 | 330,106 | 369,273 |
| Average size of .oct file, bytes: | 886,801 | 1,713,077 | 2,501,036 | 3,249,837 | 3,954,998 | 4,633,979 | 5,285,505 | 5,912,168 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 8.9237 | 17.2383 | 25.1673 | 32.7023 | 39.7982 | 46.6306 | 53.1868 | 59.4928 |
| Symmetric rmsF p2p: | 1.5165 | 1.1475 | 0.9520 | 0.8189 | 0.7171 | 0.6323 | 0.5586 | 0.4924 |
| Symmetric PSNR_1 p2p: | 63.1605 | 64.3712 | 65.1824 | 65.8364 | 66.4132 | 66.9598 | 67.4984 | 68.0461 |
| Symmetric PSNR_2 p2p: | 4.4544 | 6.8758 | 8.4982 | 9.8061 | 10.9599 | 12.0530 | 13.1301 | 14.2255 |
| Symmetric rmsF p2pl: | 0.3515 | 0.3120 | 0.2826 | 0.2568 | 0.2330 | 0.2106 | 0.1894 | 0.1694 |
| Symmetric PSNR_1 p2pl: | 69.5091 | 70.0272 | 70.4576 | 70.8731 | 71.2956 | 71.7355 | 72.1946 | 72.6804 |
| Symmetric PSNR_2 p2pl: | 17.1515 | 18.1877 | 19.0486 | 19.8797 | 20.7245 | 21.6044 | 22.5225 | 23.4941 |
| Soldier, R = 1 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 298,525 | 554,593 | 753,226 | 920,279 | 1,011,060 | 1,058,928 | 1,060,749 | 1,060,770 |
| Average size of .oct file, bytes: | 4,781,816 | 8,878,917 | 12,057,034 | 14,729,884 | 16,182,391 | 16,948,270 | 16,977,416 | 16,977,739 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 48.1183 | 89.3465 | 121.3271 | 148.2234 | 162.8396 | 170.5465 | 170.8398 | 170.8430 |
| Symmetric rmsF p2p: | 0.7867 | 0.4851 | 0.2906 | 0.1324 | 0.0469 | 0.0017 | 0.0000 | 0.0000 |
| Symmetric PSNR_1 p2p: | 66.0108 | 68.1101 | 70.3362 | 73.7484 | 78.2606 | 92.5742 | 112.3807 | Inf |
| Symmetric PSNR_2 p2p: | 6.5947 | 10.7933 | 15.2455 | 22.0699 | 31.0944 | 59.7214 | 99.3344 | Inf |
| Symmetric rmsF p2pl: | 0.2672 | 0.1826 | 0.1110 | 0.0557 | 0.0199 | 0.0008 | 0.0000 | 0.0000 |
| Symmetric PSNR_1 p2pl: | 70.7010 | 72.3536 | 74.5152 | 77.5116 | 81.9802 | 95.8459 | 116.2297 | Inf |
| Symmetric PSNR_2 p2pl: | 15.9752 | 19.2803 | 23.6035 | 29.5964 | 38.5334 | 66.2649 | 107.0324 | Inf |
| Soldier, R = 2 | O = 1 | O = 2 | O = 3 | O = 4 | O = 5 | O = 6 | O = 7 | O = 8 |
|---|---|---|---|---|---|---|---|---|
| Average number of output points: | 78,169 | 151,269 | 221,122 | 287,916 | 350,702 | 411,306 | 469,731 | 526,048 |
| Average size of .oct file, bytes: | 1,256,069 | 2,425,706 | 3,543,359 | 4,612,076 | 5,616,648 | 6,586,314 | 7,521,122 | 8,422,194 |
| Average number of input points: | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 | 795,010 |
| Average bits per input point: | 12.6395 | 24.4093 | 35.6560 | 46.4102 | 56.5190 | 66.2765 | 75.6833 | 84.7506 |
| Symmetric rmsF p2p: | 1.5565 | 1.1815 | 0.9842 | 0.8503 | 0.7489 | 0.6649 | 0.5922 | 0.5272 |
| Symmetric PSNR_1 p2p: | 63.0473 | 64.2443 | 65.0378 | 65.6730 | 66.2245 | 66.7409 | 67.2443 | 67.7490 |
| Symmetric PSNR_2 p2p: | 0.6678 | 3.0617 | 4.6487 | 5.9190 | 7.0221 | 8.0549 | 9.0618 | 10.0711 |
| Symmetric rmsF p2pl: | 0.3544 | 0.3203 | 0.2942 | 0.2705 | 0.2483 | 0.2271 | 0.2067 | 0.1871 |
| Symmetric PSNR_1 p2pl: | 69.4744 | 69.9128 | 70.2828 | 70.6468 | 71.0190 | 71.4072 | 71.8164 | 72.2488 |
| Symmetric PSNR_2 p2pl: | 13.5218 | 14.3986 | 15.1387 | 15.8666 | 16.6112 | 17.3875 | 18.2058 | 19.0707 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumic, E.; Bjelopera, A.; Nüchter, A. Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression. Sensors 2022, 22, 197. https://doi.org/10.3390/s22010197
Dumic E, Bjelopera A, Nüchter A. Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression. Sensors. 2022; 22(1):197. https://doi.org/10.3390/s22010197
Chicago/Turabian StyleDumic, Emil, Anamaria Bjelopera, and Andreas Nüchter. 2022. "Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression" Sensors 22, no. 1: 197. https://doi.org/10.3390/s22010197
APA StyleDumic, E., Bjelopera, A., & Nüchter, A. (2022). Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression. Sensors, 22(1), 197. https://doi.org/10.3390/s22010197








