Shack-Hartmann Wavefront Sensing of Ultrashort Optical Vortices
Abstract
1. Introduction
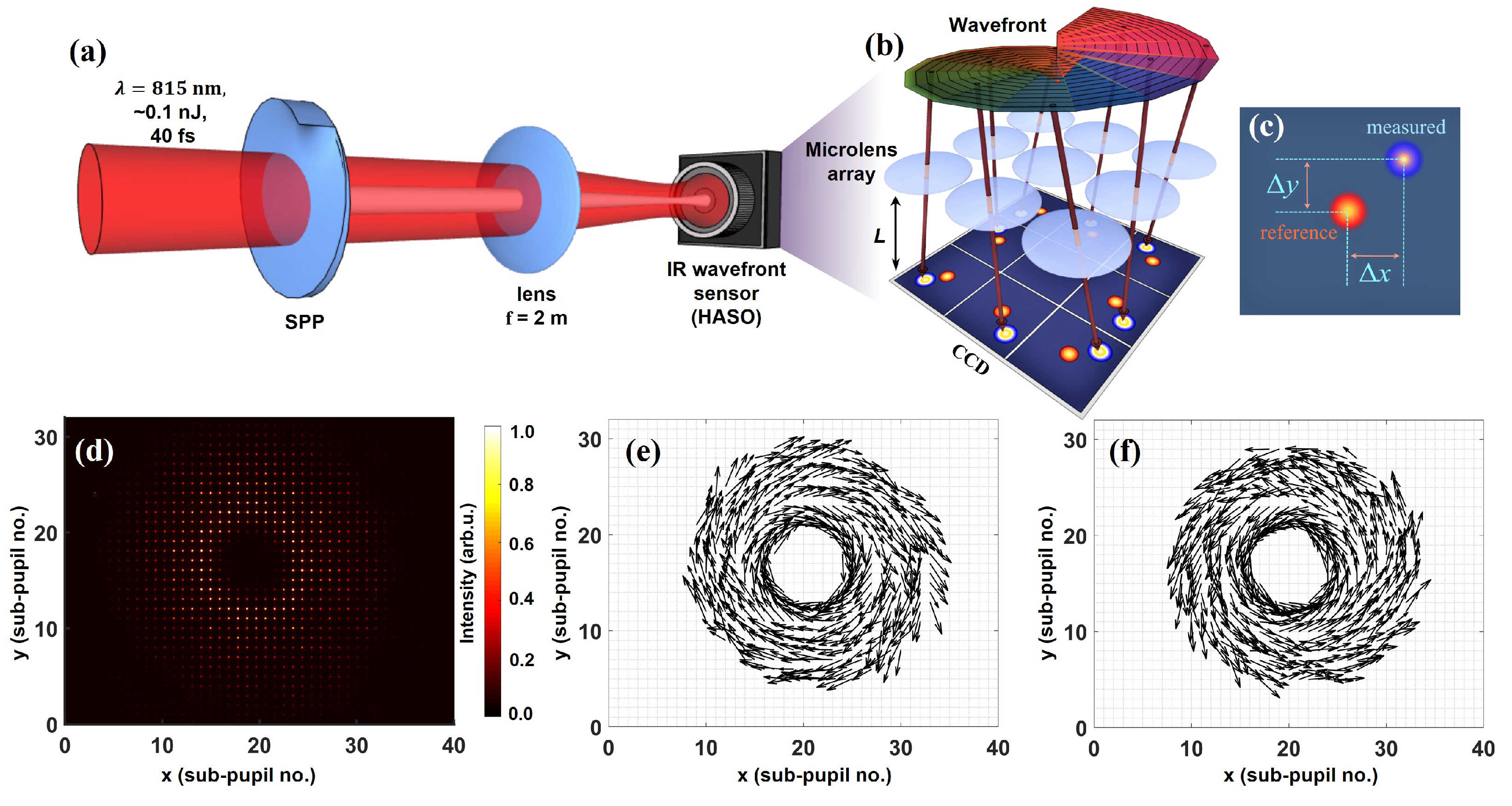
2. Experimental Setup and Methods for Wavefront Characterization of Ultrashort Vortex Beams
Optical Vortex Detection and Wavefront Reconstruction
3. Results
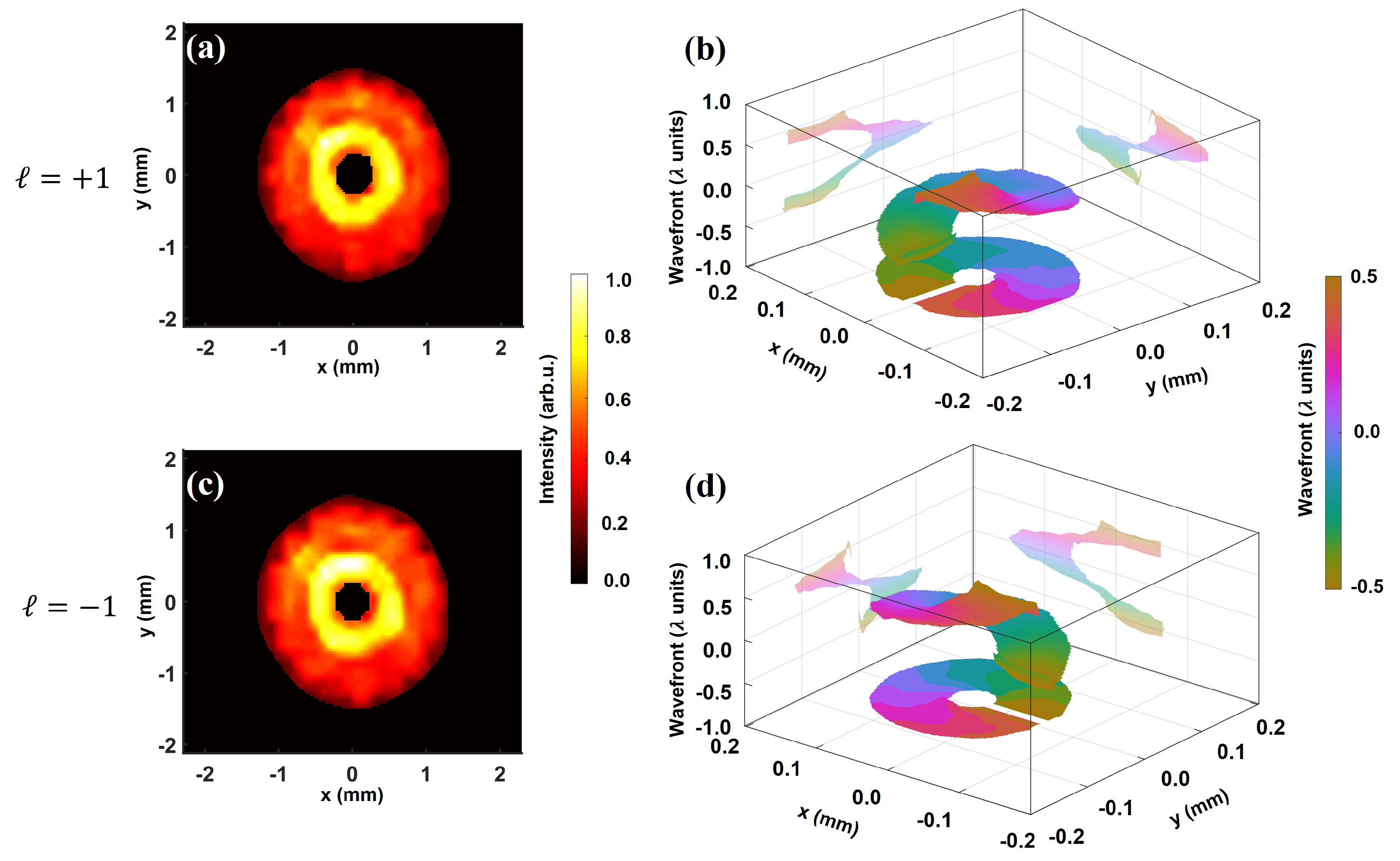
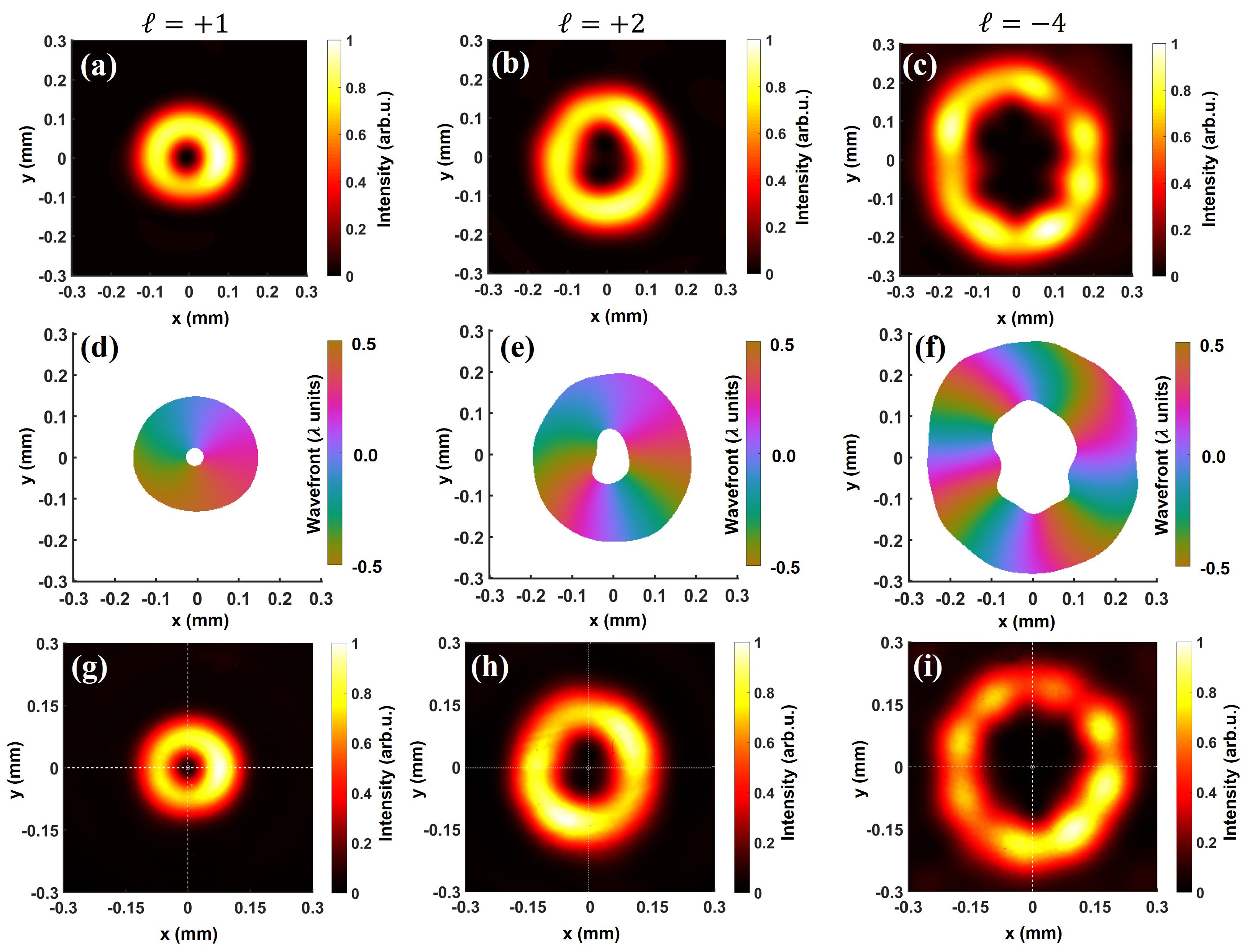
3.1. Intensity and Wavefront Characterization of Ultrashort Vortex Beams
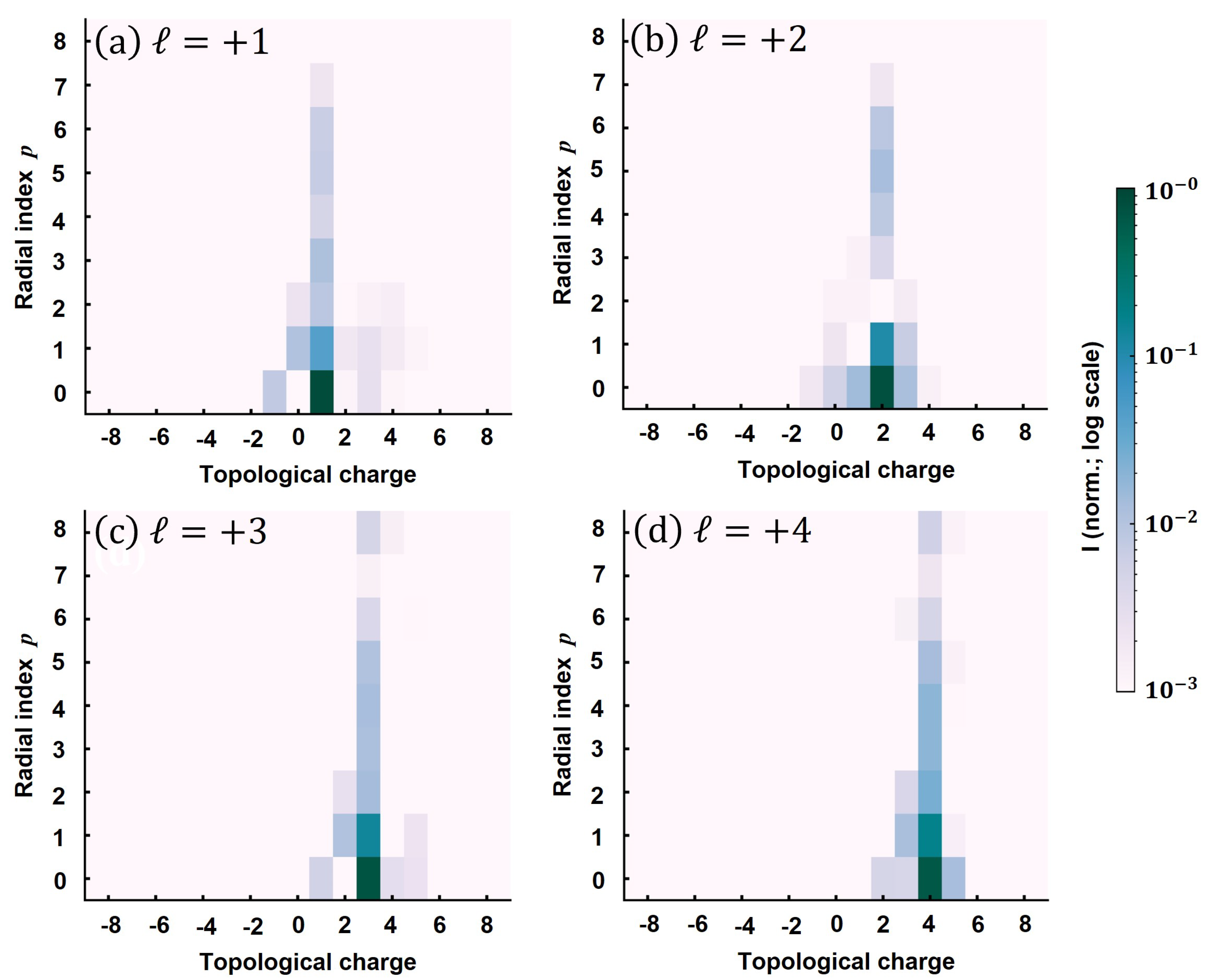
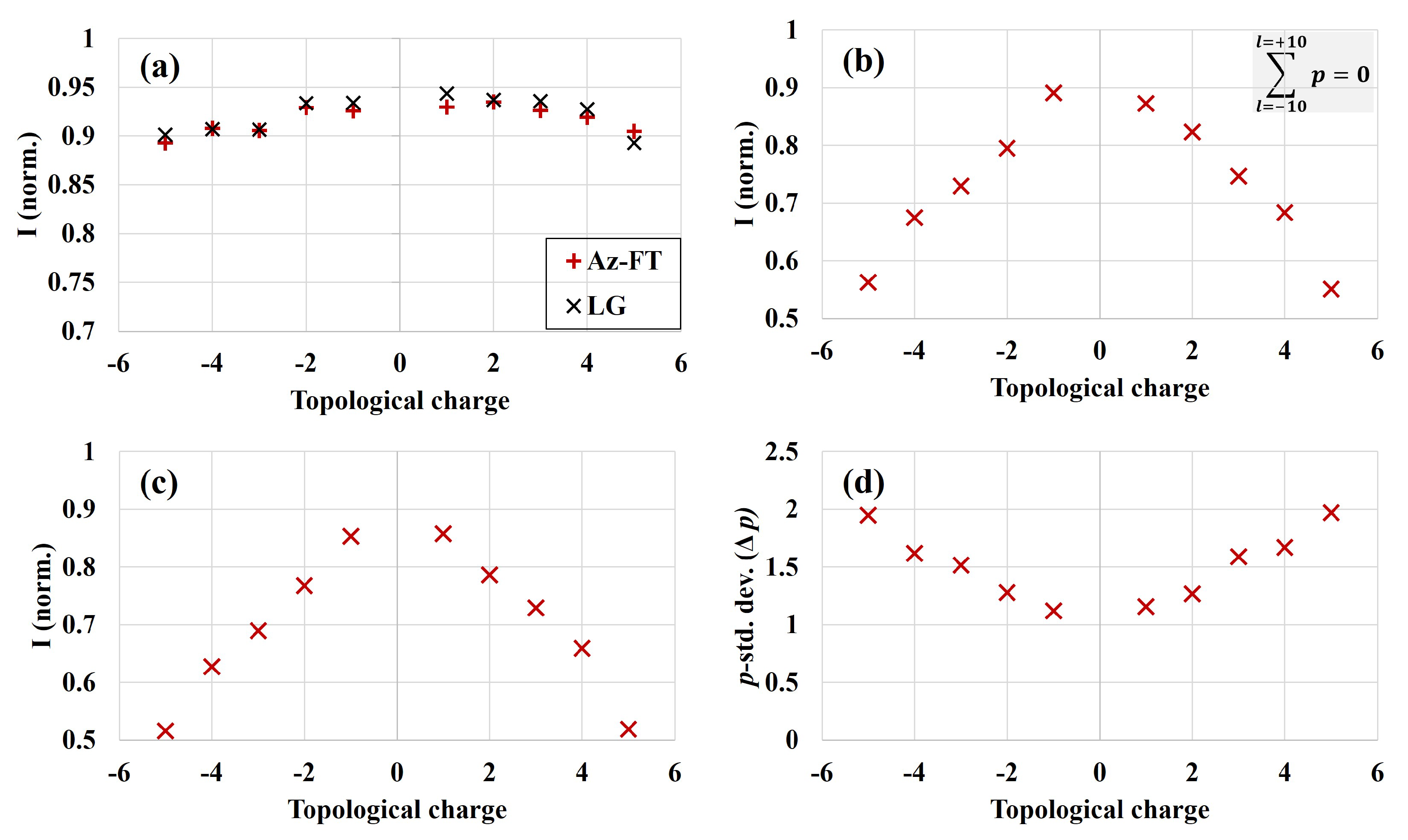
3.2. Modal Purity of the Vortex Beams
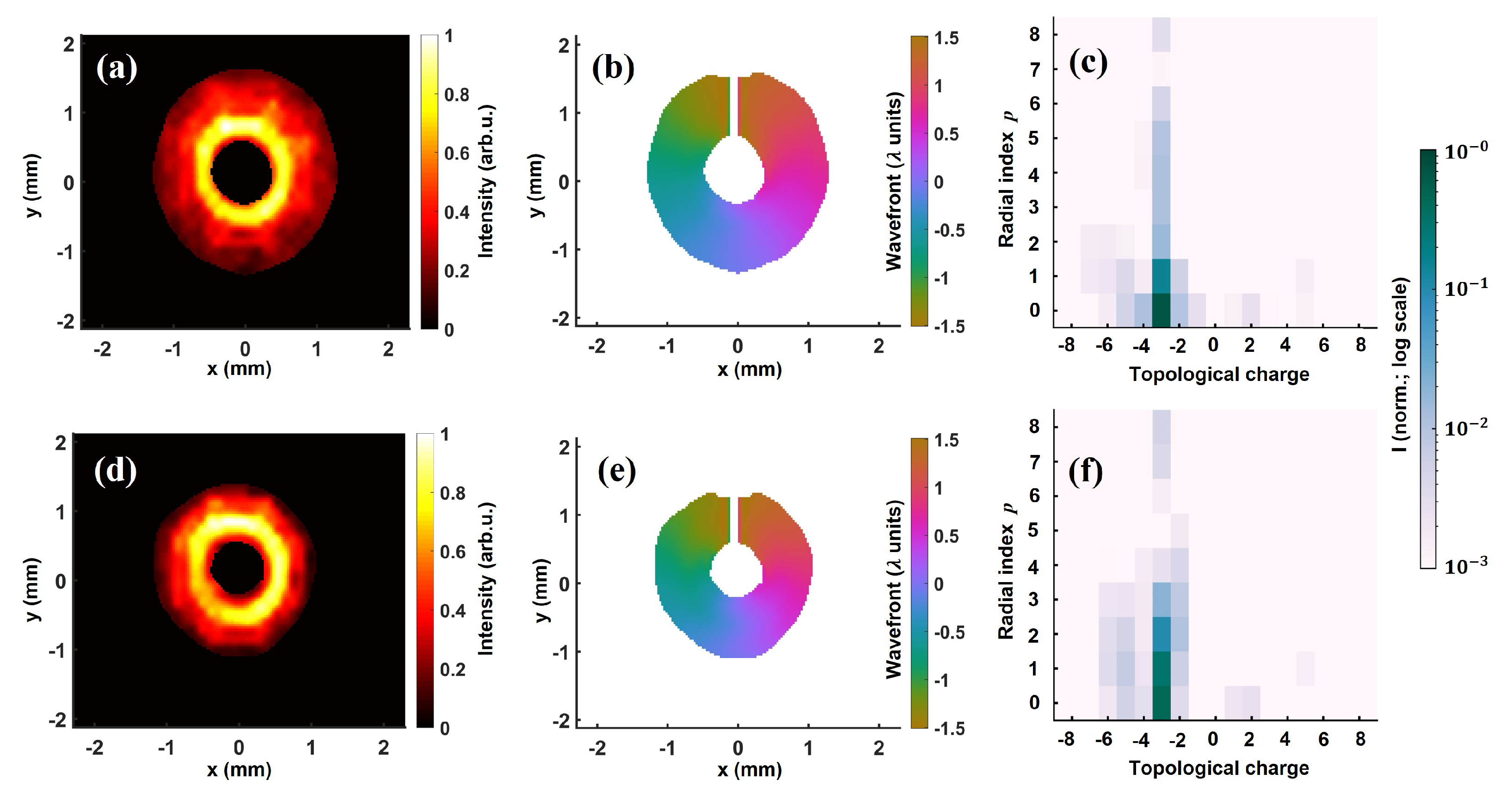
3.3. Effect of Radial Aperturing on Modal Content
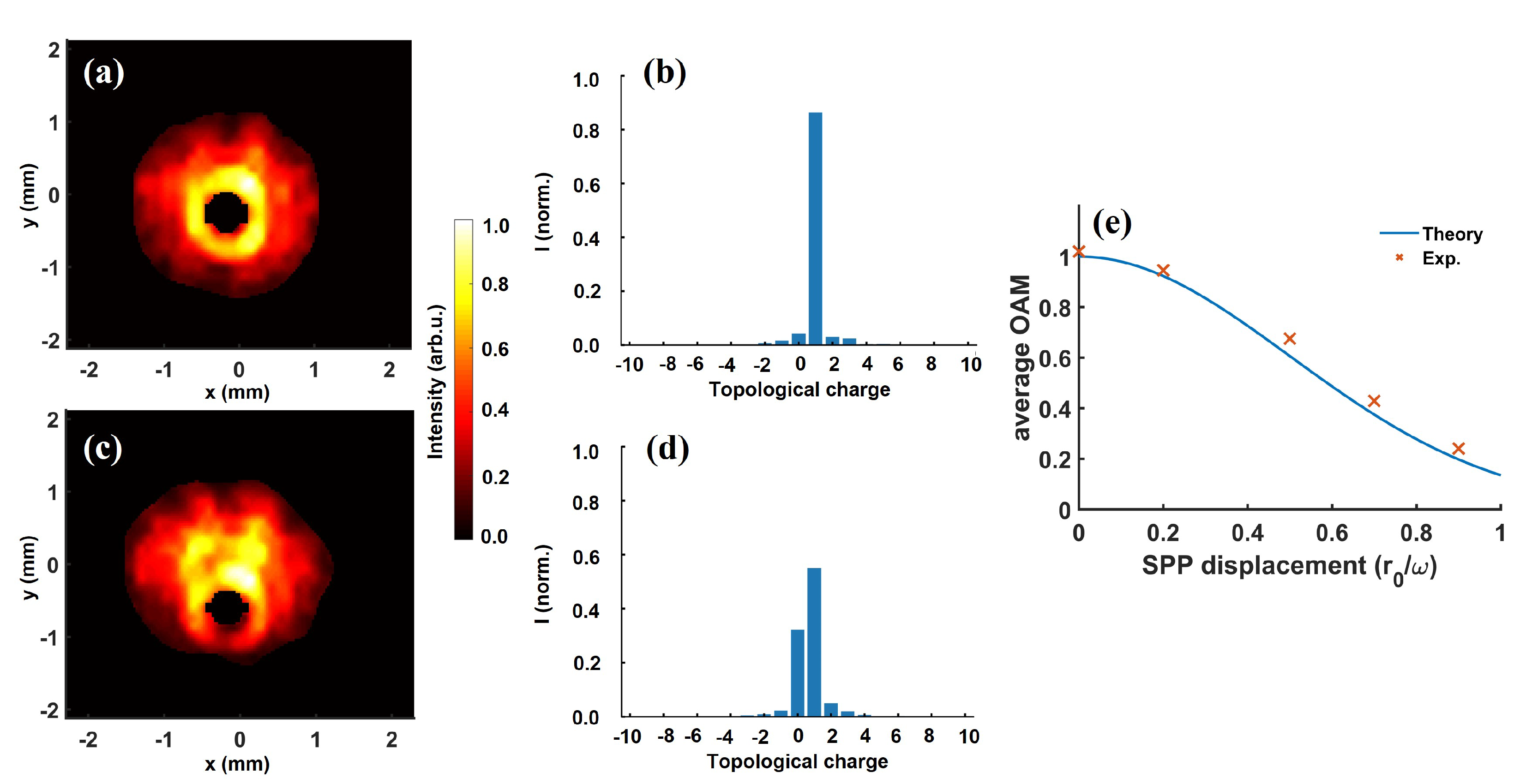
3.4. Effect of Spiral Phase Plate Displacement on the Modal Composition
3.5. Topological Charge Measurement at 10 Hz
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Molina-Terriza, G.; Vaziri, A.; Řeháček, J.; Hradil, Z.; Zeilinger, A. Triggered Qutrits for Quantum Communication Protocols. Phys. Rev. Lett. 2004, 92, 167903. [Google Scholar] [CrossRef]
- Iketaki, Y.; Bokor, N. Super-resolution microscope using a two-color phase plate for generating quasi-Laguerre–Gaussian beam. Opt. Commun. 2012, 285, 3798–3804. [Google Scholar] [CrossRef]
- Vicidomini, G.; Bianchini, P.; Diaspro, A. STED super-resolved microscopy. Nat. Methods 2018, 15, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Gahagan, K.T.; Swartzlander, G.A. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using Optical Vortex To Control the Chirality of Twisted Metal Nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef] [PubMed]
- Syubaev, S.; Zhizhchenko, A.; Kuchmizhak, A.; Porfirev, A.; Pustovalov, E.; Vitrik, O.; Kulchin, Y.; Khonina, S.; Kudryashov, S. Direct laser printing of chiral plasmonic nanojets by vortex beams. Opt. Express 2017, 25, 10214–10223. [Google Scholar] [CrossRef]
- Berkhout, G.C.G.; Beijersbergen, M.W. Method for Probing the Orbital Angular Momentum of Optical Vortices in Electromagnetic Waves from Astronomical Objects. Phys. Rev. Lett. 2008, 101, 100801. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Molina-Terriza, G.; Anzolin, G. Twisting of light around rotating black holes. Nat. Phys. 2011, 7, 195–197. [Google Scholar] [CrossRef]
- Sederberg, S.; Kong, F.; Hufnagel, F.; Zhang, C.; Karimi, E.; Corkum, P.B. Vectorized optoelectronic control and metrology in a semiconductor. Nat. Photonics 2020, 14, 680–685. [Google Scholar] [CrossRef]
- Jana, K.; Herperger, K.R.; Kong, F.; Mi, Y.; Zhang, C.; Corkum, P.B.; Sederberg, S. Reconfigurable electronic circuits for magnetic fields controlled by structured light. Nat. Photonics 2021, 15, 622–626. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef]
- De Ninno, G.; Wätzel, J.; Ribič, P.R.; Allaria, E.; Coreno, M.; Danailov, M.B.; David, C.; Demidovich, A.; Di Fraia, M.; Giannessi, L.; et al. Photoelectric effect with a twist. Nat. Photonics 2020, 14, 554–558. [Google Scholar] [CrossRef]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef]
- Fanciulli, M.; Bresteau, D.; Vimal, M.; Luttmann, M.; Sacchi, M.; Ruchon, T. Electromagnetic theory of helicoidal dichroism in reflection from magnetic structures. Phys. Rev. A 2021, 103, 013501. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Harris, M.; Hill, C.; Vaughan, J. Optical helices and spiral interference fringes. Opt. Commun. 1994, 106, 161–166. [Google Scholar] [CrossRef]
- Soskin, M.S.; Gorshkov, V.N.; Vasnetsov, M.V.; Malos, J.T.; Heckenberg, N.R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 1997, 56, 4064–4075. [Google Scholar] [CrossRef]
- Leach, J.; Courtial, J.; Skeldon, K.; Barnett, S.M.; Franke-Arnold, S.; Padgett, M.J. Interferometric Methods to Measure Orbital and Spin, or the Total Angular Momentum of a Single Photon. Phys. Rev. Lett. 2004, 92, 013601. [Google Scholar] [CrossRef] [PubMed]
- Hickmann, J.M.; Fonseca, E.J.S.; Soares, W.C.; Chávez-Cerda, S. Unveiling a Truncated Optical Lattice Associated with a Triangular Aperture Using Light’s Orbital Angular Momentum. Phys. Rev. Lett. 2010, 105, 053904. [Google Scholar] [CrossRef] [PubMed]
- Mourka, A.; Baumgartl, J.; Shanor, C.; Dholakia, K.; Wright, E.M. Visualization of the birth of an optical vortex using diffraction from a triangular aperture. Opt. Express 2011, 19, 5760–5771. [Google Scholar] [CrossRef]
- Mazilu, M.; Mourka, A.; Vettenburg, T.; Wright, E.M.; Dholakia, K. Simultaneous determination of the constituent azimuthal and radial mode indices for light fields possessing orbital angular momentum. Appl. Phys. Lett. 2012, 100, 231115. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J. Measuring Orbital Angular Momentum (OAM) States of Vortex Beams with Annular Gratings. Sci. Rep. 2017, 7, 40781. [Google Scholar] [CrossRef] [PubMed]
- Alperin, S.N.; Niederriter, R.D.; Gopinath, J.T.; Siemens, M.E. Quantitative measurement of the orbital angular momentum of light with a single, stationary lens. Opt. Lett. 2016, 41, 5019–5022. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.G.; Permangatt, C.; Prabhakar, S.; Anwar, A.; Banerji, J.; Singh, R.P. Divergence of optical vortex beams. Appl. Opt. 2015, 54, 6690–6693. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, S.J.; Zhu, F.Q.; Shao, W.; Chen, M.S. Dimensional properties of Laguerre–Gaussian vortex beams. Appl. Opt. 2017, 56, 3556–3561. [Google Scholar] [CrossRef]
- Ohtake, Y.; Ando, T.; Fukuchi, N.; Matsumoto, N.; Ito, H.; Hara, T. Universal generation of higher-order multiringed Laguerre-Gaussian beams by using a spatial light modulator. Opt. Lett. 2007, 32, 1411–1413. [Google Scholar] [CrossRef] [PubMed]
- Beijersbergen, M.; Coerwinkel, R.; Kristensen, M.; Woerdman, J. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for high intensity laser pulses. Opt. Express 2004, 12, 3548–3553. [Google Scholar] [CrossRef] [PubMed]
- Longman, A.; Fedosejevs, R. Mode conversion efficiency to Laguerre-Gaussian OAM modes using spiral phase optics. Opt. Express 2017, 25, 17382–17392. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Romanato, F. Generation of high-order Laguerre–Gaussian modes by means of spiral phase plates. Opt. Lett. 2014, 39, 5094–5097. [Google Scholar] [CrossRef]
- Janicijevic, L.; Topuzoski, S. Gaussian laser beam transformation into an optical vortex beam by helical lens. J. Mod. Opt. 2016, 63, 164–176. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Pre-turbulence compensation of orbital angular momentum beams based on a probe and the Gerchberg–Saxton algorithm. Opt. Lett. 2016, 41, 3185–3188. [Google Scholar] [CrossRef]
- Chang, H.; Yin, X.L.; Cui, X.Z.; Zhang, Z.C.; Ma, J.X.; Wu, G.H.; Zhang, L.J.; Xin, X.J. Adaptive optics compensation of orbital angular momentum beams with a modified Gerchberg–Saxton-based phase retrieval algorithm. Opt. Commun. 2017, 405, 271–275. [Google Scholar] [CrossRef]
- Esashi, Y.; Liao, C.T.; Wang, B.; Brooks, N.; Dorney, K.M.; Hernández-García, C.; Kapteyn, H.; Adams, D.; Murnane, M. Ptychographic amplitude and phase reconstruction of bichromatic vortex beams. Opt. Express 2018, 26, 34007–34015. [Google Scholar] [CrossRef]
- Yamane, K.; Yang, Z.; Toda, Y.; Morita, R. Frequency-resolved measurement of the orbital angular momentum spectrum of femtosecond ultra-broadband optical-vortex pulses based on field reconstruction. New J. Phys. 2014, 16, 053020. [Google Scholar] [CrossRef]
- D’Errico, A.; D’Amelio, R.; Piccirillo, B.; Cardano, F.; Marrucci, L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams. Optica 2017, 4, 1350–1357. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the Orbital Angular Momentum of a Single Photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef] [PubMed]
- Vasnetsov, M.V.; Torres, J.P.; Petrov, D.V.; Torner, L. Observation of the orbital angular momentum spectrum of a light beam. Opt. Lett. 2003, 28, 2285–2287. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Yan, J.; Hao, H.; Wu, Y.K. Phase retrieval for short wavelength orbital angular momentum beams using knife-edge diffraction. Opt. Commun. 2020, 474, 126077. [Google Scholar] [CrossRef]
- Kulkarni, G.; Sahu, R.; Magaña-Loaiza, O.S.; Boyd, R.W.; Jha, A.K. Single-shot measurement of the orbital-angular-momentum spectrum of light. Nat. Commun. 2017, 8, 1054. [Google Scholar] [CrossRef]
- Neal, D.R.; Copland, J.; Neal, D.A. Shack-Hartmann wavefront sensor precision and accuracy. In Proceedings of the Advanced Characterization Techniques for Optical, Semiconductor, and Data Storage Components, Seattle, WA, USA, 11 November 2002. [Google Scholar] [CrossRef]
- Chernyshov, A.; Sterr, U.; Riehle, F.; Helmcke, J.; Pfund, J. Calibration of a Shack–Hartmann sensor for absolute measurements of wavefronts. Appl. Opt. 2005, 44, 6419–6425. [Google Scholar] [CrossRef]
- Pandey, A.K.; Guilbaud, O.; Sanson, F.; Papagiannouli, I.; Kabacinski, A.; Tissandier, F.; Harms, F.; Beaugrand, G.; Dovillaire, G.; Baynard, E.; et al. Single-shot wavefront characterization of high topological charge extreme-ultraviolet vortex. In Proceedings of the International Conference on X-ray Lasers 2020, Online, 8–10 December 2020. [Google Scholar] [CrossRef]
- Sanson, F.; Pandey, A.K.; Papagiannouli, I.; Harms, F.; Dovillaire, G.; Baynard, E.; Demailly, J.; Guilbaud, O.; Lucas, B.; Neveu, O.; et al. Highly multimodal structure of high topological charge extreme ultraviolet vortex beams. Opt. Lett. 2020, 45, 4790–4793. [Google Scholar] [CrossRef]
- Leach, J.; Keen, S.; Padgett, M.J.; Saunter, C.; Love, G.D. Direct measurement of the skew angle of the Poynting vector in a helically phased beam. Opt. Express 2006, 14, 11919–11924. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, H.; Matsui, Y.; Tanaka, H.; Toyoda, H.; Inoue, T.; Liu, H. Aberration-resistible topological charge determination of annular-shaped optical vortex beams using Shack–Hartmann wavefront sensor. Opt. Express 2019, 27, 7803–7821. [Google Scholar] [CrossRef] [PubMed]
- Stoklasa, B.; Motka, L.; Rehacek, J.; Hradil, Z.; Sánchez-Soto, L.L. Wavefront sensing reveals optical coherence. Nat. Commun. 2014, 5, 3275. [Google Scholar] [CrossRef] [PubMed]
- Grunwald, R.; Elsaesser, T.; Bock, M. Spatio-temporal coherence mapping of few-cycle vortex pulses. Sci. Rep. 2014, 4, 7148. [Google Scholar] [CrossRef] [PubMed]
- Starikov, F.A.; Kochemasov, G.G.; Kulikov, S.M.; Manachinsky, A.N.; Maslov, N.V.; Ogorodnikov, A.V.; Sukharev, S.A.; Aksenov, V.P.; Izmailov, I.V.; Kanev, F.Y.; et al. Wavefront reconstruction of an optical vortex by a Hartmann-Shack sensor. Opt. Lett. 2007, 32, 2291–2293. [Google Scholar] [CrossRef]
- Murphy, K.; Burke, D.; Devaney, N.; Dainty, C. Experimental detection of optical vortices with a Shack-Hartmann wavefront sensor. Opt. Express 2010, 18, 15448–15460. [Google Scholar] [CrossRef]
- Murphy, K.; Dainty, C. Comparison of optical vortex detection methods for use with a Shack-Hartmann wavefront sensor. Opt. Express 2012, 20, 4988–5002. [Google Scholar] [CrossRef]
- Huang, C.; Huang, H.; Toyoda, H.; Inoue, T.; Liu, H. Correlation matching method for high-precision position detection of optical vortex using Shack–Hartmann wavefront sensor. Opt. Express 2012, 20, 26099–26109. [Google Scholar] [CrossRef]
- Luo, J.; Huang, H.; Matsui, Y.; Toyoda, H.; Inoue, T.; Bai, J. High-order optical vortex position detection using a Shack-Hartmann wavefront sensor. Opt. Express 2015, 23, 8706–8719. [Google Scholar] [CrossRef]
- Pandey, A.K.; Papagiannouli, I.; Sanson, F.; Baynard, E.; Demailly, J.; Kazamias, S.; Pittman, M.; Neveu, O.; Lucas, B.; Marec, A.L.; et al. Towards subpicosecond pulses from solid target plasma based seeded soft X-ray laser. Opt. Express 2020, 28, 28924–28941. [Google Scholar] [CrossRef]
- Fried, D.L. Adaptive optics wave function reconstruction and phase unwrapping when branch points are present. Opt. Commun. 2001, 200, 43–72. [Google Scholar] [CrossRef]
- De Las Heras, A.; Kumar Pandey, A.; Román, J.S.; Plaja, L.; Baynard, E.; Dovillaire, G.; Pittman, M.; Durfee, C.G.; Kazamias, S.; Guilbaud, O.; et al. Generation of Coherent Extreme-Ultraviolet Vector-Vortex beams. In Proceedings of the 2021 Conference on Lasers and Electro-Optics Europe European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 21–25 June 2021. [Google Scholar] [CrossRef]
- Pandey, A.K.; de Las Heras, A.; Román, J.S.; Plaja, L.; Baynard, E.; Dovillaire, G.; Pittman, M.; Kazamias, S.; Guilbaud, O.; Hernández-García, C. Extreme-Ultraviolet Vortices of very high Topological Charge. In Proceedings of the 2021 Conference on Lasers and Electro-Optics Europe European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 21–25 June 2021. [Google Scholar] [CrossRef]
- Pandey, A.K.; de Las Heras, A.; Larrieu, T.; Román, J.S.; Serrano, J.; Plaja, L.; Baynard, E.; Dovillaire, G.; Pittman, M.; Kazamias, S.; et al. Characterization of Extreme-Ultraviolet Vortex Beams with very High Topological Charge; Laboratoire Irène Joliot-Curie, Université Paris-Saclay: Paris, France, 2021; Submitted and under Review. [Google Scholar]
- Southwell, W. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Padgett, M.; Allen, L. The Poynting vector in Laguerre-Gaussian laser modes. Opt. Commun. 1995, 121, 36–40. [Google Scholar] [CrossRef]
- Hernández-García, C.; Picón, A.; San Román, J.; Plaja, L. Attosecond Extreme Ultraviolet Vortices from High-Order Harmonic Generation. Phys. Rev. Lett. 2013, 111, 083602. [Google Scholar] [CrossRef] [PubMed]
- Rego, L.; Román, J.S.; Picón, A.; Plaja, L.; Hernández-García, C. Nonperturbative Twist in the Generation of Extreme-Ultraviolet Vortex Beams. Phys. Rev. Lett. 2016, 117, 163202. [Google Scholar] [CrossRef] [PubMed]
- Yao, E.; Franke-Arnold, S.; Courtial, J.; Barnett, S.; Padgett, M. Fourier relationship between angular position and optical orbital angular momentum. Opt. Express 2006, 14, 9071–9076. [Google Scholar] [CrossRef]
- Vallone, G. Role of beam waist in Laguerre–Gauss expansion of vortex beams. Opt. Lett. 2017, 42, 1097–1100. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, D. Optical vortices generated by multi-level achromatic spiral phase plates for broadband beams. Opt. Commun. 2008, 281, 7–11. [Google Scholar] [CrossRef]
- Ohland, J.B.; Eisenbarth, U.; Roth, M.; Bagnoud, V. A study on the effects and visibility of low-order aberrations on laser beams with orbital angular momentum. Appl. Phys. B 2019, 125, 202. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Asymmetric Gaussian optical vortex. Opt. Lett. 2017, 42, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Franke-Arnold, S.; Barnett, S.M.; Yao, E.; Leach, J.; Courtial, J.; Padgett, M. Uncertainty principle for angular position and angular momentum. New J. Phys. 2004, 6, 103. [Google Scholar] [CrossRef]
- Kotlyar, V.; Kovalev, A.; Porfirev, A.; Kozlova, E. Orbital angular momentum of a laser beam behind an off-axis spiral phase plate. Opt. Lett. 2019, 44, 3673–3676. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, A.K.; Larrieu, T.; Dovillaire, G.; Kazamias, S.; Guilbaud, O. Shack-Hartmann Wavefront Sensing of Ultrashort Optical Vortices. Sensors 2022, 22, 132. https://doi.org/10.3390/s22010132
Pandey AK, Larrieu T, Dovillaire G, Kazamias S, Guilbaud O. Shack-Hartmann Wavefront Sensing of Ultrashort Optical Vortices. Sensors. 2022; 22(1):132. https://doi.org/10.3390/s22010132
Chicago/Turabian StylePandey, Alok Kumar, Tanguy Larrieu, Guillaume Dovillaire, Sophie Kazamias, and Olivier Guilbaud. 2022. "Shack-Hartmann Wavefront Sensing of Ultrashort Optical Vortices" Sensors 22, no. 1: 132. https://doi.org/10.3390/s22010132
APA StylePandey, A. K., Larrieu, T., Dovillaire, G., Kazamias, S., & Guilbaud, O. (2022). Shack-Hartmann Wavefront Sensing of Ultrashort Optical Vortices. Sensors, 22(1), 132. https://doi.org/10.3390/s22010132





