Development and Evaluation of BenchBalance: A System for Benchmarking Balance Capabilities of Wearable Robots and Their Users
Abstract
:1. Introduction
2. Materials and Methods
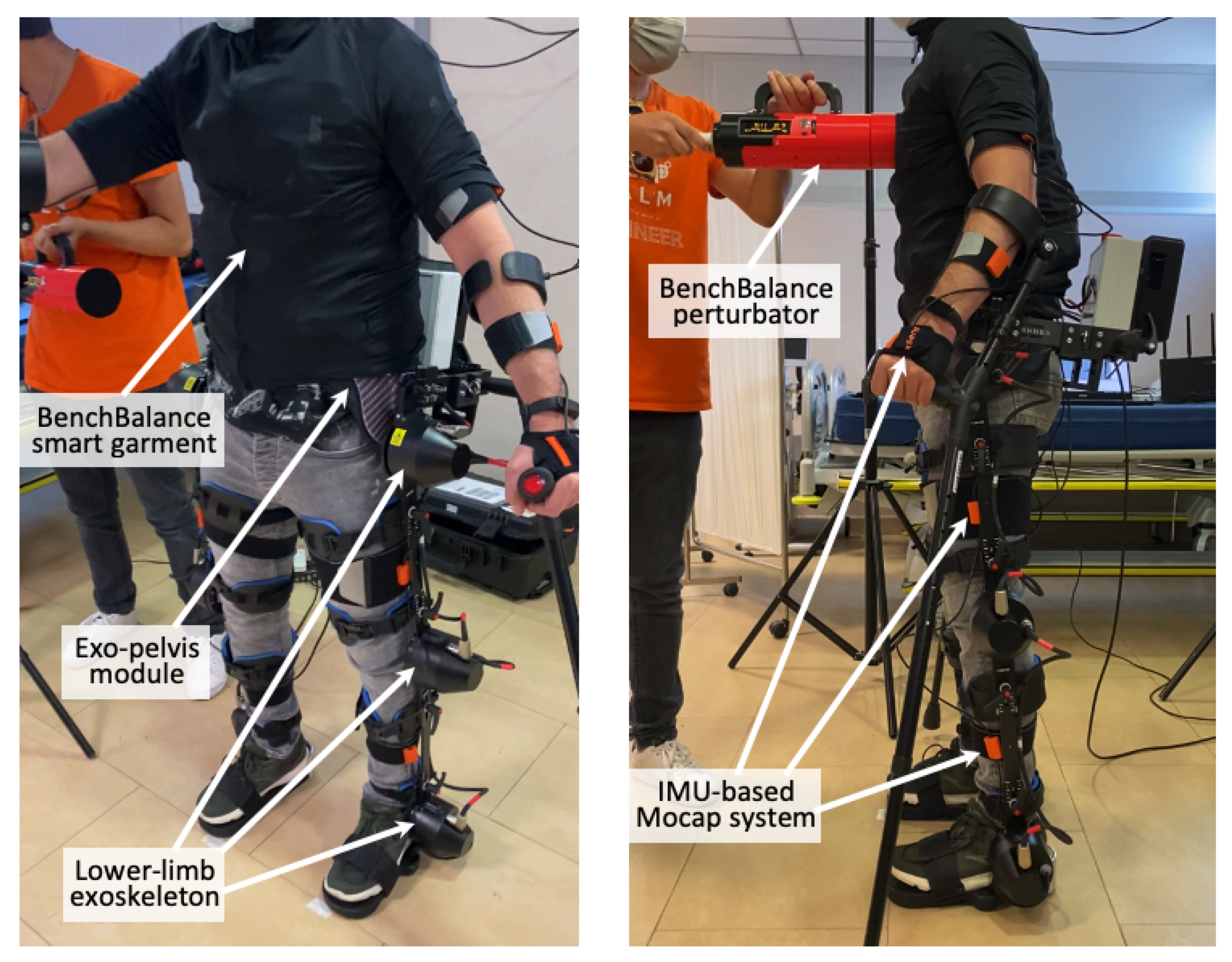
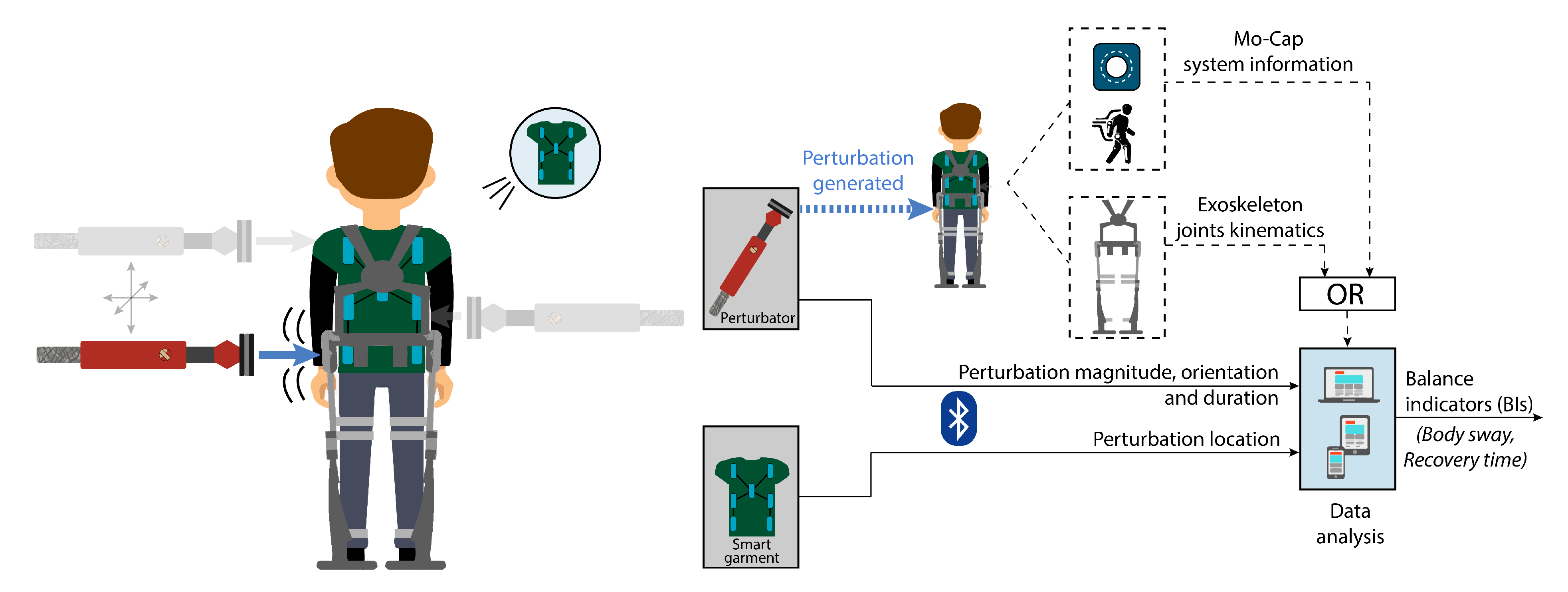
2.1. BenchBalance System
- Quantify the disturbance applied in terms of force magnitude and orientation;
- Quantify where a perturbation is applied on the human body, since balance recovery strategies might differ depending on the location of such perturbation;
- Ensure an appropriate synchronization of the perturbation with the user’s response;
- Provide real-time feedback to the experimenter to augment the ability of providing perturbations in a consistent way;
- Calculate outcome indicators to quantify the balance response by using kinematic data collected either with any motion capture system (Mocap) or with the on-board exoskeleton sensors.
2.1.1. Perturbator
Electronics and Signal Processing
- A three-axial force sensor, K3D60a (ME Systeme GmbH, Hennigsdorf, Germany). The nominal force of the sensor is 500 N with an accuracy of 0.2% in all directions, which was a requirement to properly quantify the magnitude of the perturbation applied to the user.
- An inertial measurement unit (IMU) MTi-3 AHRS (Xsens, Enschede, The Netherlands). Together with another inertial sensor integrated in the smart garment subsystem, it is used to estimate the relative orientation of the perturbation with respect to the human.
- Amplifier with ADC 24 bits (HX711), used to measure the force detected by the force sensor.
- LCD display, New Haven, NHD-2.8-25664UMY3, included in the command panel to show relevant real-time information to the experimenter, i.e., perturbation amplitude, impulse, and orientation.
- Micro SD card, used to pre-store the data of the experiment that will be later transferred to the host computer (sampling frequency of data collected: 30 Hz).
- Battery Management System (BMS), to control a one-cell lithium polymer (LiPo) battery (3.7 V, 2000 mAh) used to supply the microprocessor board and the sensors.
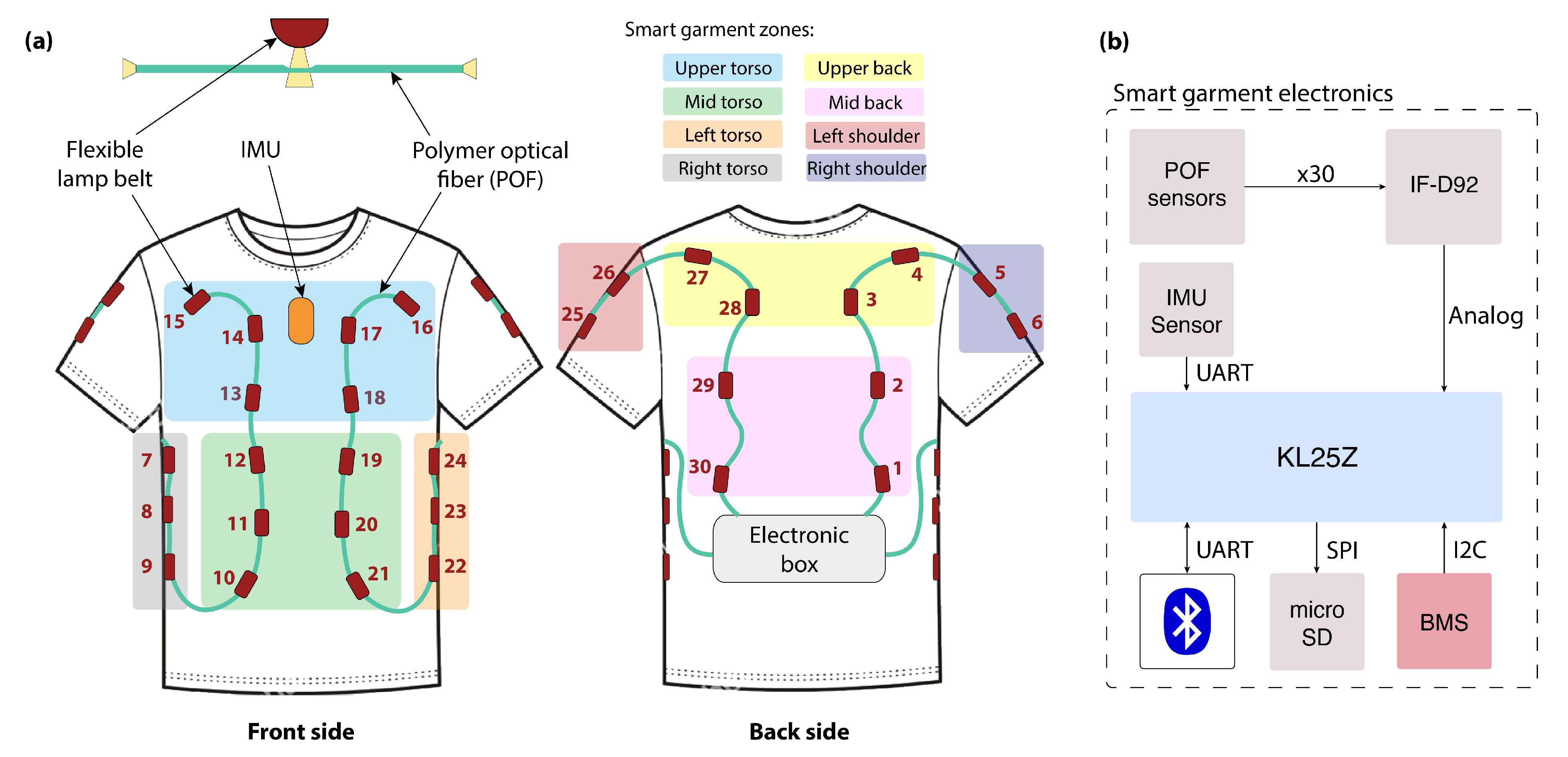
2.1.2. Smart Garment
Electronics and Signal Processing
- Four high-sensitive phototransistor detectors (Industrial Fiberoptics, IF-D92) to transform the light intensities into voltages.
- Micro SD card module to pre-store the data collected during the experiment that later will be transferred to the host computer (sampling frequency of data collected: 30 Hz).
- BMS (SparkFun Battery Babysitter) to monitor a LiPo battery (3.7 V, 2000 mAh), which is used to supply the microprocessor board and the sensors.
2.2. Data Recording and Metrics Derivation
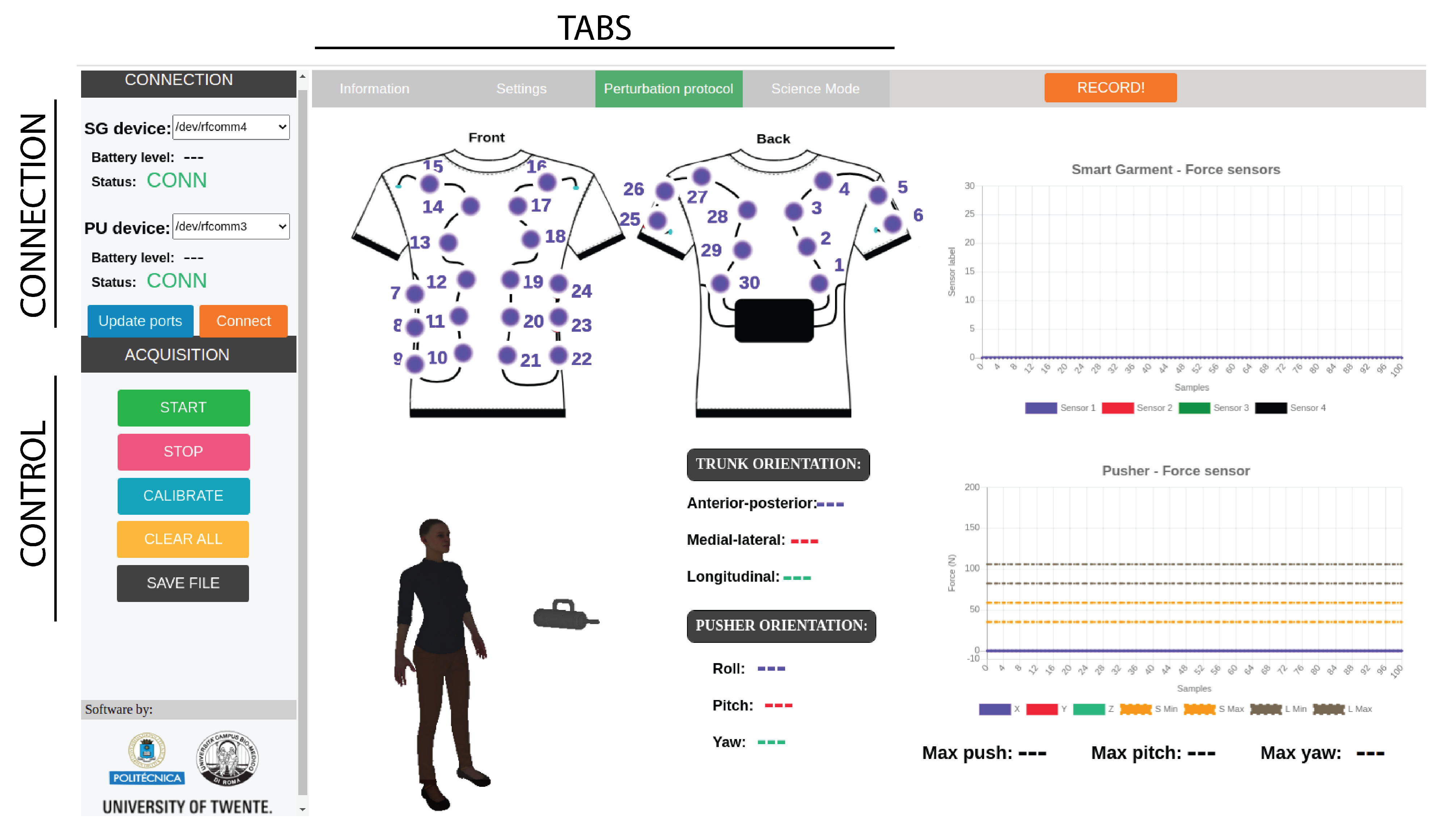
2.2.1. User Control Interface
2.2.2. Controlled Variables and Protocol
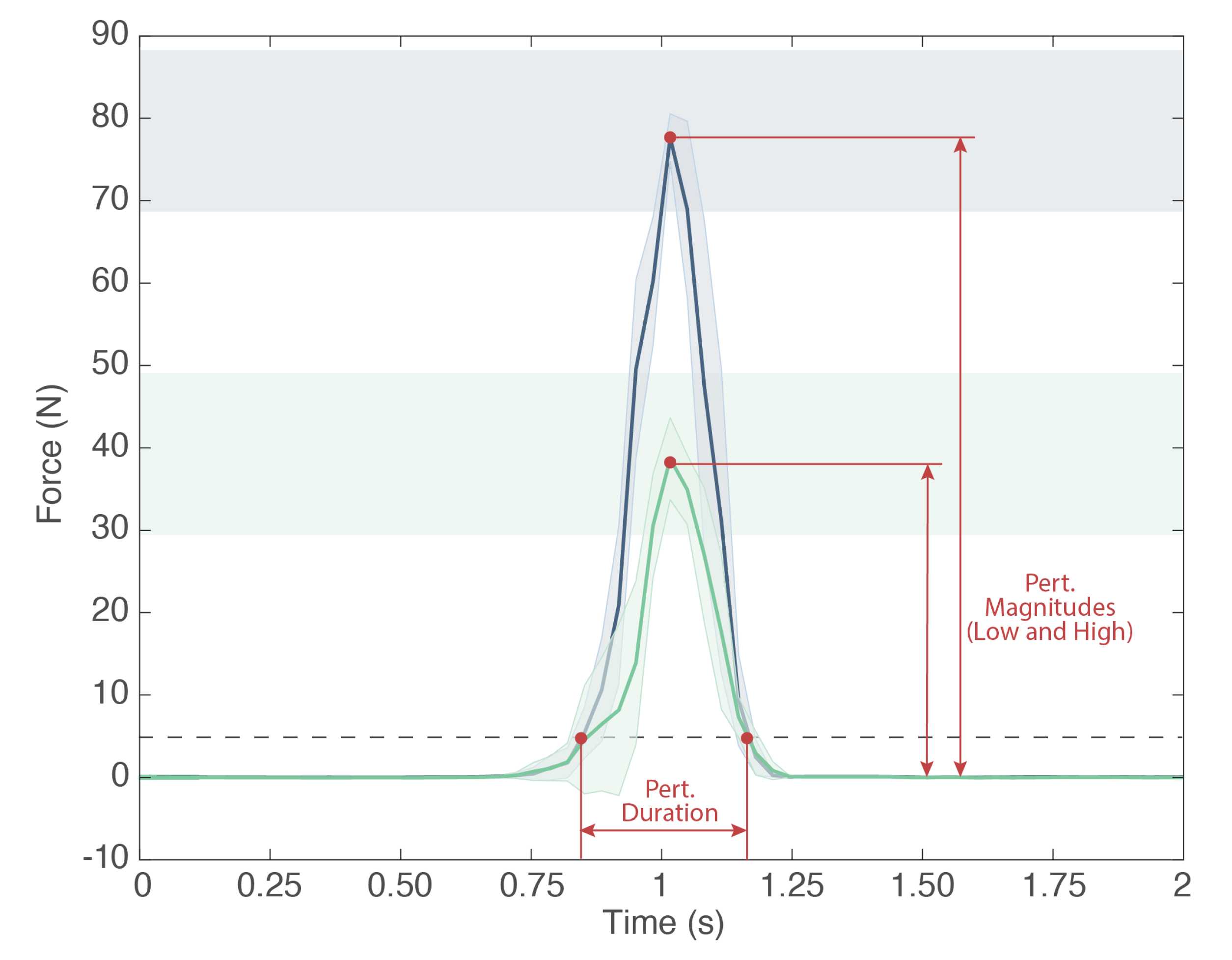
- Perturbation magnitude: It is the maximum amplitude of the force (N) applied by the experimenter to the subject by means of the perturbator. In particular, the perturbator monitors the forces along all three axes, and we calculate the magnitude of the resultant vector. Within the BenchBalance protocol (Table 1), we consider two levels of perturbation magnitude: “Low”, computed as 8 ± 2% of the total mass (body mass plus mass of the exoskeleton, if present); and “High”, computed as 16 ± 2% of the total mass (Figure 5).
- Perturbation duration: It is the time interval along which the force is applied by the experimenter by means of the perturbator. It is calculated as the elapsed time of the force exceeding a (“no force”) threshold of 5 N, and it is expressed in seconds (Figure 5). For the BenchBalance protocol, an acceptable value of the perturbation duration is 0.35 ± 0.15 s for all conditions.
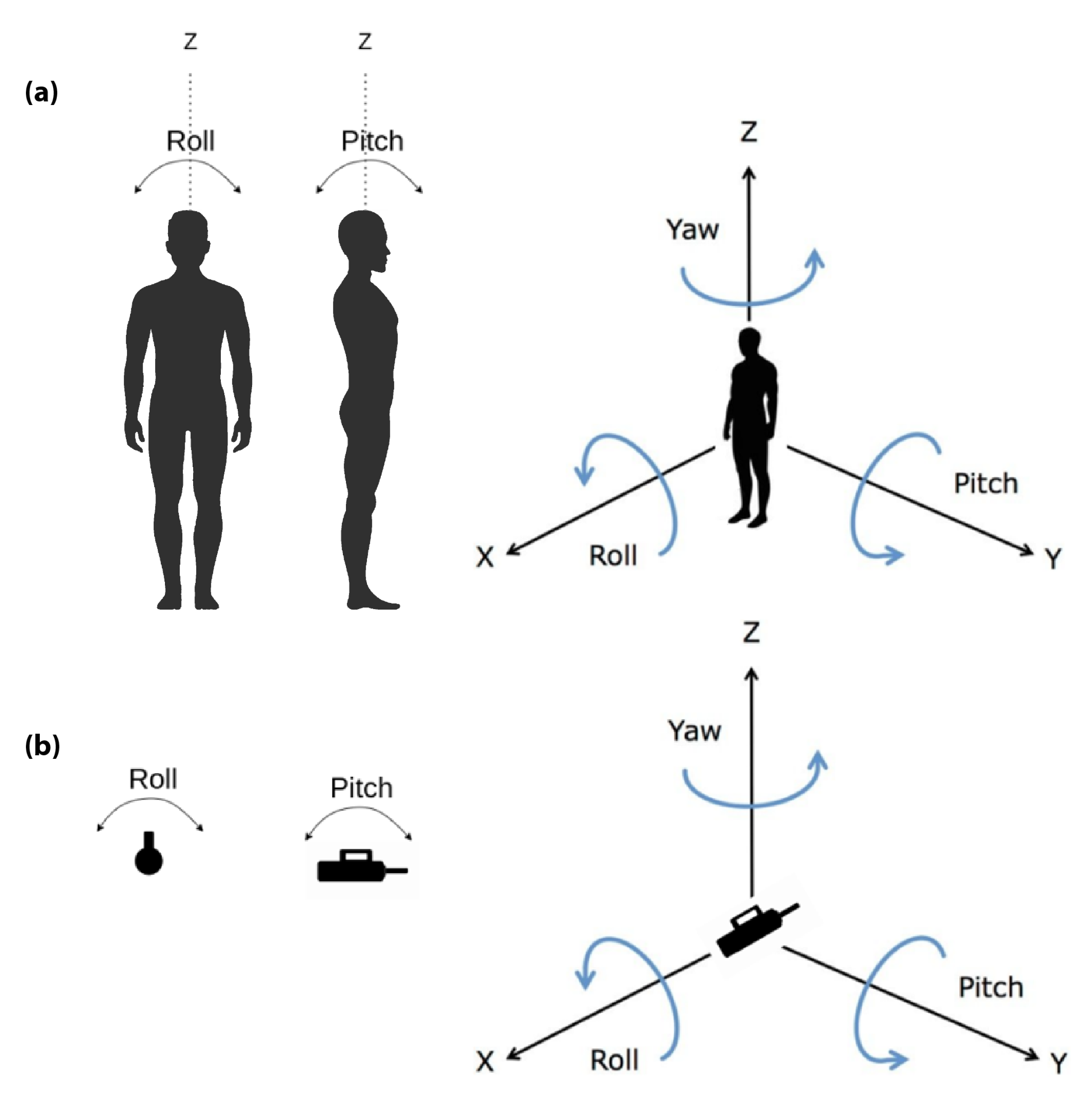
- Perturbation orientation: It is the relative orientation between the human upper body and the direction of the force vector applied to the subject. It is measured by means of the IMUs of the smart garment and the perturbator, and it is expressed as pitch, yaw, and roll components (see reference frames in Figure 6). Within the BenchBalance protocol, we consider acceptable perturbations applied perpendicular to the human body with a tolerance of ±30 degrees in pitch and yaw angles for all conditions.
- Perturbation location: It is the area of the subject’s upper body where the force is applied. This location is extracted by checking the number of the four most active sensors in the smart garment, identifying them based on the zones reported in Figure 3.
- Exoskeleton: It is a Boolean value indicating the presence or not of the exoskeleton in the experiment (0: user without exoskeleton; 1: user with exoskeleton). If an exoskeleton is present, its characteristics (dimensions and mass distribution) are considered for BIs calculation, as described in the following section.
| Condition Order | Perturbation Location | Sensors | Perturbation Magnitude | Perturbation Type |
|---|---|---|---|---|
| 1 | Mid back | 1–2–29–30 | 8 ± 2% M | Low |
| 2 | Upper back | 3–4–27–28 | 8 ± 2% M | Low |
| 3 | Mid back | 1–2–29–30 | 16 ± 2% M | High |
| 4 | Upper back | 3–4–27–28 | 16 ± 2% M | High |
| 5 | Mid torso | 10–11–12–19–20–21 | 8 ± 2% M | Low |
| 6 | Upper torso | 13–14–15–16–17–18 | 8 ± 2% M | Low |
| 7 | Mid torso | 10–11–12–19–20–21 | 16 ± 2% M | High |
| 8 | Upper torso | 13–14–15–16–17–18 | 16 ± 2% M | High |
| 9 | Right side torso | 7–8–9 | 8 ± 2% M | Low |
| 10 | Right side shoulder | 5–6 | 8 ± 2% M | Low |
| 11 | Right side torso | 7–8–9 | 16 ± 2% M | High |
| 12 | Right side shoulder | 5–6 | 16 ± 2% M | High |
| 13 | Left side torso | 22–23–24 | 8 ± 2% M | Low |
| 14 | Left side shoulder | 25–26 | 8 ± 2% M | Low |
| 15 | Left side torso | 22–23–24 | 16 ± 2% M | High |
| 16 | Left side shoulder | 25–26 | 16 ± 2% M | High |
2.2.3. Balance Indicators (BIs)
- Left and right legs are considered identical and symmetrically placed.
- Only ankle, knee, and hip pure flexion/extension angles were considered for the sagittal plane model, and only pure hip add/abduction was used to define the orientation for the frontal plane model. Each joint angle was derived by comparing the relative orientations of the proximal and distal segments around each joint.
- Left/right angles were considered equal (left/right average of collected data).
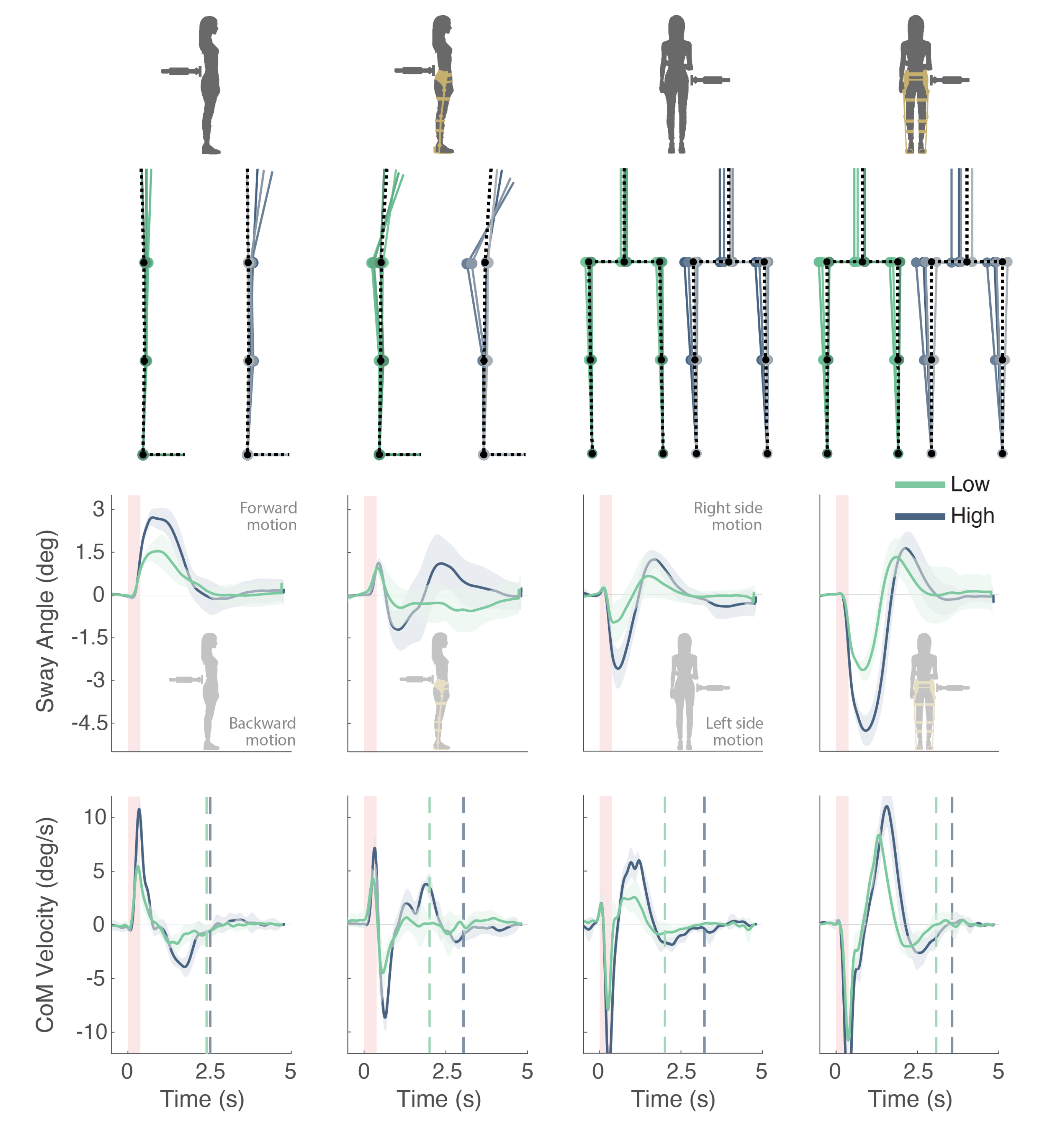
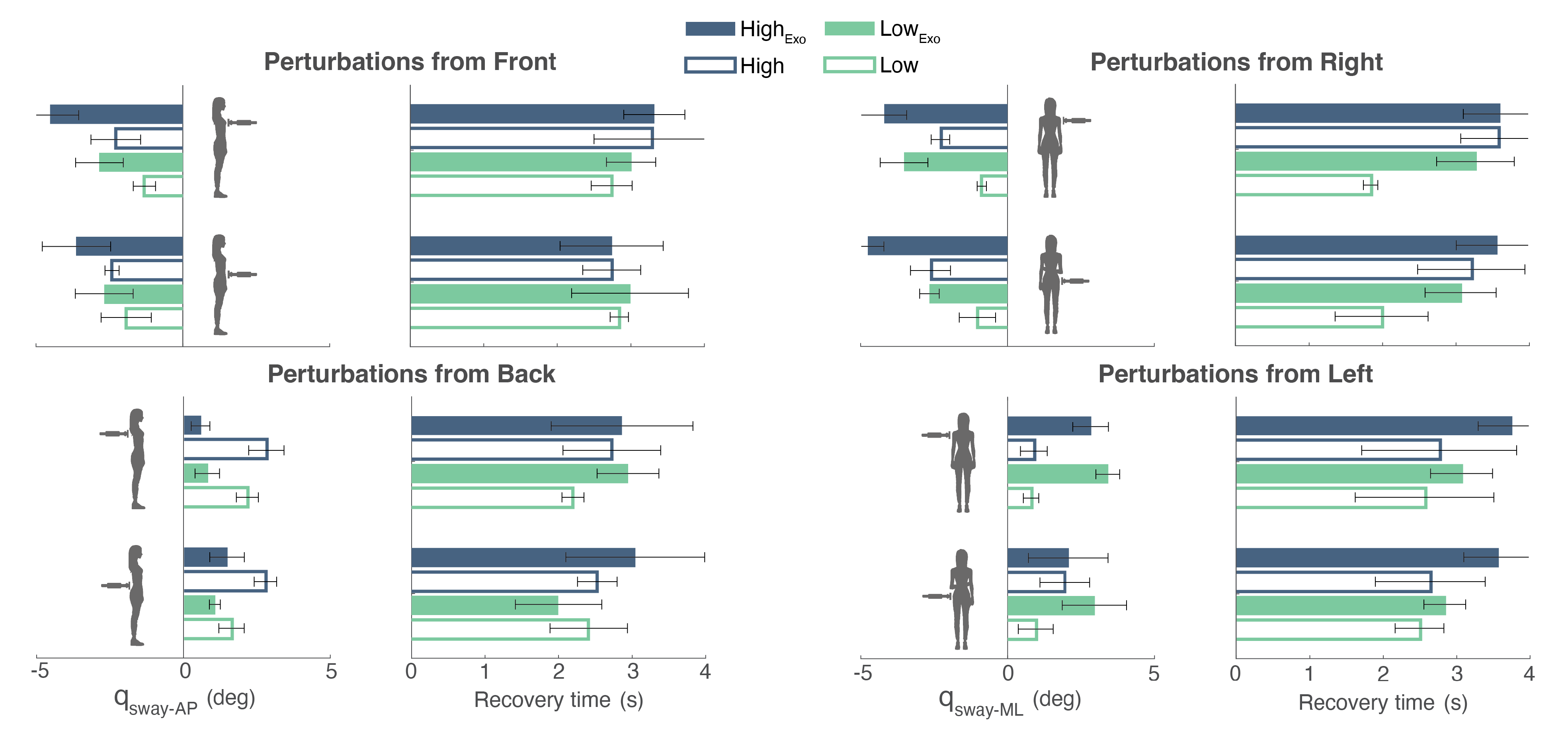
- Body sway (): It represents the maximum body angle in response to a perturbation. A high value of the indicates less ability of the subject in maintaining balance. This BI was evaluated separately for AP and ML (Figure 7a,b). Considering the Cartesian coordinates of the combined (, , ), was calculated as:
- Recovery time: It stands for the time spent to recover from a perturbation, i.e., the time needed to get the back to the rest position within a certain error tolerance. Here, we consider that the position is being recovered if the sway velocity is lower than a threshold of 0.86 deg/s for at least 0.5 s after the perturbation onset.
2.3. Proof of Principle
3. Results
3.1. Performance of the BenchBalance System
3.2. Participant and Exoskeleton Performances
4. Discussion
5. Conclusions
Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Without Exoskeleton | With Exoskeleton | |||
|---|---|---|---|---|
| Condition Order | Sway Angle (deg) | Recovery Time (s) | Sway Angle (deg) | Recovery Time (s) |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
Appendix B
| Plane | BI | r | RMSE (deg) |
|---|---|---|---|
| Sagittal | 0.9849 ± 0.0127 | 0.2556 ± 0.1692 | |
| Frontal | 0.8897 ± 0.1014 | 0.4286 ± 0.2139 |
Appendix C
References
- Agrawal, A.; Harib, O.; Hereid, A.; Finet, S.; Masselin, M.; Praly, L.; Ames, A.D.; Sreenath, K.; Grizzle, J.W. First Steps Towards Translating HZD Control of Bipedal Robots to Decentralized Control of Exoskeletons. IEEE Access 2017, 5, 9919–9934. [Google Scholar] [CrossRef] [Green Version]
- Mummolo, C.; Peng, W.Z.; Agarwal, S.; Griffin, R.; Neuhaus, P.D.; Kim, J.H. Stability of Mina V2 for robot-assisted balance and locomotion. Front. Neurorobot. 2018, 12, 62. [Google Scholar] [CrossRef] [PubMed]
- Ugurlu, B.; Doppmann, C.; Hamaya, M.; Forni, P.; Teramae, T. Variable ankle stiffness improves balance control: Experiments on a bipedal exoskeleton. IEEE Trans. Mechatron. 2016, 21, 79–87. [Google Scholar] [CrossRef]
- Bayon, C.; Emmens, A.R.; Afschrift, M.; Van Wouwe, T.; Keemink, A.; Van Der Kooij, H.; van Asseldonk, E. Can Momentum Based Control Predict Human Balance Recovery Strategies? IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2015–2024. [Google Scholar] [CrossRef]
- Thatte, N.; Geyer, H. Toward Balance Recovery with Leg Prostheses using Neuromuscular Model Control. IEEE Trans. Biomed. Eng. 2015, 63, 904–913. [Google Scholar] [CrossRef]
- Zhao, G.; Sharbafi, M.A.; Vlutters, M.; Asseldonk, E.V.; Seyfarth, A. Bio-Inspired Balance Control Assistance Can Reduce Metabolic Energy Consumption in Human Walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1760–1769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afschrift, M.; Jonkers, I.; De Schutter, J.; De Groote, F. Mechanical effort predicts the selection of ankle over hip strategies in nonstepping postural responses. J. Neurophysiol. 2016, 116, 1937–1945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jackson, R.W.; Collins, S.H. Heuristic-Based Ankle Exoskeleton Control for Co-Adaptive Assistance of Human Locomotion. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2059–2069. [Google Scholar] [CrossRef] [PubMed]
- Monaco, V.; Tropea, P.; Aprigliano, F.; Martelli, D.; Parri, A.; Cortese, M.; Molino-Lova, R.; Vitiello, N.; Micera, S. An ecologically-controlled exoskeleton can improve balance recovery after slippage. Sci. Rep. 2017, 7, 46721. [Google Scholar] [CrossRef] [PubMed]
- Bayón, C.; Keemink, A.; van Mierlo, M.; Rampeltshammer, W.; van der Kooij, H.; van Asseldonk, E.H.F. Cooperative ankle-exoskeleton control can reduce effort to recover balance after unexpected disturbances during walking. J. NeuroEng. Rehabil. 2021. [Google Scholar] [CrossRef]
- Torricelli, D.; Gonzalez-Vargas, J.; Veneman, J.F.; Mombaur, K.; Tsagarakis, N.; Del-Ama, A.J.; Gil-Agudo, A.; Moreno, J.C.; Pons, J.L. A unified scheme for humanoids, wearable robots, and humans. IEEE Robot. Autom. Mag. 2015, 22, 103–115. [Google Scholar] [CrossRef] [Green Version]
- del Pôbil, A.P. Why do We Need Benchmarks in Robotics Research? In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Mancini, M.; Horak, F.B. The relevance of clinical balance assessment tools to differentiate balance deficits. Eur. J. Phys. Rehabil. Med. 2010, 46, 239–248. [Google Scholar] [PubMed]
- Shirota, C.; Asseldonk, E.V.; Matja, Z.; Vallery, H.; Barralon, P.; Maggioni, S.; Buurke, J.H.; Veneman, J.F. Robot-supported assessment of balance in standing and walking. J. Neuroeng. Rehabil. 2017, 14, 80. [Google Scholar] [CrossRef] [Green Version]
- Visser, J.; Carpenter, M.; van der Kooij, H.; Bloem, B. The clinical utility of posturography. Clin. Neurophysiol. 2008, 119, 2424–2436. [Google Scholar] [CrossRef]
- Horak, F.B.; Mancini, M. Objective biomarkers of balance and gait for Parkinson’s disease using body-worn sensors. Mov. Disord. 2013, 28, 1544–1551. [Google Scholar] [CrossRef] [Green Version]
- Vlutters, M.; Van Asseldonk, E.H.F.; Van Der Kooij, H. Reduced center of pressure modulation elicits foot placement adjustments, but no additional trunk motion during anteroposterior-perturbed walking. J. Biomech. 2018, 68, 93–98. [Google Scholar] [CrossRef]
- Matjačić, Z.; Zadravec, M.; Bizovičar, N.; Goljar, N.; Olenšek, A. Novel Perturbation-Based Approaches Using Pelvis Exoskeleton Robot in Gait and Balance Training After Stroke. In Wearable Robotics: Challenges and Trends; Springer: Cham, Switzerland, 2019; pp. 91–95. [Google Scholar] [CrossRef]
- Matjaž, Z.; Andrej, O.; Marko, R.; Nataša, B.; Nika, G.; Zlatko, M. Assessment of dynamic balancing responses following perturbations during slow walking in relation to clinical outcome measures for high-functioning post-stroke subjects. J. NeuroEng. Rehabil. 2020, 17, 85. [Google Scholar]
- Emmens, A.; Asseldonk, E.V.; Masciullo, M.; Arquilla, M.; Pisotta, I.; Tagliamonte, N.L.; Tamburella, F.; Molinari, M.; Kooij, H.V.D. Improving the Standing Balance of Paraplegics through the use of a Wearable Exoskeleton. In Proceedings of the 7th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Enschede, The Netherlands, 26–29 August 2018. [Google Scholar]
- Leal-Junior, A.G.; Frizera, A.; José Pontes, M. Sensitive zone parameters and curvature radius evaluation for polymer optical fiber curvature sensors. Opt. Laser Technol. 2018, 100, 272–281. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Díaz, C.R.; Marques, C.; Pontes, M.J.; Frizera, A. Multiplexing technique for quasi-distributed sensors arrays in polymer optical fiber intensity variation-based sensors. Opt. Laser Technol. 2019, 111, 81–88. [Google Scholar] [CrossRef]
- Boonstra, T.A.; Schouten, A.C.; Van Der Kooij, H. Identification of the contribution of the ankle and hip joints to multi-segmental balance control. J. NeuroEng. Rehabil. 2013, 10, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noamani, A.; Nazarahari, M.; Lewicke, J.; Vette, A.H.; Rouhani, H. Validity of using wearable inertial sensors for assessing the dynamics of standing balance. Med. Eng. Phys. 2020, 77, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.D. An Optimal Control Model for Analyzing Human Postural Balance. IEEE Trans. Biomed. Eng. 1995, 42, 87–101. [Google Scholar] [CrossRef] [PubMed]
- EUROBENCH. Eurobench Framework Documentation. 2021. Available online: https://eurobench.github.io/sofware_documentation/latest/data_format.html#Eurobench%20Data%20Format (accessed on 12 November 2021).
- Winter, D. Anthropometry. In Biomechanics and Motor Control of Human Movements, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009; pp. 82–106. [Google Scholar]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors. Xsens Technol. 2013, 3, 1–9. [Google Scholar]
- Bortole, M.; Venkatakrishnan, A.; Zhu, F.; Moreno, J.C.; Francisco, G.E.; Pons, J.L.; Contreras-Vidal, J.L. The H2 robotic exoskeleton for gait rehabilitation after stroke: Early findings from a clinical study. J. NeuroEng. Rehabil. 2015, 12, 54. [Google Scholar] [CrossRef] [Green Version]
- Mergner, T.; Lippi, V. Posture control-human-inspired approaches for humanoid robot benchmarking: Conceptualizing tests, protocols and analyses. Front. Neurorobotics 2018, 12, 21. [Google Scholar] [CrossRef] [Green Version]
- Tokur, D.; Grimmer, M.; Seyfarth, A. Review of balance recovery in response to external perturbations during daily activities. Hum. Mov. Sci. 2020, 69, 102546. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayón, C.; Delgado-Oleas, G.; Avellar, L.; Bentivoglio, F.; Di Tommaso, F.; Tagliamonte, N.L.; Rocon, E.; van Asseldonk, E.H.F. Development and Evaluation of BenchBalance: A System for Benchmarking Balance Capabilities of Wearable Robots and Their Users. Sensors 2022, 22, 119. https://doi.org/10.3390/s22010119
Bayón C, Delgado-Oleas G, Avellar L, Bentivoglio F, Di Tommaso F, Tagliamonte NL, Rocon E, van Asseldonk EHF. Development and Evaluation of BenchBalance: A System for Benchmarking Balance Capabilities of Wearable Robots and Their Users. Sensors. 2022; 22(1):119. https://doi.org/10.3390/s22010119
Chicago/Turabian StyleBayón, Cristina, Gabriel Delgado-Oleas, Leticia Avellar, Francesca Bentivoglio, Francesco Di Tommaso, Nevio L. Tagliamonte, Eduardo Rocon, and Edwin H. F. van Asseldonk. 2022. "Development and Evaluation of BenchBalance: A System for Benchmarking Balance Capabilities of Wearable Robots and Their Users" Sensors 22, no. 1: 119. https://doi.org/10.3390/s22010119
APA StyleBayón, C., Delgado-Oleas, G., Avellar, L., Bentivoglio, F., Di Tommaso, F., Tagliamonte, N. L., Rocon, E., & van Asseldonk, E. H. F. (2022). Development and Evaluation of BenchBalance: A System for Benchmarking Balance Capabilities of Wearable Robots and Their Users. Sensors, 22(1), 119. https://doi.org/10.3390/s22010119








