A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges
Abstract
1. Introduction
- mathematical formulation and explanation of the SS models which take into account the impact of NU variations, DT adaptations, and both, on the probability of ED,
- presentation of the algorithm developed for simulating ED performance on differently modulated OFDM signals detected in MA, RA, and combined RA and MA based implementations,
- a systematic investigation based on extensive simulations on how the different OFDM modulations and corresponding Tx powers, the SNRs in the position of SU, the levels of NUs, the sample quantity, and the false alarm probability impact on the probability of signal detection in the ED process with DT adaptation,
- explanation of the limitations of ED as one of the local SS methods, with discussion on future research challenges and opportunities related to the improvement of the ED technique.
2. Related Works on the SS of OFDM Signals
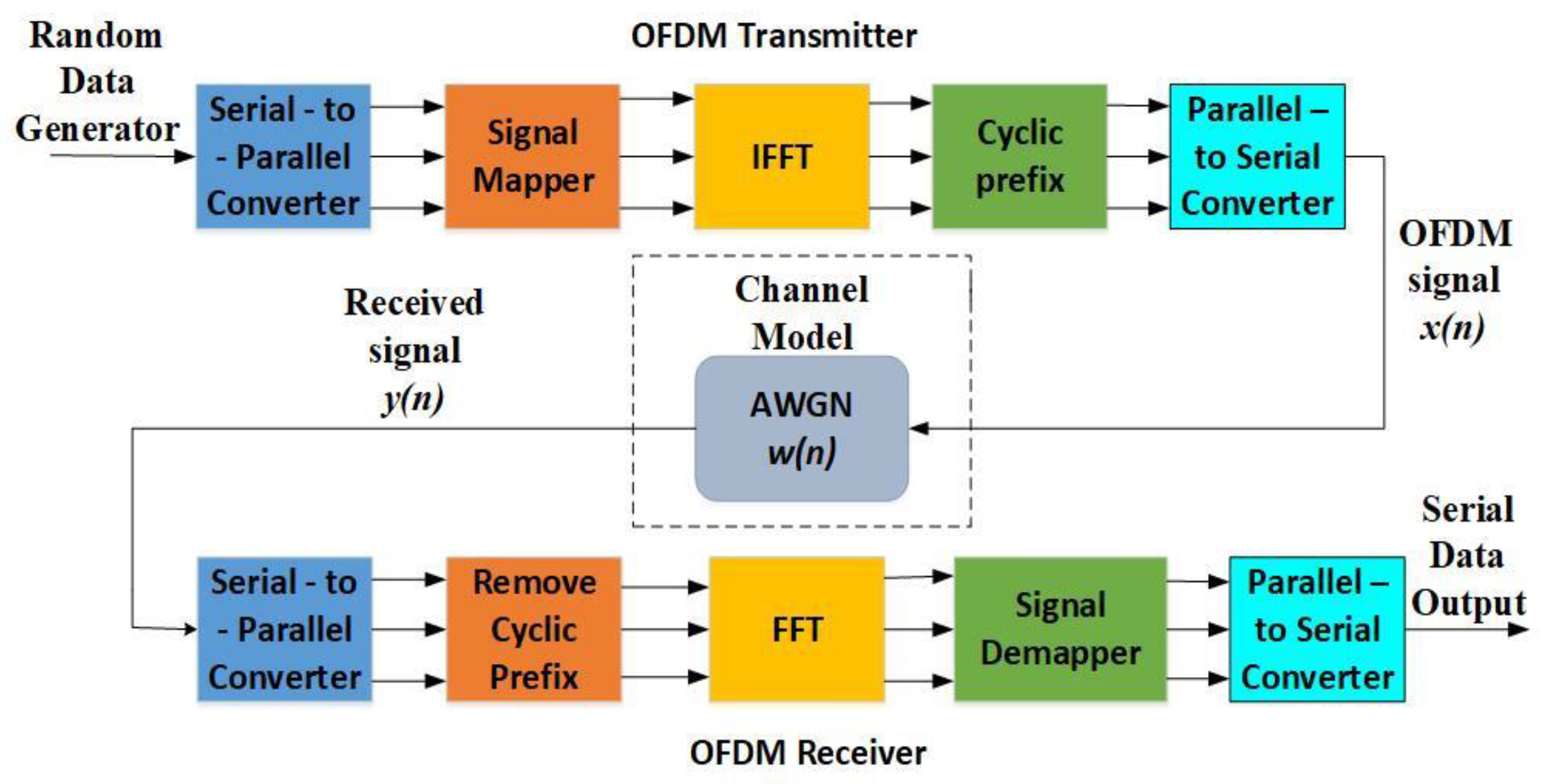
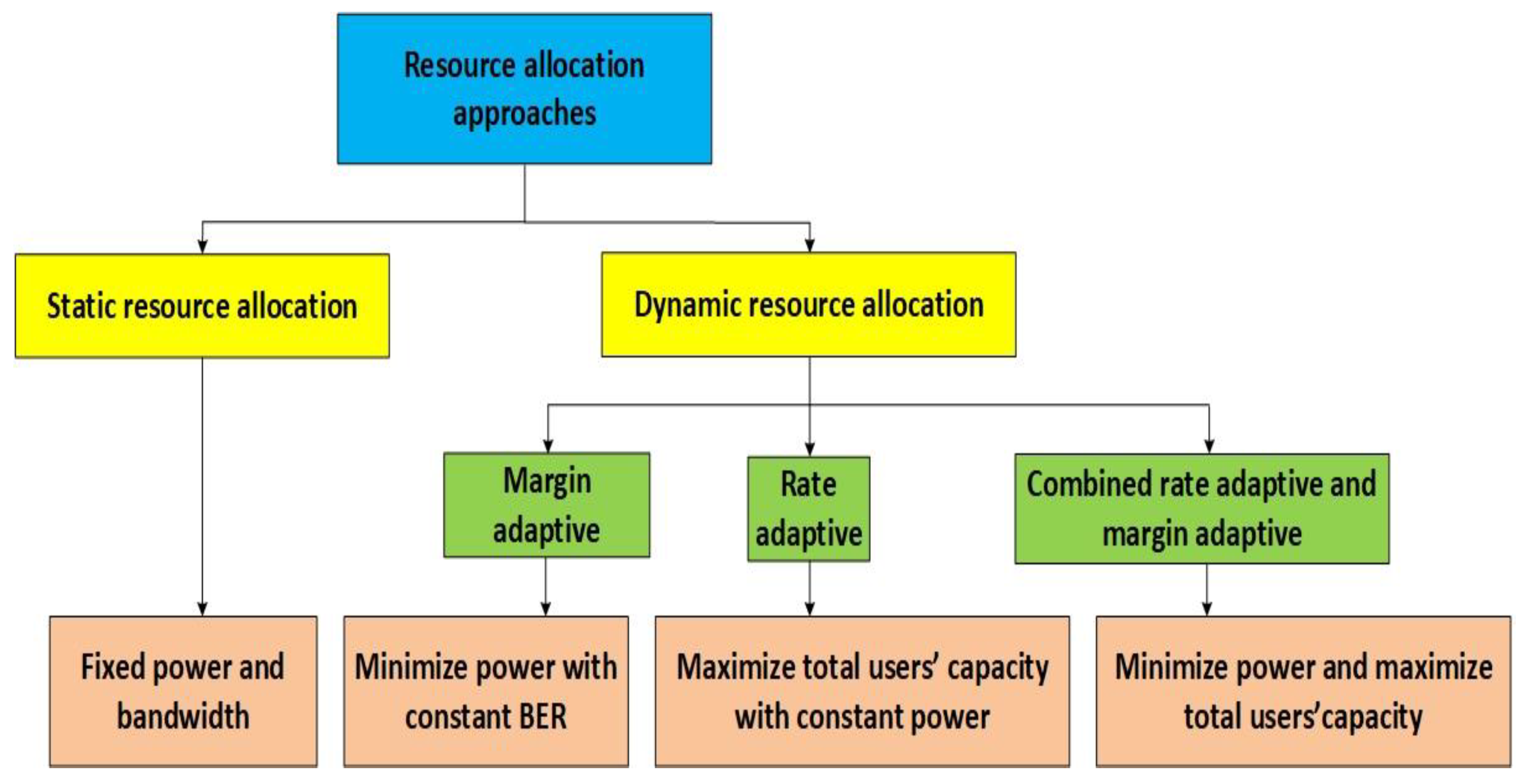
3. Design of Different OFDM Based Systems
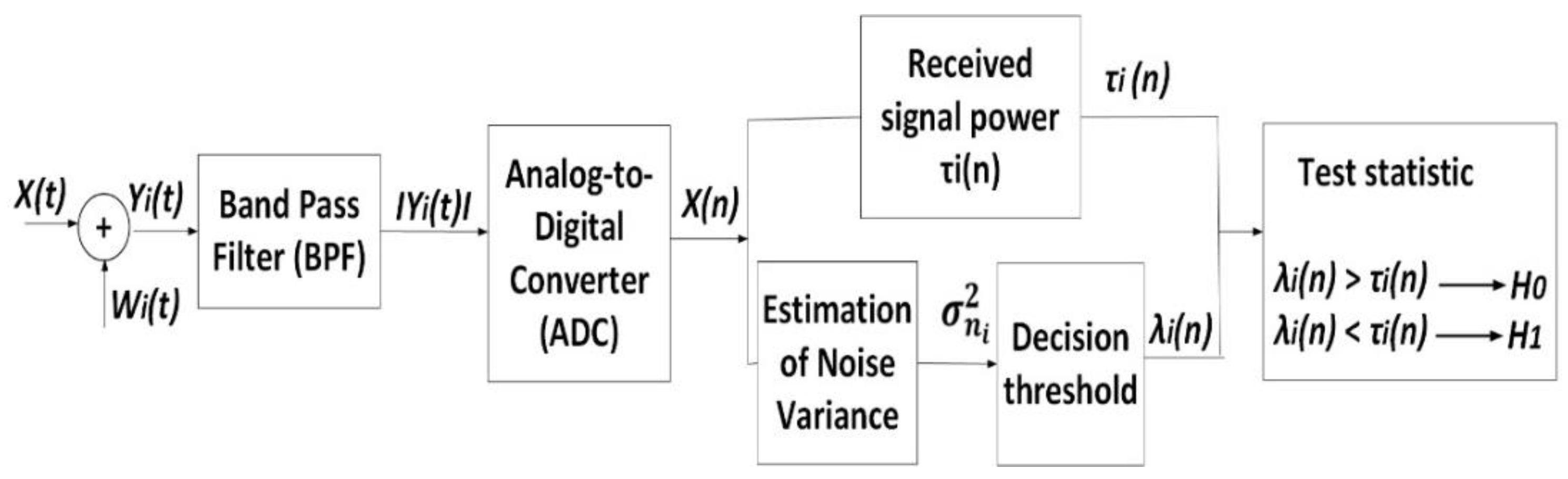
4. Energy Detection Model
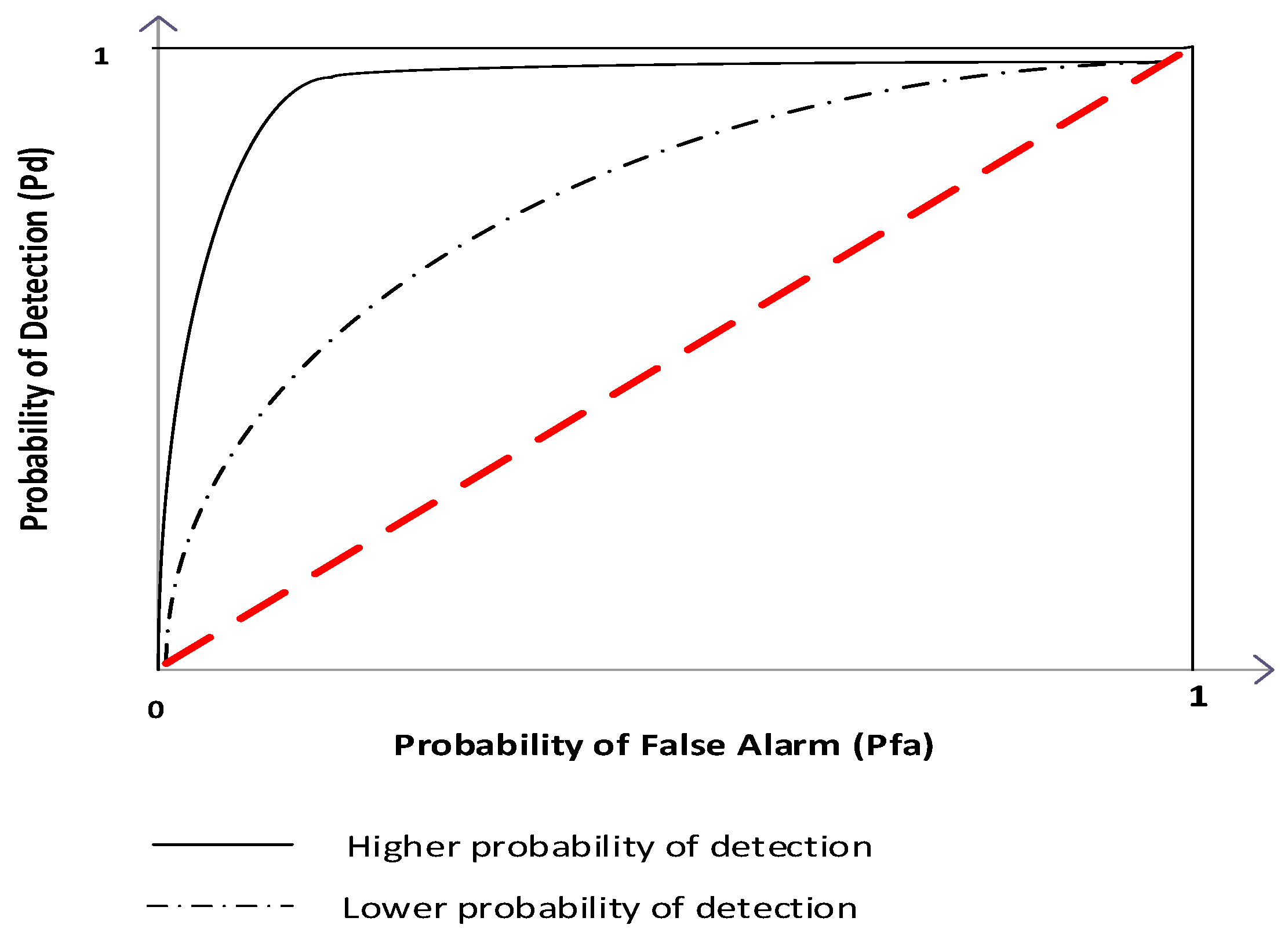
4.1. Receiver Operating Characteristic Curves
5. Energy Detection Process
5.1. Detection and False Alarm Probabilities
5.2. Detection Threshold Estimation
5.3. Noise Uncertainty Estimation
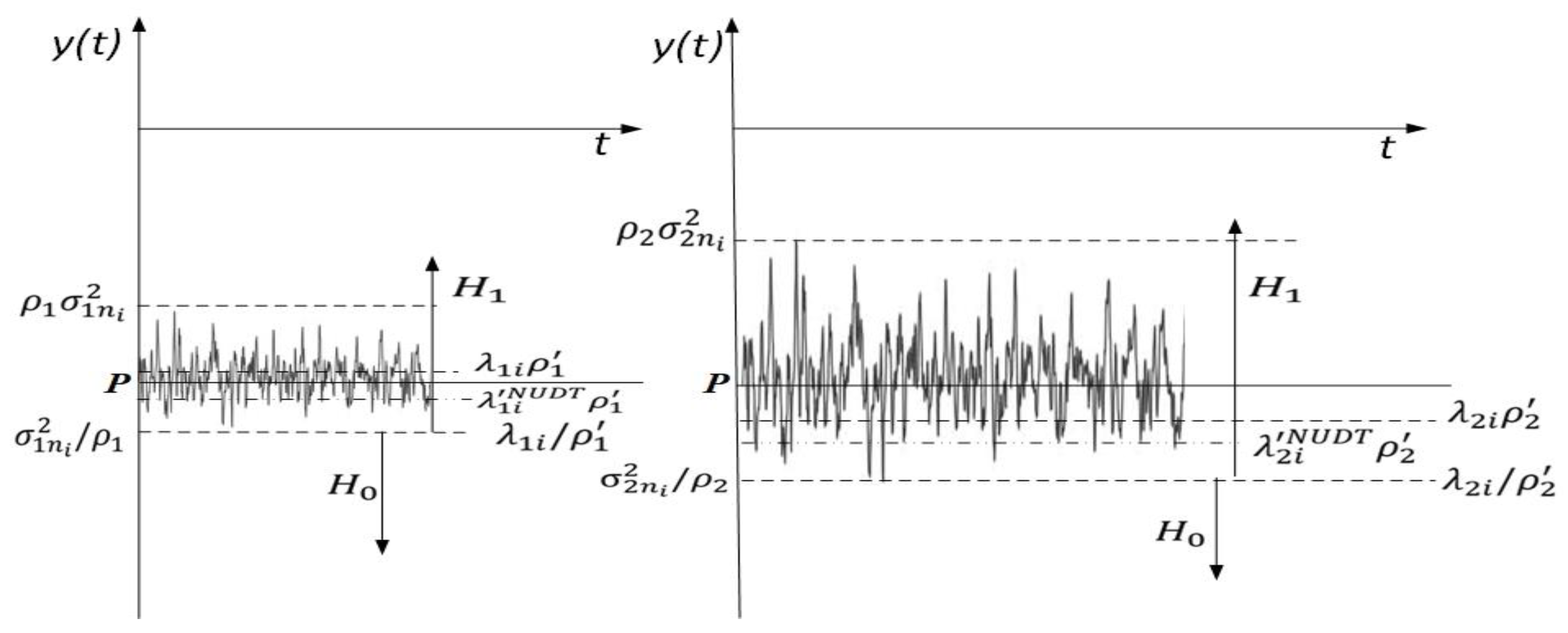
5.4. Energy Detection with NU and DT Adaptation
6. Energy Detection Algorithm
| Algorithm 1 Simulation of ED process |
| 1:INPUT:OFDM signal (ofdm_signal), len_ofdm_data, sample quantity (N), SNR, NU factor (ρ), DT factor (), noise variance (), length of (), and number of Monte Carlo simulations (kk) 2: OUTPUT: Detection probability () 3: INITIALISE: OFDM signal (ofdm_signal) Step 1: Simulation Detection probability () vs. Probability of False Alarm () based on (13, 18, 21, 25) 4: set kk = number of Monte Carlo simulations 5: set Pfa = false alarm probability in interval [0,1] 6: FOR p = 1:length (); 7: i1 = 0; i2 = 0; 8: FOR kk = 1:10,000; Step 2: Generate AWGN noise () with zero mean and variance 9: Noise_1 (ρ = 1.00,> 1.00) = sqrt (). *randn (1, len_ofdm_data); 10: Noise_2 (ρ > 1.00,> 1.00) = sqrt (. *randn (1, len_ofdm_data); Step 3: Generate PU signal(t) and Received signal(t) calculation 11: final_ofdm_signal = sqrt(SNR).*ofdm_signal; 12: received_signal_1 = final_ofdm_signal + Noise_1; 13: received_signal_2 = final_ofdm_signal + Noise_2; Step 4: Received signal energy calculation 14: energy_calc_1 = abs(received_signal_1).^2; 15: energy_calc_2 = abs(received_signal_2).^2; Step 5: Test statistic calculation using (2) 16: test_stat_1 = (1/N).*sum(energy_calc_1); 17: test_stat_2 = (1/N).*sum(energy_calc_2); Step 6: Threshold evaluation using (17) and (23) 18: thresh1(p) = ((qfuncinv((p))./sqrt(N))+ 1)./; 19: thresh2(p) = ((qfuncinv((p)).* ρ./sqrt(N))+ ρ)./; Step 7: Decision making using (7) and (8) 20: IF (test_stat_1 >= thresh1(p)); 21: i1 = i1+1; 22: END 23: IF (test_stat_2 >= thresh2(p)); 24: i2 = i2 + 1; 25: END 26: END Step 8: Monte Carlo simulation-determining (1) 27: 1(p) = i1/kk; 28: 2(p) = i2/kk; 29:END 30:UNTIL = [0,1] |
7. Results of Simulations
7.1. Parameters of Simulation
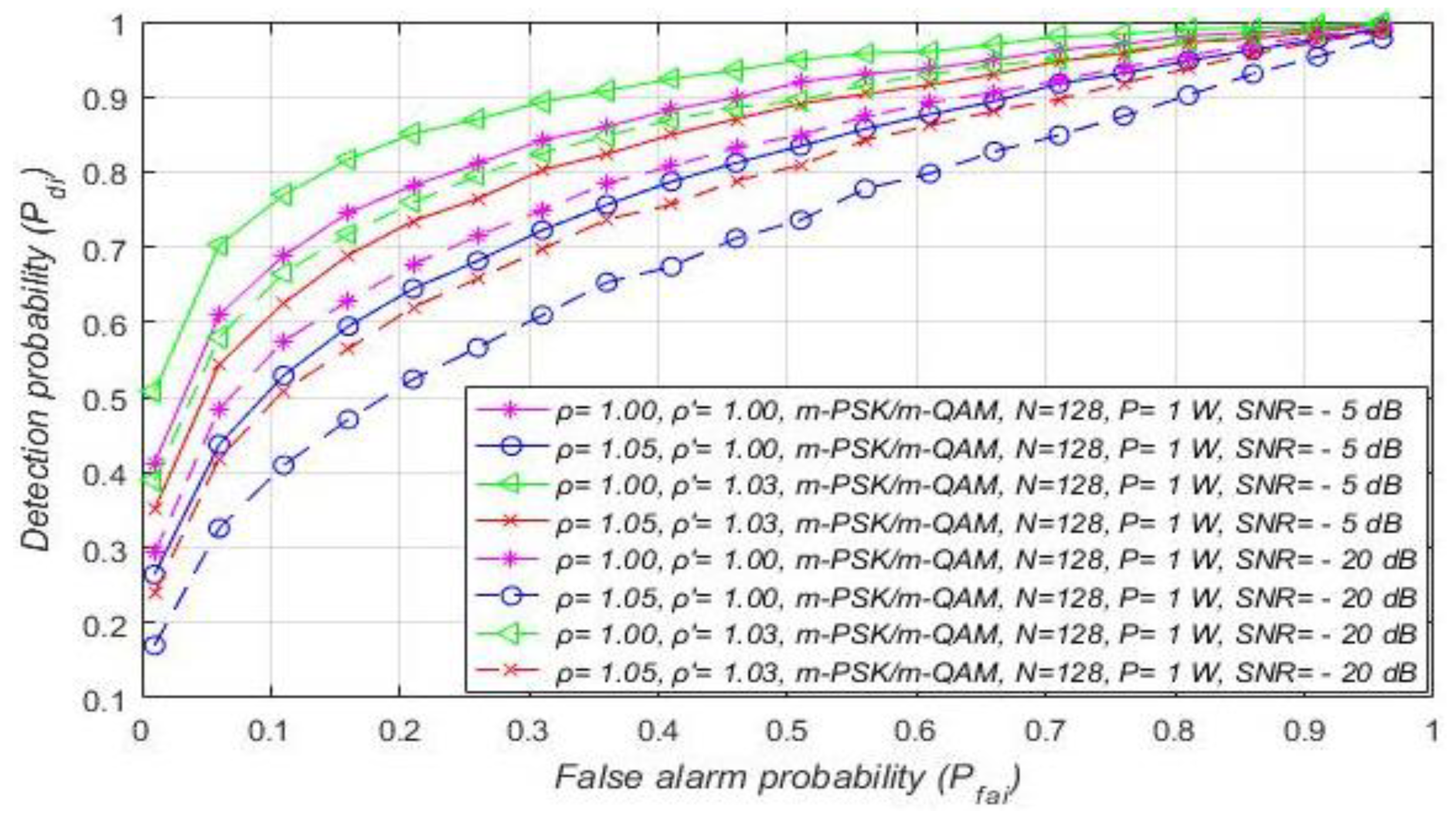
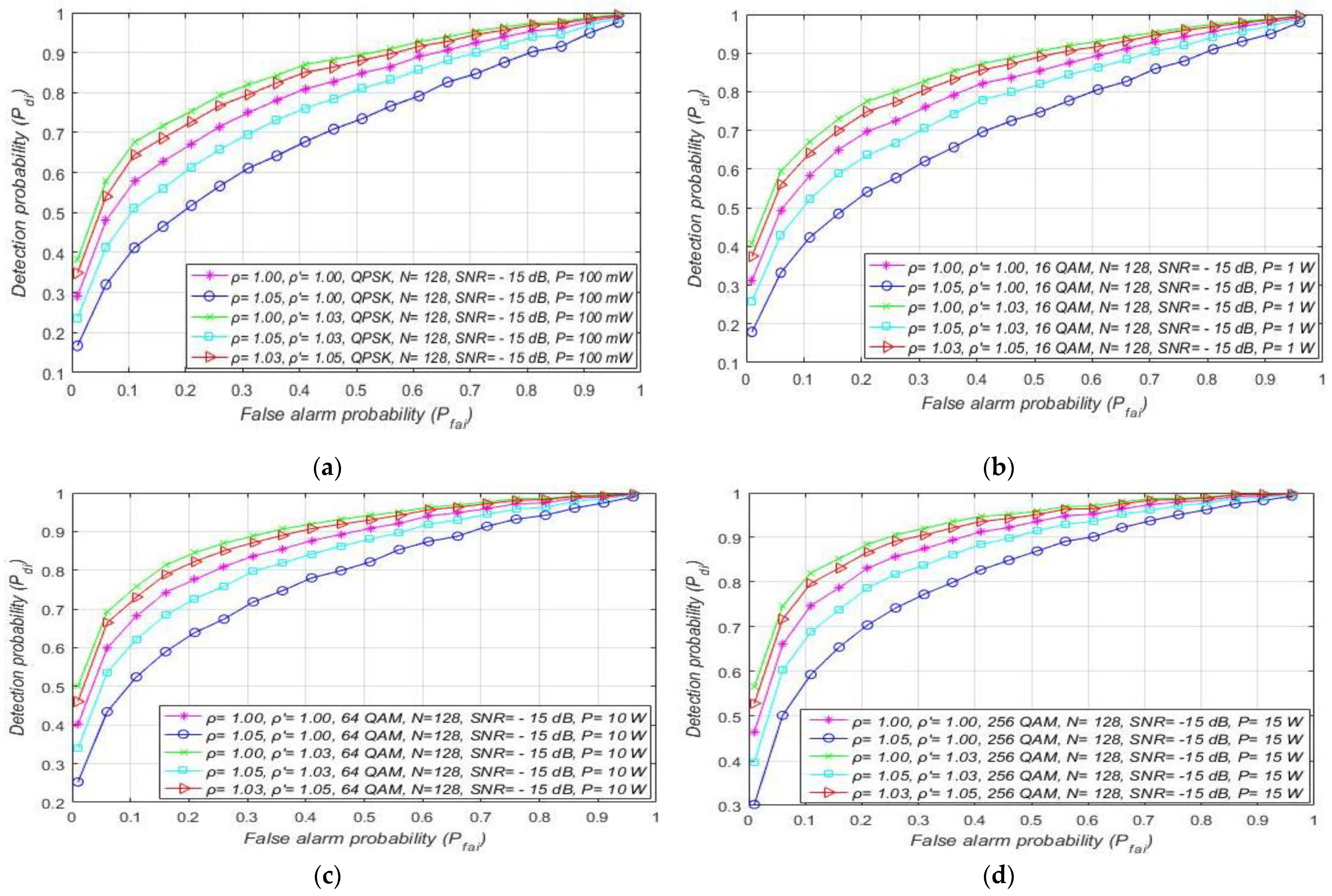
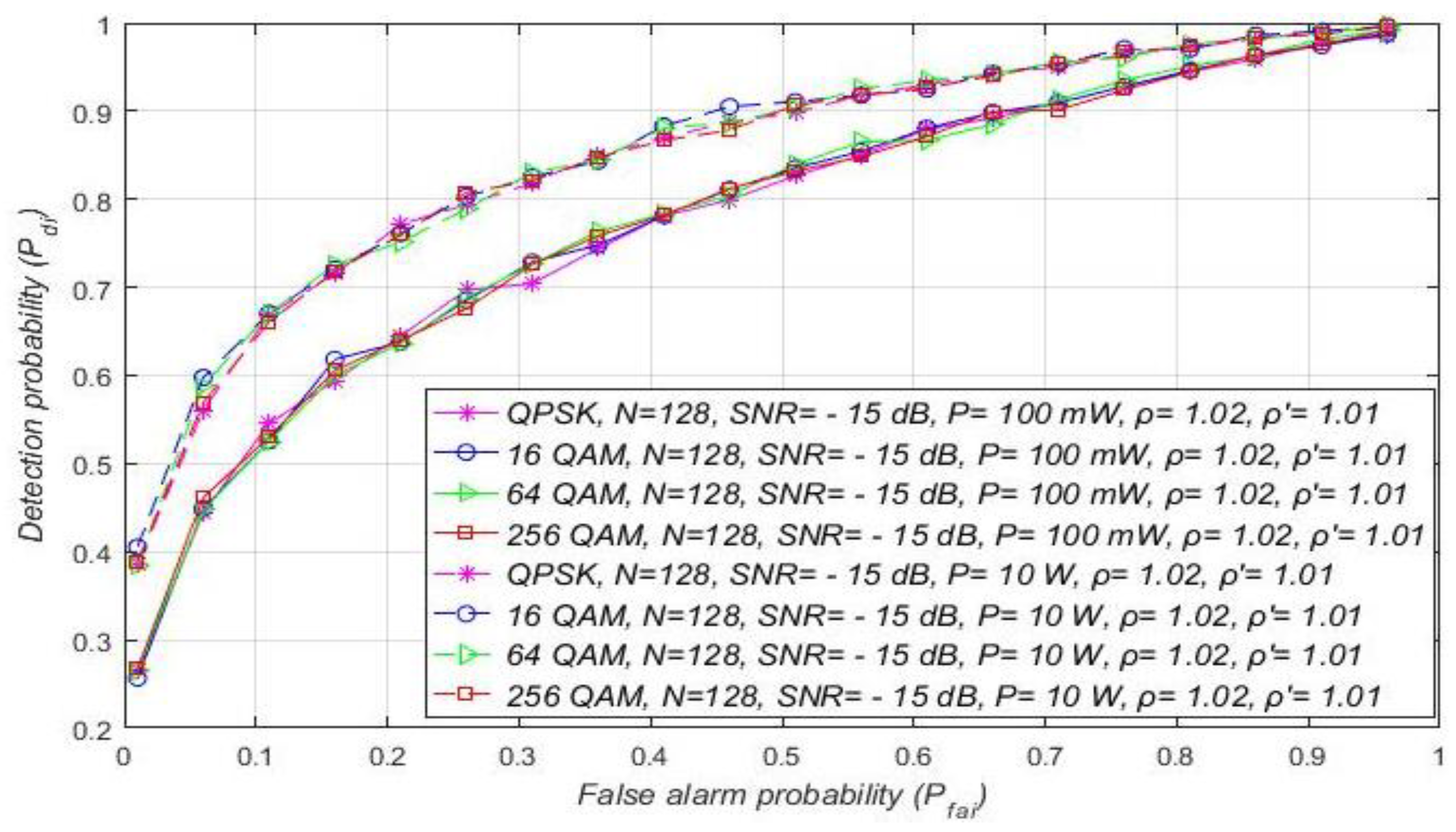
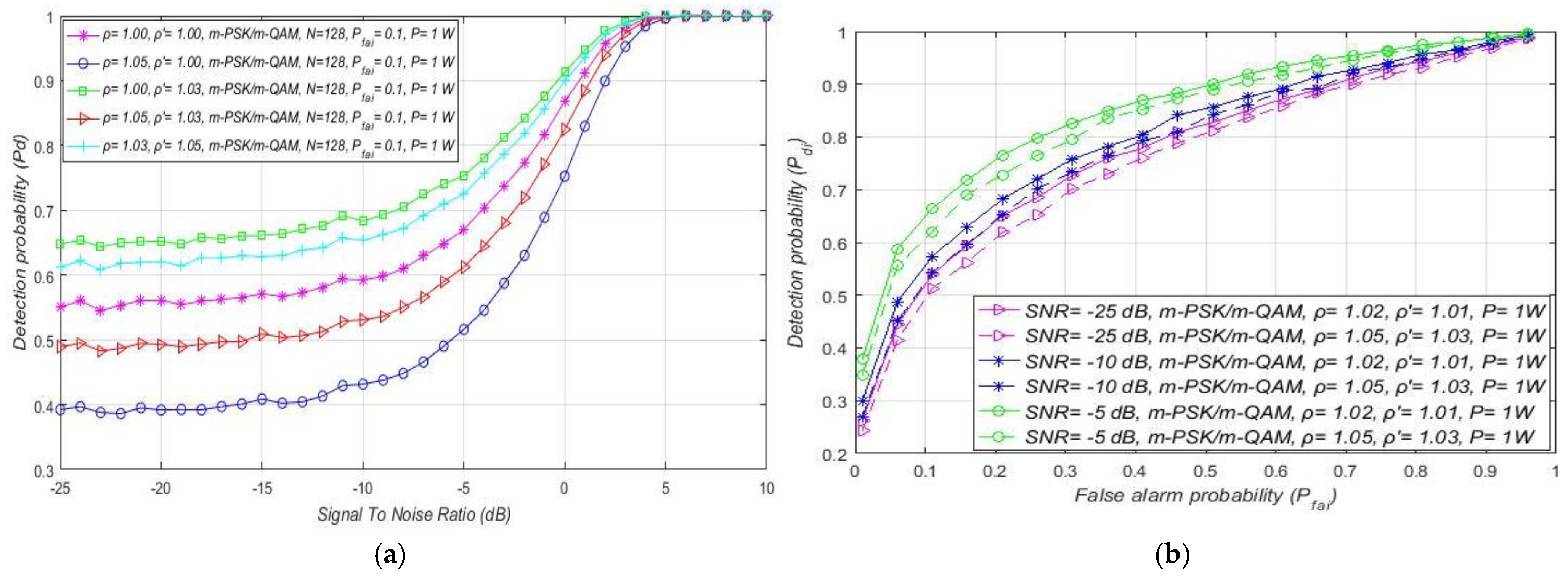
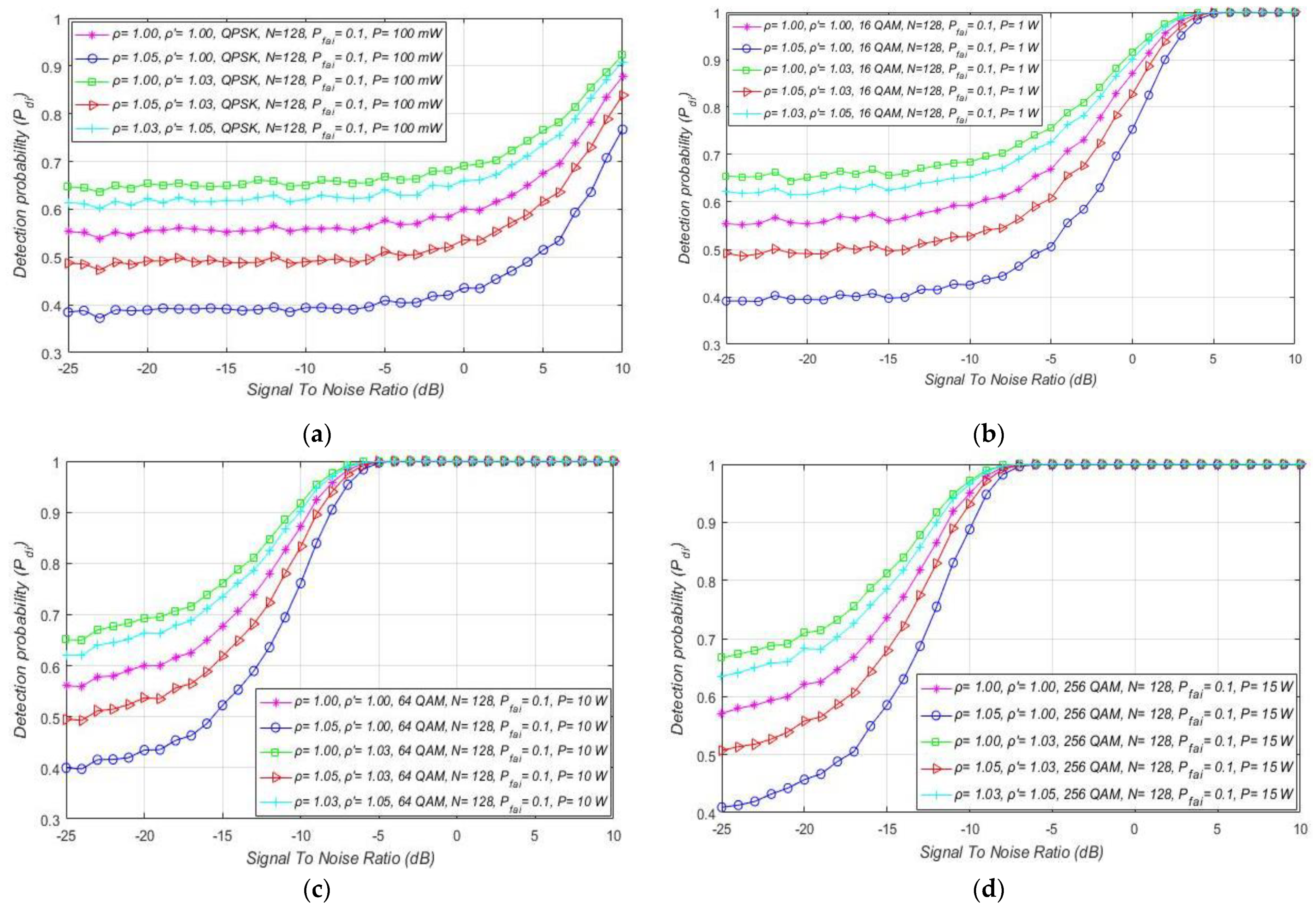
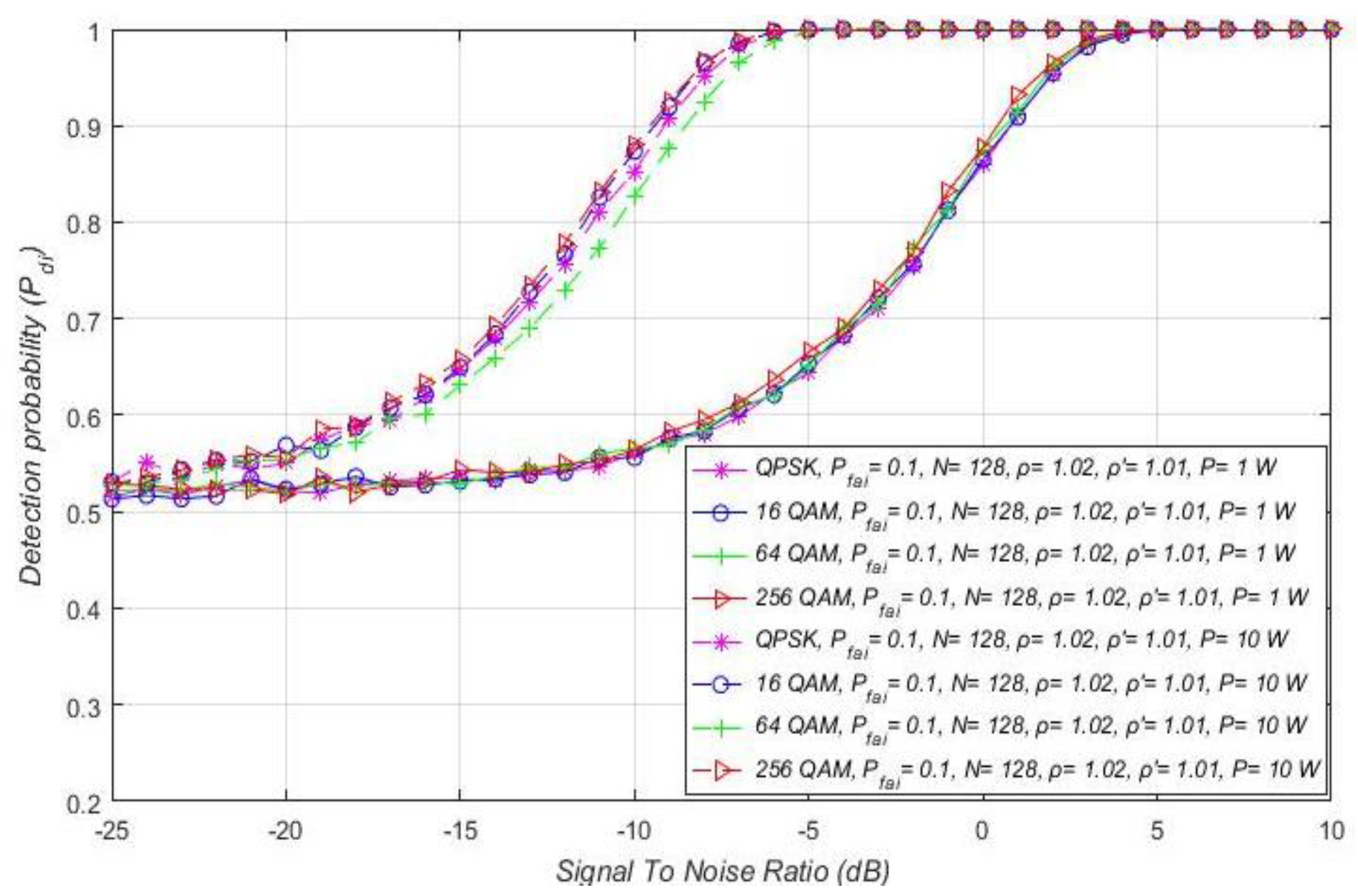
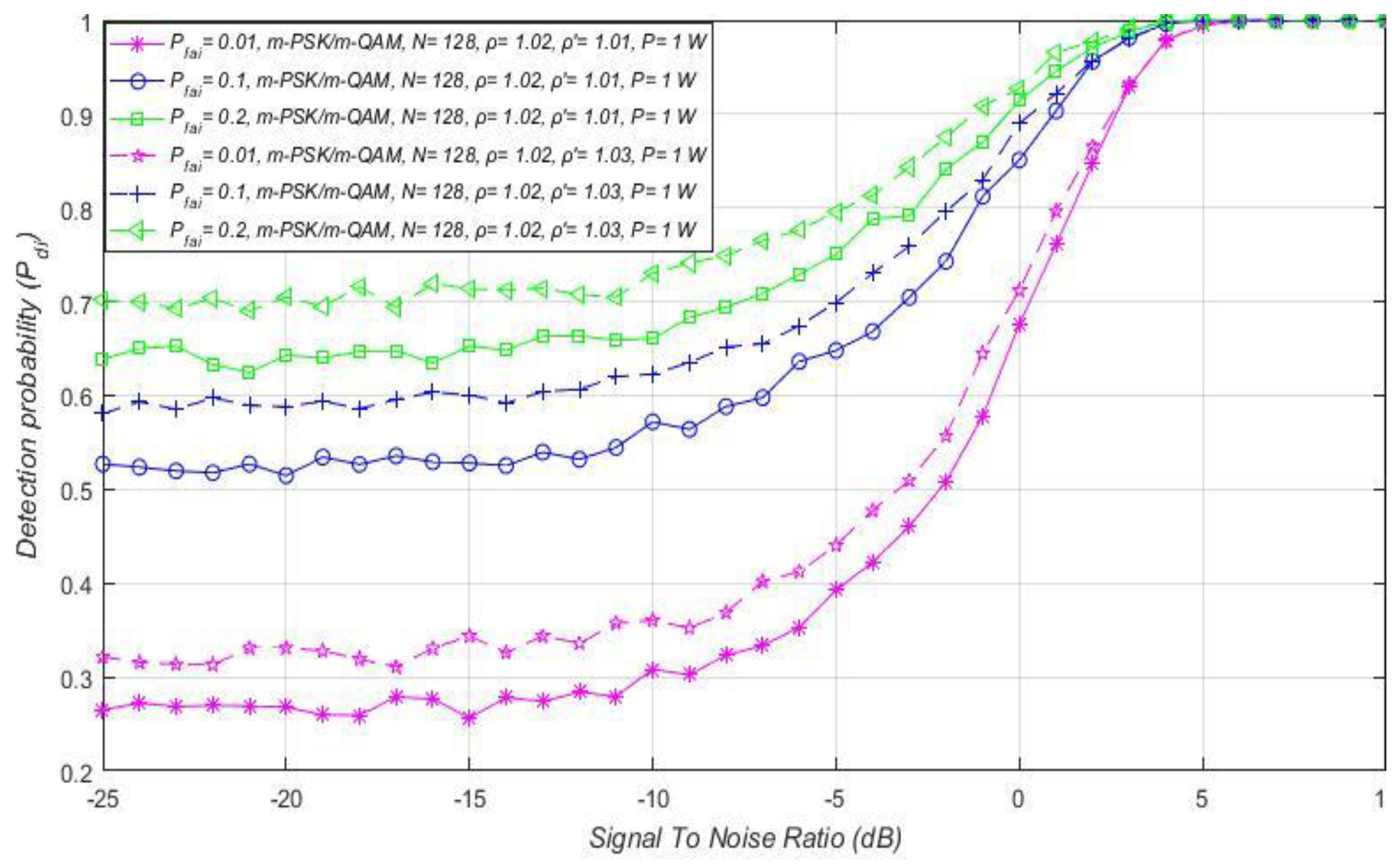
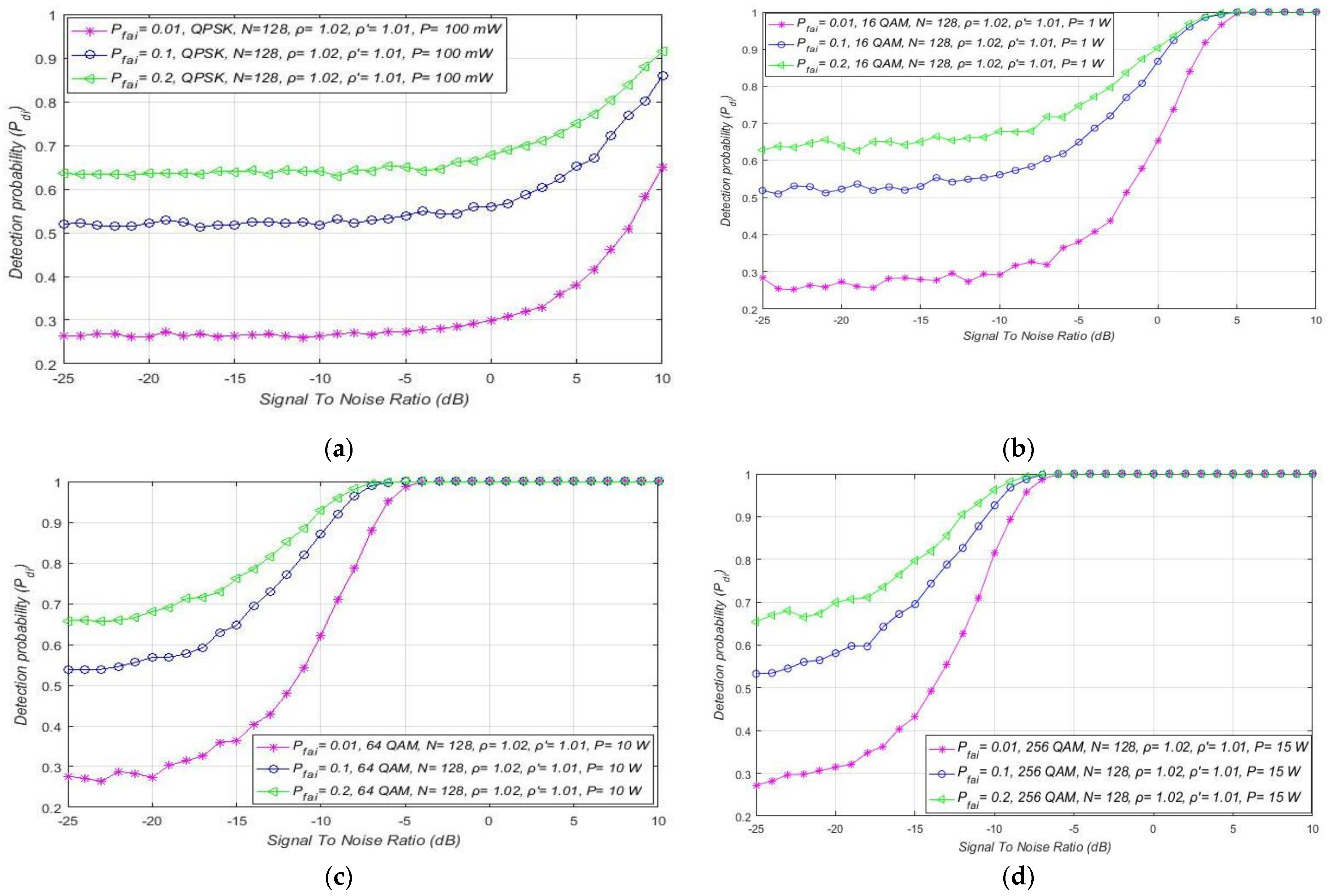
7.2. Influence of DT Adaptation on Performance of ED
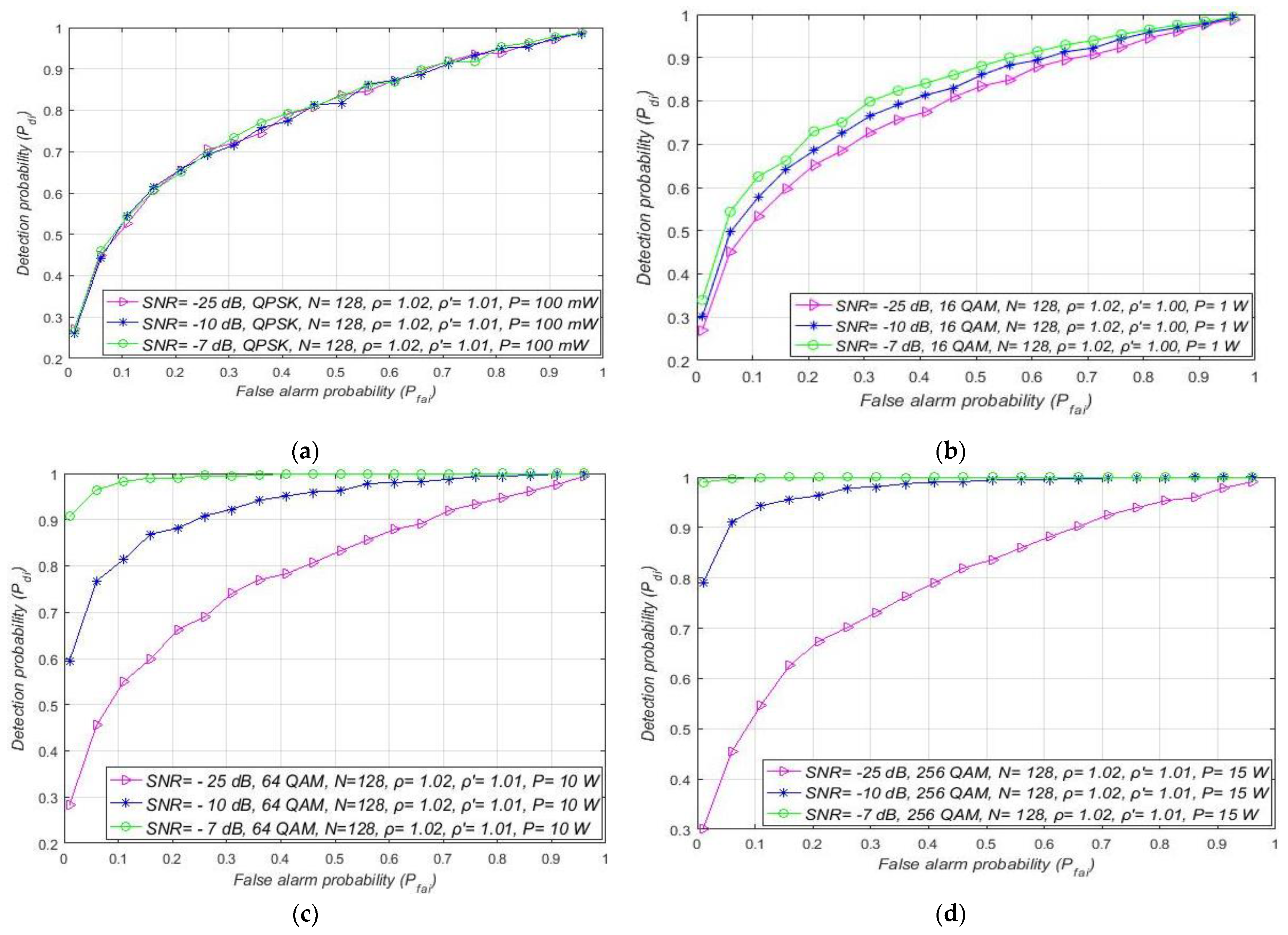
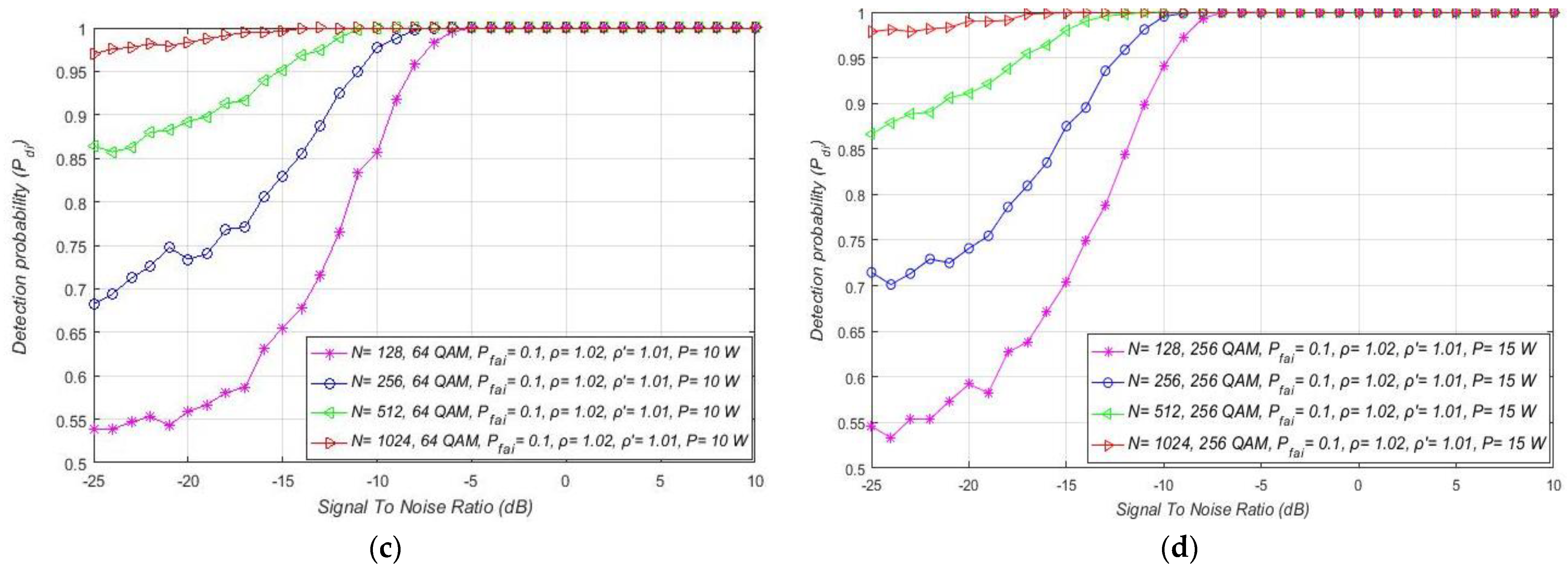
7.3. Impact of SNR on the ED Performance
7.4. Impact of the Sample Quantity on the ED Performance
7.5. Influence of the False Alarm Probability on the ED Performance
8. Future Challenges for the Enhancement of ED Limitations
8.1. Research Challenges Related to Noise Uncertainty
8.2. Research Challenges Related to the ED Degradation at Low SNRs
8.3. Research Challenges Related to Sensing Duration
8.4. Research Challenges Related to the Different SS Methods
8.5. Research Challenges Related to the Fading Channels and Hidden Node Problem
8.6. Research Challenges Related to the Users’ Distinction, Interference and Wideband Sensing
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ADC | Analogue to digital converter |
| AWGN | Additive white Gaussian noise |
| BER | Bit Error Rate |
| BPF | Band-pass filter |
| BPSK | Binary Phase Shift Keying |
| CDF | Cumulative distribution function |
| CDR | Constant detection rate |
| CFAR | Constant false alarm rate |
| CFD | Cyclostationary feature detection |
| CP | Cyclic prefix |
| CR | Cognitive radio |
| CRN | Cognitive radio networks |
| CWSN | Cognitive wireless sensor networks |
| DT | Dynamic threshold |
| EBD | Eigenvalue based detection |
| ED | Energy detection |
| END | Entropy detection |
| FFT | Fast Fourier transform |
| GFTD | Goodness of fit test detection |
| GI | Guard interval |
| IEEE | The Institute of Electrical and Electronics Engineers |
| IFFT | Inverse Fast Fourier Transform |
| IoT | Internet of Things |
| ISI | Inter-symbol interference |
| LTE | Long Term Evolution |
| LTE-A | Long Term Evolution-Advanced |
| MA | Margin adaptive |
| MFD | Matched filter detection |
| NU | Noise uncertainty |
| OFDM | Orthogonal frequency division multiplexing |
| OFDMA | Orthogonal frequency division multiplexing access |
| Probability density functions | |
| PU | Primary user |
| QAM | Quadrature Amplitude Modulation |
| QoS | Quality of service |
| QPSK | Quadrature Phase-Shift Keying |
| RA | Rate adaptive |
| RF | Radio frequency |
| ROC | Receiver Operating Characteristic |
| SINR | Signal to Interference plus Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| SS | Spectrum sensing |
| SU | Secondary user |
| WBD | Waveform based detection |
| WiMAX | Worldwide Interoperability for Microwave Access |
| WLAN | Wireless Local Area Network |
| WRAN | Wireless Regional Area Networks |
| 5G network | 5th generation network |
References
- Yin, S.; Chen, D.; Zhang, Q.; Liu, M.; Li, S. Mining spectrum usage data: A large-scale spectrum measurement study. IEEE Trans. Mob. Comput. 2012, 11, 1033–1046. [Google Scholar]
- Fortuna, C.; Mohorčič, M. Trends in the development of communication networks: Cognitive networks. Comput. Netw. 2009, 53, 1354–1376. [Google Scholar] [CrossRef]
- Pandit, S.; Singh, G. Spectrum sensing in cognitive radio networks: Potential challenges and future perspective in spectrum sharing in cognitive radio networks. In Spectrum Sharing in Cognitive Radio Networks, 1st ed.; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 35–73. [Google Scholar]
- Shi, Z.; Wu, Z.; Yin, Z.; Cheng, Q. Novel spectrum sensing algorithms for OFDM cognitive radio networks. Sensors 2015, 15, 13966–13993. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ghosh, M.; Challapali, K. Emerging cognitive radio applications: A survey. IEEE Commun. Mag. 2011, 49, 74–81. [Google Scholar] [CrossRef]
- Xiao, Y.; Hu, F. Cognitive Radio Networks, 1st ed.; Auerbach Publications: Boca Raton, FL, USA, 2008; pp. 3–37. [Google Scholar]
- Eduard, A.F.; Caballero, R.G.G. Experimental Evaluation of Performance for Spectrum Sensing: Matched Filter vs. Energy Detector. In Proceedings of the IEEE Colombian Conference on Communication and Computing (IEEE COLCOM 2015), Popayan, Colombia, 13–15 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Gorcin, A.; Qaraqe, K.A.; Celebi, H.; Arslan, H. An Adaptive Threshold Method for Spectrum Sensing in Multi-Channel Cognitive Radio Networks. In Proceedings of the 17th International Conference on Telecommunications, Doha, Qatar, 4–7 April 2010; pp. 425–429. [Google Scholar] [CrossRef]
- Thuo, N. An Adaptive Threshold Energy Detection Technique with Noise Variance Estimation for Cognitive Radio Sensor Networks. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2015. [Google Scholar]
- Wang, N.; Gao, Y.; Cuthbert, L. Spectrum Sensing Using Adaptive Threshold Based ED for OFDM Signals. In Proceedings of the 2014 IEEE International Conference on Communication Systems, Macau, China, 19–21 November 2014; pp. 359–363. [Google Scholar] [CrossRef]
- Rwodzi, J. Energy-Detection Based Spectrum Sensing for Cognitive Radio on a Real-Time SDR Platform. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2016. [Google Scholar]
- Ghasemi, A.; Sousa, E.S. Spectrum sensing in cognitive radio networks: Requirements, challenges and design trade-offs. IEEE Commun. Mag. 2008, 46, 32–39. [Google Scholar] [CrossRef]
- Çakir, A.C.; Yiğit, H. Spectrum Sensing Performance with Adaptive Threshold in MIMO Cognitive Radio. In Proceedings of the Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15 May 2017; pp. 1923–1926. [Google Scholar] [CrossRef]
- Dang, W.; Tao, M.; Mu, H.; Huang, J. Subcarrier-pair based resource allocation for cooperative multi-relay OFDM systems. IEEE Trans. Wirel. Commun. 2010, 9, 1640–1649. [Google Scholar] [CrossRef]
- Roy, P.; Dutta, S.; Dey, N.; Dey, G.; Chakraborty, S.; Ray, R. Adaptive Thresholding: A Comparative Study. In Proceedings of the 2014 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kanyakumari District, India, 10–11 July 2014; pp. 1182–1186. [Google Scholar] [CrossRef]
- Arar, A.M.; Masri, A.M.; Ghannam, H.O.; Tumar, I.K. A proposed scheme for dynamic threshold versus noise uncertainty in cognitive radio networks (DTNU). Wirel. Personal. Commun. 2017, 96, 4543–4555. [Google Scholar] [CrossRef]
- Yu, G.; Shao, Y.; Long, H.; Yue, G. Dynamic Threshold Based Spectrum Detection in Cognitive Radio Systems. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Nandhakumar, P.; Kumar, A. Analysis of OFDM system with energy detection spectrum sensing. Indian J. Sci. Technol. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Chen, Z.; Luan, T.; Zhang, X.D. Sensing orthogonal frequency division multiplexing systems for cognitive radio with cyclic prefix and pilot tones. IET Commun. 2012, 6, 97–106. [Google Scholar] [CrossRef]
- Zarrinkoub, H. Understanding LTE with MATLAB: From Mathematical Foundation to Simulation, Performance Evaluation and Implementation, 1st ed.; John Wiley & Sons: West Sussex, UK, 2014; pp. 72–85. [Google Scholar]
- Ndujiuba, C.U.; Oni, O.; Ibhaze, A.E. Comparative analysis of digital modulation techniques in LTE 4G systems. J. Wirel. Netw. Commun. 2015, 5, 60–66. [Google Scholar]
- Bedeer, E.; Dobre, O.A.; Ahmed, M.H.; Baddour, K.E. Optimal Bit and Power Loading for OFDM Systems with Average BER and Total Power Constraints. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 3685–3689. [Google Scholar]
- Makni, M.; Baklouti, M.; Niar, S.; Biglari-Abhari, M.; Abid, M. Heterogeneous Multi-Core Architecture for a 4G Communication in High-Speed Railway. In Proceedings of the 2015 10th International Design & Test Symposium (IDT), Amman, Jordan, 14–16 December 2015; pp. 26–31. [Google Scholar] [CrossRef]
- Dalai, J.; Patra, S.K. Spectrum Sensing for WLAN and WIMAX Using Energy Detection Technique. In Proceedings of the 2013 IEEE International Conference on Emerging Trends in Computing, Communication and Nanotechnology (ICECCN), Tirunelveli, India, 25–26 March 2013; pp. 620–624. [Google Scholar] [CrossRef]
- Hammouda, M.A.; Wallace, J.W. Noise Uncertainty in Cognitive Radio Sensing: Analytical Modeling and Detection Performance. In Proceedings of the 2012 International ITG Workshop on Smart Antennas (WSA), Dresden, Germany, 7–8 March 2012; pp. 287–293. [Google Scholar] [CrossRef]
- Axell, E.; Larsson, E.G. Optimal and suboptimal spectrum sensing of OFDM signals in known and unknown noise variance. IEEE J. Sel. Areas Commun. 2011, 29, 290–304. [Google Scholar] [CrossRef]
- Chin, W.L.; Kao, C.W.; Le, T.N. Advanced Spectrum Sensing for OFDM-Based Cognitive Radio Networks Using Cyclic Prefix. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Lei, Z.; Chin, F.P.S. Sensing OFDM systems under frequency-selective fading channels. IEEE Trans. Veh. Technol. 2010, 59, 1960–1968. [Google Scholar]
- Shi, Z.; McLernon, D.; Ghogho, M.; Wu, Z. Improved spectrum sensing for OFDM cognitive radio in the presence of timing offset. EURASIP J. Wirel. Commun. Netw. 2014, 1–9. [Google Scholar] [CrossRef]
- Awin, F.; Abdel-Raheem, E.; Tepe, K. Blind spectrum sensing approaches for interweaved cognitive radio system: A tutorial and short course. IEEE Commun. Surv. Tutor. 2019, 21, 238–259. [Google Scholar] [CrossRef]
- El Bahi, F.Z.; Ghennioui, H.; Zouak, M. Spectrum sensing technique of OFDM signal under noise uncertainty based on mean ambiguity function for cognitive radio. Phys. Commun. 2019, 33, 142–150. [Google Scholar] [CrossRef]
- Lorincz, J.; Begušić, D.; Ramljak, I. Misdetection Probability Analyses of OFDM Signals in Energy Detection Cognitive Radio Systems. In Proceedings of the 2018 26th International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 13–15 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zeng, Y.; Liang, Y.C.; Pham, T.H. Spectrum sesning for OFDM signals using pilot induced auto-corelations. IEEE J. Sel. Areas Commun. 2013, 31, 353–363. [Google Scholar] [CrossRef]
- Hwang, C.H.; Lai, G.L.; Chen, S.C. Spectrum sensing in wideband OFDM cognitive radios. IEEE Trans. Signal Proc. 2010, 58, 709–719. [Google Scholar] [CrossRef]
- Kumar, A.; NandhaKumar, P. OFDM system with cyclostationary feature detection spectrum sensing. ICT Express 2019, 5, 21–25. [Google Scholar] [CrossRef]
- Lorincz, J.; Ramljak, I.; Begušić, D. A review of the noise uncertainty impact on energy detection with different OFDM system designs. Comput. Commun. 2019, 148, 185–207. [Google Scholar] [CrossRef]
- Martian, A.; Al Sammarraie, M.J.A.; Vlădeanu, C.; Popescu, D.C. Three-event energy detection with adaptive threshold for spectrum sensing in cognitive radio systems. Sensors 2020, 20, 3614. [Google Scholar] [CrossRef]
- Hassan, S.M.; Eltholth, A.; Ammar, A.H. Double threshold weighted energy detection for asynchronous PU activities in the presence of noise uncertainty. IEEE Access 2020, 8, 177682–177692. [Google Scholar] [CrossRef]
- Sarkar, S.; Muralishankar, R.; Gurugopinath, S. Dynamic Threshold Correction Based on the Exact Statistics of Energy Detection in Spectrum Sensing. In Proceedings of the 2019 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2019; pp. 430–434. [Google Scholar] [CrossRef]
- Kockaya, K.; Develi, I. Spectrum sensing in cognitive radio networks: Threshold optimization and analysis. EURASIP J. Wirel. Commun. Netw. 2020, 255, 1–19. [Google Scholar]
- Wylie-Green, M. Dynamic Spectrum Sensing by Multiband OFDM Radio for Interference Mitigation. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MA, USA, 8–11 November 2005; pp. 619–625. [Google Scholar] [CrossRef]
- Takaharu, N. Radio Parameters of LTE-Advanced; Fujitsu Limited: Beijing, China, 2009. [Google Scholar]
- Tareco, P. WiMAX Capacity vs. Channel Bandwidth. Master’s. Thesis, University of Lisboa, Lisbon, Portugal, 2011. [Google Scholar]
- Martínez, D.M.; Andrade, Á.G. On the Reduction of the Noise Uncertainty Effects in Energy Detection for Spectrum Sensing in Cognitive Radios. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 1975–1979. [Google Scholar] [CrossRef]
- Yu, G.; Long, C.; Xiang, M.; Xi, W. A novel energy detection scheme based on dynamic threshold in cognitive radio systems. J. Comput. Inf. Syst. 2012, 8, 2245–2252. [Google Scholar]
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy Detection for Spectrum Sensing in Cognitive Radio; Springer: New York, NY, USA, 2014; pp. 11–38. [Google Scholar]
- Chabbra, K.; Banerjee, P. Effect of Dynamic Threshold & Noise Uncertainty in Energy Detection Spectrum Sensing Technique for Cognitive Radio Systems. In Proceedings of the 2014 International Conference on Signal Processing and Integrated Networks (SPIN), Delhi, India, 20–21 February 2014; pp. 361–377. [Google Scholar] [CrossRef]
- Plata, D.M.M.; Reátiga, Á.G.A. Evaluation of energy detection for spectrum sensing based on the dynamic selection of detection-threshold. Procedia Eng. 2012, 35, 135–143. [Google Scholar] [CrossRef]
- Ye, Z.; Memik, G.; Grosspietsch, J. Energy Detection Using Estimated Noise Variance for Spectrum Sensing in Cognitive Radio Networks. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March–3 April 2008; pp. 711–716. [Google Scholar] [CrossRef]
- Riviello, D.G. Spectrum Sensing Algorithms and Software-Defined Radio Implementation for Cognitive Radio Systems. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2016. [Google Scholar]
- Weidling, F.; Datla, D.; Petty, V.; Krishnan, P.; Minden, G. A Framework for RF Spectrum Measurements and Analysis. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MA, USA, 8–11 November 2005; pp. 573–576. [Google Scholar] [CrossRef]
- Oh, D.C.; Lee, Y.H. Energy detection based spectrum sensing for sensing error minimization in cognitive radio networks. Int. J. Commun. Netw. Inf. Sec. (IJCNIS) 2009, 1, 1–5. [Google Scholar]
- Lehtomaki, J.; Vartiainen, J.; Juntti, M.; Saarnisaari, H. Spectrum Sensing with Forward Methods. In Proceedings of the MILCOM 2006–2006 IEEE Military Communications Conference, Washington, DC, USA, 23–25 October 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Vartiainen, J.; Sarvanko, H.; Lehtomki, J.; Juntti, M.; Latva-Aho, M. Spectrum Sensing with LAD-Based Methods. In Proceedings of the 2007 IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007; pp. 1–5. [Google Scholar] [CrossRef]
- Tandra, R.; Sahai, A. SNR walls for signal detection. IEEE J. Sel. Top. Signal Process 2008, 2, 4–17. [Google Scholar] [CrossRef]
- Tandra, R.; Sahai, A. Fundamental Limits on Detection in Low SNR Under Noise Uncertainty. In Proceedings of the 2005 International Conference on Wireless Networks, Communications and Mobile Computing, Maui, HI, USA, 13–16 June 2005; pp. 464–469. [Google Scholar] [CrossRef]
- Gong, S.; Wang, P.; Liu, W.; Zhuang, W. Performance Bounds of Energy Detection with Signal Uncertainty in Cognitive Radio Networks. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2238–2246. [Google Scholar] [CrossRef]
- Lopez-Benitez, M.; Casadevall, F. Signal uncertainty in spectrum sensing for cognitive radio. IEEE Trans. Commun. 2013, 61, 1231–1241. [Google Scholar] [CrossRef]
- Lim, C.H. Adaptive energy detection for spectrum sensing in unknown white Gaussian noise. IET Commun. 2012, 6, 1884–1889. [Google Scholar] [CrossRef]
- Joshi, D.R.; Popescu, D.C.; Dobre, O.A. Adaptive Spectrum Sensing with Noise Variance Estimation for Dynamic Cognitive Radio Systems. In Proceedings of the 2010 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, NY, USA, 17–19 March 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Bao, Z.; Wu, B.; Ho, P.; Ling, X. Adaptive Threshold Control for Energy Detection Based Spectrum Sensing in Cognitive Radios. In Proceedings of the 2011 IEEE Global Telecommunications Conference—GLOBECOM 2011, Kathmandu, Nepal, 5–9 December 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Kumar, A.; Thakur, P.; Pandit, S.; Singh, G. Fixed and Dynamic Threshold Selection Criteria in Energy Detection for Cognitive Radio Communication Systems. In Proceedings of the 2017 Tenth International Conference on Contemporary Computing (IC3), Uttar Pradesh, India, 10–12 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Muralidharan, A.; Venkateswaran, P.; Ajay, S.G.; Prakash, D.A.; Arora, M.; Kirthiga, S. An Adaptive Threshold Method for Energy Based Spectrum Sensing in Cognitive Radio Networks. In Proceedings of the 2015 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kumaracoil, India, 18–19 December 2015; pp. 8–11. [Google Scholar]
- Sarker, M. Energy Detector Based Spectrum Sensing by Adaptive Threshold for Low SNR in CR Networks. In Proceedings of the 2015 24th Wireless and Optical Communication Conference (WOCC), Taipei, Taiwan, 7 December 2015; pp. 118–122. [Google Scholar] [CrossRef]
- Arjoune, Y.; Mrabet, Z.E.; Ghazi, H.E.; Tamtaoui, A. Spectrum Sensing: Enhanced Energy Detection Technique Based on Noise Measurement. In Proceedings of the 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–10 January 2018; pp. 828–834. [Google Scholar] [CrossRef]
- Yucek, T.; Arslan, H. A survey of spectrum sensing algorithms for cognitive radio applications. IEEE Commun. Surv. Tutor. 2009, 11, 116–130. [Google Scholar] [CrossRef]
- Wang, B.; Ray Liu, K.J. Advances in cognitive radio networks: A survey. IEEE J. Sel. Top. Signal Process. 2011, 5, 5–23. [Google Scholar] [CrossRef]
- Kim, H.; Shin, K.G. In-Band Spectrum Sensing in Cognitive Radio Networks: Energy Detection or Feature Detection? In Proceedings of the 14th Annual International Conference on Mobile Computing and Networking, MOBICOM 2008, San Francisco, CA, USA, 14–19 September 2008; pp. 14–25. [Google Scholar] [CrossRef]
- Torrieri, D.J. Principles of Military Communication Systems, 3rd ed.; Artech House Publishers: Dedham, MA, USA, 1981. [Google Scholar]
- Lehtomäki, J. Analysis of Energy Based Signal Detection. Ph.D. Thesis, University of Oulu, Oulu, Finland, 2005. [Google Scholar]
- Olivieri, M.P.; Barnett, G.; Lackpour, A.; Davis, A.; Ngo, P. A Scalable Dynamic Spectrum Allocation System with Interference Mitigation for Teams of Spectrally Agile Software Defined Radios. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 170–179. [Google Scholar] [CrossRef]
- Bhargavi, D.; Murthy, C.R. Performance Comparison of Energy, Matched-Filter and Cyclostationarity-Based Spectrum Sensing. In Proceedings of the 2010 IEEE 11th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Marrakech, Morocco, 20–23 June 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, C.; Li, M.; Jin, M.L. Blind energy-based detection for spatial spectrum sensing. IEEE Wirel. Commun. Lett. 2015, 4, 98–101. [Google Scholar] [CrossRef]
- Haykin, S.; Thomson, D.J.; Reed, J.H. Spectrum sensing for cognitive radio. Proc. IEEE 2009, 97, 849–877. [Google Scholar] [CrossRef]
- Cormiob, C.; Chowdhury, K.R. A survey on MAC protocols for cognitive radio networks. Ad Hoc Netw. 2009, 7, 1315–1329. [Google Scholar] [CrossRef]
- Liang, Y.C.; Zeng, E.P.Y.; Hoang, A.T. Sensing-Throughput Trade off for Cognitive Radio Networks. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 5330–5335. [Google Scholar] [CrossRef]
- Men, S. Spectrum Sensing Techniques in Cognitive Wireless Sensor Networks. Ph.D. Thesis, Université Bretagne Loire, Rennes, France, 2016. [Google Scholar]
- Joshi, G.P.; Nam, S.Y.; Kim, S.W. Cognitive radio wireless sensor networks: Applications, challenges and research trends. Sensors 2011, 13, 11196–11228. [Google Scholar] [CrossRef]
- Zahmati, A.S. Optimization of Spectrum Sensing Schemes in Cognitive Sensor Networks. Ph.D. Thesis, Ryerson University, Toronto, ON, Canada, 2013. [Google Scholar]
- Akan, O.B.; Karli, O.B.; Ergul, O. Cognitive radio sensor networks. IEEE Network 2009, 23, 34–40. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Arslan, H. Cognitive Radio, Software Defined Radio, and Adaptive Wireless Systems; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Nair, P.R.; Vinod, A.P.; Krishna, A.K. An Adaptive Threshold Based Energy Detector for Spectrum Sensing in Cognitive Radios at Low SNR. In Proceedings of the 2010 IEEE International Conference on Communication Systems, Singapore, 17–19 November 2010; pp. 574–578. [Google Scholar] [CrossRef]
- Arjoune, Y.; Mrabet, Z.E.; Kaabouch, N. Multi-attributes, utility-based, channel quality ranking mechanism for cognitive radio networks. Appl. Sci. 2018, 8, 628. [Google Scholar] [CrossRef]
- Airoldi, R.; Nurmi, J. Design of Matched Filter for Timing Synchronization. In Proceedings of the 2013 Conference on Design and Architectures for Signal and Image Processing, Cagliari, Italy, 8–10 October 2013; pp. 247–251. [Google Scholar]
- Arjoune, Y.; Kaabouch, N. A Comprehensive survey on spectrum sensing in cognitive radio networks: Recent advances, new challenges, and future research directions. Sensors 2019, 19, 126. [Google Scholar] [CrossRef] [PubMed]
- Tang, H. Some Physical Layer Issues of Wide-Band Cognitive Radio Systems. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 151–159. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. Spectrum Sensing via Energy Detector in Low SNR. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Lunden, J.; Koivunen, V.; Huttunen, A.; Poor, H. Spectrum Sensing in Cognitive Radios Based on Multiple Cyclic Frequencies. In Proceedings of the 2007 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Orlando, FL, USA, 1–3 August 2007; pp. 37–43. [Google Scholar] [CrossRef]
- Cabric, D.; Brodersen, R.W. Physical Layer Design Issues Unique to Cognitive Radio Systems. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; pp. 759–763. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, G.; Sun, C. Performance of Cyclostationary Features Based Spectrum Sensing Method in a Multiple Antenna Cognitive Radio System. In Proceedings of the 2009 IEEE Wireless Communications and Networking Conference, Budapest, Hungary, 12 May 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Verma, M.; Dua, R. Performance analysis of energy detection, matched filter detection & cyclostationary feature detection spectrum sensing techniques. Indian Streams Res. J. 2012, 2, 1296–1301. [Google Scholar]
- Turunen, V.; Kosunen, M.; Huttunen, A.; Kallioinen, S.; Ikonen, P.; Parssinen, A.; Ryynanen, J. Implementation of Cyclostationary Feature Detector for Cognitive Radios. In Proceedings of the 2009 4th International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Hannover, Germany, 22–24 June 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Srinu, S. Entropy Based Reliable Cooperative Spectrum Sensing for Cognitive Radio Networks. Ph.D. Thesis, University of Hyderabad, Hyderabad, India, 2013. [Google Scholar]
- Nagaraj, S.V. Entropy-based spectrum sensing in cognitive radio. Signal Process. 2009, 89, 174–180. [Google Scholar] [CrossRef]
- Srinu, S.; Sabat, S.L. FPGA implementation and performance study of spectrum sensing based on entropy estimation using cyclic features. Comput. Electr. Eng. 2012, 38, 1658–1669. [Google Scholar] [CrossRef]
- Zeng, Y.; Koh, C.L.; Liang, Y.C. Maximum Eigenvalue Detection: Theory and Application. In Proceedings of the 2008 IEEE International Conference on Communications, Beijing, China, 19–23 May 2008; pp. 4160–4164. [Google Scholar] [CrossRef]
- Penna, F.; Garello, R.; Spirito, M.A. Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in wishart matrices. IEEE Commun. Lett. 2009, 13, 507–509. [Google Scholar] [CrossRef]
- Zeng, Y.; Liang, Y.C. Eigenvalue-based spectrum sensing algorithms for cognitive radio. IEEE Trans. Commun. 2009, 57, 1784–1793. [Google Scholar] [CrossRef]
- Yang, X.; Lei, K.; Peng, S.; Cao, X. Blind detection for primary user based on the sample covariance matrix in cognitive radio. IEEE Commun. Lett. 2011, 15, 40–42. [Google Scholar] [CrossRef]
- Kortun, A.; Ratnarajah, T.; Sellathurai, M.; Zhong, C.; Papadias, C.B. On the performance of eigenvalue-based cooperative spectrum sensing for cognitive radio. IEEE J. Sel. Top. Signal Process. 2011, 5, 49–55. [Google Scholar] [CrossRef]
- Pillay, N.; Xu, H. Blind eigenvalue-based spectrum sensing for cognitive radio networks. IET Commun. 2012, 6, 1388–1396. [Google Scholar] [CrossRef]
- Bollig, A.; Mathar, R. MMME and DME: Two New Eigenvalue-Based Detectors for Spectrum Sensing in Cognitive Radio. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 1210–1213. [Google Scholar] [CrossRef]
- Huang, L.; Fang, J.; Liu, K.; So, H.C.; Li, H. An eigenvalue-moment-ratio approach to blind spectrum sensing for cognitive radio under sample-starving environment. IEEE Trans. Veh. Technol. 2015, 64, 3465–3480. [Google Scholar] [CrossRef]
- Shen, L.; Wang, H.; Zhang, W.; Zhao, Z. Blind spectrum sensing for cognitive radio channels with noise uncertainty. IEEE Trans. Wirel. Commun. 2011, 10, 1721–1724. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Koo, I. Empirical distribution-based event detection in wireless sensor networks: An approach based on evidence theory. IEEE Sens. J. 2012, 12, 2222–2228. [Google Scholar] [CrossRef]
- Kundargi, N.; Liu, Y.; Tewfik, A. A framework for inference using goodness of fit tests based on ensemble of phi- divergences. IEEE Trans. Signal Process. 2013, 61, 945–955. [Google Scholar] [CrossRef]
- Jin, M.; Guo, Q.; Xi, J.; Yu, Y. Spectrum sensing based on goodness of fit test with unilateral alternative hypothesis. Electron. Lett. 2014, 50, 1645–1646. [Google Scholar] [CrossRef]
- Patel, D.K.; Trivedi, Y.N. Goodness-of-fit-based non-parametric spectrum sensing under middleton noise for cognitive radio. Electron. Lett. 2015, 51, 419–421. [Google Scholar] [CrossRef]
- Scheers, B.; Teguig, D.; Nir, V.L. Wideband Spectrum Sensing Technique Based on Goodness-of-Fit Testing. In Proceedings of the 2015 International Conference on Military Communications and Information Systems (ICMCIS), Krakow, Poland, 18–19 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Teguig, D.; Nir, V.L.; Scheers, B. Spectrum sensing method based on goodness of fit test using chi-square distribution. Electron. Lett. 2014, 50, 713–715. [Google Scholar] [CrossRef]
- Teguig, D.; Nir, V.L.; Scheers, B. Spectrum sensing method based on likelihood ratio goodness-of-fit test. Electron. Lett. 2015, 51, 253–255. [Google Scholar] [CrossRef]
- Wang, H.; Yang, E.H.; Zhao, Z.; Zhang, W. Spectrum sensing in cognitive radio using goodness of fit testing. IEEE Trans. Wirel. Commun. 2009, 8, 5427–5430. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X.; Liang, Y.C.; Liu, J. Fast and robust spectrum sensing via Kolmogorov-Smirnov test. IEEE Trans. Commun. 2010, 58, 3410–3416. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Collaborative Spectrum Sensing for Opportunistic Access in Fading Environments. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 131–136. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Opportunistic spectrum access in fading channels through collaborative sensing. J. Commun. 2007, 2, 71–82. [Google Scholar] [CrossRef]
- Kostylev, V.I. Energy Detection of a Signal with Random Amplitude. In Proceedings of the 2002 IEEE International Conference on Communications, New York, NY, USA, 28 April–2 May 2002; pp. 1606–1610. [Google Scholar] [CrossRef]
- Digham, F.F.; Alouini, M.S.; Simon, M.K. On the energy detection of unknown signals over fading channels. IEEE Trans. Commun. 2007, 55, 3575–3579. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Impact of User Collaboration on the Performance of Sensing Based Opportunistic Spectrum Access. In Proceedings of the IEEE Vehicular Technology Conference, Montreal, QC, Canada, 25–28 September 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Cabric, D.; Tkachenko, A.; Brodersen, R. Spectrum Sensing Measurements of Pilot, Energy, and Collaborative Detection. In Proceedings of the MILCOM 2006–2006 IEEE Military Communications conference, Washington, DC, USA, 23–25 October 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Cabric, D. Addressing the feasibility of cognitive radios. IEEE Signal Process. Mag. 2008, 25, 85–93. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks. IEEE Trans. Wirel. Commun. 2007, 200, 3139–3143. [Google Scholar]
- Ganesan, G.; Li, Y.G. Agility Improvement Through Cooperation Diversity in Cognitive Radio. In Proceedings of the GLOBECOM ‘05. IEEE Global Telecommunications Conference, St. Louis, MO, USA, 28 November–2 December 2005; pp. 2505–2509. [Google Scholar] [CrossRef]
- Yoo, S.K.; Sofotasios, P.C.; Cotton, S.L.; Muhaidat, S.; Badarneh, O.S.; Karagiannidis, G.K. Entropy and energy detection-based spectrum sensing over F composite fading channels. IEEE Trans. Commun. 2019, 67, 4641–4653. [Google Scholar] [CrossRef]
- Zhang, W.; Letaief, K.B. Cooperative spectrum sensing with transmit and relay diversity in cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 7, 4761–4766. [Google Scholar] [CrossRef]
- Letaief, K.B.; Zhang, W. Cooperative communications for cognitive radio networks. Proc. IEEE 2009, 97, 878–893. [Google Scholar] [CrossRef]
- Jiang, H.; Lai, L.; Fan, R.; Poor, H. Optimal selection of channel sensing order in cognitive radio. IEEE Trans. Wirel. Commun. 2009, 8, 297–307. [Google Scholar] [CrossRef]
- Xie, S.; Liu, Y.; Zhang, Y.; Yu, R. A parallel cooperative spectrum sensing in cognitive radio networks. IEEE Trans. Veh. Technol. 2010, 59, 4079–4092. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Weiss, T.; Jondral, F.K. Calculation of detection and false alarm probabilities in spectrum pooling systems. IEEE Commun. Lett. 2005, 9, 349–351. [Google Scholar] [CrossRef]
- Suwanboriboon, S.; Lee, W. A Novel Two-Stage Spectrum Sensing for Cognitive Radio System. In Proceedings of the 2013 13th International Symposium on Communications and Information Technologies (ISCIT), Surat Thani, Thailand, 4–6 September 2013; pp. 176–181. [Google Scholar] [CrossRef]
- Wu, J.; Luo, T.; Yu, G. An Energy Detection Algorithm Based on Double-Threshold in Cognitive Radio Systems. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009; pp. 493–496. [Google Scholar] [CrossRef]
- Cabric, D.; Mishra, S.M.; Brodersen, R.W. Implementation Issues in Spectrum Sensing for Cognitive Radios. In Proceedings of the Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004; pp. 772–776. [Google Scholar] [CrossRef]
- Salahdine, F.; Ghazi, H.E.; Kaabouch, N.; Fihri, W.F. Matched Filter Detection with Dynamic Threshold for Cognitive Radio Networks. In Proceedings of the 2015 International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Kapoor, S.; Rao, S.; Singh, G. Opportunistic Spectrum Sensing by Employing Matched Filter in Cognitive Radio Network. In Proceedings of the 2011 International Conference on Communication Systems and Network Technologies, Katra, Jammu, India, 3–5 June 2011; pp. 580–583. [Google Scholar] [CrossRef]
- Iqbal, M.; Ghafoor, A. Analysis of Multiband Joint Detection Framework for Waveform-Based Sensing in Cognitive Radios. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Umar, R.; Sheikh, A.U.H.; Deriche, M.A. Unveiling the hidden assumptions of energy detector based spectrum sensing for cognitive radios. IEEE Commun. Surv. Tutor. 2013, 16, 713–728. [Google Scholar] [CrossRef]
- Yue, W.; Zheng, B. A Two-Stage Spectrum Sensing Technique in Cognitive Radio Systems Based on Combining Energy Detection and One-Order Cyclostationary Feature Detection. In Proceedings of the 2009 International Symposium on Web Information Systems and Applications, Nanchang, China, 22–24 May 2009; pp. 327–330. [Google Scholar]
- Nair, P.R.; Vinod, A.P.; Krishna, A.K. A Fast Two Stage Detector for Spectrum Sensing in Cognitive Radios. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011; pp. 1–5. [Google Scholar] [CrossRef]
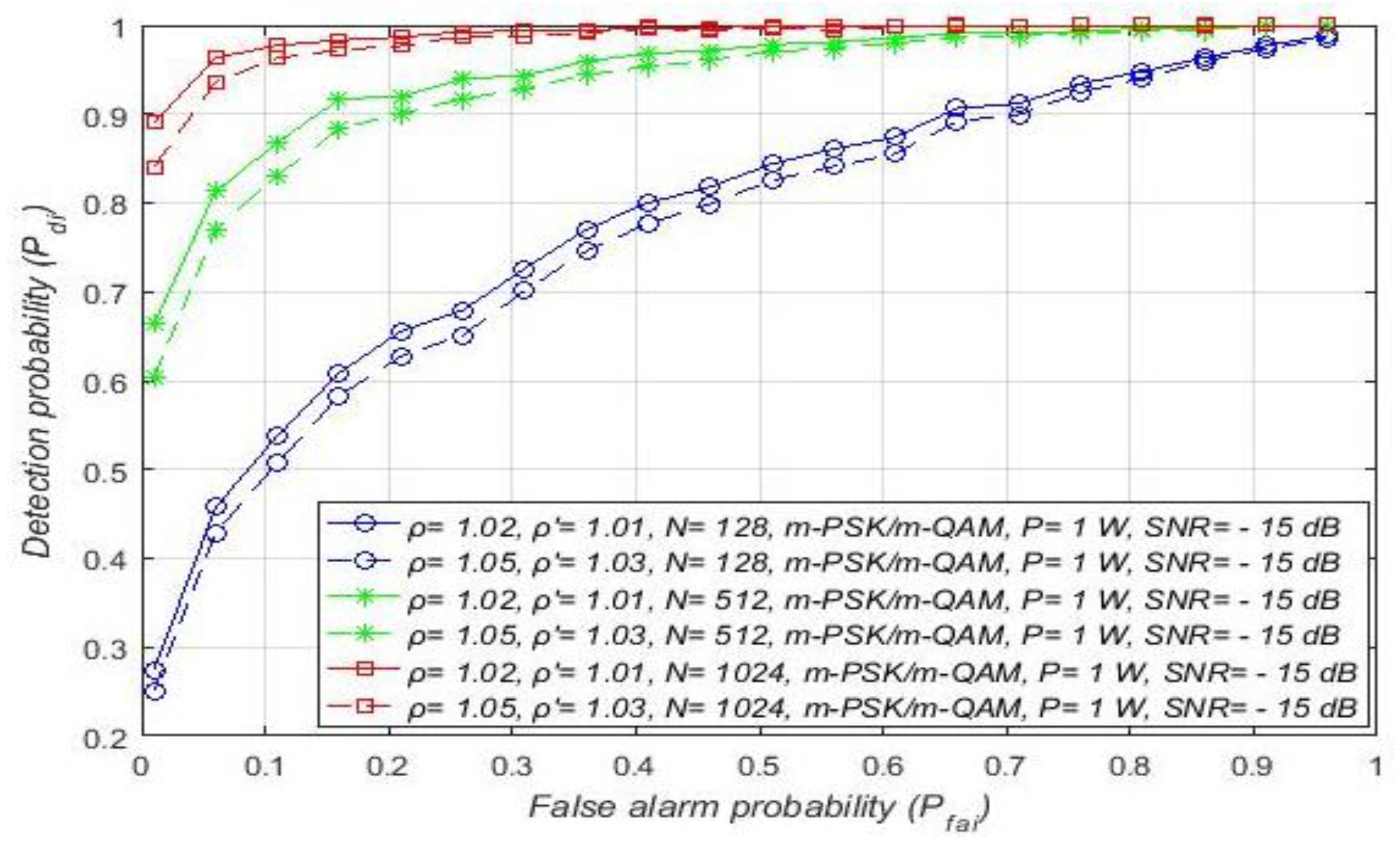
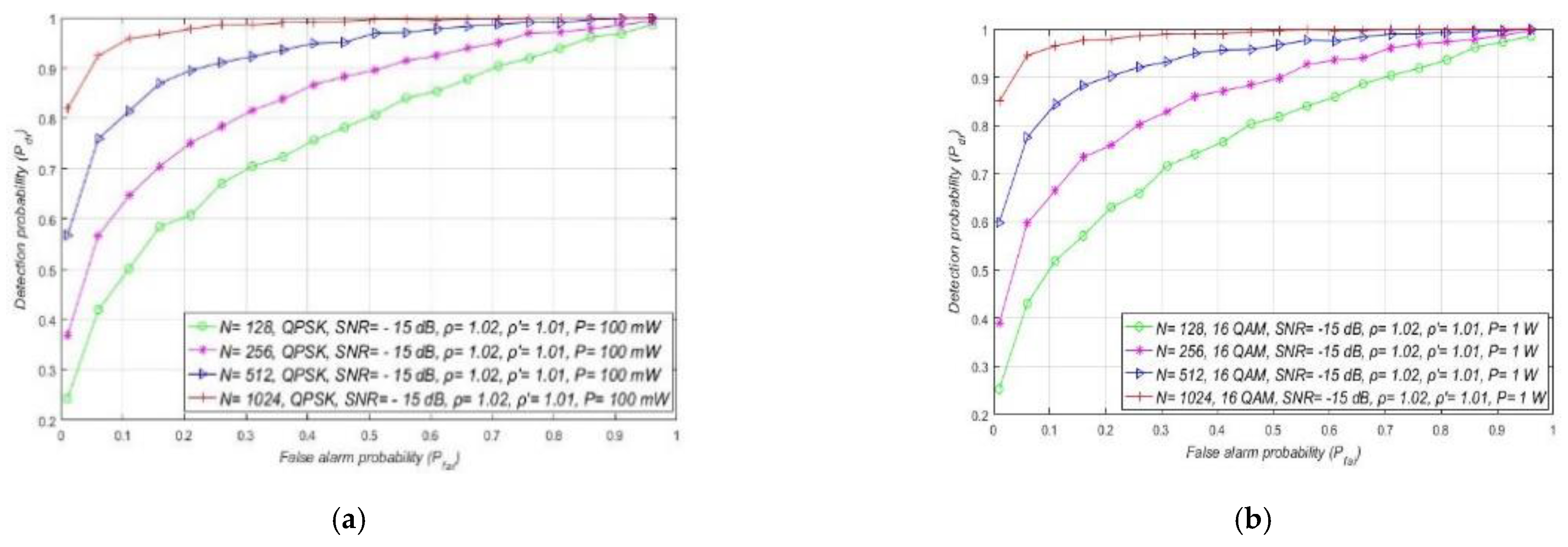
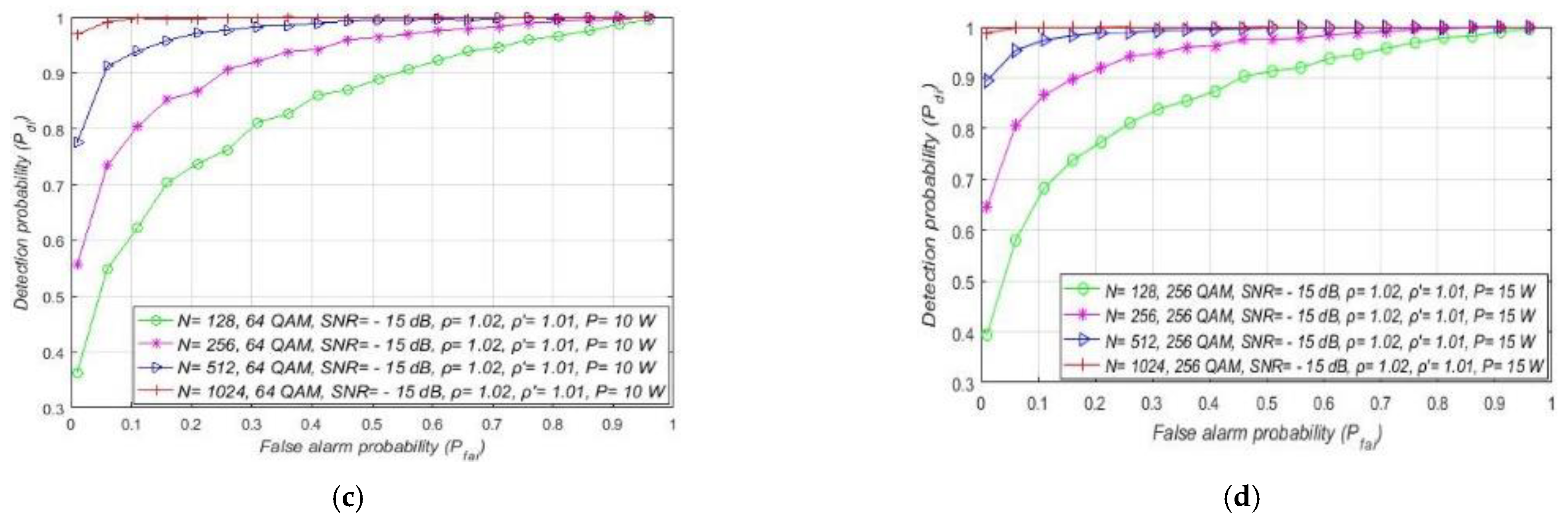
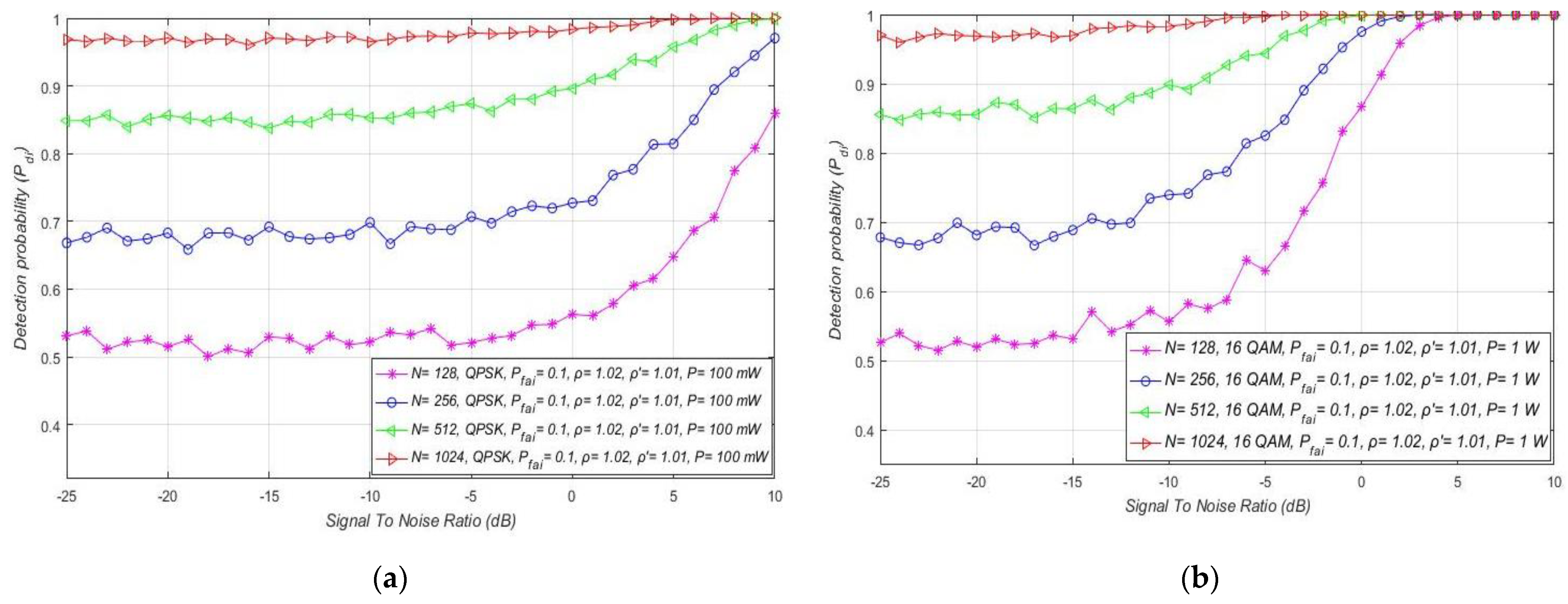
| Approach Analysed in the Literature | Description of the Analysed Approach | The Merit of the Analysed Approach |
|---|---|---|
| Only the ED approach with fixed detection threshold [7,18,24,27,34] | No influence related to the impact of NU and DT adaptation | The strong impact of NU and lack of DT adaptation significantly degrade the reliability of ED performance |
| The ED approach impacted by NU and without DT adaptation [12,25,26,28,30,31,32,36] | Analyses of ED performance taking into account the impact of the NU variations | Reduced detection probability of ED method due to impact of NU variation caused by thermal noise and interference from neighbor communication systems |
| The ED approach with DT adaptation and without the impact of NU variations [8,10,11,13,37] | Analyses of ED performance based on the selection of the appropriate value of the DT | Somewhat improved detection probability of ED method due to exploitation of DT adaptation but less realistic due to neglecting the impact of NU variations |
| The ED approach impacted by NU variations and performed using DT adaptation [9,16,17,38,39,40] | Analyses of ED performance based on the selection of the appropriate value of the DT impacted by the NU variations | The best detection probability of ED method and the most realistic approach for simulation and analyses |
| Index | Description |
|---|---|
| Hypothesis which determines the absence of the PU signal | |
| Hypothesis which determines the presence of the PU signal | |
| Averaged received signal for i-th SU and for n-th sample | |
| (n) | AWGN signal for i-th SU |
| Variance of AWGN signal for i-th SU without NU variations and DT adaptation | |
| AWGN variance (interval) for ED with NU variations and DT adaptation | |
| AWGN variance (interval) for ED with NU variations | |
| Transmitted i-th signal from the PU | |
| Energy test statistic signal level of the detected signal | |
| Detection threshold of i-th SU for ED without NU variations and DT adaptation | |
| Detection threshold based on CDR and without NU variations and DT adaptation | |
| False alarm threshold based on CFAR and without NU variations and DT adaptation | |
| DT (interval) for ED without NU variation | |
| DT (interval) for ED with DT adaptation and NU variation | |
| Detection probability for ED without NU and DT | |
| False alarm probability for ED without NU and DT | |
| Detection probability for ED with DT adaptation | |
| False alarm probability for ED with DT adaptation | |
| Detection probability for ED with NU variation | |
| False alarm probability for ED with NU variation | |
| Detection probability for ED with DT adaptation and NU variation | |
| False alarm probability for ED with DT adaptation and NU variation | |
| ρ | NU factor |
| DT factor | |
| Q | Standard Gaussian complementary CDF |
| Inverse standard Gaussian Complementary CDF | |
| Average received PU signal power at position of SU | |
| N | Overall sample quantity for ED without DT adaptation and NU variation |
| Overall sample quantity for ED with DT adaptation | |
| Overall sample quantity for ED with NU variation | |
| Overall sample quantity for ED with DT adaptation and NU variation |
| Parameters | Quantity |
|---|---|
| Modulation of PU signal | OFDM |
| Type of OFDM (constellation) | QPSK, 16 QAM, 64 QAM, 256 QAM |
| Type of channel noise | AWGN |
| Quantity N of samples (FFT size) | 128, 256, 512, 1024 |
| SNR range at SU position (dB) | −25–10 |
| The range of detection and false alarm probabilities | 0–1 |
| Quantity of Monte Carlo iterations per simulation | 10,000 |
| in the case of DT (ρ = 1.00) | 1.00 |
| in the case of NU and DT (ρ > 1.00, > 1.00) | 1.01 |
| 1.00, 1.02, 1.03, 1.05 | |
| 1.00, 1.01, 1.03, 1.05 |
| Major ED Disadvantages | Challenges in Future ED Research | Possible Enhancements |
|---|---|---|
| Reduction of detection precision as a consequence of variations in noise power (NU) [3,8,10,16,45,47,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64] | Implementation of new algorithms for optimal selection of DT and its assessment | Improvement of ED accuracy in environments impaired with noise fluctuations (NU) |
| Degradation of detection accuracy at low SNRs [55,56,65,66,67,68,69,70,71] | Development of new noise estimation techniques | Improvement of ED accuracy at lower SNRs |
| Reduction of detection accuracy for a low sample quantity [72,73,74,75,76,77,78,79,80,81,82] | Optimising detection time (sample quantity) for exact detection | Increase in throughput of SU, reduction in SU energy consumption (in CWSN) |
| The existence of more accurate local SS methods [7,77,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114] | Combining the ED approach with other approaches for SS at the same SU node | Ensuring desired sensing performance or accurate detection of specific idle bands |
| Degradation of detection accuracy due to fading channels and hidden node problem [66,68,115,116,117,118,119,120,121,122,123,124] | Novel collaboration approaches among SUs for reducing the impact of fading or hidden node problem | Improvement of ED robustness in fading channels and elimination of any hidden node problems |
| Inability to differentiate between interference, PU and SU signals [118,125,126,127,128,129] | Collaboration among distributed SUs based on combining ED with other detection methods in collaborative sensing | Elimination of the problem of PU, SU and interference distinction, and contribution to the improvement of wideband sensing |
| Parameters for Comparison with ED Method | Matched Filter Detection (MFD) | Cyclostationary Feature Detection (CFD) | Entropy Detection Method (END) | Waveform Based Detection (WBD) | Goodness of Fit Test Detection (GFTD) | Eigenvalue Based Detection (EBD) |
|---|---|---|---|---|---|---|
| [7,83,84,85,86,129,132,133] | [77,84,86,89,90,91,92,93,104] | [85,94,95,96] | [77,87,88,134,135] | [77,105,106,107,108,109,110,111,112,113,114] | [77,97,98,99,100,101,102,103,104] | |
| Detection accuracy at all SNRs compared to ED | Significantly better | Better | Better | Significantly better | Somewhat better | Better |
| Amount of prior PU information compared to ED | Significantly higher | Higher | Equal (no PU information) | Higher | Equal (no PU information) | Equal (no PU information) |
| Sensing time (sample quantity) for accurate | Lower | Similar | Similar | Lower | Lower | Similar |
| Robustness against NU compared to ED | More robust | Significantly more robust | More robust | More robust | Similar | More robust |
| Computational complexity compared to ED | More complex | Significantly complex | More complex | More complex | Somewhat complex | More complex |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorincz, J.; Ramljak, I.; Begušić, D. A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges. Sensors 2021, 21, 3080. https://doi.org/10.3390/s21093080
Lorincz J, Ramljak I, Begušić D. A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges. Sensors. 2021; 21(9):3080. https://doi.org/10.3390/s21093080
Chicago/Turabian StyleLorincz, Josip, Ivana Ramljak, and Dinko Begušić. 2021. "A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges" Sensors 21, no. 9: 3080. https://doi.org/10.3390/s21093080
APA StyleLorincz, J., Ramljak, I., & Begušić, D. (2021). A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges. Sensors, 21(9), 3080. https://doi.org/10.3390/s21093080








