Impact of Transmitter Positioning and Orientation Uncertainty on RSS-Based Visible Light Positioning Accuracy †
Abstract
1. Introduction
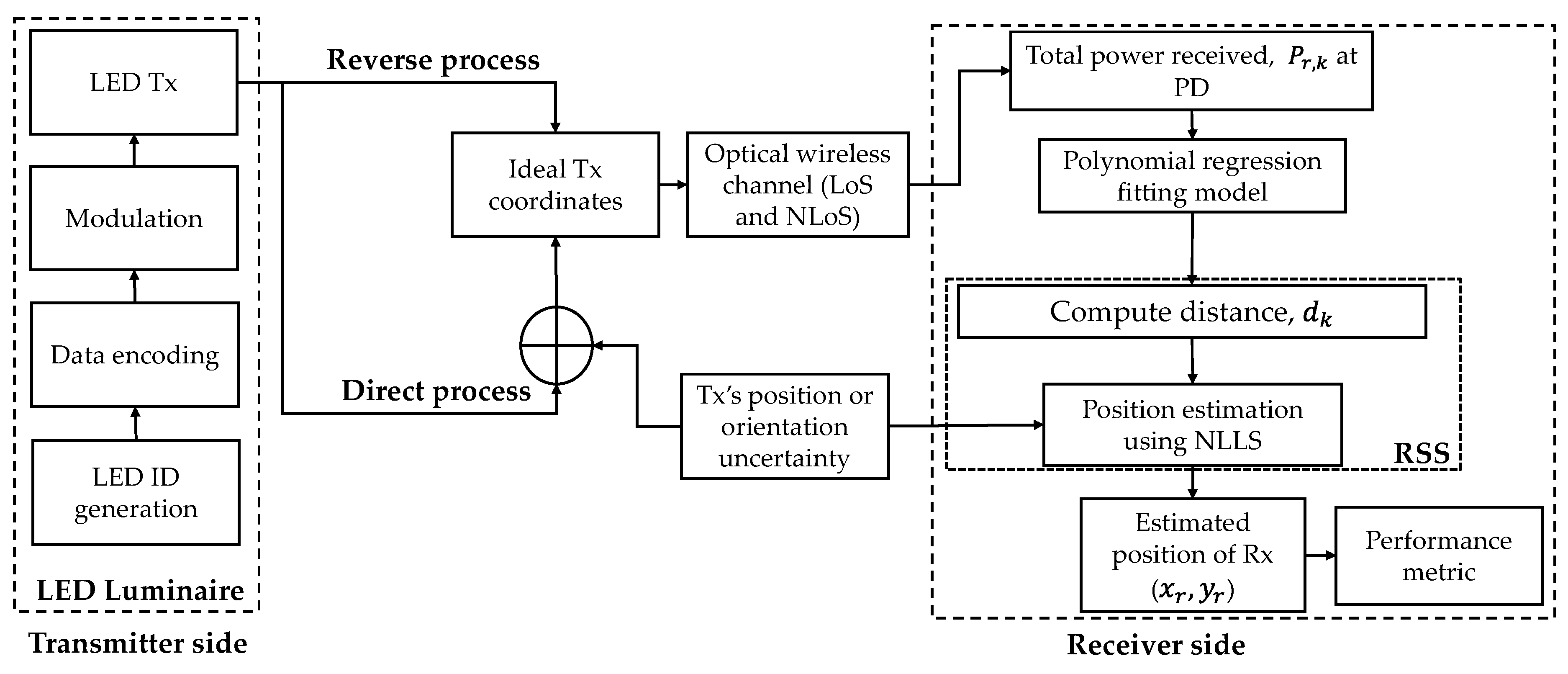
2. VLP System Modelling
2.1. Channel Model
2.2. RSS-Based Positioning
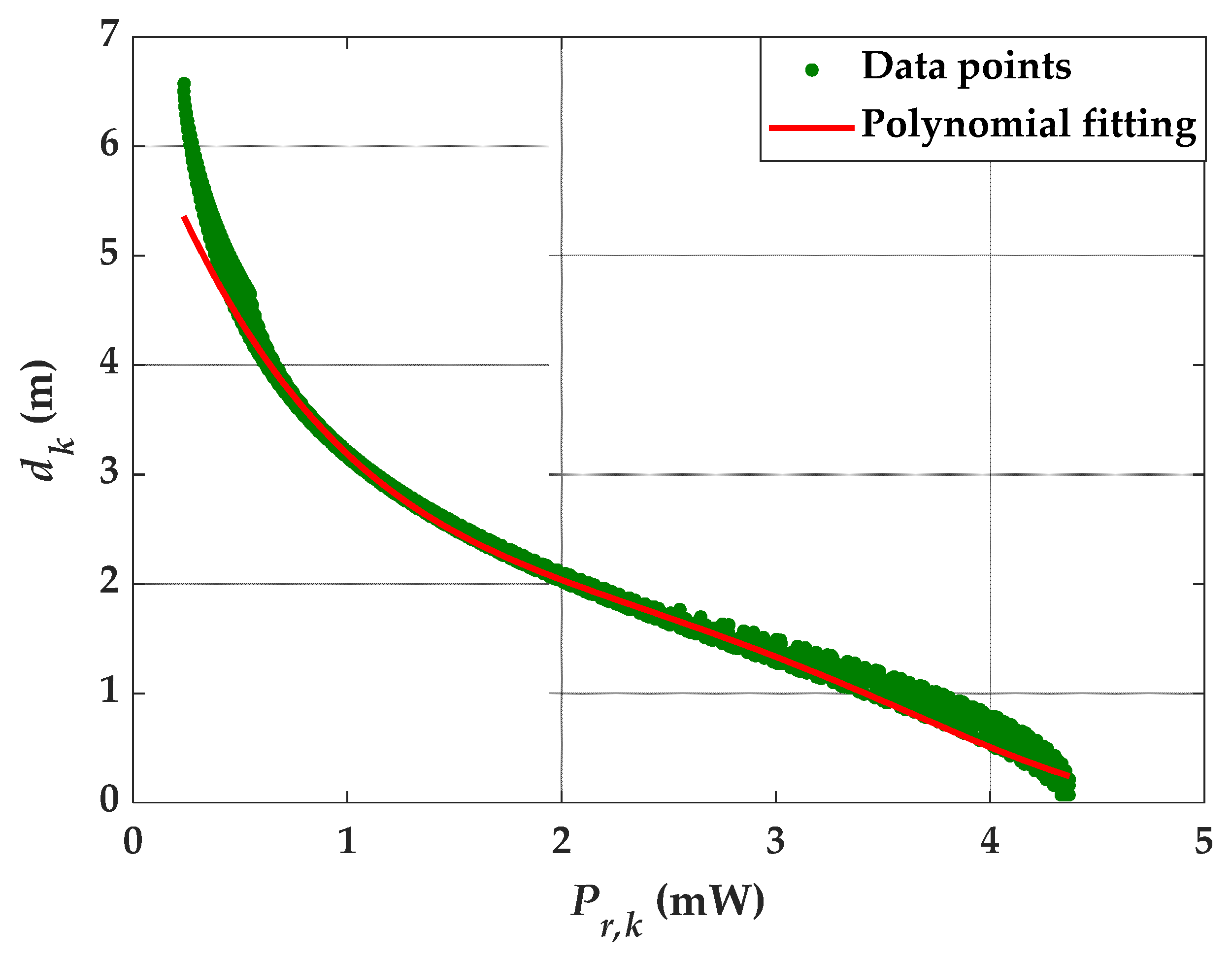
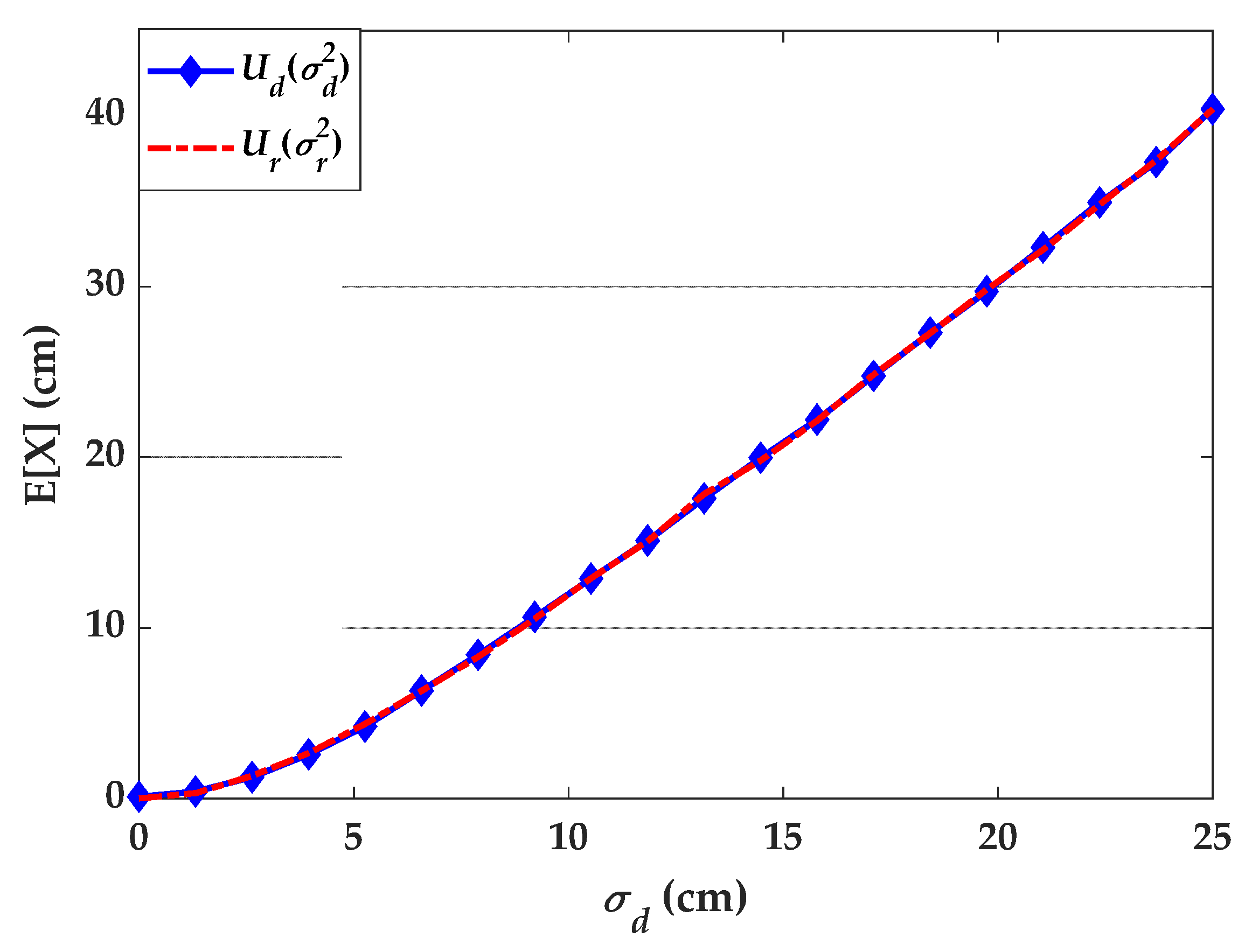
2.3. Distance Estimation Using Polynomial Regression
2.4. Estimation Using Nonlinear Least Squares
2.5. Performance Metrics
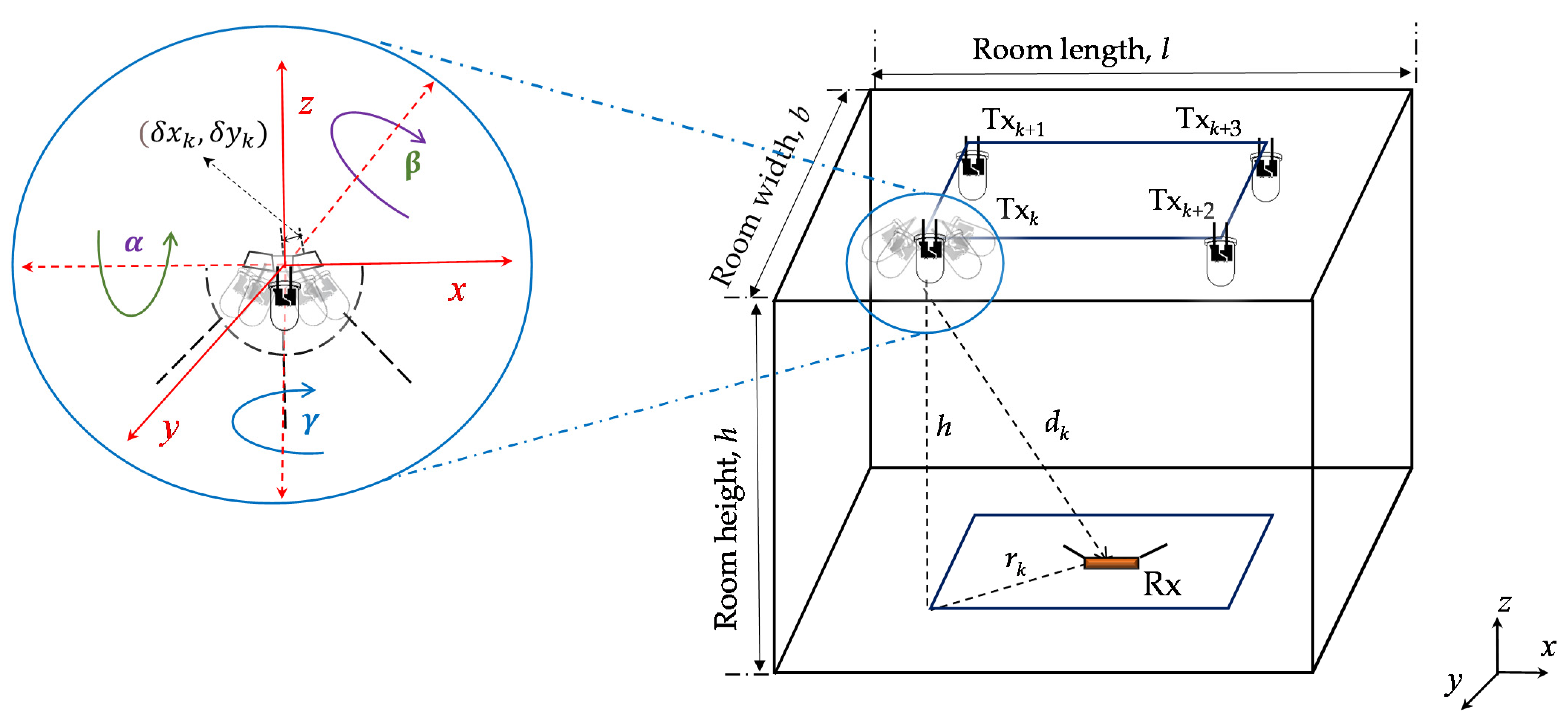
3. Set-Up Uncertainties
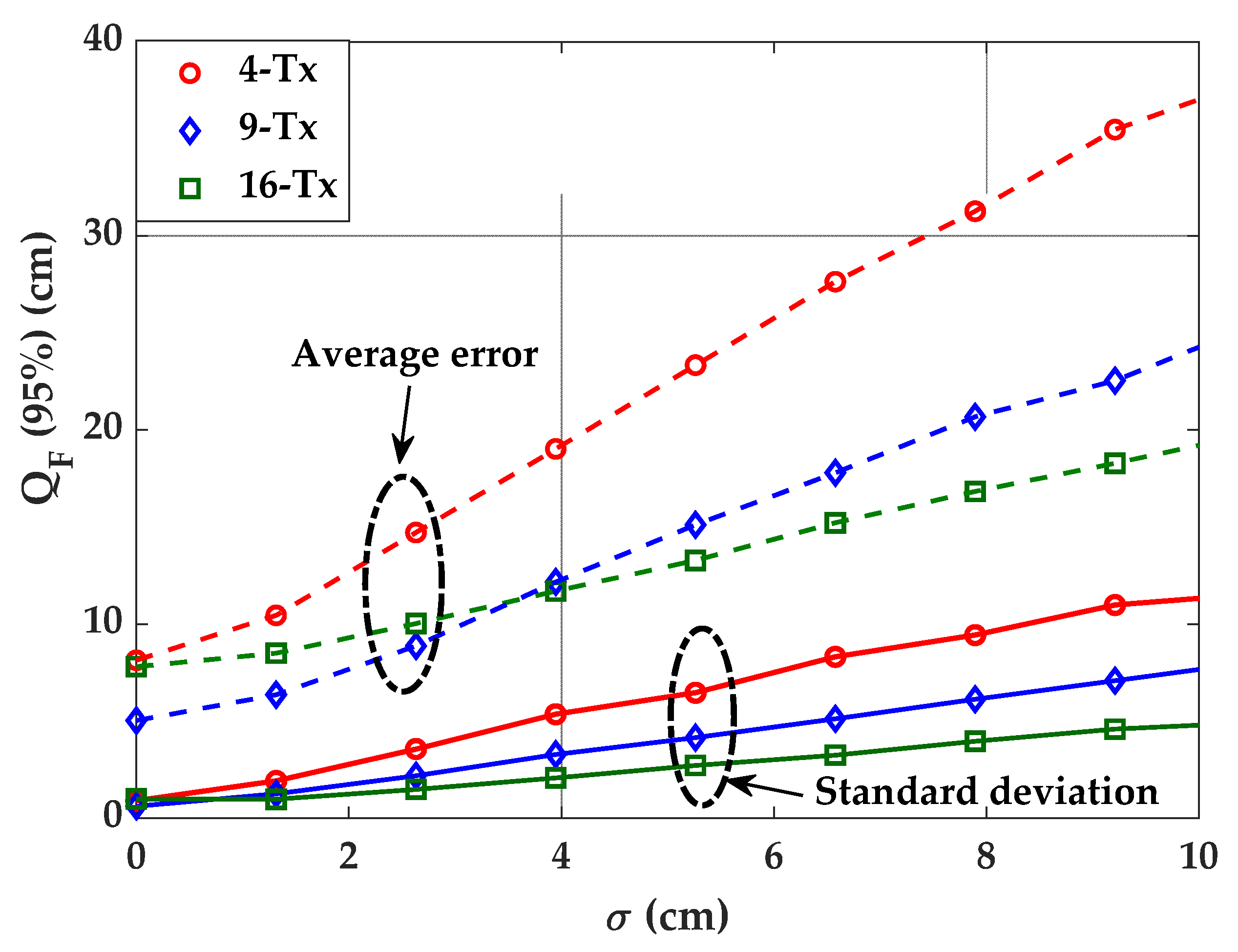
3.1. Uncertainties of the Tx’s Position
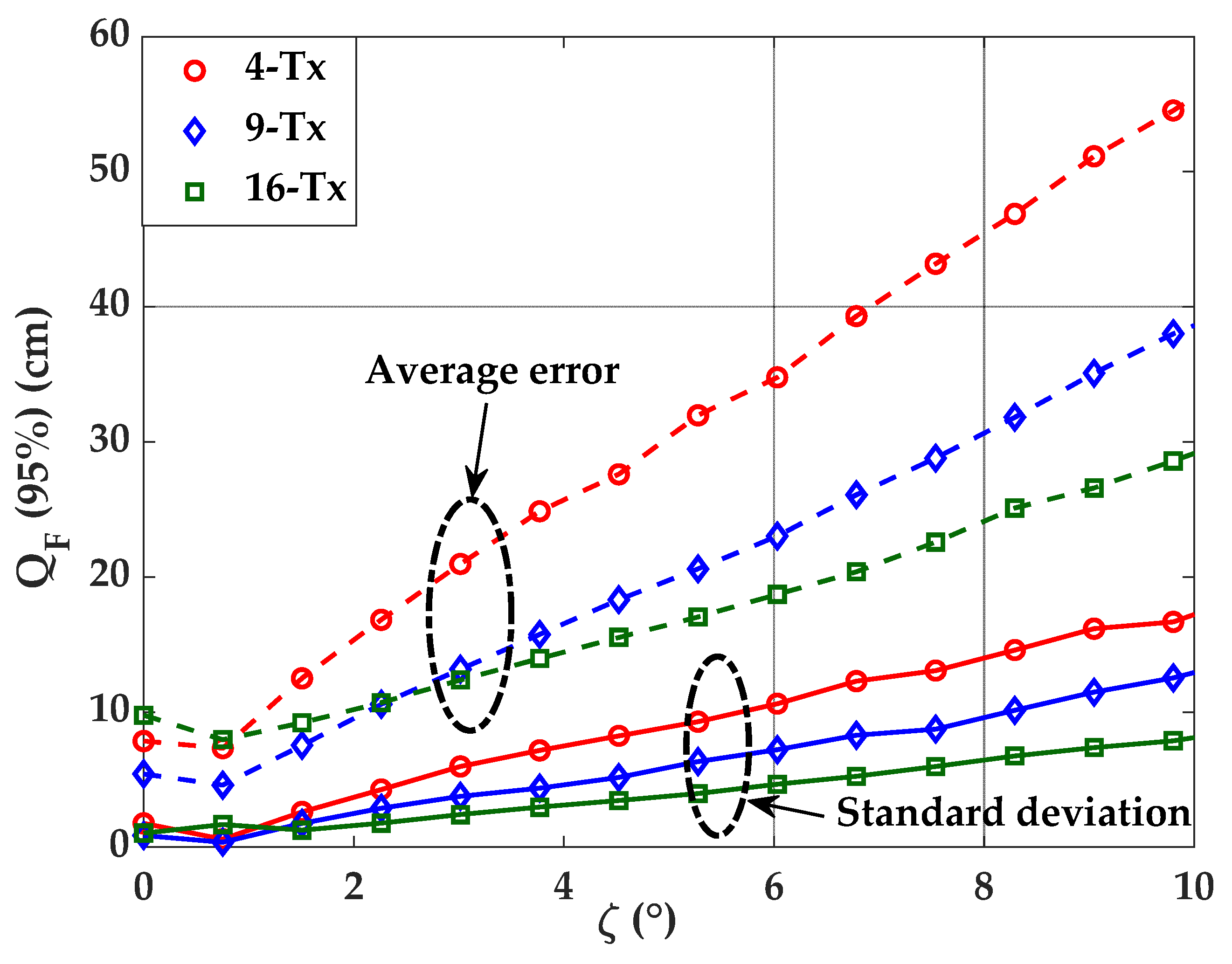
3.2. Uncertainties of the Tx’s Orientation
3.3. Lighting Uniformity
4. Simulation Results
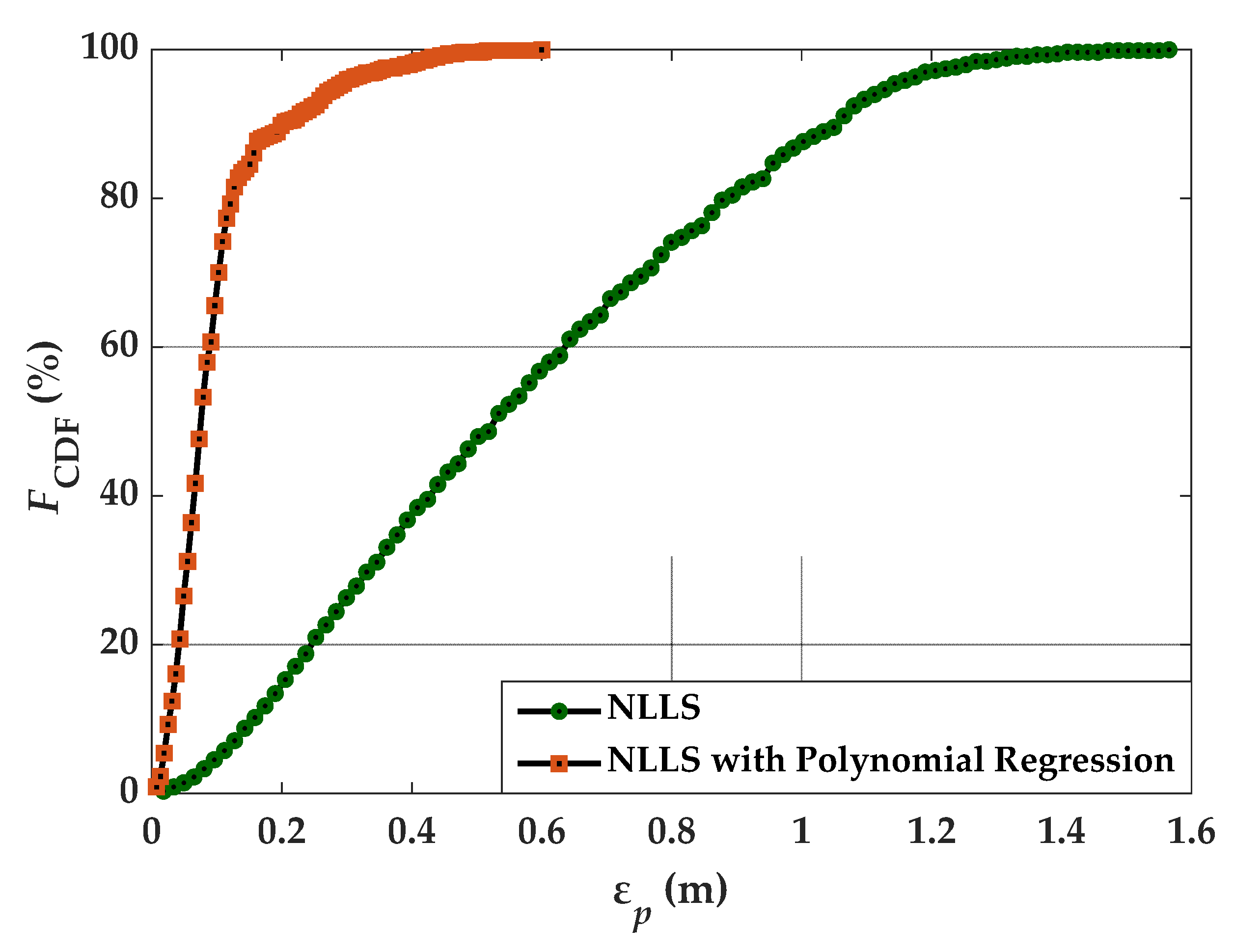
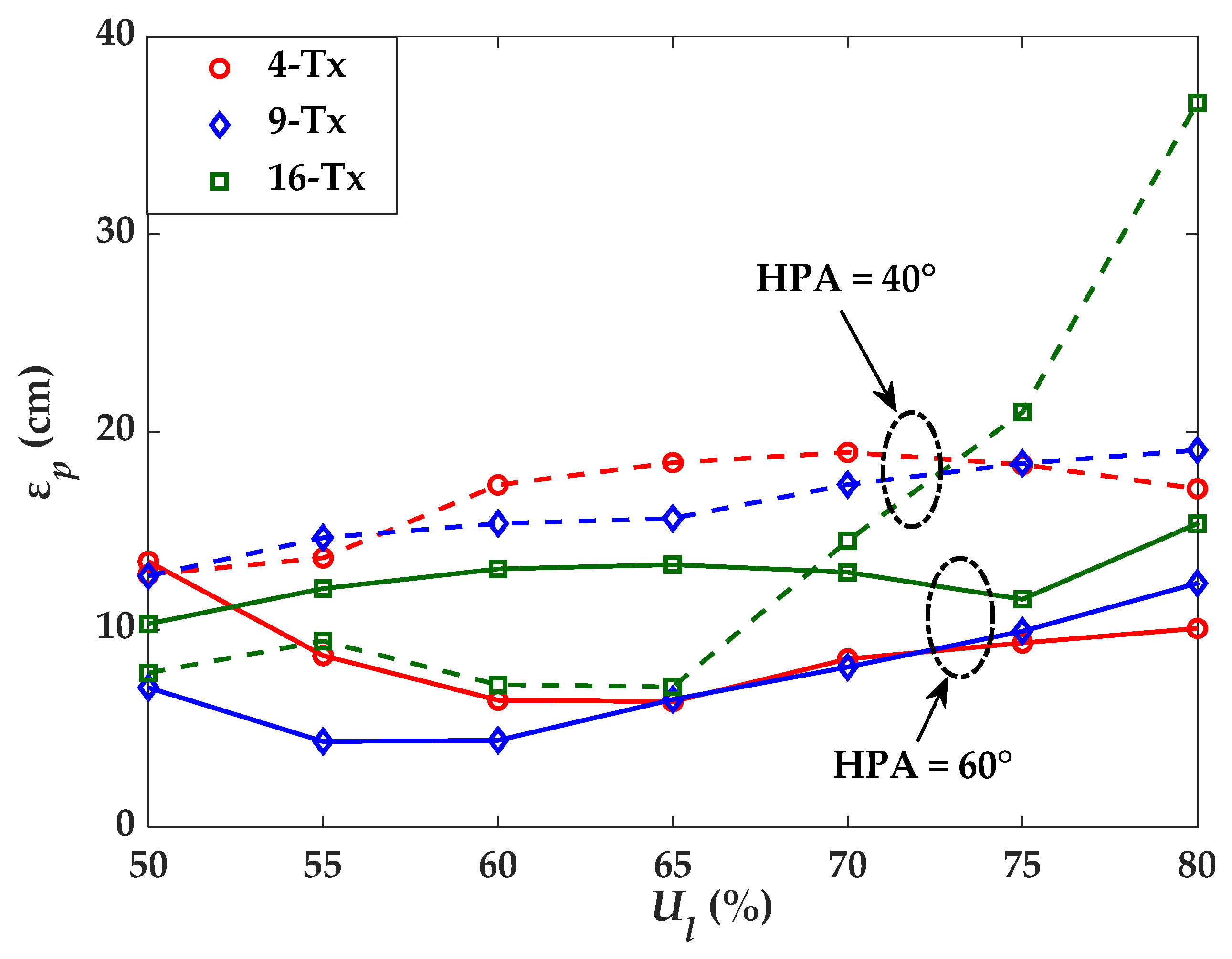
4.1. Positioning Error Dependence on Lighting Uniformity
4.2. Impact of Tx’s Position and Orientation Uncertainty on Error Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ADOA | Angle difference of arrival |
| ANN | Artificial neural network |
| AOA | Angle of arrival |
| CDF | Cumulative distribution function |
| FOV | Field of view |
| GPS | Global positioning system |
| HPA | Half power angle |
| IoT | Internet of things |
| IP | Indoor positioning |
| LEDs | Light-emitting diodes |
| LLS | Linear least square |
| LOS | Line of sight |
| NLLS | Nonlinear least square |
| NLOS | Non-line of sight |
| OOK | On-off keying |
| PD | Photodiode |
| Probability distribution function | |
| PR | Polynomial regression |
| RF | Radio frequency |
| RFID | Radio frequency identification |
| RSS | Received signal strength |
| Rx | Receiver |
| SNR | Signal-to-noise ratio |
| TDOA | Time difference of arrival |
| TOA | Time of arrival |
| Tx | Transmitter |
| UWB | Ultra-wide band |
| VLC | Visible light communication |
| VLP | Visible light positioning |
References
- Chaudhary, N.; Alves, L.N.; Ghassemblooy, Z. Current Trends on Visible Light Positioning Techniques. In Proceedings of the 2019 2nd West Asian Colloquium on Optical Wireless Communications (WACOWC), Tehran, Iran, 27–28 April 2019; pp. 100–105. [Google Scholar]
- Do, T.-H.; Yoo, M. An In-Depth Survey of Visible Light Communication Based Positioning Systems. Sensors 2016, 16, 678. [Google Scholar] [CrossRef] [PubMed]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef]
- Gezici, S.; Tian, Z.; Giannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, H.V.; Sahinoglu, Z. Localization via Ultra-Wideband Radios: A Look at Positioning Aspects for Future Sensor Networks. IEEE Signal Process. Mag. 2005, 22, 70–84. [Google Scholar] [CrossRef]
- Tariq, Z.B.; Cheema, D.M.; Kamran, M.Z.; Naqvi, I.H. Non-GPS Positioning Systems: A Survey. ACM Comput. Surv. 2017, 50, 1–34. [Google Scholar] [CrossRef]
- Luo, J.; Fan, L.; Li, H. Indoor Positioning Systems Based on Visible Light Communication: State of the Art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- Armstrong, J.; Sekercioglu, Y.; Neild, A. Visible Light Positioning: A Roadmap for International Standardization. IEEE Commun. Mag. 2013, 51, 68–73. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, Q.; Shi, M.; Cao, P.; Qi, L.; Yang, J. Low-Power Centimeter-Level Localization for Indoor Mobile Robots Based on Ensemble Kalman Smoother Using Received Signal Strength. IEEE Internet Things J. 2019, 6, 6513–6522. [Google Scholar] [CrossRef]
- Zhu, B.; Cheng, J.; Wang, Y.; Yan, J.; Wang, J. Three-Dimensional VLC Positioning Based on Angle Difference of Arrival With Arbitrary Tilting Angle of Receiver. IEEE J. Sel. Areas Commun. 2018, 36, 8–22. [Google Scholar] [CrossRef]
- Xu, J.; Gong, C.; Xu, Z. Experimental Indoor Visible Light Positioning Systems With Centimeter Accuracy Based on a Commercial Smartphone Camera. IEEE Photonics J. 2018, 10, 1–17. [Google Scholar] [CrossRef]
- Naeem, A.; Hassan, N.U.; Pasha, M.A.; Yuen, C.; Sikora, A. Performance Analysis of TDOA-Based Indoor Positioning Systems Using Visible LED Lights. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, 20–21 September 2018; pp. 103–107. [Google Scholar]
- Xie, C.; Guan, W.; Wu, Y.; Fang, L.; Cai, Y. The LED-ID Detection and Recognition Method Based on Visible Light Positioning Using Proximity Method. IEEE Photonics J. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Stevens, N.; Martens, L.; Joseph, W. Monte-Carlo Simulation of the Impact of LED Power Uncertainty on Visible Light Positioning Accuracy. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar]
- Gu, W.; Aminikashani, M.; Deng, P.; Kavehrad, M. Impact of Multipath Reflections on the Performance of Indoor Visible Light Positioning Systems. J. Light. Technol. 2016, 34, 2578–2587. [Google Scholar] [CrossRef]
- Mousa, F.I.K.; Almaadeed, N.; Busawon, K.; Bouridane, A.; Binns, R.; Elliot, I. Indoor Visible Light Communication Localization System Utilizing Received Signal Strength Indication Technique and Trilateration Method. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Wang, X.; Shen, J. Machine Learning and Its Applications in Visible Light Communication Based Indoor Positioning. In Proceedings of the 2019 International Conference on High Performance Big Data and Intelligent Systems (HPBD&IS), Shenzhen, China, 9–11 May 2019; pp. 274–277. [Google Scholar]
- Shawky, S.; El-Shimy, M.A.; El-Sahn, Z.A.; Rizk, M.R.M.; Aly, M.H. Improved VLC-Based Indoor Positioning System Using a Regression Approach with Conventional RSS Techniques. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 904–909. [Google Scholar]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W. An Analysis of the Impact of LED Tilt on Visible Light Positioning Accuracy. Electronics 2019, 8, 389. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W. Performance Assessment of Artificial Neural Networks on the RSS-Based Visible Light Positioning Accuracy with Random Transmitter Tilt. In Proceedings of the CSNDSP, Porto, Portugal, 20–22 July 2020; Volume 8, p. 389. [Google Scholar]
- Chaudhary, N.; Alves, L.N.; Ghassemlooy, Z. Impact of Transmitter Positioning Uncertainty on RSS-Based Visible Light Positioning Accuracy. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20 July 2020; pp. 1–6. [Google Scholar]
- Shi, G.; Li, Y.; Cheng, W. Accuracy Analysis of Indoor Visible Light Communication Localization System Based on Received Signal Strength in Non-Line-of-Sight Environments by Using Least Squares Method. Opt. Eng. 2019, 58, 1. [Google Scholar] [CrossRef]
- Ghassemblooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab®; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chaudhary, N.; Alves, L.N.; Ghassemblooy, Z. Feasibility Study of Reverse Trilateration Strategy with a Single Tx for VLP. In Proceedings of the 2019 2nd West Asian Colloquium on Optical Wireless Communications (WACOWC), Tehran, Iran, 27–28 April 2019; pp. 121–126. [Google Scholar]
- Sun, X.; Duan, J.; Zou, Y.; Shi, A. Impact of Multipath Effects on Theoretical Accuracy of TOA-Based Indoor VLC Positioning System. OSA Publishing: Washington, DC, USA, 2015; Volume 4. [Google Scholar]
- Chaudhary, N.; Younus, O.I.; Alves, L.N.; Ghassemlooy, Z.; Zvanovec, S.; Le-Minh, H. An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy. Sensors 2021, 21, 920. [Google Scholar] [CrossRef] [PubMed]
- Shiquan, W. Computation of a Trust Region Step. ACTA Math. Appl. Sin. 1991, 7, 354–362. [Google Scholar]
- Hu, Y.; Luo, M.R.; Yang, Y. A Study on Lighting Uniformity for LED Smart Lighting System. In Proceedings of the 2015 12th China International Forum on Solid State Lighting (SSLCHINA), Shenzhen, China, 2–4 November 2015; pp. 127–130. [Google Scholar]



| Polynomial Coefficient | |||||
|---|---|---|---|---|---|
| Value | 7.4 |
| Parameter | Value |
|---|---|
| Room size | 6 × 6 × 3 m3 |
| Number of LED Txs | 4/9/16 |
| Transmit power of each Tx | 1 W |
| Rx’s field of view | 75° |
| Reflection coefficient | 0.7 |
| Area of PD | 10−4 m2 |
| Responsivity of PD | 0.5 A/W |
| Tx elevation | −90° |
| Tx azimuth | 0° |
| Rx elevation | 90° |
| Rx azimuth | 0° |
| Number of Txs | Uniformity | Distance between Txs (m) | HPA (°) |
|---|---|---|---|
| 4 | 0.65 | 2.4 | 60 |
| 9 | 0.55 | 1.3 | 60 |
| 16 | 0.65 | 1.34 | 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, N.; Alves, L.N.; Ghassemlooy, Z. Impact of Transmitter Positioning and Orientation Uncertainty on RSS-Based Visible Light Positioning Accuracy. Sensors 2021, 21, 3044. https://doi.org/10.3390/s21093044
Chaudhary N, Alves LN, Ghassemlooy Z. Impact of Transmitter Positioning and Orientation Uncertainty on RSS-Based Visible Light Positioning Accuracy. Sensors. 2021; 21(9):3044. https://doi.org/10.3390/s21093044
Chicago/Turabian StyleChaudhary, Neha, Luis Nero Alves, and Zabih Ghassemlooy. 2021. "Impact of Transmitter Positioning and Orientation Uncertainty on RSS-Based Visible Light Positioning Accuracy" Sensors 21, no. 9: 3044. https://doi.org/10.3390/s21093044
APA StyleChaudhary, N., Alves, L. N., & Ghassemlooy, Z. (2021). Impact of Transmitter Positioning and Orientation Uncertainty on RSS-Based Visible Light Positioning Accuracy. Sensors, 21(9), 3044. https://doi.org/10.3390/s21093044








