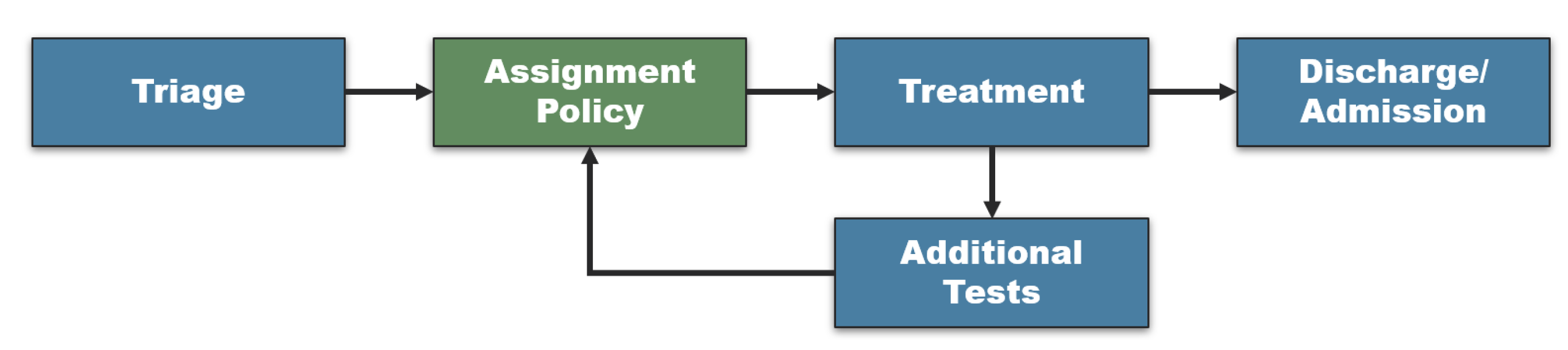
The patient–physician matching is directed at getting the right patient to the right physician at the right time, given the ED’s constraints. Specifically, given a preliminary evaluation of the patient upon arrival (commonly done by a triage nurse) and the available medical staff, a decision has to be made as to
when the patient should receive treatment and by
which physician. Currently, the patient–physician assignment process focuses almost entirely on assigning each patient a severity level using triage scales (e.g., between 1 and 5, 1 being the highest [
42]), which in turn translates into an
upper bound on the desired patient’s waiting time, leaving the decision as to
when and which medical professional should provide the treatment entirely in the hands of the triage nurse(s). Unfortunately, due to the time-critical environment, the multiple partially-conflicting objectives of the ED (as discussed next) and multiple interruptions, decisions are often inadequately made and are mainly based on conventional scheduling heuristics and experience which do not necessarily fully align with optimizing the ED’s objectives (e.g., [
4,
5,
6]). Specifically, while EDs have been computationally investigated for over 70 years [
43], mainly focusing on modeling the patient arrival flow and required staffing levels, to the best of our knowledge, the patient–physician assignment problem has yet to be addressed by computational means. To address this shortcoming, we make use of our approach (
Section 3) and adapt it to the ED domain.
Our approach provides the ED with an effective and efficient policy targeted at optimizing the hospital-specific objectives given the hospital’s available resources and expected patient flow.
To ensure the validity of the application of our approach to the ED domain from a medical perspective, we recruited four medical professionals (who did not co-author this article), namely a triage nurse, a physician’s assistant, an attending physician and an ED director, from three large hospitals in Israel. We refer to these medical professionals as the expert panel in this study.
4.1.2. The Optimization Problem
We start by modeling the two main sets of actors in the ED, patients and physicians and their interaction. Our modeling is based on existing literature and common clinical practices as prescribed by the expert panel.
Patients. A patient
is represented as a pair
where
is defined using a common triage scale (such as the popular Emergency Severity Index (ESI) [
5]) (Using the ESI, each patient is assigned a number between 1 and 5 representing the acuity of her condition (with 1 being the most acute).) and
, which defines the type of injury or condition based on the patients’ symptoms (e.g.,
Orthopedic,
Internal, etc.). According to clinical guidelines,
is associated with the maximal time she is permitted to wait for the initial physician’s treatment, denoted
and, if needed, the second physician’s treatment
. Patients may arrive at time
t to the ED based on an estimated distribution
, commonly assumed to follow an estimated distribution learned from past data [
34,
44]. We assume that, upon arrival to the ED,
’s characteristics are correctly identified by the triage nurse. After leaving the triage station (or when
’s test results arrive, see
Figure 1), she is scheduled to meet one of the physicians
.
Physicians. A physician is represented as a pair : is defined based on the physician’s qualifications over a discrete set (In Israel, as in most countries), c’s is classified to one the following (from lowest to highest): physician’s assistant, intern, resident and attending physician.) and indicates if the physician has “special training” in a specific injury type defined over the same set of injury types which characterize the patients (NONE otherwise). As a result, different physicians may have different required treatment times and varying levels of care quality. The set of available physicians, as well as their characteristics, is assumed to be known in advance and does not change during a shift.
Objective. The principal purpose of the ED is to ensure that patients receive the level and quality of care appropriate to their clinical needs and that the ED resources are most usefully applied to this end [
45]. Unfortunately, explicitly quantifying the above purpose is highly complex [
46], which often leads hospitals and governmental agencies to define multiple, often partially conflicting, objectives [
47]. These objectives primarily focus on minimizing the following measures: (1) risk of adverse consequences to patients [
48] (e.g., misdiagnosis, inappropriate medication); (2) ED over-crowdedness [
49]; (3) interruptions to physicians [
50]; (4) patients’ wait times [
51]; and (5) patients’ length of stay in the ED [
52].
With the help of the expert panel (who are familiar with Rambam hospital’s practices and Israel’s guidelines), we instantiate the ED’s objective and constants of our model which are not directly observable from data. Namely, we formulate the primary ED objectives as follows:
(1) Minimizing risk of adverse consequences. Each examination () performed by on has some risk of an adverse consequence. For example, a physician’s assistant with no specific specialty may be very well equipped to perform a first examination of minor orthopedic injuries with only a minimal risk of an adverse consequence, while severe head injuries should be examined by a qualified physician. We use as an indicator of whether was examined by in her eth examination. denotes the risk of adverse consequences associated with such an examination.
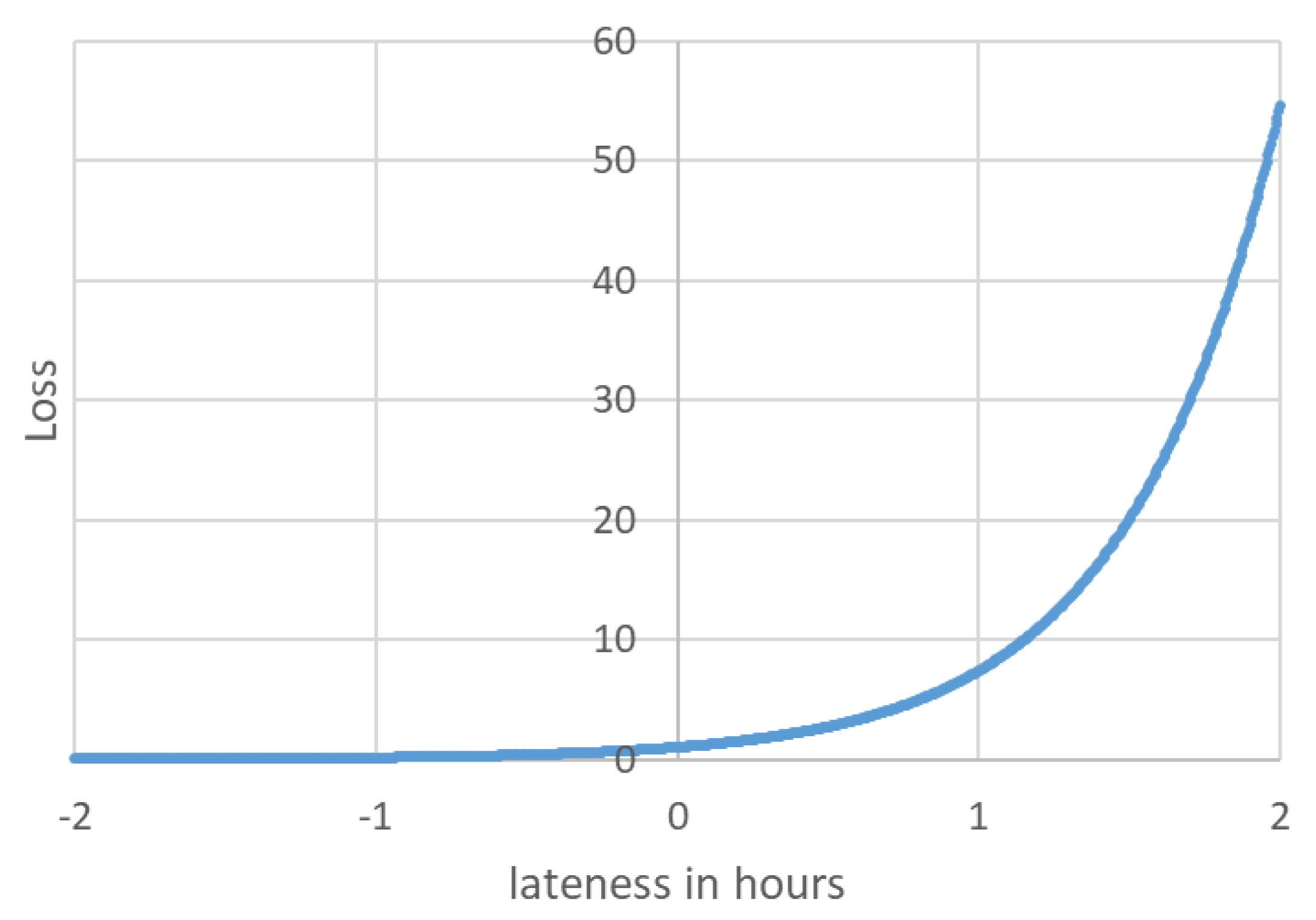
(2) Minimizing patients’ waiting time. Each patient , has to wait for her first (and second) examination for minutes. Given ’s and (as defined by the triage scale), the ED seeks to minimize the wait time and avoid exceeding the wait time limits. The penalty for exceeding the limits is provided by where is the excess wait time.
(3) Minimizing patients’ length of stay. Each patient spends minutes from the time she arrives at the ED to the time she is discharged or admitted to a hospital ward. This includes the time waits for examinations, the treatment time needed by the physicians, denoted and (if needed) lab test time between the two examinations. denotes the nominal treatment time and denotes the physician’s time efficiency factor, capturing the relative “examination speed” which varies between physicians.
(4) Minimizing over-crowdedness. At any point in time, one can measure the number of patients currently waiting and being treated in the ED, denoted , where t indicates continuous time.
(5) Minimizing interruption to physicians. Unfortunately, in some (extreme) cases, a physician may be asked to stop the treatment of one patient in order to treat another. This preemption may be very costly. The number of preemptions during ’s eth examination is denoted as . The penalty for each interruption is given by .
The ED must choose, for each patient
, which physician
will provide the examination/treatment
e and at what time
t. Let
be indicator decision variables denoting that patient
is assigned to physicians
for her
eth examination at time
t. We assume that the ED is evaluated based on some metric, defined by stakeholders and governmental agencies, over the above five objectives, e.g., using a linear objective which summarizes the weighted objectives over all patients, examinations and time as proposed in Equation (
1). Note, however, that the objective need not be linear, and, in the interest of generality, we do not assume it to be in the following sections.
Table 1 summarizes the paper’s notations.
When the patients’ arrival times and characteristics are known in advance, optimal patient–physician assignment can be derived over a discrete finite horizon
using the following Mathematical Problem (MP):
The MP consists of an ED-specific objective function (e.g., Equation (
1)) and the following constraints: Equations (3) and (4) enforce that at most one patient is treated at a time by each physician and, similarly, at most one physician can treat a patient at a given time. Equations (5)–(7) extract the treatment start time and Equations (8) and (9) extract the treatment end time. Equations (10) and (12) enforce a valid treatment duration, while Equation (11) extracts the time in which a patient becomes available for her second treatment.
Note that is assumed to be given in the offline setting. Equations (13) and (14) extract each patient’s
and
, respectively. Next, Equation (15) makes sure that the time physicians are assigned to a patient is appropriate and Equation (16) extracts the preemptions that took place. For simplicity, the above MP assumes each patient is treated twice.
Note that the patient–physician assignment problem is akin to the well studied job shop scheduling problem of unrelated machines with preemption, with the analogy of physicians to machines and patients to incoming jobs, as discussed below. This problem is known to be NP-hard [
53].
4.1.7. Experimental Results
To evaluate our approach, we use real-world data and compare our LBA approach with the conventional online heuristic deployed in EDs. This heuristic is often known as First-Come-First-Served-with-Urgencies (FCFSwU) which, according to our expert panel, is the backbone of most ED assignment decisions, including those at Rambam hospital. FCFSwU works as follows: patients of severity Levels 3–5 are treated as a single “non-urgent” type and are admitted in a first-come-first-served fashion to a physician who specializes in the relevant injury type or to a physician with no specialty. Specifically, a patient would not be assigned to a specialist who specialized in a different injury type. Patients of severity Level 1 or 2 are treated as a single “urgent” type and, upon arrival, the most senior specialized physician who is not already treating another urgent patient is called (or interrupted) in order to provide the needed treatment.
We examined two scenarios:
normal patient flow and
heavy patient flow. The normal patient flow is provided in the literature [
34], whereas the heavy patient flow is derived by multiplying the distribution parameters, resulting in twice the number of patients on expectancy. We trained two LBA DNNs, one for the normal patient flow case, denoted
, and one for the heavy patient flow case, denoted
.
We randomly generated 500 scenarios for each flow type, which in turn were optimally solved using the Gurobi solver [
35]. The results are translated into two training sets for
and
. We evaluated both
and
versus the FCFSwU heuristic on a series of 100 simulations of eight-hour shifts sampled according to the parameters discussed earlier. Both approaches were evaluated using the expert panel objective function available in our code.
Interestingly, for all 100 sampled instances, the approach outperforms the FCFSwU heuristic. The difference is statistically significant, for both the normal and heavy patient flow types, using a paired samples t-test, .
We further evaluated the results based on the five major ED objectives. We encounter the following results:
Risk of Adverse Consequences: The average risk of adverse consequences was reduced by 10% (normal flow) and 15% (heavy flow) compared to FCFSwU.
Wait times: The average wait time was slightly reduced by an average of 20 s per patient, across both patient flow conditions, compared to FCFSwU.
Length of stay: The average length of stay was reduced by 5% (normal flow) and 11% (heavy flow) compared to FCFSwU.
Crowdedness: There were no significant differences.
Interruptions: The most prominent difference was measured in the number and cost of preemptions. Specifically, a treatment is approximately 10 times more likely to be interrupted using the FCFSwU compared to LBA. By weighting the interruptions by their associated penalties, we see a penalty that is 20 times higher per shift.
The results further show that there is no apparent trade-off between the approach and the FCFSwU heuristic. Specifically, based on the results, the use of LBA improved four out of the five performance metrics while having no impact on the fifth. Namely, our approach provides a Pareto improvement over the existing practices.
All code and data used for evaluating our approach in this domain are available at
https://goo.gl/rXaBRh (accessed on 25 April 2021).