On the Performance Analysis of Switched Diversity Combining Receivers over Fisher–Snedecor ℱ Composite Fading Channels
Abstract
1. Introduction
- (a)
- We derive an exact and novel analytical expression of the probability density function (PDF) for bivariate Fisher–Snedecor distribution with arbitrary fading parameters, along with its compact form, using the generalized Lauricella series function.
- (b)
- The analytical expressions of the statistical properties of the output SNR for a dual-branch SSC scheme are deduced in different scenarios, including independent or correlated and identical or non-identical fading cases. To reduce complicated calculations, only the i.i.d. case is considered for SEC and SECps. Noted that some novel analytical expressions of the moment-generating function (MGF) and the qth moments of the output SNR for the SECps scheme are presented in the context of the multivariate Fox’s H-function.
- (c)
- A thorough performance investigation of SSC, SEC, and SECps is presented. The performance metrics of interest comprise the average SNR, amount of fading (AoF), outage probability (OP), average bit error probability and average symbol error probability (ABEP/ASEP), and the average channel capacity. In particular, a novel and exact expression of the ASEP of M-ary quadrature amplitude modulation (MQAM) is also obtained in terms of the multivariate Fox’s H-function. Furthermore, the optimal analysis of the performance metrics in the i.i.d. case is discussed in detail.
- (d)
- Based on the numerical analysis and simulations, certain significant insights are obtained as follows: (i) the impact of the multipath parameter on the system performance is more than those of the other parameters, including the shadowing parameter, the correlation coefficient, and the average SNR; (ii) to explore the potential gains of the SDC systems, the switching threshold should not be too large or too small compared to the average SNR, and there exists an optimal threshold for optimal performance under certain fading scenarios; (iii) SEC and SECps with more than two branches can provide more benefits than SSC when an appropriate switching threshold is chosen. Note that the above new insights will be meaningful and help to enhance the system reliability in the design and deployment of future communications systems.
2. Fisher–Snedecor Fading Channel Model
2.1. Univariate Fisher–Snedecor Distribution
2.2. Bivariate Fisher–Snedecor Distribution
2.2.1. Joint PDF of Bivariate Fisher–Snedecor Composite Envelope
2.2.2. Joint PDF of the Instantaneous Output SNR
2.2.3. Joint CDF of the Instantaneous Output SNR
3. Dual-Branch SSC Receiver
3.1. PDF
3.2. CDF
3.3. MGF
3.4. The qth Moments
4. Multi-Branch SEC Receiver
4.1. SEC Receiver
4.2. SECps Receiver
5. Performance Analysis and Optimization
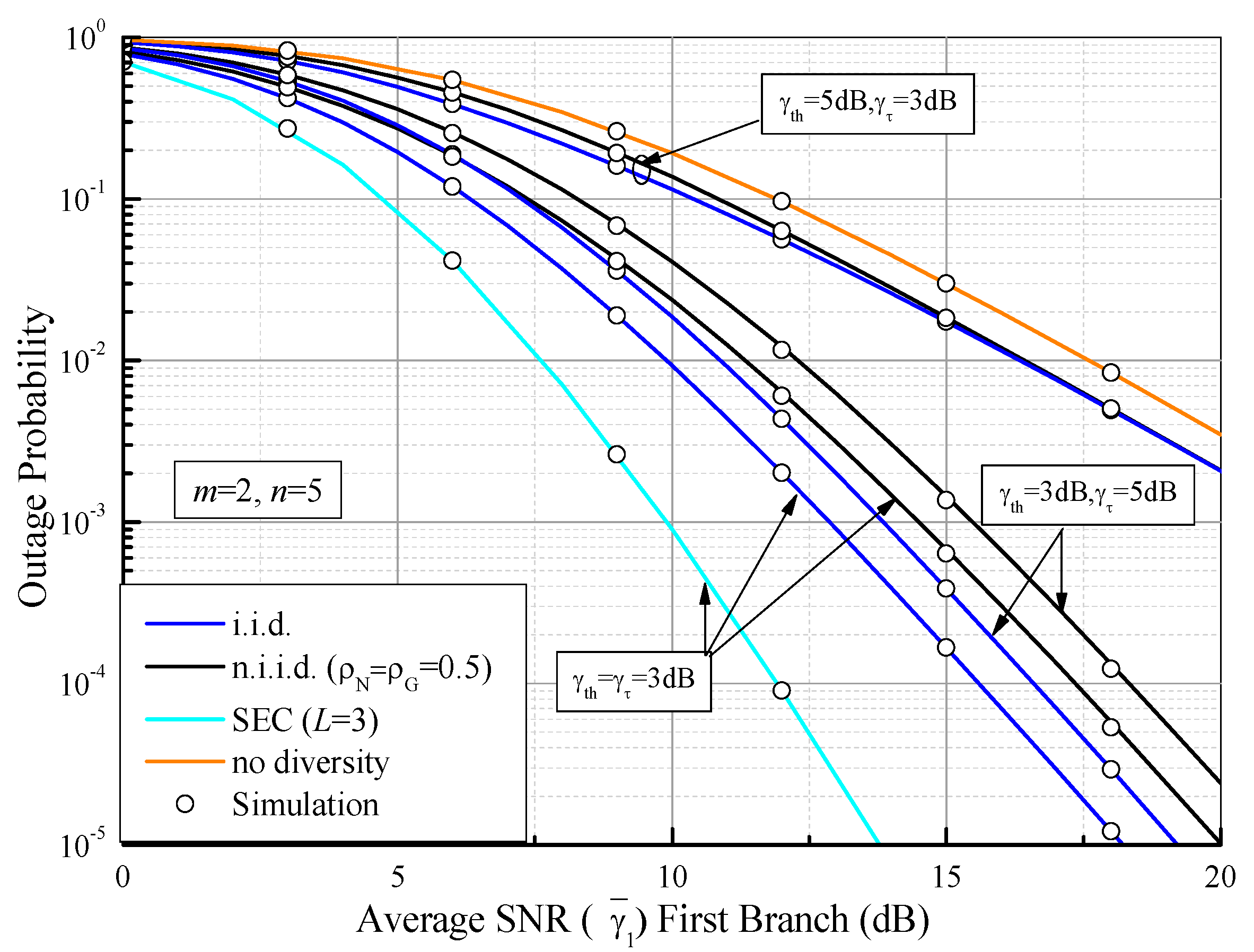
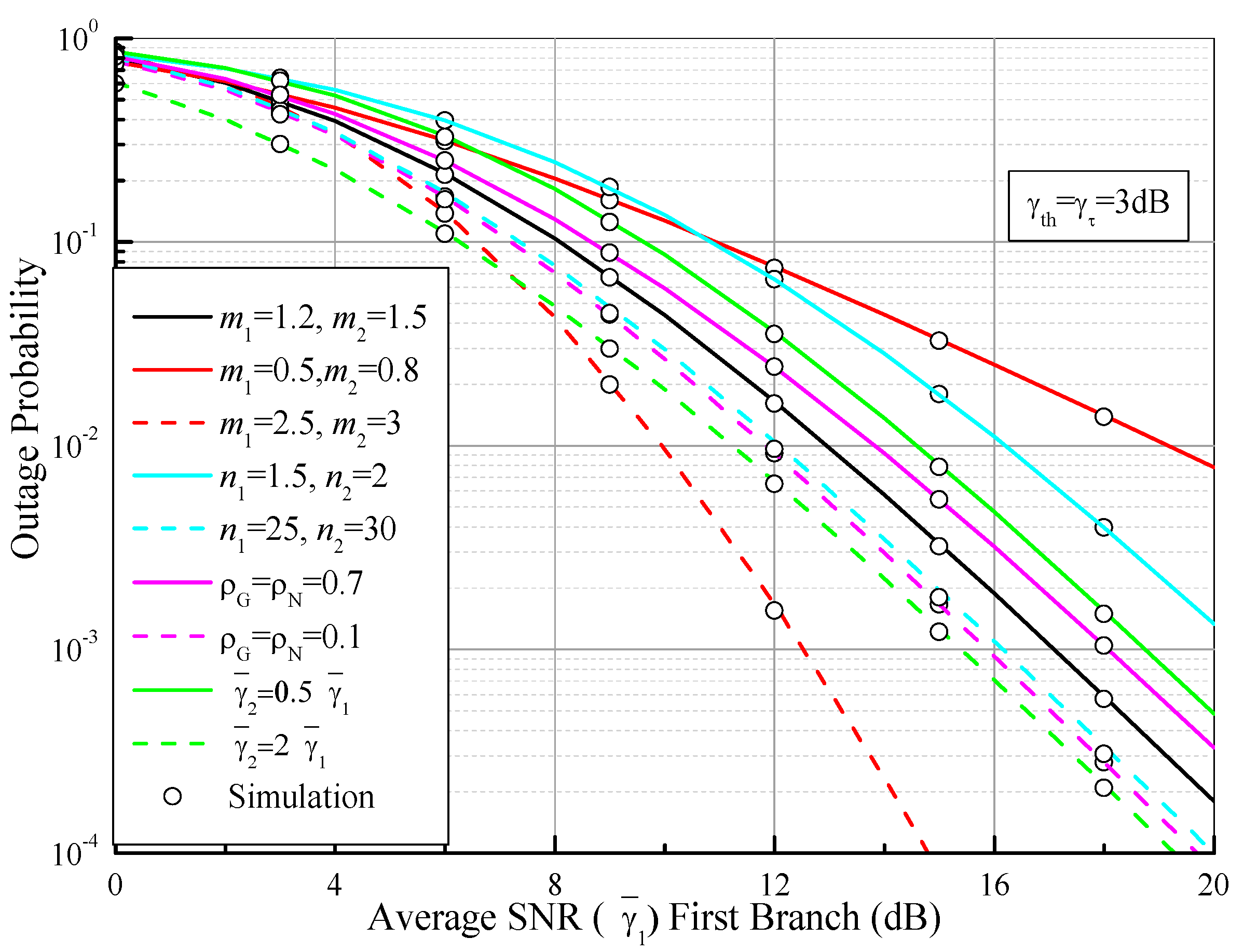
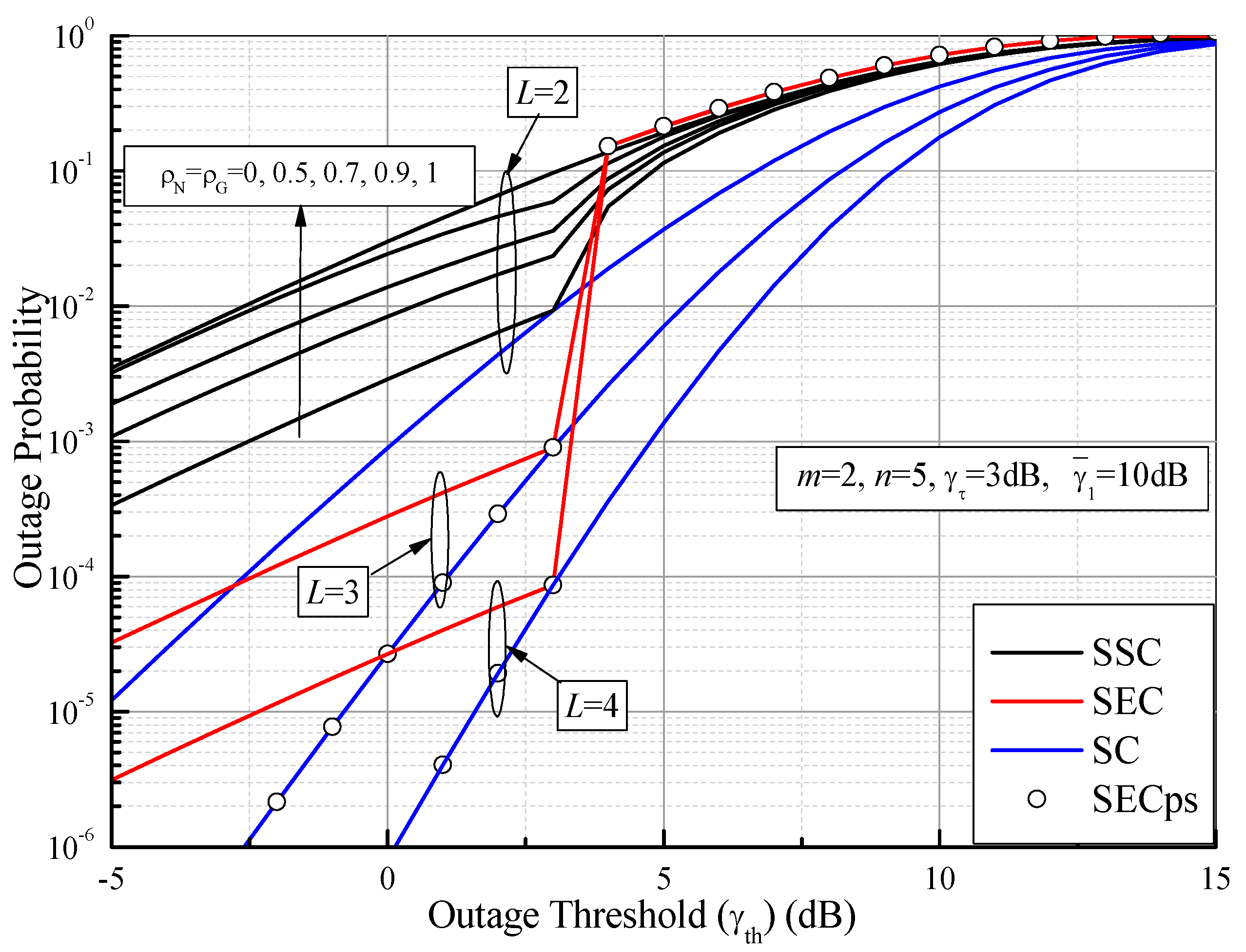
5.1. Outage Probability
5.2. Average Output SNR and Amount of Fading
5.2.1. Average Output SNR
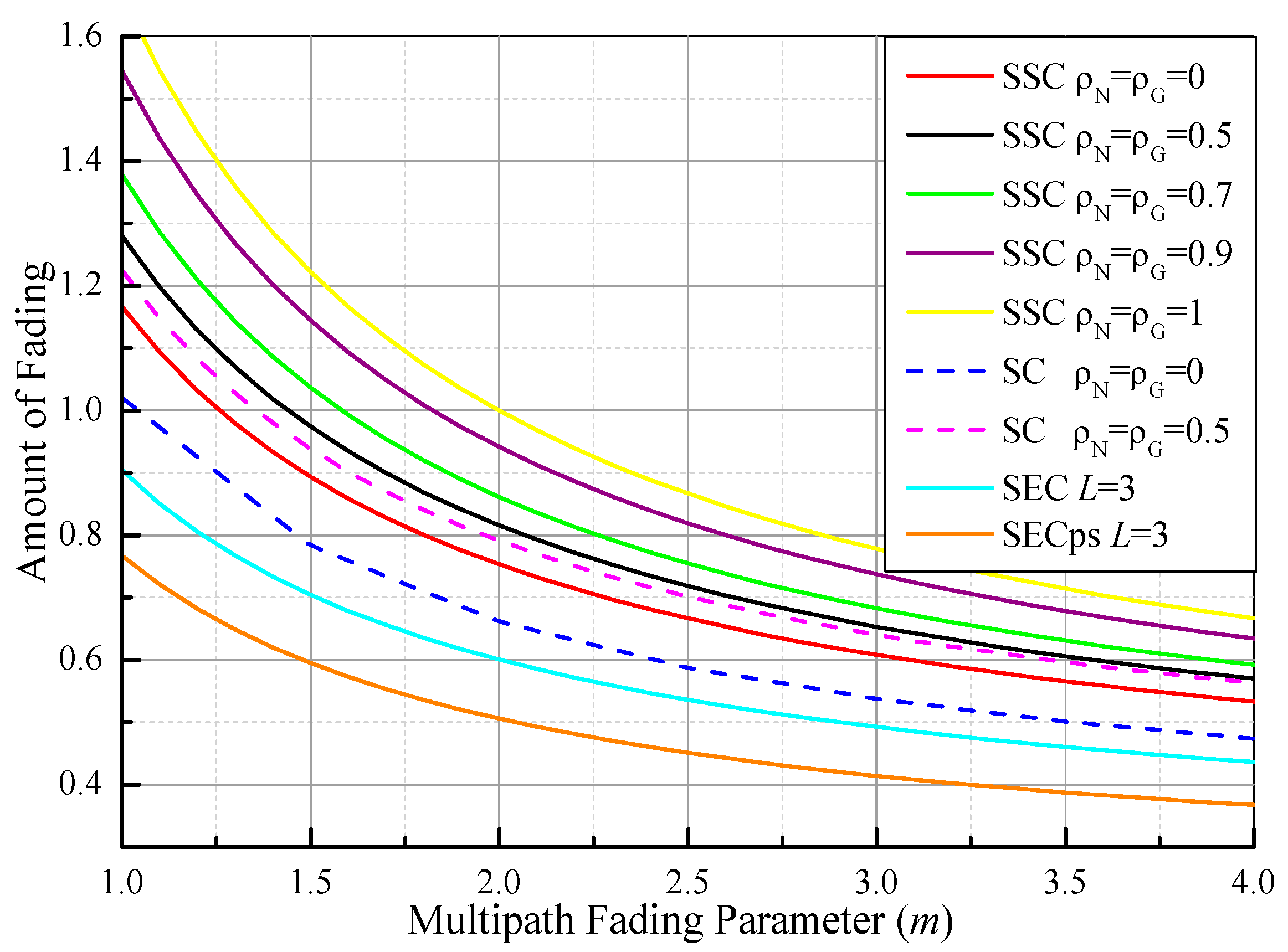
5.2.2. Amount of Fading
5.3. Average BEP/SEP
5.3.1. ABEP for NCBFSK and BDPSK
5.3.2. ABEP for BPSK and BFSK
5.3.3. ASEP for MQAM
5.4. Ergodic Capacity
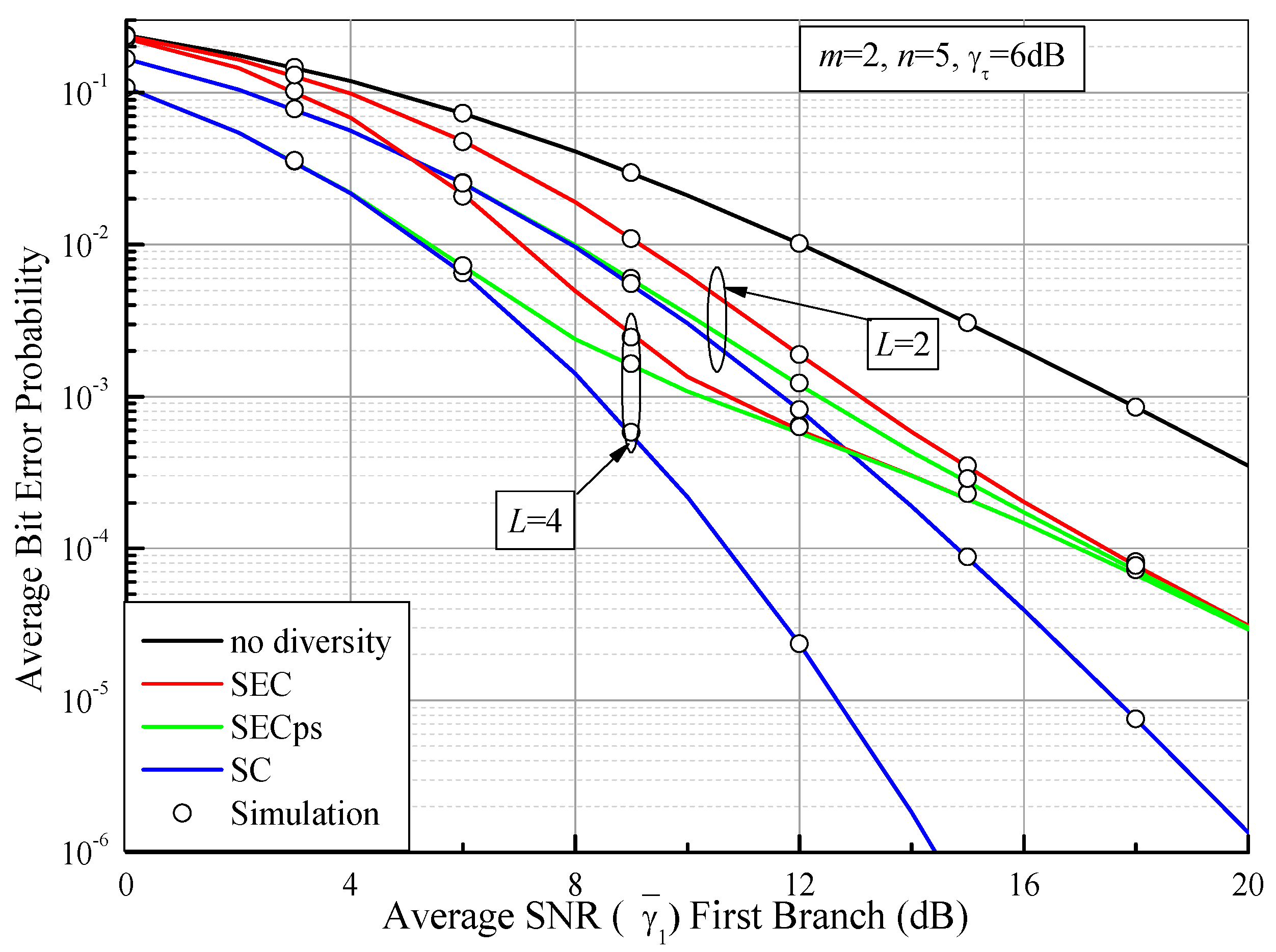
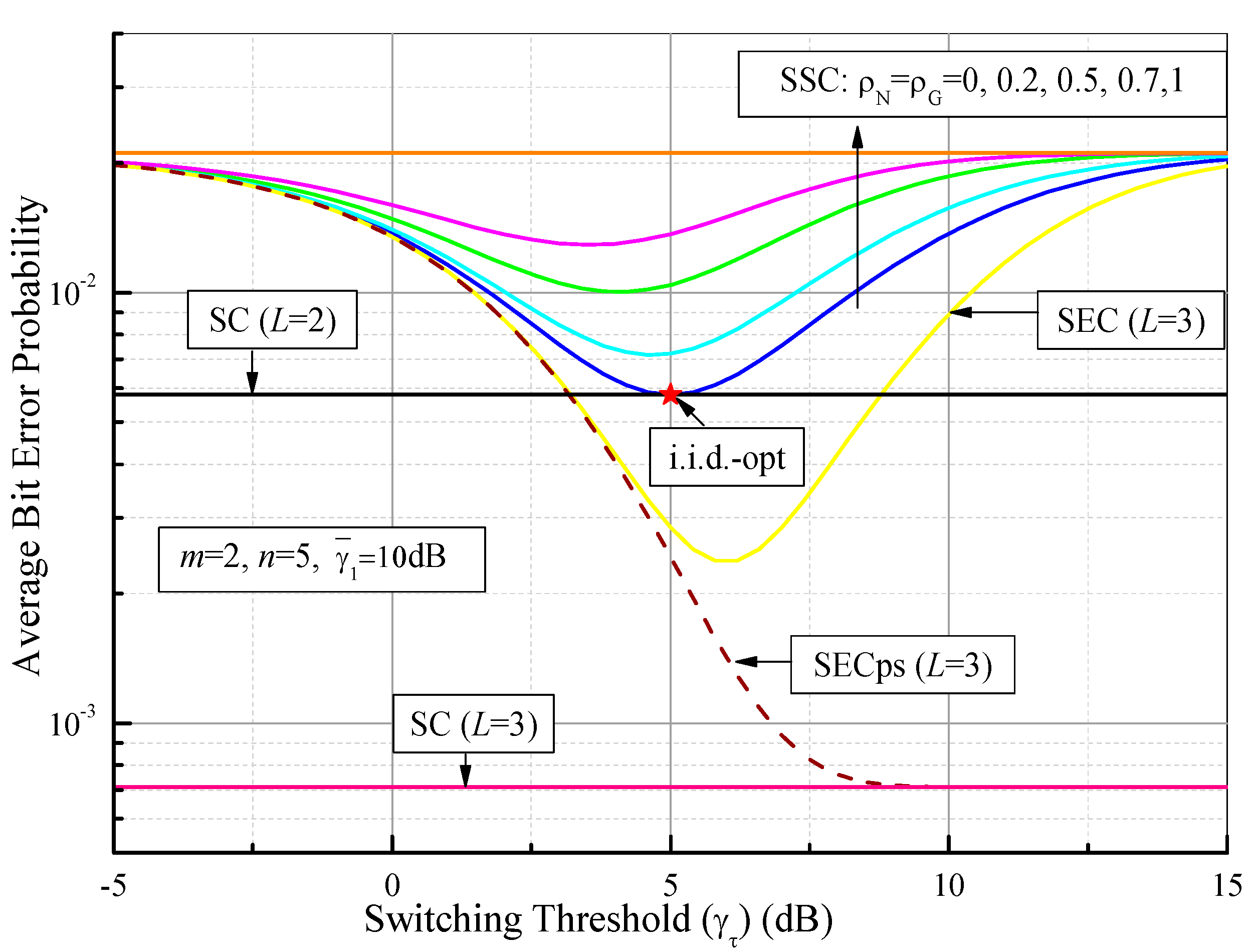
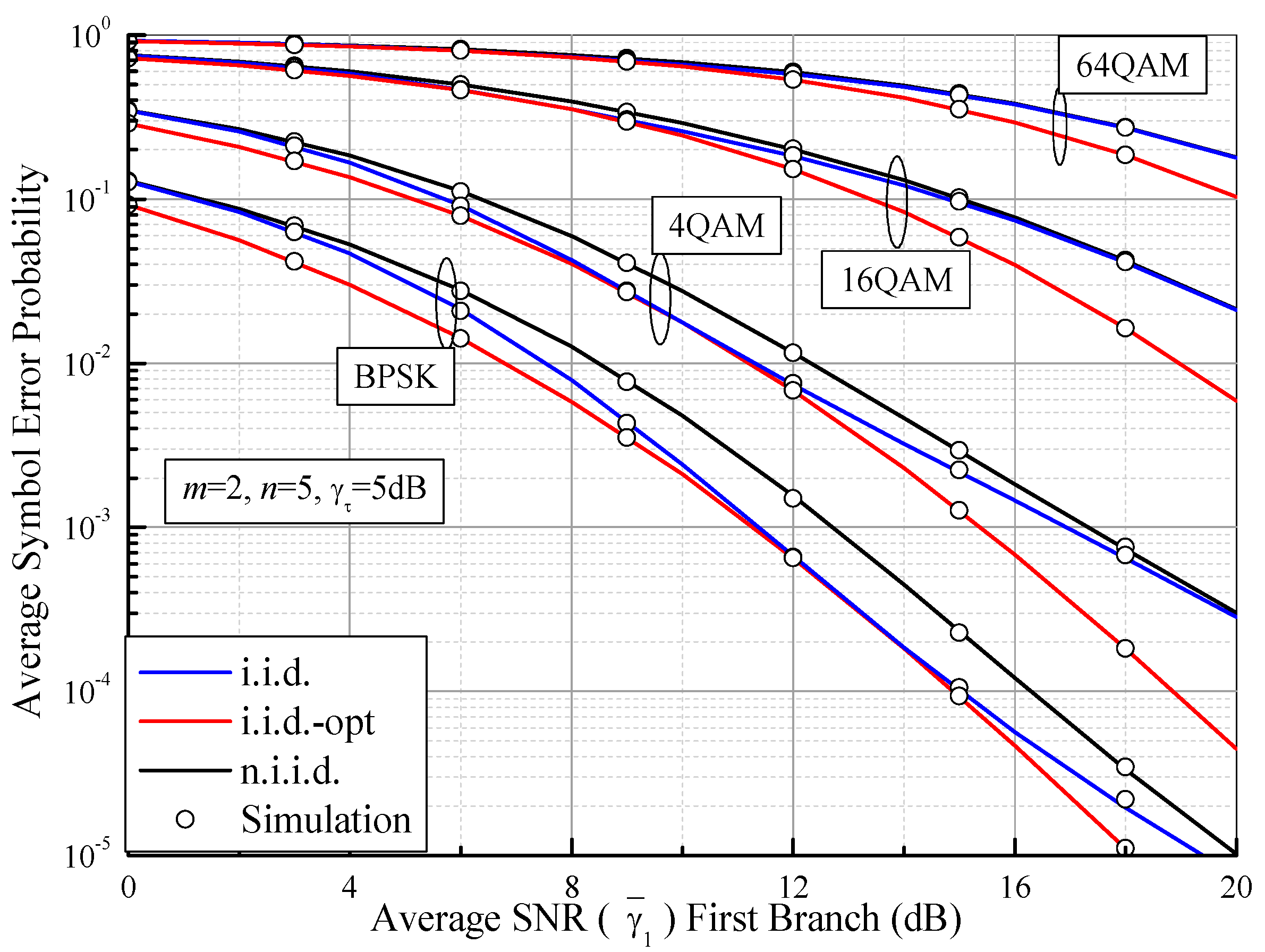
6. Numerical Results and Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Simon, M.K.; Alouini, M.-S. Digital Communication over Fading Channels, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Yoo, S.K.; Cotton, S.L.; Scanlon, W.G. Switched diversity techniques for indoor off-body communication channels: An Experimental Analysis and Modeling. IEEE Trans. Antennas Propag. 2016, 64, 3201–3206. [Google Scholar] [CrossRef]
- Yang, H.-C.; Alouini, M.-S. Performance analysis of multibranch switched diversity systems. IEEE Trans. Commun. 2003, 51, 782–794. [Google Scholar] [CrossRef]
- Yang, H.C.; Alouini, M.S. Improving the performance of switched diversity with post-examining selection. IEEE Trans. Wirel. Commun. 2006, 5, 67–71. [Google Scholar] [CrossRef]
- Tellambura, C.; Annamalai, A.; Bhargava, V.K. Unified analysis of switched diversity systems in independent and correlated fading channels. IEEE Trans. Commun. 2001, 49, 1955–1965. [Google Scholar] [CrossRef]
- Xiao, L.; Dong, X. New results on the BER of switched diversity combining over Nakagami fading channels. IEEE Commun. Lett. 2005, 9, 136–138. [Google Scholar] [CrossRef]
- Sagias, N.C.; Mathiopoulos, T. Switched diversity receivers over generalized gamma fading channels. IEEE Commun. Lett. 2005, 9, 871–873. [Google Scholar] [CrossRef]
- Sari, K. Performance analysis of switch and stay combining diversity system over κ-μ fading channels. AEU Int. J. Electron. Commun. 2015, 69, 475–486. [Google Scholar] [CrossRef]
- Sari, K. On the channel capacity of SSC diversity system in η-μ and κ-μ fading environments. AEU Int. J. Electron. Commun. 2015, 69, 1683–1699. [Google Scholar] [CrossRef]
- Mohamed, R.; Ismail, M.H.; Mourad, H.M. Performance of dual selection and switch-and-stay combining diversity receivers over the α-μ fading channel with co-channel interference. In Proceedings of the 2012 International Symposium on Signals, Systems, and Electronics, Potsdam, Germany, 3–5 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Mathiopoulos, P.T.; Sagias, N.C. Switch-and-examine diversity over arbitrarily correlated nakagami- m fading channels. IEEE Trans. Veh. Technol. 2010, 59, 2080–2087. [Google Scholar] [CrossRef]
- Anastasov, J.A.; Stefanović, M.Č. Impact of fading/shadowing correlation on outage performance of SSC receiver. In Proceedings of the 22nd Telecommunications Forum Telfor, Belgrade, Serbia, 25–27 November 2014; pp. 376–382. [Google Scholar] [CrossRef]
- AlQuwaiee, H.; Alouini, M. On the ergodic capacity of dual-branch correlated Log-normal fading channels with applications. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (Spring), Glasgow, UK, 11–14 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Srivastava, S.; Pradeep, U.; Shreyas, M.R.; Gowtham, N.R.; Manoj, B.R. Investigation of Switch and Stay Combiner performance over ‘independent’ and ‘i.i.d.’ K fading channels. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 26–28 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Manoj, B.R.; Sahu, P.R. Performance analysis of dual-switch and stay combiner over correlated KG fading channels. In Proceedings of the 2013 National Conference on Communications, New Delhi, India, 15–17 February 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Stefanovic, C.; Djosic, D.; Stefanovic, D.; Jovkovic, S.; Stefanovic, M. The performance analysis of wireless macro-diversity switch and stay receiver in the presence of gamma shadowed Kappa-Mu fading. In Proceedings of the 2016 International Symposium on Industrial Electronics (INDEL), Banja, Luka, 3–5 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Hmood, H. A mixture gamma distribution based performance analysis of switch and stay combining scheme over α-κ-μ shadowed fading channels. In Proceedings of the 2017 Annual Conference on New Trends in Information & Communications Technology Applications (NTICT), Baghdad, Iraq, 7–9 March 2017; pp. 292–297. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Scanlon, W.G.; Conway, G.A. An experimental evaluation of switched combining based macro-diversity for wearable communications operating in an outdoor environment. IEEE Trans. Wirel. Commun. 2017, 16, 5338–5352. [Google Scholar] [CrossRef]
- Arya, S.; Chung, Y.H. Non-line-of-sight ultraviolet communication with receiver diversity in atmospheric turbulence. IEEE Photonics Technol. Lett. 2018, 30, 895–898. [Google Scholar] [CrossRef]
- Arya, S.; Chung, Y.H. A novel blind spectrum sensing technique for multi-user ultraviolet communications in atmospheric turbulence channel. IEEE Access 2019, 7, 58314–58323. [Google Scholar] [CrossRef]
- Alcaraz López, O.L.; Mahmood, N.H.; Alves, H. Enabling URLLC for low-cost IoT devices via diversity combining schemes. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Al-Juboori, S.; Fernando, X.; Deng, Y.; Nallanathan, A. Impact of interbranch iorrelation on multichannel spectrum sensing with SC and SSC diversity combining schemes. IEEE Trans. Veh. Technol. 2019, 68, 456–470. [Google Scholar] [CrossRef]
- Aruna, G. Performance analysis of SSC and SEC diversity receivers in indoor MM wave mobile network. In Proceedings of the 2016 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 23–25 March 2016; pp. 2104–2108. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, B.; Huang, Y.; Guo, D. Secrecy outage analysis of multiuser downlink wiretap networks with SECps scheduling in Nakagami-m channel. IEEE Wirel. Commun. Lett. 2016, 5, 492–495. [Google Scholar] [CrossRef]
- Xia, J.; Fan, L.; Yang, N.; Deng, Y.; Duong, T.Q.; Karagiannidis, G.K.; Nallanathan, A. Opportunistic access point selection for mobile edge computing networks. IEEE Trans. Wirel. Commun. 2021, 20, 695–709. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, B.; Huang, Y.; Guo, D. Outage analysis of multi-relay networks with hardware impairments using SECps scheduling scheme in shadowed-Rician shannel. IEEE Access 2017, 5, 5113–5120. [Google Scholar] [CrossRef]
- Gupta, J.; Dwivedi, V.K.; Karwal, V.; Ansari, I.; Karagiannidis, G.K. Free space optical communications with distributed switch-and-stay combining. IET Commun. 2018, 12, 727–735. [Google Scholar] [CrossRef]
- Bithas, P.S.; Kanatas, A.G.; Matolak, D.W. Exploiting shadowing stationarity for antenna selection in V2V communications. IEEE Trans. Veh. Technol. 2019, 68, 1607–1615. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Sofotasios, P.C.; Matthaiou, M.; Valkama, M.; Karagiannidis, G.K. The Fisher-Snedecor distribution: A simple and accurate composite fading model. IEEE Commun. Lett. 2017, 21, 1661–1664. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, L.; Salem, A.S.; Alouini, M. Ergodic capacity under power adaption over Fisher-Snedecor fading channels. IEEE Commun. Lett. 2019, 23, 546–549. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Karagiannidis, G.K.; Ai, B. Effective rate of MISO systems over Fisher-Snedecor Fading Channels. IEEE Commun. Lett. 2018, 22, 2619–2622. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Security performance analysis of physical layer over Fisher-Snedecor fading channels. arXiv 2017, arXiv:1805.07652. [Google Scholar]
- Badarneh, O.S.; Sofotasios, P.C.; Muhaidat, S.; Cotton, S.L.; Rabie, K.M.; Aldhahir, N. Achievable physical-layer security over composite fading channels. IEEE Access 2020, 8, 195772–195787. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Da Costa, D.B.; Sofotasios, P.C.; Muhaidat, S.; Cotton, S.L. On the sum of Fisher-Snedecor variates and its application to maximal-ratio combining. IEEE Wirel. Commun. Lett. 2018, 7, 966–969. [Google Scholar] [CrossRef]
- Du, H.; Zhang, J.; Cheng, J.; Ai, B. Sum of Fisher-Snedecor Random Variables and Its Applications. IEEE Open J. Commun. Soc. 2020, 1, 342–356. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Selection Combining Scheme over Non-identically Distributed Fisher-Snedecor Fading Channels. IEEE Wirel. Commun. Lett. 2020, 9. [Google Scholar] [CrossRef]
- Shankar, H.; Kansal, A. Performance analysis of MRC receiver over Fisher Snedecor composite fading channels. Wirel. Pers. Commun. 2020, 7, 1–23. [Google Scholar] [CrossRef]
- Cheng, W.; Wang, X. Bivariate Fisher–Snedecor distribution and its applications in wireless communication systems. IEEE Access 2020, 8, 146342–146360. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Sofotasios, P.C.; Muhaidat, S.; Cotton, S.L.; Da Costa, D.B. Product and ratio of product of Fisher-Snedecor variates and their applications to performance evaluations of wireless communication systems. IEEE Access 2020, 8, 215267–215286. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Sofotasios, P.C.; Muhaidat, S.; Badarneh, O.S.; Karagiannidis, G.K. Entropy and energy detection-based spectrum sensing over Fisher-Snedecor composite fading channels. IEEE Trans. Commun. 2019, 67, 4641–4653. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, J.; Peppas, K.P.; Ng, D.W.K.; Ai, B. Dual-Hop Relaying Communications Over Fisher-Snedecor Fading Channels. IEEE Trans. Commun. 2020, 68, 2695–2710. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Derbas, R.; Almehmadi, F.S.; Bouanani, F.E.; Muhaidat, S. Performance Analysis of FSO Communications over Turbulence Channels with Pointing Errors. IEEE Commun. Lett, 2021; 25, 926–930. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 7th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
- Reig, J.; Rubio, L.; Cardona, N. Bivariate Nakagami-m distribution with arbitrary fading parameters. Electron. Lett. 2002, 38, 1715–1717. [Google Scholar] [CrossRef]
- Yoo, S.K.; Sofotasios, P.C.; Cotton, S.L.; Muhaidat, S.; Lopez-Martinez, F.J.; Romero-Jerez, J.M.; Karagiannidis, G.K. A comprehensive analysis of the achievable channel capacity in composite fading channels. IEEE Access 2019, 7, 34078–34094. [Google Scholar] [CrossRef]
- Saad, N.; Hall, R.L. Integrals containing confluent hypergeometric functions with applications to perturbed singular potentials. J. Phys. A Math. Gen. 2003, 36, 7771–7788. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nguyen, T.H.; Yakubovich, S.B. The Double Mellin-Barnes Type Integrals and Their Applications to Convolution Theory; World Scientific: Hackensack, NJ, USA, 1992. [Google Scholar]
- Wolfram Research, Gamma2. Available online: http://functions.wolfram.com/GammaBetaErf/Gamma2/ (accessed on 20 October 2020).
- Nam, H.; Alouini, M. Optimization of multi-branch switched diversity systems. IEEE Trans. Commun. 2009, 57, 2960–2970. [Google Scholar] [CrossRef]
- Adamchik, V.S.; Marichev, O.I. The algorithm for calculating integrals of hypergeometric type functions and its realization in REDUCE system. In Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC’90), Tokyo, Japan, 20–24 August 1990; pp. 212–224. [Google Scholar] [CrossRef]
- Alhennawi, H.R.; El Ayadi, M.M.; Ismail, M.H.; Mourad, H.-A.M. Closed-form exact and asymptotic expressions for the symbol error rate and capacity of the H-function fading channel. IEEE Trans. Veh. Technol. 2015, 65, 1957–1974. [Google Scholar] [CrossRef]
- Ko, Y.C.; Alouini, M.-S.; Simon, M.K. Analysis and optimization of switched diversity systems. IEEE Trans. Veh. Technol. 2000, 49, 1813–1831. [Google Scholar] [CrossRef]
- Wolfram Research, Beta3. Available online: http://functions.wolfram.com/GammaBetaErf/Beta3/ (accessed on 20 October 2020).




| References | Research Topic | System Models | Fading Channels |
|---|---|---|---|
| [2] | Indoor off-body communication | SSC, SEC, and SECps | Nakagami-m |
| [18] | Outdoor wearable communication | SSC, SEC, and SECps | Nakagami-m |
| [19] | Ultra-ultraviolet communications | SSC | gamma–gamma |
| [20] | Multiuser ultraviolet communication | SSC | gamma–gamma |
| [21] | Low-power ultra-reliable low-latency downlink communications | PSC and SSC | Nakagami-m |
| [22] | Multichannel spectrum sensing | PSC and SSC | correlated Nakagami-m |
| [23] | Indoor millimeter wave communications | SSC and SEC | Rayleigh |
| [24] | Multiuser downlink wiretap networks | SECps | Nakagami-m |
| [25] | Mobile edge computing network | PSC and SSC | Nakagami-m |
| [26] | free space optical communications | distributed SSC | generalized Málaga and Gamma–Gamma |
| [27] | Multi-relay networks | SECps | shadowed Rician |
| Acronym | Description | Acronym | Description |
|---|---|---|---|
| ABEP/ASEP | Average Bit/Symbol Error Probability | n.i.i.d. | Non-Independent and Identically Distributed |
| AoF | amount of fading | NCBFSK | non-coherent binary frequency shift keying |
| AWGN | additive white Gaussian noise | OP | outage probability |
| BDPSK | binary differential phase-shift keying | probability density function | |
| CDF | cumulative distribution function | PSC | pure selection combining |
| i.i.d. | independent and identically distributed | SEC | switch-and-examine combining |
| i.n.i.d. | independent and non-identically distributed | SECps | SEC with post-examining selection |
| MGF | Moment-generating function | SDC | Switched diversity combining |
| MRC | maximum ratio combining | SNR | output signal-to-noise ratio |
| MQAM | M-ary quadrature amplitude modulation | SSC | switch-and-stay combining |
| n.i.n.i.d. | non-independent and non-identically distributed |
| L | α | ||
|---|---|---|---|
| m = 2, n = 5 | m = 2, n = 100 | m = 2 (Nakagami-m) [50] | |
| 2 | 1 | 1 | 1 |
| 3 | 1.1874 | 1.1595 | 1.1582 |
| 4 | 1.3345 | 1.2790 | 1.2763 |
| 5 | 1.4571 | 1.3750 | 1.3710 |
| 6 | 1.5628 | 1.4554 | 1.4503 |
| 7 | 1.6564 | 1.5248 | 1.5185 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Wang, X.; Ma, T.; Wang, G. On the Performance Analysis of Switched Diversity Combining Receivers over Fisher–Snedecor ℱ Composite Fading Channels. Sensors 2021, 21, 3014. https://doi.org/10.3390/s21093014
Cheng W, Wang X, Ma T, Wang G. On the Performance Analysis of Switched Diversity Combining Receivers over Fisher–Snedecor ℱ Composite Fading Channels. Sensors. 2021; 21(9):3014. https://doi.org/10.3390/s21093014
Chicago/Turabian StyleCheng, Weijun, Xiaoting Wang, Tengfei Ma, and Gang Wang. 2021. "On the Performance Analysis of Switched Diversity Combining Receivers over Fisher–Snedecor ℱ Composite Fading Channels" Sensors 21, no. 9: 3014. https://doi.org/10.3390/s21093014
APA StyleCheng, W., Wang, X., Ma, T., & Wang, G. (2021). On the Performance Analysis of Switched Diversity Combining Receivers over Fisher–Snedecor ℱ Composite Fading Channels. Sensors, 21(9), 3014. https://doi.org/10.3390/s21093014






