4.1. The Analysis of the Influence of Input Variables on Prediction Accuracy
The random forest algorithm learned the model using selected 20 input variables, and the general rule is that RF does not need to reduce the number of input variables [
18]. However, in practice, the selection is nevertheless necessary because the prediction time, when using an unlimited number of input variables, can be significantly increased in real models. Furthermore, the transfer and processing of a smaller amount of data is always an advantage because such systems are generally faster and more flexible.
Upon finding the most successful combination of input variables and the most successful data mining algorithm, the influence of individual input variables or groups of variables on the output result is additionally analyzed, as well as the evaluation of the performance.
The influence of input variables on the prediction result (
Figure 1) is proportional to the importance of individual attributes in building random forest models. However, the out of bag (OOB) method cannot know with certainty how the attributes would behave if some were removed because in that scenario the tree would be built differently. Equally, it is not possible to know whether all scenarios of external navigation conditions are covered, i.e., whether a sufficient amount of data has been collected and whether the model has been overlearned. Therefore, expert interpretation of the results for different combinations of input variables is required.
Discretization is performed for easier applicability in ship operations where it is important to timely predict the class of fuel consumption as support when making decisions related to the operation of the ship. Outlet variable, i.e., main propulsion engine fuel consumption, is divided into five groups (labels) which correspond to the fuel consumption according to the charter party: class a < 1333, 1333 ≤ b < 1583, 1583 ≤ c < 1770, 1770 ≤ d ≤ 1916, and e > 1916, in kg/h. Classes can be further optimized depending on the need to compare the numeric results, such as a comparison with the fuel consumption from the SEEMP, the values measured during the sea trial, or from the factory test bench.
The random forest classification algorithm built the model in 5.31 s with 18,018 out of 18,499, or 97.40% of, correctly classified instances and an RMSE of 0.0895. The confusion matrix is shown in the
Appendix B as
Table A1.
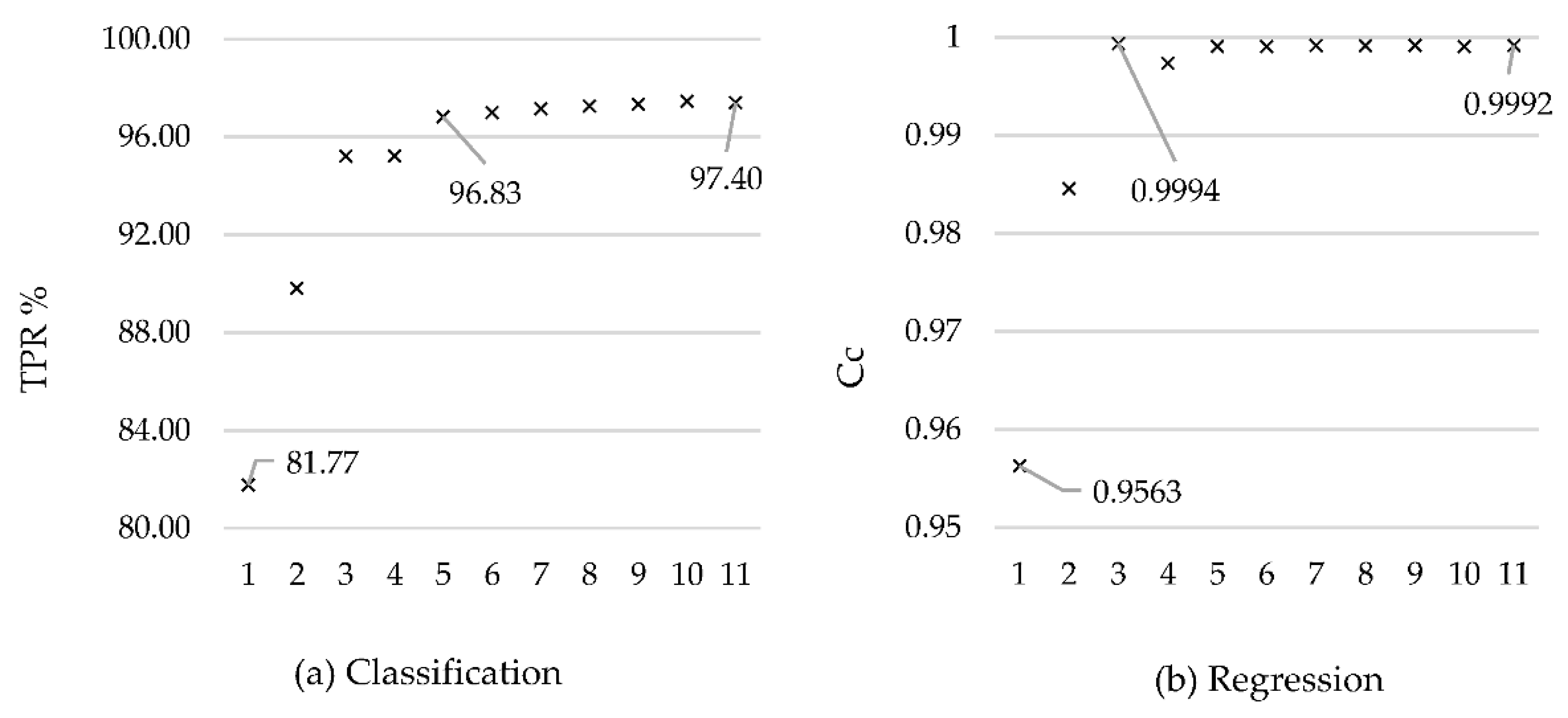
A graphical presentation (
Figure 2) of accurately classified instances (TPR) (classification/left) and correlation coefficients (Cc) (regression/right) in combinations of input signals according to the groups (1–11) described in
Table 6 gives an overview on how input variable selection affects random forest classification and regression result.
Similar prediction results for classification and regression are to be expected, given that both models are learned on the same data with the same input signals, only the output variable is written differently—once as a classification, and the second time as a numerical value for regression.
The model with only one input variable, i.e., ME rpm (group 1,
Table 6) is able to predict fuel consumption with 81.77% classification accuracy or 0.9563 correlation coefficient in regression. Without this variable it is impossible to predict fuel consumption for a ship in navigation, so it remains in the model in all combinations.
Data from the ship’s noon reports (group 2) achieve a weaker result than collected publicly available meteorological and oceanographic data (group 3), contributing more to model construction. By including meteorological and oceanographic data and noon report data, a model was built to predict fuel consumption with an already acceptable accuracy of 95.23% of the classification, and correlation coefficient 0.9974 in regression (group 4). The reason for the weaker results of external influences from ship noon reports may be a larger time interval and a smaller total number of variables, and a human factor that does not read with complete accuracy. Humans are a potentially reliable measuring instrument for measuring a range of quantities. However, it is an entirely different question of how metrically accurate and usable this measurement will be. The influence of wind direction and speed from the ship’s anemometer corrects the previously mentioned external factors and improves the overall prediction. This information can be used in future research as a measure of the assessment of collected publicly available oceanographic and meteorological wind data (group 5). The next input variable is the course over ground (group 6), whose significance is in determining the counter angle of external factors to the ship (the input variable of the actual navigation direction is excluded because such information is impossible to know in the future). Air temperature (group 7) and sea temperature (group 8) are equally important, however their real importance in an operational setup is lower than significance derived from the RF model (
Figure 1). The explanation stems from the very nature of the collected data, where the adverse weather was in a high percentage accompanied by air (and sea) temperature drop, and therefore the contribution of air and seawater temperature as the manifestation of the swift change of weather conditions is recognized by RF model as highly important (0.44) (
Figure 1). Still, in the context of expert explanation when selecting the input variables and their combinations, the temperature significance is lower (
Figure 2). The trim (group 9) contributes to the accuracy of the prediction while the list (group 10), despite the fact that significance derived from the RF model is equal to that of the ship’s trim (0.42) (
Figure 1), does not contribute to the quality of prediction in an operational setup (
Figure 2). The reason stems from the crew’s effort to maintain the ship transversely aligned, while the trim depends on the condition of the cargo, and at the same time, contributes more to fuel consumption. The draft (group 11) moderately contributes to the prediction despite a relatively high impact of 0.24 from the RF attribute significance analysis (
Figure 1). In tankers, especially those for the transport of liquefied gases, the draft does not change continuously but it is rather binary, defined by the state of the cargo, i.e., the ship in ballast or cargo condition.
The random forest algorithm can successfully learn the model through the number of revolutions of the main propulsion machine and external parameters (group 5) in the case of classification with 96.83% of accurately classified instances, while in regression, by combining the number of revolutions of the main propulsion machine and publicly available meteorological and oceanographic data (group 3), can predict fuel consumption with a 0.9994 correlation coefficient. This result is explained by the fact that at the time of data collection, the ship was in navigation at a constant steaming, and the consumption under calm weather conditions is mostly dependent on the number of revolutions of the main propulsion machine. Other variables contribute to the quality of prediction in adverse weather conditions.
In general, it can be concluded that the influence of individual variable follows the importance of attributes in the construction of random forest model (
Figure 1). Still, an expert insight into the study of the interdependence of variables is necessary to set up a model that will successfully predict the operating parameters for all cases of the ship’s operating envelope, and subsequently contribute to better energy efficiency. In the case of the random forest, and where the speed of data prediction is at stake, it is possible to exclude one or more variables based on graphically presented results (
Figure 2) and discussion of the influences of different combinations of input variables from the previous text. The results indicate that both regression and classification have satisfactory performance in groups 3 and 5, where we include 9 and 14 input variables, respectively. In the case of the need for high precision and the readiness of the model to external conditions that differ greatly from those processed, and when the construction time of the model is not crucial, it is recommended to use all input variables (
Table 6).
4.2. The Selection of the Output Variables
The selection of output variables followed factors related to propulsion and hull efficiency through the energy efficiency design index (EEDI), SEEMP (parts 1 and 2) [
19,
20], and other standard operational procedures that can improve the ship energy efficiency. Main output variables are, therefore, main propulsion engine total and specific fuel consumption, ship apparent slip ratio, speed of the ship (over the ground), the longitudinal inclination of the ship (trim), and the need for liquefaction of cargo, while the remaining variables may be calculated by including the known values.
The main propulsion engine fuel oil consumption (FOC) is selected as the primary output variable because the main propulsion engine is, as always, the largest single energy consumer, and it is possible to achieve the most significant energy savings which meet the SEEMP plans and the criteria of the EEDI. The results of RF prediction are presented in the previous section.
The ship’s speed over ground (SOG) is used as an independent variable when calculating the energy efficiency indicators of navigation, due to its operational significance when selecting the most favorable route according to sea and weather conditions. Since the classification does not have too many foundations in practical use, only a random forest regression algorithm was used. The RF algorithm built the model in 8.73 s with a Cc of 0.9989, RMSE of 0.1542, and RAE 3.1917%.
Ship Energy Efficiency Operational Indicator (EEOI) is a common energy efficiency indicator calculated within a given time period:
where
MCO2 is the mass of carbon dioxide (t),
Mc is the mass of the cargo carried (t), and
d is the total distance (nm).
It follows from the above formula that the EEOI depends on fuel consumption (speed, optimization of ship/engine construction), the quantity of cargo, length of travel, part of the journey carried out in ballast, and time spent at anchor, delays in port, repairs, or other inactive conditions.
From the above, the EEOI can be calculated as per:
where
Fc is the fuel consumption (t/hr), C
f is the dimensionless coefficient for converting the consumption into the amount of CO
2 emitted,
Mc is the mass of the transported cargo (t), and
v is the speed of the ship (knot).
Results of EEOI prediction are the product of the prediction results of the main propulsion engine FOC and the SOG. The fuel consumption of other equipment can be easily predicted because it does not depend on weather conditions and the set speed.
To monitor and measure energy efficiency, various
Energy Performance Indicators (EnPI) built into the SEEMP are used, which can be simple parameters, or more complex, which are considered to represent the energy efficiency of the ship. EnPI for fuel consumption is usually calculated according to the following expression:
where
FC is fuel consumption (t) and
FCB is initial or comparative fuel consumption. EnPI represents the difference (%) in fuel consumption according to a predetermined basic consumption. Results of
prediction are equal to the results for main propulsion FOC alone.
The specific fuel oil consumption (SFOC) of the main propulsion engine is used in the calculation of EEDI and, despite the high correlation with the fuel consumption of the main propulsion engine, provides useful information in confirming the actual fuel consumption of the machine according to load and by the manufacturer’s default values. SFOC is calculated in g/kW as the ratio of fuel consumption to the power delivered to the shaft line and represents the efficiency of converting the chemical energy of the fuel into useful work. The SFOC value indicates not only the efficiency of the engine combustion process but also the fuel economy. The RF regression prediction algorithm built the model in 5.87 s with a C
C of 0.9887, RMSE of 12.0096, and 9.4625% RAE. For classification purposes, SFOC is divided into four classes corresponding to the consumption according to the test drive results: a < 161, 161 ≤ b < 175, 175 ≤ c ≤ 189, d > 189. Classes can be optimized depending on the results comparison, such as the comparison with the targeted fuel consumption from the SEEMP, or the values measured on the factory test bench. The classification algorithm of the RF method built the model in 5.55 s with 17,962 out of 18,499, or 97.1% of, correctly classified instances, RMSE of 0.103, and the confusion matrix, as shown in the
Appendix B,
Table A2.
Ship’s slip is the ratio of the actual speed of the ship and the invested speed of the ship’s propeller. Since the ship’s propeller is immersed in the sea, its actual axial shift is never equal to its pitch, as is the case with a classic screw in a solid material [
21]. Therefore, the slip is the ratio between the theoretical and the actual movement, i.e., the propeller pitch and the actual shift, or the loss in propeller pitch. The RF regression prediction built the model in 9.52 s with a C
C of 0.995, RMSE of 1.593, and 5.857% RAE. The apparent slip ratio for classification purposes is divided into four classes corresponding to the experimental data: a < 0, 0 ≤ b < 5, 5 ≤ c ≤ 10, d > 10. The RF classification algorithm built the model in 7.34 s with 16,933 out of 18,499, or 91.53% of, correctly classified instances, and RMSE of 0.1856. More information on the results of the classification can be seen in the confusion matrix (
Appendix B,
Table A3).
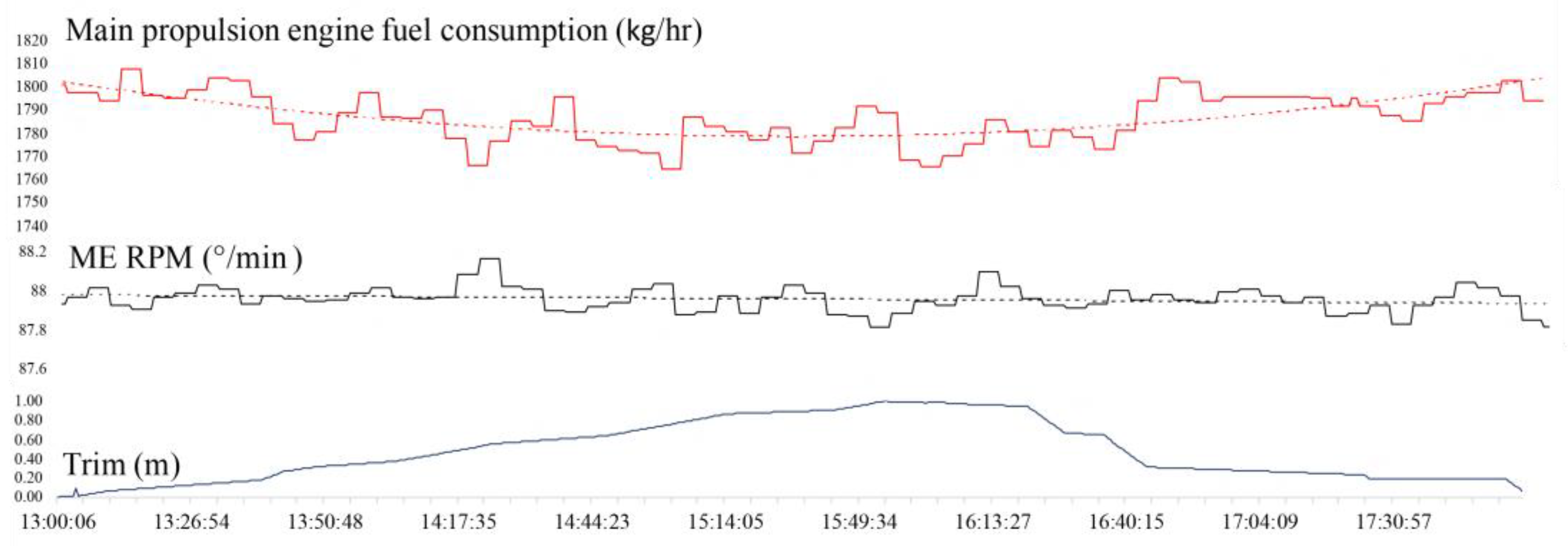
Ship’s trim is used to optimize energy consumption, especially in larger vessels, where the energy savings are more significant (
Figure 3). Trim is changed by ballasting or by longitudinally distributing the cargo within the ship cargo holds. In a period of 5 h, the ship’s trim was changed (by ballasting) from the initial 0 m to 1 m of immersion in the bow and back to 0 m. The ship was loaded with 48,394.6 MT of cargo, the weather conditions and the state of the sea did not change, and the control lever was set to 88 rpm and kept stable within 1 rpm. It can be concluded that the subject ship has a lower propulsion fuel consumption when the bow is immersed 1 m more than the stern.
The RF regression prediction algorithm built the model in 7.00 s with a C
C of 0.9992, RMSE of 0.0499, and 2.2963% RAE. For classification, trim is divided into five classes corresponding to the limit values from experimental data: a < −1, −1 ≤ b < 0, 0 ≤ c < 1, 1 ≤ d ≤ 2, e > 2. As no measurements were recorded over the −1 m group (ship inclined longitudinally towards the bow over 1 m), the group was omitted from the classification evaluation table. The RF classification algorithm built the model in 4.09 s with 18,116 out of 18,499, or 97.93% of, correctly classified instances, and an RMSE of 0.0879. More information on the results of the classification can be seen in the confusion matrix (
Appendix B,
Table A4). The set ML model is capable of learning the trim on known data and adequately predicting trim that needs to be maintained in order to match the predicted consumption.
The need for liquefaction of cargo on the case of a ship for the transport of liquefied petroleum gas is represented by the total electrical load of the main switchboard. The effective power of electricity required to liquefy cargo is higher than any other operation on a liquefied petroleum gas carrier; hence it is used to monitor the cargo liquefaction. For classification purposes, electrical power is divided into three classes corresponding to the limit values from experimental data and ship’s electrical load analyses drawing: a < 700, 700 ≤ b ≤ 900, d > 900. All three values represent the consumption in navigation so that the first represents the electrical load with reduced consumption, the second normal consumption, and the third consumption with the operation of the cargo liquefaction plant. RF classification algorithm built the model in 5.34 s with 18,145 out of 18,499, or 98.09% of, correctly classified cases, and an RMSE of 0.103. More information on the results of the classification can be seen in the confusion matrix (
Appendix B,
Table A5). To be able to use liquefaction forecasting as support when planning liquefaction in the future, it is a prerequisite that the decision on liquefaction in the data used for learning is correct. Future research should introduce cargo-related data to make predictions more accurate.