Dual-Mode Radar Sensor for Indoor Environment Mapping
Abstract
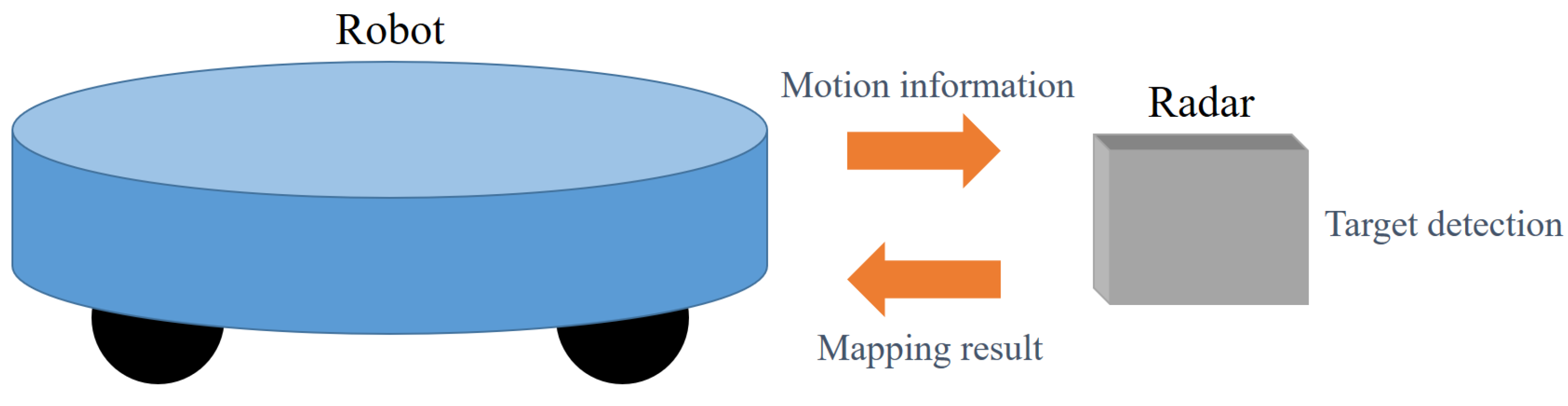
:1. Introduction
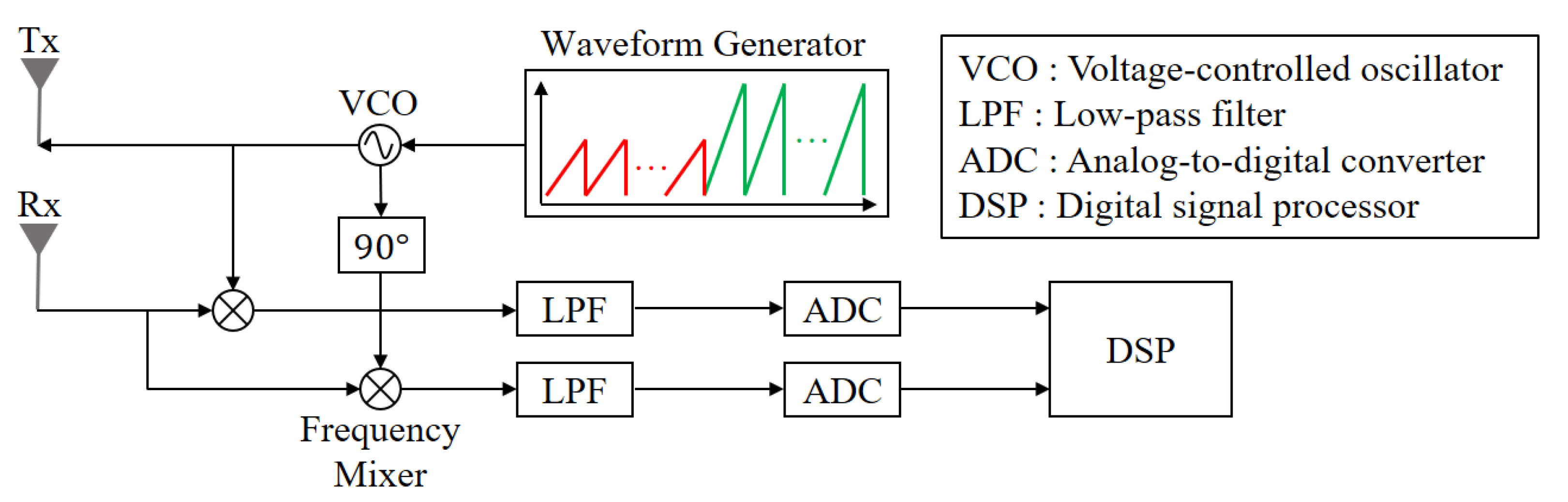
2. Dual-Mode FMCW Radar Sensor
3. Radar Signal Analysis
3.1. Distance and Velocity Estimation Using FMCW Radar Signals
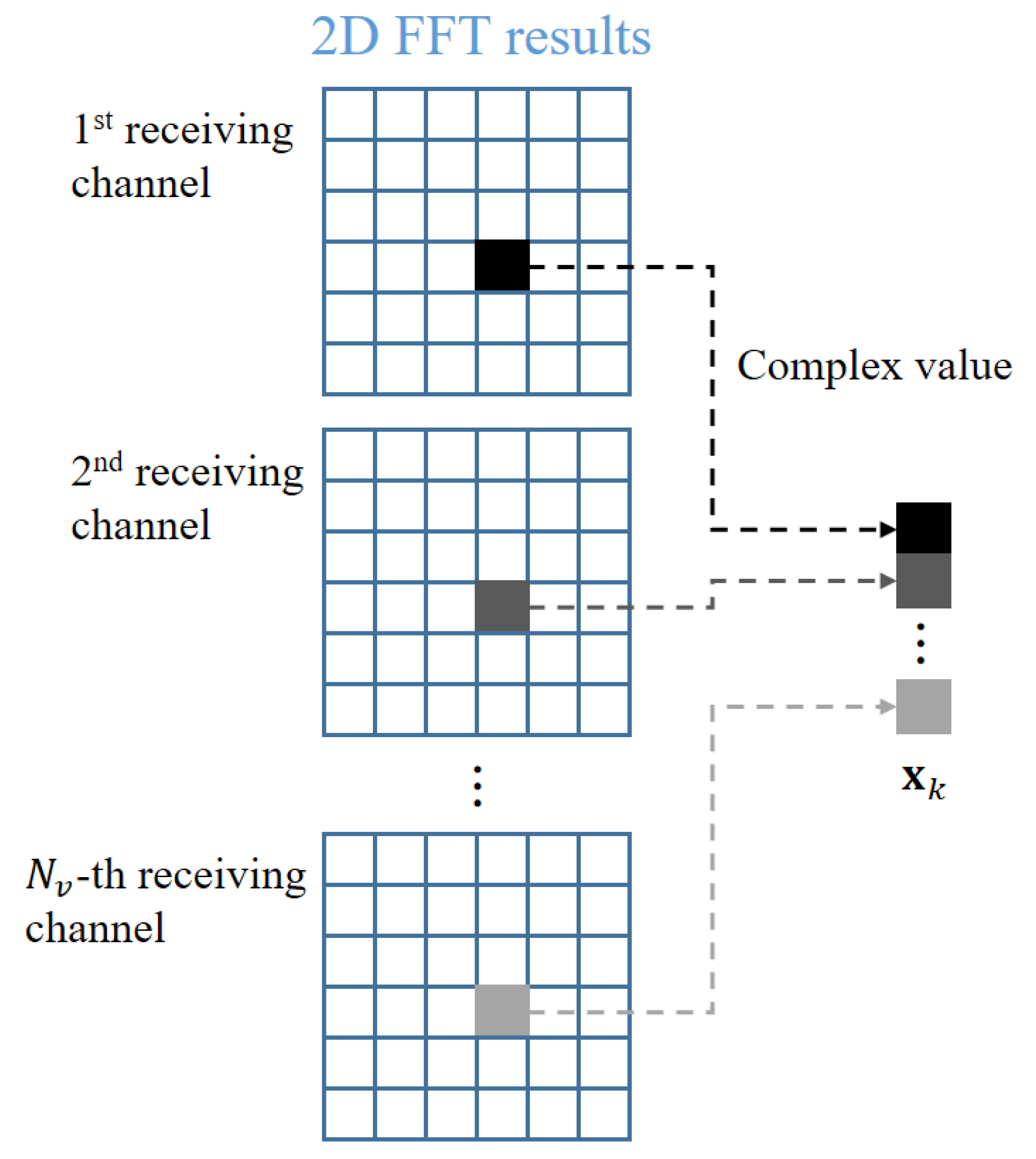
3.2. Angle Estimation Using Multiple Antenna Elements
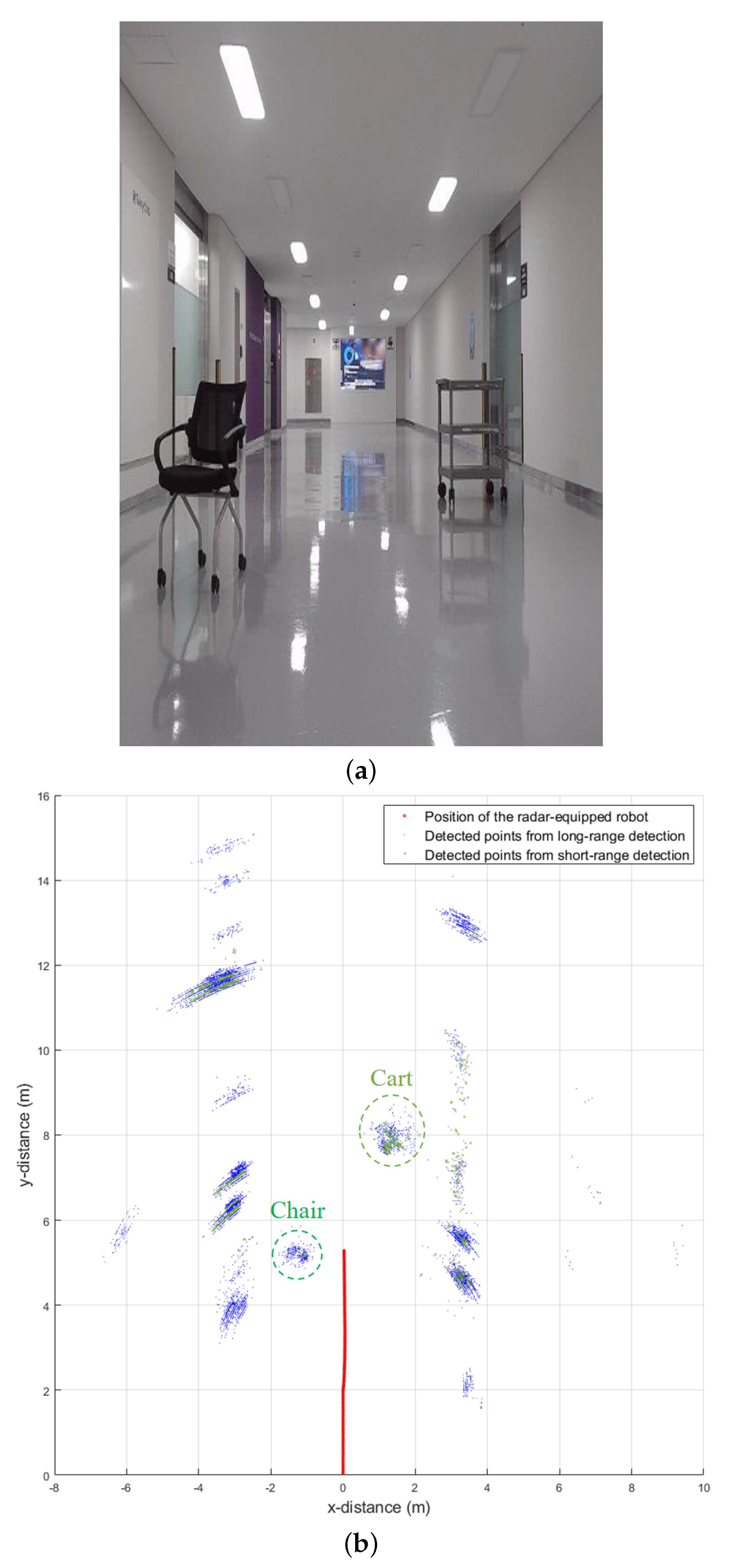
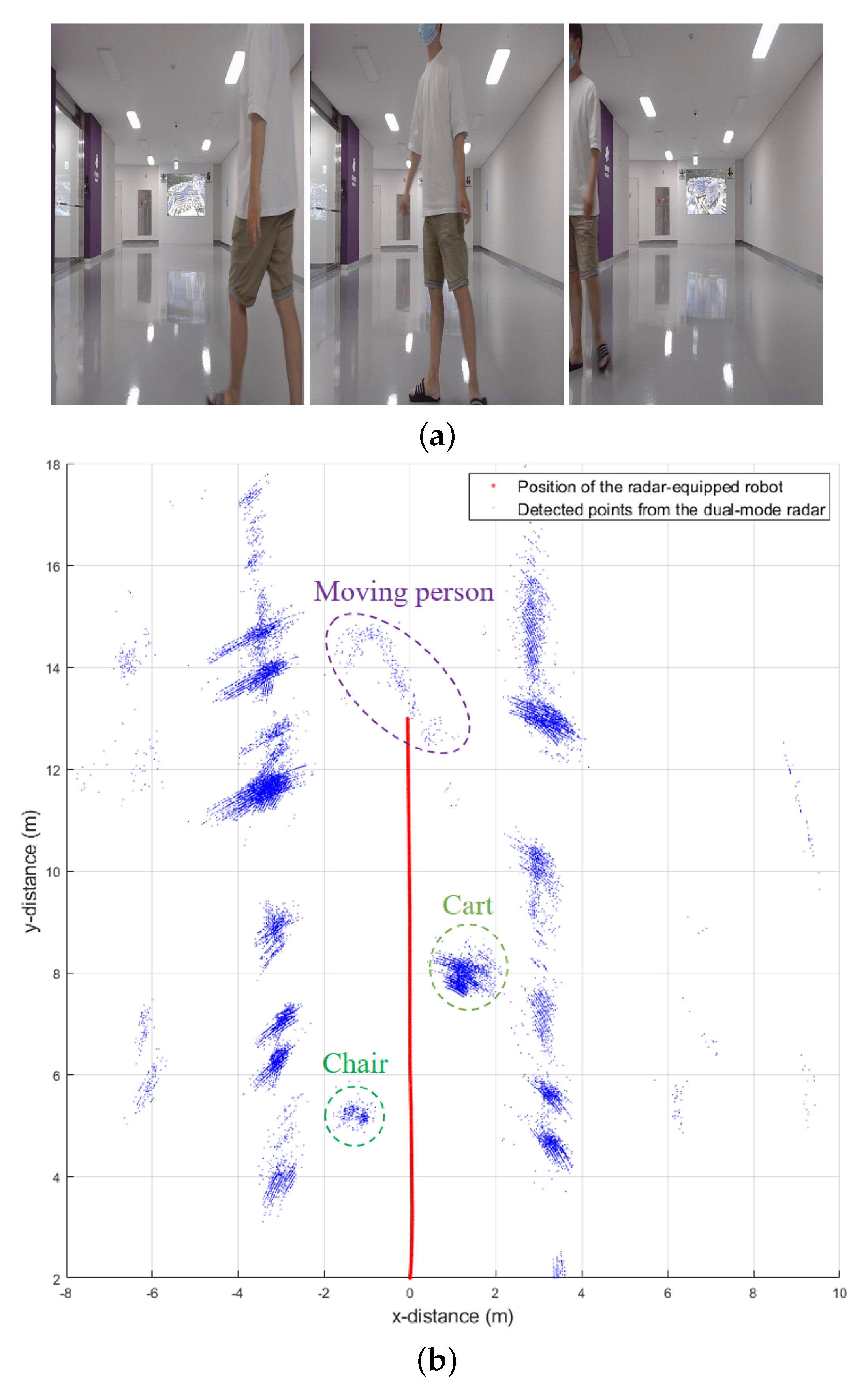
3.3. Detection Results in Dual-Mode
4. Indoor Environment Mapping Using Dual-Mode Radar Detection Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| ESPRIT | Estimation of signal parameters via rotational invariance techniques |
| FFT | Fast Fourier transform |
| FHR | Fraunhofer Institute for High Frequency Physics and Radar Techniques |
| FMCW | Frequency-modulated continuous wave |
| FOV | Field of view |
| MIMO | Multiple-input multiple-output |
| MUSIC | Multiple signal classification |
| PCB | Printed circuit board |
| RANSAC | Random sample consensus |
| SIMO | Single-input multiple-output |
| SLAM | Simultaneous localization and mapping |
References
- Deißler, T.; Thielecke, J. Feature based indoor mapping using a bat-type UWB radar. In Proceedings of the IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–11 September 2009; pp. 475–479. [Google Scholar]
- Guerra, A.; Guidi, F.; Ahtaryieva, L.; Decarli, N.; Dardari, D. Crowd-based personal radars for indoor mapping using UWB measurements. In Proceedings of the IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Nanjing, China, 16–19 October 2016; pp. 1–4. [Google Scholar]
- Schouten, G.; Steckel, J. RadarSLAM: Biomimetic SLAM using ultra-wideband pulse-echo radar. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Schouten, G.; Stecke, J. A biomimetic radar system for autonomous navigation. IEEE Trans. Robot. 2019, 35, 539–548. [Google Scholar] [CrossRef]
- Marck, J.W.; Mohamoud, A.; vd Houwen, E.; van Heijster, R. Indoor radar SLAM: A radar application for vision and GPS denied environments. In Proceedings of the European Radar Conference, Nuremberg, Germany, 9–11 October 2013; pp. 471–474. [Google Scholar]
- Fritsche, P.; Wagner, B. Modeling structure and aerosol concentration with fused radar and LiDAR data in environments with changing visibility. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2685–2690. [Google Scholar]
- Mielle, M.; Magnusson, M.; Lilienthal, A.J. A comparative analysis of radar and lidar sensing for localization and mapping. In Proceedings of the European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019; pp. 1–6. [Google Scholar]
- Park, Y.S.; Kim, J.; Kim, A. Radar localization and mapping for indoor disaster environments via multi-modal registration to prior LiDAR Map. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 1307–1314. [Google Scholar]
- Cohen, M.N. An overview of high range resolution radar techniques. In Proceedings of the National Telesystems Conference Proceedings, Atlanta, GA, USA, 26–27 March 1991; pp. 107–115. [Google Scholar]
- Stove, A.G. Linear FMCW radar techniques. IEE Proc. F Radar Signal Process. 1992, 139, 343–350. [Google Scholar] [CrossRef]
- MIMO Radar. Available online: Https://www.ti.com/lit/an/swra554a/swra554a.pdf (accessed on 1 March 2021).
- Friedlander, B. Direction finding using an interpolated array. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 2951–2954. [Google Scholar]
- Kahrilas, P.J. Design of electronic scanning radar systems (ESRS). Proc. IEEE 1968, 56, 1763–1771. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Zhang, P.; Xu, S.; Zhang, E. Velocity measurement research of moving object for mobile robot in dynamic environment. In Proceedings of the 10th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 25–26 August 2018; pp. 235–238. [Google Scholar]
- Crouch, S. Velocity measurement in automotive sensing: How FMCW radar and lidar can work together. IEEE Potentials 2020, 39, 15–18. [Google Scholar] [CrossRef]
- Jung, J.; Lee, S.; Lim, S.; Kim, S. Machine learning-based estimation for tilted mounting angle of automotive radar sensor. IEEE Sens. J. 2020, 20, 2928–2937. [Google Scholar] [CrossRef]
- Winkler, V. Range Doppler detection for automotive FMCW radars. In Proceedings of the 2007 European Microwave Conference, Munich, Germany, 9–12 October 2007; pp. 1445–1448. [Google Scholar]
- Moffet, A.T. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, AP-16, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-Y.; Vaidyanathan, P.P. Minimum redundancy MIMO radars. In Proceedings of the IEEE International Symposium on Circuits and Systems, Seattle, WA, USA, 18–21 May 2008; pp. 45–48. [Google Scholar]
- Schmid, C.M.; Feger, R.; Pfeffer, C.; Stelzer, A. Motion compensation and efficient array design for TDMA FMCW MIMO radar systems. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 1746–1750. [Google Scholar]
- Tuncer, T.E.; Yasar, T.K.; Friedlander, B. Direction of arrival estimation for nonuniform linear arrays by using array interpolation. Radio Sci. 2007, 42, 1–11. [Google Scholar] [CrossRef]
- Bartlett, M.S. Smoothing periodograms from time series with continuous Spectra. Nature 1948, 161, 686–687. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Kailath, T. ESPRIT—Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef] [Green Version]
- Gross, F.B. Smart Antennas for Wireless Communications with MATLAB, 2nd ed.; McGraw-Hill Professional: New York, NY, USA, 2005. [Google Scholar]
- Lee, H.-B. Efficient Parameter Estimation Methods for Automotive Radar Systems. Ph.D. Thesis, Department of Electrical and Computer Engineering, College of Engineering, Seoul National University, Seoul, Korea, 2016. [Google Scholar]
- Godara, L.C. Application of antenna arrays to mobile communications, Part II: Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef] [Green Version]
- Shahi, S.N.; Emadi, M.; Sadeghi, K. High resolution DOA estimation in fully coherent environments. Prog. Electromagn. Res. C 2008, 5, 135–148. [Google Scholar]
- Lim, S.; Lee, S.; Kim, S.-C. Clustering of Detected Targets Using DBSCAN in Automotive Radar Systems. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–7. [Google Scholar]
- Lim, S.; Lee, S. Hough transform based ego-velocity estimation in automotive radar system. Electron. Lett. 2021, 57, 80–82. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]







| Detection Mode | Long-Range Mode | Short-Range Mode |
|---|---|---|
| Bandwidth, B (GHz) | 1.5 | 3 |
| The number of chirps, and | 256 | 256 |
| The number of time samples, N | 128 | 128 |
| Maximum detectable range (m) | 20 | 10 |
| Range resolution (m) | 0.1 | 0.05 |
| Maximum detectable velocity (m/s) | 8 | 8 |
| Velocity resolution (m/s) | 0.315 | 0.315 |
| FOV (deg.) | −20∼20 | −60∼60 |
| Transmit power (dBm) | 10 | 10 |
| Total transmission time (ms) | 50 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kwon, S.-Y.; Kim, B.-J.; Lim, H.-S.; Lee, J.-E. Dual-Mode Radar Sensor for Indoor Environment Mapping. Sensors 2021, 21, 2469. https://doi.org/10.3390/s21072469
Lee S, Kwon S-Y, Kim B-J, Lim H-S, Lee J-E. Dual-Mode Radar Sensor for Indoor Environment Mapping. Sensors. 2021; 21(7):2469. https://doi.org/10.3390/s21072469
Chicago/Turabian StyleLee, Seongwook, Song-Yi Kwon, Bong-Jun Kim, Hae-Seung Lim, and Jae-Eun Lee. 2021. "Dual-Mode Radar Sensor for Indoor Environment Mapping" Sensors 21, no. 7: 2469. https://doi.org/10.3390/s21072469






