1. Introduction
Many critical services in our society, such as healthcare, transportation, and security, require a robust, reliable, and undisrupted supply of electricity. This requires on the one hand a reliable and redundant infrastructure, and on the other hand, the ability to maintain the performance of the infrastructure. As such, the ability to detect faults and to act accordingly is of critical importance for maintaining a high availability of the network [
1]. Many components of the power generation and distribution network can be directly monitored with specific sensors. However, it is not possible nor cost efficient for all the components and all the fault types. Therefore, for some of the components, the monitoring can only be performed indirectly through the behavior of the electrical current. For example, insulation damages in power systems, such as generators or defects in medium-voltage cables [
2], can be monitored by detecting localized pulses in the electrical current, namely, partial discharges (PD).
According to the IEC 60270 international standard, partial discharges are “localized electrical discharges that only partially bridge the insulation between conductors”. In fact, the presence of PD can be indicative of anomalies in many electrical systems and can cause further degradation of the insulation. The high-voltage discharges deteriorate the insulation materials and can have impacts on the entire system. Their detection is, therefore, of utmost importance to assess the condition of electrical components and has been a long-standing challenge [
3]. As such, the literature is extremely vast. PD detection has been studied in many systems such as in transformers [
4], gas-insulated high-voltage switchgear [
5], power plants [
6], and power lines [
7]. The main challenge in PD detection lies in the detection of extremely short and temporally localized events: their wavelength is at the micro-second scale. It requires, therefore, extremely high-frequency data (several tens of MHz). In addition, only few pulses can occur per period of the current utility frequency (usually 50 or 60 Hz) [
3]. In brief, PD signs in the electrical current represent roughly 1/20,000-th of the data. Until the very recent development of technologies able to capture and store such vast amount of data, the detection of PD patterns had to be performed online.
Among the traditional approaches, a group of approaches takes advantage of the property that for some systems, PD always occurs at the same phase in the electrical current. These approaches are also referred to as the phase-resolved partial discharge (PRPD) detection methods [
8]. They consist in detecting pulses in the electrical current, whereby the simplest method to detect a pulse is to apply a maximum filter. Subsequently, the detected rate of occurrence (n) of pulses is plotted as a function of their voltage amplitude (Q) and of their phase value (
). It can be implemented online and experts can inspect PRPD graphs to recognize the patterns generated by the different types of PD [
9]. However, to obtain meaningful occurrence rates, these methods require the aggregation of pulses over several hundreds or thousands of periods. Overall, these methods are expensive, as experts need to constantly monitor the
-Q-n diagrams. The interpretation of the diagrams also becomes difficult in the presence of noise or of superimposed pulses.
As all types of PD are not necessarily resolved in the phase domain, statistical approaches are also frequently used [
10]. They aim at characterizing the pulses with engineered features. The features become a multidimensional space where decision boundaries are established, for example with traditional classifiers such as random forest [
7], support vector machines (SVM) [
11,
12], or deep learning methods such as artificial neural networks (ANN) [
13], convolutional neural networks (CNN) [
14,
15], autoencoders [
16], and recurrent neural networks (long short-term memory networks (LSTM)) [
17,
18,
19]. For a more exhaustive overview, the reader is referred to the literature reviews in [
20,
21]. These methods are time consuming and expensive due to the difficulty of extracting and engineering the relevant features. It requires years of domain expertise for a profound understanding of the system. Additionally, the methods suffer from degradation performances when pulses are superimposed.
To address the aforementioned challenges, we propose to take advantage of the recent advances in Deep Learning (DL) applied to time series (TS) anomaly detection. For example, DL has already been successfully applied to identify cardiac abnormalities in electrocardiography (ECG) data [
22]. In particular, convolutional neural networks (CNN) have recently demonstrated very good performances for TS classification [
23,
24], forecasting [
25], and anomaly detection [
26]. In fact, temporal convolutions are able to learn meaningful filters in the time domain, adjusted to the signature of the analyzed events, and are, thus, often compared to learnable spectral features [
27].
In this paper, we propose an end-to-end learning framework for partial discharge detection in time series. The framework comprises two parts: (1) the automatic PD detection without any feature engineering and (2) the subsequent extraction of pulse activation maps that provide the domain experts a possibility to interpret the results. The difficulty met by previous research in the detection of partial discharges lies in the discrimination between PD and non-PD related pulses. Therefore, we propose here to extract a collection of pulses for each period of the utility frequency. We train a temporal convolution neural network with the binary information of whether PD are present in the original time series or not. Since all pulses of the collection are processed with the same temporal filters, a well-performing model should be able learn the PD pulse signatures. Learning these signatures is, in fact, particularly valuable for the experts to potentially distinguish between different types of PD. Therefore, we design our framework to provide both competitive results in terms of partial discharge detection, and a visualization of the neural network processing of the inputs through the pulse activation maps. These activation maps provide interpretability and explainability of the results and allow the experts to diagnose for each time series, which pulses and which part of the pulses where dominant in the final score of the network. It gives an extremely fine interpretation of the network decision. We demonstrate the performance of the proposed approach by achieving rank 4 on private leaderboard of the Kaggle VSB Power Line Fault Detection competition. The aim is to identify damaged power lines from the observed PD in the electrical voltage [
2,
28]. Furthermore, we also demonstrate the added value of each part of the proposed framework with an ablation study.
The paper is organized as follows.
Section 2 presents each step of the framework, including the preprocessing, network architecture, and pulse activation map devising.
Section 3 details the experiments we performed to quantify the results presented in
Section 4. The final results are discussed in
Section 5.
2. Methodology
An overview of the proposed framework is presented in
Figure 1. For each measurement (1), each phase is handled independently. Low frequencies, in particular the utility frequency, are filtered first (2). Pulses are identified and ranked with a simple maximum filter and extracted into a pulse collection (3). Each phase is estimated independently by the same neural network (4). The final decision on the power line takes the results from the three phases into account and applies a global threshold (5). Last, a pulse activation map (6) is computed to understand which part of the input led to the networks classification results.
2.1. Preprocessing
The main assumption of the proposed framework relies on the inherent definition of a PD signature as a pulse in the electric current. Thus, inspired by the PRPD analysis, in the very first step, we identify and extract the pulses with a simple maximum filter. This requires first the removal of the low frequencies.
Data filtering—
Figure 1 (2). PDs are due to insulation failures and typically occur at very specific voltage changes. Their frequency is much higher than the utility frequency
. Thus, we first implement a high-pass filter with cut-off frequency
. In this work, we apply a Butterworth filter of order 5 [
29]. However, other filters could be explored. An example before and after the filtering of an electric current recording over one period is shown in
Figure 1 (2), where the sampling frequency
MHz,
kHz and
Hz. Low frequencies such as the underlying sine wave are eliminated after the high-pass filter, while the high frequency pulses remain unchanged.
Pulse extraction—
Figure 1 (3). As the partial discharge signature is inherently a pulse in the electric potential, we propose as a second step to extract a large collection of pulses from the recordings that will be used as inputs to the neural network (NN). The goal of the NN is to learn to recognize if there is a PD pulse signature within the input collection. Due to the nature of partial discharge, we can expect some periodicity in the occurrence of the pulses with respect to the utility frequency. We create therefore, for each period of the utility frequency, a 2D array where each row represents a single pulse. The columns represent the time dimension. The number of columns corresponds to the number of timestamps
w collected for each pulse.
The pulses are identified with a maximum filter on the absolute value of the electric potential. The filter extracts the local maximal values which are further apart than a given window size. For simplicity purposes, we set this window to
w. We extract in the filtered data, the
w timestamps around each of the
largest local maxima, with an offset of
. That is, if the
i-th local maximum is localized at timestamp
, we extract the interval
. The collection of pulses is, therefore, a 2D array of shape
.
Figure 1 (3) illustrates the pulse extraction and the resulting collection for one period and phase of the utility frequency.
and w are hyperparameters of the proposed approach. Expert domain knowledge could help to identify relevant values for these hyperparameters. The selected values would primarily depend on the noise level for the selection of (some noise pulses may dominate the PD pulses), and on the expected frequency of the pulses for the selection of w. Yet, if this knowledge is not available, as in our case, these hyperparameters can be selected based on cross-validation.
2.2. Temporal Convolutional Neural Network
Convolutional neural network (CNN). Inspired by the recent advances in computer vision and more recently also in time series classification tasks, using CNN architectures, we propose to apply a CNN for this PD detection task. For the applied architecture, we propose a deep learning neural network architecture with a similar structure to VGG neural networks [
30]. Yet, the architecture requires several adaptations to the high-frequency time series data as used in this case study. Unlike in images, where the neighborhood of a pixel has a clear meaning in both the
X and the
Y dimensions, in the extracted pulses, only the temporal dimension contains a physically meaningful neighborhood relationship. The pulses have been ordered by decreasing amplitudes and not by their relationships in the signal. We, therefore, apply 1D convolutions instead of 2D kernels. This also means that the temporal filters are applied identically to each pulse, performing operations similar to spectral analysis.
Global Average Pooling (GAP). A limitation when using CNN is that the convolutional layers preserve the dimensionality of their inputs. Therefore, as predictions are usually vectors (with one element per class), it is necessary to flatten the latent space in order to transition toward fully connected layers. A consequence is an explosion in the number of model parameters, often leading to overfitting effects and harming the generalization ability of the network. We propose, therefore, to use the Global Average Pooling (GAP) as a structural regularizer [
31,
32]. GAP takes the average over the feature maps channel-wise and thus shrinks the size of the last latent space before its vectorization.
Proposed CNN Architecture. The proposed network architecture takes advantage of 1D CNN and the GAP layer. It contains 2 blocks comprising 2 successive convolutional layers and a max pooling layer. The 2 blocks are followed by a GAP layer, a fully connected (FC) layer, and a single neuron layer for binary classification.
2.3. Pulse Activation Maps (PAM)
To provide more interpretability and more insights on the network decision to classify a collection of pulses as belonging to a damaged line or not, we propose to devise the Class Activation Maps (CAM) of our network [
33]. Following the methodology in [
33], we devise in this section the pulse activation map (PAM) for the proposed network architecture. The PAM enables to interpret which part of the pulse has contributed most to the classification result (in this case, PD, or non-PD). There are two differences to the original contribution. First, our network has a binary output. We devise a single PAM per input, instead of a per-class activation map. Second, our network contains a fully connected layer between the GAP and the output. In the following, we demonstrate that the CAM (or here, the PAM) can still be computed in such cases, as long as the activation functions used by the intermediate fully connected layers are piece-wise linear.
As the first two blocks of our network use 1-D convolution filters, the latent space M after the last block can be written as , where is the number of pulses used as input to the network, is the resulting size after the successive max-pooling (here ), and is the number of filters of the last convolution. In the following, we denote the size of M as .
The
j-th neuron of the GAP layer performs the operation:
The GAP layer is connected to a fully connected layer of size
with the weights and bias
, we have for the
i-th neuron, before activation:
After the piece-wise linear activation function, the
i-th activated neuron
is given by
where
Note that the definition of can be generalized to any piece-wise linear activation function. Under this assumption, it is also worth noticing that Equation (3) can be generalized to as many successive fully-connected layers as required.
Last, the activated neurons are combined into a last dense layer of output size 1. Denoting its weights and bias by
. The final score before the sigmoid is obtained as
Finally, the pulse activation map
for each input is a collection of
vectors of size
and is defined as
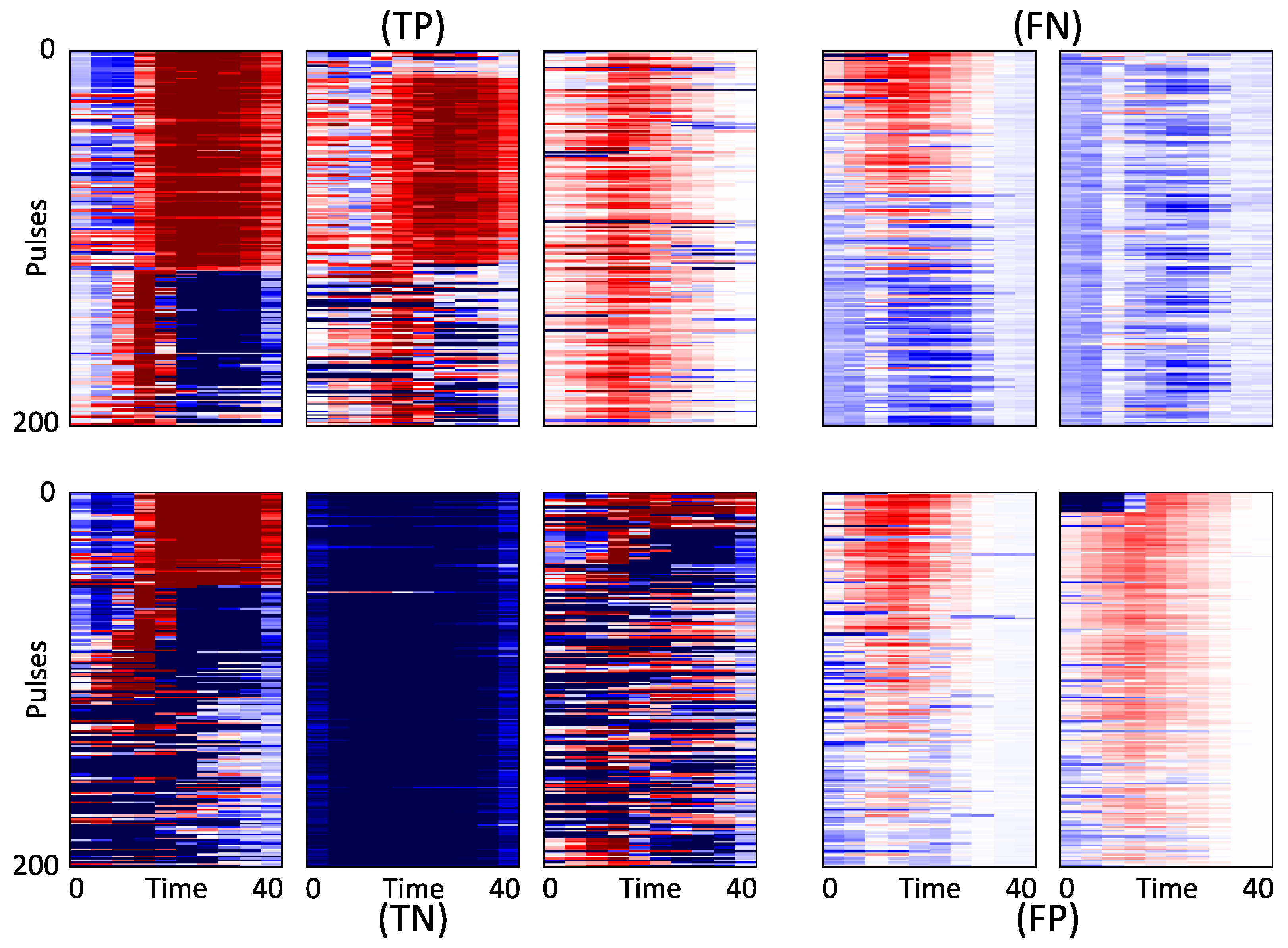
As the decision of the network is taken after applying the sigmoid operation to the value Equation (5), we can interpret the PAM as follows. A map whose average is positive corresponds to a score above 0.5 after the sigmoid operation, and is thus originating from pulses containing PD. On the contrary, a map whose average is negative corresponds to a non-PD pulse. The activation maps can be used by domain experts to further evaluate the pulses and possibly to distinguish between different types of PD.
3. Experiments
3.1. Datasets
To demonstrate the benefit of our approach, we apply the proposed methodology on the VSB dataset, generated and released by the Technical University of Ostrava [
28]. The goal of the case study is to detect damaged three-phase, medium-voltage overhead power lines [
2]. According to the dataset description, damaged power lines can be identified through the observed PD patterns [
28]. To this end, the electric voltage is recorded over one period of the grid utility frequency, 50 Hz, for the three phases simultaneously. The sampling frequency is 40 MHz such that each recording contains 800,000 values. An example signal is shown in
Figure 1 (1).
The VSB dataset contains two sets of measurements. The training set contains 8712 samples with 3 labels: the measurement ID, the phase, and whether the power line insulation was damaged at the time of recording. Damaged power lines should contain PD, however no additional information is provided on the PD types, shapes, or location. In this set, 575 samples are labeled as damaged power lines.
The second set contains 20,037 samples with two labels: the measurement ID and the phase. No ground truth is provided with respect to the presence of PD. However, the predictions of the health state can be evaluated online through the Matthew Correlation Coefficient (MCC).
To the best of our knowledge, no other published study outside of the competition leaderboard reported results on the second test dataset. In [
12,
18,
19], the reported results are computed on a subset of the labeled dataset. In [
12], results are reported on the full training set and might therefore be overfitted. In [
18], results are reported on an artificially augmented set containing 807 non-PD signals and 935 signals with PD, which might also therefore suffer overfitting. We report anyway their results in Table 2, where we recompute the value of the metrics they would achieve on our set, assuming constant sensitivity and specificity of their model. This cannot be done for the work in [
19], as the numbers of tested samples with and without PD are not reported.
3.2. Network Architecture and Training
The proposed neural network architecture as presented in
Figure 1 (4) comprises two convolutional blocks: The first block contains two temporal convolutional layers with 16 kernels of size 15. The second block has two temporal convolutional layers with 8 kernels of size 10. Each block is followed by a 1D temporal max-pooling layer with kernel size 2. Therefore, the input size is
, the latent space size after the first block is
, the latent space size after the second block is
, and the latent space size after the GAP layer is 8. In particular, we have
in Equation (6). The fully connected layer after the GAP layer is of size 32. All layers but the last output layer use
ReLU as activation function. The hyperparameters of this architecture (number of blocks, kernel number, and size) were inferred from a grid search with a 5-fold stratified cross-validation.
We implemented the network with Keras and TensorFlow. For the training, we used the
ADAM [
34] optimizer with constant learning rate of
,
, and
. We used the binary cross entropy loss:
where
y is the ground truth and
p is the network output.
3.3. Threshold Setting
The problem at hand is a binary classification problem. The output is, therefore, designed as a single neuron output layer, activated with a sigmoid function such that the output is continuous between 0 and 1. The traditional baseline consists in using a threshold at value 0.5 on the network output value. Compared to the baseline approach, we propose to explore two modifications: first, the inference of an optimized threshold based on a validation set, and second, the consideration of the three phases as a single indicator of the power line health. We propose, thus, to compare four different postprocessing approaches of the network output:
- (i)
Baseline: Round the output (threshold ).
- (ii)
‘1=3’-Phase Classification: Round the prediction of the three phases. If one phase is estimated as damaged, the whole power line (the three phases) is considered as being damaged.
- (iii)
1-Phase Optimized Threshold: Infer the threshold with cross-validation, and consider each phase independently.
- (iv)
Proposed 3-Phase Global threshold: Using the threshold devised in (iii), apply the 3-Phase Global threshold, , to the sum of the output values for the three phases.
Please note that in (iv), the direct inference of the
with cross-validation instead of using
may have enhanced the performance. This is, however, not possible as in the training set, some samples do not have all the three phases recorded as damaged. Using 5-fold stratified cross validation to maximize the MCC (defined below in
Section 3.4), we define
.
3.4. Evaluation Metrics
As part of the competition, a tool is provided to evaluate the test set online. It provides an evaluation of the results with the Matthews Correlation Coefficient (
) [
35]:
where
is the number of true positives,
is the number of true negatives,
is the number of false positives, and
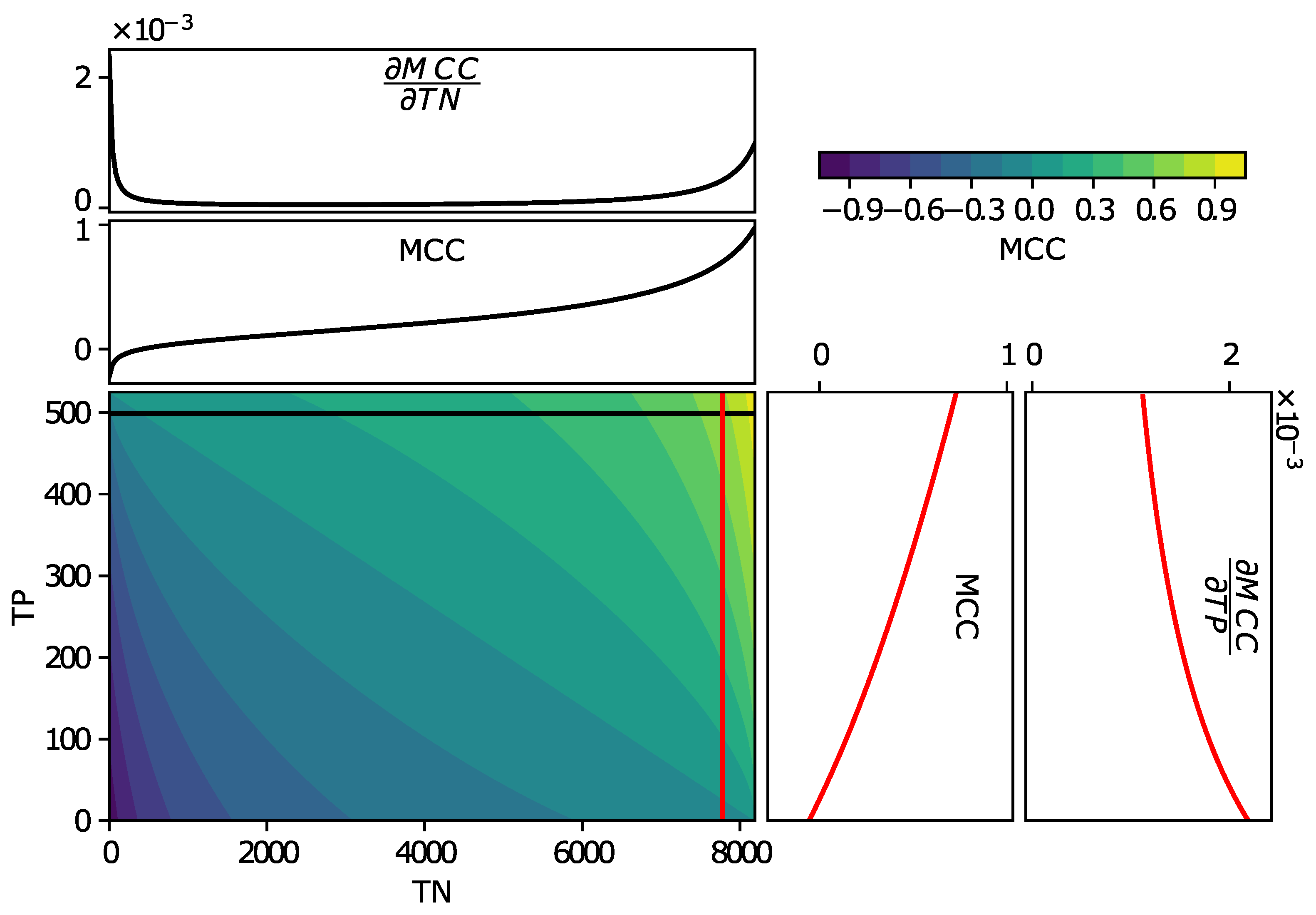
is the number of false negatives. This metric varies from −1 to 1, where 1 indicates an optimal solution, 0 a solution no better than a random guess, and −1 a total disagreement with the ground truth.
To enrich our evaluation of the network performance, we propose to use in addition three common evaluation metrics for binary classification problems, namely,
Accuracy,
Precision, and
Recall, as defined in Equations (9)–(11).
where
is the total number of samples.
If the Accuracy can give a false sense of performance of the model in a strongly imbalanced dataset (a naive model always classifying to the main class would have high Accuracy), its derivatives with respect to and are identical and constant. Changes in Accuracy are, therefore, easier to interpret than in other metrics.
6. Conclusions
In this paper, we proposed a new framework for the detection of damaged power lines. The proposed approach offers several improvements with respect to traditional power-line diagnostics. First, the proposed framework does not require any feature engineering and is able to handle raw measurements with extremely little preprocessing. Second, it provides competitive detection results at the power-line level, but also at the phase level. The proposed approach is robust and can detect damages in power lines from a single period of utility frequency. It provides a significant speed up compared to the more traditional PRPD approaches that require first, the processing of several hundreds of periods, and second, an expert analysis of the diagrams.
In addition, we proposed to extract the Pulse Activation Maps to improve the interpretability and to gain understanding on which part of the electrical signals are learned by the network as being a signature of a damaged power line. PAM can be used by the domain experts to gain more insights in the decisions of the proposed neural networks and to perform the diagnostics. PAM provides the information on which pulses and which part of the pulses dominated the decision of the neural network and allows to verify the network’s decision.
It can be pointed out that one limit of the task we tackled here is the relatively small size of the training dataset (from a deep learning perspective). Even though very competitive results were obtained, we believe our approach can showcase its full potential when more and more data will be available. Training the framework with more data will allow for a more precise tuning of the hyperparameters. Furthermore, if samples were identified per power-line, timestamped and collected over a long time period (which was not the case in the considered case study), the monitoring of the PAM evolution over time would be a very promising follow-up research. We could expect that, as a power-line damage increases, the PAM would become more and more positively activated, and such monitoring would have a potentially large benefit for the utility operators.