Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying
Abstract
1. Introduction
2. Materials and Methods
2.1. Low-Cost Receiver and Antenna
2.2. Reference Data and Measurements
2.3. Experiment Setup and Processing Strategies
2.3.1. Static Measurements
2.3.2. RTK and NRTK
3. Results and Discussion
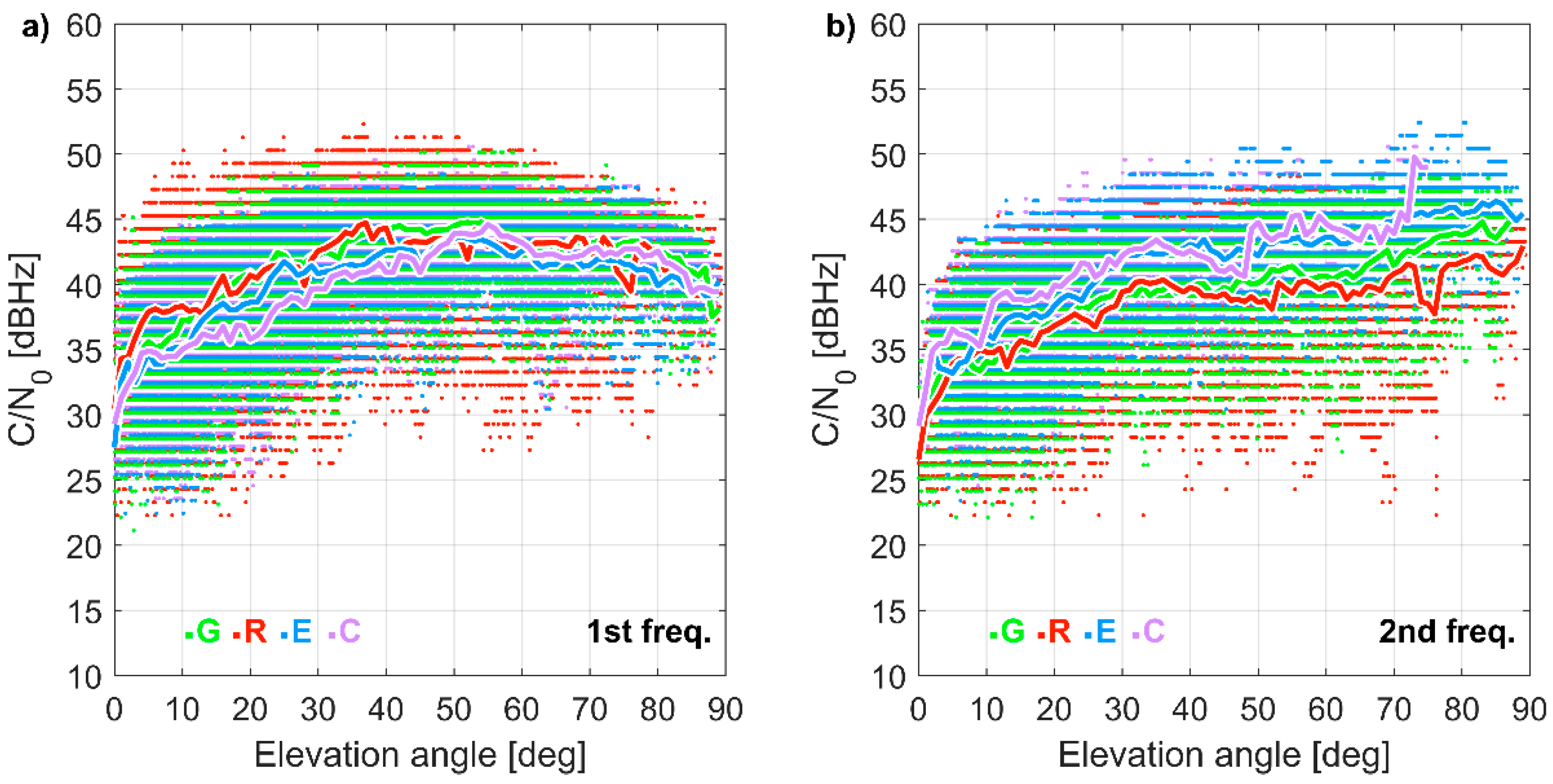
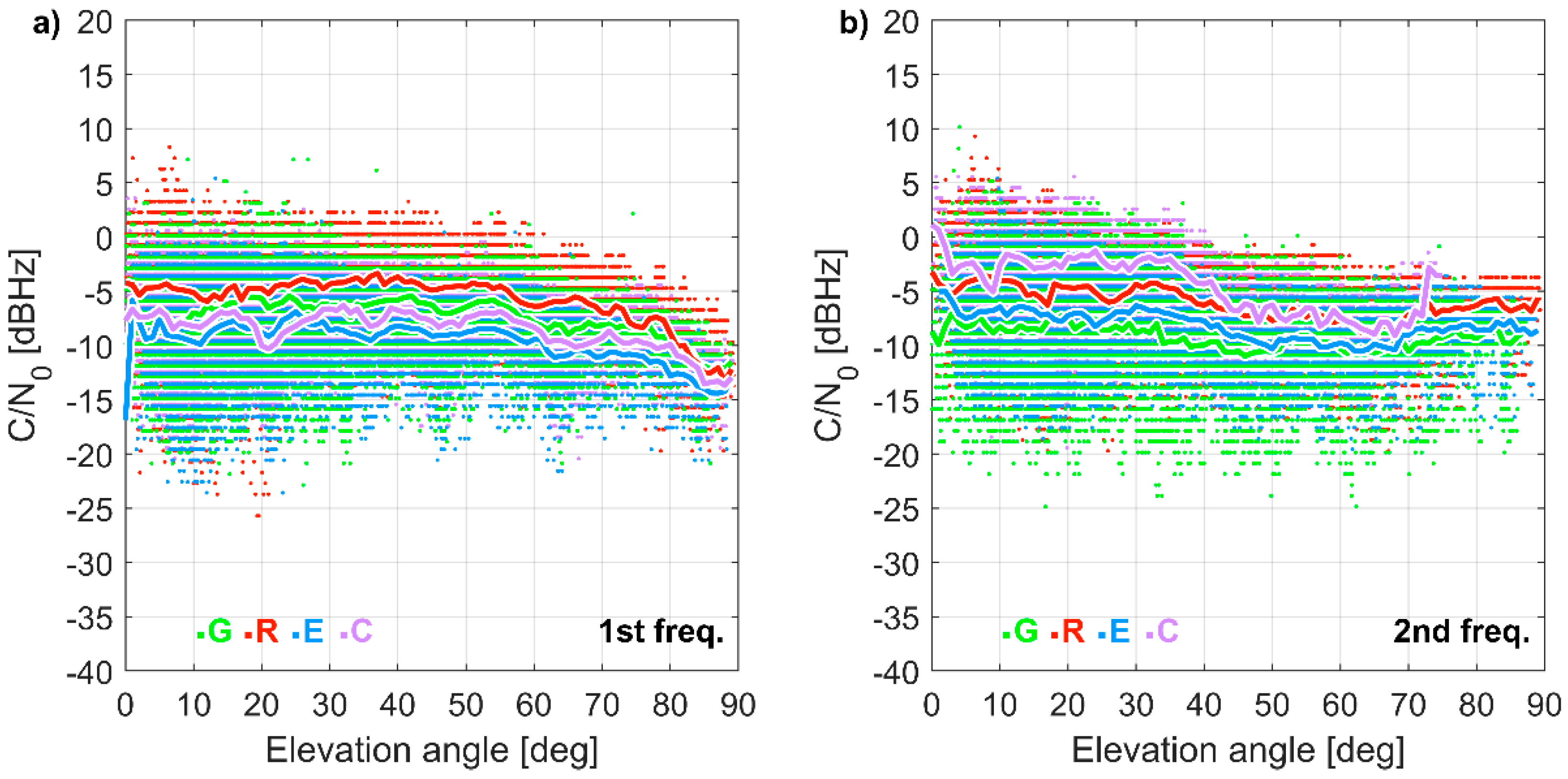
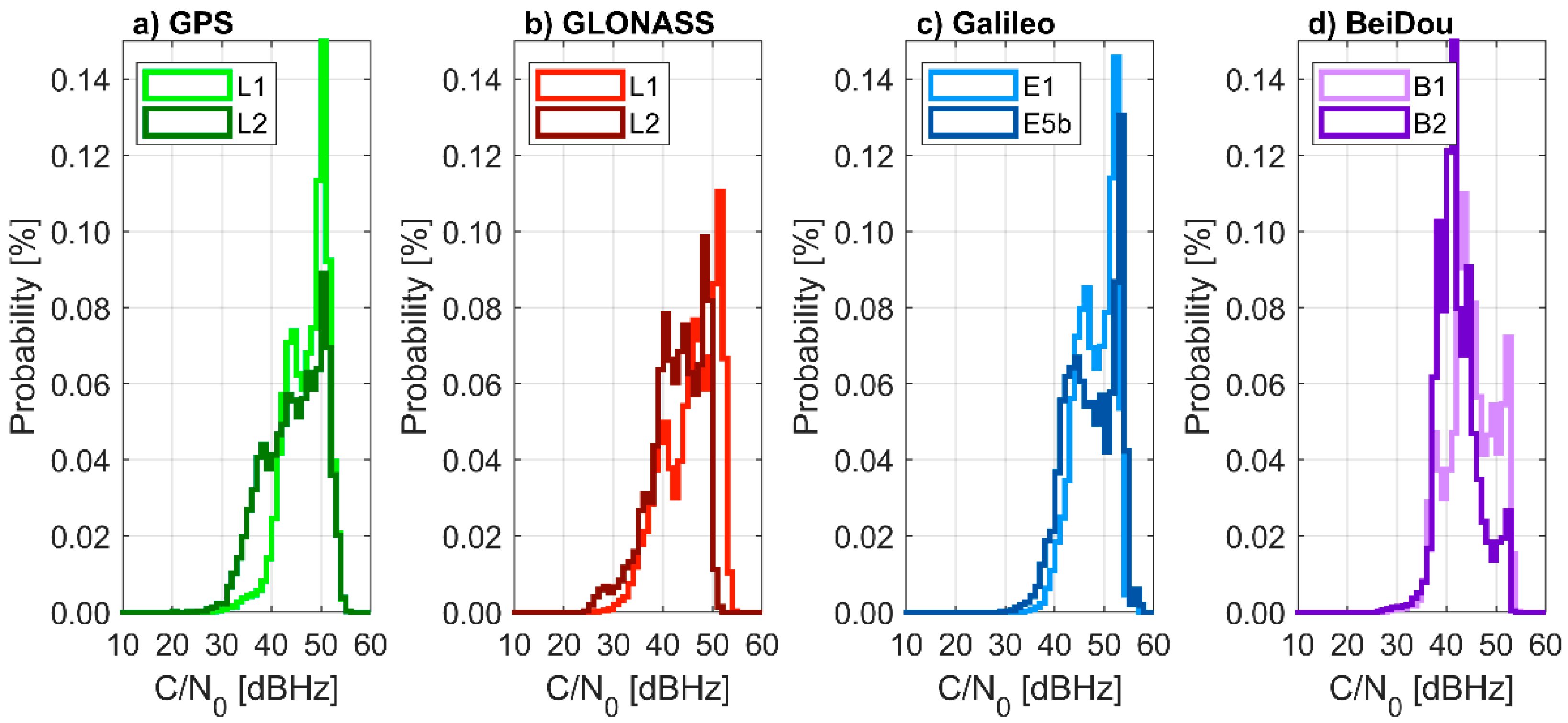
3.1. Carrier-to-Noise Ratio Analysis
3.2. Static Positioning
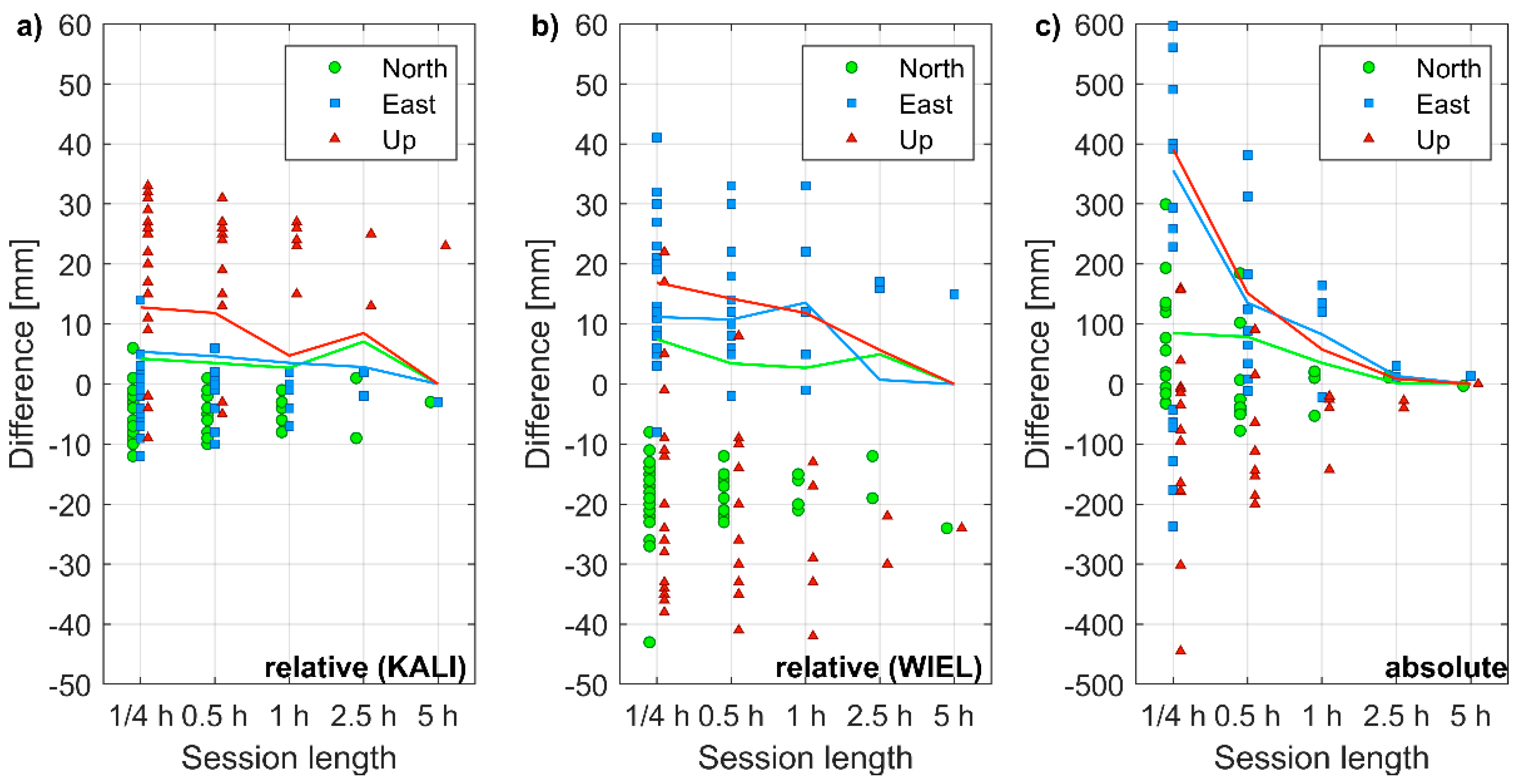
3.2.1. Session Length
3.2.2. Positioning Confidence and Accuracy
3.3. RTK and NRTK
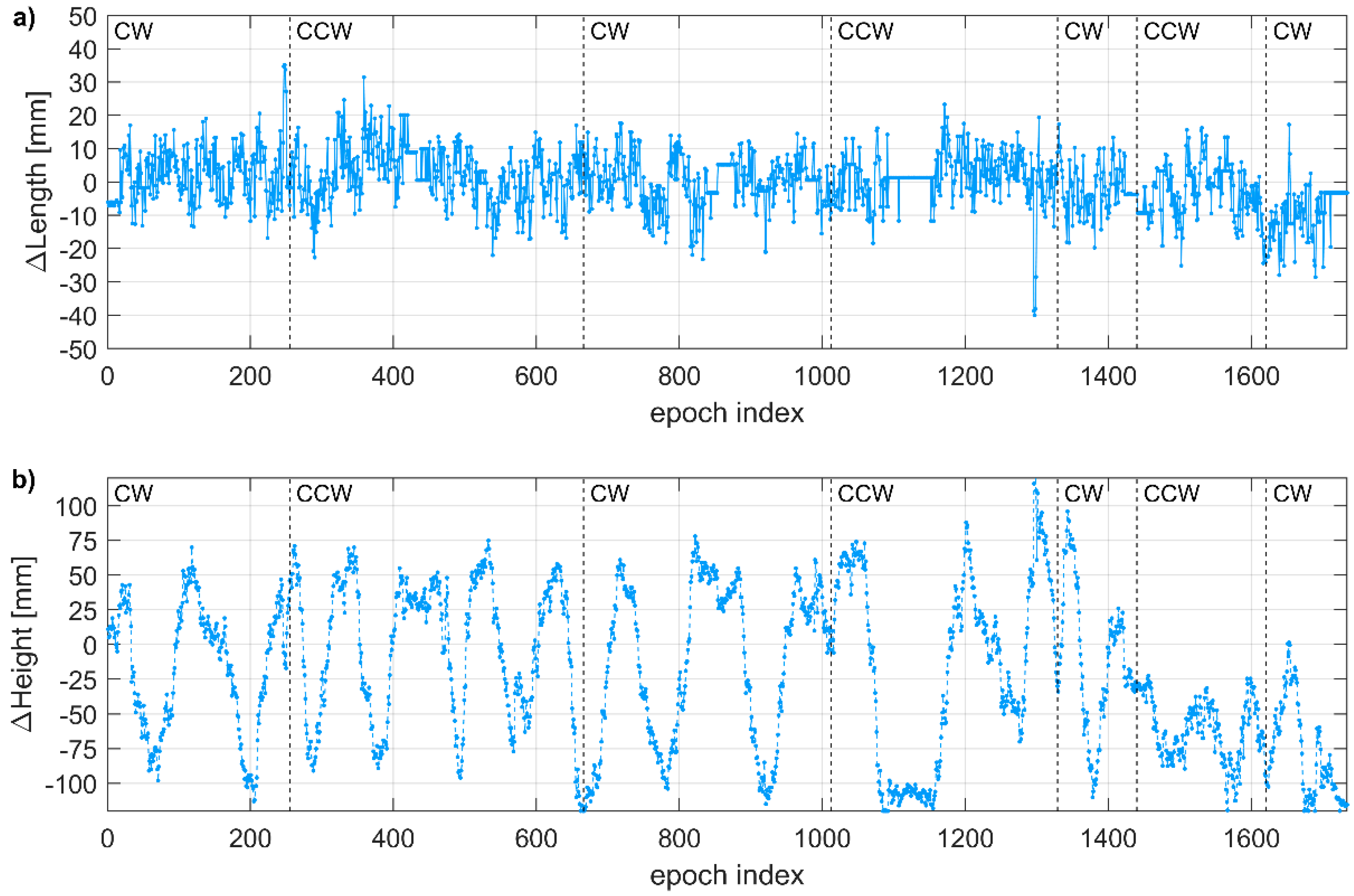
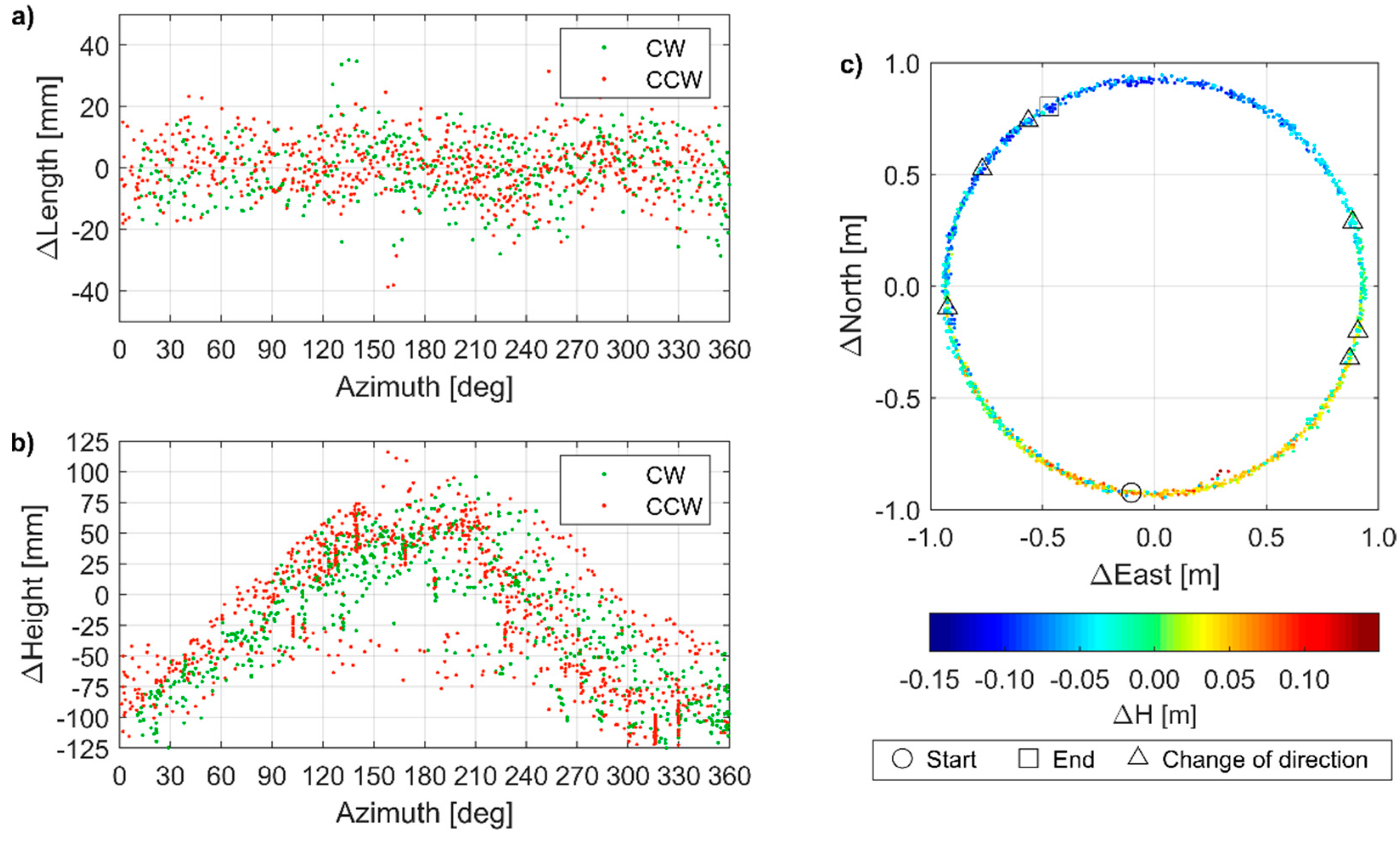
3.3.1. Baseline Precision
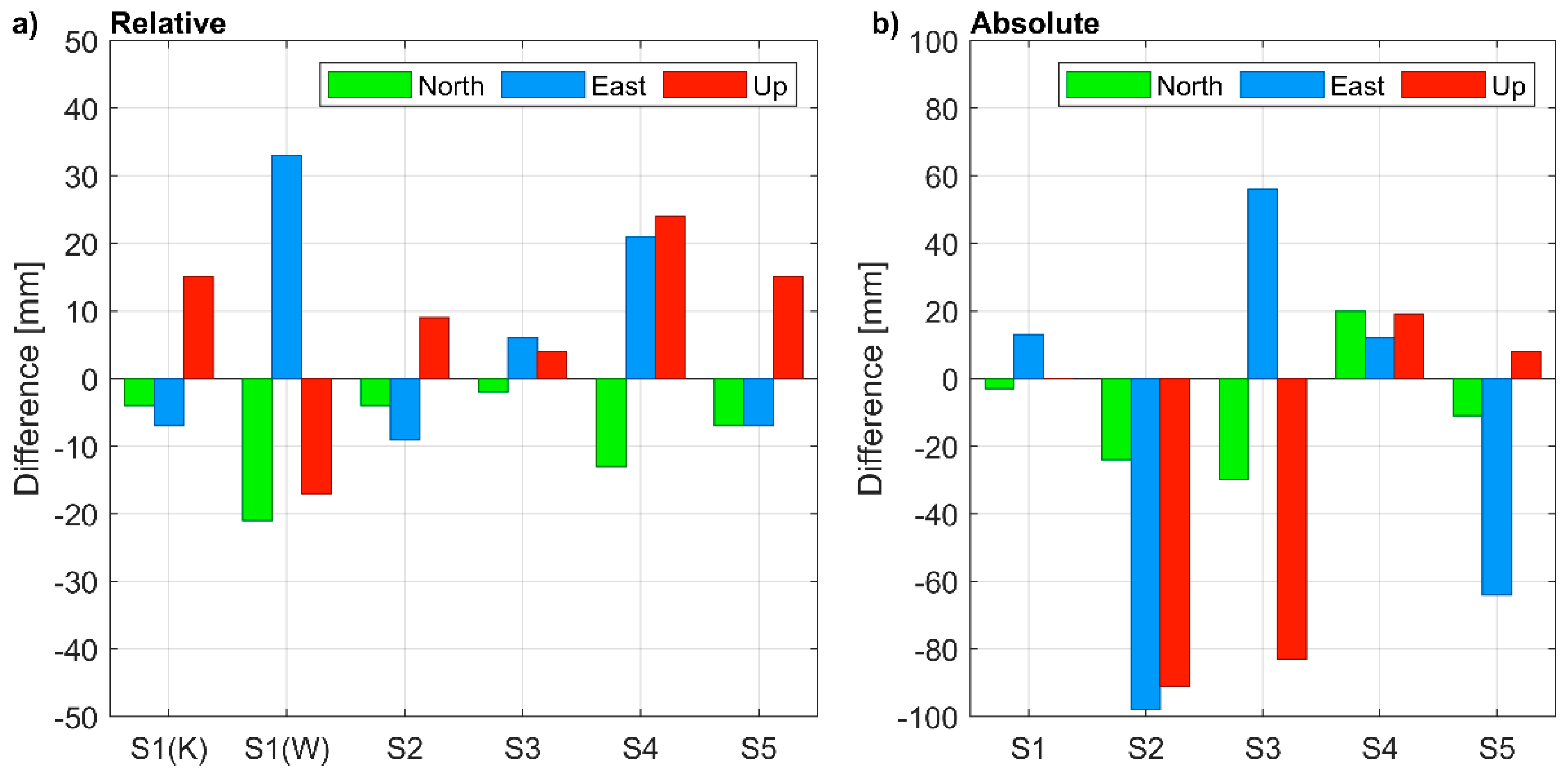
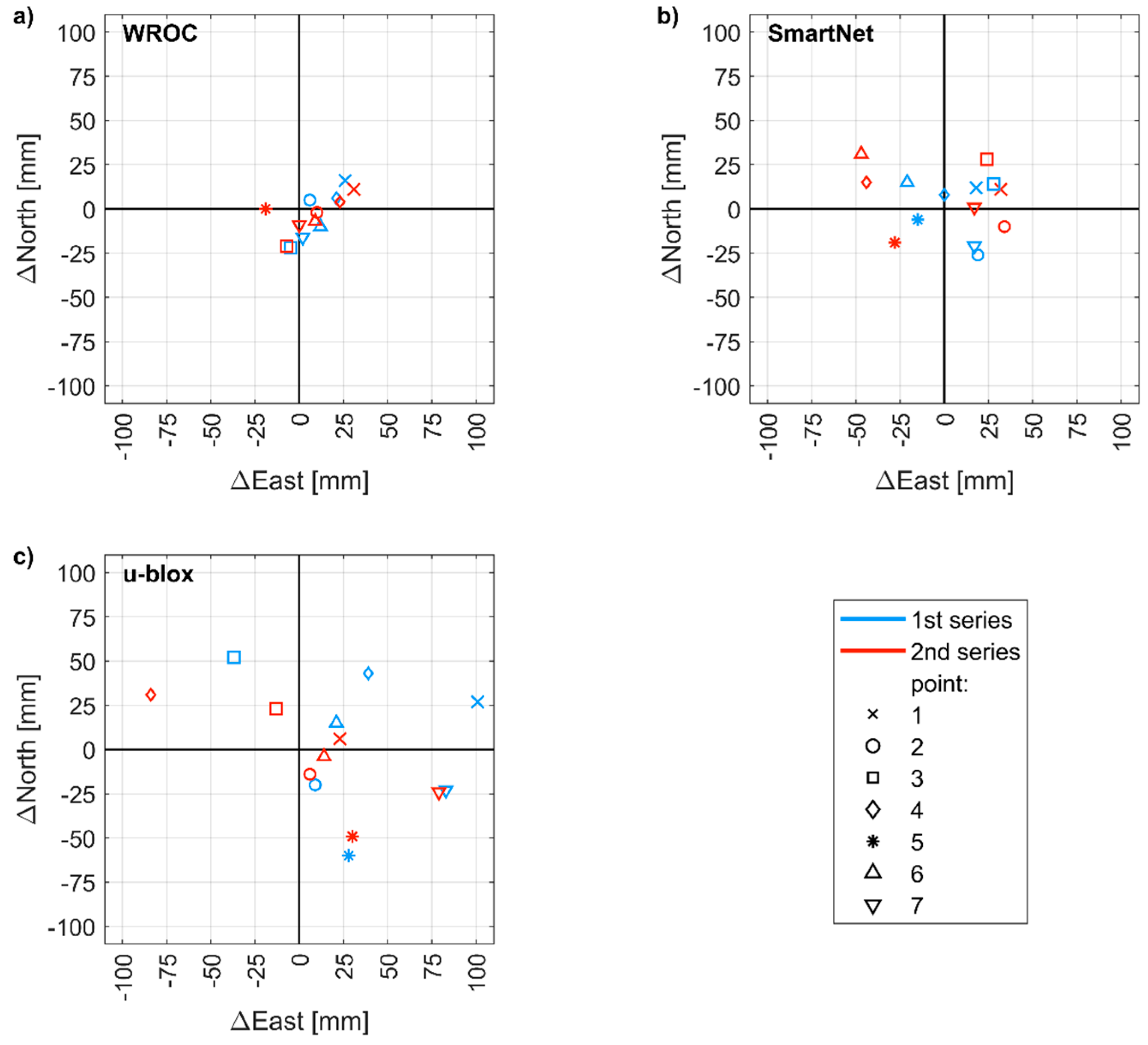
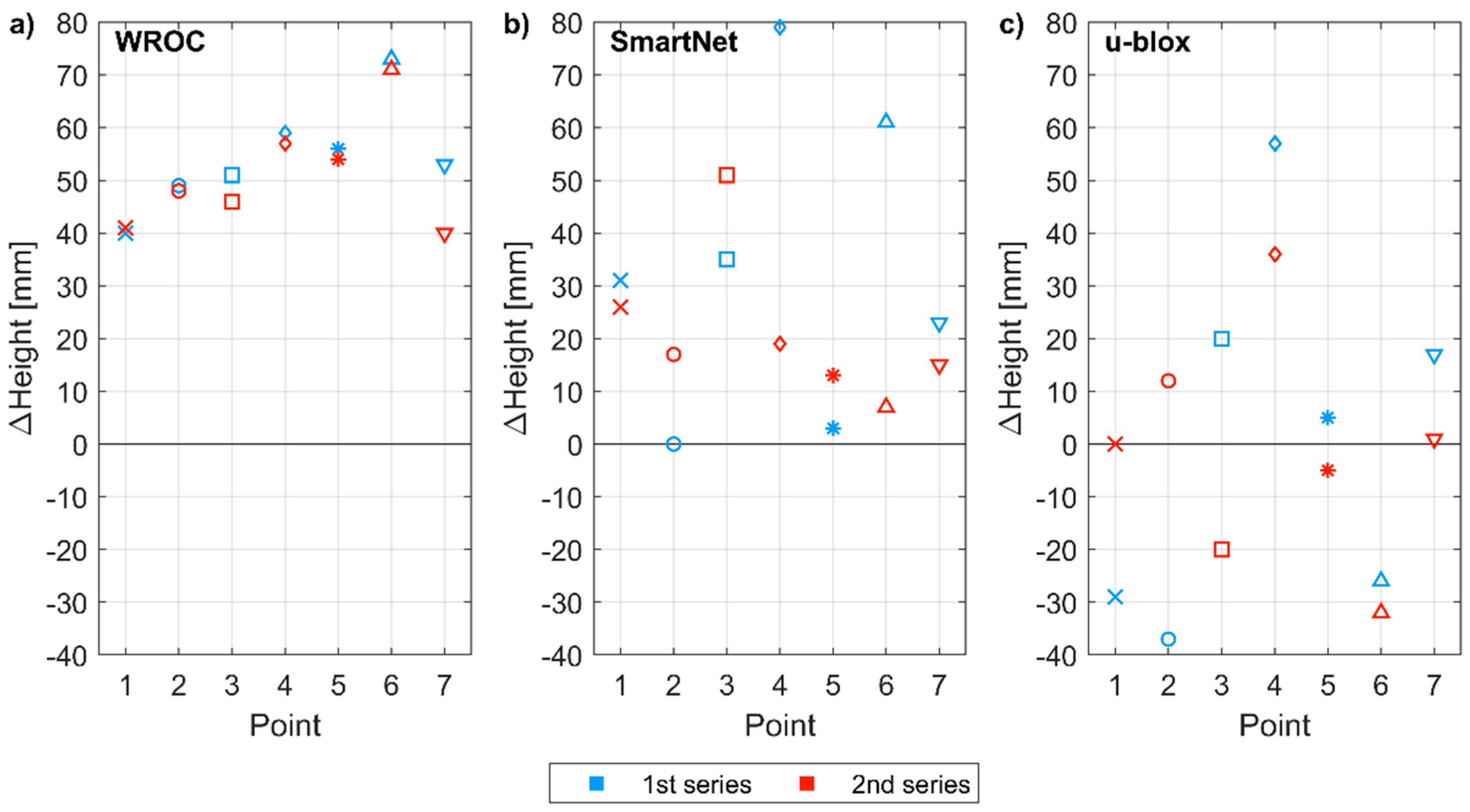
3.3.2. Positioning Accuracy
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Freymueller, J. Geodynamics. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1063–1106. ISBN 978-3-319-42928-1. [Google Scholar]
- Kreemer, C.; Blewitt, G.; Klein, E.C. A Geodetic Plate Motion and Global Strain Rate Model. Geochem. Geophys. Geosystems 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
- Martín, A.; Anquela, A.B.; Dimas-Pagés, A.; Cos-Gayón, F. Validation of Performance of Real-Time Kinematic PPP. A Possible Tool for Deformation Monitoring. Measurement 2015, 69, 95–108. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and Radar Interferometric Data for a 3D Surface Displacement Monitoring of Landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Nie, Z.; Zhang, R.; Liu, G.; Jia, Z.; Wang, D.; Zhou, Y.; Lin, M. GNSS Seismometer: Seismic Phase Recognition of Real-Time High-Rate GNSS Deformation Waves. J. Appl. Geophys. 2016, 135, 328–337. [Google Scholar] [CrossRef]
- Jakowski, N.; Béniguel, Y.; Franceschi, G.D.; Pajares, M.H.; Jacobsen, K.S.; Stanislawska, I.; Tomasik, L.; Warnant, R.; Wautelet, G. Monitoring, Tracking and Forecasting Ionospheric Perturbations Using GNSS Techniques. J. Space Weather Space Clim. 2012, 2, A22. [Google Scholar] [CrossRef]
- Bosy, J.; Kaplon, J.; Rohm, W.; Sierny, J.; Hadas, T. Near Real-Time Estimation of Water Vapour in the Troposphere Using Ground GNSS and the Meteorological Data. Ann. Geophys. 2012, 30, 1379–1391. [Google Scholar] [CrossRef]
- Padró, J.-C.; Muñoz, F.-J.; Planas, J.; Pons, X. Comparison of Four UAV Georeferencing Methods for Environmental Monitoring Purposes Focusing on the Combined Use with Airborne and Satellite Remote Sensing Platforms. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Melendez-Pastor, C.; Ruiz-Gonzalez, R.; Gomez-Gil, J. A Data Fusion System of GNSS Data and On-Vehicle Sensors Data for Improving Car Positioning Precision in Urban Environments. Expert Syst. Appl. 2017, 80, 28–38. [Google Scholar] [CrossRef]
- Rizos, C. Surveying. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1011–1037. ISBN 978-3-319-42928-1. [Google Scholar]
- Rizos, C. Network RTK Research and Implementation: A Geodetic Perspective. J. Glob. Position. Syst. 2002, 1, 144–150. [Google Scholar] [CrossRef]
- Lindqwister, U.J.; Zumberge, J.F.; Webb, F.H.; Blewitt, G. Few Millimeter Precision for Baselines in the California Permanent GPS Geodetic Array. Geophys. Res. Lett. 1991, 18, 1135–1138. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Anquela, A.B.; Martín, A.; Berné, J.L.; Padín, J. GPS and GLONASS Static and Kinematic PPP Results. J. Surv. Eng. 2013, 139, 47–58. [Google Scholar] [CrossRef]
- Cina, A.; Piras, M. Performance of Low-Cost GNSS Receiver for Landslides Monitoring: Test and Results. Geomat. Nat. Hazards Risk 2015, 6, 497–514. [Google Scholar] [CrossRef]
- Biagi, L.; Grec, F.C.; Negretti, M. Low-Cost GNSS Receivers for Local Monitoring: Experimental Simulation, and Analysis of Displacements. Sensors 2016, 16, 2140. [Google Scholar] [CrossRef]
- Gill, M.; Bisnath, S.; Aggrey, J.; Seepersad, G. Precise Point Positioning (PPP) Using Low-Cost and Ultra-Low-Cost GNSS Receivers. In Proceedings of the 30th International Technical Meeting of The Satellite Division of The Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 226–236. [Google Scholar]
- Takasu, T.; Yasuda, A. Evaluation of RTK-GPS Performance with Low-Cost Single-Frequency GPS Receivers. In Proceedings of International Symposium on GPS/GNSS; Tokyo University of Marine Science and Technology: Tokyo, Japan, 2008. [Google Scholar]
- Notti, D.; Cina, A.; Manzino, A.; Colombo, A.; Bendea, I.H.; Mollo, P.; Giordan, D. Low-Cost GNSS Solution for Continuous Monitoring of Slope Instabilities Applied to Madonna Del Sasso Sanctuary (NW Italy). Sensors 2020, 20, 289. [Google Scholar] [CrossRef] [PubMed]
- Zribi, M.; Motte, E.; Fanise, P.; Zouaoui, W. Low-Cost GPS Receivers for the Monitoring of Sunflower Cover Dynamics. Available online: https://www.hindawi.com/journals/js/2017/6941739/ (accessed on 29 December 2020).
- Poluzzi, L.; Tavasci, L.; Corsini, F.; Barbarella, M.; Gandolfi, S. Low-Cost GNSS Sensors for Monitoring Applications. Appl. Geomat. 2020, 12, 35–44. [Google Scholar] [CrossRef]
- Garrido-Carretero, M.S.; de Lacy-Pérez de los Cobos, M.C.; Borque-Arancón, M.J.; Ruiz-Armenteros, A.M.; Moreno-Guerrero, R.; Gil-Cruz, A.J. Low-Cost GNSS Receiver in RTK Positioning under the Standard ISO-17123-8: A Feasible Option in Geomatics. Measurement 2019, 137, 168–178. [Google Scholar] [CrossRef]
- Tsakiri, M.; Sioulis, A.; Piniotis, G. The Use of Low-Cost, Single-Frequency GNSS Receivers in Mapping Surveys. Surv. Rev. 2018, 50, 46–56. [Google Scholar] [CrossRef]
- Jackson, J.; Saborio, R.; Ghazanfar, S.A.; Gebre-Egziabher, D.; Davis, B. Evaluation of Low-Cost, Centimeter-Level Accuracy OEM GNSS Receivers; Minnesota Department of Transportation: Saint Paul, MN, USA, 2018. [Google Scholar]
- Nie, Z.; Liu, F.; Gao, Y. Real-Time Precise Point Positioning with a Low-Cost Dual-Frequency GNSS Device. GPS Solut. 2019, 24, 9. [Google Scholar] [CrossRef]
- Krietemeyer, A.; van der Marel, H.; van de Giesen, N.; ten Veldhuis, M.-C. High Quality Zenith Tropospheric Delay Estimation Using a Low-Cost Dual-Frequency Receiver and Relative Antenna Calibration. Remote Sens. 2020, 12, 1393. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Ambrožič, T.; Turk, G.; Sterle, O. Testing Multi-Frequency Low-Cost GNSS Receivers for Geodetic Monitoring Purposes. Sensors 2020, 20, 4375. [Google Scholar] [CrossRef] [PubMed]
- Catania, P.; Comparetti, A.; Febo, P.; Morello, G.; Orlando, S.; Roma, E.; Vallone, M. Positioning Accuracy Comparison of GNSS Receivers Used for Mapping and Guidance of Agricultural Machines. Agronomy 2020, 10, 924. [Google Scholar] [CrossRef]
- Arul Elango, G.; Sudha, G.F.; Francis, B. Weak Signal Acquisition Enhancement in Software GPS Receivers – Pre-Filtering Combined Post-Correlation Detection Approach. Appl. Comput. Inform. 2017, 13, 66–78. [Google Scholar] [CrossRef]
- Bramanto, B.; Gumilar, I.; Taufik, M.; Hermawan, I.M.D.A. Long-Range Single Baseline RTK GNSS Positioning for Land Cadastral Survey Mapping. E3s Web Conf. 2019, 94, 01022. [Google Scholar] [CrossRef]
- Gumilar, I.; Bramanto, B.; Rahman, F.F.; Hermawan, I.M.D.A. Variability and Performance of Short to Long-Range Single Baseline RTK GNSS Positioning in Indonesia. E3s Web Conf. 2019, 94, 01012. [Google Scholar] [CrossRef]


| Relative Positioning | Absolute Positioning | |
|---|---|---|
| Software/service | RTKLib | CSRS-PPP |
| GNSS | GPS + GLONASS + Galileo | GPS + GLONASS |
| Satellite orbits and clocks | MGEX Final (COM) | MGEX Final (COM) |
| Technique | double-differencing | PPP |
| Frequencies | L1 + L2/L5 | Ionosphere-free from L1 + L2 |
| Measurement frequency | 1 Hz | 1 Hz |
| Elevation mask | 10° | 7.5° |
| Satellite PCO/PCV | igs14.atx | igs14.atx |
| Antenna PCO/PCV | none | none |
| Troposphere delay | Saastamoinen | estimated |
| Ambiguities | fixed | float |
| Session Length | Reference Station: KALI | Reference Station: WIEL | ||||
|---|---|---|---|---|---|---|
| min | max | Average | min | max | Average | |
| 15 min | 43.3 | 97.9 | 78.2 | 0.0 | 94.1 | 41.3 |
| 30 min | 61.2 | 95.3 | 79.5 | 10.5 | 85.3 | 53.0 |
| 1 h | 71.5 | 88.8 | 79.5 | 35.4 | 86.7 | 55.6 |
| 2.5 h | 78.4 | 81.2 | 79.8 | 46.2 | 68.2 | 57.2 |
| 5 h | 79.9 | 79.9 | 79.9 | 58.0 | 58.0 | 58.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wielgocka, N.; Hadas, T.; Kaczmarek, A.; Marut, G. Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying. Sensors 2021, 21, 1956. https://doi.org/10.3390/s21061956
Wielgocka N, Hadas T, Kaczmarek A, Marut G. Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying. Sensors. 2021; 21(6):1956. https://doi.org/10.3390/s21061956
Chicago/Turabian StyleWielgocka, Natalia, Tomasz Hadas, Adrian Kaczmarek, and Grzegorz Marut. 2021. "Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying" Sensors 21, no. 6: 1956. https://doi.org/10.3390/s21061956
APA StyleWielgocka, N., Hadas, T., Kaczmarek, A., & Marut, G. (2021). Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying. Sensors, 21(6), 1956. https://doi.org/10.3390/s21061956








