1. Introduction
With increasing spectral demands, the use of millimeter-wave (mm-wave) frequencies is envisaged in the near future [
1]. The potential of several mm-wave bands has been investigated for mobile or vehicular applications [
2,
3], with the 28 GHz band becoming a part of the 5G New Radio (NR) standard, while the 60 GHz band is promising in terms of its unlicensed access to spectra [
4]. The mm-wave bands beyond 52 GHz are currently under investigation for use in 5G NR Release 17 [
5]. Due to the excellent resolution they offer, mm-waves have also shown their potential for precise localization [
6]. In contrast to the currently most-used microwave frequencies, usually in the sub-6 GHz band, mm-waves offer channel bandwidths in the range of hundreds of MHz. In total, more than 11 GHz of bandwidth is available in mm-waves if both the licensed as well as the unlicensed parts of the spectrum are included.
The Orthogonal Frequency Division Multiplex (OFDM) is currently the most widespread technique applied in wideband wireless communication standards including LTE, 5G or WiFi local area networks, while for point-to-point links, the single-carrier M-ary Quadrature Amplitude Modulation (MQAM) is often used. In the last few years, several waveforms with reduced out-of-band emissions have been designed as complements or envisaged successors of OFDM, such as the Filter Bank Multi Carrier (FBMC) [
7], the Generalized Frequency Division Multiplexing (GFDM) [
8,
9] or the Filtered OFDM (F-OFDM) [
10].
Important research activities dealing with the effects of radio frequency (RF) front-end impairments [
11] on various communication waveforms have been carried out recently. The outcomes of theoretical analyses, together with impairment compensation techniques, have been thoroughly experimentally verified at microwave frequencies [
12,
13,
14]. Although some early-bird mm-wave setups have already been used for experiments with multicarrier signals [
15] and some completely new software defined radios for mm-waves have been built [
16], there are still many works [
17] dealing with advanced multicarrier waveforms and RF front-end compensation by computer simulations only, often due to the lack of affordable instrumentation for mm-waves.
One of the most severe RF front-end impairments is power amplifier (PA) nonlinearity [
18]. This results not only in out-of-band radiation that is actually less problematic in the mm-waves due to the spatial separation of the links, but also in in-band signal distortion that needs to be compensated. Such in-band distortion manifests in the increased spreading of constellation points, which can be quantified by the Error Vector Magnitude (EVM) metric [
19]. A perfect way of compensating for PA nonlinearity is to use the digital predistortion (DPD) method for linearization [
20,
21]. In order to track the changes of the component parameters and their dependency on the center frequency, output power or working temperature, DPD needs to be implemented in an adaptive manner, imposing the requirements on the additional circuitry (an observation receiver is necessary) and signal processing.
Despite the continuing research into advanced front-end architectures [
22], a direct conversion (homodyne) concept is still very attractive due to its reduced cost and easy on-chip integration without bulky external filters. On the other hand, the direct conversion architecture [
23] suffers from the modulator/demodulator phase and gain imbalances. The spectral images arising due to these impairments result in a significant reduction of the achievable rate, as has been shown in [
24] and as we further developed experimentally for the case of the 60 GHz transceiver [
25].
Another important RF front-end impairment is phase noise, especially for commercial RF transceiver designs with a low-cost variable frequency synthesis and wide signal bandwidth. In contrast to the gain and phase mismatch or PA nonlinearity [
26], receiver performance degradation due to phase noise can be eliminated only by careful design; this is especially true for high-quality frequency synthesis [
27]. To a certain extent, the effect of phase noise can be reduced by increasing the symbol time; e.g., by using an increased number of subcarriers in the OFDM system [
28]. Otherwise, only a constant phase rotation due to phase noise can be reduced, but not the random time fluctuation of the received symbols.
Note that the influence of the above-mentioned transceiver imperfections is further accentuated in the wideband channels of the mm-wave systems. To date, for wider bandwidths, analog predistortion has usually been employed [
29]. A smart combination of analog tunable delay lines has also been recently used for the compensation of 60 GHz beamformers, as presented in [
30]. In recent years, increased attention has been paid to the application of digital predistorters [
31], including for wideband signals. That makes DPD attractive for mm-wave engineers. The state-of-the-art experimental research is mainly based on expensive universal measurement devices such as high-speed arbitrary waveform generators (AWG) and real-time spectrum analyzers or fast oscilloscopes [
32,
33,
34]. A multi-Gb/s general-purpose AWG and oscilloscope have also been used in a recent demonstration of DPD in the 28 GHz band [
35]. The use of such general-purpose equipment significantly increases the costs of the overall system and prohibits the wider deployment of predistortion in commercial mm-wave applications. Alternatively, some works have evaluated the performance of DPD using simulations or models scaled to lower frequency bands [
36]. Some of the existing test-beds, such as our time-domain channel sounder [
37], are able to process the wide bandwidths of several GHz, but without the capability of transmitting I/Q data, whereas other mm-wave setups allow for arbitrary I/Q data transmission, but with the bandwidths limited far below 100 MHz [
15].
In this paper, we present our wideband (up to 900 MHz bandwidth without predistortion) experimental 60 GHz transmitter test-bed with an observation receiver (denoted below simply as the receiver), which was developed not using expensive laboratory instruments [
32,
33,
34,
35] but with affordable development kits and discrete components selected to target low-phase noise and sampling clock jitter. The described test-bed is fully MATLAB-controlled and, in contrast to similar recent setups, it contains digital compensation for the RF front-end including amplitude and phase mismatch and power amplifier linearization using digital predistortion. Thus, as summarized in
Table 1, the presented test-bed achieves a much higher transmission power, with a bandwidth and linearity performance comparable to or exceeding the state-of-the art works in [
38] or [
16]. In addition to our recently published conference contribution [
39] or our recent paper showing early predistortion results [
40], this manuscript presents a much more detailed description of the hardware as well as the compensation algorithms and also provides in-depth results of the digital predistortion application for three examples of typical communication waveforms—MQAM, OFDM and FBMC—and two cases of power amplifiers.
2. Hardware of the Test-Bed
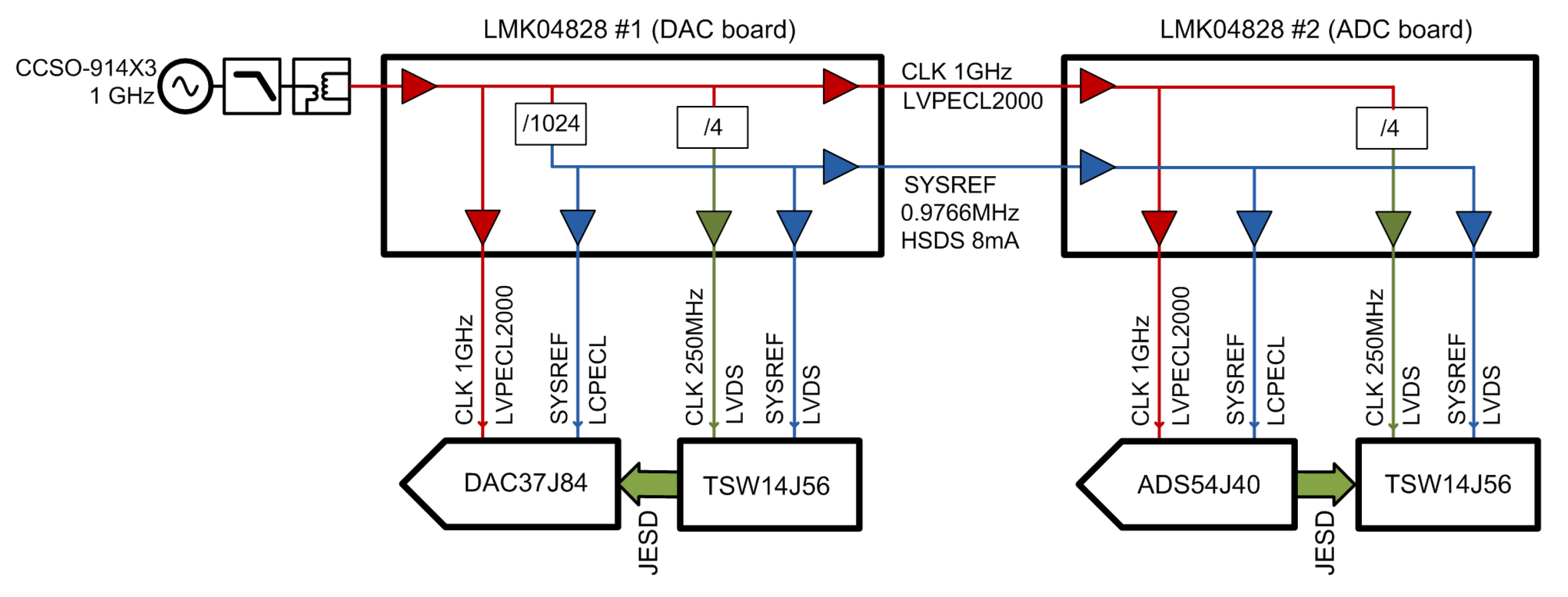
A block diagram and a photo of our digitally compensated test-bed for the 60 GHz band are shown in
Figure 1 and
Figure 2, respectively. As an evolution of our previous narrowband setup [
41], the setup is also based on the Infineon BGT60 evaluation board [
42]. In contrast to the CompuGen/CompuScope cards with maximal sampling frequencies of 300/400 MHz which we used in the previous setup, the described test-bed is based on the development kits of commercially available Analog-to-Digital (A/D) and Digital-to-Analog (D/A) converters from Texas Instruments accompanied with FPGA data acquisition cards. We developed application interface libraries for MATLAB to fully control BGT60 and data converter parameters from a host PC. The baseband data processing (signal generation, demodulation) and control of the test-bed thus proceeds completely through the MATLAB environment. Each of the crucial parts of the test-bed is described in the following sections.
The whole test-bed uses DC-coupled fully differential signaling, as it offers many benefits over a single-ended design; namely, ground returns and noisy grounds are less of an issue. Moreover, DC offset compensation is sufficiently stable for a standard range of lab temperatures and does not require re-calibration before each measurement. Due to mechanical reasons (the waveguide system at RF ports), baseband units with A/D and D/A converters are connected to the RF front-end (BGT60) via the baseband cables. Despite the unstable contact resistance being sensitive to movements of the cable connections, the lack of available differential 100 cables with connectors led us to use standard Serial ATA (SATA) cables for this application.
2.1. RF Section
The whole RF section (depicted in violet on the block diagram in
Figure 1) was built from standard WR-15 waveguide components. Waveguides were preferred over coaxial cables due to their better phase stability. To allow for the estimation of RF impairments, an observation receiver is necessary. For this reason, part of the signal from the transmitter (TX) output is coupled back to the BGT60 receiver (RX) port by a directional coupler. The directional coupler had to be designed and manufactured in-house due to the BGT60’s non standard TX/RX port spacing of 0.96 inches. Its design was described in detail in our previous work [
43]. The BGT60 output signal is also monitored with the Rohde and Schwarz spectrum analyzer FSUP equipped with an FS-Z75 harmonic mixer.
The experiments with digital predistortion were carried out on two power amplifiers—an internal power amplifier integrated within the Infineon BGT60 transceiver module and an external QuinStar power amplifier QPW QPW-50662330. More details about the power amplifiers can be found in
Section 4.1, together with digital linearization performance results. Note that the attenuators are used at the input/output of PA and at the input of the observation receiver to adjust the power levels.
2.2. BGT60 Transceiver
The BGT60 chip [
42] is a V-band direct conversion transceiver with more than 1 GHz bandwidth, manufactured by Infineon in SiGe technology. It features a fully differential design, an integrated Voltage Controlled Oscillator (VCO) with a prescaler-divider and a 12 dBm (1 dB compression) integrated PA. The BGT60 can be operated in full-duplex mode, but only on the same RF frequency (sharing the integrated VCO). This perfectly suits the intended application, where the receiver serves as the observation path to estimate transmitter impairments. The VCO supports an RF frequency range of 57–64 GHz, controlled by the analog tuning voltage. The Phase Locked Loop (PLL) is external to the transceiver chip, and the one populated on the BGT60 evaluation board is based on the ADF4158 circuit. A 40 MHz PLL reference clock is taken from an on-board Temperature Compensated Crystal Oscillator (TCXO) and is thus non-coherent to the rest of the system. The frequency of the Phase Frequency Detector (PFD) is 20 MHz, and a loop filter is designed for a 2.5 mA current. The baseband ports of TX have 100
input impedance; however, the RX baseband ports need to be loaded with 400
impedance, which complicated the process of matching to standard 100
filters and cables.
In the framework of our cooperation with the Institute of Telecommunications, TU Wien, Austria, we measured the phase noise performance of the BGT60 transmitter using a Rohde & Schwarz signal and spectrum analyzer FSW with a phase noise measurement option. The measured results are shown in
Table 2, together with the values specified by the BGT60 datasheet. The data are in good agreement.
2.3. Analog to Digital and Digital to Analog Converters
To profit from BGT60’s baseband bandwidth of approximately 1 GHz, we chose a sampling rate of 1 Gsps (complex baseband) for both the D/A converter (DAC) and A/D converter (ADC). We selected the ADS54J40 (dual channel, 14 bit resolution, maximal sampling rate of 1.0 Gsps) and the DAC37J84 (quad channel, 16 bit resolution, maximal sampling rate of 1.6 Gsps) as the ADC and DAC, respectively.
To facilitate implementation, we used the evaluation modules from Texas Instruments for both the ADS54J40 and DAC37J84 converters with some necessary changes. The default analog physical interface of these boards—the passive baluns and SMA connectors—were removed from the modules, and custom analog interface boards were designed to provide differential connections to the DAC and ADC. The custom analog interface boards have physical dimensions enabling them to fit over the analog area of the original D/A and A/D converter boards. In the case of the DAC, this custom analog interface board also contains the TX baseband circuitry described in
Section 2.4, while the ADC only serves to connect ADC inputs to a SATA cable and the RX baseband circuitry is joined to the BGT60 module, as shown in
Figure 2.
In the digital domain, each DAC and ADC module is connected to an Altera Arria V FPGA-based TSW14J56 pattern generator/data capture card from Texas Instruments, populated with DDR3 SDRAM memory. For a 16 bit sample width, the capacity of 32 Gb of SDRAM allows us to store up to 2 Giga-samples for both transmitted and received signals. The pattern generator cards are connected to the host PC via a USB 3.0 interface.
2.4. Baseband Signal Circuity
The signal at the outputs of the D/A converters is passed through an in-house made board with a pair of reconstruction filters, amplifiers and noise-limiting filters. This interface board is physically located at the DAC printed circuit board (PCB) and connected to the BGT60 evaluation board with a SATA cable. The reconstruction filter is a fifth-order passive elliptic filter. The DAC is loaded with a load impedance = 25 single-ended (50 differential) and matched to the filter’s load = 100 by a resistor divider. The common-mode voltage at the reconstruction filter is 0.60 V. The gain stage follows, based on an LMH5401 circuit, providing a necessary common-mode shift to 1.62 V for BGT60’s TX baseband (BB) ports. This also improves reconstruction filter matching and serves to isolate the filter from the BGT60. The amplifier is configured for a minimum stable gain of 6 dB (including termination loss), as gain boost is not needed in the TX baseband path. The usable bandwidth is well over 4 GHz in this configuration, which is more than sufficient with respect to BGT60 bandwidth. A simple third-order elliptic noise-limiting filter is used after the gain stage to limit wideband noise and to improve the overall lowpass frequency response. The TX baseband path as a whole has a cutoff frequency of approximately 480 MHz (at −6 dB) with about 20 dB gain drop at a Nyquist frequency of 500 MHz.
Conversely, the downconverted baseband signal from the BGT60 receiver is first filtered by a pair of discrete anti aliasing (AA) filters, amplified by a 12 dB gain stage and then passed to the ADC board through a SATA cable connection. The board with these RX baseband components is mounted directly on the BGT60 module to prevent noise pickup in sensitive high-impedance traces. A seventh-order elliptic filter designed for 100 characteristic impedance, with a cutoff frequency of 450 MHz (−6 dB), is used as the AA filter. Besides gain, the ADC driver and the gain stage based on the LMH5401 circuit also provides a common mode shift from 1.38 V to 2.01 V.
In order to match the 400 impedance of the BGT60 RX baseband outputs to the AA filter input impedance, an active matching stage (400 to 100 ) based on the ADA4960 circuit was tested in the initial phase of design. The results were unsatisfactory, with either too high gain with respect to remaining circuitry or problems with stability when the gain was lowered. Therefore, the active matching stage was replaced by a passive resistive impedance matching circuit, compromising the overall baseband RX gain by a value of 6 dB. Although this solution resulted in the inability to fully drive the ADC (−7 dBFS with receiver driven to 1dB compression) and the reduction of the available dynamic range, the receiver chain still provides a 65 dB Spurious Free Dynamic Range (SFDR). Note that the most significant spurious signals are located at ±250 MHz, as the actual sampling frequency of the ADS54J40 interleaving (4 × 250 Msps) A/D converters. A further significant contribution to spurious emissions comes from a JESD interface reference clock to FPGA (250 MHz).
2.5. Sampling Clock
High-speed acquisition systems come with strict requirements regarding the jitter of the sampling clock source [
44]. It is desirable to have significantly lower sampling clock jitter than aperture jitter of the ADC to avoid the available Signal-to-Noise Ratio (SNR) of the ADC being degraded. A standard solution for generating sampling clocks in the 1–3 GHz range is to use PLL and a Voltage Controlled Temperature Compensated Crystal Oscillator (VCTCXO) in the typical range of 100 MHz as a reference. This was also the default solution for the used ADC and DAC evaluation boards, with a 122.88 MHz reference oscillator and LMK04828 chip as a PLL/clock distributor. A broad range of output frequencies can be generated by two internal VCOs (2 or 3 GHz core) and appropriate dividers.
If variable clock frequency is not needed, lower jitter can be achieved using a dedicated oscillator at a fixed frequency. We adopted this solution, which also avoids the use of PLLs in the clock system, in our test-bed. The LMK04828 then serves as a clock distributor only.
A clock tree block diagram of the test-bed is shown in
Figure 3. The sampling clock source is the ultra-low-phase-noise SAW (Surface Acoustic Wave) oscillator Crystek CCSO-914X3 (1 GHz) with a sinusoidal output. The clock signal is filtered by a simple low-pass filter to suppress higher harmonics (there are no subharmonics). A balun is used to create a differential clock routed to the DAC board. After this point, all clocks down the clock tree are differential. The secondary clocks (a 250 MHz FPGA interface clock and f/1024 periodic SYSREF) are derived from this 1 GHz clock source in the
clock distributor LMK04828#1 located on the DAC evaluation board. Through unused clock outputs on the DAC board, the main clock and SYSREF are forwarded to the
clock distributor LMK04828#2 present on the ADC board. Note that several distinct digital voltage standards are used to meet the different common-mode voltage requirements of the individual circuits. The clock to data converters are DC coupled and use LVPECL and LCPECL, while clocks for the FPGA boards use LVDS.
The phase noise and the RMS jitter of the sampling clock for the standard PLL-based and selected fixed frequency solutions with SAW oscillators are summarized in
Table 3. According to our simulations, the achievable RMS jitter of the manufacturer’s default solution with PLL would approximately be 86 fs. In bypass mode (with PLL disabled), the additive RMS jitter of each clock distributor was estimated to be about 16 fs at 1 GHz, resulting in approximately 26 fs RMS jitter at the ADC; i.e., after the second clock distributor. As the ADS54J40 has a typical internal aperture jitter of 120 fs RMS, the SNR and SFDR performance is mainly affected by the used A/D converters.
3. Digital Compensation of RF Impairments
Prior to digital predistortion, there were several transceiver impairments that needed to be compensated or at least taken into account, as listed below.
Phase noise of local oscillators;
Sampling clock jitter;
Carrier frequency offset between TX and RX;
Sampling frequency offset between TX and RX;
DC offset at TX and RX;
Gain and phase imbalance of TX and RX quadrature modulators dependent on frequency.
Phase noise and sampling clock jitter cannot be substantially compensated by any digital methods, except for the compensation of a constant rotation caused by phase noise [
28], resulting in only marginal performance improvement. It is only possible to limit their effect by careful design. That was the reason why we used an ultra-low-phase-noise SAW oscillator at a fixed frequency as a clock source as described in
Section 2.5.
In general-purpose wireless transceivers, the carrier frequency offset and the sampling frequency offset between TX and RX represent serious issues [
27]. In the designed test-bed, the RX part serves as the observation receiver [
45,
46] for DPD adaptation and there is neither carrier nor sampling frequency mismatch as the RF local oscillator and the clock source of A/D and D/A converters are shared for both TX and RX sides. We thus limit our description here mainly to DC offset and gain and phase imbalance compensation.
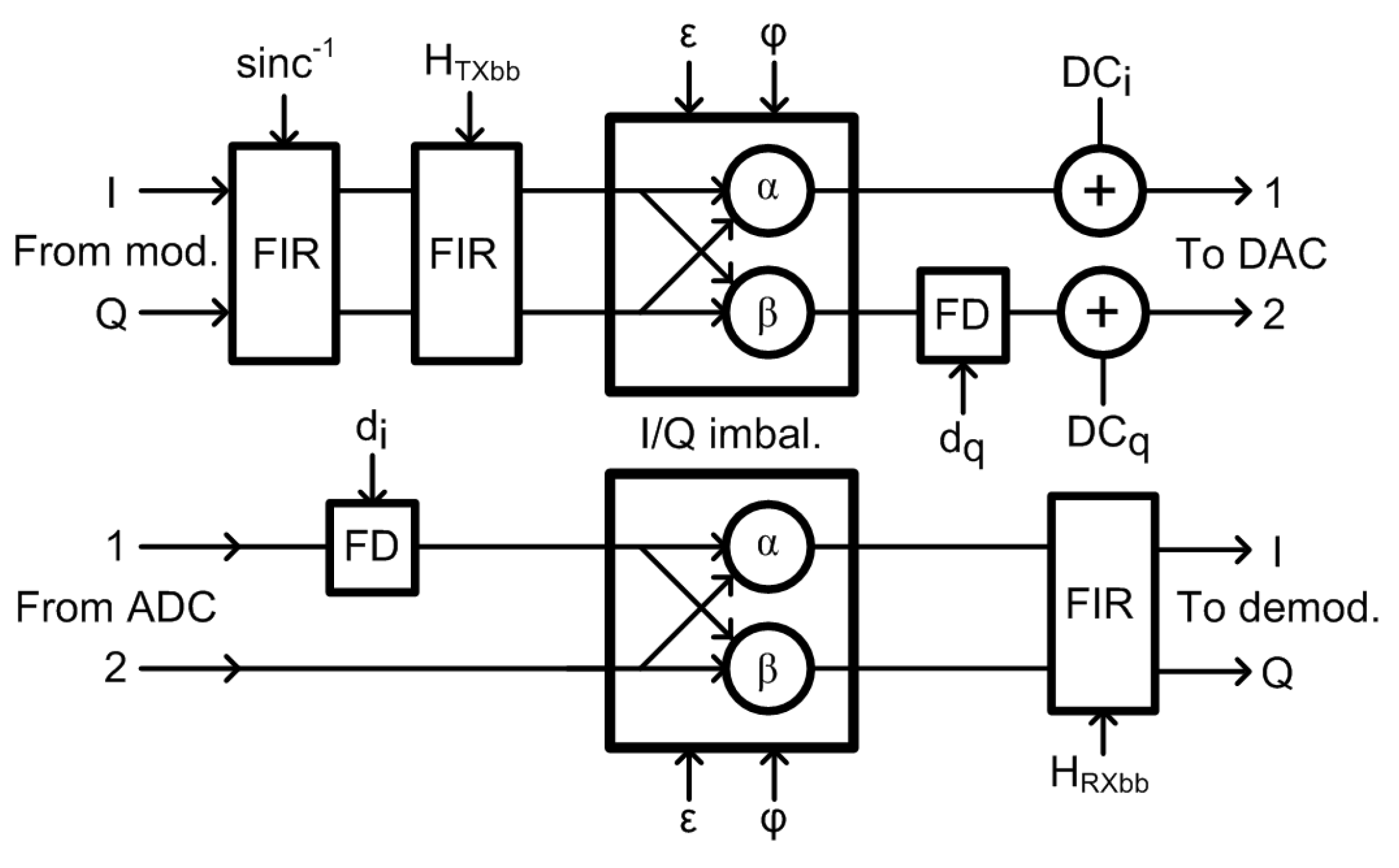
Figure 4 shows the overall schematics of the implemented digital compensations for amplitude and phase mismatches and DC offset, all applied at digital baseband stages of TX and RX.
3.1. Gain and Phase Imbalance Compensation
Besides the compensation of imbalances induced by the quadrature modulators, the roll-off of D/A converters have to be corrected. At the TX stage, this is done by an inverse sinc time domain Finite Impulse Response (FIR) filter through which the baseband samples are passed.
Due to the wide bandwidth of our test-bed, we assumed that the gain and phase mismatch of both transmitter and receiver are frequency-dependent. The effect of this mismatch on the transmitted signal is often expressed in the frequency domain as [
47]
with
where
and
are components of the original, and the I/Q-impaired signal at frequencies
f,
and
correspond to frequency-dependent gain and phase imbalances.
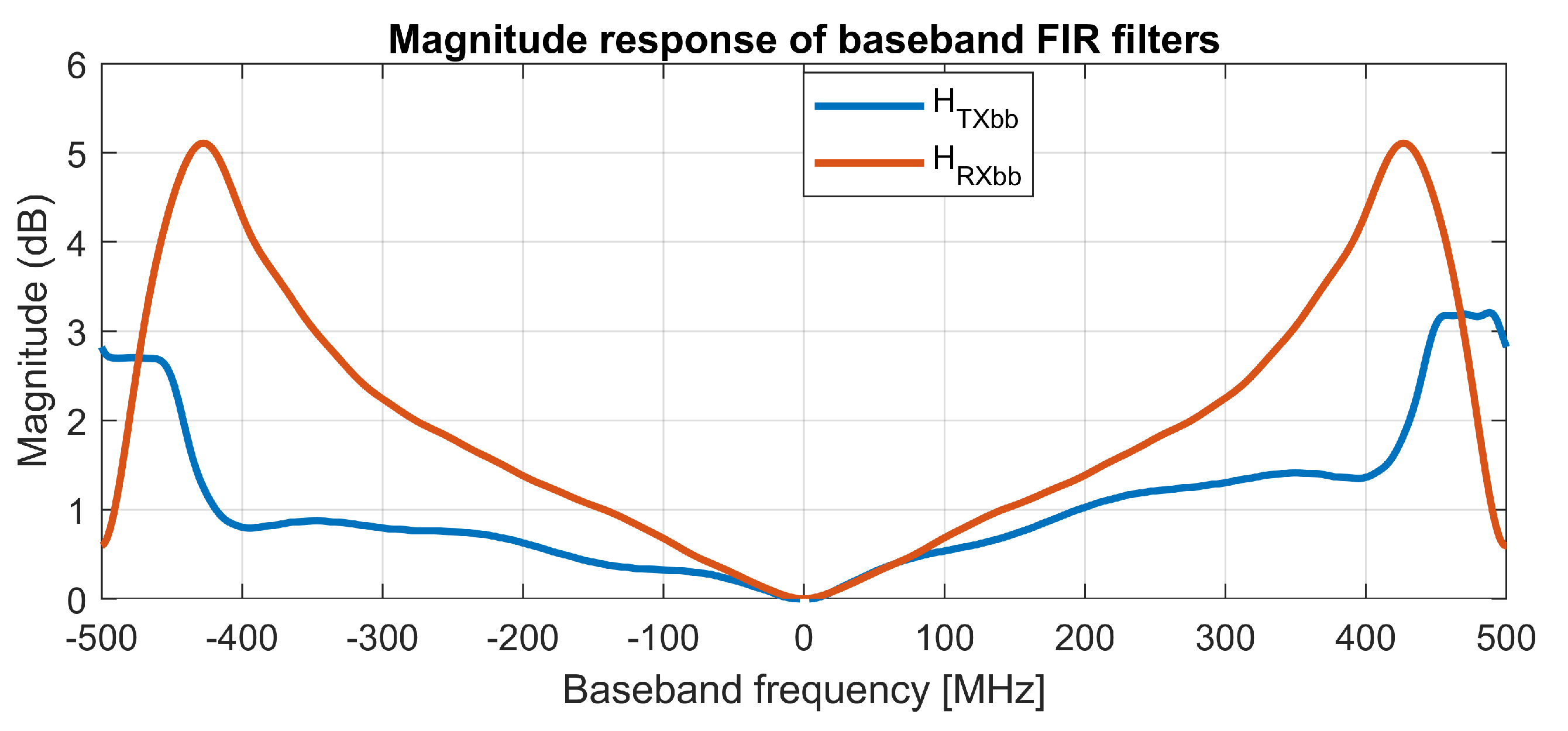
In the described test-bed, the compensation of frequency-dependent gain and phase imbalances is done in three steps. First, the frequency dependent amplitude variations are corrected by an FIR filter
with the complex coefficients allowing for non-symmetrical frequency characteristic, with the measured magnitude response shown in
Figure 5. For the second step, the frequency-independent imbalances of the quadrature I/Q modulator are corrected with the values obtained by the measurements summarized in
Table 4. In the third step, a first-order frequency-dependent phase imbalance is corrected by a fractional delay
introduced into the quadrature path of TX. The fractional delays
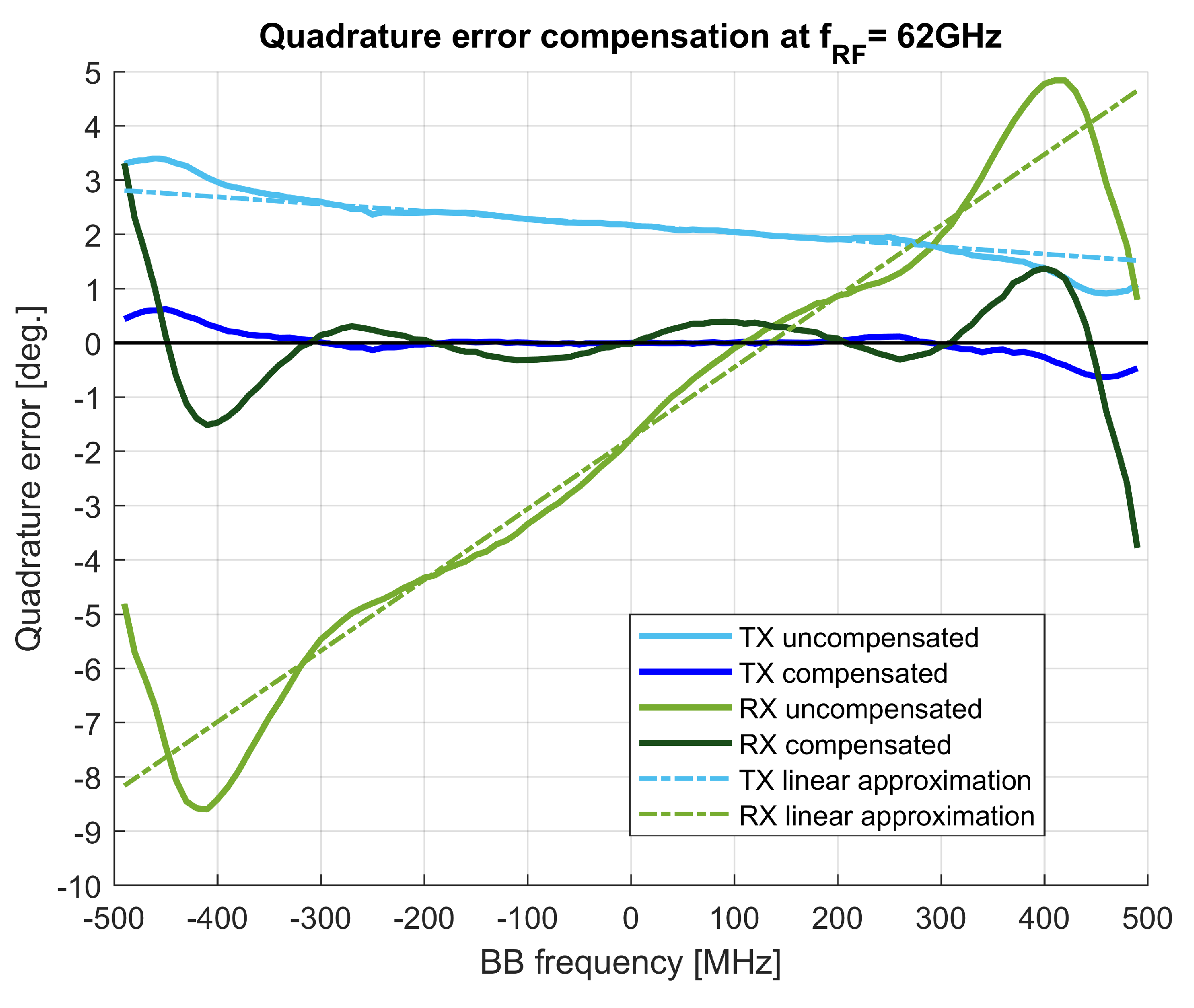
were calculated from slopes of linear approximations of the quadrature error. The measured phase imbalances (sometimes denoted as quadrature errors) before and after compensation are shown in
Figure 6 for both the transmitter and the receiver.
At the receiver side, the compensation of imbalances is equivalent to that of the transmitter, but with an inverted order of operations. A fractional delay is inserted first, and then a frequency-independent I/Q compensation is applied; as a last step, the baseband amplitude response is corrected by an FIR filter with a frequency characteristic of .
To summarize, the employed compensation at the TX side reduced the frequency-dependent phase imbalance from the initial range of (+0.9,+3.4) degrees to approximately (−0.5,+0.5) degrees in the 900 MHz bandwidth. At the RX side, the initial phase imbalance in the range of (−7,+4) degrees was reduced to the range close to (−0.5,+0.5) degrees for a bandwidth of almost 700 MHz.
3.2. DC Offset Correction
The BGT60 transceiver supports internal DC offset settings [
42] for the TX path. However, we found experimentally that setting TX DC compensation outside default (center) values degraded the baseband harmonic distortion characteristics. Therefore, the transmitter DC offset correction is applied to the baseband signal prior to sending the samples to DAC (see
Figure 4), where it is denoted as
.
On the contrary, DC offset at the receiver side is not corrected in the digital domain but is compensated by the current sources at the ADC driver amplifier inputs, meaning that DC offset is not amplified by the ADC drivers with high gain.
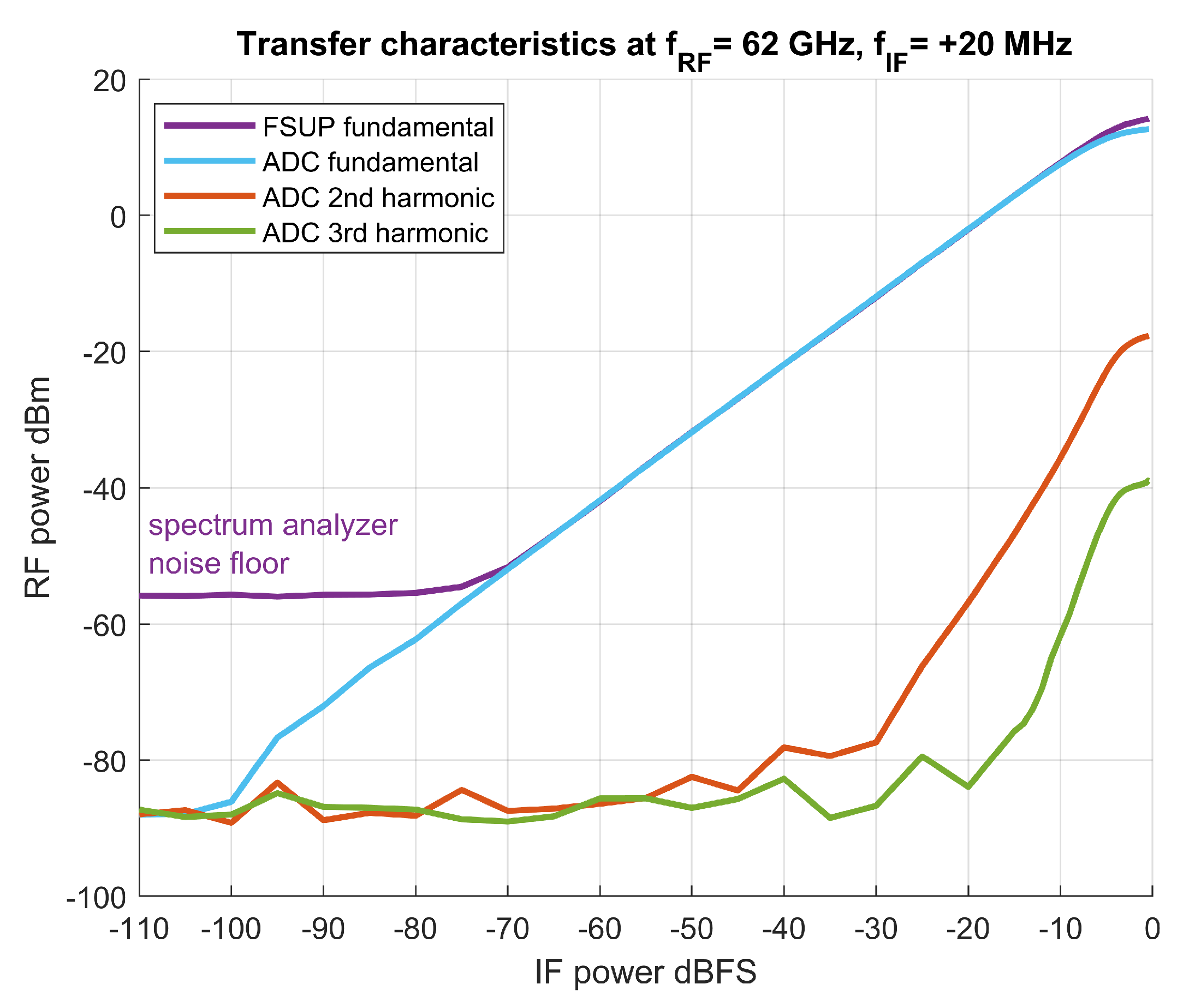
3.3. Overall Transfer Characteristics of the Transmitter-Observation Receiver Chain
An example of the transfer characteristics of the whole transmitter–observation receiver chain at an RF frequency of 62 GHz is shown in
Figure 7. The output power was also measured by an FSUP spectrum analyzer (a violet trace) and the observation receiver path gain was calculated and applied accordingly. At maximum power, the FSUP trace indicates that the transmitter is driven to approximately 2 dB compression. Additionally, ADC power and FSUP power traces are separated, indicating that the receiver is driven to compression (about 1.5 dB below the FSUP trace).