Experimental Comparison of Radon Domain Approaches for Resident Space Object’s Parameter Estimation
Abstract
1. Introduction
- 1.
- SIRTA-CM: The Spectrogram Inverse Radon Transform based Algorithm—Concentration Measure (SIRTA-CM) is the algorithm introduced by the same authors in [27]. This algorithm to estimate the rotation period of the object exploits the IRT of the received signal. In particular, the period is estimated from the IRT displaying the maximum Concentration Measure (CM).
- 2.
- SIRTA-LP: SIRTA-LP is correspondent to SIRTA-CM except for the fact that instead of using the CM to estimate the period from the IRT, it considers the largest peak of the IRT.
- 3.
- AF-CM: Autocorrelation Function—Concentration Measure (AF-CM) relies on two main steps. In the first step the period is estimated by exploiting the autocorrelation function of the signal. However, since the AF-based estimation may suffer from ambiguities due to the level of noise or to the geometry of the object, a refinement step is added. This second step consist in applying the SIRTA-CM methodology on a smaller subset respect to full domain of candidate periods. The subset domain is constructed from the period estimated during the first step by taking values around it and around a number of its multiples.
- 4.
- AF-LP: AF-LP corresponds to AF-CM except for the fact that instead of using the CM to estimate the period from the IRT, it considers the largest peak of the IRT.
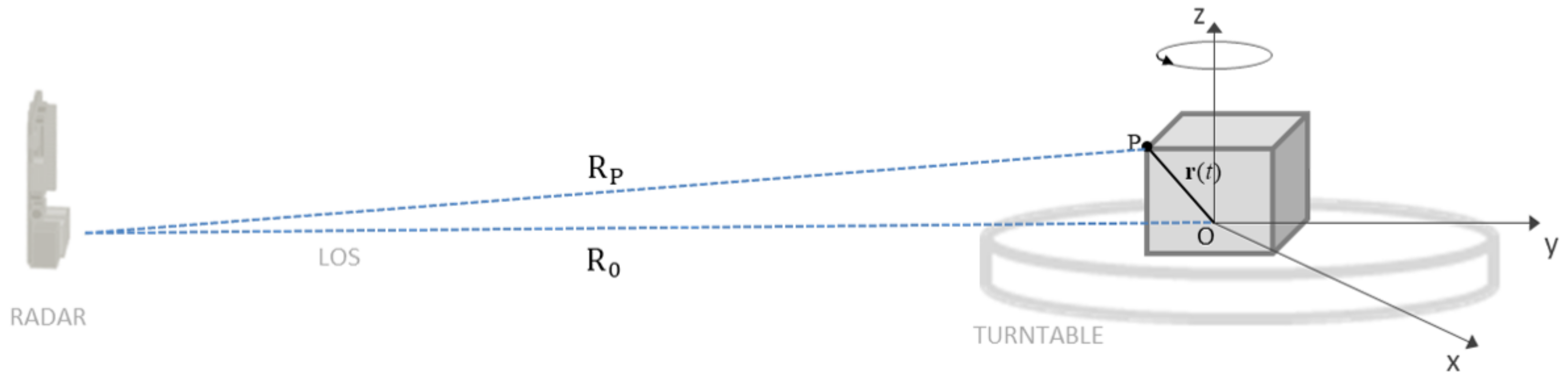
2. Signal Model
3. Periodicity Estimation Methods
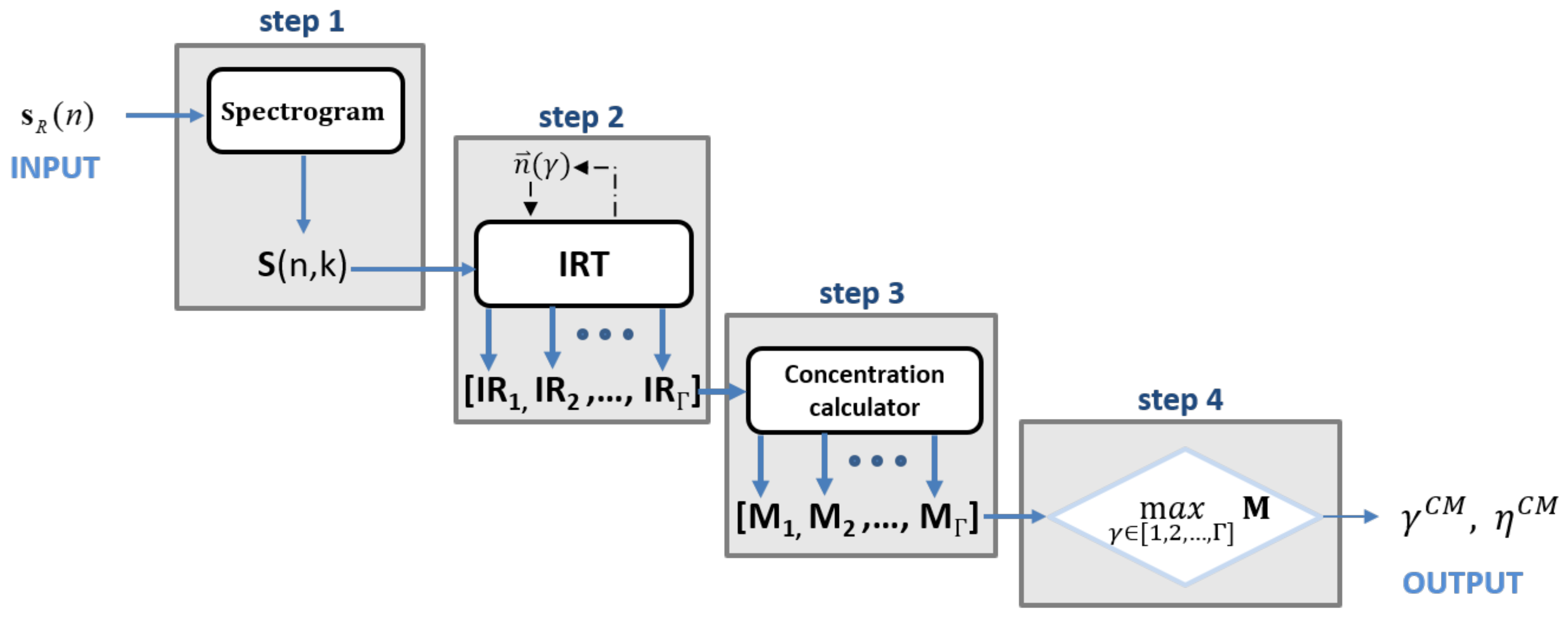
3.1. SIRTA-CM
- step 1: the spectrogram is calculated from the received signal (in the discrete domain).
- step 2: the IRT is calculated for each value contained in the set of candidates values
- step 3: the CM is calculated from (13) by considering each element of the set of values in IR = [].
- step 4: is found by searching for the index corresponding with the maximum value of the CM vector M = [ ].
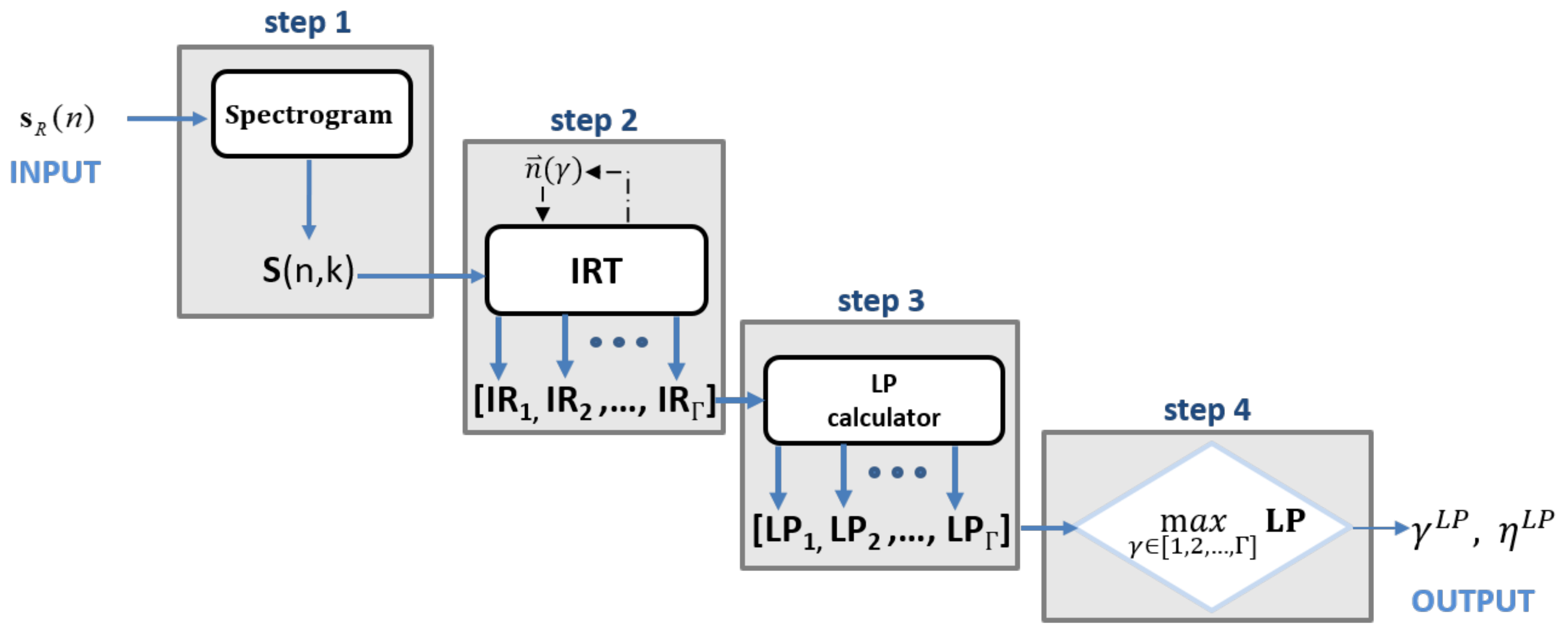
3.2. SIRTA-LP
- step 1: the spectrogram is calculated from the received signal
- step 2: the IRT is calculated for each value contained in the set of candidates values
- step 3: the LP for all the IRT images contained in the set IR = [] is derived and stored in the vector LP = [ ].
- step 4: is found by searching for the index corresponding to the maximum of the vector LP.
3.3. AF-CM
3.4. AF-LP
4. Performance Comparison Analysis
4.1. Simulation Set Up
4.2. Simulation Results
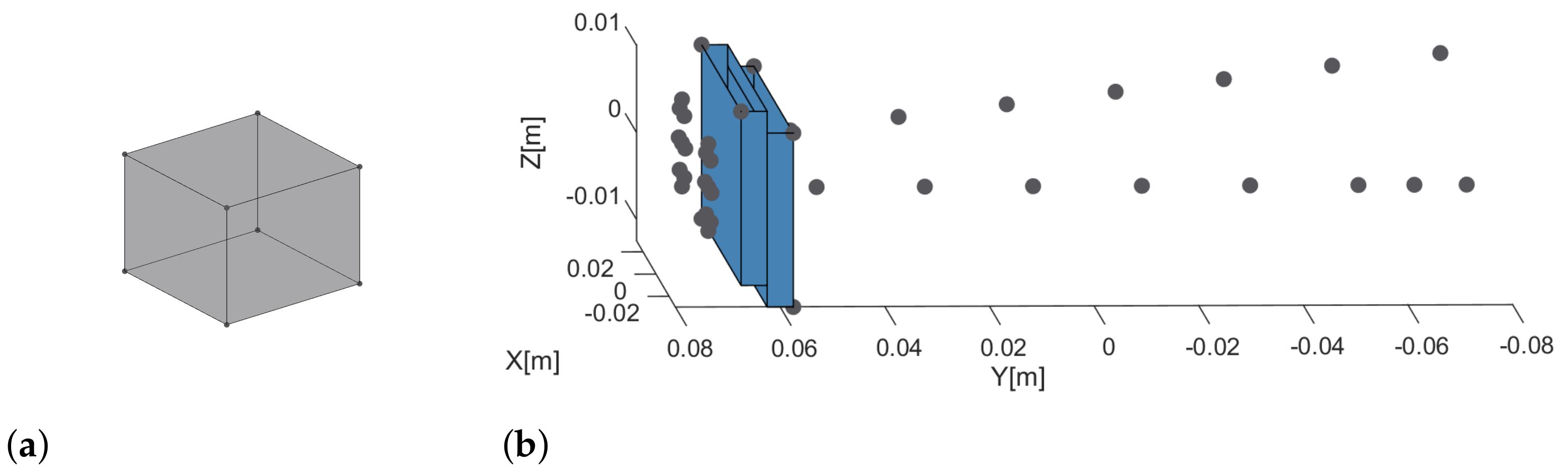
4.3. Experimental Set-Up
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CM | Concentration Measure |
| FMCW | Frequency Modulated Continuous Wave |
| IRT | Inverse Radon Transform |
| ISAR | Inverse Synthetic Aperture Radar |
| LOS | Line Of Sight |
| LP | largest peak |
| NRMSE | Normalized Root Mean Square Error |
| PRI | Pulse Repetition Interval |
| RMSE | Root Mean Square Error |
| SIRTA | Spectrogram - Inverse Radon Transform based Algorithm |
| SSA | Space Situational Awareness |
| STFT | Short Time Fourier Transform |
Appendix A
Appendix Normalized Root Mean Square Error
Appendix B
Appendix Spectrogram Definition
References
- Portree, D.S.; Loftus, J.P., Jr. Orbital Debris: A Chronology; NASA: Washington, DC, USA, 1999. [Google Scholar]
- Johnson, N.L. Orbital Debris: The Growing Threat to Space Operations; NASA: Washington, DC, USA, 2010. [Google Scholar]
- Janson, S. 25 Years of Small Satellites; The Aerospace Corporation: El Segundo, CA, USA, 2011. [Google Scholar]
- Rees, J.M.; King-Hele, D. Table of the artificial earth satellites launched in 1957–1962. Planet. Space Sci. 1963, 11, 1053–1081. [Google Scholar] [CrossRef]
- King-Hele, D.; Quinn, E. Table of the artificial earth satellites launched in 1963. Planet. Space Sci. 1964, 12, 681–701. [Google Scholar] [CrossRef]
- King-Hele, D.; Quinn, E. Table of the artificial earth satellites launched in 1964. Planet. Space Sci. 1965, 13, 707–722. [Google Scholar] [CrossRef]
- King-Hele, D.; Quinn, E. Table of the earth satellites launched in 1965. Planet. Space Sci. 1966, 14, 817–838. [Google Scholar] [CrossRef]
- Quinn, E.; King-Hele, D. Table of the earth satellites launched in 1966. Planet. Space Sci. 1967, 15, 1181–1201. [Google Scholar] [CrossRef]
- Rossi, A. The earth orbiting space debris. Serbian Astron. J. 2005, 170, 1–12. [Google Scholar] [CrossRef]
- Kessler, D.J.; Johnson, N.L.; Liou, J.; Matney, M.; Colorado, B. The Kessler Syndrome: Implications to Future Space Operations. Adv. Astronaut. Sci. 2010, 137, 2010. [Google Scholar]
- Su, S.Y.; Kessler, D. Contribution of explosion and future collision fragments to the orbital debris environment. Adv. Space Res. 1985, 5, 25–34. [Google Scholar] [CrossRef]
- Kessler, D.J.; Cour-Palais, B.G. Collision frequency of artificial satellites: The creation of a debris belt. J. Geophys. Res. Space Phys. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Klinkrad, H. Space Debris: Models and Risk Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Dawson, J.A.; Bankston, C.T. Space debris characterization using thermal imaging systems. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 14–17 September 2010; p. 40. [Google Scholar]
- Kervin, P.W.; Africano, J.L.; Sydney, P.F.; Hall, D. Small satellite characterization technologies applied to orbital debris. Adv. Space Res. 2005, 35, 1214–1225. [Google Scholar] [CrossRef]
- Linares, R.; Crassidis, J.; Jah, M.; Kim, H. Astrometric and photometric data fusion for resident space object orbit, attitude, and shape determination via multiple-model adaptive estimation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 8341. [Google Scholar]
- Lichter, M.D.; Dubowsky, S. State, shape, and parameter estimation of space objects from range images. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA ’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; Volume 3, pp. 2974–2979. [Google Scholar]
- Czerwinski, M.G.; Usoff, J.M. Development of the haystack ultrawideband satellite imaging radar. Linc. Lab. J. 2014, 21, 28–44. [Google Scholar]
- Mehrholz, D.; Leushacke, L.; Flury, W.; Jehn, R.; Klinkrad, H.; Landgraf, M. Detecting, tracking and imaging space debris. ESA Bull. 2002, 109, 128–134. [Google Scholar]
- Chen, V.C.; Li, F.; Ho, S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Dakovic, M.; Stankovic, L. Estimation of sinusoidally modulated signal parameters based on the inverse Radon transform. In Proceedings of the 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA), Trieste, Italy, 4–6 September 2013; pp. 302–307. [Google Scholar] [CrossRef]
- Wang, C.; Fu, X.; Li, T.; Shi, L.; Gao, M. Micro-Doppler feature extraction using single-frequency radar for high-speed targets. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Cilliers, A.; Nel, W.A.J. Helicopter parameter extraction using joint time-frequency and tomographic techniques. In Proceedings of the 2008 International Conference on Radar, Adelaide, Australia, 2–5 September 2008; pp. 598–603. [Google Scholar] [CrossRef]
- He, Z.; Tao, F.; Duan, J.; Luo, J. Research on Radar Micro-Doppler Feature Parameter Estimation of Propeller Aircraft. J. Phys. Conf. Ser. 2018, 960, 012049. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F.; Xing, M.; Bao, Z. High Resolution ISAR Imaging of Targets with Rotating Parts. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2530–2543. [Google Scholar] [CrossRef]
- Ghio, S.; Martorella, M. Estimation of Rotating RSO Parameters using Radar Data and Joint Time-Frequency Transforms. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017. [Google Scholar]
- Ghio, S.; Martorella, M.; Staglianó, D.; Petri, D.; Lischi, S.; Massini, R. Practical implementation of the spectrogram-inverse Radon transform based algorithm for resident space objects parameter estimation. IET Sci. Meas. Technol. 2019, 13, 1254–1259. [Google Scholar] [CrossRef]
- Ghio, S.; Martorella, M. A comparison of Radon domain approaches for resident space object’s parameter estimation. In Proceedings of the 2020 21st International Radar Symposium (IRS), Warsaw, Poland, 4–8 October 2020; pp. 318–322. [Google Scholar] [CrossRef]
- Stankovic, L. Measure of some time-frequency distributions concentration. Signal Process. 2001, 81, 621–631. [Google Scholar] [CrossRef]
- Ghio, S.; Martorella, M. Multi-Bistatic Radar for Resident Space Objects Feature Estimation. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–11. [Google Scholar]


| Symbol | Description | Value |
|---|---|---|
| Carrier frequency | 23.5 GHz | |
| Observation Time | 7.2 s | |
| Sampling frequency | 100 Hz | |
| Pulse Width | 0.125 s | |
| Pulse Repetition Interval | 10 ms |
| SNR [dB] | SIRTA-CM | SIRTA-LP | AF-CM | AF-LP | AF |
|---|---|---|---|---|---|
| −5 | 0.0202 | 0.4051 | 0.0194 | 0.2208 | 2.0116 |
| 0 | 0.0127 | 0.0285 | 0.0139 | 0.0292 | 2.0115 |
| 5 | 0.0053 | 0.0311 | 0.0092 | 0.0304 | 2.0115 |
| 10 | 0 | 0.0352 | 0.0044 | 0.0336 | 2.0115 |
| 15 | 0 | 0.0410 | 0.0037 | 0.0394 | 2.0115 |
| 20 | 0 | 0.0471 | 0.0037 | 0.0449 | 2.0115 |
| SNR [dB] | SIRTA-CM | SIRTA-LP | AF-CM | AF-LP | AF |
|---|---|---|---|---|---|
| −5 | 0.1371 | 0.7943 | 0.8351 | 2.3723 | 1.7843 |
| 0 | 0.0106 | 0.0359 | 0.0117 | 0.6240 | 1.3392 |
| 5 | 0.0026 | 0.0217 | 0.0091 | 0.0195 | 1.3404 |
| 10 | 0 | 0.0245 | 0.0069 | 0.0201 | 1.3408 |
| 15 | 0 | 0.0258 | 0.0063 | 0.0212 | 1.3412 |
| 20 | 0 | 0.0271 | 0.0041 | 0.0254 | 1.3405 |
| Object | SIRTA-CM | SIRTA-LP | AF-CM | AF-LP | AF |
|---|---|---|---|---|---|
| First object | 0 | 0.0620 | 0.0039 | 0.0582 | 1.6102 |
| Second object | 0 | 0 | 0.0548 | 0.0548 | 1.4675 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghio, S.; Martorella, M.; Staglianò, D.; Petri, D.; Lischi, S.; Massini, R. Experimental Comparison of Radon Domain Approaches for Resident Space Object’s Parameter Estimation. Sensors 2021, 21, 1298. https://doi.org/10.3390/s21041298
Ghio S, Martorella M, Staglianò D, Petri D, Lischi S, Massini R. Experimental Comparison of Radon Domain Approaches for Resident Space Object’s Parameter Estimation. Sensors. 2021; 21(4):1298. https://doi.org/10.3390/s21041298
Chicago/Turabian StyleGhio, Selenia, Marco Martorella, Daniele Staglianò, Dario Petri, Stefano Lischi, and Riccardo Massini. 2021. "Experimental Comparison of Radon Domain Approaches for Resident Space Object’s Parameter Estimation" Sensors 21, no. 4: 1298. https://doi.org/10.3390/s21041298
APA StyleGhio, S., Martorella, M., Staglianò, D., Petri, D., Lischi, S., & Massini, R. (2021). Experimental Comparison of Radon Domain Approaches for Resident Space Object’s Parameter Estimation. Sensors, 21(4), 1298. https://doi.org/10.3390/s21041298







