Extracting the Resistive Current Component from a Surge Arrester’s Leakage Current without Voltage Reference
Abstract
1. Introduction
- atmospheric discharges, and
- consequences of switch devices’ manipulations.
2. Physical Background of the Arrester Monitoring Principle
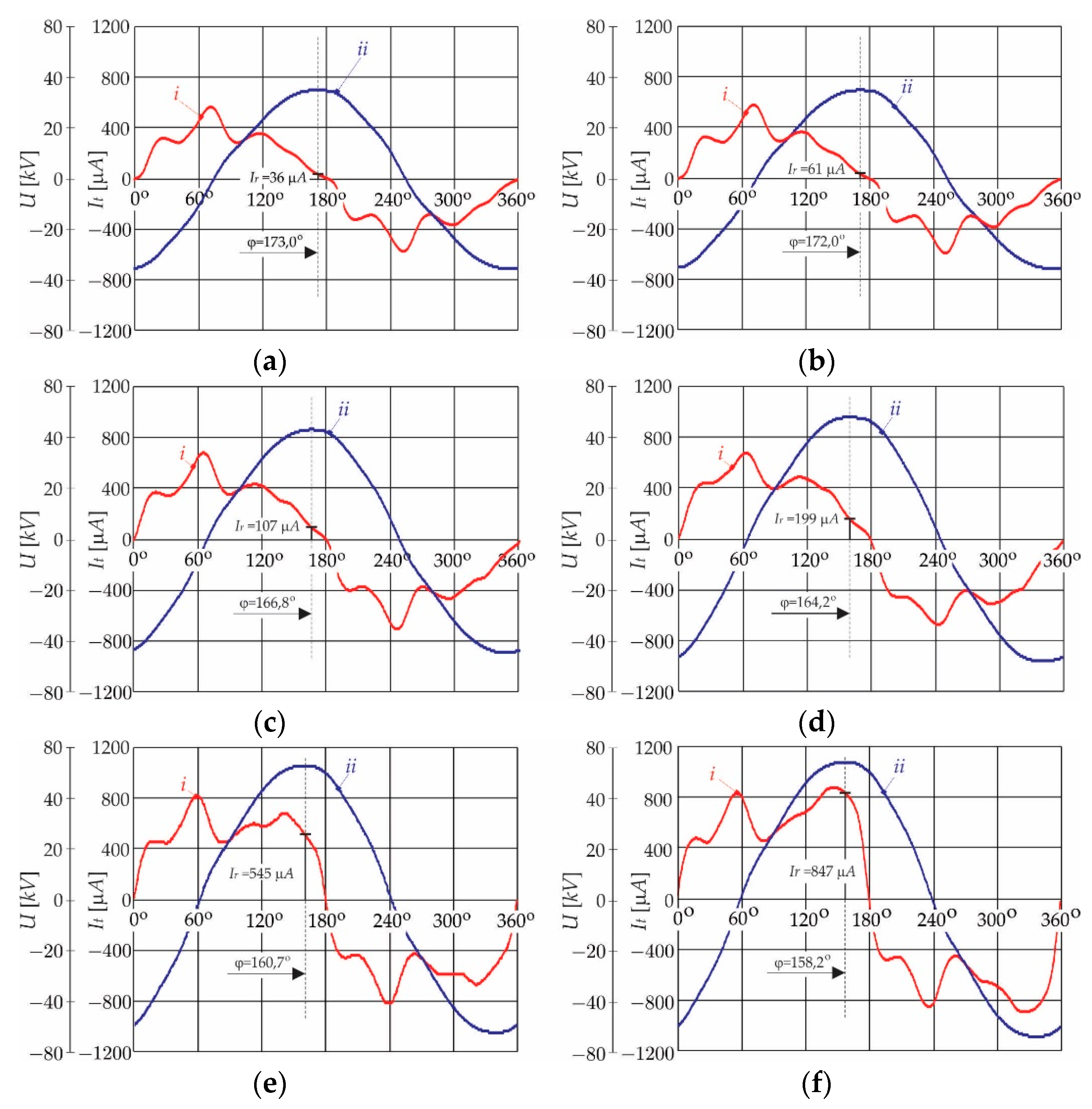
2.1. Extraction of the Resistive Current Magnitudes from the Arrester’s Leakage Current
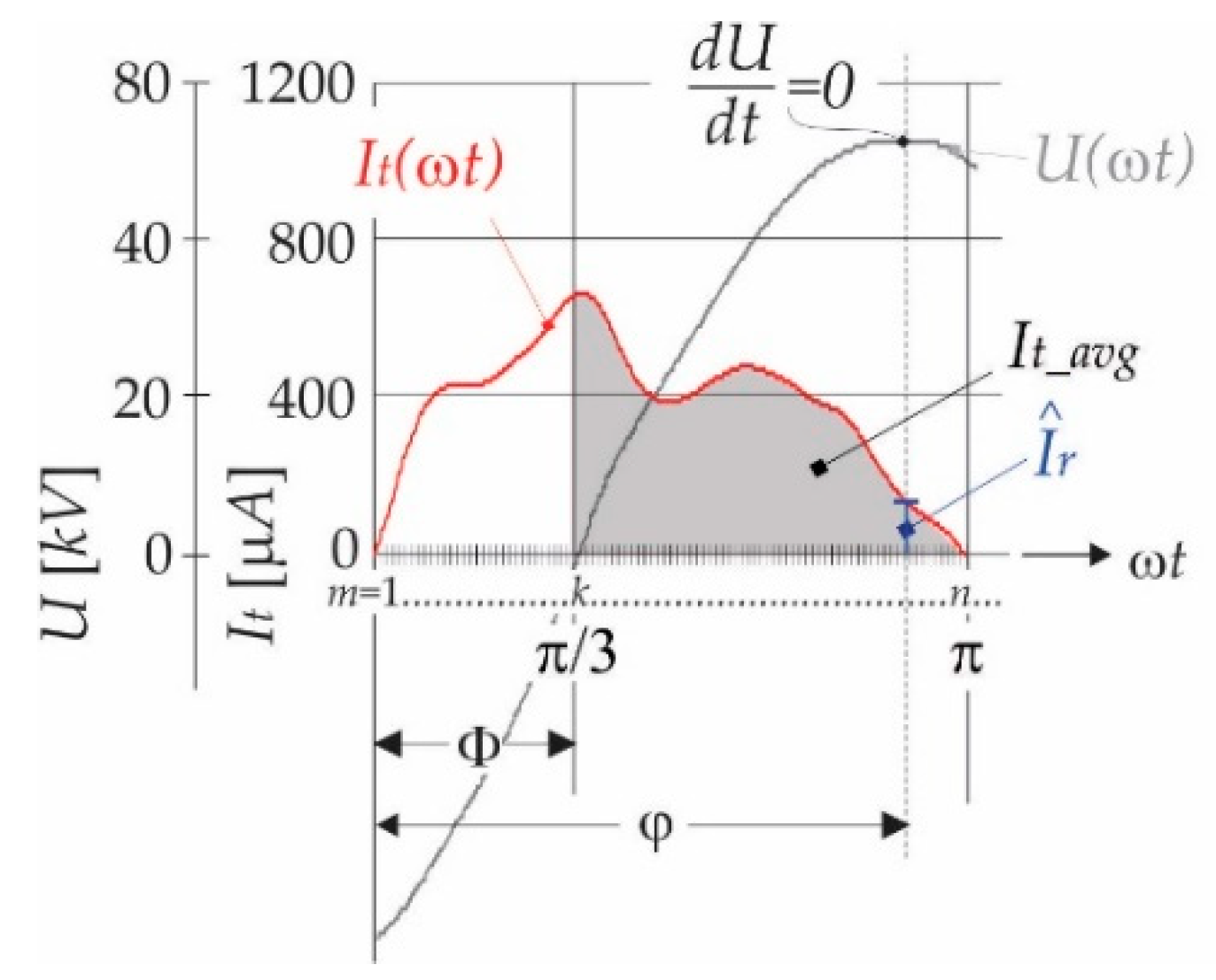
2.2. Description of the Measurement Principle for the Average Value of Leakage Current at Certain Intervals
- when ;
- when ;
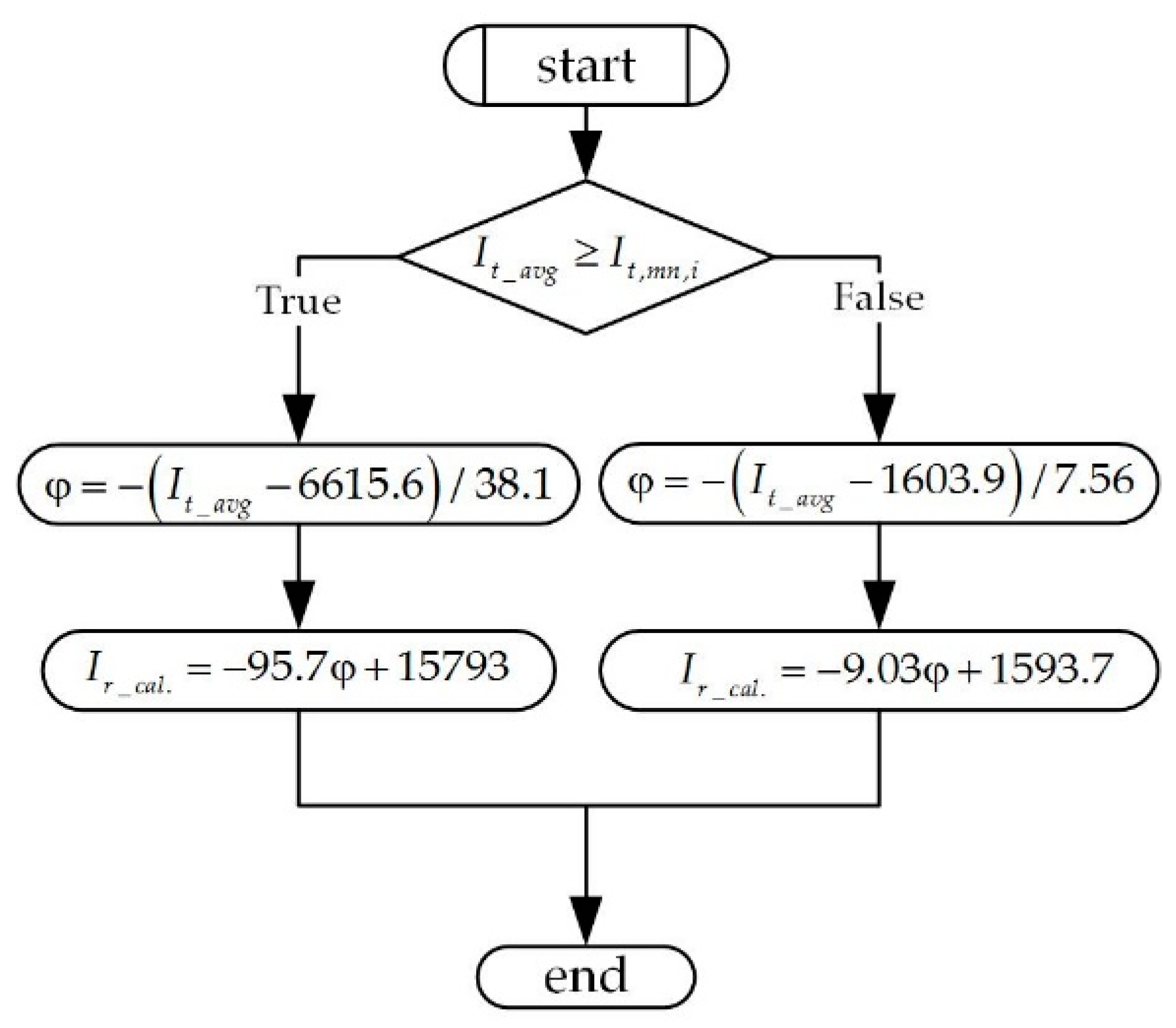
2.3. Verification of the Proposed Algorithm
3. Surge Arrester Monitoring Device (SAMD)
- galvanic isolation of the measured signal (safety reasons);
- acquire and prepare the analogue signal for digital conversion;
- collection of current samples in the range ; and,
- prepare information for wireless transfer to an off-line server.
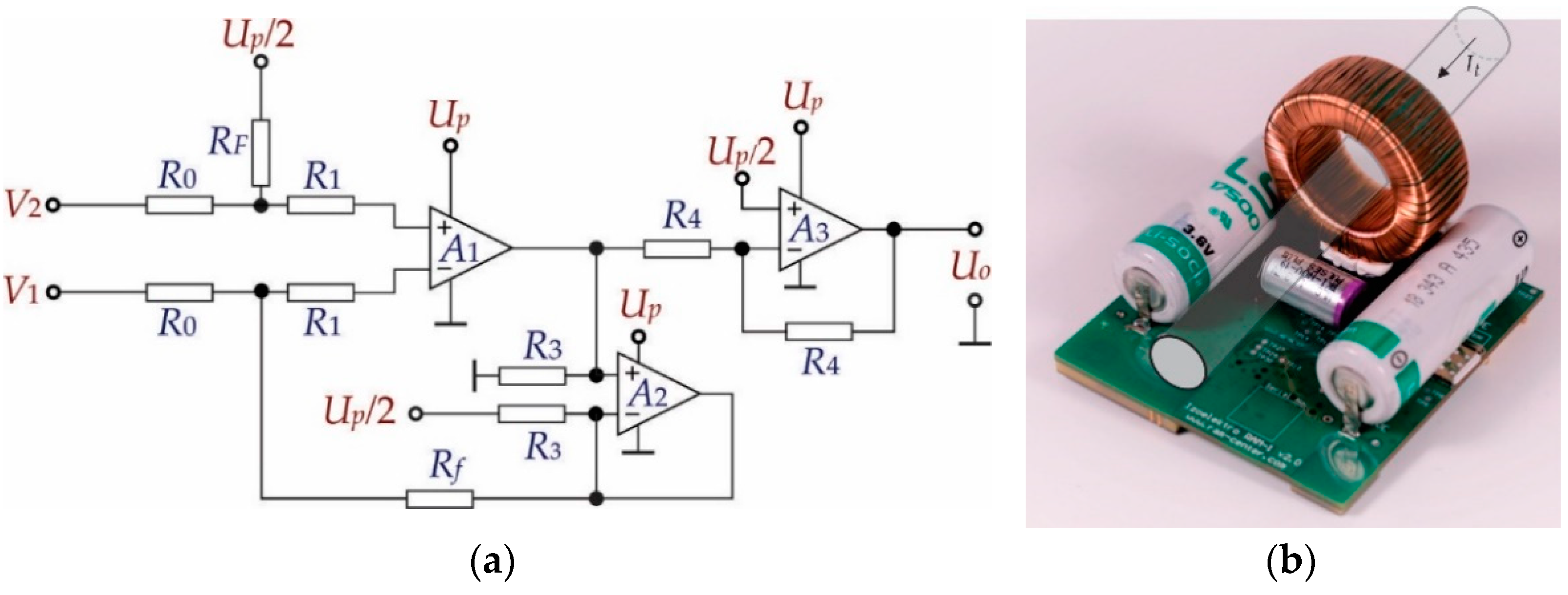
3.1. Electronic Circuits
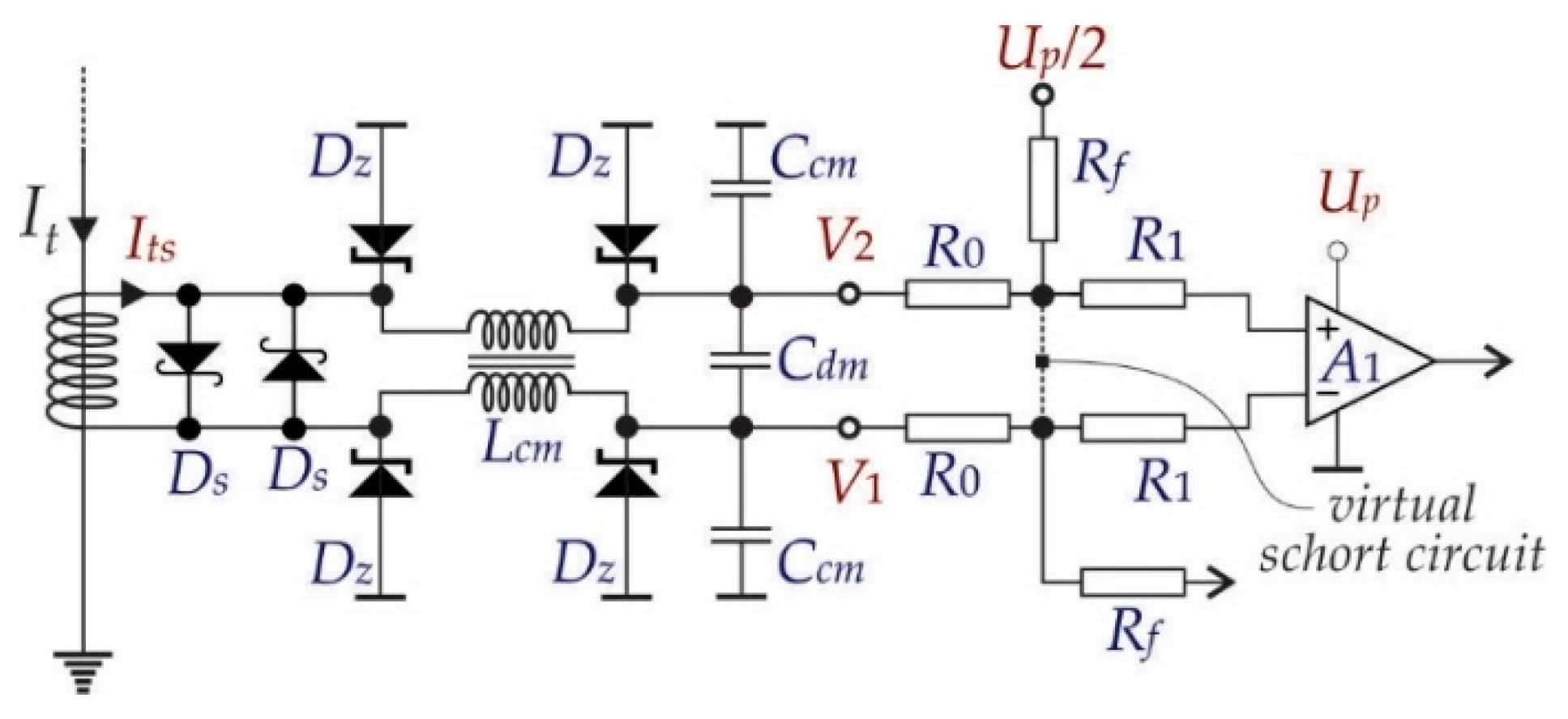
3.1.1. Protection Circuit
3.1.2. Signal Acquisition Circuit
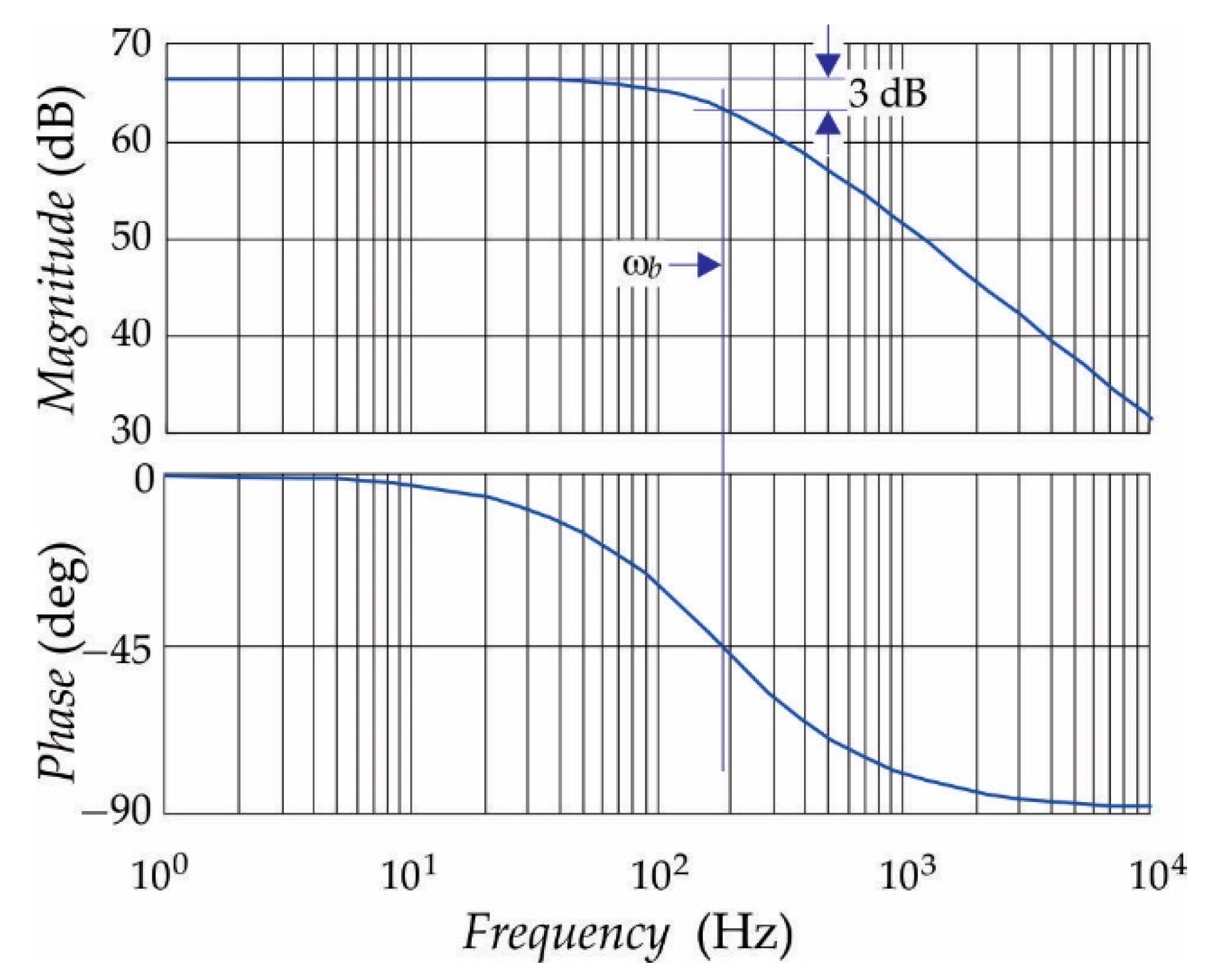
3.1.3. Microcontroller and Communication Unit
- 12-bit analogue-digital converter (ADC),
- operational amplifier,
- two ultra-low-power comparators with reach communication interfaces, and
- development supports, etc.
3.1.4. Battery
4. Experimental Results
4.1. Experimental Test-Bench
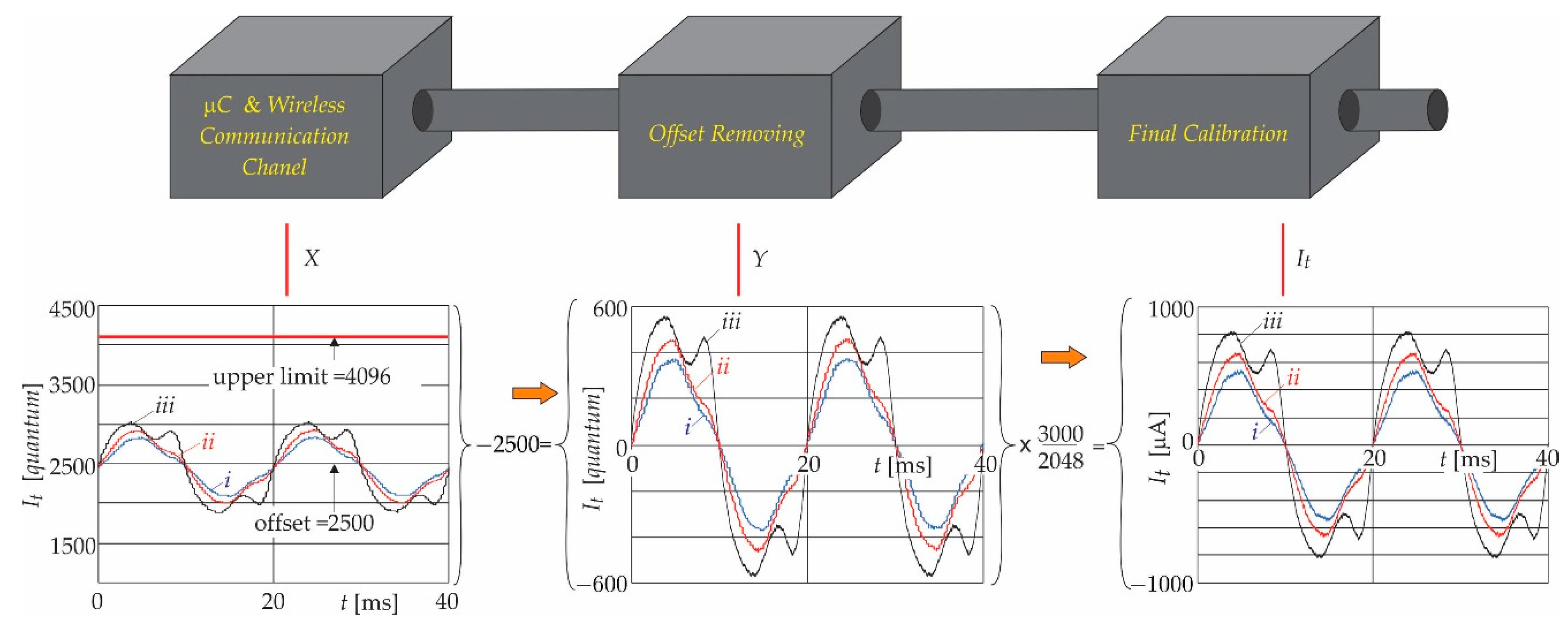
4.2. Calibration of the Measurement Devices
4.2.1. Measurement Constant
4.2.2. Verification of the Calibration Process
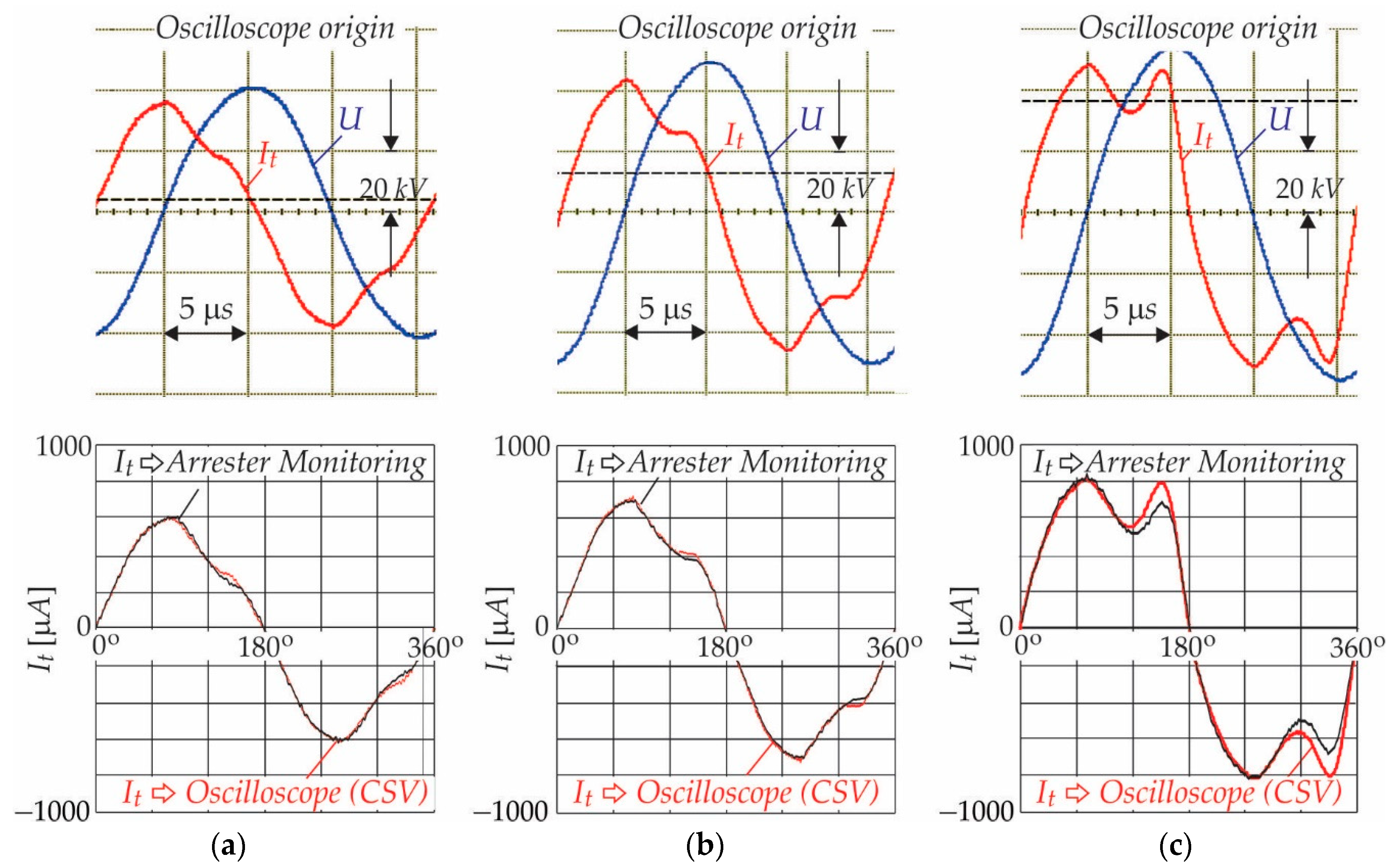
4.3. Measurement Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bokoro, P.; Jandrell, I. Failure Analysis of Metal Oxide Arresters under Harmonic Distortion. SAIEE Afr. Res. J. 2016, 107, 167–176. [Google Scholar] [CrossRef]
- George, R.; Lira, S.; Costa, E.G. MOSA Monitoring Technique Based on Analysis of Total Leakage Current. IEEE Trans. Power Deliv. 2013, 28. [Google Scholar] [CrossRef]
- Metwally, I.A. Performance of Distribution-Class Surge Arresters under Dry and Artificial Pollution Conditions. Electr. Eng. 2010, 93, 55–62. [Google Scholar] [CrossRef]
- Khodsuz, M.; Mirzaie, M.; Seyyedbarzegar, S. Metal Oxide Surge Arrester Condition Monitoring Based on Analysis of Leakage Current Components. Int. J. Electr. Power Energy Syst. 2015, 66, 188–193. [Google Scholar] [CrossRef]
- Lundquist, J.; Stenstrom, L.; Schei, A.; Hansen, B. New Method for Measurement of the Resistive Leakage Currents of Metal-Oxide Surge Arresters in Service. IEEE Trans. Power Deliv. 1990, 5, 1811–1822. [Google Scholar] [CrossRef]
- Metwally, I.A. Measurement and Calculation of Surge-Arrester Residual Voltages. Measurement 2011, 44, 1945–1953. [Google Scholar] [CrossRef]
- Khodsuz, M.; Mirzaie, M. Harmonics Ratios of Resistive Leakage Current as Metal Oxide Surge Arresters’ Diagnostic Tools. Measurement 2015, 70, 148–155. [Google Scholar] [CrossRef]
- Latiff, N.A.A.; Illias, H.A.; Bakar, A.H.A.; Dabbak, S.Z.A. Measurement and Modelling of Leakage Current Behaviour in ZnO Surge Arresters under Various Applied Voltage Amplitudes and Pollution Conditions. Energies 2018, 11, 875. [Google Scholar] [CrossRef]
- Novizon, Y.; Abdul-Malek, Z. Electrical and Temperature Correlation to Monitor Fault Condition of ZnO Surge Arrester. In Proceedings of the 3rd International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Semarang, Indonesia, 18–20 October 2016. [Google Scholar]
- Vita, V.; Christodoulou, C.A. Comparison of ANN and Finite Element Analysis Simulation Software for the Calculation of the Electric Field around Metal Oxide Surge Arresters. Electr. Power Syst. Res. 2016, 133, 87–92. [Google Scholar] [CrossRef]
- Costa, E.G.; Barros, R.M.R.; Alves, H.M.M.; Bastos, M.A. Thermal Behavior Analysis of ZnO Polymeric Surge Arrester Using the Finite Elements Method. In Proceedings of the 2014 ICHVE International Conference on High Voltage Engineering and Application, Poznan, Poland, 8–11 September 2014. [Google Scholar]
- Dlamini, A.; Bokoro, P.; Doorsamy, W. The Effect of Thermal Transient on the Leakage Current of Metal Oxide Arresters. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA, Cape Town, South Africa, 29–31 January 2020. [Google Scholar]
- Xu, J.; Ye, Z.; Luo, L.; Kubis, A.; Zhou, K. Electromagnetic Field and Thermal Distribution Optimization in Shell-Type Traction Transformers. IET Electr. Power Appl. 2013, 7, 627–632. [Google Scholar] [CrossRef]
- Hoang, T.T.; Cho, M.-Y.; Alam, M.N.; Tuan Vu, Q. A Novel Differential Particle Swarm Optimization for Parameter Selection of Support Vector Machines for Monitoring Metal-Oxide Surge Arrester Conditions. Swarm Evol. Comput. 2018, 38, 120–126. [Google Scholar] [CrossRef]
- Dobrić, G.; Stojanović, Z.; Stojković, Z. The Application of Genetic Algorithm in Diagnostics of Metal-Oxide Surge Arrester. Electr. Power Syst. Res. 2015, 119, 76–82. [Google Scholar] [CrossRef]
- Zhu, H.; Raghuveer, M.R. Influence of Representation Model and Voltage Harmonics on Metal Oxide Surge Arrester Diagnostics. IEEE Power Eng. Rev. 2001, 21, 62. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Zheng, H.; Guo, W. Decomposition Method for the Total Leakage Current of MOA Based on Multiple Linear Regression. IEEE Trans. Power Deliv. 2016, 31, 1422–1428. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, J.; Bretas, A.; Ou, Y.; Zhou, G. Measurement Method for Resistive Current Components of Metal Oxide Surge Arrester in Service. IEEE Trans. Power Deliv. 2018, 33, 2246–2253. [Google Scholar] [CrossRef]
- Munir, A.; Abdul-Malek, Z.; Arshad, R.N. Resistive Component Extraction of Leakage Current in Metal Oxide Surge Arrester: A Hybrid Method. Measurement 2020. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Surge Arresters—Part5: Selection and Application Recommendations; IEC 60099-5:2013; International Electrotechnical Commission: Geneva, Switzerland, 2013. [Google Scholar]
- Electric Power Transmission and Distribution Losses (% of Output)—World, European Union, Slovenia. 2003. Available online: https://data.worldbank.org/indicator/EG.ELC.LOSS.ZS?end=2014&locations=1W-EU-SI&most_recent_value_desc=false&start= (accessed on 24 March 2020).
- Phillips, A.J.; Engelbrecht, C.; Lynch, R.C.; Major, J.M. Sensor to Monitor Health of Metal Oxide Arresters. U.S. Patent 10209293, 19 February 2019. [Google Scholar]
- Raschke, P. Monitoring Device for a Surge Arrester and Monitoring System Comprising a Monitoring Device. U.S. Patent 20170108550A1, 20 April 2017. [Google Scholar]
- Li, D.; Lu, J. System, Method, and Apparatus for Remotely Monitoring Surge Arrester Conditions. U.S. Patent 20140176336A1, 26 June 2014. [Google Scholar]
- Schillert, H.; Schubert, M.; Steinfeld, K. Device for Monitoring the Leakage Current of a Surge Arrester. U.S. Patent 7336193B2, 26 February 2008. [Google Scholar]
- Rostron, J.; Keister, J.; Anand, R. Arrester Temperature Monitor. U.S. Patent 20180108461A1, 19 April 2018. [Google Scholar]
- Khatri, M.; Comber, F. Temperature Monitoring of High Voltage Distribution System Components. U.S. Patent 20160265978, 15 September 2016. [Google Scholar]
- Luo, Y.F. Study on Metal-Oxide-Arrester on-line Monitoring Distributed-Control-System. Master’s Thesis, Xi’an Jiao tong University, Xi’an, China, 2003. [Google Scholar]
- Ultra-Low-Power with FPU Arm Cortex-M4 MCU 80 MHz with 256 Kbytes of Flash Memory, LCD, USB. Available online: https://www.st.com/en/microcontrollers-microprocessors/stm32l433cc.html (accessed on 28 January 2021).
- Saft LS17500 A 3.6V Primary Lithium Battery. Available online: https://www.atbatt.com/saft-ls17500-a-3-6v-primary-lithium-battery/ (accessed on 28 January 2021).
- Kirianaki, N.V.; Yurish, S.Y.; Shpak, N.O.; Deynega, V.P. Data Acquisition and Signal Processing for Smart Sensors; John Wiley & Sons Ltd.: New York, NY, USA, 2002; pp. 1–27. [Google Scholar]
- Wu, Q.; Chung, H.-H. Management protocols for sensors in smart grid networks. In Wireless Sensor Networks and Ecological Monitoring; Mukhopadhyay, S.C., Jiang, J.-A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 125–150. [Google Scholar]
- Buchholz, B.M.; Styczynski, Z. Smart Grids—Fundamentals and Technologies in Electricity Networks; Springer: Berlin/Heidelberg, Germany, 2014; pp. 62–66. [Google Scholar]
- Quectel MC60 Ultra-Small LCC Quad-band GSM/GPRS/GNSS Module. Available online: https://www.quectel.com/UploadFile/Product/Quectel_MC60_GSM_Specification_V1.2.pdf (accessed on 28 January 2021).
- Velasco-Quesada, G.; Conesa-Roca, A.; Román-Lumbreras, M. Technologies for electric current sensors. In Smart Sensors for Industrial Applications; Iniewski, K., Ed.; CRC Press Taylor & Francis Group, LLC.: Boca Raton, FL, USA, 2013; pp. 125–150. [Google Scholar]





| Annual for 1 MOSA | Annual for 12,090 pcs of MOSA | |
|---|---|---|
| Power losses [MWh] | 0.486 | 5.872 |
| Financial losses [€] | 35.4 | 428.312 |
| Carbon footprint [t] | 0.133 | 16.4416 |
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | … | Sample N | Mean Val. | Relative σ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φ1 [°] | [μA] | φ2 [°] | [μA] | φ3 [°] | [μA] | φ4 [°] | [μA] | .… | φN [°] | [μA] | φ [°] | [μA] | Urms [kV] | σφ [%] | [%] |
| 157 | 812 | 158 | 847 | 158 | 847 | 155 | 755 | …. | 156 | 750 | 157 | 802 | 39 | 0.31 | 3.9 |
| 159 | 510 | 160 | 521 | 161 | 545 | 160 | 475 | …. | 159 | 480 | 160 | 500 | 37 | 0.36 | 4.3 |
| 162 | 220 | 163 | 214 | 165 | 199 | 162 | 195 | …. | 163 | 183 | 163 | 202 | 36 | 0.59 | 7.3 |
| 165 | 107 | 166 | 102 | 167 | 107 | 164 | 95 | …. | 166 | 102 | 166 | 103 | 33 | 0.67 | 4.8 |
| 168 | 66 | 169 | 56 | 169 | 61 | 171 | 56 | …. | 171 | 60 | 170 | 59 | 31 | 0.88 | 5.8 |
| 173 | 33 | 172 | 33 | 173 | 36 | 174 | 36 | …. | 173 | 37 | 173 | 35 | 25 | 0.39 | 5.5 |
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | … | Sample N | Mean | Relative σ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φ [°] | It_avg,1 [μA] | φ [°] | It_avg,2 [A] | φ [°] | It_avg,3 [μA] | φ [°] | It_avg,4 [μA] | … | φ [°] | It_avg,N [μA] | φ [°] | It,mn [μA] | Urms [kV] | σφ [%] | σIt,mn [%] |
| 157 | 643 | 158 | 665 | 158 | 664 | 155 | 621 | … | 156 | 640 | 157 | 646 | 39 | 0.73 | 2.5 |
| 159 | 546 | 160 | 548 | 161 | 545 | 160 | 523 | … | 159 | 522 | 160 | 537 | 37 | 0.43 | 2.2 |
| 162 | 426 | 163 | 420 | 165 | 418 | 162 | 380 | … | 163 | 401 | 163 | 409 | 35 | 0.68 | 4.1 |
| 165 | 359 | 166 | 353 | 167 | 356 | 164 | 340 | … | 166 | 365 | 166 | 355 | 33 | 0.46 | 2.4 |
| 168 | 329 | 169 | 319 | 169 | 318 | 171 | 314 | … | 171 | 321 | 170 | 320 | 31 | 0.72 | 1.5 |
| 173 | 298 | 172 | 294 | 173 | 301 | 174 | 305 | … | 173 | 310 | 173 | 299 | 25 | 0.27 | 2.0 |
| Measured Values | Phase | Calculated (15)–(18) | Scope Value | Relative Error |
|---|---|---|---|---|
| It_avg [μA] | φ [°] | [μA] | [μA] | ε [%] |
| 665 | 156.25 | 839 | 847 | 0.9 |
| 643 | 156.86 | 783 | 812 | 3.6 |
| 522 | 160.01 | 480 | 480 | 0.0 |
| 418 | 162.74 | 218 | 199 | −9.8 |
| 356 | 165.06 | 103 | 107 | 3.5 |
| 319 | 169.95 | 59 | 56 | −5.4 |
| 298 | 172.72 | 34 | 33 | −3.0 |
| 570 | 158.75 | 600 |
| SAMD Measured | Oscilloscope Measured | Relative Error |
|---|---|---|
| It_avg [μA] | It_avg [μA] | εrel [%] |
| 327.3 | 331.4 | −1.24 |
| 372.1 | 375.8 | −0.98 |
| 605.2 | 642.5 | −5.81 |
| SAMD Measured | Calculated (15)–(18) | Reference Scope Value | Absolute | Relative |
|---|---|---|---|---|
| It_avg [μA] | [μA] | [μA] | εabs [μA] | εrel [%] |
| 327.3 | 69.0 | 79.1 | 10.1 | −12.8 |
| 372.1 | 103.2 | 97.0 | 6.2 | 6.3 |
| 409.7 | 197.0 | 195.3 | 1.7 | 0.9 |
| 411.1 | 201.1 | 204.2 | −3.1 | −1.6 |
| 457.0 | 316.5 | 311.0 | 5.5 | 1.6 |
| 581.2 | 628.5 | 628.0 | 0.5 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vončina, V.; Pihler, J.; Milanovič, M. Extracting the Resistive Current Component from a Surge Arrester’s Leakage Current without Voltage Reference. Sensors 2021, 21, 1257. https://doi.org/10.3390/s21041257
Vončina V, Pihler J, Milanovič M. Extracting the Resistive Current Component from a Surge Arrester’s Leakage Current without Voltage Reference. Sensors. 2021; 21(4):1257. https://doi.org/10.3390/s21041257
Chicago/Turabian StyleVončina, Vid, Jože Pihler, and Miro Milanovič. 2021. "Extracting the Resistive Current Component from a Surge Arrester’s Leakage Current without Voltage Reference" Sensors 21, no. 4: 1257. https://doi.org/10.3390/s21041257
APA StyleVončina, V., Pihler, J., & Milanovič, M. (2021). Extracting the Resistive Current Component from a Surge Arrester’s Leakage Current without Voltage Reference. Sensors, 21(4), 1257. https://doi.org/10.3390/s21041257








