Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis
Abstract
1. Introduction
2. Methodology
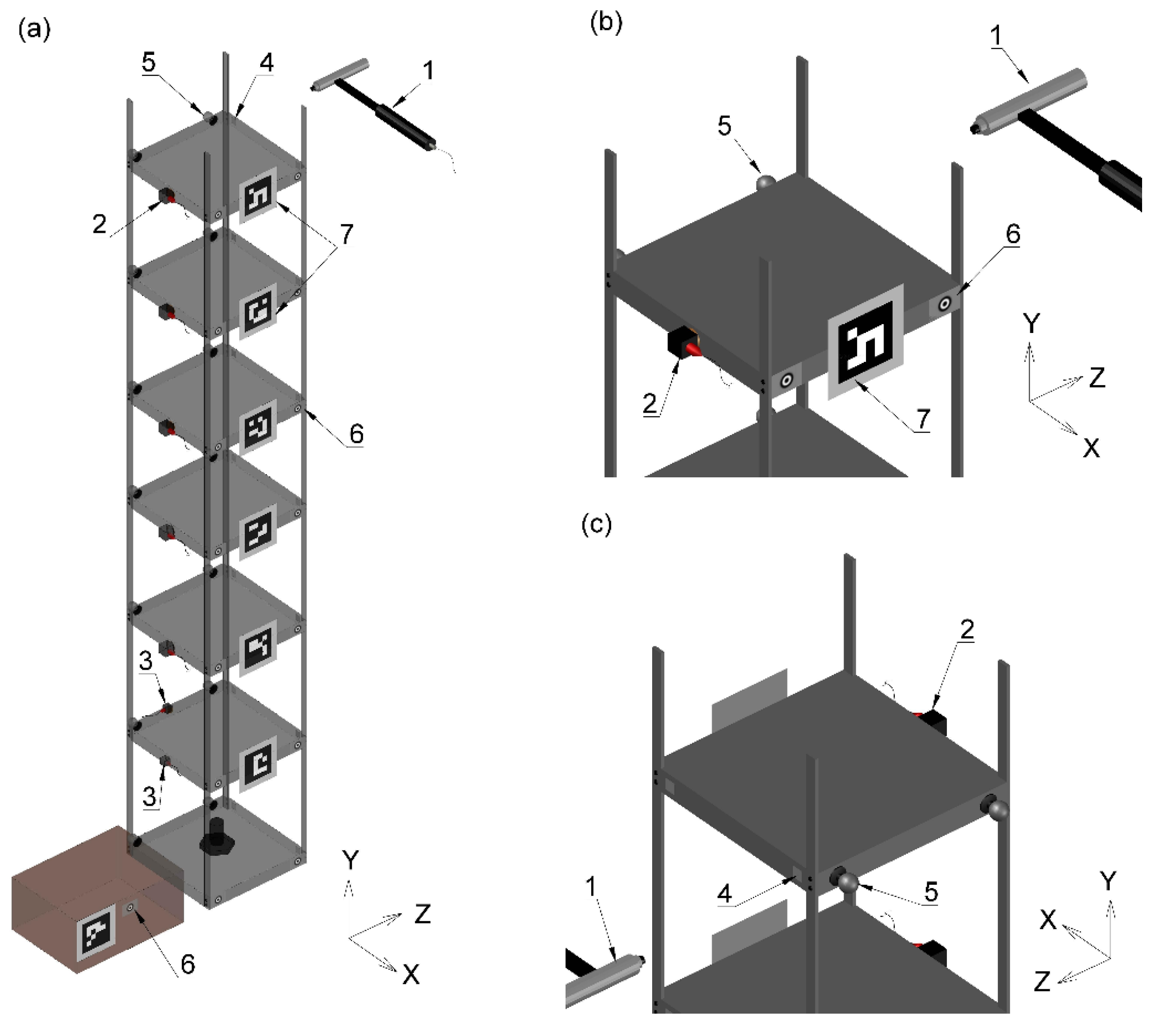
2.1. Tested Structure
2.2. Instrumentation
2.2.1. Accelerometers
2.2.2. Imetrum
2.2.3. OptiTrack
2.2.4. Polytec Laser Doppler Vibrometer (LDV)
2.2.5. Consumer-Grade Camera (CGC)
Feature-Based Template Matching (ArUco)
Area-Based Template Matching
2.2.6. Instrumented Hammer
2.2.7. Lux Meter
2.3. Fiducial Markers
2.3.1. Light-Reflective Markers
2.3.2. Light-Emitting Markers
2.3.3. Shape- and Pattern-Based Markers
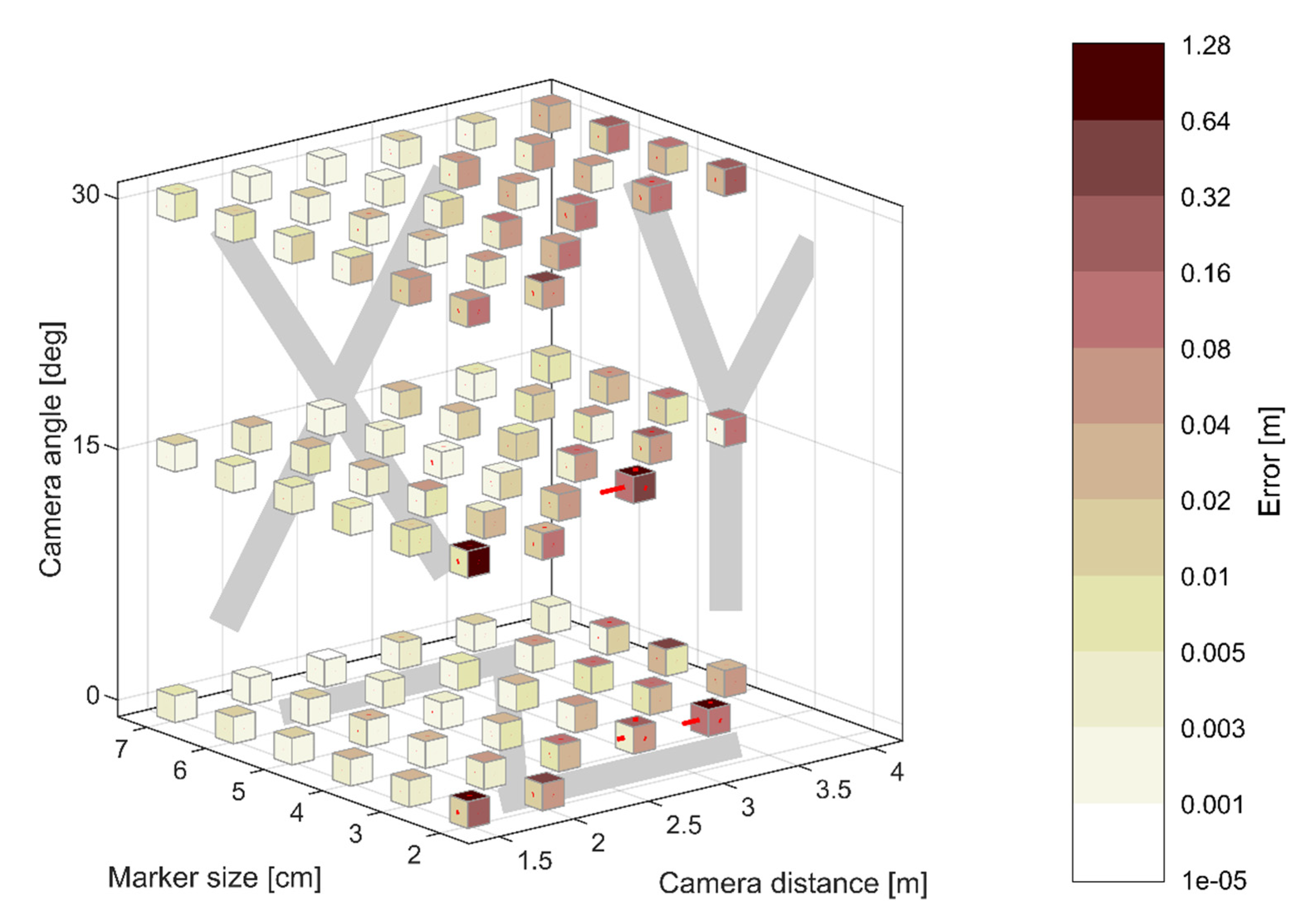
2.4. ArUco Pose Accuracy Assessment
2.5. Modal Testing and Analysis
2.6. Initial Displacement Testing and Analysis
3. Results and Discussion
3.1. ArUco Pose Accuracy Results
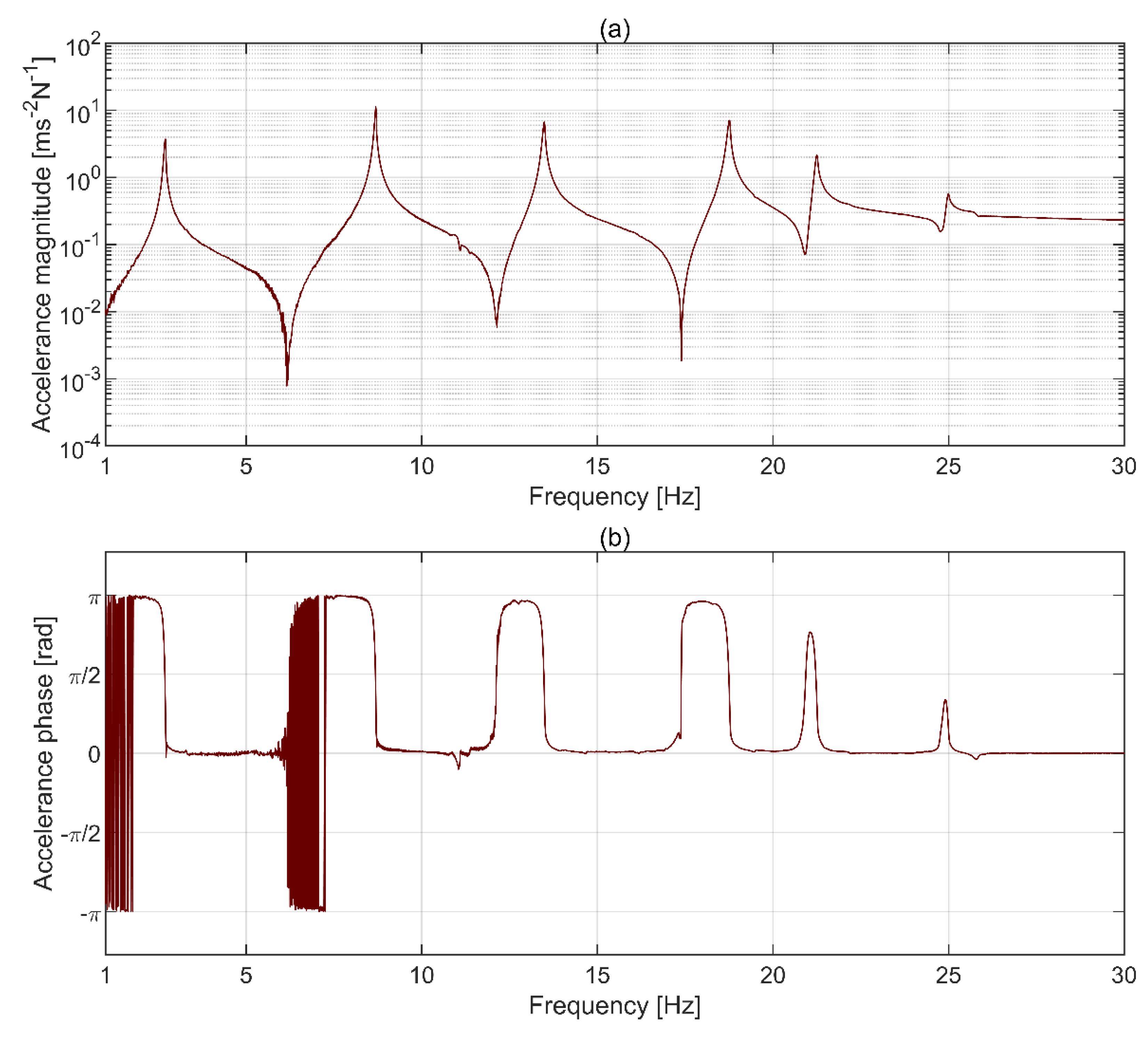
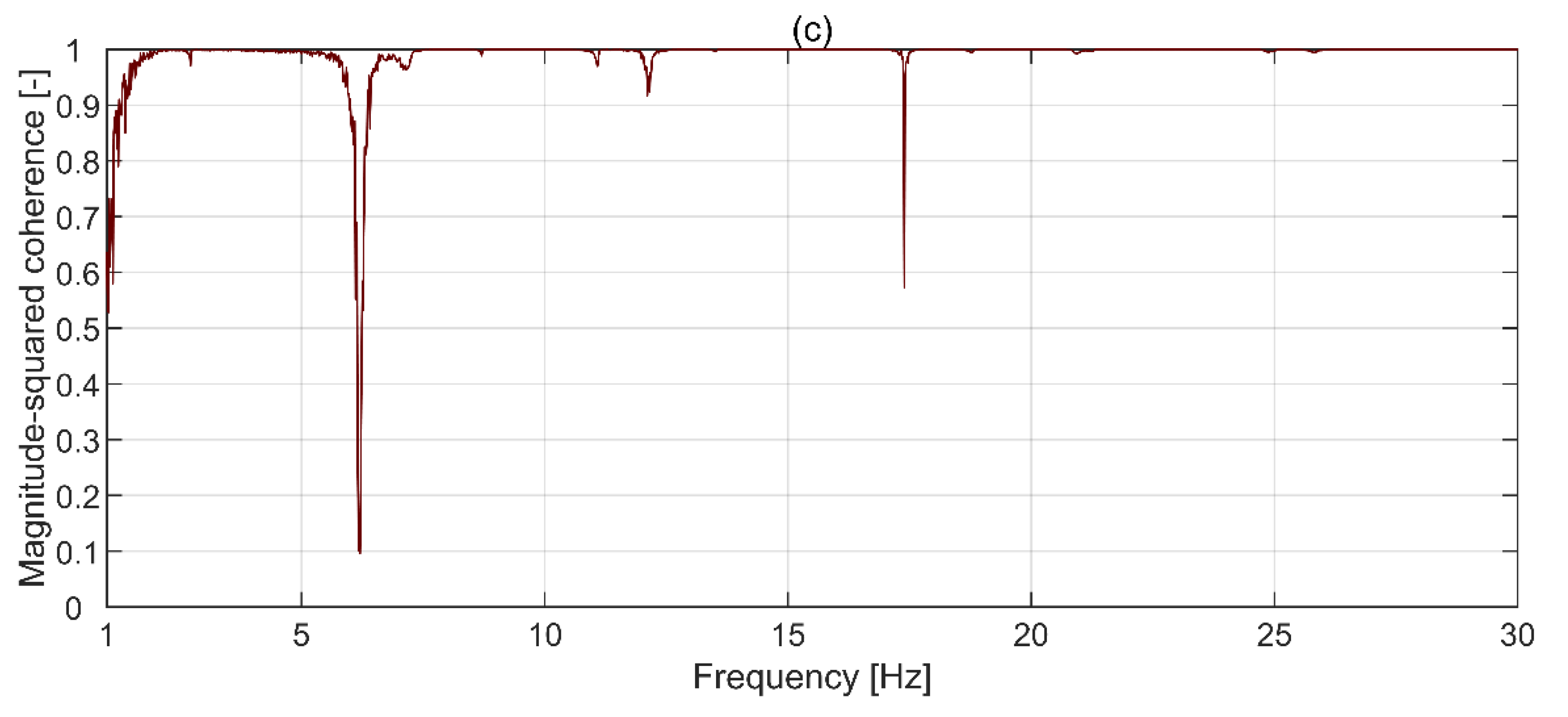
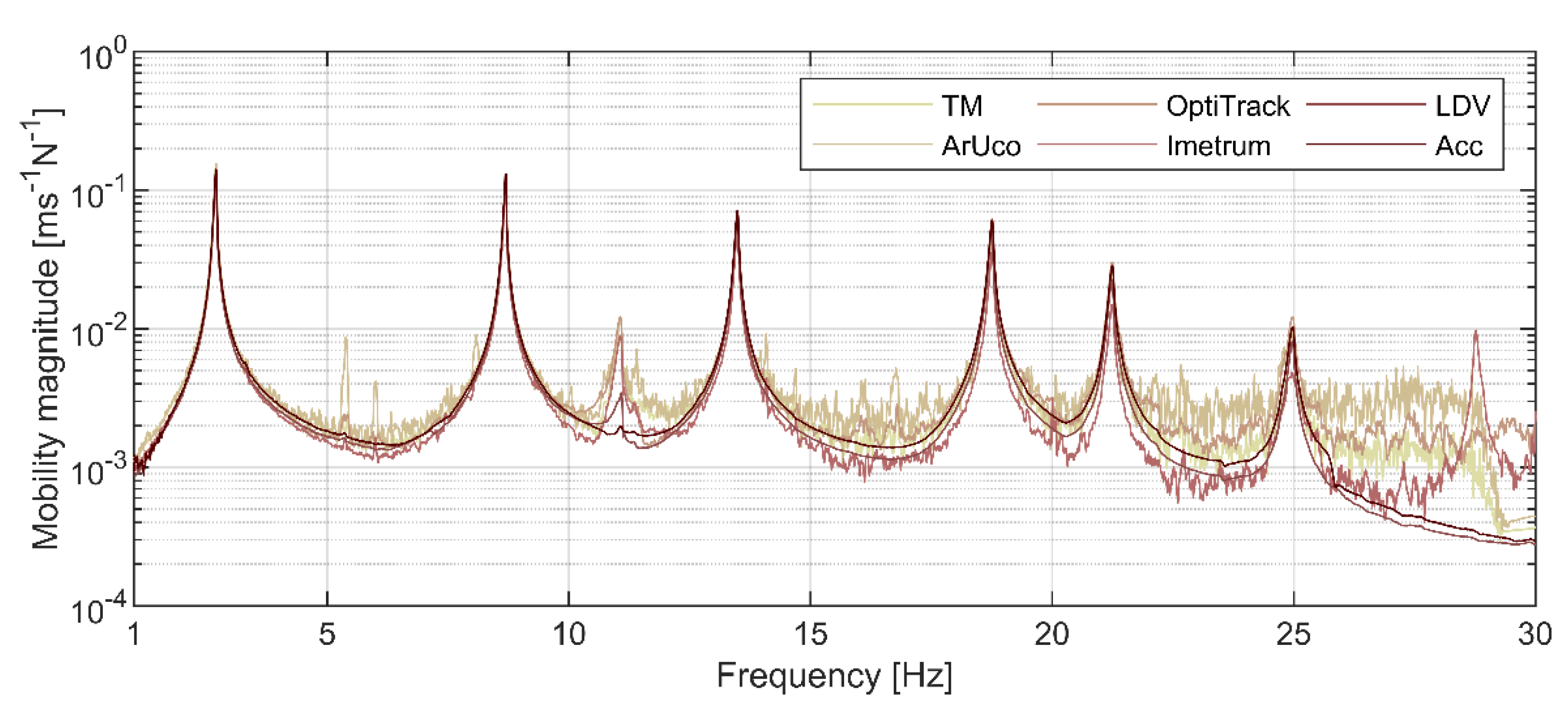
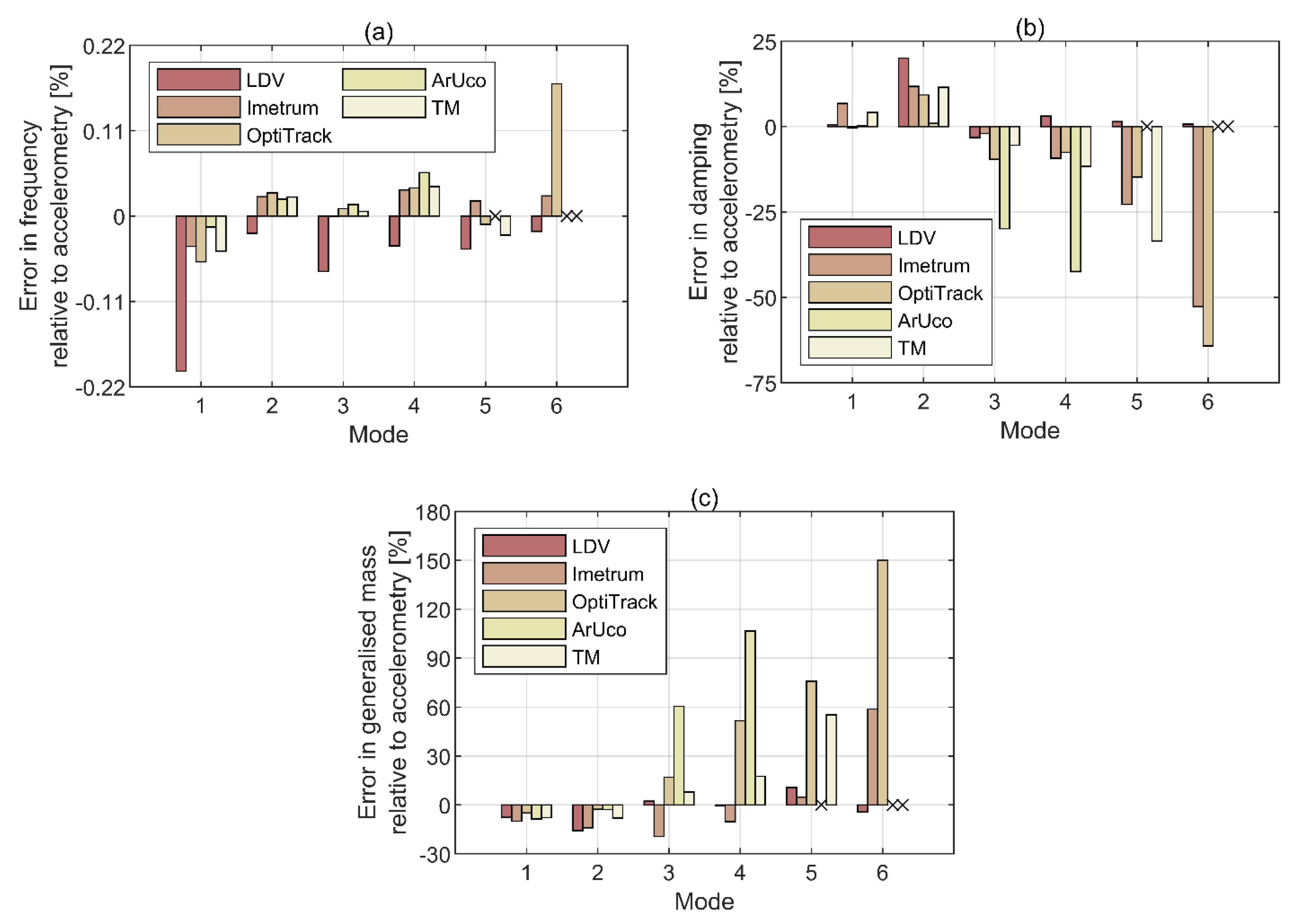
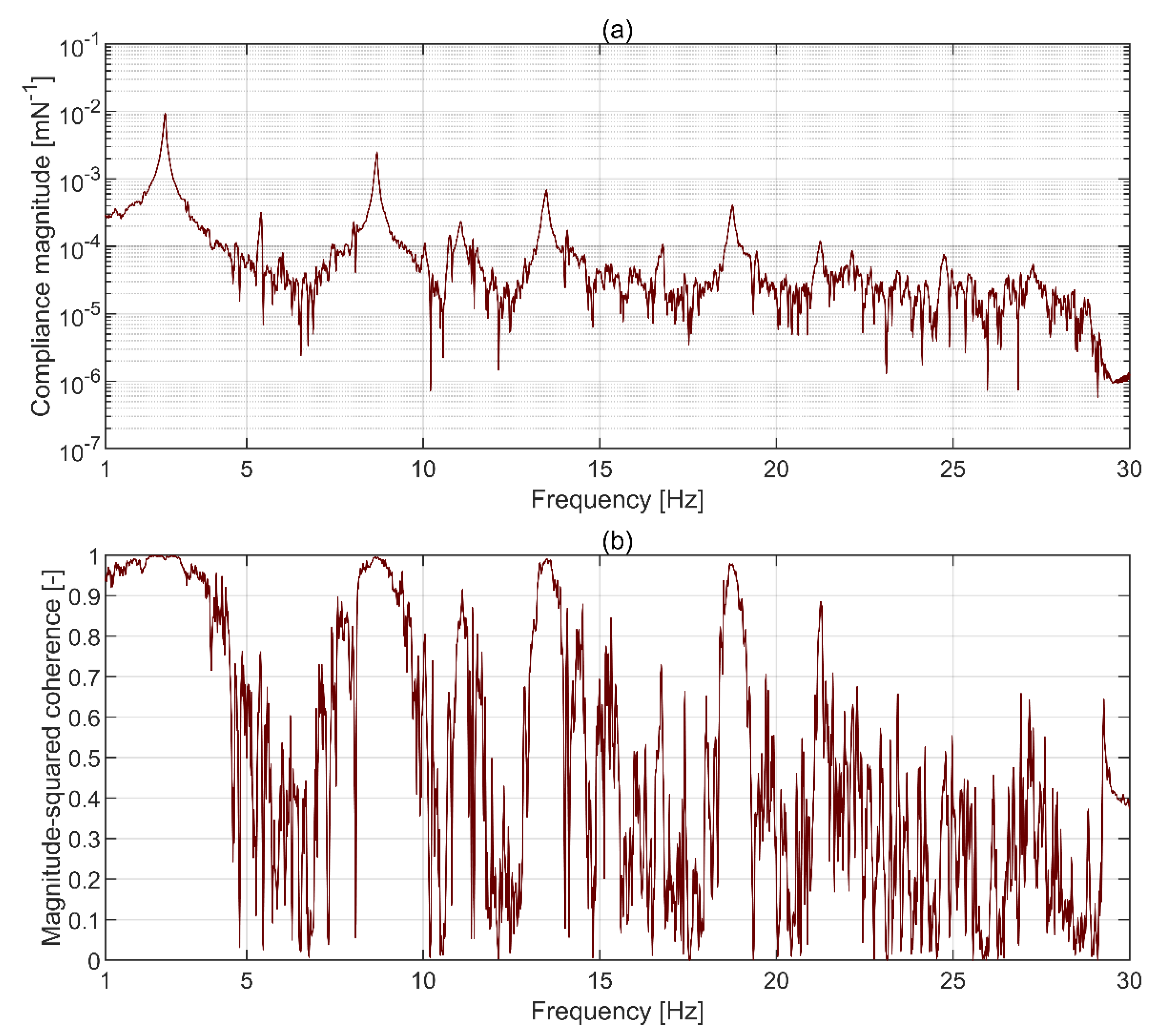
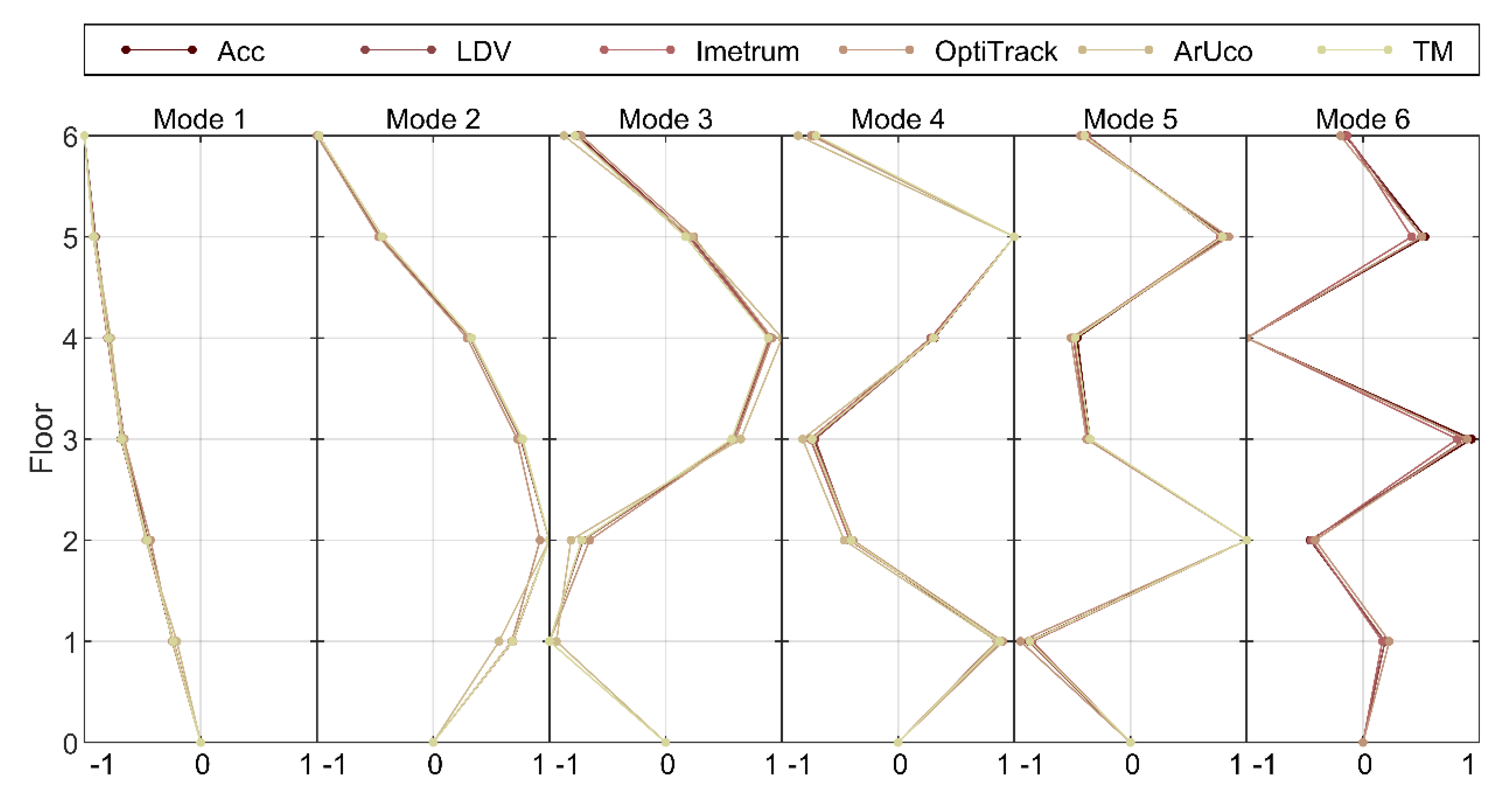
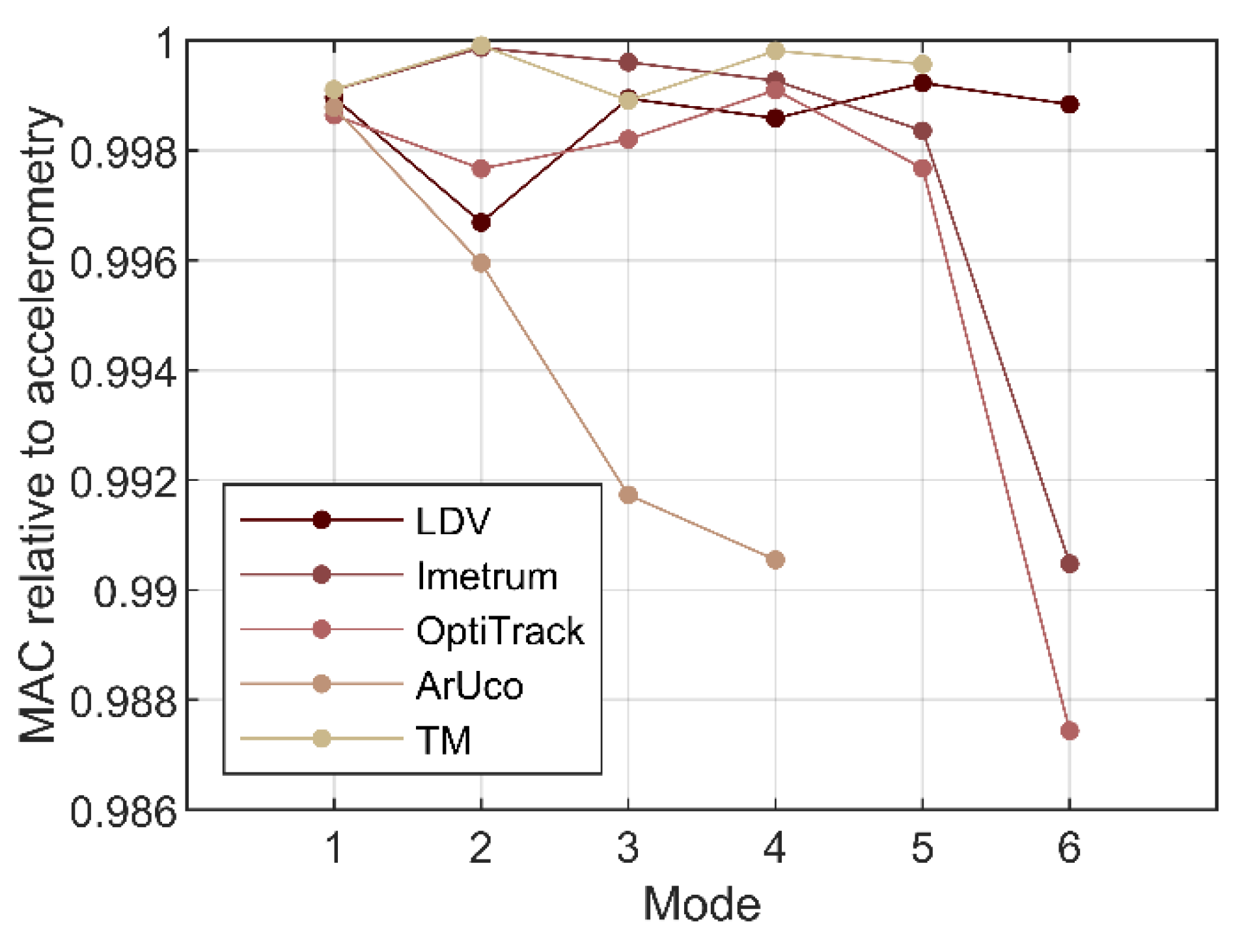
3.2. Modal Testing Results
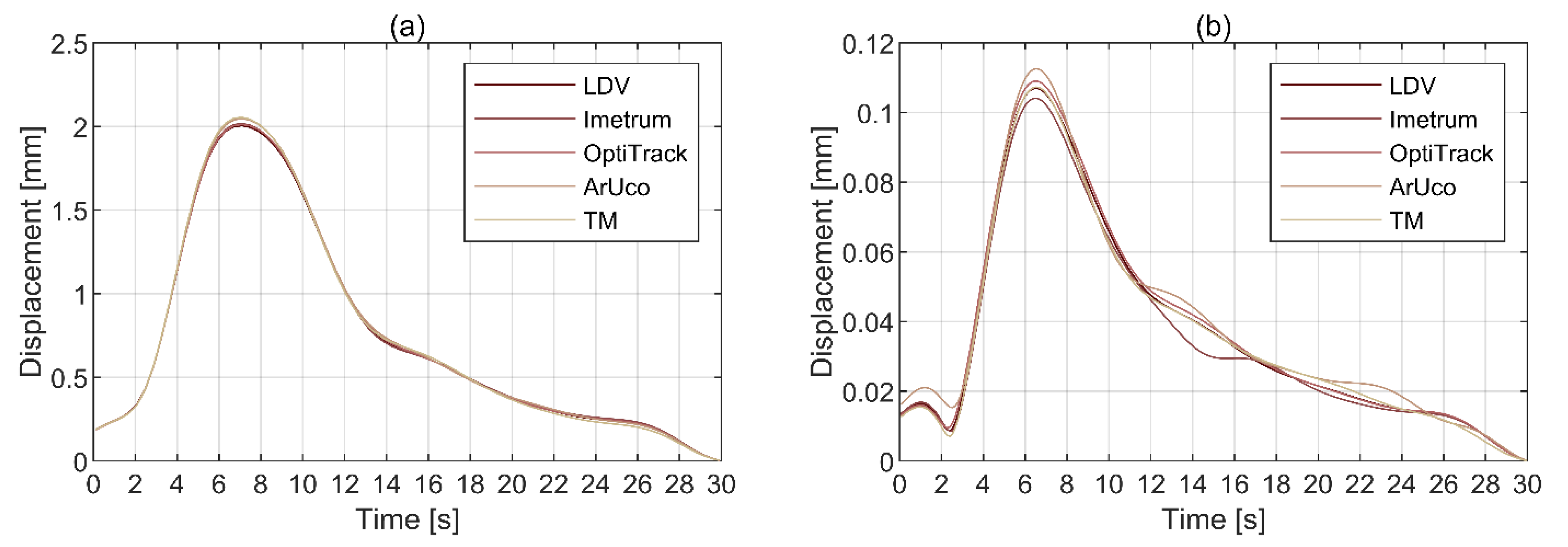
3.3. Initial Displacement Testing Results
3.3.1. Vibration Amplitude
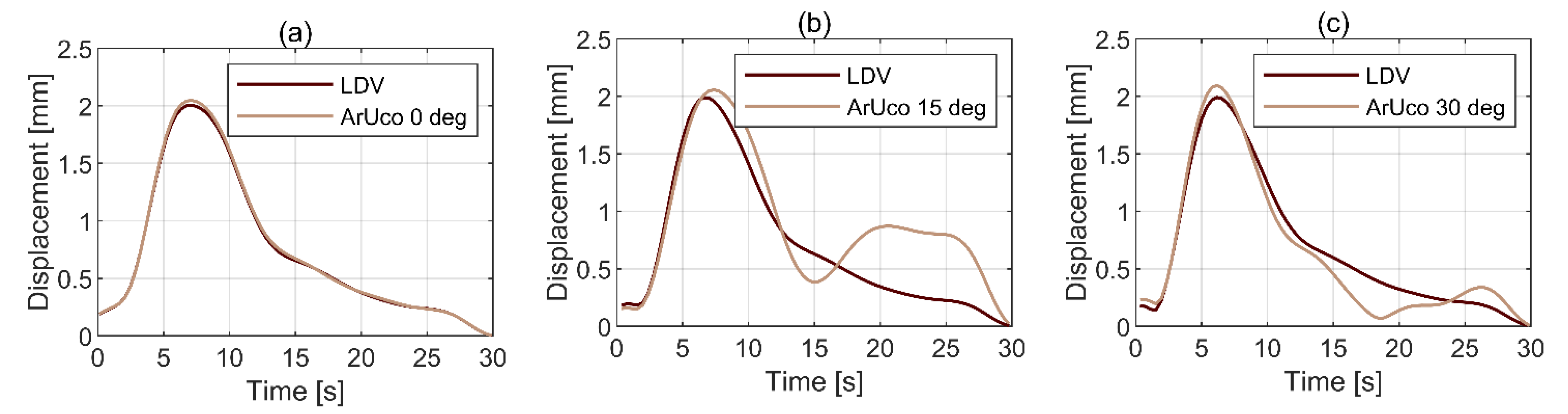
3.3.2. Influence of the Angle of Incidence of CGC
3.4. Limitations of This Study and Deployment Considerations on In Situ Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Health Monit. 2018, 8, 91–110. [Google Scholar] [CrossRef]
- Spencer, B.F.; Hoskere, V.; Narazaki, Y. Advances in computer vision-based civil infrastructure inspection and monitoring. Engineering 2019, 5, 199–222. [Google Scholar] [CrossRef]
- Park, S.W.; Park, H.S.; Kim, J.H.; Adeli, H. 3D displacement measurement model for health monitoring of structures using a motion capture system. Meas. J. Int. Meas. Confed. 2015, 59, 352–362. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Hester, D.; Xu, Y.; Bassitt, J.; Koo, K. Viability of optical tracking systems for monitoring deformations of a long span bridge. In Proceedings of the 6th European Conference on Structural Control, Sheffield, UK, 11–13 July 2016; European Association for the Control of Structures: Sheffield, UK, 2016. [Google Scholar]
- Luo, L.; Feng, M.Q.; Wu, Z.Y. Robust vision sensor for multi-point displacement monitoring of bridges in the field. Eng. Struct. 2018, 163, 255–266. [Google Scholar] [CrossRef]
- Patil, K.; Srivastava, V.; Baqersad, J. A multi-view optical technique to obtain mode shapes of structures. Meas. J. Int. Meas. Confed. 2018, 122, 358–367. [Google Scholar] [CrossRef]
- Kromanis, R.; Xu, Y.; Lydon, D.; Martinez del Rincon, J.; Al-Habaibeh, A. Measuring structural deformations in the laboratory environment using smartphones. Front. Built Environ. 2019, 5. [Google Scholar] [CrossRef]
- Zhao, X.; Ri, K.; Wang, N. Experimental verification for cable force estimation using handheld shooting of smartphones. J. Sens. 2017, 1–13. [Google Scholar] [CrossRef]
- Feldbusch, A.; Sadegh-Azar, H.; Agne, P. Vibration analysis using mobile devices (smartphones or tablets). Procedia Eng. 2017, 199, 2790–2795. [Google Scholar] [CrossRef]
- Lydon, D.; Lydon, M.; Taylor, S.; Del Rincon, J.M.; Hester, D.; Brownjohn, J. Development and field testing of a vision-based displacement system using a low cost wireless action camera. Mech. Syst. Signal Process. 2019, 121, 343–358. [Google Scholar] [CrossRef]
- Fonseca, L.M.G.; Manjunath, B.S. Registration techniques for multisensor remotely sensed imagery. Photogramm. Eng. Remote Sens. 1996, 62, 1049–1056. [Google Scholar]
- Xu, Y.; Brownjohn, J.; Kong, D. A non-contact vision-based system for multipoint displacement monitoring in a cable-stayed footbridge. Struct. Control Health Monit. 2018, 25, 1–23. [Google Scholar] [CrossRef]
- Abdelbarr, M.; Chen, Y.L.; Jahanshahi, M.R.; Masri, S.F.; Shen, W.M.; Qidwai, U.A. 3D dynamic displacement-field measurement for structural health monitoring using inexpensive RGB-D based sensor. Smart Mater. Struct. 2017, 26. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.Q.; Shinozuka, M. Cost-effective vision-based system for monitoring dynamic response of civil engineering structures. Struct. Control Health Monit. 2010, 17, 918–936. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Theiler, J.; Kenyon, G.; Farrar, C.; Mascareñas, D. Reference-free detection of minute, non-visible, damage using full-field, high-resolution mode shapes output-only identified from digital videos of structures. Struct. Health Monit. 2018, 17, 514–531. [Google Scholar] [CrossRef]
- Dong, C.-Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2020, 1475921720935585. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; John Wiley & Sons: Baldock, UK, 2000. [Google Scholar]
- Guillaume, P.; Brussel, V.U.; De Troyer, T.; Brussel, V.U.; Devriendt, C.; Brussel, V.U.; De Sitter, G.; Brussel, V.U. OMAX—A combined experimental-operational modal analysis approach. In Proceedings of the International Conference on Noise and Vibration Engineering, ISMA 2006, Heverlee, Belgium, 18–20 September 2006; KTH: Stockholm, Sweden, 2006; pp. 2985–2996. [Google Scholar]
- Reynders, E. System identification methods for (operational) modal analysis: Review and comparison. Arch. Comput. Methods Eng. 2012, 19, 51–124. [Google Scholar] [CrossRef]
- Aenlle, M.; Juul, M.; Brincker, R. Modal mass and length of mode shapes in structural dynamics. Shock Vib. 2020, 2020, 8648769. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Brandt, A.; Berardengo, M.; Manzoni, S.; Cigada, A. Scaling of mode shapes from operational modal analysis using harmonic forces. J. Sound Vib. 2017, 407, 128–143. [Google Scholar] [CrossRef]
- Oh, B.K.; Hwang, J.W.; Kim, Y.; Cho, T.; Park, H.S. Vision-based system identification technique for building structures using a motion capture system. J. Sound Vib. 2015, 356, 72–85. [Google Scholar] [CrossRef]
- Reu, P.L.; Rohe, D.P.; Jacobs, L.D. Comparison of DIC and LDV for practical vibration and modal measurements. Mech. Syst. Signal Process. 2017, 86, 2–16. [Google Scholar] [CrossRef]
- Yoon, H.; Elanwar, H.; Choi, H.; Golparvar-Fard, M.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control Health Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Hoskere, V.; Park, J.W.; Yoon, H.; Spencer, B.F. Vision-based modal survey of civil infrastructure using unmanned aerial vehicles. J. Struct. Eng. 2019, 145, 1–14. [Google Scholar] [CrossRef]
- Imetrum. Available online: https://www.imetrum.com/ (accessed on 20 April 2020).
- Hester, D.; Brownjohn, J.; Bocian, M.; Xu, Y. Low cost bridge load test: Calculating bridge displacement from acceleration for load assessment calculations. Eng. Struct. 2017, 143, 358–374. [Google Scholar] [CrossRef]
- Macdonald, J.H.G.; Dagless, E.L.; Thomas, B.T.; Taylor, C.A. Dynamic measurements of the Second Severn Crossing. Proc. Inst. Civ. Eng. Transp. 1997, 123, 241–248. [Google Scholar] [CrossRef]
- OptiTrack. Available online: https://optitrack.com/ (accessed on 20 April 2020).
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly Media: Sebastopol, CA, USA, 2008. [Google Scholar]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Popescu, D.C.; Cernaianu, M.O.; Ghenuche, P.; Dumitrache, I. An assessment on the accuracy of high precision 3D positioning using planar fiducial markers. In Proceedings of the 21st International Conference on System Theory, Control and Computing, ICSTCC 2017, Sinaia, Romania, 19–23 October 2017; pp. 471–476. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q.; Ozer, E.; Fukuda, Y. A vision-based sensor for noncontact structural displacement measurement. Sensors 2015, 15, 16557–16575. [Google Scholar] [CrossRef]
- British Standards Institution. BS EN 12464-1:2002. Light and Lighting—Lighting of Work Places—Part 1: Indoor Work; BSI: London, UK, 2002. [Google Scholar]
- Ye, X.W.; Ni, Y.Q.; Wai, T.T.; Wong, K.Y.; Zhang, X.M.; Xu, F. A vision-based system for dynamic displacement measurement of long-span bridges: Algorithm and verification. Smart Struct. Syst. 2013, 12, 363–379. [Google Scholar] [CrossRef]
- Ozbek, M.; Rixen, D.J.; Erne, O.; Sanow, G. Feasibility of monitoring large wind turbines using photogrammetry. Energy 2010, 35, 4802–4811. [Google Scholar] [CrossRef]
- Wahbeh, A.M.; Caffrey, J.P.; Masri, S.F. A vision-based approach for the direct measurement of displacements in vibrating systems. Smart Mater. Struct. 2003, 12, 785–794. [Google Scholar] [CrossRef]
- Dong, C.Z.; Ye, X.W.; Liu, T. Non-contact structural vibration monitoring under varying environmental conditions. Vibroeng. Procedia 2015, 5, 217–222. [Google Scholar]
- Olaszek, P. Investigation of the dynamic characteristic of bridge structures using a computer vision method. Meas. J. Int. Meas. Confed. 1999, 25, 227–236. [Google Scholar] [CrossRef]
- Peeters, B.; Lowet, G.; Van der Auweraer, H.; Leuridan, J. A new procedure for modal parameter estimation. Sound Vib. 2004, 38, 24–29. [Google Scholar]
- Peeters, B.; Van Der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Guillaume, P.; Verboven, P.; Vanlanduit, S. A poly-reference implementation of the least-squares complex frequency-domain estimator. In Proceedings of the 21st International Modal Analysis Conference, Kissimmee, FL, USA, 3–6 February 2003. [Google Scholar]
- Peeters, B.; Guillaume, P. The new PolyMAX Plus method: Confident modal parameter estimation even in very noisy cases. In Proceedings of the International Conference on Noise and Vibration Engineering, ISMA 2012/International Conference on Uncertainty in Structural Dynamics, USD 2012, Leuven, Belgium, 17–19 September 2012; pp. 2801–2814. [Google Scholar]
- Smith, J.W. Vibration of Structures; Chapman & Hall: London, UK, 1988. [Google Scholar]
- Bocian, M.; Macdonald, J.H.G.; Burn, J.F. Probabilistic criteria for lateral dynamic stability of bridges under crowd loading. Comput. Struct. 2014, 136, 108–119. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Bocian, M.; Hester, D.; Quattrone, A.; Hudson, W.; Moore, D.; Goh, S.; Lim, M.S. Footbridge system identification using wireless inertial measurement units for force and response measurements. J. Sound Vib. 2016, 384, 339–355. [Google Scholar] [CrossRef]
- White, R.E.; Alexander, N.A.; Macdonald, J.H.G.; Bocian, M. Characterisation of crowd lateral dynamic forcing from full-scale measurements on the Clifton Suspension Bridge. Structures 2020, 24, 415–425. [Google Scholar] [CrossRef]
- Nikitas, N.; Macdonald, J.H.G.; Jakobsen, J.B. Identification of flutter derivatives from full-scale ambient vibration measurements of the Clifton Suspension Bridge. Wind Struct. Int. J. 2011, 14, 221–238. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Allemang, R.J. The modal assurance criterion—Twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Allemang, R.J.; Brown, D.L. A correlation coefficient for modal vector analysis. In Proceedings of the 1st International Modal Analysis Conference, Orlando, FL, USA, 8–10 November 1982; pp. 110–116. [Google Scholar]
- Balmes, E. GARTEUR group on ground vibration testing. Results from the test of a single structure by 12 laboratories in Europe. In Proceedings of the 15th International Modal Analysis Conference, Orlando, FL, USA, 3–6 February 1997; Volume 2, pp. 1346–1352. [Google Scholar]
- Park, H.S.; Young Kim, J.; Gi Kim, J.; Woon Choi, S.; Kim, Y. A new position measurement system using a motion-capture camera for wind tunnel tests. Sensors 2013, 13, 12329–12344. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Dai, K.; Ren, X.; Chen, Q.; Zhao, B. Case studies of LDV-aided dynamic testing. Appl. Mech. Mater. 2012, 226–228, 2066–2071. [Google Scholar] [CrossRef]






| System | Sensor | Quantity | Sampling Frequency and Resolution | Distance Relative to the Markers | Fiducial Marker |
|---|---|---|---|---|---|
| Polytec LDV | PSV-500-HM | 3 | 200 Hz and 0.02 µm/s | 3 m |  |
| OptiTrack | Prime 13 with 5.5 mm lens | 8 | 120 fps at 1.3 MP | 1–3 m |  |
| Imetrum | Manta G-223 B NIR with 16 mm lens | 2 | 50 fps at 2 MP | 3 m |  |
| Accelerometers | PCB 356 A16 PCB 333 B30 | 5 2 | 64 Hz at 100 mV/g 64 Hz at 100 mV/g | Direct contact Direct contact | N/A |
| CGC (used with feature-based ArUco and area-based template matching) | Cannon EOS 200 D with DIGIC 7 processor and 20 mm Canon lens | 1 | 59.94 fps at 24.2 MP | 1.5 m |  |
| Modal Frequency [Hz] | ||||||
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | |
| Accelerometry | 2.681 (N/A) | 8.673 (N/A) | 13.471 (N/A) | 18.730 (N/A) | 21.223 (N/A) | 24.943 (N/A) |
| LDV | 2.676 (−0.20%) | 8.671 (−0.02%) | 13.462 (−0.07%) | 18.723 (−0.04%) | 21.214 (−0.04%) | 24.938 (−0.02) |
| OptiTrack | 2.680 (−0.04%) | 8.675 (0.02%) | 13.471 (0.00%) | 18.737 (0.03%) | 21.227 (0.02%) | 24.949 (0.03%) |
| Imetrum | 2.680 (−0.06%) | 8.676 (0.03%) | 13.473(0.01%) | 18.737 (0.04%) | 21.221 (−0.01%) | 24.985 (0.17%) |
| ArUco | 2.681 (−0.01%) | 8.675 (0.02%) | 13.473 (0.01%) | 18.741 (0.06%) | N/A | N/A |
| Template matching | 2.680 (−0.05%) | 8.675 (0.02%) | 13.472 (0.01%) | 18.738 (0.04%) | 21.218 (−0.02%) | N/A |
| Modal damping ratio [%] | ||||||
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | |
| Accelerometry | 0.706 (N/A) | 0.224 (N/A) | 0.251 (N/A) | 0.227 (N/A) | 0.238 (N/A) | 0.233 (N/A) |
| LDV | 0.710 (0.54%) | 0.269 (20.14%) | 0.243 (−3.24%) | 0.234 (3.05%) | 0.241 (1.46%) | 0.235 (0.70%) |
| OptiTrack | 0.754 (6.79%) | 0.250 (11.77%) | 0.246 (−2.03%) | 0.206 (−9.25%) | 0.184 (−22.77%) | 0.110 (−52.73%) |
| Imetrum | 0.704 (−0.31%) | 0.245 (9.29%) | 0.227 (−9.59%) | 0.210 (−7.52%) | 0.203 (−14.76%) | 0.083 (−64.23%) |
| ArUco | 0.707 (0.21%) | 0.226 (0.93%) | 0.176 (−29.95%) | 0.130 (−42.47%) | N/A | N/A |
| Template matching | 0.735 (4.13%) | 0.249 (11.51%) | 0.237 (−5.47%) | 0.200 (−11.68%) | 0.158 (−33.54%) | N/A |
| Generalised mass [kg] | ||||||
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | |
| Accelerometry | 19.55 (N/A) | 20.74 (N/A) | 17.71 (N/A) | 15.55 (N/A) | 13.80 (N/A) | 10.78 (N/A) |
| LDV | 18.05 (−7.66%) | 17.47 (−15.78%) | 18.11 (2.27%) | 15.44 (−0.72%) | 15.26 (10.59%) | 10.31 (−4.38%) |
| OptiTrack | 17.57 (−10.11%) | 17.83 (−14.04%) | 14.27 (−19.41%) | 13.95 (−10.26%) | 14.45 (4.71%) | 17.13 (58.92%) |
| Imetrum | 18.58 (−4.93%) | 20.18 (−2.72%) | 20.72 (16.98%) | 23.58 (51.65%) | 24.25 (75.76%) | 26.95 (149.99%) |
| ArUco | 17.85 (−8.65%) | 20.13 (−2.92%) | 28.42 (60.50%) | 32.12 (106.6%) | N/A | N/A |
| Template matching | 18.02 (−7.83%) | 19.06 (−8.07%) | 19.11 (7.93%) | 18.28 (17.57%) | 21.43 (55.34%) | N/A |
| MCS | Number of Cameras | Mode 1 | Mode 2 |
|---|---|---|---|
| RMS Error [mm] | RMS Error [mm] | ||
| OptiTrack | 8 | 6.74 × 10−3 | 1.23 × 10−3 |
| Imetrum | 2 | 7.15 × 10−3 | 2.61 × 10−3 |
| ArUco | 1 | 1.74 × 10−2 | 3.12 × 10−3 |
| Template matching | 1 | 1.98 × 10−2 | 1.34 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalybek, M.; Bocian, M.; Nikitas, N. Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis. Sensors 2021, 21, 1239. https://doi.org/10.3390/s21041239
Kalybek M, Bocian M, Nikitas N. Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis. Sensors. 2021; 21(4):1239. https://doi.org/10.3390/s21041239
Chicago/Turabian StyleKalybek, Maksat, Mateusz Bocian, and Nikolaos Nikitas. 2021. "Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis" Sensors 21, no. 4: 1239. https://doi.org/10.3390/s21041239
APA StyleKalybek, M., Bocian, M., & Nikitas, N. (2021). Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis. Sensors, 21(4), 1239. https://doi.org/10.3390/s21041239






