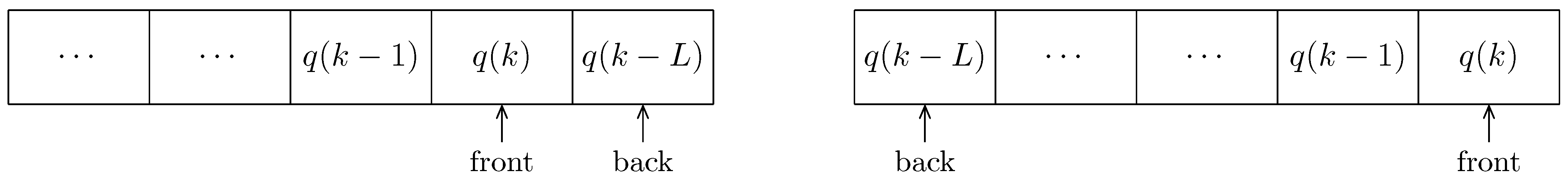Abstract
Broadband adaptive beamformers have been widely used in many areas due to their ability of filtering signals in space domain as well as in frequency domain. However, the space-time array employed in broadband beamformers requires presteering delays to align the signals coming from a specific direction. Because the presteering delays are direction dependent, it is difficult to make precise delays in practice. A common way to eliminate the presteering delays is imposing constraints on the weight vector of the space-time array. However, the structure of the constraint matrix is not taken into account in the existing methods, leading to a computational complexity of when updating the weight vector. In this paper, we describe a new kind of constraint method in time domain that preserves the block diagonal structure of the constraint matrix. Based on this structure, we design an efficient weight vector update algorithm that has a computational complexity of . In addition, the proposed algorithm does not contain matrix operations (only scalar and vector operations are involved), making it easy to be implemented in chips such as FPGA. Moreover, the constraint accuracy of the proposed method is as high as the frequency constraint method when the fractional bandwidth of the signal is smaller than . Numerical experiments show that our method achieves the same performance of the state-of-the-art methods while keeping a simpler algorithm structure and a lower computational cost.
1. Introduction
Beamforming has become a fundamental technique for sensor arrays and received considerable attention in recent decades [1,2,3,4,5]. Besides providing the ability of performing spatial filtering, the broadband beamformers can also control the frequency response in a given direction [6], which makes it a power tool in various areas such as radar, sonar, mobile communications, satellite navigations, and radio astronomy. The space-time adaptive processing is one of the widely used approaches to implement broadband beamforming. An adaptive broadband beamformer based on space-time array was proposed in [7], which uses the least mean square (LMS) algorithm to compute the weight vector of the array. This method has been used in a wide range of applications due to its low computational complexity and good numerical stability. Another commonly used technique for broadband beamforming is the space-frequency adaptive processing [8,9], which splits the frequency band of the incident signal into several narrow subbands and then uses narrowband beamformers to deal with the narrowband signals. The space-frequency processing has a faster convergence rate than space-time processing when the number of taps is large (e.g., hundreds or thousands). Nevertheless, space-frequency beamformer has a larger processing delay than space-time beamformer [10,11]. Therefore, space-time adaptive processing is still the first choice for delay sensitive applications such as satellite navigations [12,13].
To obtain a desired frequency response in the direction of the signal of interest (SOI), constraints should be imposed on the weight vector of the beamformer. Most of these constraints require that the array has been presteered toward the direction of SOI. However, it is difficult to implement precise delays in practice [14,15], especially for the situations that sensor array has to form multiple beams [16,17]. In addition, the presteering errors may cause signal cancellation in the direction of SOI, leading to performance degradation of the beamformer [18,19]. Therefore, it is very important to eliminate the presteering delays in broadband beamformers. A type of convolution constraint method was proposed in [20] to remove the presteering delays. This method has a simple procedure to implement; however, it is computationally expensive. The authors in [21] described another technique to remove the presteering delays, which multiplies the received signal by a matrix whose elements are the inverse Fourier transform of the steering vector. Thus, it is computationally expensive too. By introducing a set of frequency domain constraints (FDC), the authors in [22] developed a simple technique to eliminate the presteering delays, which requires less tapped delay-lines (TDLs) than the convolution constraint method. Moreover, it can incorporate the sensor patterns into the beamforming algorithm and thus can be applied to conformal arrays [23]. The FDC method based on generalized sidelobe canceller (FDC-GSC) was presented in [24], which is mathematically equivalent to FDC but with fewer computations. To further reduce the number of TDLs, infinite impulse response filter can be used [25,26]. However, all of these methods destroy the block diagonal structure of the constraint matrix, making the computational complexity of weight vector update increased from to .
To reduce the computational complexity of weight vector update, we design a new kind of time domain approximate constraint (TDAC) method, which does not require the presteering delays while preserving the block diagonal structure of the constraint matrix. The constraint accuracy of TDAC is as high as the FDC method if the fractional bandwidth is smaller than . This is a reasonable assumption because the fractional bandwidth of most radar and communication systems is smaller than . Moreover, by exploiting the block diagonal structure of the constraint matrix, a new efficient weight vector update algorithm with a complexity of is also developed. In fact, the computations involved in each iteration of the proposed algorithm is only half of that of the conventional Frost algorithm (CFA). Both LMS and normalized LMS (NLMS) algorithms can be used to update the weight vector of the space-time array. We shall study the NLMS-based algorithm in this paper because the one based on LMS can be easily obtained from NLMS.
The rest of this paper is organized as follows. Section 2 reviews the signal model of space-time array and the conventional Frost algorithm. Section 3 describes the details of the proposed method, including algorithm design, geometrical interpretation, and complexity analysis. Numerical simulations are presented in Section 4, followed by conclusions in Section 5.
Notation: We use lowercase letters (a), lowercase boldface letters (), uppercase boldface letters (), and uppercase calligraphy letters () to represent scalars, vectors, matrices and sets, respectively. The superscripts , , , and stand for complex conjugate, transpose, conjugate transpose, orthogonal complement, and inverse, respectively. The symbol ⊗ denotes the Kronecker product, represents the Euclid norm, stands for the mathematical expectation, and means “on the order of”.
2. Space-Time Adaptive Beamformer
This section reviews the signal model of space-time array and the conventional Frost algorithm, including space-time steering vector, frequency-wavenumber response (FWR), and weight vector update methods of Frost algorithm based on LMS and NLMS.
2.1. Signal Model of Space-Time Array
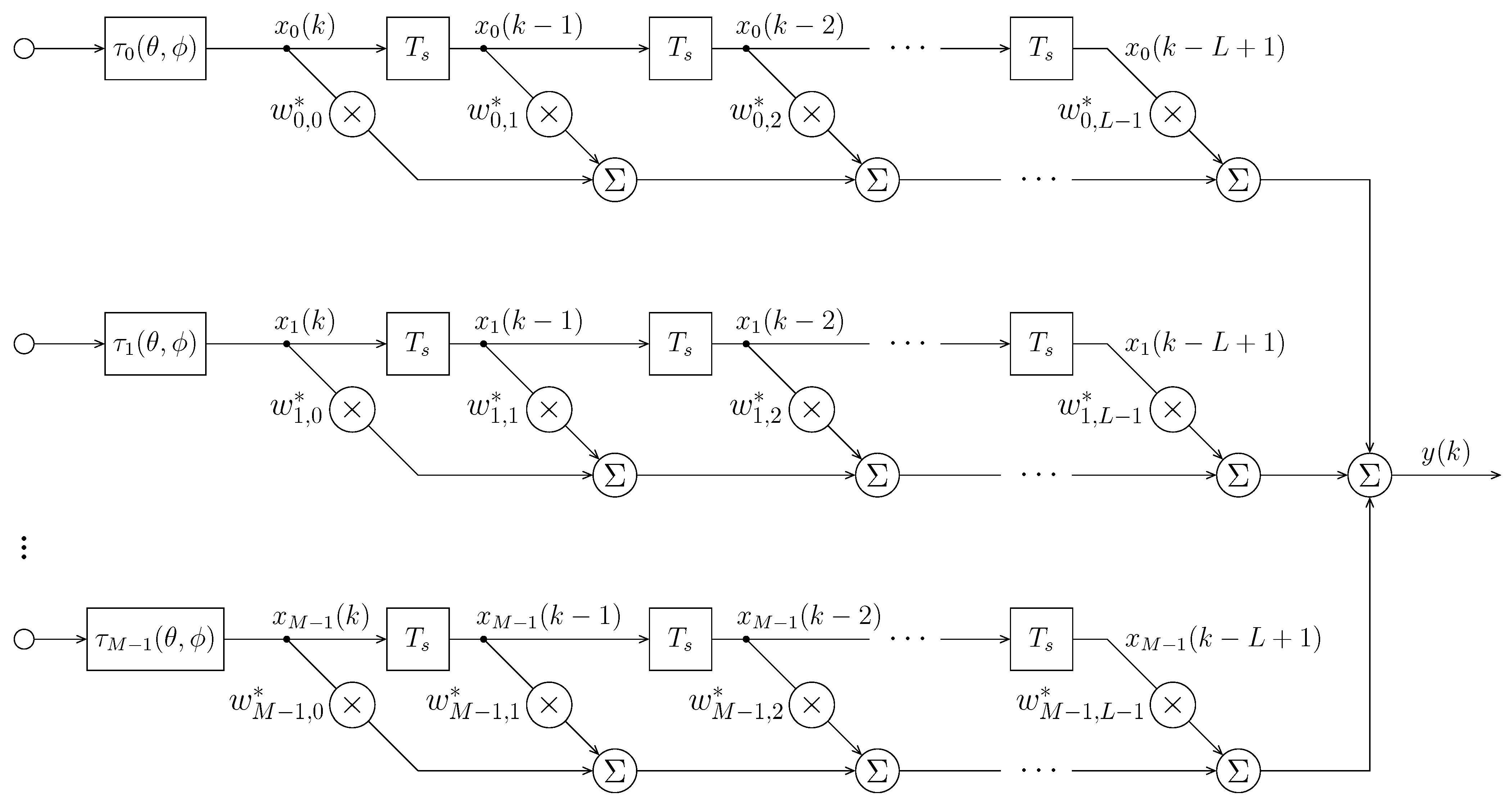
Figure 1 shows a space-time array with M sensors and each sensor is followed by a time delay unit and a finite impulse response (FIR) filter of L taps (the radio frequency chain and the analog-to-digital converter are omitted for simplicity). The aim of presteering delays is to align the signal coming from the direction of SOI so that there is no phase difference among the SOI received by different sensors. The total degrees of freedom of the array, i.e., the number of free weights [6], is , and the baseband signal vector at the kth time instant is given by
where is the signal vector at the lth tap for . Similarly, the weight vector is given by
where is the weight vector at the lth tap.
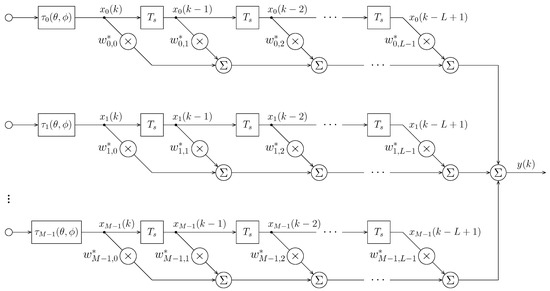
Figure 1.
The structure of a space-time array (see also [7]).
If there are no presteering delays, the FWR of the array for the signal coming from at frequency can be expressed as [27]
where is the wavevector of the impinging signal, is the carrier frequency, is the baseband frequency, c is the speed of light, is the propagation direction, is the position vector of the mth sensor, and is the sampling period of the baseband signal. The steering vector of the space-time array can be expressed as [28]
where
is the temporal steering vector and
is the spatial steering vector.
2.2. The Conventional Frost Algorithm
The linearly constrained minimum variance beamformer is a widely used technique to suppress the interferences while keeping the SOI, which minimizes the output power of the array subject to J linear constraints as follows
where is the space-time covariance matrix of the received signal, is the constraint matrix whose columns are linearly independent and is the gain vector. The solution of (7) is given by [27]
It is not advisable to compute the weight vector by solving the above equation for real-time processing applications, because one has to estimate the covariance matrix and compute the matrix inversion (or solve linear systems of equations). Frost developed an adaptive approach to compute the weight vector based on the LMS algorithm as follows [7]:
where is the step size parameter,
is the quiescent weight vector in the column space of , denoted by , and
is the projection matrix onto the orthogonal complement of , denoted by . The normalized version of (9) is given by [29]
3. The Proposed Method
Although the CFA (9) (or (12)) is simple, it requires the presteering delays. In this section, we first introduce a new kind of constraint for the space-time array, which eliminates the presteering delays and enables the weight vector to be updated efficiently. Then, inspired by [7], we give a geometric interpretation of the proposed algorithm. Finally, the comparison of computational complexity of our method and the existing methods is provided.
3.1. The Approximate Constraints in Time Domain
Suppose that the number of constraints J in (7) is equal to the number of taps L of the array, and let , then the FWR (3) of the space-time array can be expressed as
where is the normalized frequency [30]. To keep the symbols consistent with (7), we define , i.e., . If is independent of , then is equal to the discrete Fourier transform (DFT) of an FIR filter whose lth coefficient is equal to the inner product of and .
Equation (13) shows that the broadband beamformers can perform frequency filtering as well as spatial filtering. If the frequency response in the direction of SOI is determined by an FIR filter with coefficients , we can impose constraints on in the form of . However, because the wavevector depends on baseband frequency , the coefficients in (13) depend on too. Nevertheless, for systems that operate with a small fractional bandwidth, the difference between and is small and can be approximated by . Thus, we obtain the following approximate constraints for the weight vector
The above approximation is reasonable for many practical broadband systems that operate with a fractional bandwidth smaller than , such as radar [28], satellite navigations [12], and wireless communications [31]. The benefit of this approximation is that it allows an efficient implementation of the weight vector update.
The constraints given by (14) can be rewritten as , which takes the same form of the constraint given in (7). The constraint matrix has a block diagonal structure as follows
where is the identity matrix. The main computations of (12) come from the projection operation. Thus, we should derive a simple form for the projection matrix . By using the properties and [32], we have
and
Let
where is the normalized spatial steering vector. Then the projection matrix can be written as
Expressing the projection matrix by an projection matrix is the key point of the efficient algorithm, which will be described in the next subsection.
3.2. An Efficient Weight Vector Update Algorithm
Because is independent of time instant k, only the second term on the right hand side of (12) needs updating. Let
where
Then can be decomposed into two terms as follows
We call the adaptive weight vector because it is updated adaptively according to the input signal vectors .
Since is the projection matrix onto and , we have . Thus,
By using the idempotent property of the projection matrix [33], we have
Hence,
Next we show how to compute and efficiently. Because, as shown in Figure 1, has a time delay structure ,
has a similar time delay structure. It follows from (1) and (19) that
where
Therefore, only needs to be computed at each iteration, which involves complex additions and complex multiplications. Although can be computed by with complex additions and N complex multiplications. However, there exists a more efficient method to compute as follows
where the time delay properties and are used. Since has already been calculated and each term on the right hand side of the above equation is real, there are only M complex additions and M complex multiplications in computing if we store the quantities .
A circular array [34] is employed in our method to store the latest quantities of for , , ⋯, . The circular array, denoted by , is shown in Figure 2, where the position front points at the current quantity and the position back points at the Lth previous quantity . When new data arrives, the circular array overwrites with .

Figure 2.
The circular array that stores for , , ⋯, .
The final description of our algorithm is summarized in Algorithm 1. Please note that there are no matrix operations in our algorithm, which means that the algorithm can be implemented at the level of scalar and vector operations. This feature is very important when the algorithm is implemented in chips such as field programmable gate array (FPGA) and digital signal processor (DSP).
| Algorithm 1: The TDAC algorithm based on NLMS. |
 |
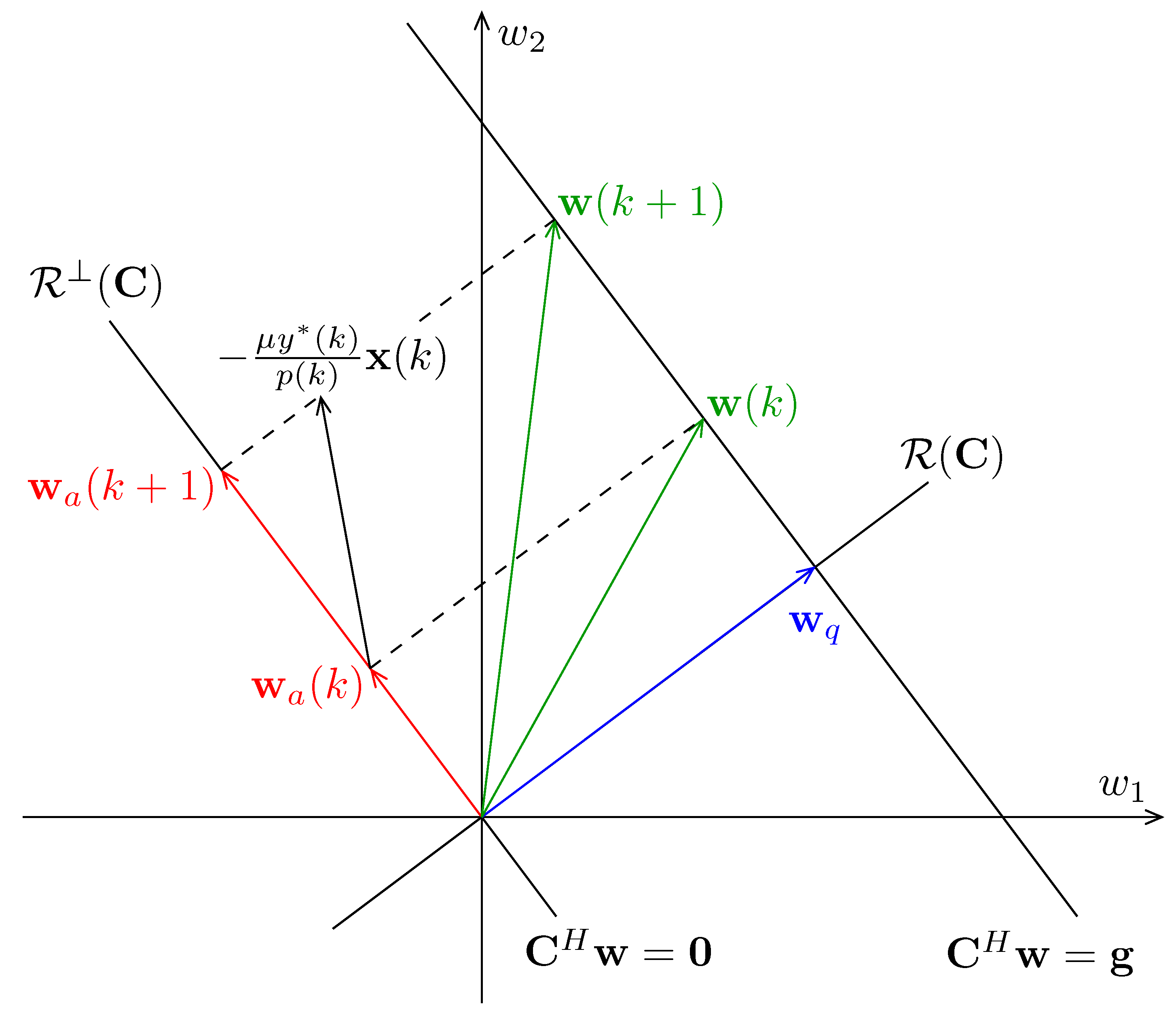
3.3. Geometrical Interpretation
The new weight vector update algorithm has a simple geometrical interpretation as shown in Figure 3, where and define the constraint subspace and the constraint plane, respectively. It follows from (16) that . Thus, it is perpendicular to the constraint subspace . Meanwhile, because satisfies the constraint equation , it terminates on the constraint plane. In addition, as defined by (20), is the projection of onto . Thus, it lies in the constraint subspace.
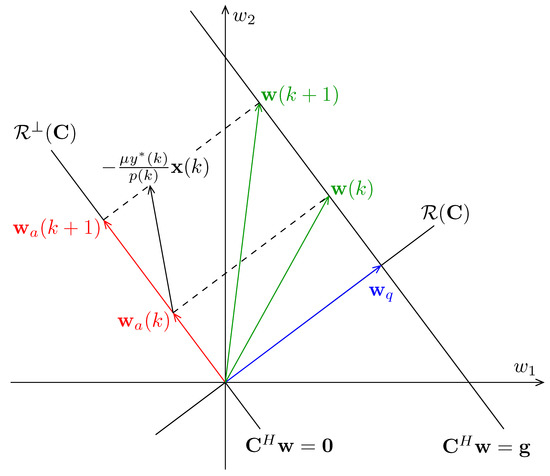
Figure 3.
Geometrical interpretation of the proposed algorithm.
From Algorithm 1 we know that only is updated during the iterations. To minimize the output power at the kth time instant, an increment , based on the NLMS criterion, is added to the adaptive vector . However, this change may move off the constraint subspace. Thus, the projection of the increment is used to update to ensure that lies in the constraint subspace.
3.4. Computational Complexity Analysis
The computations involved in each iteration of CFA, FDC, FDC-GSC, and TDAC, in terms of complex additions and complex multiplications, are shown in Table 1. We see from the table that our method (TDAC) has the least computations, which is even more efficient than CFA. In contrast, FDC and FDC-GSC increase the weight vector update complexity from to .

Table 1.
Computations in each iteration of CFA, DFC, DFC-GSC, and TDAC.
In addition, computing the projection matrix at the initial stage of FDC requires a complexity of , where J is the number of constraint points in frequency band. Similarly, computing the blocking matrix at the initial stage of FDC-GSC requires a complexity of . The convolution constraint method has the same update complexity of FDC. However, it needs DFT operations to form the constraint matrix, leading to a higher complexity than FDC. In contrast to FDC and FDC-GSC, the proposed method only requires N additions and multiplications at the initial stage.
4. Simulation Results
In this section, we present some numerical experiments to compare the performance of the proposed algorithm with other methods. A space-time array is employed in the first experiment. More specifically, a uniform linear array (ULA) located along the z-axis is considered. The array consists of 10 isotropic antennas whose interelement spacing is where is the wavelength corresponding to the carrier frequency. In baseband, each sensor is connected to an FIR filter with 10 TDLs. The distortionless gain vector is set to . One desired signal and two uncorrelated interferences impinge on the array from , and , respectively. Noises are assumed to be spatially and temporally uncorrelated zero-mean Gaussian random processes with equal power. The signal-to-noise ratio (SNR) is 10 dB and the interference-to-noise ratios (INR) are 40 dB and 30 dB respectively. Both the signal and interferences occupy a bandwidth of 100 MHz around the carrier frequency of 1000 MHz, i.e., the fractional bandwidth is . We compare our method (TDAC) with the methods of CFA [7], FDC [22], and FDC-GSC [24]. The NLMS-based update Equation (12) with is used for all of the tested algorithms. For the FDC method, 10 constraint points are uniformly selected in the frequency band.
The performance of broadband beamformer is measured in terms of array output power and signal-to-interference-plus-noise ratio (SINR). The output SINR is defined as
where is the correlation matrix of the desired signal and is the correlation matrix of interferences plus noise. We assume that the power spectral densities of the desired signal and the interferences are flat in the bandwidth of considered. We also assume that the signal, interferences, and noise are statistically independent. Under these assumptions, the correlation between the lth tap after the mth sensor and the pth tap after the qth sensor for the dth impinging wave can be expressed as [35]
where is the power of the dth signal, is the propagation delay of the dth signal at the mth sensor with respect to the origin, and is the bandwidth of the dth signal. For the simulation scenario described above, , , where is the noise power.
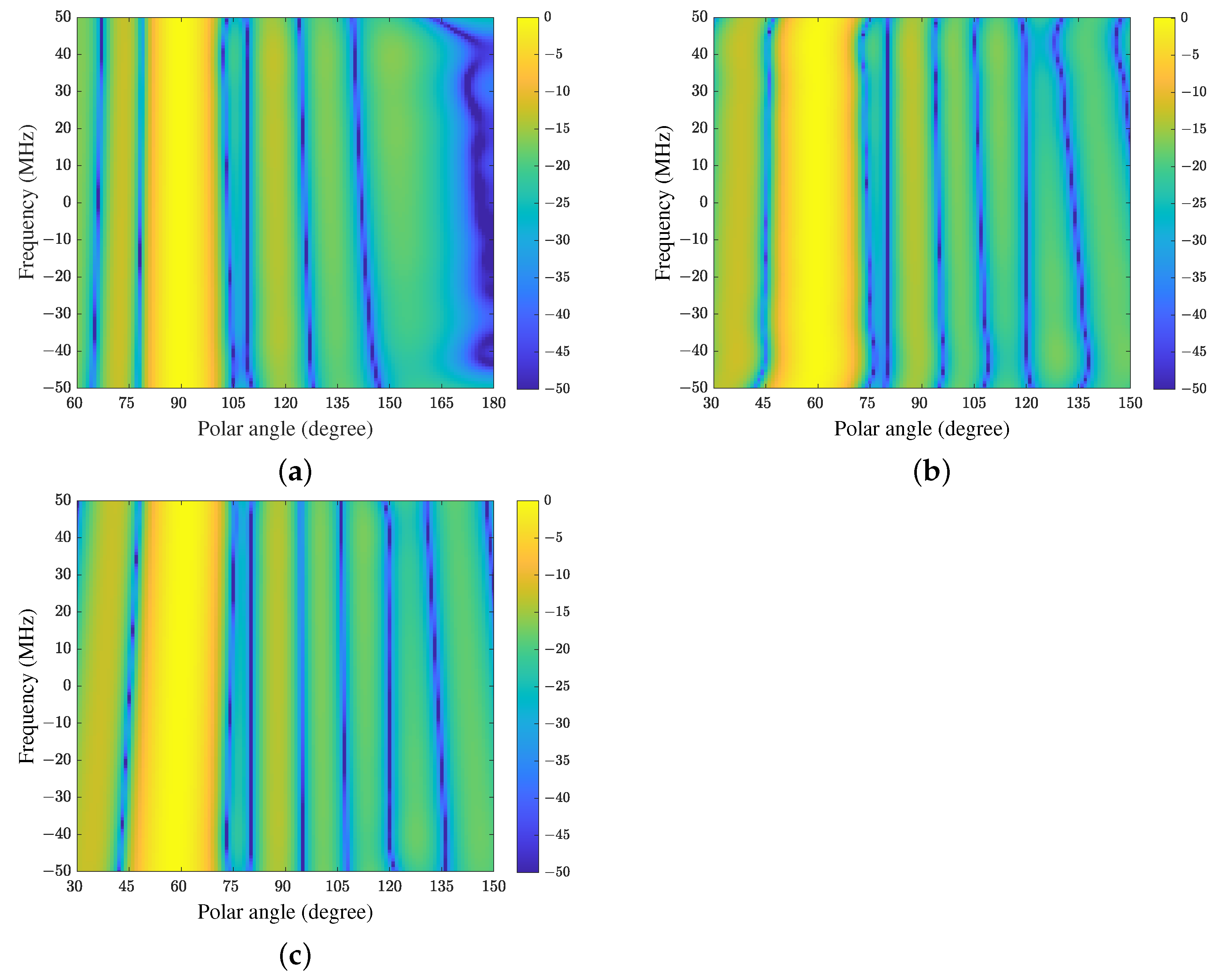
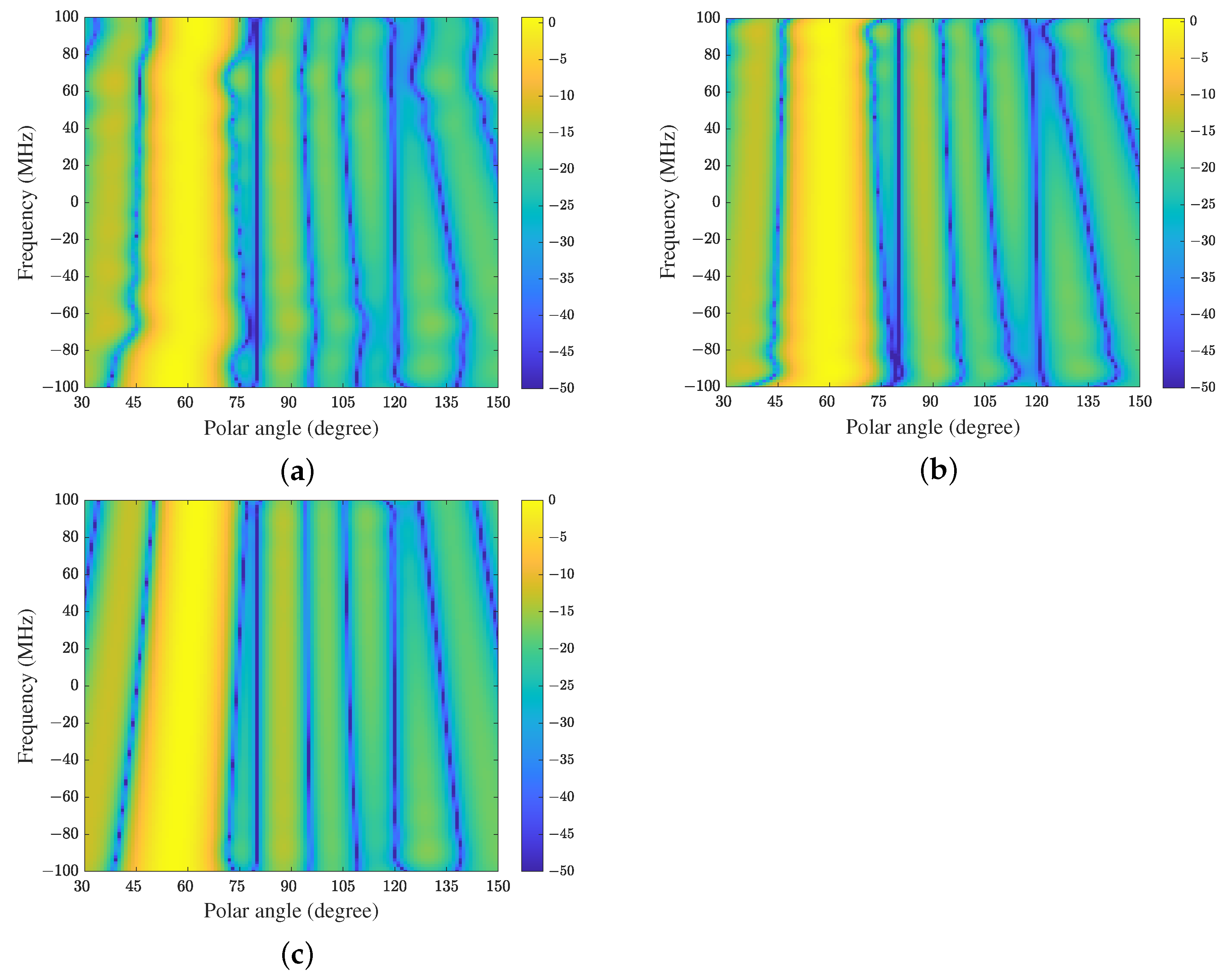
Figure 4 shows the FWRs of CFA, FDC and TDAC when the adaptive algorithms have converged (for ULA located along the z-axis, FWR depends on frequency and polar angle). Because the FWR of FDC-GSC is the same as FDC, it is not shown here. It can be seen that all methods have constant magnitude responses at the constrained direction while placing nulls at the interference directions in the whole frequency band. Because the array is presteered toward the direction of SOI by CFA, the equivalent directions of interferences are also changed. In this example, the equivalent directions of the desired signal and interferences are , and respectively, which can be verified in Figure 4a. In addition, we see from Figure 4b,c that the FWR of TDAC is smoother than that of FDC. Hence TDAC may have better SINR performance than FDC in this experiment due to the better sidelobe structure.
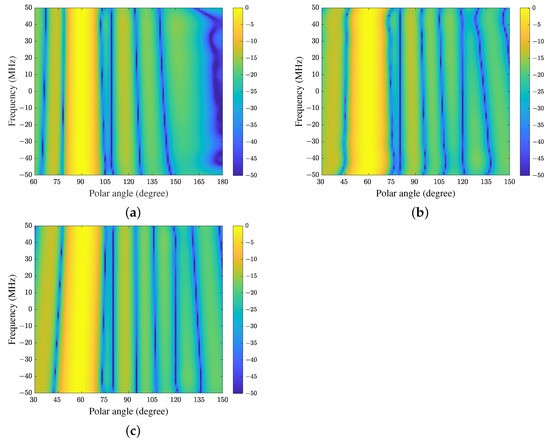
Figure 4.
The FWRs of a space-time array with a fractional bandwidth of : (a) CFA, (b) FDC, and (c) the proposed method (TDAC).
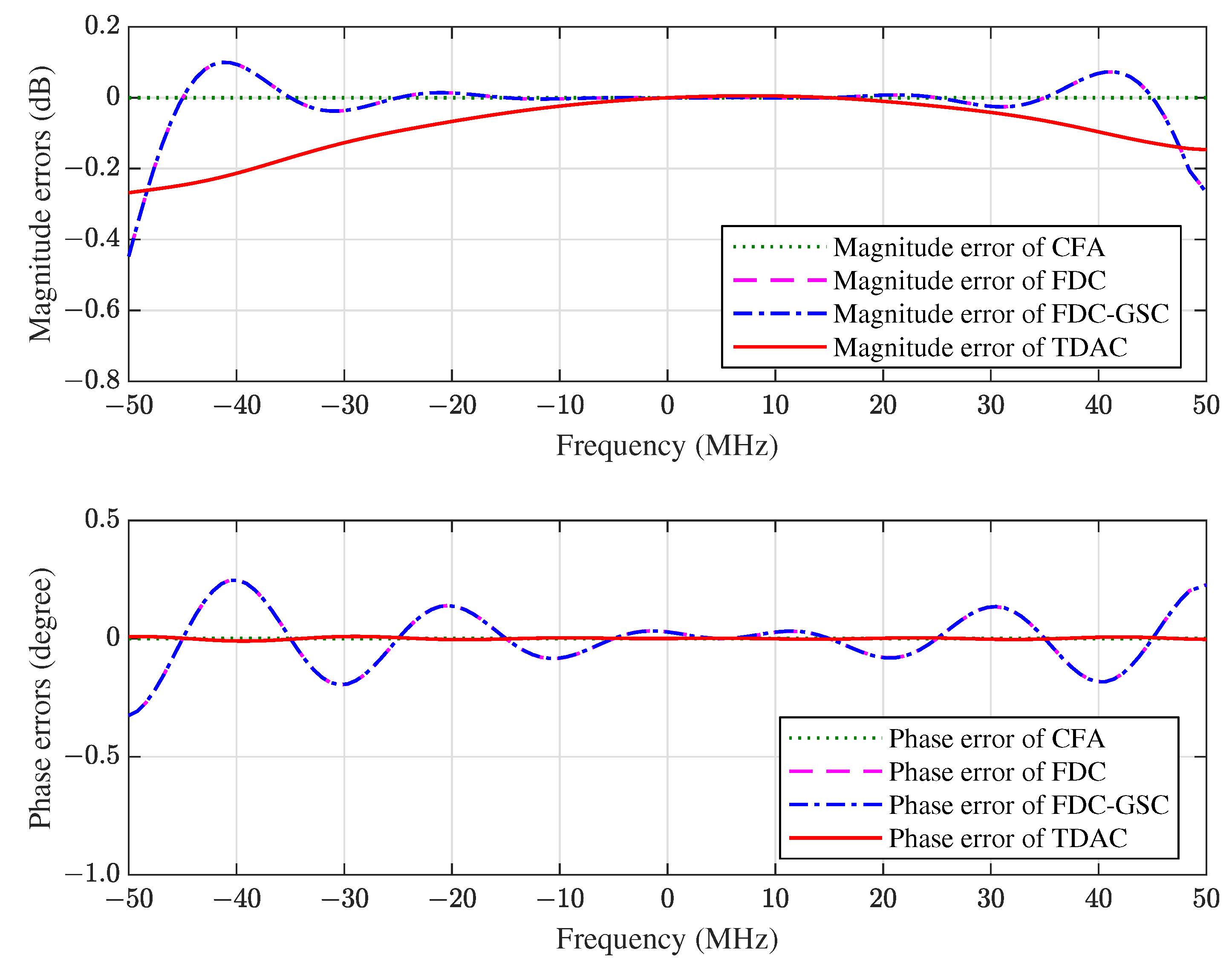
The magnitude and phase errors in the constrained direction of CFA, FDC, FDC-GSC and TDAC are plotted in Figure 5. It can be seen that (i) the constrained response is equal to the distortionless response when the array is precisely presteered by CFA; (ii) FDC and FDC-GSC have the same frequency response since they are equivalent; (iii) there exist ripples in the frequency response of FDC, this is because only 10 frequency points are constrained by FDC and the responses between these constrained points are not guaranteed; (iv) both FDC and TDAC provide good approximations to the desired frequency response; and (v) TDAC has a smaller phase error than FDC.
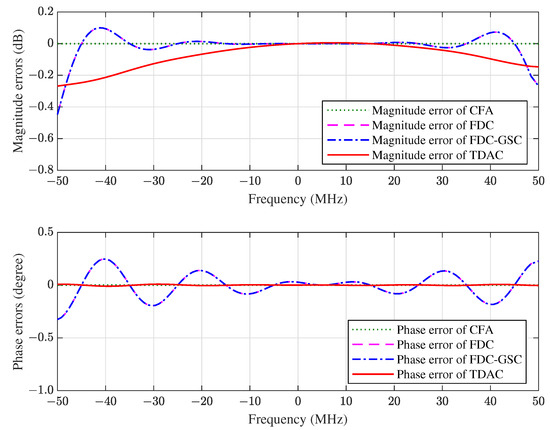
Figure 5.
The magnitude and phase errors of the space-time array in the direction of SOI.
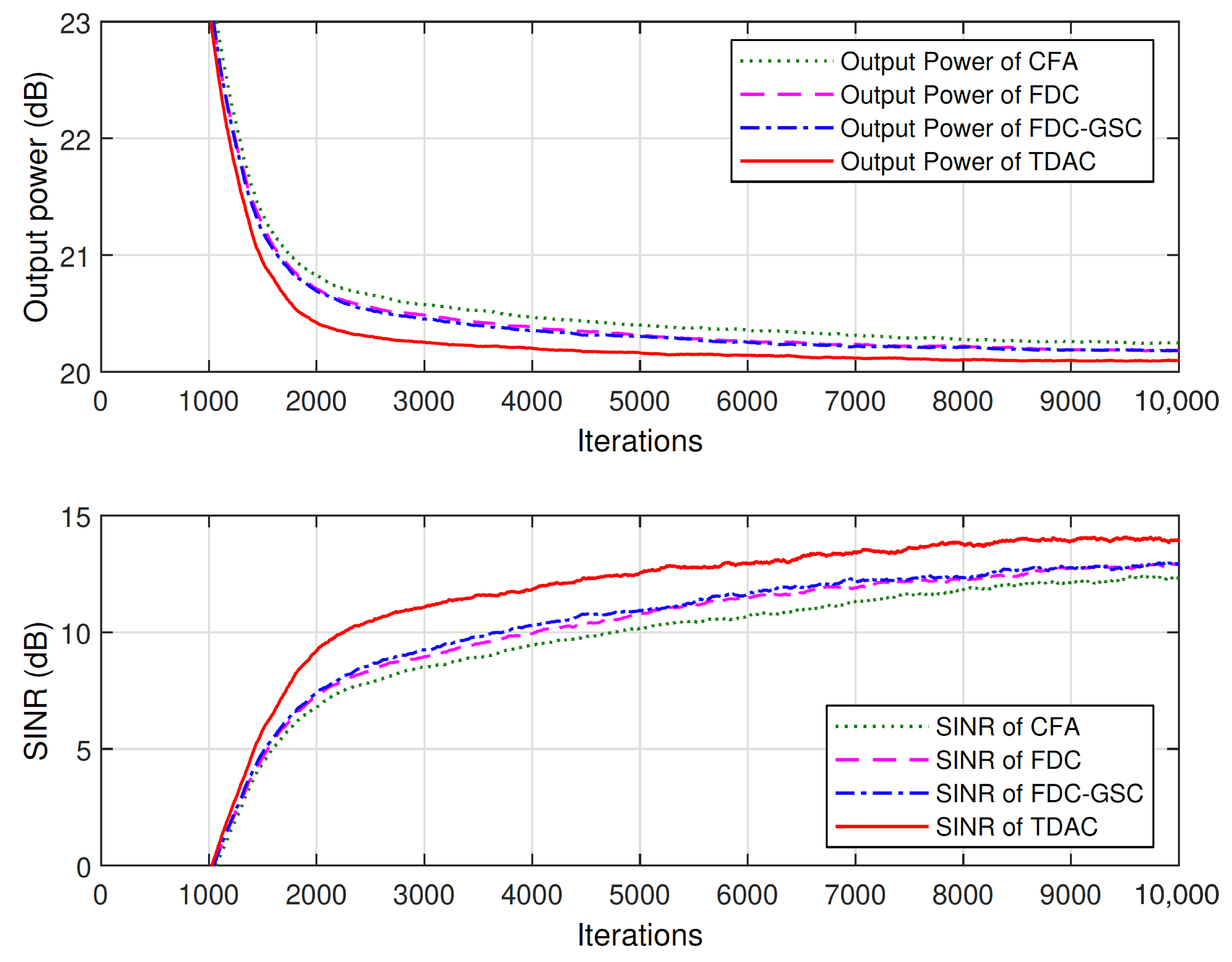
Figure 6 shows the learning curves of the output power and SINR of different methods averaged over 100 independent trials. As shown in Figure 6, the four tested methods have the same convergence rate, but our method has the best steady-state SINR performance. The reason CFA has a smaller SINR than other methods is that when the array is presteered toward the direction of SOI, the directions of interferences are also changed. Thus, the array faces a different interference environment, leading to different SINR performance. Although FDC can impose accurate constraints in frequency domain, the frequency responses between the constrained points are not guaranteed, leading to ripples in frequency band as shown in Figure 5. Therefore, similar to the proposed method that approximates the FWR in time domain, FDC is also a type of approximate method that approximates the FWR in frequency domain.
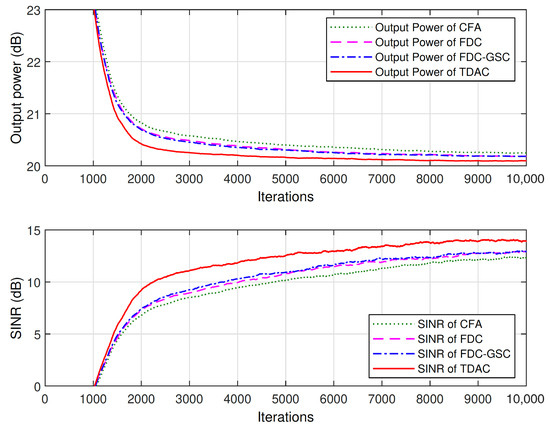
Figure 6.
The output power and SINR of the space-time array averaged over 100 trials.
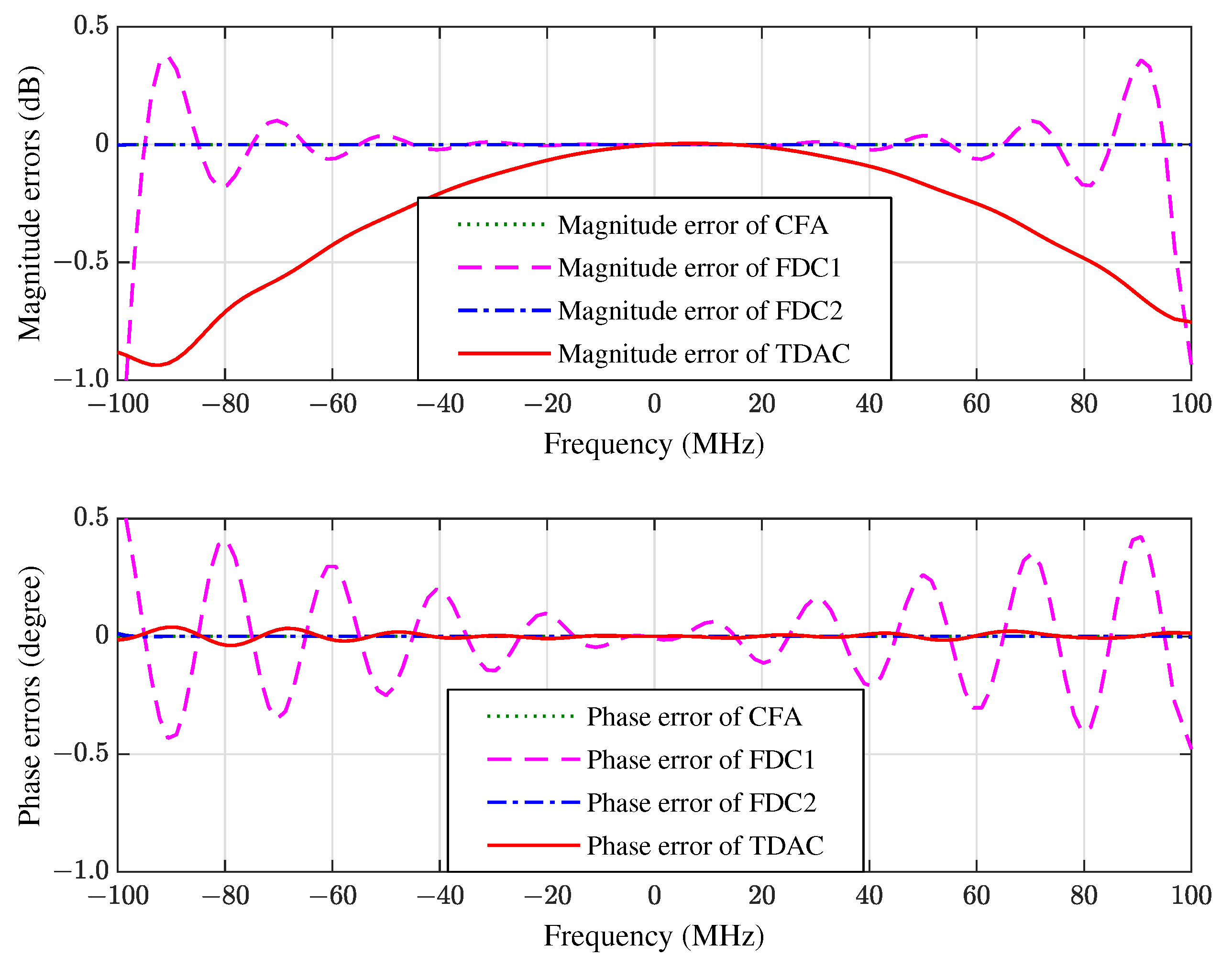
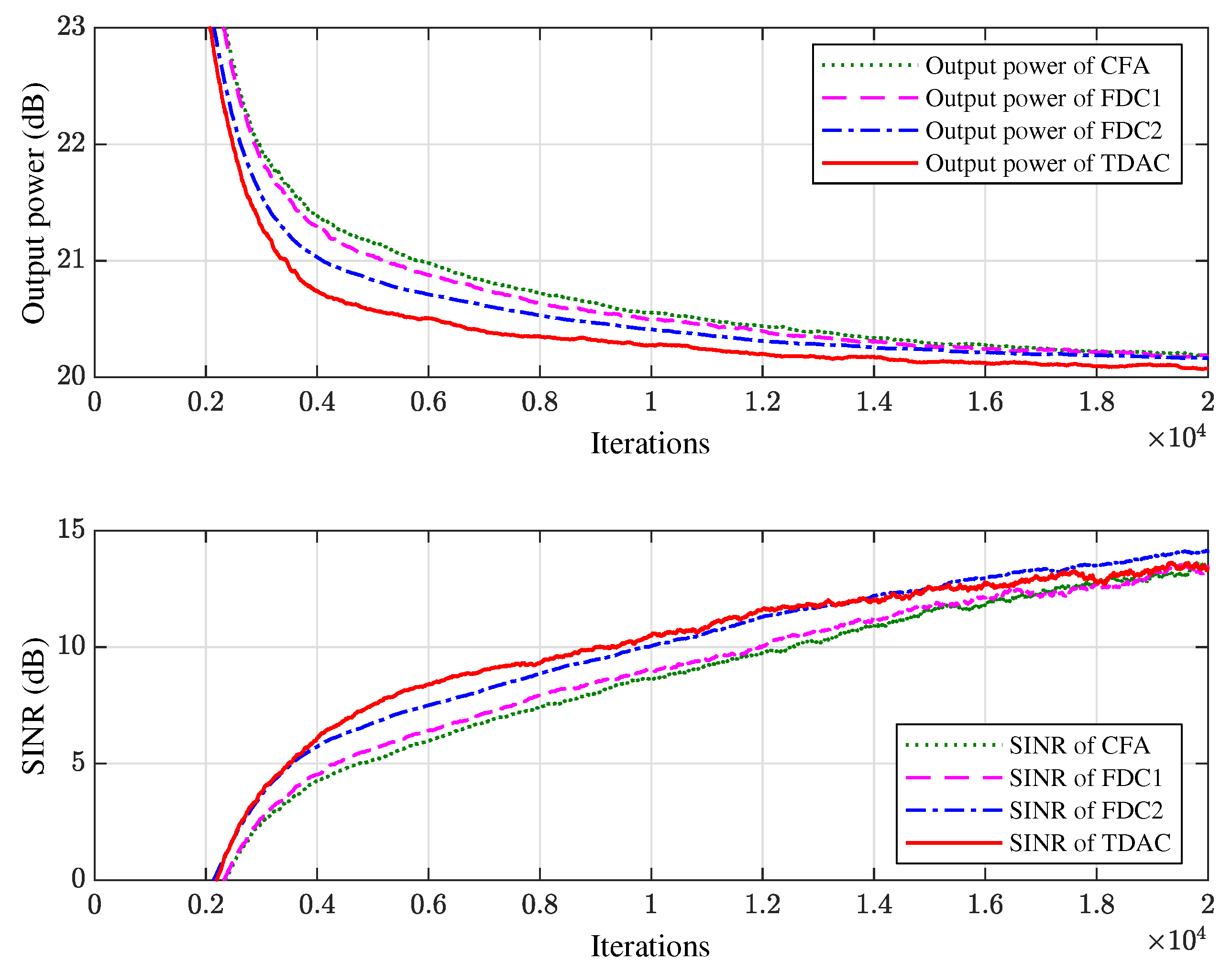
In the second experiment we change the bandwidth from 100 MHz to 200 MHz while keeping the carrier frequency fixed at 1000 MHz, i.e., the fractional bandwidth is . We also change the length of FIR filter from 10 to 20, i.e., we use a space-time array. The proposed algorithm is compared with the FDC methods with 20 constraint points (denoted by FDC1) and 30 constraint points (denoted by FDC2) respectively. The simulation results of FWRs, constraint errors, and learning curves are shown in Figure 7, Figure 8 and Figure 9, respectively.
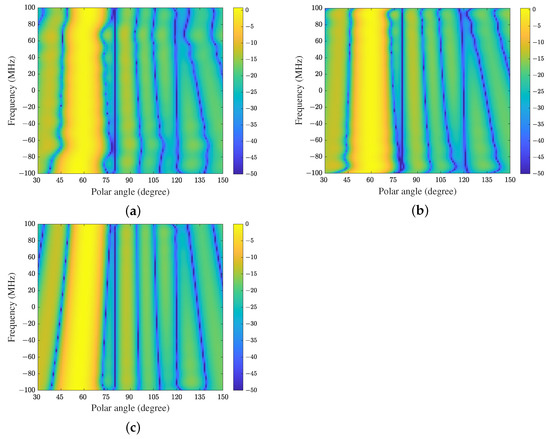
Figure 7.
The FWRs of a space-time array with a fractional bandwidth of : (a) FDC with 20 constraint points (FDC1), (b) FDC with 30 constraint points (FDC2), and (c) the proposed method.
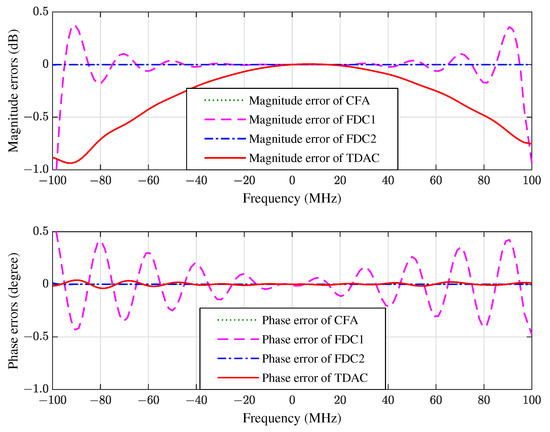
Figure 8.
The magnitude and phase errors of the space-time array in the direction of SOI.
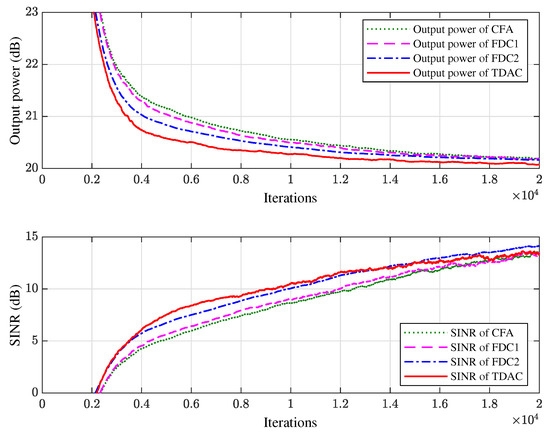
Figure 9.
The output power and SINR of the space-time array averaged over 100 trials.
5. Conclusions
An efficient implementation of the broadband adaptive beamformer without presteering delays was studied in this paper. A new kind of approximate constraint in time domain has been proposed to eliminate the presteering delays of the space-time array. In addition, a new weight vector update algorithm was developed by using the block diagonal structure of the constraint matrix, leading to a computational complexity of in each iteration. In contrast, the computational complexity of the frequency constraint methods is in each iteration. Moreover, the new algorithm does not contain matrix operations and can be implemented at the level of scalar and vector operations. This feature is very important for real-time applications, in which the algorithms should be implemented in chips such as FPGA and DSP. Numerical experiments shown that the approximate accuracy of the proposed method is as high as the frequency constraint method for systems with a fractional bandwidth smaller than , while our method has a simpler algorithm structure and a lower computational cost than the existing methods.
Author Contributions
Conceptualization, M.Z., X.W. and A.Z.; methodology, M.Z. and X.W.; software and validation, M.Z. and X.W.; writing–original draft preparation, M.Z.; writing–review and editing, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China grant 61801368 and in part by the China Postdoctoral Science Foundation grant 2018M640990.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Godara, L.C. Application of antenna arrays to mobile communications, part II: Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]
- Fante, R.L.; Vaccaro, J. Wideband cancellation of interference in a GPS receive array. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 549–567. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Fa, R. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity. IET Signal Proc. 2016, 10, 150–161. [Google Scholar] [CrossRef]
- Felici-Castell, S.; Navarro, E.A.; Pérez-Solano, J.J.; Segura-García, J.; García-Pineda, M. Practical considerations in the implementation of collaborative beamforming on wireless sensor networks. Sensors 2017, 17, 237. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Al-Rizzo, H. Beamforming optimization in internet of things applications using robust swarm algorithm in conjunction with connectable and collaborative sensors. Sensors 2020, 20, 2048. [Google Scholar] [CrossRef] [PubMed]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE Aerosp. Electron. Syst. Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Frost, O.L. An algorithm for linearly constrained adaptive array processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Chen, Y.H.; Fang, H.D. Frequency-domain implementation of Griffiths-Jim adaptive beamformer. J. Acoust. Soc. Am. 1992, 91, 3354–3366. [Google Scholar] [CrossRef]
- Liu, W.; Langley, R.J. An adaptive wideband beamforming structure with combined subband decomposition. IEEE Trans. Antennas Propag. 2009, 57, 2204–2207. [Google Scholar] [CrossRef]
- Boroujeny, B.F.; Jahromi, M.R.S. Analysis of the frequency-domain block LMS algorithm. IEEE Trans. Signal Process. 2000, 48, 2332–2342. [Google Scholar] [CrossRef]
- Valero, M.L.; Mabande, E.; Habets, A.P. An alternative complexity reduction method for partitioned-block frequency-domain adaptive filters. IEEE Signal Process Lett. 2016, 23, 668–672. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS/GNSS, Principles and Applications, 3rd ed.; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Martin, A.; Parry, M.; Soundy, A.W.; Panckhurst, B.J.; Brown, P.; Molteno, T.C.; Schumayer, D. Improving real-time position estimation using correlated noise models. Sensors 2020, 20, 5913. [Google Scholar] [CrossRef]
- Guo, W.; Yan, Y.; Jia, M.; Wu, X.; Tang, C. Cascaded interpolation-filter-decimation algorithm without additional delay. IET Signal Proc. 2017, 11, 554–565. [Google Scholar] [CrossRef]
- Liu, X.; Kolpatzeck, K.; Häring, L.; Balzer, J.C.; Czylwik, A. Wideband beam steering concept for terahertz time-domain spectroscopy: Theoretical considerations. Sensors 2020, 20, 5568. [Google Scholar] [CrossRef]
- De Lorenzo, D.S.; Sherman, C.L.; Enge, P.K.; Rife, J. Calibrating adaptive antenna arrays for high-integrity GPS. GPS Solut. 2011, 16, 221–230. [Google Scholar] [CrossRef]
- Song, Y.; Zhu, Y.; Nan, T.; Hou, J.; Du, S.; Song, S. Accelerating faceting wide-field imaging algorithm with FPGA for SKA radio telescope as a vast sensor array. Sensors 2020, 20, 4070. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, A.X.; Yang, Q.Q. Robust adaptive beamforming based on conjugate gradient algorithms. IEEE Trans. Signal Process. 2016, 64, 6046–6057. [Google Scholar] [CrossRef]
- Zhang, B.; Ma, H.; Sun, X.L.; Tan, Q.; Pan, H. Robust anti-jamming method for high dynamic global positioning system receiver. IET Signal Proc. 2016, 10, 342–350. [Google Scholar] [CrossRef]
- Godara, L.C.; Chan, K.S. Convolution constraints for broadband antenna arrays. IEEE Trans. Antennas Propag. 2007, 55, 3146–3154. [Google Scholar] [CrossRef]
- Godara, L.C.; Jahromi, M.R.S. Presteering broadband antenna arrays without using steering delays. In Proceedings of the IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 2562–2567. [Google Scholar]
- Ebrahimi, R.; Seydnejad, S.R. Elimination of pre-steering delays in space-time broadband beamforming using frequency domain constraints. IEEE Commun. Lett. 2013, 17, 769–772. [Google Scholar] [CrossRef]
- Rasekh, M.; Seydnejad, S.R. Design of an adaptive wideband beamforming algorithm for conformal arrays. IEEE Commun. Lett. 2014, 18, 1955–1958. [Google Scholar] [CrossRef]
- Wu, K.; Su, T.; Habets, A.P. Design of generalised sidelobe canceller-based adaptive wideband beamformer without pre-steering delays. Electron. Lett. 2016, 52, 177–179. [Google Scholar] [CrossRef]
- Duan, H.; Ng, B.P.; See, C.M.S.; Fang, J. Broadband beamforming using TDL-form IIR filters. IEEE Trans. Signal Process. 2007, 55, 990–1002. [Google Scholar] [CrossRef]
- Seydnejad, S.R.; Ebrahimi, R. Broadband beamforming using Laguerre filters. Signal Process. 2012, 92, 1093–1100. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- De Campos, M.L.R.; Werner, S.; Apolinário, J.A. Constrained adaptation algorithms employing householder transformation. IEEE Trans. Signal Process. 2002, 50, 2087–2095. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sidiropoulos, N.D.; Lathauwer, L.D.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Meyer, C.D. Matrix Analysis and Applied Linear Algebra; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Weiss, M.A. Data Structures and Algorithm Analysis in C++, 4th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Zhang, M.; Zhang, A.X.; Li, J.X. Fast and accurate rank selection methods for multistage Wiener filter. IEEE Trans. Signal Process. 2016, 64, 973–984. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).