Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals
Abstract
1. Introduction
2. Characteristics of AE Signals during Grinding Brittle Materials
3. Wheel’s Life Cycle Experiments
3.1. Experimental Instruments
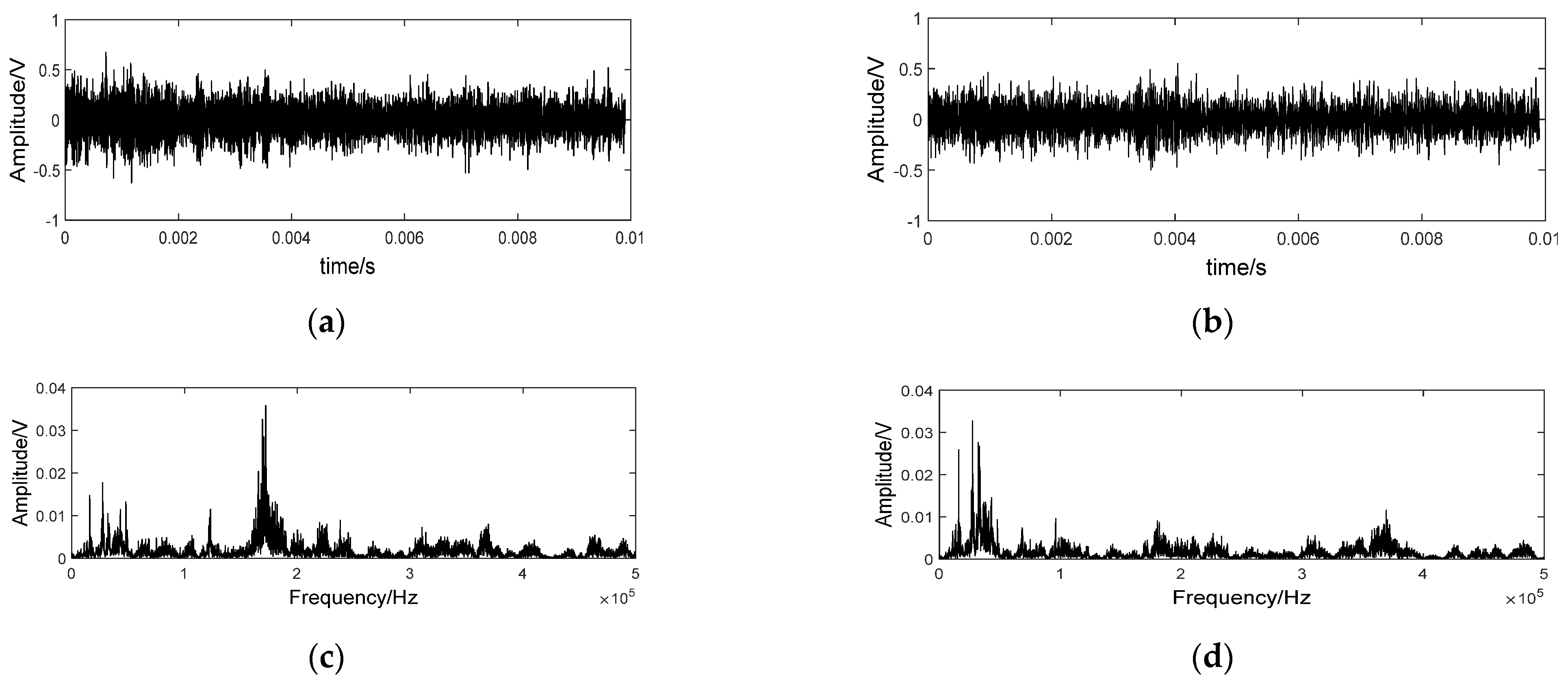
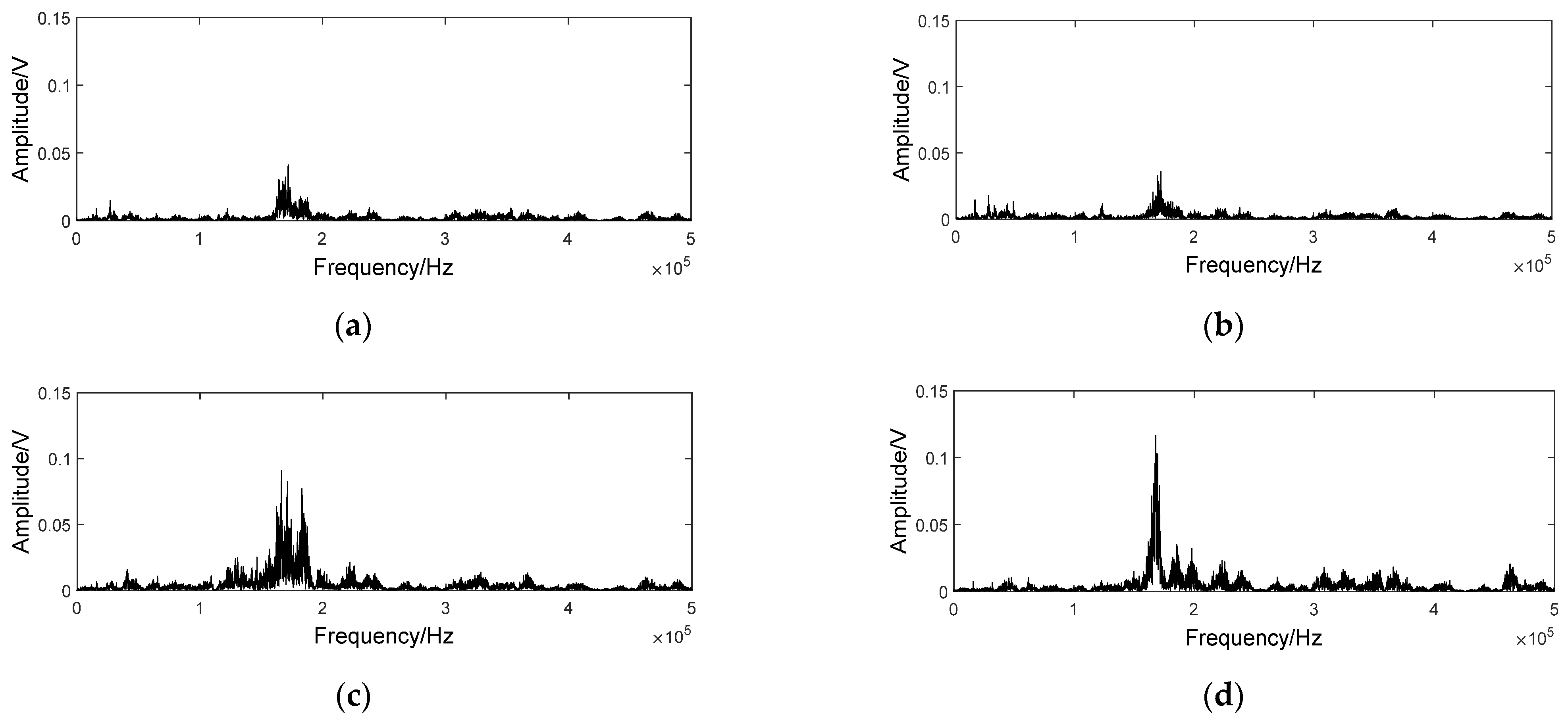
3.2. Basic Analysis of AE Signals
4. Wheel State Classification Based on Original AE Time Waveform
4.1. CNN Model of Wheel State Classification
4.2. Multi-Class Classification of Wheel State Based on CNN
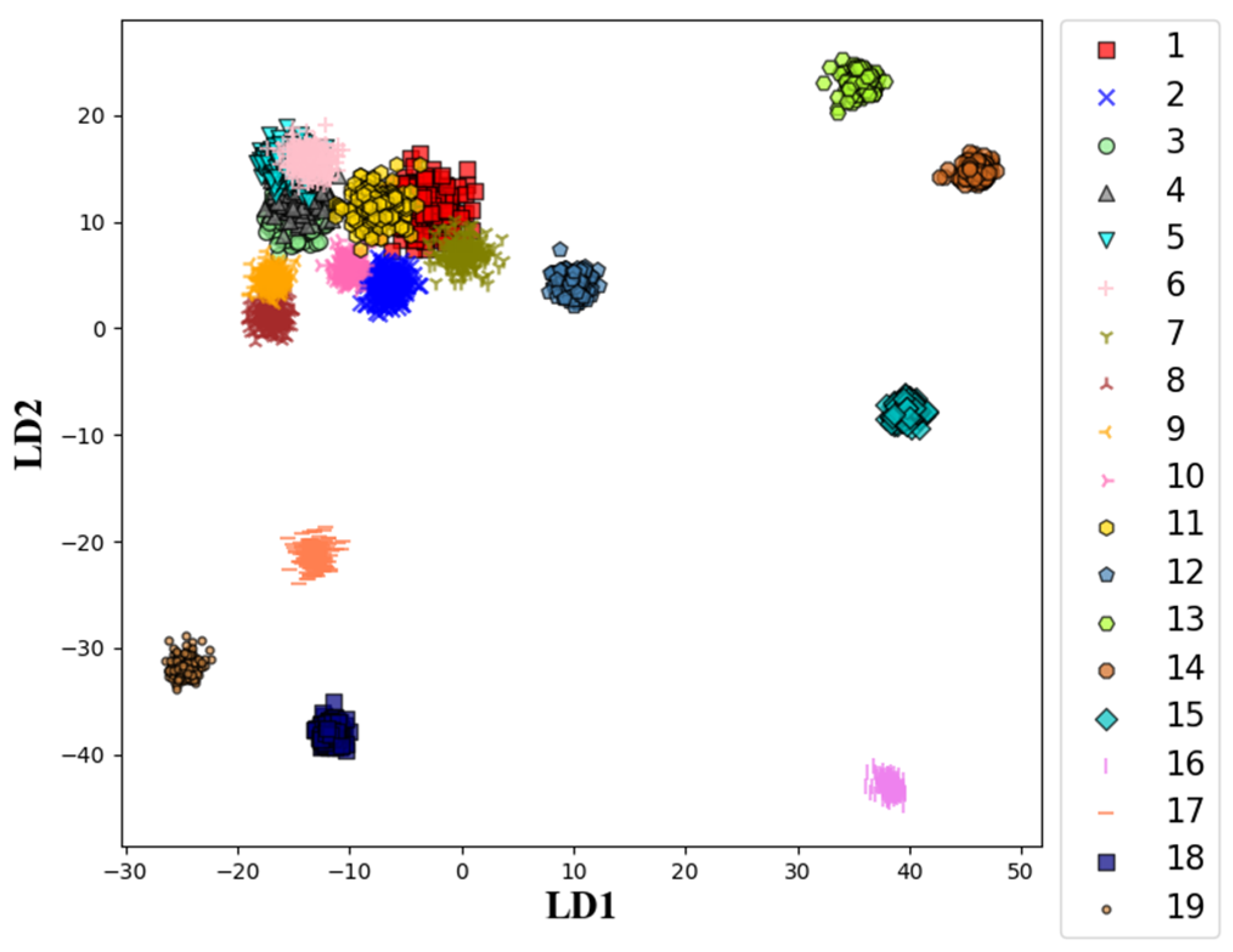
4.3. Visualization and Analysis of Convolution Output
5. LSTM for Wheel State Classification
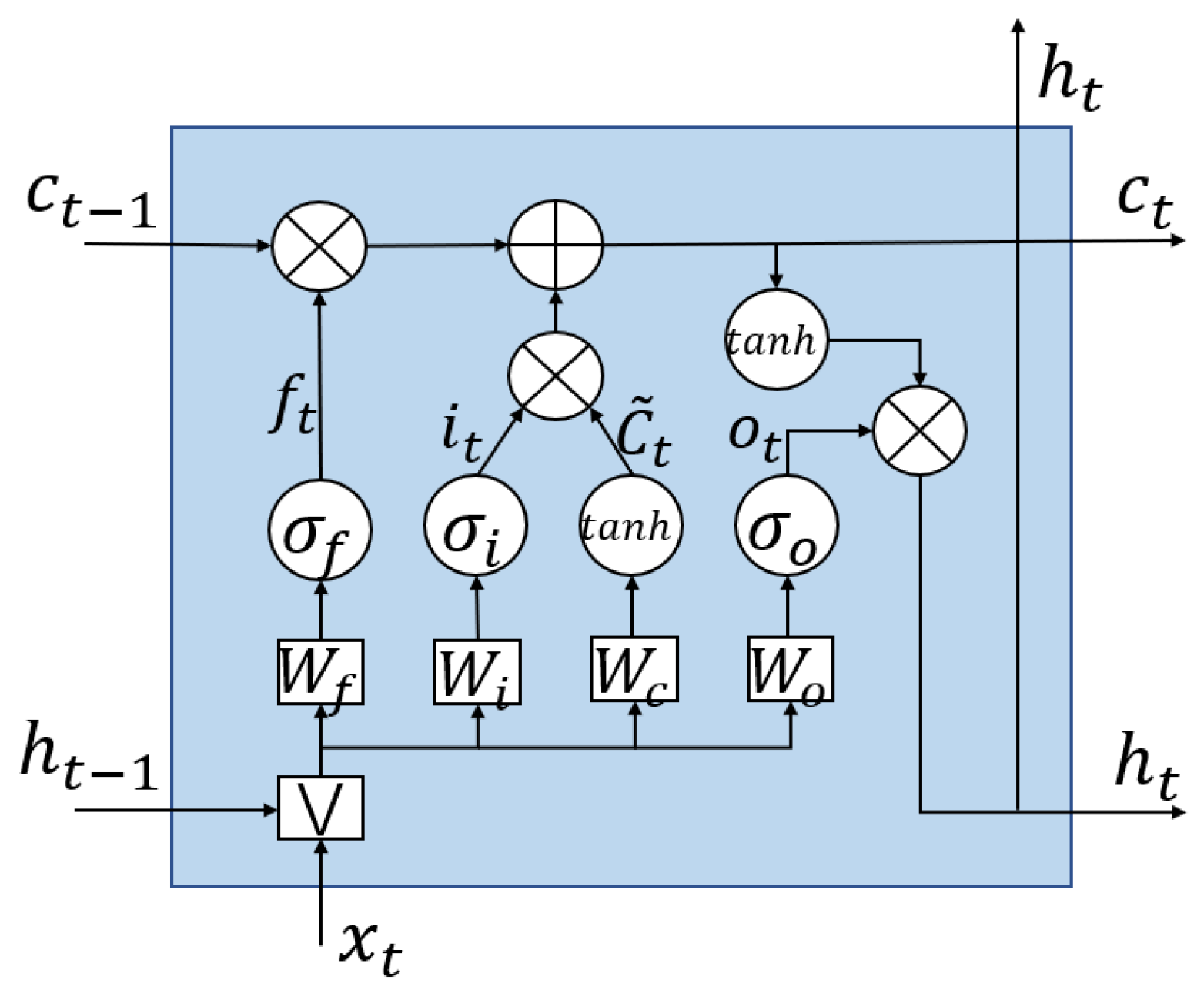
5.1. Basic Principle of LSTM
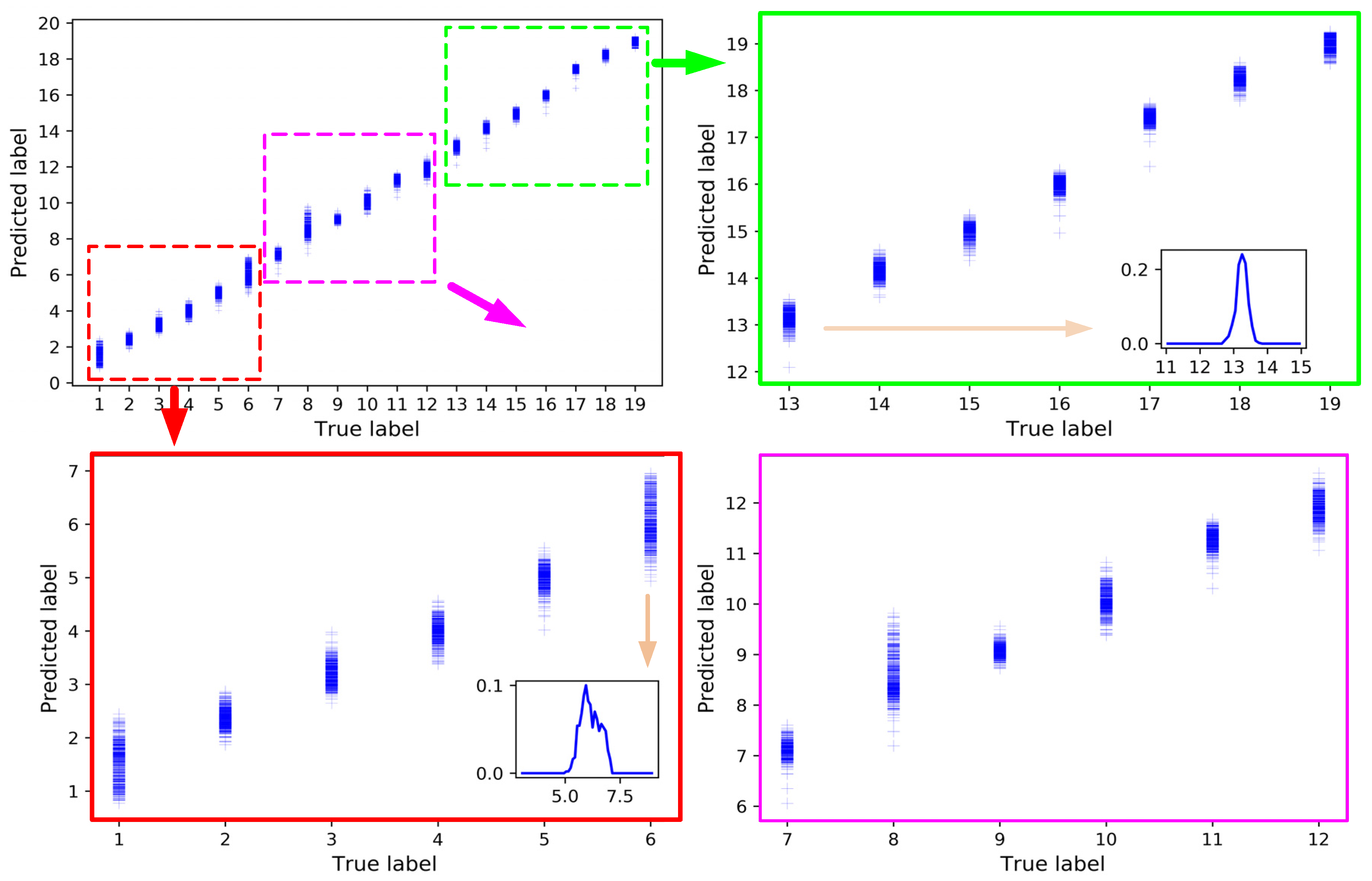
5.2. Regression Analysis of Wheel State Based on LSTM
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AE | acoustic emission |
| b-AE | burst-type AE |
| c-AE | continuous-type AE |
| CNN | convolution neural network |
| LSTM | long short-term memory |
| AE signal | |
| frequency factor | |
| Fourier transform of (the positive-frequency part) | |
| the base of natural logarithms | |
| the delta function | |
| the unit step signal | |
| the damping factor | |
| the amplitude of b-AE | |
| the output of LSTM cells | |
| the internal state of LSTM cells | |
| the input of LSTM cells | |
| the output of the Sigmoid gate of forgetting | |
| the output of the Sigmoid gate of input | |
| the output of the Sigmoid gate of output | |
| the output of the tanh gate | |
| the bias parameter of the Sigmoid gate of forgetting | |
| the bias parameter of the Sigmoid gate of input | |
| the bias parameter of the tanh gate of the LSTM cell | |
| the bias parameter of the Sigmoid gate of output | |
| the forgetting weight matrix | |
| the input weight matrix | |
| the output weight matrix | |
| the state weight matrix of the LSTM cell | |
| the Sigmoid function | |
| the Sigmoid gate of forgetting | |
| the Sigmoid gate of input | |
| the Sigmoid gate of output |
References
- Wegener, K.; Hoffmeister, H.W.; Karpuschewski, B.; Kuster, F.; Hahmann, W.C.; Rabiey, M. Conditioning and monitoring of grinding wheels. CIRP Ann. Manuf. Technol. 2011, 60, 757–777. [Google Scholar] [CrossRef]
- Morgan, M.N.; Cai, R. Design and implementation of an intelligent grinding assistant system. Int. J. Abrasive Technol. 2007, 1, 106–135. [Google Scholar] [CrossRef]
- Liang, S.Y.; Hecker, R.L.; Landers, R.G. Machining Process Monitoring and Control: The State-of-the-Art. J. Manuf. Sci. Eng. 2004, 126, 297–310. [Google Scholar] [CrossRef]
- Kuntolu, M.; Aslan, A.; Pimenov, D.Y.; Usca, Ü.A.; Salur, E.; Gupta, M.K.; Mikolajczyk, T.; Giasin, K.; Kapłonek, W.; Sharma, S. A Review of Indirect Tool Condition Monitoring Systems and Decision-Making Methods in Turning: Critical Analysis and Trends. Sensors 2021, 21, 108. [Google Scholar] [CrossRef] [PubMed]
- Inasaki, I. Application of Acoustic Emission Sensor for Monitoring Machining Processes. Ultrason 1998, 36, 273–281. [Google Scholar] [CrossRef]
- Lee, S.H. Analysis of ductile mode and brittle transition of AFM nanomachining of silicon. Int. J. Mach. Tools Manuf. 2012, 61, 71–79. [Google Scholar] [CrossRef]
- Liao, T.W.; Tang, F.M.; Qu, J.; Blau, P.J. Grinding wheel condition monitoring with boosted minimum distance classifiers. Mech. Syst. Signal Process. 2008, 22, 217–232. [Google Scholar] [CrossRef]
- Alexandre, F.A.; Lopes, W.N.; Dotto, F.R.L.; Ferreira, F.I.; Aguiar, P.R.; Bianchi, E.C.; Lopes, J.C. Tool condition monitoring of aluminum oxide grinding wheel using AE and fuzzy model. Int. J. Adv. Manuf. Technol. 2018, 96, 67–79. [Google Scholar] [CrossRef]
- Alexandre, F.A.; Lopes, J.C.; Fernandes, L.D.M.; Ribeiro, F.S.F.; Fernandez, B.O.; De Angelo Sanchez, L.E.; De Oliveira, R.F.M.; De Mello, H.J.; Aguiar, P.O.; Bianchi, E.C. Depth of dressing optimization in CBN wheels of different friabilities using acoustic emission (AE) technique. Int. J. Adv. Manuf. Technol. 2020, 106, 5225–5240. [Google Scholar] [CrossRef]
- Hassan, M.; Sadek, A.; Damir, A.; Attia, M.H.; Thomson, V. A novel approach for real-time prediction and prevention of tool chipping in intermittent turning machining. CIRP Ann. Manuf. Technol. 2018, 67, 41–44. [Google Scholar] [CrossRef]
- Bhaskaran, J.; Murugan, M.; Balashanmugam, N.; Chellamalai, M. Monitoring of hard turning using acoustic emission signal. J. Mech. Sci. Technol. 2012, 26, 609–615. [Google Scholar] [CrossRef]
- Sutowski, P.; Plichta, S. An investigation of the grinding wheel wear with the use of root-mean-square value of acoustic emission. Arch. Civ. Mech. Eng. 2006, 6, 87–98. [Google Scholar] [CrossRef]
- Stephenson, D.J.; Sun, X.; Zervos, C. A study on ELID ultra precision grinding of optical glass with acoustic emission. Int. J. Mach. Tools Manuf. 2006, 46, 1053–1063. [Google Scholar] [CrossRef]
- Aguiar, P.R.; Serni, P.J.A.; Dotto, F.R.L.; Bianchi, E.C. In-process grinding monitoring through acoustic emission. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 118–124. [Google Scholar] [CrossRef]
- Mokbel, A.A.; Maksoud, T.M.A. Monitoring of the condition of diamond grinding wheels using acoustic emission technique. J. Mater. Process. Technol. 2000, 101, 292–297. [Google Scholar] [CrossRef]
- Liao, T.W.; Ting, C.F.; Blau, P.J. A wavelet-based methodology for grinding wheel condition monitoring. Int. J. Mach. Tools Manuf. 2007, 47, 580–592. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, Z.; Xie, C.; Huang, Y. Application of Hilbert–Huang Transform to acoustic emission signal for burn feature extraction in surface grinding process. Measurement 2014, 47, 14–21. [Google Scholar] [CrossRef]
- Liao, T.W. Feature extraction and selection from acoustic emission signals with an application in grinding wheel condition monitoring. Eng. Appl. Artif. Intell. 2010, 23, 74–84. [Google Scholar] [CrossRef]
- Lv, L.S.; Deng, Z.H.; Liu, T.; Li, Z.Y.; Liu, W. Intelligent technology in grinding process driven by data: A review—ScienceDirect. J. Manuf. Process. 2020, 58, 1039–1051. [Google Scholar] [CrossRef]
- Lezanski, P. An intelligent system for grinding wheel condition monitoring. J. Mater. Process. Technol. 2001, 109, 258–263. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, Z. Grinding wheel wear monitoring based on wavelet analysis and support vector machine. Int. J. Adv. Manuf. Technol. 2012, 62, 107–121. [Google Scholar] [CrossRef]
- Nakai, M.E.; Aguiar, P.R.; Guillardi, H.J.; Bianchi, E.C.; Spatti, D.H.; D’Addona, D.M. Evaluation of neural models applied to the estimation of tool wear in the grinding of advanced ceramics. Expert Syst. Appl. 2015, 42, 7026–7035. [Google Scholar] [CrossRef]
- Pandiyan, V.; Caesarendra, W.; Tjahjowidodo, T.; Tan, H.K. In-process tool condition monitoring in compliant abrasive belt grinding process using support vector machine and genetic algorithm. J. Manuf. Process. 2018, 31, 199–213. [Google Scholar] [CrossRef]
- Guo, W.; Li, B.; Shen, S.; Zhou, Q. An intelligent grinding burn detection system based on two-stage feature selection and stacked sparse autoencoder. Int. J. Adv. Manuf. Technol. 2019, 103, 2837–2847. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Serin, G.; Sener, B.; Ozbayoglu, A.M.; Unver, H.O. Review of tool condition monitoring in machining and opportunities for deep learning. Int. J. Adv. Manuf. Technol. 2020, 109, 953–974. [Google Scholar] [CrossRef]
- Tönshoff, H.K.; Jung, M.; Mnnel, S.; Rietz, W. Using acoustic emission signals for monitoring of production processes. Ultrasonics 2000, 37, 681–686. [Google Scholar] [CrossRef]
- Li, X. A brief review: Acoustic emission method for tool wear monitoring during turning. Int. J Mach. Tools Manuf. 2002, 42, 157–165. [Google Scholar] [CrossRef]
- Dias, E.A.; Pereira, F.B.; Filho, S.L.M.R.; Brandão, L.C. Monitoring of through-feed centreless grinding processes with acoustic emission signals. Measurement 2016, 94, 71–79. [Google Scholar] [CrossRef]
- Li, S.Y.; Wang, Z.; Wu, Y.L. Relationship between subsurface damage and surface roughness of optical materials in grinding and lapping processes. J. Mater. Process. Technol. 2008, 205, 34–41. [Google Scholar] [CrossRef]
- Lambropoulos, J.C.; Jacobs, S.D.; Ruckman, J.; Trans, C. Material removal mechanisms from grinding to polishing. Ceram. Trans. 1999, 102, 113–128. [Google Scholar]
- Suratwala, T.; Steele, R.; Shen, N.; Ray, N.; Wong, L.; Miller, P.E.; Feit, M. Lateral cracks during sliding indentation on various optical materials. J. Am. Ceram. Soc. 2019, 103, 1343–1357. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Accornero, F.; Mpalaskas, A.C.; Aggelis, D.G. Influence of damage in the acoustic emission parameters. Cem. Concr. Compos. 2013, 44, 9–16. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Soulioti, D.V.; Gatselou, E.A.; Barkoula, N.M.; Matikas, T.E. Monitoring of the mechanical behavior of concrete with chemically treated steel fibers by acoustic emission. Constr. Build. Mater. 2013, 48, 1255–1260. [Google Scholar] [CrossRef]
- Hase, A.; Mishina, H.; Wada, M. Correlation between features of acoustic emission signals and mechanical wear mechanisms. Wear 2012, 292–293, 144–150. [Google Scholar] [CrossRef]
- Grafakos, L. Classical Fourier Analysis, 2nd ed.; World Publishing Corporation: Beijing, China, 2012. [Google Scholar]
- Webb, A.R. Statistical Pattern Recognition, 2nd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2003. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Ren, L.; Sun, Y.; Wang, H.; Zhang, L. Prediction of Bearing Remaining Useful Life with Deep Convolution Neural Network. IEEE Access 2018, 6, 13041–13049. [Google Scholar] [CrossRef]
- Kothuru, A.; Nooka, S.P.; Liu, R. Application of deep visualization in CNN-based tool condition monitoring for end milling. Procedia Manuf. 2019, 34, 995–1004. [Google Scholar] [CrossRef]
- Zhang, W. Shift-invariant pattern recognition neural network and its optical architecture. In Proceedings of the Annual Conference of the Japan Society of Applied Physics, Tokyo, Japan, 24–26 August 1988; pp. 4790–4797. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
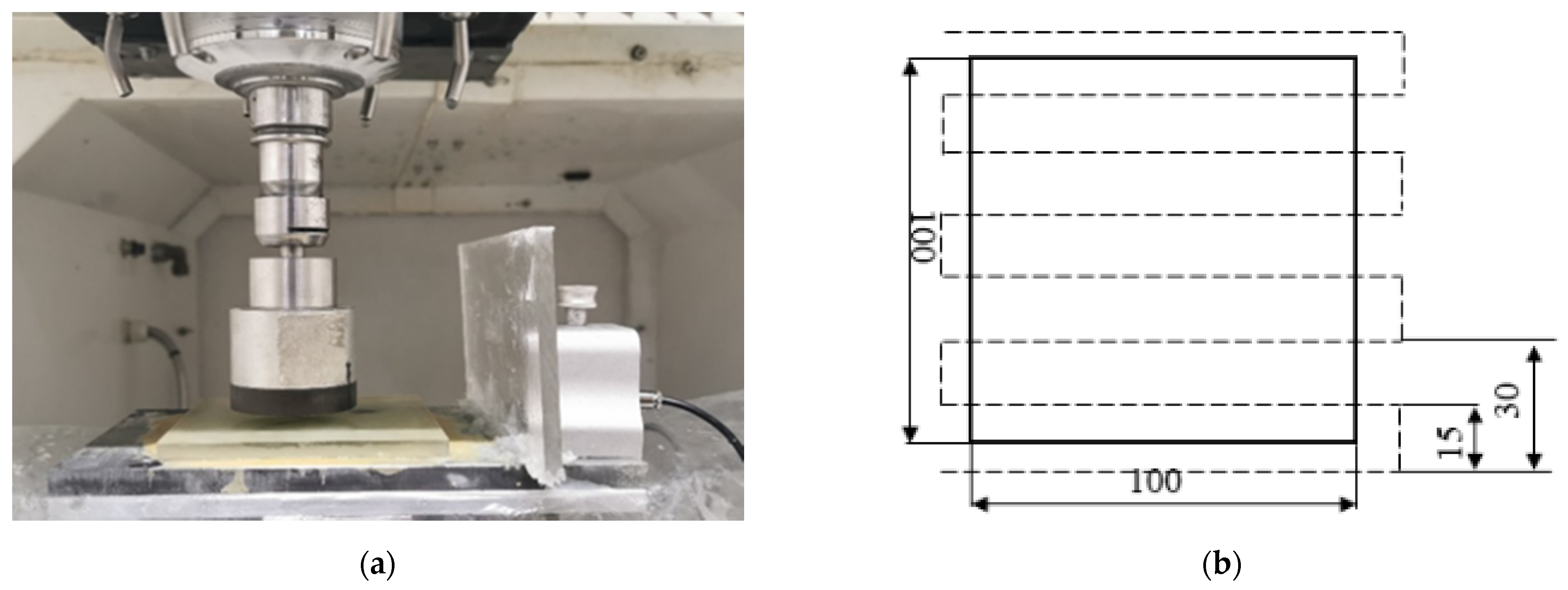

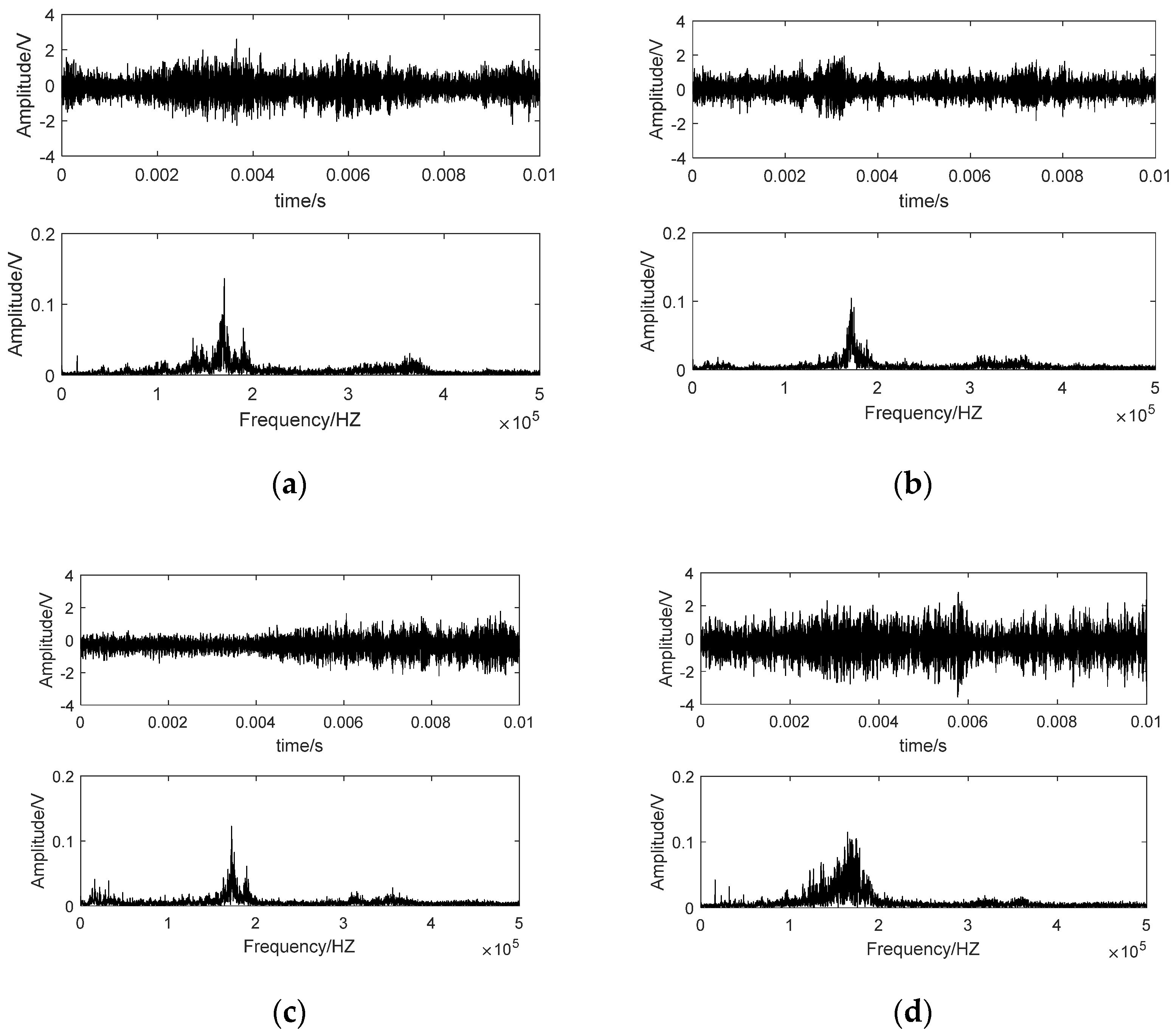
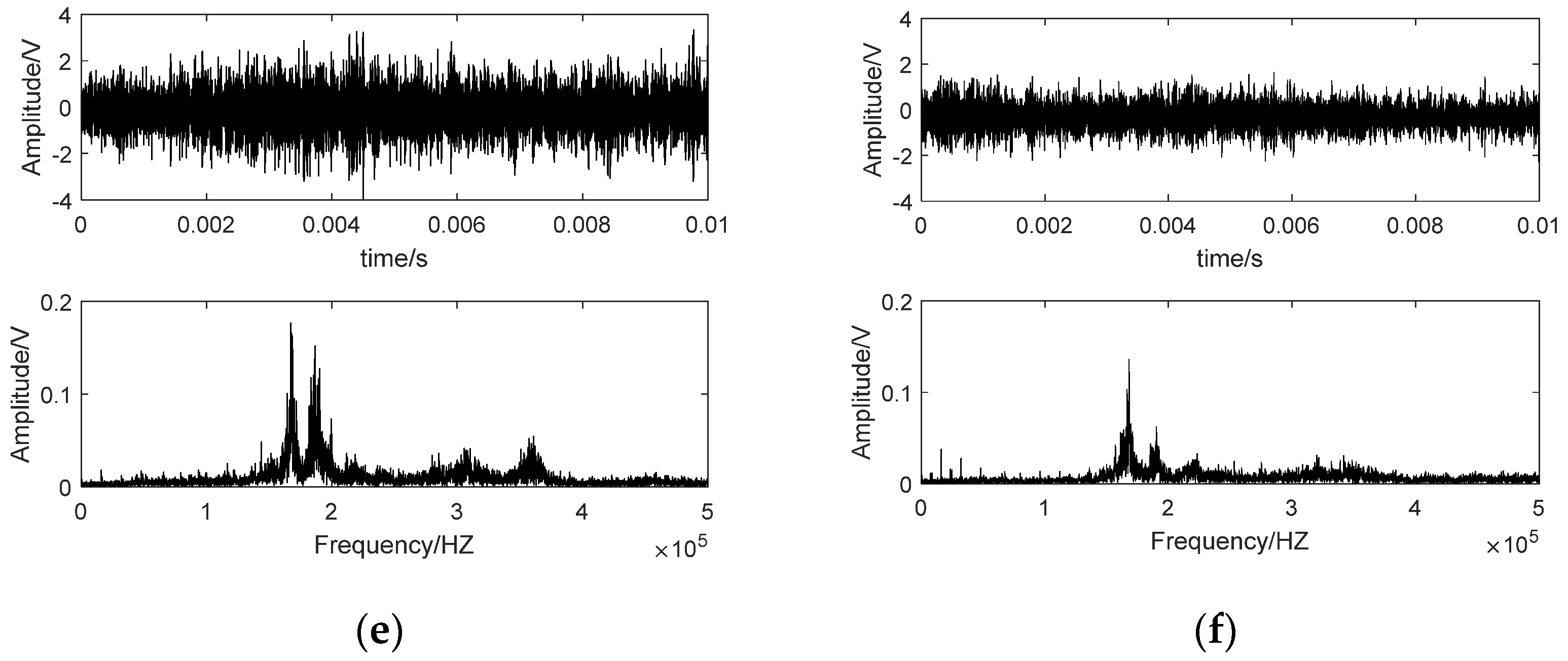




| Cup wheel | abrasive | bond | Diameter | mesh grain size | Concentration | |||
| diamond | Resin bond | 50 mm | 400# | 100% | ||||
| workpiece | Young’s modulus | Shear modulus | Modulus of rupture | Knoop hardness (100 g load) | Density | Softening point | Specific heat | Thermal conductivity |
| 73 GPa | 31 GPa | 52.4 MPa | 522 kg/mm2 | 2.2 g/cm3 | 1585 ℃ | 0.770 J/(g K) | 1.38 W/(m K) | |
| Grinding processing | observation nodes | volume of material removal () | spindle speed (n/s) | cutting depth (µm) | grinding grating interval (mm) | workpiece speed (mm/min) | ||
| 1~19 | 0.1:0.1:1.9 | 50 | 5 | 15 | 600 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, G.; Liu, S.; Su, S.; Wang, Z. Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals. Sensors 2021, 21, 1054. https://doi.org/10.3390/s21041054
Bi G, Liu S, Su S, Wang Z. Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals. Sensors. 2021; 21(4):1054. https://doi.org/10.3390/s21041054
Chicago/Turabian StyleBi, Guo, Shan Liu, Shibo Su, and Zhongxue Wang. 2021. "Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals" Sensors 21, no. 4: 1054. https://doi.org/10.3390/s21041054
APA StyleBi, G., Liu, S., Su, S., & Wang, Z. (2021). Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals. Sensors, 21(4), 1054. https://doi.org/10.3390/s21041054






