A Possible World-Based Fusion Estimation Model for Uncertain Data Clustering in WBNs
Abstract
1. Introduction
2. Related Works
3. Preliminaries
3.1. Definition of Possible World
3.2. Definition of Kullback–Leibler Divergence
3.3. Some Assumptions
4. Possible World-Based Fusion Estimation Model (PWFWM)
4.1. Data Fusion Estimation
4.2. Distance Calculation Method Based on KL Divergence-Based Distance
4.3. The Clustering Method Based on the Possible World
| Algorithm 1 for Matrix Pruning: |
| Input: the matrix S ∈ Rn×n and pruning threshold p The processing: Removing step: For i = 1 to n For j = 1 to n If sij < p sij = 0 End if End for End for Normalization step: For i = 1 to n For j = 1 to n End for End for |
| Algorithm 2 for processing S: |
| Input: the matrix S ∈ Rn×n and clustering threshold Th The processing: is the set of eigenvalues of Ls is the set of eigenvectors of Ls If k = r End if |
4.4. Updating
| Algorithm 3 for Clustering Updating: |
| Input: the center of each cluster , and the number of cluster members of training set and the test set . The processing: Clustering step: = . For i = n + 1 to n + p If clusteri = clusteri’ Oi belongs to clusteri. Else if Oi belongs to clusteri’ Else Oi belongs to clusteri End if End if End for Centers updating step: For i = n + 1 to n + p If Oi belongs to clusteri End if End for |
5. Simulations
| Algorithm 4 The Generation Method from Numerical Data to Uncertain Data (Gaussian Type). |
| Input: the numerical data and the standard deviation of each attribute Output: the corresponding uncertain data For i = 1 to n x = random, 0 < x ≤ 1 End for |
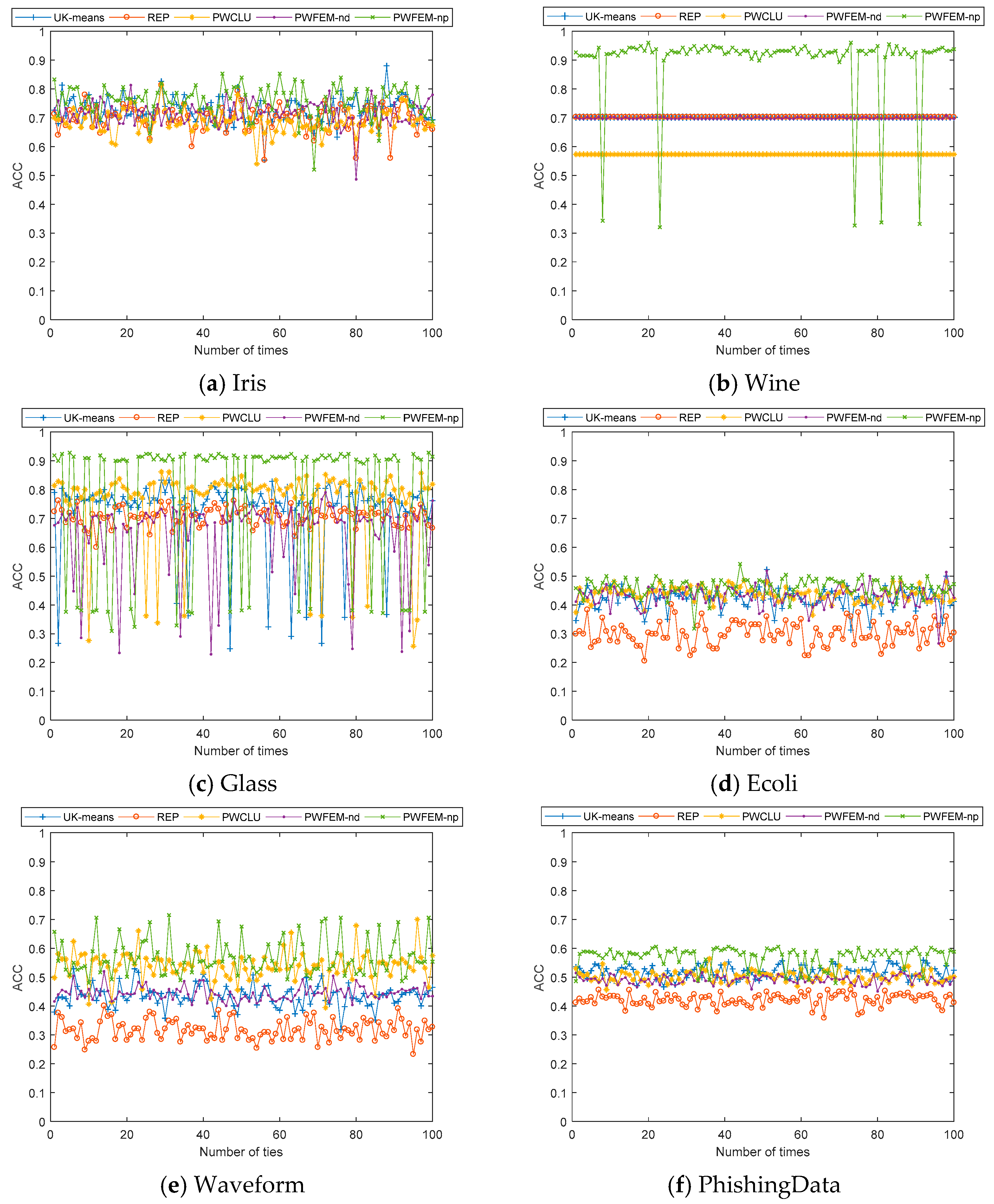
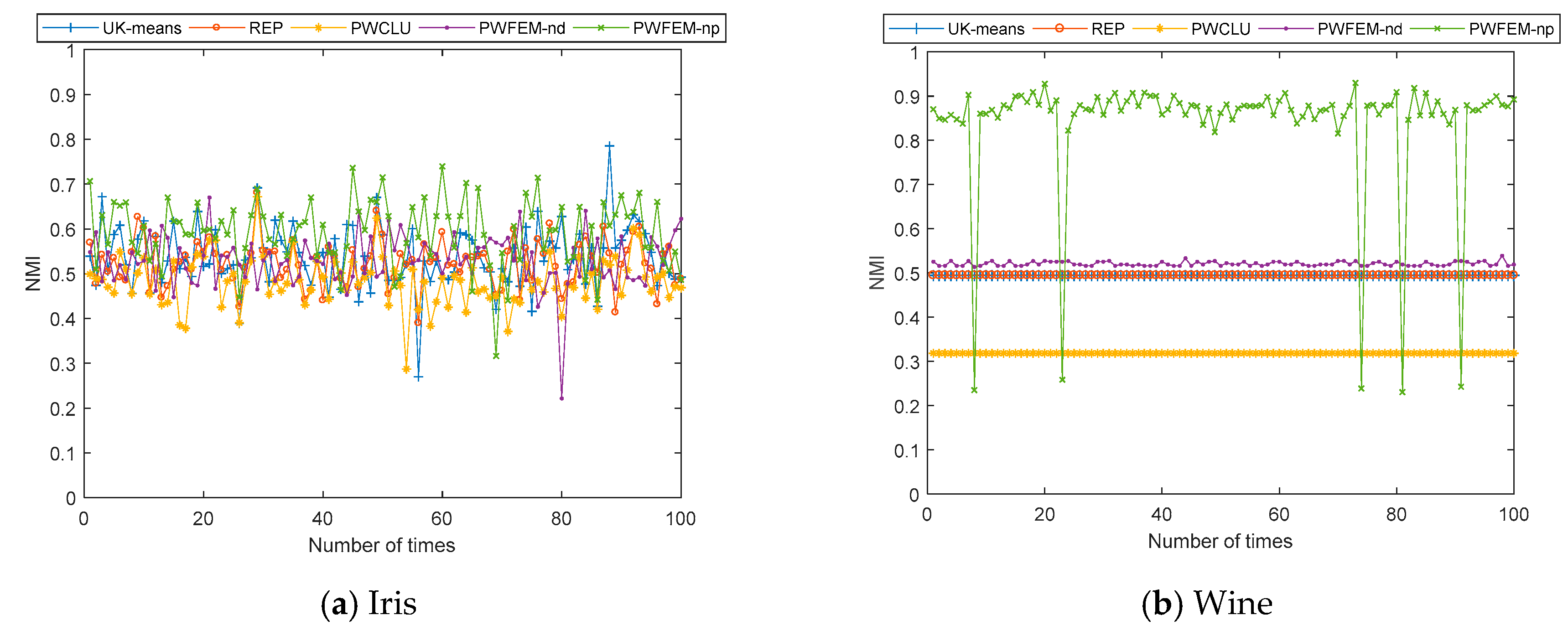
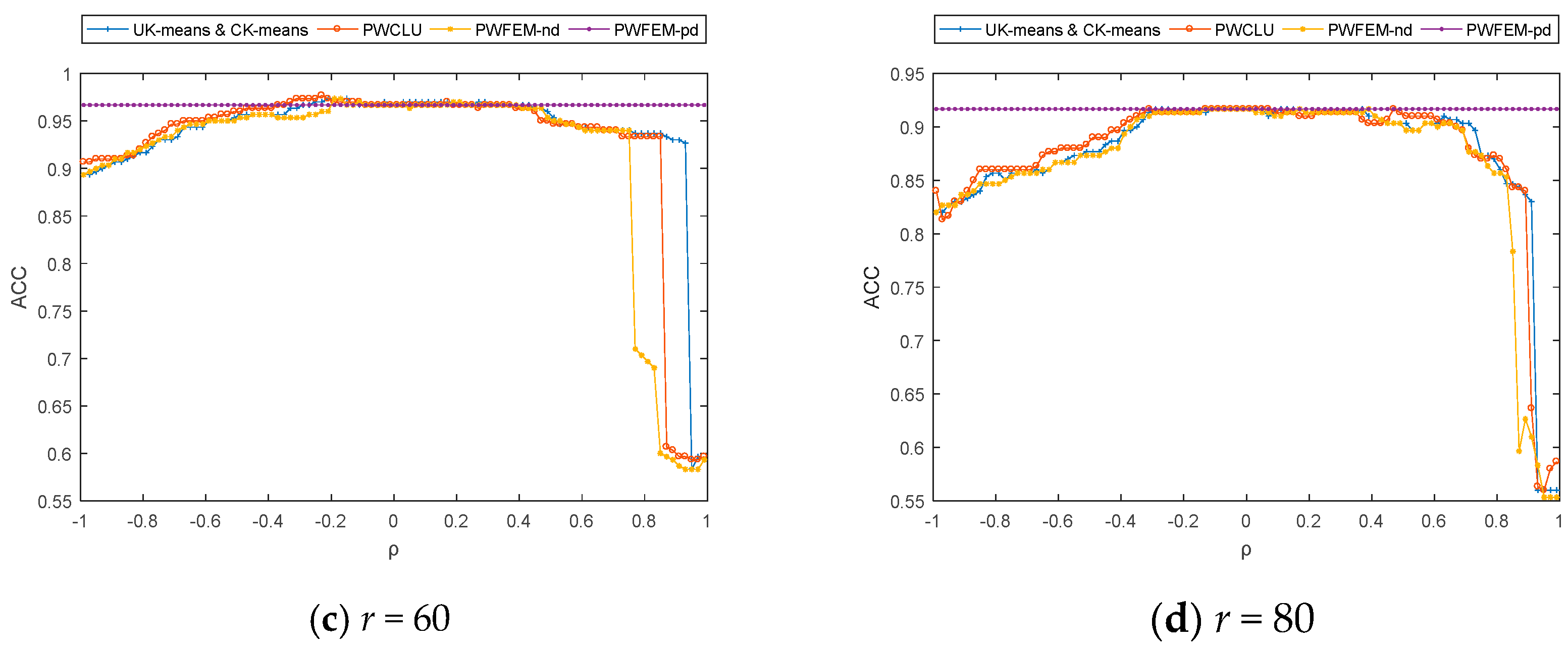
5.1. The Clustering Accuracy
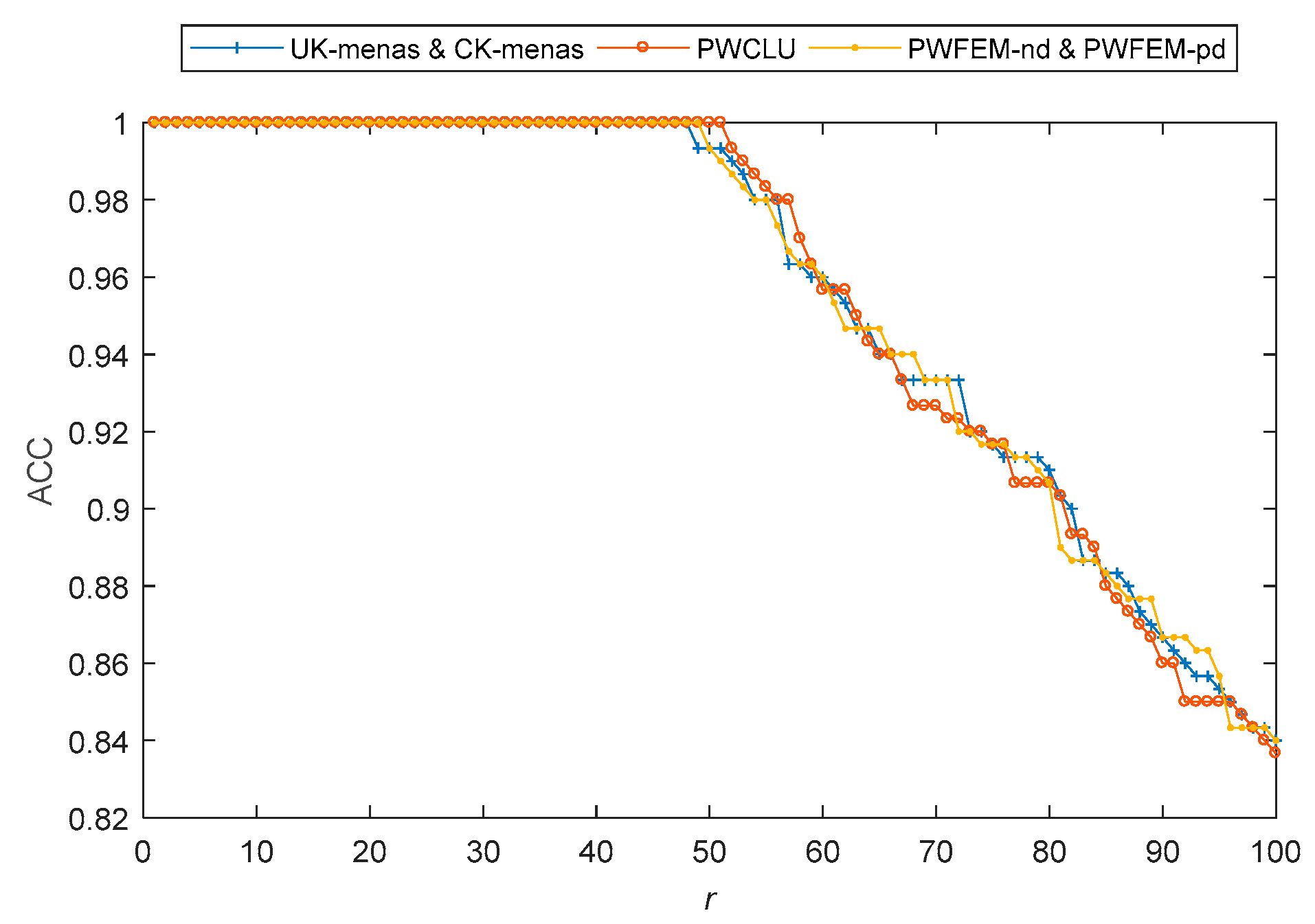
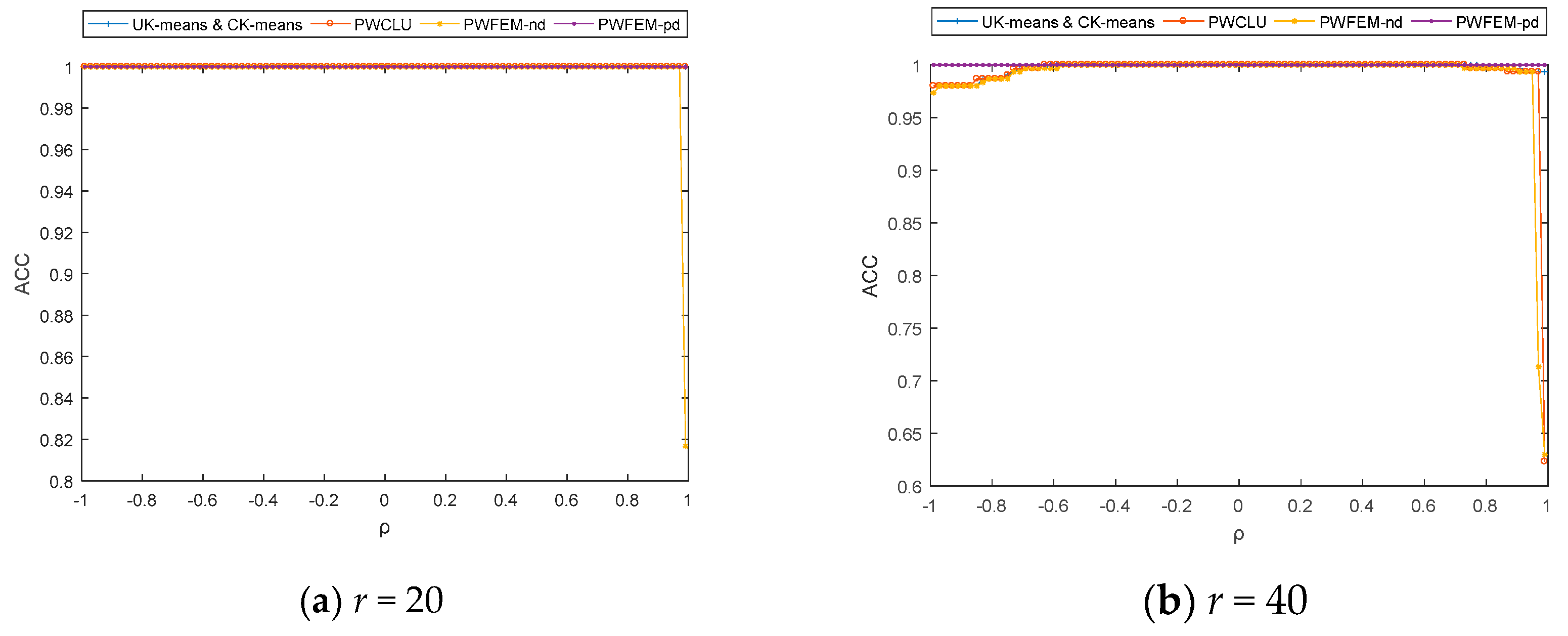
5.2. The Simulation with a Specific Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Delias, P.; Doumpos, M.; Grigoroudis, E.; Manolitzas, P.; Matsatsinis, N. Supporting healthcare management decisions via robust clustering of event logs. Knowl. Based Syst. 2015, 84, 203–213. [Google Scholar] [CrossRef]
- Gaglio, S.; Re, G.L.; Morana, M. Human Activity Recognition Process Using 3-D Posture Data. IEEE Trans. Hum. Mach. Syst. 2017, 45, 586–597. [Google Scholar] [CrossRef]
- Waller, L.A.; Turnbull, B.W.; Clark, L.C.; Nasca, P. Chronic disease surveillance and testing of clustering of disease and exposure: Application to leukemia incidence and TCE-contaminated dumpsites in upstate New York. Environmetrics 1992, 3, 281–300. [Google Scholar] [CrossRef]
- Matthews, G.; Warm, J.S.; Shaw, T.H.; Finomore, V.S. Predicting battlefield vigilance: A multivariate approach to assessment of attentional resources. Ergonomics 2014, 57, 856–875. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Yuan, D.; Ström, E.G.; Brännström, F. Cluster-Based Radio Resource Management for D2D-Supported Safety-Critical V2X Communications. IEEE Trans. Wirel. Commun. 2015, 15, 1. [Google Scholar] [CrossRef]
- Zagouras, A.; Pedro, H.T.C.; Coimbra, C.F.M. Clustering the solar resource for grid management in island mode. Sol. Energy 2014, 110, 507–518. [Google Scholar] [CrossRef]
- Li, M.; Xu, D.; Zhang, D.; Zou, J. The seeding algorithms for spherical k-means clustering. J. Glob. Optim. 2019, 76, 695–708. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, R.; Li, S.; Li, X. Spectral Segmentation via Midlevel Cues Integrating Geodesic and Intensity. IEEE Trans. Cybern. 2013, 43, 2170–2178. [Google Scholar] [CrossRef]
- Sokoloski, S. Implementing a Bayes Filter in a Neural Circuit: The Case of Unknown Stimulus Dynamics. Neural Comput. 2017, 29, 2450–2490. [Google Scholar] [CrossRef][Green Version]
- Sinopoli, B.; Schenato, L.; Franceschetti, M.; Poolla, K.; Jordan, M.I.; Sastry, S.S. Kalman filtering with intermittent observations. IEEE Trans. Autom. Control 2004, 49, 1453–1464. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Zeadally, S.; Chao, H.C.; Leung, V. CMASM: A Multiple-algorithm Service Model for Energy-delay Optimization in Edge Artificial Intelligence. IEEE Trans. Ind. Inform. 2019, 15, 4216–4224. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Wang, L.; Chao, H.C.; Zhou, Z. Extreme learning machines with expectation kernels. Pattern Recognit. 2019, 96, 1–13. [Google Scholar] [CrossRef]
- Chau, M.; Cheng, R.; Kao, B.; Ng, J. Uncertain data mining: An example in clustering location data. In Proceedings of the Advances in Knowledge Discovery and Data Mining 10th Pacific-Asia Conference, Singapore, 9–12 April 2006. [Google Scholar]
- Kriegel, H.P.; Pfeifle, M. Hierarchical density-based clustering of uncertain data. In Proceedings of the Data Mining Fifth IEEE International Conference, Houston, TX, USA, 27–30 November 2005. [Google Scholar]
- Volk, P.B.; Rosenthal, F.; Hahmann, M.; Habich, D.; Lehner, W. Clustering Uncertain Data with Possible Worlds. In Proceedings of the Proceedings of the 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Garcia, E.; Hausotte, T.; Amthor, A. Bayes filter for dynamic coordinate measurements Accuracy improvment, data fusion and measurement uncertainty evaluation. Meas. J. Int. Meas. Confed. 2013, 46, 3737–3744. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Costa, P.J. Adaptive model architecture and extended Kalman-Bucy filters. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 525–533. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A New Approach for Filtering Nonlinear Systems. In Proceedings of the American Control Conference, Seattle, DC, USA, 21–23 June 1995. [Google Scholar]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Liu, H.; Zhang, X.; Zhang, X. Possible World-based consistency learning model for clustering and classifying uncertain data. Neural Netw. 2018, 102, 48–66. [Google Scholar] [CrossRef]
- Sinkkonen, J.; Kaski, S. Clustering Based on Conditional Distributions in an Auxiliary Space. Neural Comput. 2014, 14, 217–239. [Google Scholar] [CrossRef]
- Luxburg, U.V. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019. [Google Scholar]
- Abdelhamid, N.; Ayesh, A.; Thabtah, F. Phishing detection based Associative Classification data mining. Expert Syst. Appl. 2014, 41, 5948–5959. [Google Scholar] [CrossRef]
- Gullo, F.; Tagarelli, A. Uncertain centroid based partitional clustering of uncertain data. Proc. VLDB Endow. 2012, 5, 610–621. [Google Scholar] [CrossRef][Green Version]

| Dataset | Objects | Attributes | Classes |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Wine | 178 | 13 | 3 |
| Glass | 214 | 9 | 6 |
| Ecoli | 327 | 7 | 5 |
| Waveform | 5000 | 21 | 3 |
| PhishingData [26] | 1353 | 9 | 3 |
| UK-Means | REP | PWCLU | PWFEM-nd | PWFEM-pd | ||
|---|---|---|---|---|---|---|
| Iris | Max | 0.8800 | 0.8133 | 0.8133 | 0.8133 | 0.8533 |
| Min | 0.5533 | 0.5533 | 0.5400 | 0.4867 | 0.5200 | |
| Mean | 0.7244 | 0.6994 | 0.6869 | 0.7181 | 0.7602 | |
| Variance | 0.0022 | 0.0021 | 0.0016 | 0.0017 | 0.0028 | |
| Wine | Max | 0.7022 | 0.7022 | 0.5730 | 0.7079 | 0.9607 |
| Min | 0.7022 | 0.7022 | 0.5730 | 0.6966 | 0.3202 | |
| Mean | 0.7022 | 0.7022 | 0.5730 | 0.6989 | 0.8999 | |
| Variance | 0 | 0 | 0 | 0 | 0.0173 | |
| Glass | Max | 0.8333 | 0.7619 | 0.8618 | 0.7905 | 0.9286 |
| Min | 0.2476 | 0.6000 | 0.2571 | 0.2286 | 0.3095 | |
| Mean | 0.7239 | 0.7078 | 0.7588 | 0.6489 | 0.7818 | |
| Variance | 0.0191 | 0.0010 | 0.0204 | 0.0173 | 0.0537 | |
| Ecoli | Max | 0.5327 | 0.4953 | 0.5374 | 0.5234 | 0.5421 |
| Min | 0.3458 | 0.2056 | 0.4065 | 0.3318 | 0.4299 | |
| Mean | 0.4422 | 0.4025 | 0.4905 | 0.4527 | 0.4634 | |
| Variance | 0.0012 | 0.0035 | 0.0011 | 0.0014 | 0.0009 | |
| Waveform | Max | 0.5291 | 0.4006 | 0.7003 | 0.5199 | 0.7156 |
| Min | 0.3180 | 0.2324 | 0.3945 | 0.4006 | 0.4801 | |
| Mean | 0.4350 | 0.3177 | 0.5403 | 0.4445 | 0.5706 | |
| Variance | 0.0014 | 0.0013 | 0.0025 | 0.0006 | 0.0038 | |
| PhishingData | Max | 0.5639 | 0.4560 | 0.5647 | 0.5188 | 0.6061 |
| Min | 0.4664 | 0.3585 | 0.4568 | 0.4508 | 0.4797 | |
| Mean | 0.5183 | 0.4218 | 0.5027 | 0.4910 | 0.5719 | |
| Variance | 0.0005 | 0.0004 | 0.0004 | 0.0002 | 0.0010 | |
| UK-Means | REP | PWCLU | PWFEM-nd | PWFEM-pd | ||
|---|---|---|---|---|---|---|
| Iris | Max | 0.7854 | 0.6809 | 0.6716 | 0.6700 | 0.7396 |
| Min | 0.2694 | 0.3898 | 0.2871 | 0.2213 | 0.3162 | |
| Mean | 0.5374 | 0.5245 | 0.4834 | 0.5295 | 0.5927 | |
| Variance | 0.0050 | 0.0027 | 0.0031 | 0.0033 | 0.0054 | |
| Wine | Max | 0.4946 | 0.4946 | 0.3184 | 0.5389 | 0.9551 |
| Min | 0.4946 | 0.4946 | 0.3184 | 0.5136 | 0.3146 | |
| Mean | 0.4946 | 0.4946 | 0.3184 | 0.5209 | 0.8803 | |
| Variance | 0 | 0 | 0 | 0 | 0.0198 | |
| Glass | Max | 0.7001 | 0.6171 | 0.7522 | 0.6288 | 0.8671 |
| Min | 0.0997 | 0.4028 | 0.1643 | 0.0320 | 0.2233 | |
| Mean | 0.5511 | 0.5250 | 0.6094 | 0.4258 | 0.6911 | |
| Variance | 0.0196 | 0.0019 | 0.0223 | 0.0204 | 0.0672 | |
| Ecoli | Max | 0.6544 | 0.6544 | 0.7064 | 0.7125 | 0.7309 |
| Min | 0.3731 | 0.3731 | 0.5199 | 0.4679 | 0.3639 | |
| Mean | 0.4988 | 0.4988 | 0.6354 | 0.5629 | 0.5569 | |
| Variance | 0.0050 | 0.0050 | 0.0034 | 0.0054 | 0.0079 | |
| Waveform | Max | 0.3247 | 0.2548 | 0.4645 | 0.3104 | 0.4895 |
| Min | 0.1195 | 0.1286 | 0.1282 | 0.1919 | 0.2545 | |
| Mean | 0.2112 | 0.1909 | 0.3244 | 0.2392 | 0.3558 | |
| Variance | 0.0017 | 0.0008 | 0.0022 | 0.0005 | 0.0025 | |
| PhishingData | Max | 0.2517 | 0.1636 | 0.2416 | 0.2200 | 0.3190 |
| Min | 0.1559 | 0.0594 | 0.1452 | 0.1313 | 0.1804 | |
| Mean | 0.2088 | 0.1050 | 0.1880 | 0.1760 | 0.2803 | |
| Variance | 0.0004 | 0.0004 | 0.0005 | 0.0003 | 0.0008 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, Z.; Wei, W.; Chao, H.-C.; Liu, X. A Possible World-Based Fusion Estimation Model for Uncertain Data Clustering in WBNs. Sensors 2021, 21, 875. https://doi.org/10.3390/s21030875
Li C, Zhang Z, Wei W, Chao H-C, Liu X. A Possible World-Based Fusion Estimation Model for Uncertain Data Clustering in WBNs. Sensors. 2021; 21(3):875. https://doi.org/10.3390/s21030875
Chicago/Turabian StyleLi, Chao, Zhenjiang Zhang, Wei Wei, Han-Chieh Chao, and Xuejun Liu. 2021. "A Possible World-Based Fusion Estimation Model for Uncertain Data Clustering in WBNs" Sensors 21, no. 3: 875. https://doi.org/10.3390/s21030875
APA StyleLi, C., Zhang, Z., Wei, W., Chao, H.-C., & Liu, X. (2021). A Possible World-Based Fusion Estimation Model for Uncertain Data Clustering in WBNs. Sensors, 21(3), 875. https://doi.org/10.3390/s21030875







