A Novel Concentric Circular Coded Target, and Its Positioning and Identifying Method for Vision Measurement under Challenging Conditions
Abstract
1. Introduction
- ◼
- We have designed a novel concentric circular coded target (CCCT) in which a concentric ring is employed to resolve the eccentricity error. This improvement aims at meeting the requirements of the flat viewing angle while measuring the important information (aero-elastic deformation, attitude, position, et al.) of objects such as wind tunnel models, flight vehicles, rotating blades, and other aerospace structures, in both ground and flight testing.
- ◼
- We have proposed a positioning algorithm to precisely locate the true projected center of the CCCT. In this algorithm, the adaptive brightness adjustment has been used to address the problems of poor illumination. Concomitantly, the eccentricity error caused by flat viewing angle is corrected based on a practical error-compensation model.
- ◼
- We have presented an approach to cope with the demands of the identification of CCCTs that make its use more robust in challenging environments, especially in the unfavorable illumination and flat viewing angle.
2. Preceding Tests for Estimating the Applicability of Schneider’s Coded Targets
3. Methods
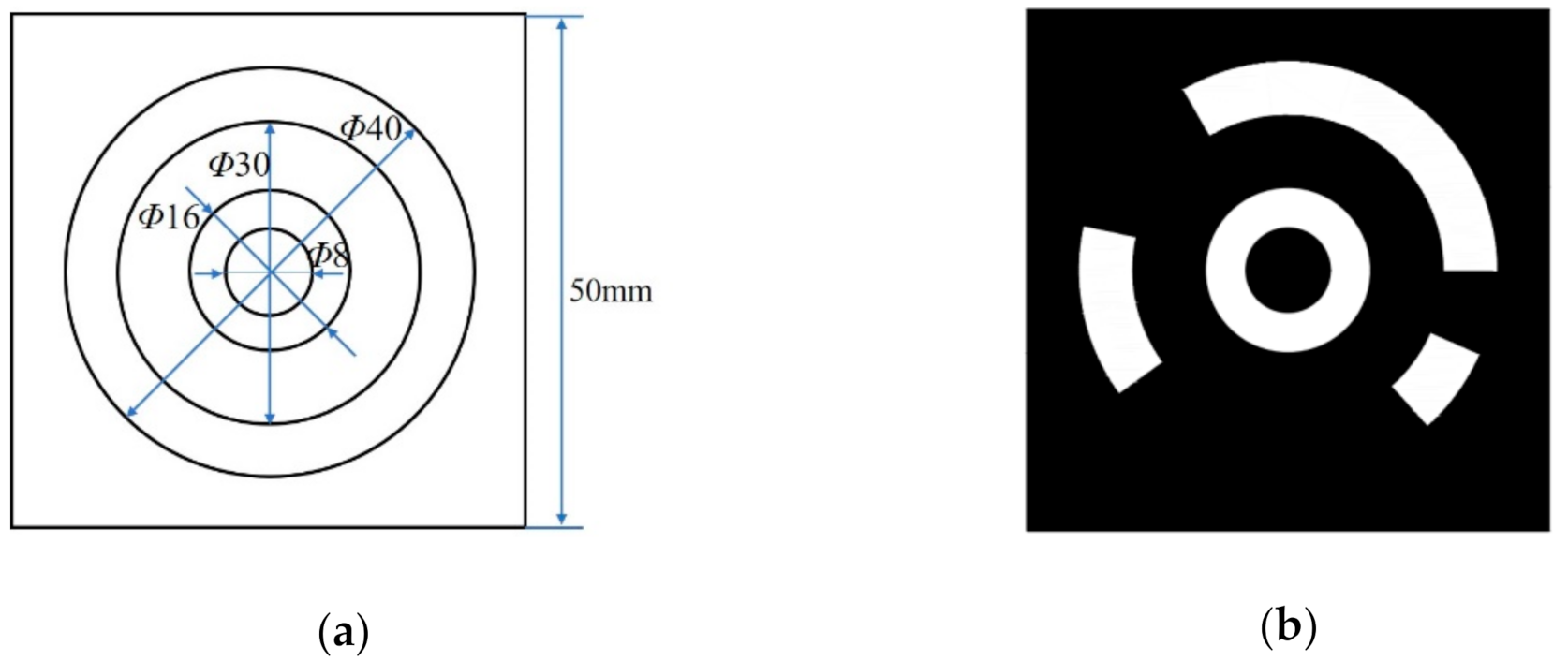
3.1. Design of the Concentric Circular Coded Target
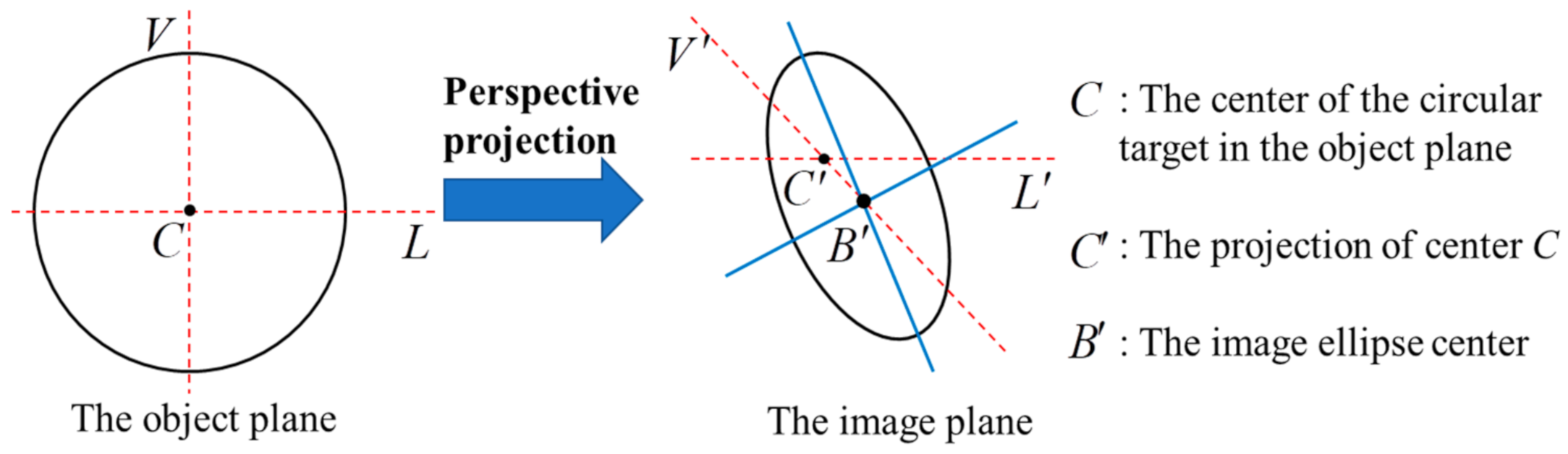
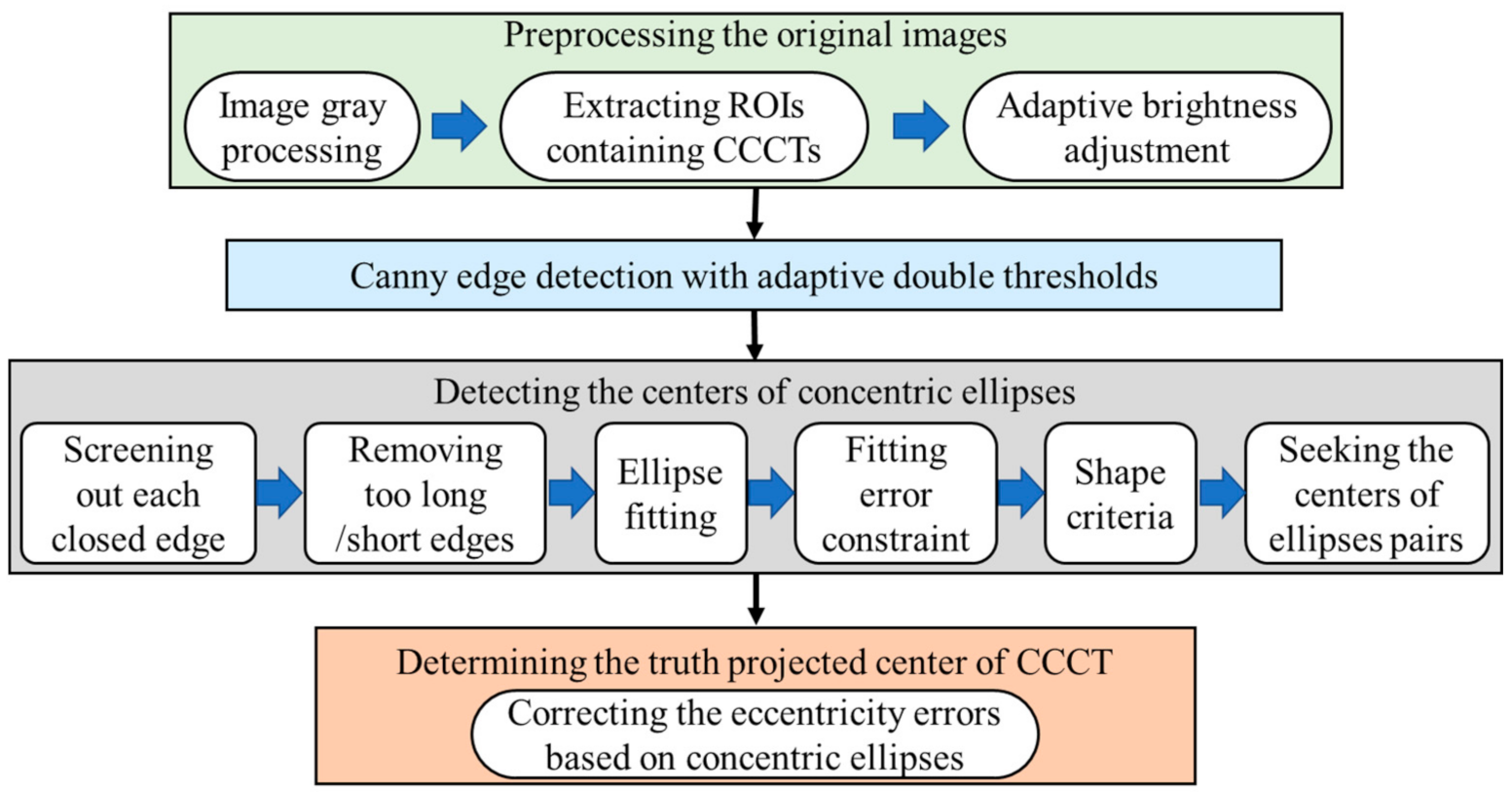
3.2. High-Precision Positioning of Concentric Circular Coded Targets
3.2.1. Preprocessing the Original Images
3.2.2. Canny Edge Detection with Adaptive Double Thresholds
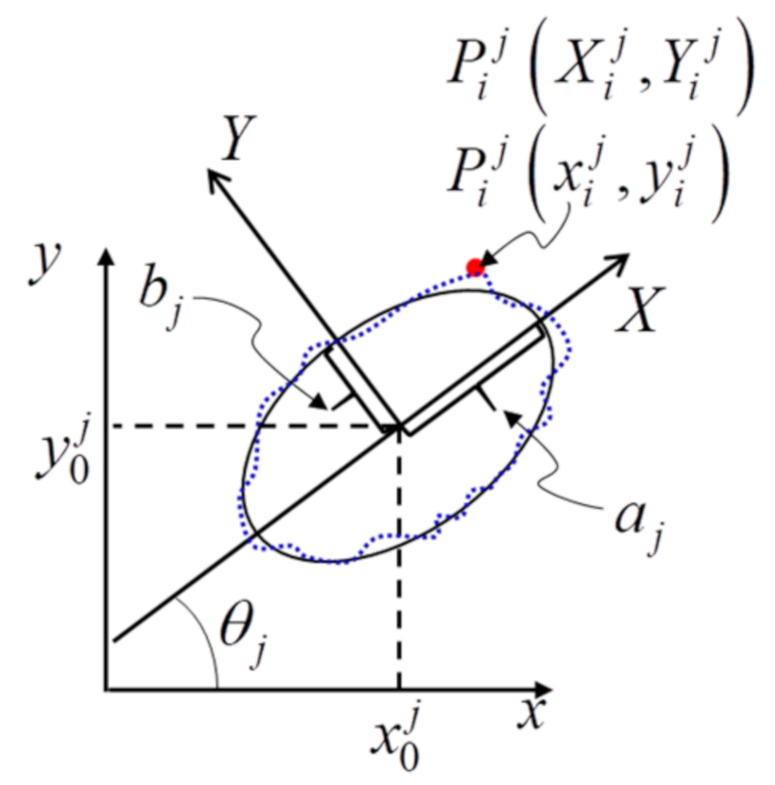
3.2.3. Detecting the Centers of Concentric Ellipse Pairs
- ◼
- Screening out each closed edge
- ◼
- Removing excessively long (short) edges
- ◼
- Ellipse fitting
- ◼
- Fitting error constraint
- ◼
- Shape criteria
- ◼
- Seeking the centers of ellipse pairs
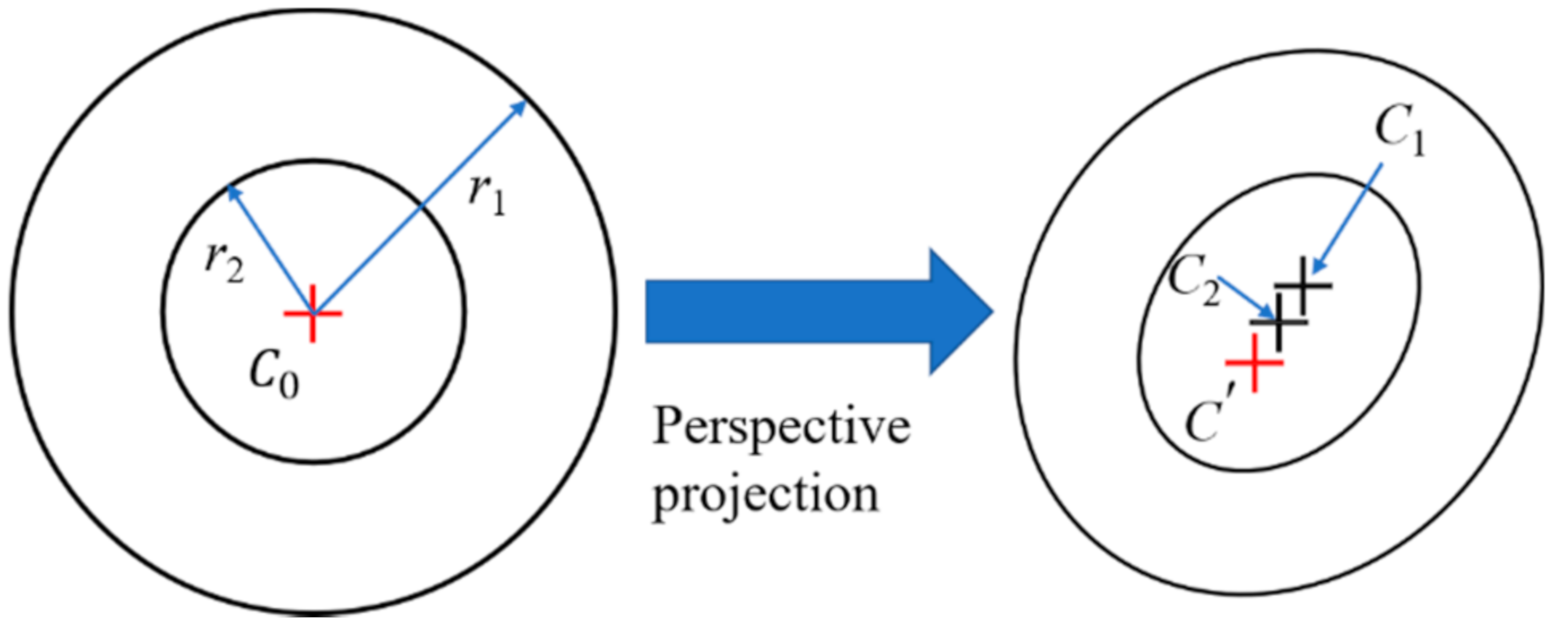
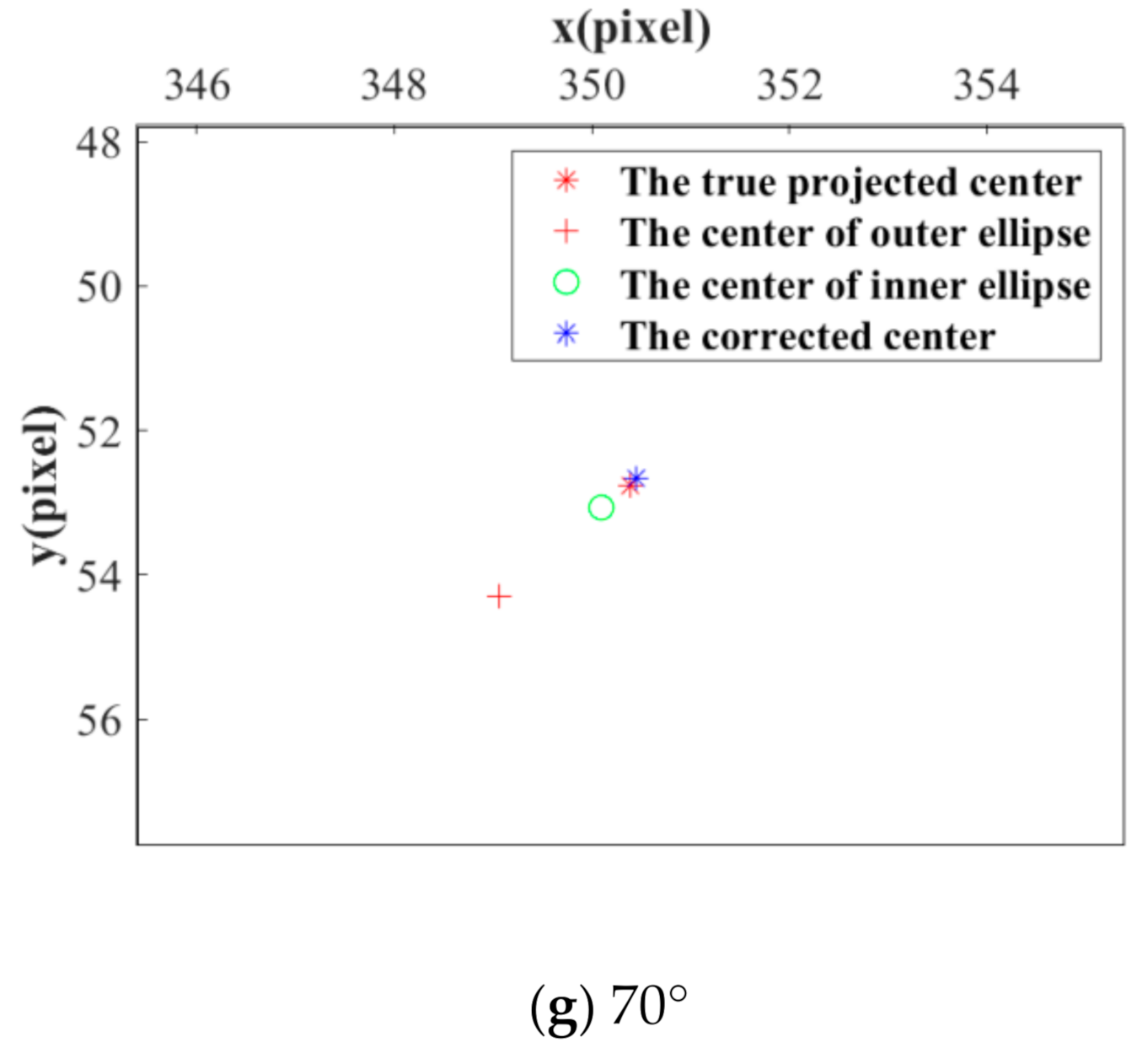
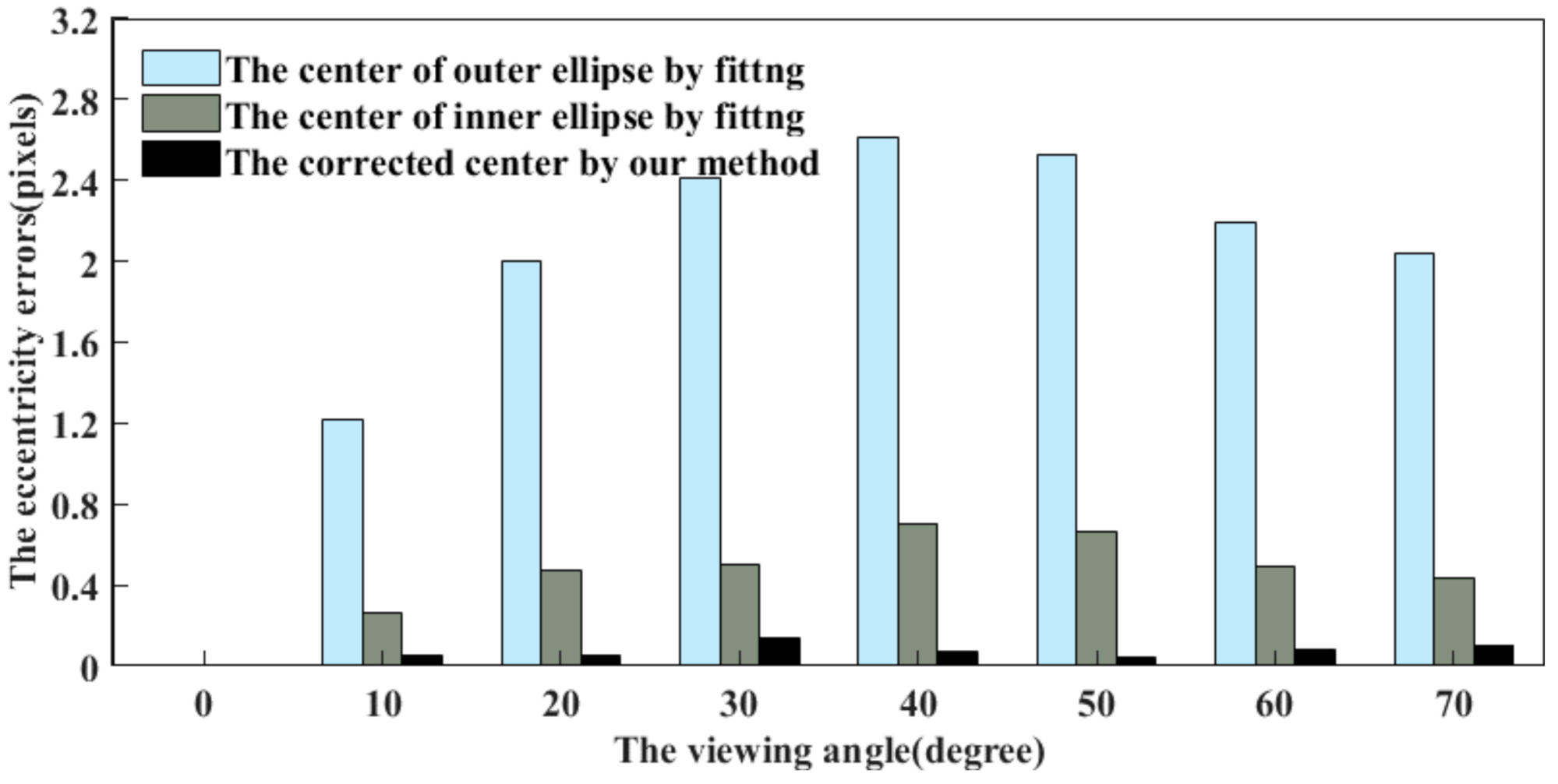
3.2.4. Determining the Truth Projected Center of CCCT
3.3. Identification of Concentric Circular Coded Targets
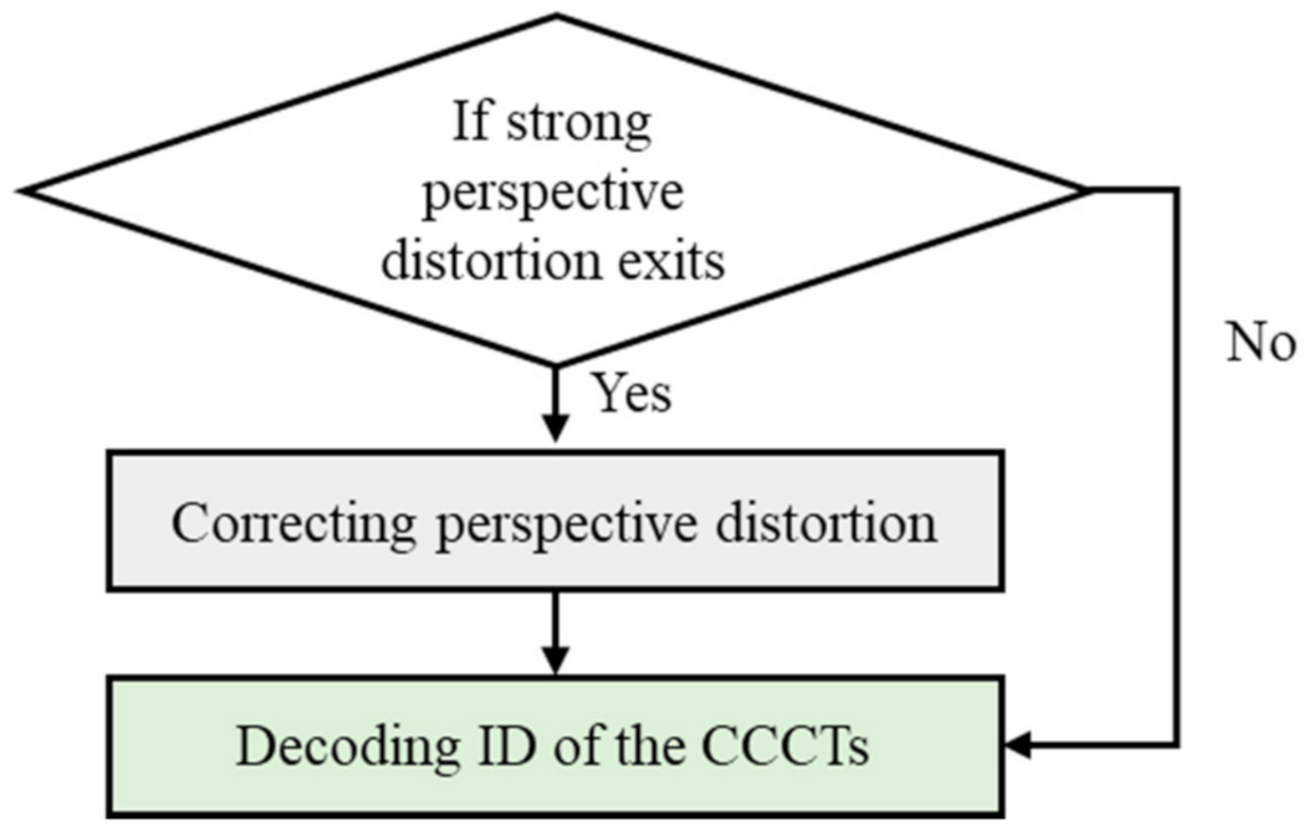
3.3.1. Correcting Perspective Distortion
3.3.2. Identifying the ID of Each CCCT
- ◼
- First, scan the outward from the center of the CCCT to search the outer and inner boundaries of the circular coded band. The Otsu algorithm is employed to calculate the average gray of the pixels contained in the outer ellipse of the coded band, Further, this average value is taken as a threshold to distinguish the black background and white target.
- ◼
- Then, for 15-bits CCCTs, rays are radiated outward from the center with an angular step of 2.4°. All pixels on each ray that fall between the outer and inner boundaries are sampled. The median gray value of these pixels is compared with the gray threshold obtained previously, and if it is greater than the threshold, the ray gray sample value is marked as “1.” Otherwise it is “0.” A 150-bits binary sequence can be obtained by scanning one circle clockwise or anticlockwise.
- ◼
- The ideal starting point to decode is from the place where the gray level fluctuates sharply to avoid the small section in the coded band being erroneously identified. Therefore, we reverse the 150-bits binary sequence until the head and tail are not the same. The reordered sequence is divided into several blocks according to consecutive “1” or “0”. The number of “1” or “0” contained in the k’th block is defined as P[k], and the “1” or “0” information of the block is placed in the array C[k].
- ◼
- Since the 15-bits binary code is adopted for the proposed CCCT, every 10 of 150 bits represent a binary bit, which is determined as
- ◼
- Finally, the 15-bits binary number is ordered, the corresponding decimal number is computed, and the minimum value is used as the ID of CCCT.
4. Experiments and Results
4.1. Positioning Accuracy Verification Experiment
4.1.1. Influence of Different Viewing Angles
4.1.2. Influence of Front-View Image Resolution
4.1.3. The Performance against the Image Noises
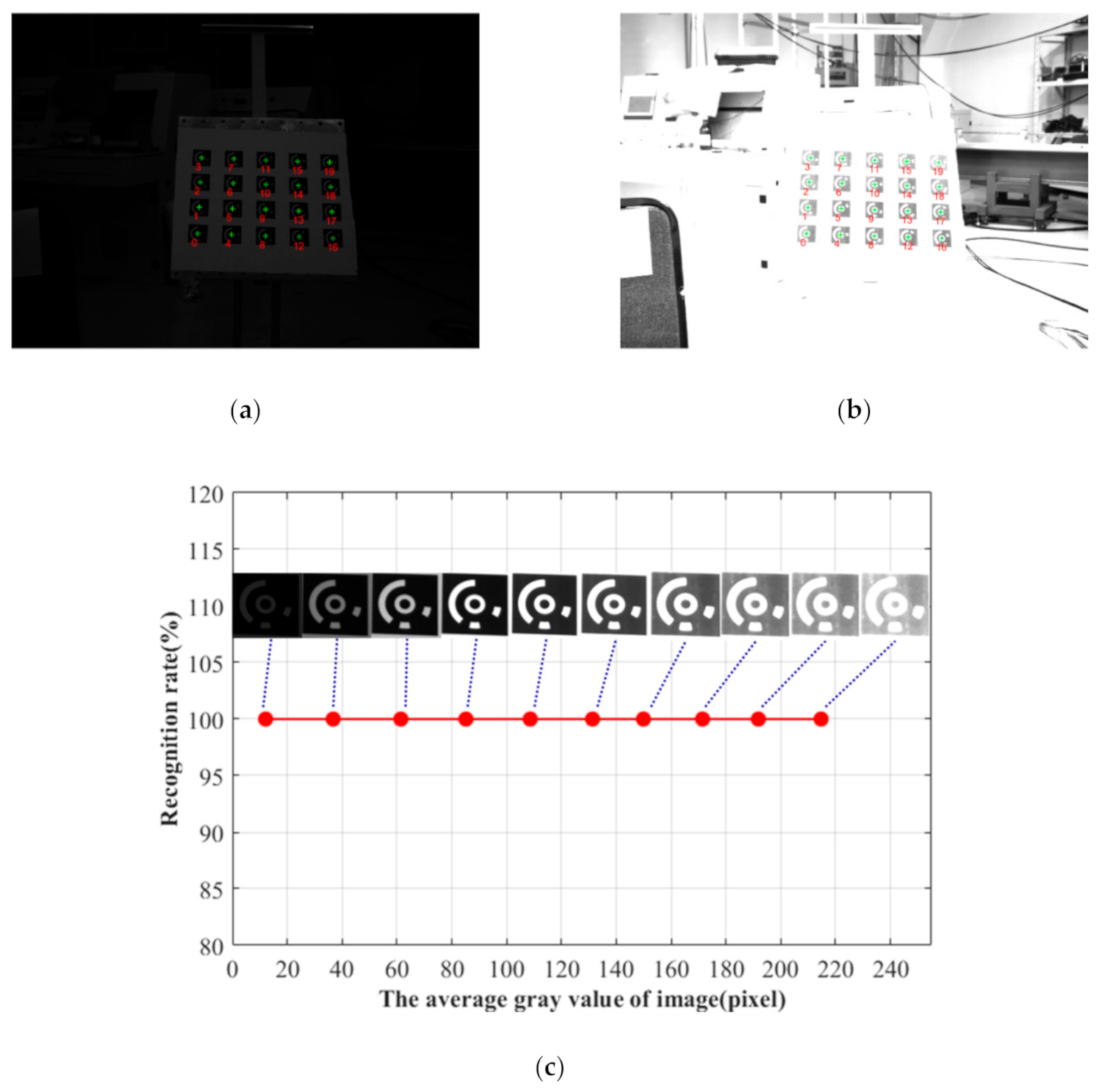
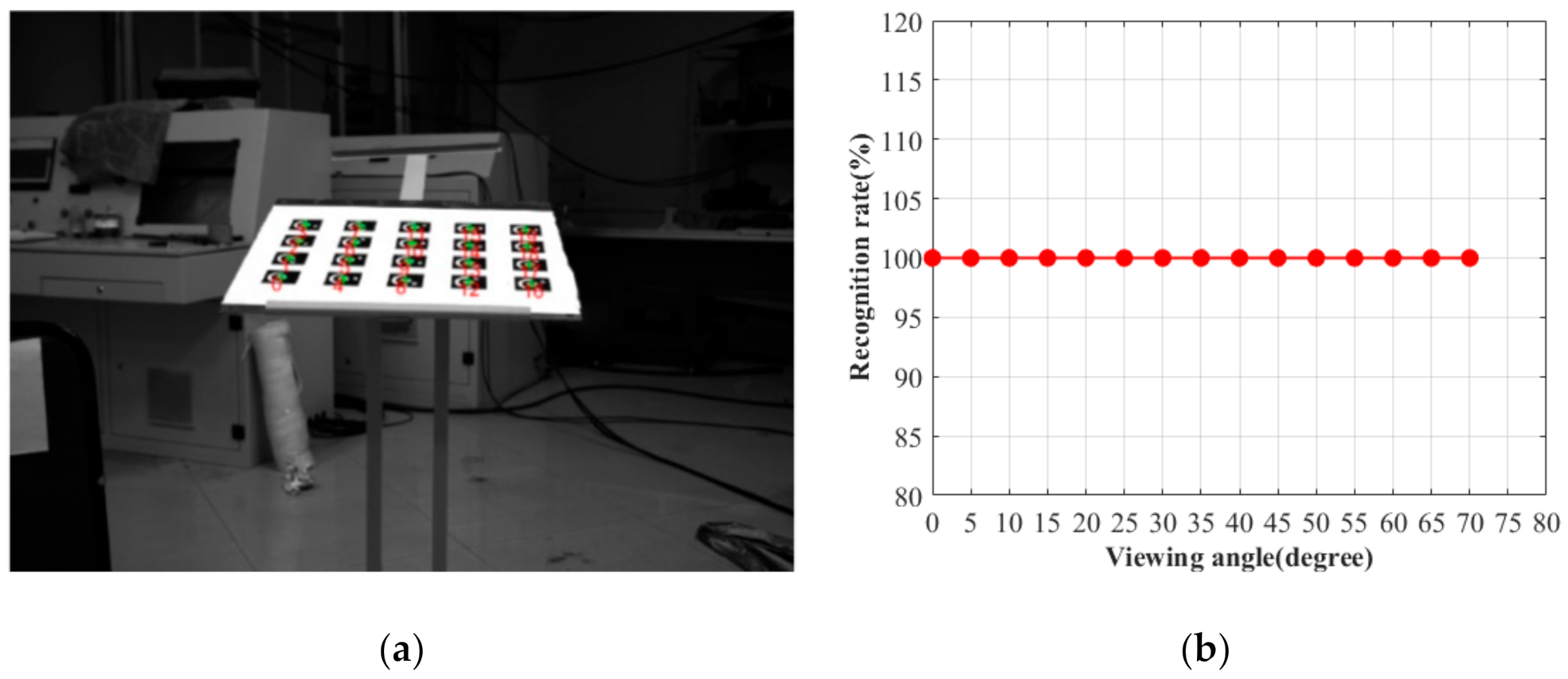
4.2. Identification Performance Verification Experiment
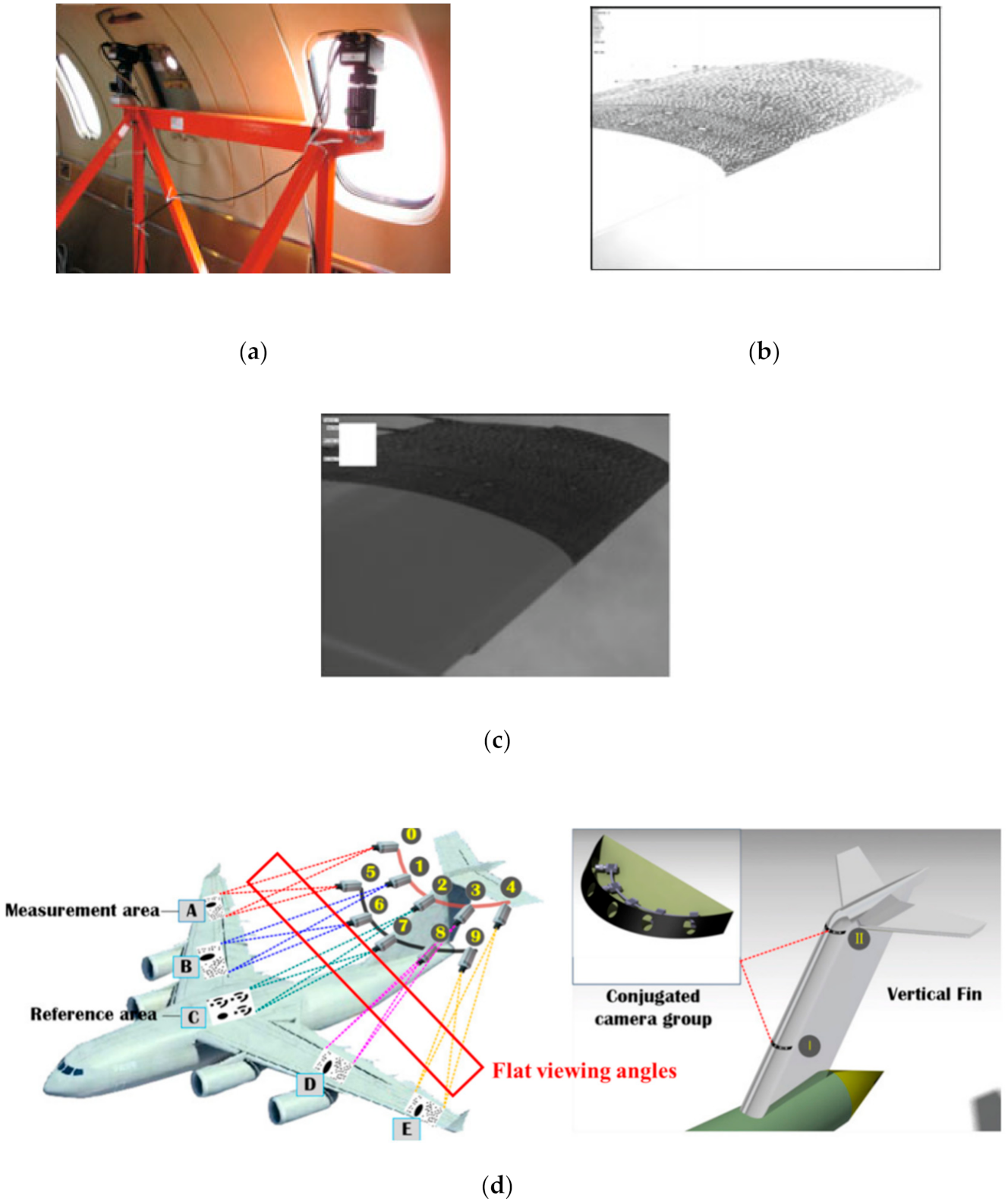
4.3. Wing Deformation Measurement Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, T.; Zhou, Z. An Improved Vision Method for Robust monitoring of Multi-Point Dynamic Displacements with Smartphones in an Interference Environment. Sensors 2020, 20, 5929. [Google Scholar] [CrossRef] [PubMed]
- Spencer, B.F.; Hoskere, V.; Narazaki, Y. Advances in computer vision-based civil infrastructure inspection and monitoring. Engineering 2019, 5, 199–248. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Li, X. Robust and Accurate Hand–Eye Calibration Method Based on Schur Matric Decomposition. Sensors 2019, 20, 4490. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Yu, C.; Chen, X.; Xi, J. Determination of optimal measurement configurations for self-calibrating a robotic visual inspection system with multiple point constraints. Int. J. Adv. Manuf. Technol. 2018, 96, 3365–3375. [Google Scholar] [CrossRef]
- Jeong, H.; Yu, J.; Lee, D. Calibration of In-Plane Center Alignment Errors in the Installation of a Circular Slide with Machine-Vision Sensor and a Reflective Marker. Sensors 2020, 20, 5916. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Li, Z.; Zhong, K.; Liu, X.; Wu, Y.; Wang, C.; Shi, Y. A Stereo-Vision System for Measuring the Ram Speed of Steam Hammers in an Environment with a Large Field of View and Strong Vibrations. Sensors 2019, 19, 996. [Google Scholar] [CrossRef]
- Dworakowski, Z.; Kohut, P.; Gallina, A.; Holak, K.; Uhl, T. Vision-based algorithms for damage detection and localization in structural health monitoring. Struct. Control. Health Monit. 2016, 23, 35–50. [Google Scholar] [CrossRef]
- Luo, L.; Feng, M.Q.; Wu, Z.Y. Robust vision sensor for multi-point displacement monitoring of bridges in the field. Eng. Struct. 2018, 163, 255–266. [Google Scholar] [CrossRef]
- Brosnan, T.; Sun, D.W. Improving quality inspection of food products by computer vision-A review. J. Food Eng. 2004, 61, 3–16. [Google Scholar] [CrossRef]
- Srivastava, B.; Anvikar, A.R.; Ghosh, S.K.; Mishra, N.; Kumar, N.; Houri-Yafin, A.; Pollak, J.J.; Salpeter, S.J.; Valecha, N. Computer-vision-based technology for fast, accurate and cost effective diagnosis of malaria. Malar. J. 2015, 14, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tateno, S.; Meng, F.; Qian, R.; Hachiya, Y. Privacy-Preserved Fall Detection Method with Three-Dimensional Convolutional Neural Network Using Low-Resolution Infrared Array Sensor. Sensors 2020, 20, 5957. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Liu, W.; Han, Z. A High-Precision Detection Approach for Catenary Geometry Parameters of Electrical Railway. IEEE Trans. Instrum. Meas. 2017, 66, 1798–1808. [Google Scholar] [CrossRef]
- Sivaraman, S.; Trivedi, M.M. Looking at Vehicles on the Road: A Survey of Vision-Based Vehicle Detection, Tracking, and Behavior Analysis. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1773–1795. [Google Scholar] [CrossRef]
- Karwowski, K.; Mizan, M.; Karkosiński, D. Monitoring of current collectors on the railway line. Transport 2016, 33, 177–185. [Google Scholar] [CrossRef]
- Liu, G.; Xu, C.; Zhu, Y.; Zhao, J. Monocular vision-based pose determination in close proximity for low impact docking. Sensors 2019, 19, 3261. [Google Scholar] [CrossRef]
- Chen, L.; Huang, P.; Cai, J.; Meng, Z.; Liu, Z. A non-cooperative target grasping position prediction model for tethered space robot. Aerosp. Sci. Technol. 2016, 58, 571–581. [Google Scholar] [CrossRef]
- Liu, T.; Burner, A.W.; Jones, T.W.; Barrows, D.A. Photogrammetric Techniques for Aerospace Applications. Prog. Aerosp. Sci. 2012, 54, 1–58. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, L.; Deng, H.; Ma, M.; Zhong, X.; Wen, P. Measurement of Unmanned Aerial Vehicle Attitude Angles Based on a Single Captured Image. Sensors 2018, 18, 2655. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, Y.; Lee, H.; Yun, H. Marker-Based Structural Displacement Measurement Models with Camera Movement Error Correction Using Image Matching and Anomaly Detection. Sensors 2020, 20, 5676. [Google Scholar] [CrossRef]
- Berveglieri, A.; Tommaselli, A.M.G. Reconstruction of Cylindrical Surfaces Using Digital Image Correlation. Sensors 2018, 18, 4183. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.; Rauh, W. Circular Coded Target for Automation of Optical 3D-Measurement and Camera Calibration. Int. J. Pattern Recognit. Artif. Intell. 2001, 15, 905–919. [Google Scholar] [CrossRef]
- Scaioni, M.; Feng, T.; Barazzetti, L.; Previtali, M.; Lu, P.; Qiao, G.; Wu, H.; Chen, W.; Tong, X.; Wang, W.; et al. Some applications of 2-D and 3-D photogrammetry during laboratory experiments for hydrogeological risk assessment. Geomat. Nat. Hazards Risk 2015, 6, 473–496. [Google Scholar] [CrossRef]
- Liu, C.; Dong, S.; Mokhtar, M.; He, X.; Lu, J.; Wu, X. Multicamera system extrinsic stability analysis and large-span truss string structure displacement measurement. Appl. Opt. 2016, 55, 8153–8161. [Google Scholar] [CrossRef] [PubMed]
- Huang, G. Study on the Key Technologies of Digital Close Range Industrial Photogrammetry and Applications. Ph.D. Thesis, Tianjin University, Tianjin, China, May 2005. [Google Scholar]
- Xiao, Z. Study on the Key Technologies of 3D Shape and Deformation Measurement Based on Industrial Photogrammetry and Computer Vision. Ph.D. Thesis, Xi’an Jiaotong University, Xi’an, China, May 2010. [Google Scholar]
- Xiao, Z.; Liang, J.; Yu, D.; Tang, Z.; Asundi, A. An accurate stereo vision system using cross-shaped target self-calibration method based on photogrammetry. Opt. Laser Technol. 2010, 48, 1251–1261. [Google Scholar] [CrossRef]
- Fraser, C.S. Innovations in automation for vision metrology systems. Photogramm. Rec. 1997, 15, 901–911. [Google Scholar] [CrossRef]
- Ahn, S.J.; Schultes, M. A new circular coded target for the automation of photogrammetric 3D surface measurements. Optical 3-D Measurement Techniques IV. In In Proceedings of the 4th Conference on Optical 3D Measurement Techniques, Zurich, Switzerland, 29 September−2 October 1997; pp. 225–234. [Google Scholar]
- Hattori, S.; Akimoto, K.; Fraser, C.; Imoto, H. Automated Procedures with Coded Targets in Industrial Vision Metrology. Photogramm. Eng. Remote Sens. 2002, 68, 441–446. [Google Scholar]
- Shortis, M.R.; Seager, J.W.; Robson, S.; Harvey, E.S. Automatic recognition of coded targets based on a Hough transform and segment matching. In Proceedings of the SPIE 5013, Santa Clara, CA, USA, 20–24 January 2003; pp. 202–208. [Google Scholar]
- Shortis, M.R.; Seager, J.W. A practical target recognition system for close range photogrammetry. Photogramm. Rec. 2015, 29, 337–355. [Google Scholar] [CrossRef]
- Sukhovilov, B.; Sartasov, E.; Grigorova, E.A. Improving the accuracy of determining the position of the code marks in the problems of constructing three-dimensional models of objects. In Proceedings of the 2nd International Conference on Industrial Engineering, Applications and Manufacturing, Chelyabinsk, Russia, 19−20 May 2016; pp. 1–4. [Google Scholar]
- Tushev, S.; Sukhovilov, B.; Sartasov, E. Architecture of industrial close-range photogrammetric system with multi-functional coded targets. In Proceedings of the 2nd International Ural Conference on Measurements, Chelyabinsk, Russia, 16−19 October 2017; pp. 435–442. [Google Scholar]
- Tushev, S.; Sukhovilov, B.; Sartasov, E. Robust coded target recognition in adverse light conditions. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing, Moscow, Russia, 15−18 May 2018; pp. 790–797. [Google Scholar]
- Knyaz, V.A.; Sibiryakov, A.V. The development of new coded targets for automated point identification and non-contact 3D surface measurements. Int. Arch. Photogramm. Remote Sens. 1998, 32, 80–85. [Google Scholar]
- Guo, Z.; Liu, X.; Wang, H.; Zheng, Z. An ellipse detection method for 3D head image fusion based on color-coded mark points. Front. Optoelectron. 2012, 5, 395–399. [Google Scholar] [CrossRef]
- Yang, J.; Han, J.D.; Qin, P.L. Correcting error on recognition of coded points for photogrammetry. Opt. Precis. Eng. 2012, 20, 2293–2299. [Google Scholar] [CrossRef]
- Deng, H.; Hu, G.; Zhang, J.; Ma, M.; Zhong, X.; Yang, Z. An Initial Dot Encoding Scheme with Significantly Improved Robustness and Numbers. Appl. Sci. 2019, 9, 4915. [Google Scholar] [CrossRef]
- Schneider, C.T.; Sinnreich, K. Optical 3-D measurement systems for quality control in industry. Int. Arch. Photogramm. Remote Sens. 1992, 29, 56–59. [Google Scholar]
- Van Den Heuvel, F.; Kroon, R.; Poole, R. Digital close-range photogrammetry using artificial targets. Int. Arch. Photogramm. Remote Sens. 1992, 29, 222–229. [Google Scholar]
- Wang, C.; Dong, M.; Lv, N.; Zhu, L. New Encode Method of Measurement Targets and Its Recognition Algorithm. Tool Technol. 2007, 17, 26–30. [Google Scholar]
- Duan, K.; Liu, X. Research on coded reference point detection in photogrammetry. Transducer Microsyst. Technol. 2010, 29, 74–78. [Google Scholar]
- Liu, J.; Jiang, Z.; Hu, H.; Yin, X. A Rapid and Automatic Feature Extraction Method for Artificial Targets Used in Industrial Photogrammetry Applications. Appl. Mech. Mater. 2012, 170, 2995–2998. [Google Scholar] [CrossRef]
- Huang, X.; Su, X.; Liu, W. Recognition of Center Circles for Encoded Targets in Digital Close-Range Industrial Photogrammetry. J. Robot. Mechatron. 2015, 27, 208–214. [Google Scholar]
- Chen, M.; Zhang, L. Recognition of Motion Blurred Coded Targets Based on SIFT. Inf. Technol. 2018, 4, 83–85. [Google Scholar]
- Miguel, F.; Carmen, A.; Bertelsen, A.; Mendikute, A. Industrial Non-Intrusive Coded-Target Identification and Decoding Application. In Proceedings of the 6th Iberian Conference on Pattern Recognition and Image Analysis, Madeira, Portugal, 5−7 June 2013; pp. 790–797. [Google Scholar]
- Scaioni, M.; Feng, T.; Barazzetti, L.; Previtali, M.; Roncella, R. Image-based Deformation Measurement. Appl. Geomat. 2015, 7, 75–90. [Google Scholar] [CrossRef]
- Bao, Y.; Shang, Y.; Sun, X.; Zhou, J. A Robust Recognition and Accurate Locating Method for Circular Coded Diagonal Target. In Proceedings of the Applied Optics and Photonics China: 3D Measurement Technology for Intelligent Manufacturing, Beijing, China, 24 October 2017; p. 104580Q. [Google Scholar]
- Jin, T.; Dong, X. Designing and Decoding Algorithm of Circular Coded Target. Appl. Res. Comput. 2019, 36, 263–267. [Google Scholar]
- Moriyama, T.; Kochi, N.; Yamada, M.; Fukmaya, N. Automatic target-identification with the color-coded-targets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 39–44. [Google Scholar]
- Wang, D. Study on the Embedded Digital Close-Range Photogrammetry System. Master’s Thesis, PLA Information Engineering University, Zhengzhou, China, April 2012. [Google Scholar]
- Yang, X.; Fang, S.; Kong, B.; Li, Y. Design of a color coded target for vision measurements. Opt. Int. J. Light Electron Opt. 2014, 125, 3727–3732. [Google Scholar] [CrossRef]
- Boden, F.; Lawson, N.; Jentink, H.W.; Kompenhans, J. Advanced In-Flight Measurement Techniques; Springer: Berlin, Germany, 2013; pp. 19–20. [Google Scholar]
- Li, L.; Liang, J.; Guo, X.; Guo, C.; Hu, H.; Tang, Z. Full-Field Wing Deformation Measurement Scheme for In-Flight Cantilever Monoplane Based on 3D Digital Image Correlation. Meas. Sci. Technol. 2014, 25, 11260–11276. [Google Scholar] [CrossRef]
- Ahn, S.; Warnecke, H. Systematic Geometric Image Measurement Errors of Circular Object Targets: Mathematical Formulation and Correction. Photogramm. Rec. 1999, 16, 485–502. [Google Scholar] [CrossRef]
- Liu, Y.; Su, X.; Guo, X.; Suo, T.; Li, Y.; Yu, Q. A novel method on suitable size selection of artificial circular targets in optical non-contact measurement. In Proceedings of the 8th Applied Optics and Photonics China, Beijing, China, 7−9 July 2019; p. 11338. [Google Scholar]
- Chen, R. Adaptive Nighttime Image Enhancement Algorithm Based on FPGA. Master’s Thesis, Guangdong University of Technology, Guangdong, China, May 2015. [Google Scholar]
- Tang, J.; Zhu, W.; Bi, Y. A Computer Vision-Based Navigation and Localization Method for Station-Moving Aircraft Transport Platform with Dual Cameras. Sensors 2020, 20, 279. [Google Scholar] [CrossRef]
- He, X.C.; Yung, N.H.C. Corner detector based on global and local curvature properties. Opt. Eng. 2008, 47, 057008. [Google Scholar]
- He, D.; Liu, X.; Peng, X.; Ding, Y.; Gao, B. Eccentricity Error Identification and Compensation for High-Accuracy 3D Optical Measurement. Meas. Sci. Technol. 2013, 24, 075402. [Google Scholar] [CrossRef]
- He, X.C.; Yung, N.H.C. Curvature Scale Space Corner Detector with Adaptive Threshold and Dynamic Region of Support. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26−26 August 2004; pp. 23–26. [Google Scholar]
- Zhang, Z.Y. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]


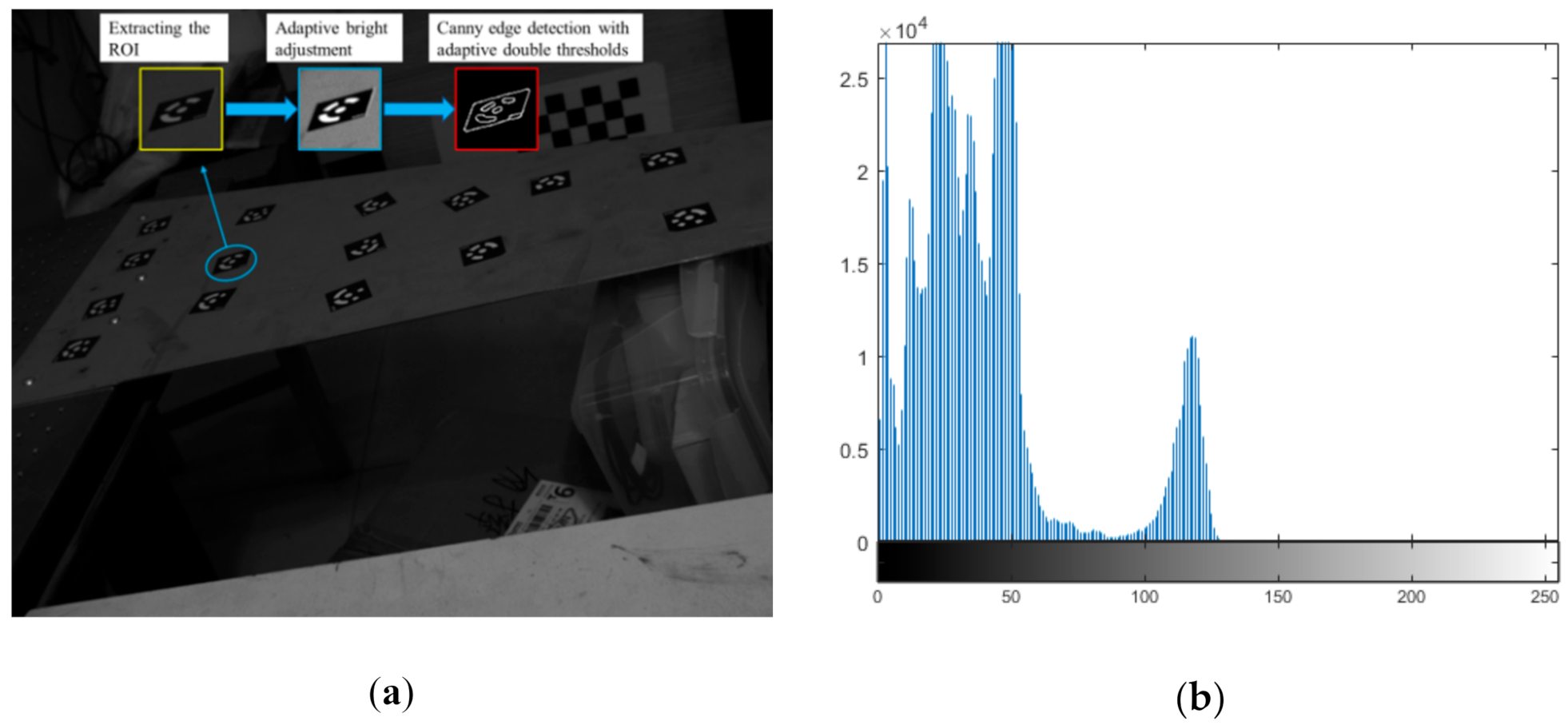






| Gaussian Noise Variance/Pepper Noise Density | The EEs of Outer Ellipse Center by Fitting | The EEs of Inner Ellipse Center by Fitting | The EEs of the CCCT Corrected Center by Our Method |
|---|---|---|---|
| 0.005 | 2.4072/2.4018 | 0.5238/0.5402 | 0.1087/0.0826 |
| 0.010 | 2.4072/2.4005 | 0.5314/0.5157 | 0.0967/0.1219 |
| 0.015 | 2.4072/2.4170 | 0.5146/0.5463 | 0.1186/0.0816 |
| 0.020 | 2.4103/2.3783 | 0.5165/0.4910 | 0.1169/0.1575 |
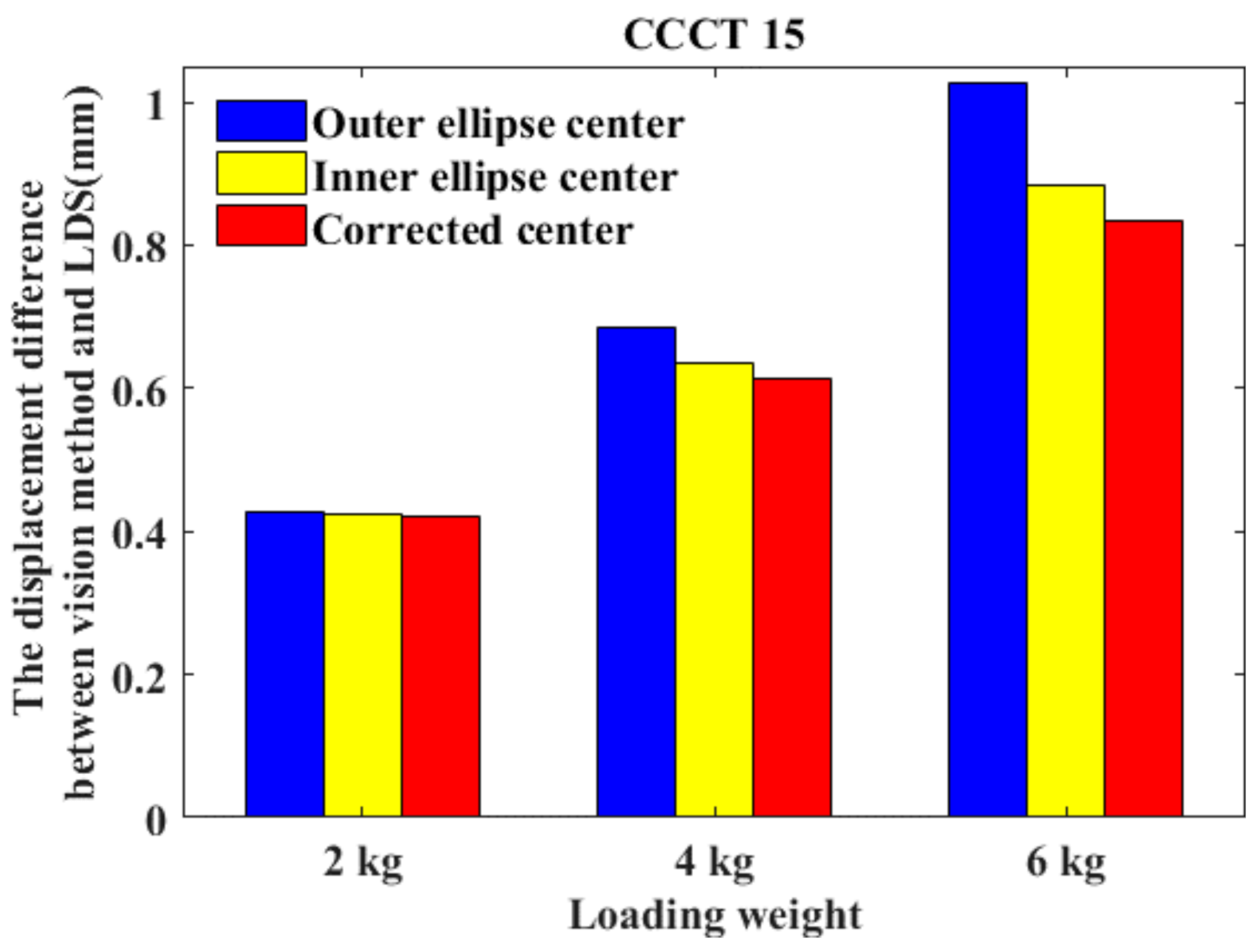
| Loading Weight | Vision Method Based on Outer Ellipse Center | Vision Method Based on Inner Ellipse Center | Vision Method Based on the Corrected Center | Laser Displacement Sensor |
|---|---|---|---|---|
| 2 kg | 10.2315 | 10.2365 | 10.2396 | 10.6599 |
| 4 kg | 20.5013 | 20.5491 | 20.5739 | 21.1859 |
| 6 kg | 30.0710 | 30.2142 | 30.2637 | 31.0984 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Su, X.; Guo, X.; Suo, T.; Yu, Q. A Novel Concentric Circular Coded Target, and Its Positioning and Identifying Method for Vision Measurement under Challenging Conditions. Sensors 2021, 21, 855. https://doi.org/10.3390/s21030855
Liu Y, Su X, Guo X, Suo T, Yu Q. A Novel Concentric Circular Coded Target, and Its Positioning and Identifying Method for Vision Measurement under Challenging Conditions. Sensors. 2021; 21(3):855. https://doi.org/10.3390/s21030855
Chicago/Turabian StyleLiu, Yan, Xin Su, Xiang Guo, Tao Suo, and Qifeng Yu. 2021. "A Novel Concentric Circular Coded Target, and Its Positioning and Identifying Method for Vision Measurement under Challenging Conditions" Sensors 21, no. 3: 855. https://doi.org/10.3390/s21030855
APA StyleLiu, Y., Su, X., Guo, X., Suo, T., & Yu, Q. (2021). A Novel Concentric Circular Coded Target, and Its Positioning and Identifying Method for Vision Measurement under Challenging Conditions. Sensors, 21(3), 855. https://doi.org/10.3390/s21030855




