Fundamental Limits of Non-Orthogonal Multiple Access (NOMA) for the Massive Gaussian Broadcast Channel in Finite Block-Length
Abstract
1. Introduction
- the traffic is characterized by a continuous data flow;
- the encoding length is over an infinite number of channel uses and, hence, without any latency constraint.
1.1. Multi-User Finite Block-Length: State of the Art
1.2. Contributions and Related Work
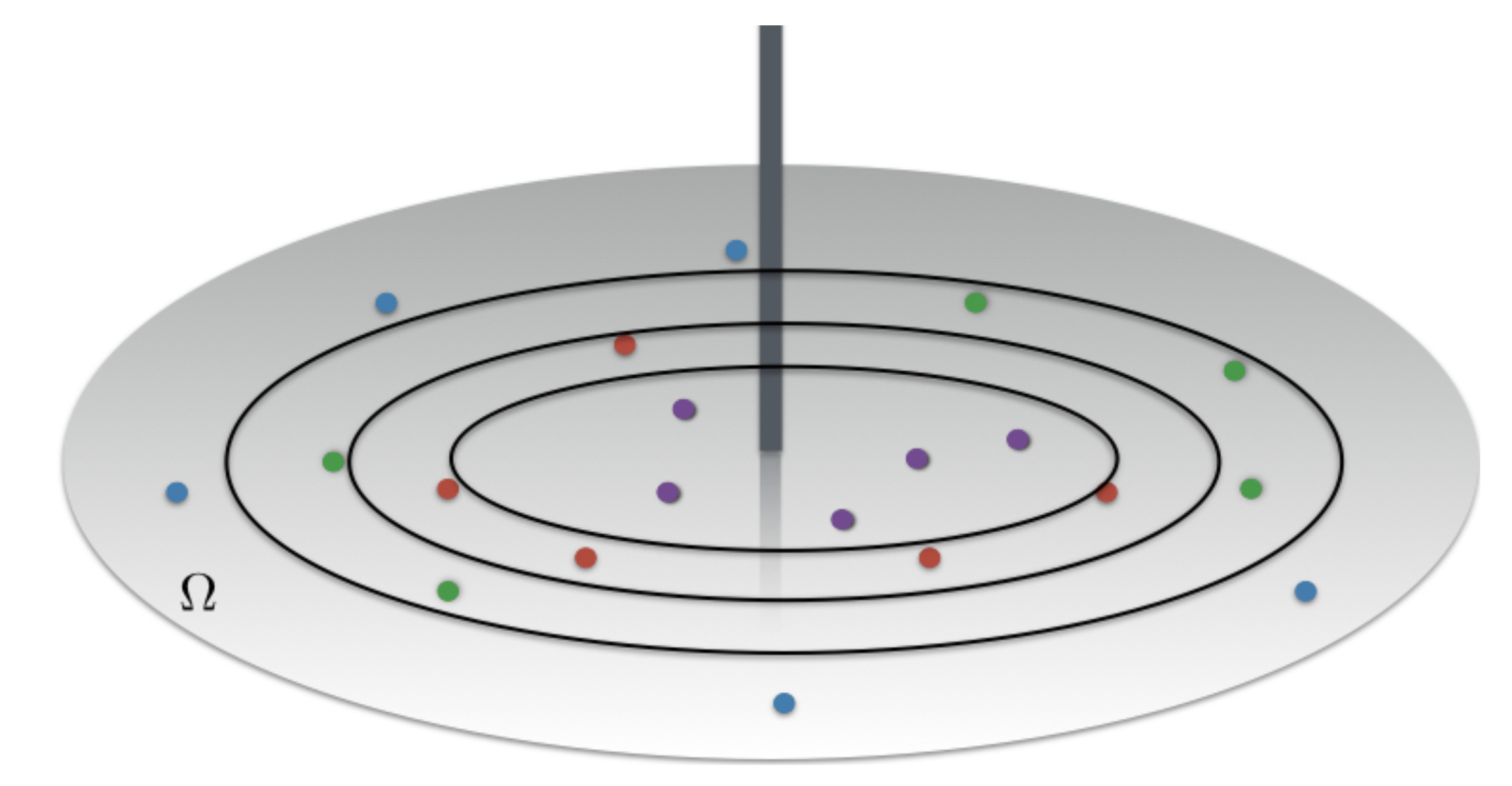
2. System Model
2.1. Model and Parameters
2.2. Reference Scenario
2.3. Superposition Coding
- The second user, with the largest equivalent noise, decodes its own signal in a Gaussian channel given byThe normalized version of this equation is given byFor this receiver the power of the equivalent additive Gaussian noise is , and its maximum achievable rate in the asymptotic regime, i.e., , is .
- The first user, with the smallest equivalent noise, has two decoding iterations. It first has to decode the second user information in the following channel:with the normalized version given byFor this receiver the power of the additive Gaussian noise is , and the achievable data rate is . Then, after canceling the second user signal, receiver one decodes its own signal:and can achieve its full achievable data rate, i.e., , in the asymptotic regime.
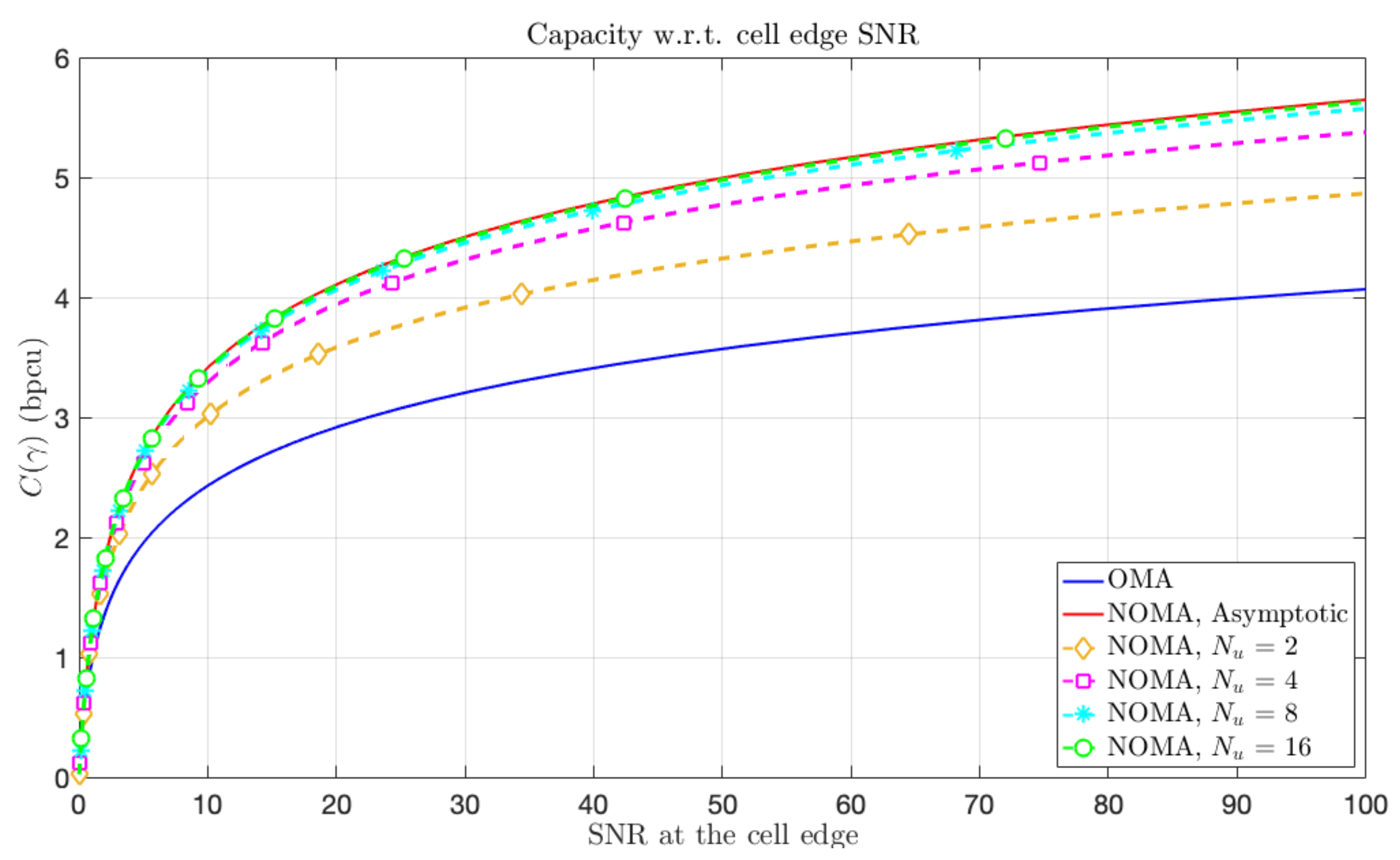
3. Symmetric Capacity in the Asymptotic Regime
3.1. Fundamental Trade-Off with SC
3.2. Fundamental Trade-Off with Orthogonal Sharing
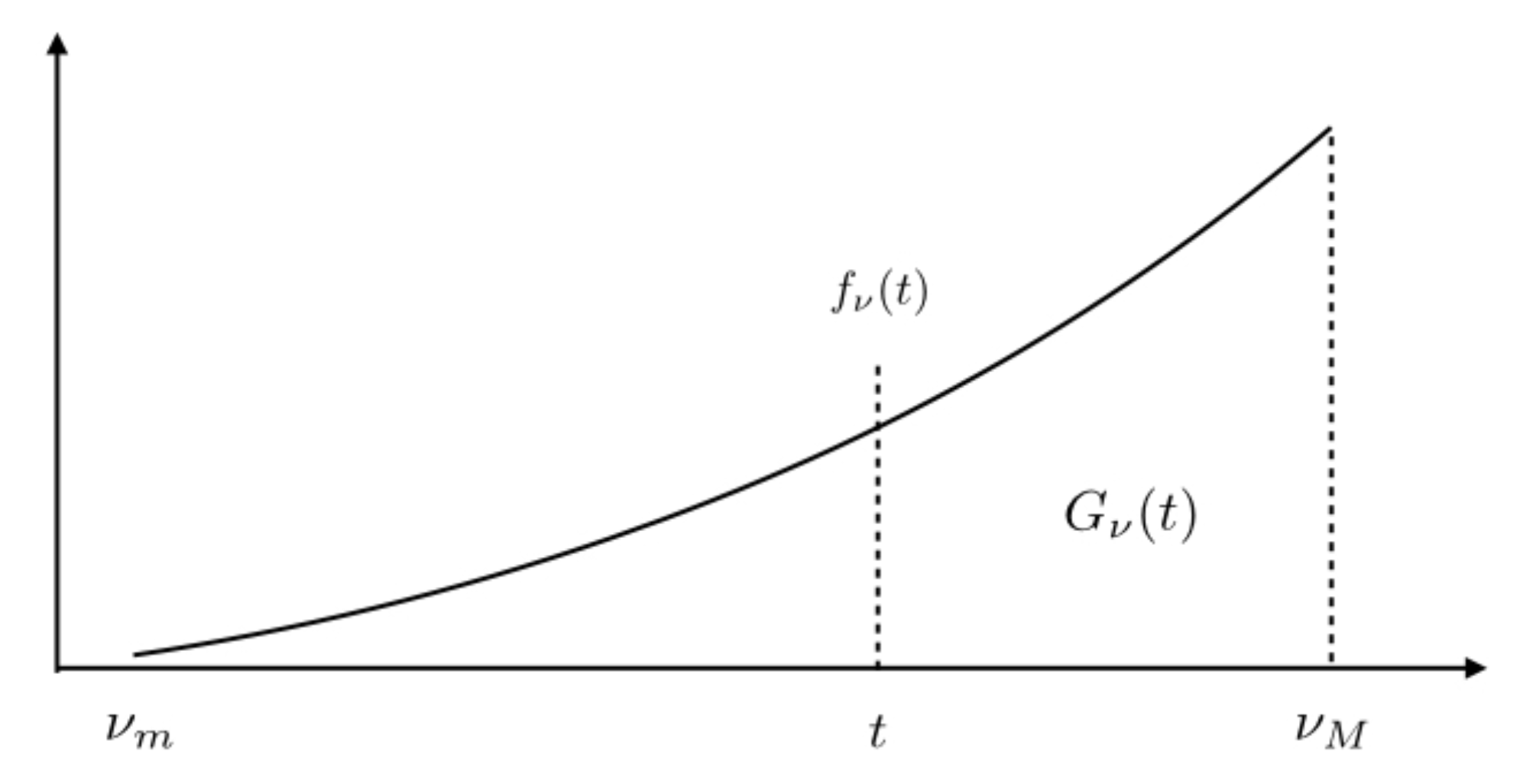
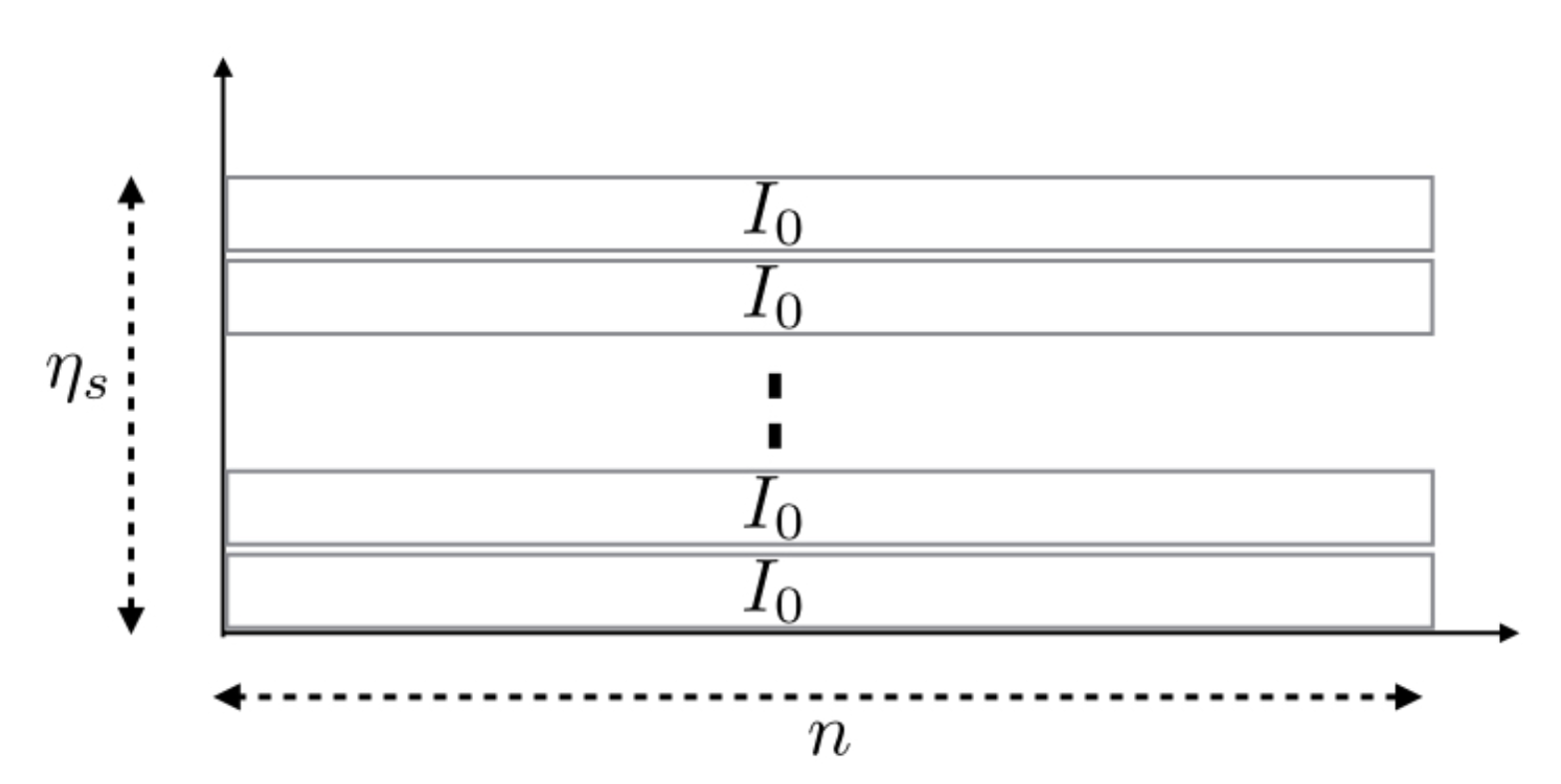
4. Finite Time Transmission Constrained Model
4.1. FTT Formulation
- a frame of channel uses of duration T, itself divided into L slots, each slot contains channel uses. One has ;
- a BS’s queue containing a random number of packets to be transmitted to a set of nodes , selected according to the PPP restricted to the subset .
4.2. Optimal Scheduling Policy
4.3. Optimal Scheduler When
4.4. Application Example
5. Finite Block-Length (FBL) Constrained Model
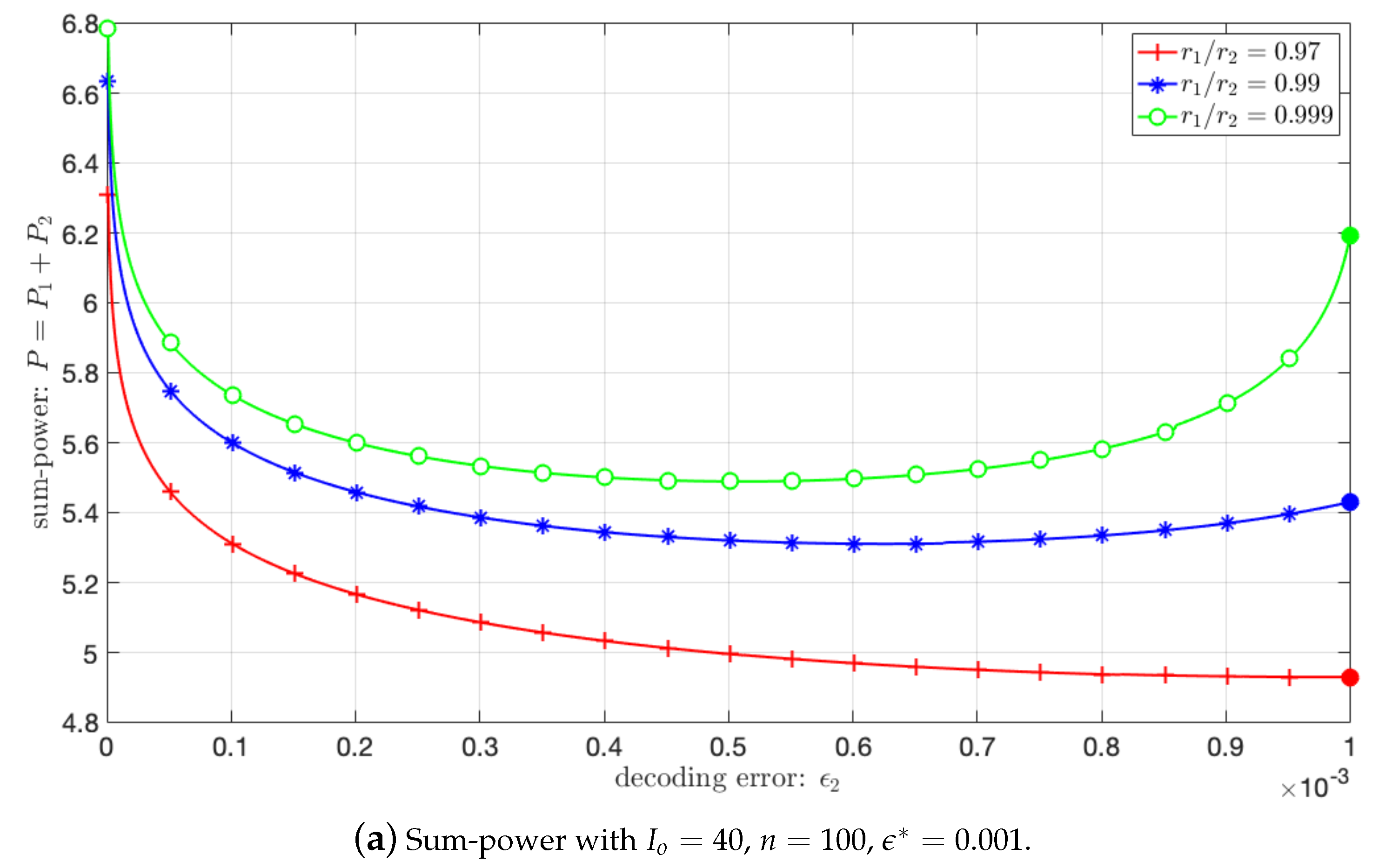
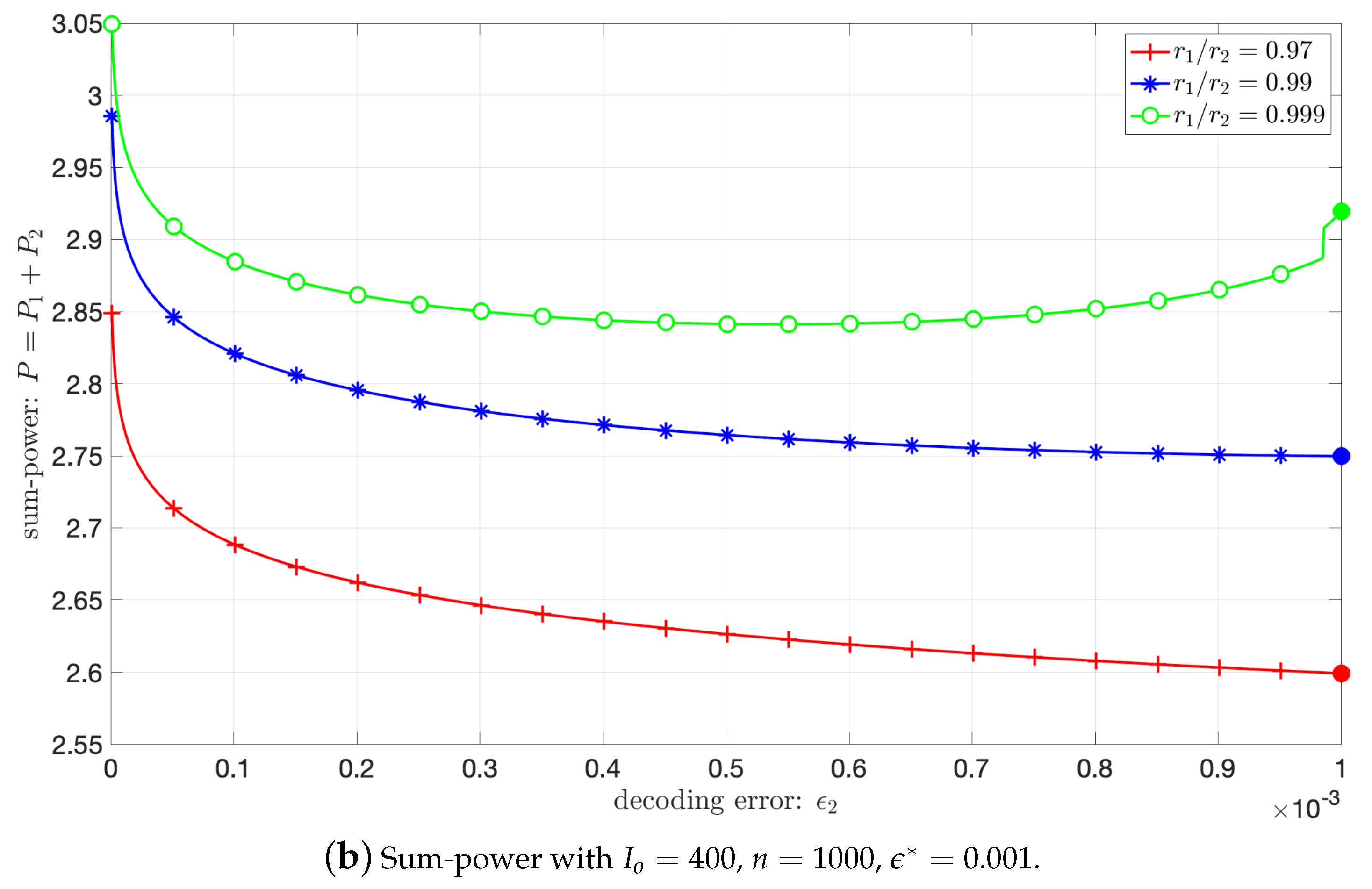
5.1. Achievable Minimal Power for the 2-User Gaussian BC
5.2. Impact of the Power Sharing between and
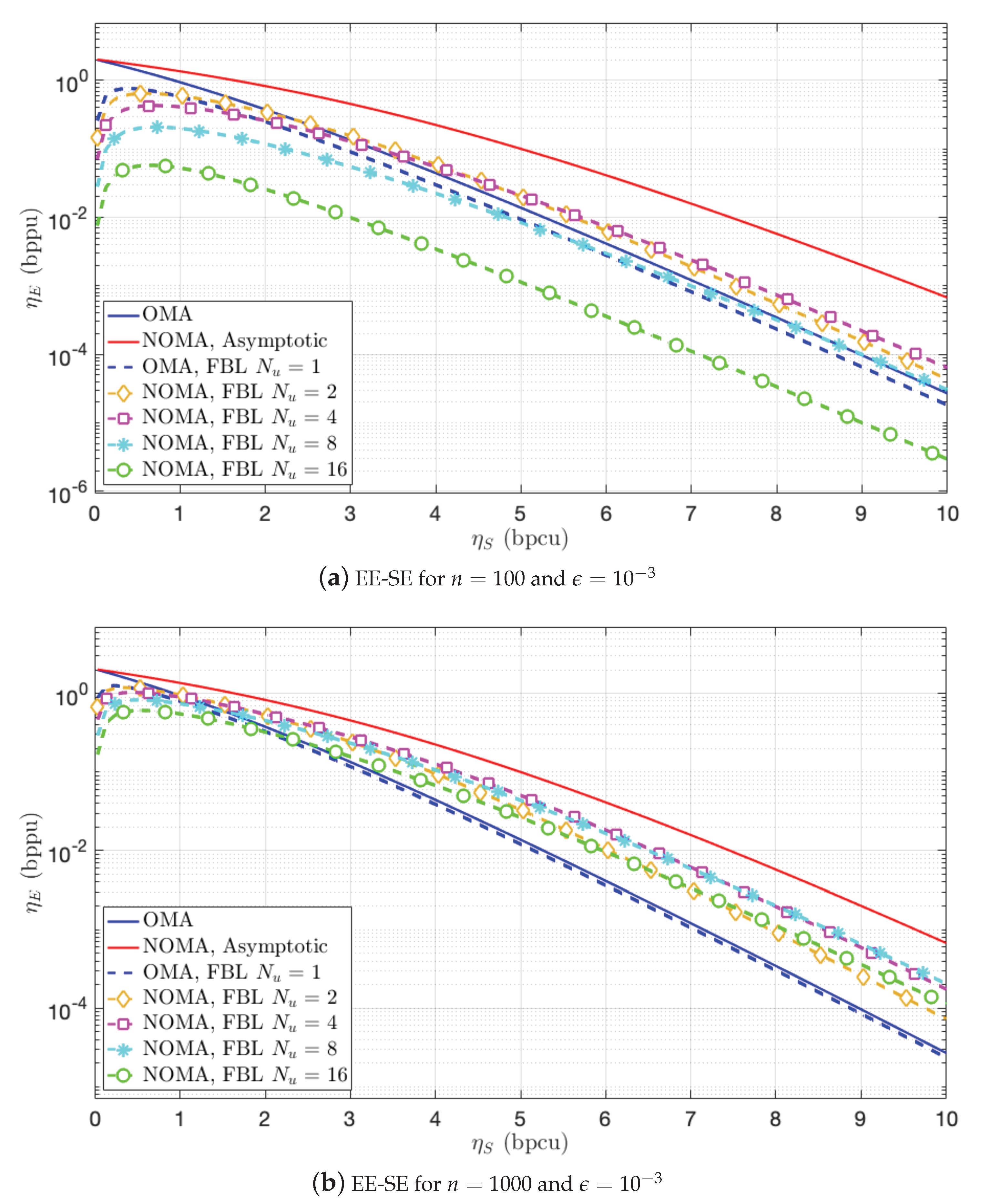
5.3. Achievable Power for the N-User BC
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AWGN | Additive White Gaussian Noise |
| BC | Broadcast Channel |
| BS | Base Station |
| ccdf | complementary cumulative distribution function |
| EE | Energy Efficiency |
| FBL | Finite block-length |
| FTT | Finite Time Transmission (constraint) |
| GSCBC | Gaussian Spatial Continuum Broadcast Channel |
| IoT | Internet of Things |
| MAC | Multiple Access Channel |
| NOMA | Non-Orthogonal Multiple Access |
| OMA | Orthogonal Multiple Access |
| probability density function | |
| PPP | Poisson Point Process |
| SC | Superposition Coding |
| SCBC | Spatial Continuum Broadcast Channel |
| SCMAC | Spatial Continuum Multiple Access Channel |
| SE | Spectral Efficiency |
| SIC | Successive Interference Cancellation |
| SINR | Signal-To-Interference-Plus-Noise Ratio |
| SNR | Signal-To-Noise Ratio |
| ULLC | Ultralow Latency Communications |
Appendix A. Proof of Lemma 1
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Vaezi, M.; Poor, H.V. NOMA: An information-theoretic perspective. In Multiple Access Techniques for 5G Wireless Networks and Beyond; Springer: Berlin/Heidelberg, Germany, 2019; pp. 167–193. [Google Scholar]
- Wu, Y.; Gao, X.; Zhou, S.; Yang, W.; Polyanskiy, Y.; Caire, G. Massive Access for Future Wireless Communication Systems. IEEE Wirel. Commun. 2020, 27, 148–156. [Google Scholar] [CrossRef]
- Verdú, S. Spectral efficiency in the wideband regime. IEEE Trans. Inf. Theory 2002, 48, 1319–1343. [Google Scholar] [CrossRef]
- Feinstein, A. A new basic theorem of information theory. IRE Trans. Inform. Theory 1954, 4, 2–22. [Google Scholar] [CrossRef]
- Shannon, C.E. Certain results in coding theory for noisy channels. Inf. Control 1957, 1, 6–25. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: Hoboken, NJ, USA, 1968. [Google Scholar]
- Polyanskiy, Y.; Poor, H.; Verdú, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Yang, W.; Durisi, G.; Koch, T.; Polyanskiy, Y. Quasi-Static Multiple-Antenna Fading Channels at Finite Blocklength. IEEE Trans. Inf. Theory 2014, 60, 4232–4265. [Google Scholar] [CrossRef]
- Hoydis, J.; Couillet, R.; Piantanida, P. The Second-Order Coding Rate of the MIMO Quasi-Static Rayleigh Fading Channel. IEEE Trans. Inf. Theory 2015, 61, 6591–6622. [Google Scholar] [CrossRef]
- Durisi, G.; Koch, T.; Östman, J.; Polyanskiy, Y.; Yang, W. Short-Packet Communications Over Multiple-Antenna Rayleigh-Fading Channels. IEEE Trans. Commun. 2016, 64, 618–629. [Google Scholar] [CrossRef]
- Mary, P.; Gorce, J.M.; Unsal, A.; Poor, H.V. Finite blocklength information theory: What is the practical impact on wireless communications? In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Jindal, N.; Vishwanath, S.; Goldsmith, A. On the duality of Gaussian multiple-access and broadcast channels. IEEE Trans. Inf. Theory 2004, 50, 768–783. [Google Scholar] [CrossRef]
- Verdu, S. Non-Asymptotic Achievability Bounds in Multi-User Information Theory. In Proceedings of the 50th Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 1–5 October 2012. [Google Scholar]
- Huang, Y.W.; Moulin, P. Finite Blocklength Coding for Multiple Access Channels. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Cambridge, MA, USA, 1–6 July 2012. [Google Scholar]
- MolavianJazi, E.; Laneman, J. A Second-Order Achievable Rate Region for Gaussian Multi-Access Channels via a Central Limit Theorem for Functions. IEEE Trans. Inf. Theory 2015, 61, 6719–6733. [Google Scholar] [CrossRef]
- Tan, V.Y.F.; Kosut, O. On the Dispersion of Three Network Information Theory Problems. IEEE Trans. Inf. Theory 2014, 60, 881–903. [Google Scholar] [CrossRef]
- Unsal, A.; Gorce, J.M. The Dispersion of Superposition Coding for Gaussian Broadcast Channels. In Proceedings of the IEEE Information Theory Workshop 2017, Kaohsiung, Taiwan, 6–10 November 2017. [Google Scholar]
- Shahi, S.; Tuninetti, D.; Devroye, N. On the capacity of strong asynchronous multiple access channels with a large number of users. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1486–1490. [Google Scholar]
- Kowshik, S.S.; Polyanskiy, Y. Quasi-static fading MAC with many users and finite payload. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 440–444. [Google Scholar]
- Chen, X.; Chen, T.Y.; Yu, W.; Guo, D. Capacity of Gaussian many-access channels. IEEE Trans. Inf. Theory 2017, 63, 3516–3539. [Google Scholar] [CrossRef]
- Cao, W.; Dytso, A.; Shkel, Y.; Feng, G.; Poor, H.V. Sum-Capacity of the MIMO Many-Access Gaussian Noise Channel. IEEE Trans. Commun. 2019, 67, 5419–5433. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, M.; Condoluci, M.; Dohler, M.; Johnson, S.J. On the Fundamental Limits of Random Non-Orthogonal Multiple Access in Cellular Massive IoT. IEEE J. Sel. Areas Commun. 2017, 35, 2238–2252. [Google Scholar] [CrossRef]
- Maatouk, A.; Assaad, M.; Ephremides, A. Minimizing the age of information: NOMA or OMA? In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Paris, France, 29 April–2 May 2019; pp. 102–108. [Google Scholar]
- Gorce, J.M.; Poor, H.V.; Kelif, J.M. Spatial continuum model: Toward the fundamental limits of dense wireless networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Gorce, J.M.; Fadlallah, Y.; Kelif, J.M.; Poor, H.V.; Gati, A. Fundamental limits of a dense IoT cell in the uplink. In Proceedings of the 15th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Paris, France, 15–19 May 2017. [Google Scholar]
- Gorce, J.M.; Mary, P.; Kélif, J.M. Towards Fundamental Limits of Bursty Multi-user Communications in Wireless Network. In Proceedings of the 10th Workshop on Information Theory Methods in Science and Engineering, Paris, France, 11–13 September 2017. [Google Scholar]
- Gorce, J.M.; Tsilimantos, D.; Ferrand, P.; Poor, H.V. Energy-Capacity Trade-off Bounds in a downlink typical cell. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014. [Google Scholar]
- Kelif, J.M.; Gorce, J.M.; Gati, A. Performance and Energy in Green Superposition Coding Wireless Networks: An Analytical Model. In Proceedings of the IEEE Globecom, Singapore, 4–8 December 2017. [Google Scholar]
- Chetot, L.; Gorce, J.M.; Kélif, J.M. Fundamental Limits in Cellular Networks with Point Process Partial Area Statistics. In Proceedings of the 17th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Avignon, France, 4–6 June 2019. [Google Scholar]
- Yu, W. On the fundamental limits of massive connectivity. In Proceedings of the 2017 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 12–17 February 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zwillinger, D.; Moll, V.; Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 8th ed.; Academic Press: Boston, MA, USA, 2014. [Google Scholar]
- Anade, D.; Gorce, J.M.; Mary, P.; Perlaza, S.M. An Upper Bound on the Error Induced by Saddlepoint Approximations—Applications to Information Theory. Entropy 2020, 22, 690. [Google Scholar] [CrossRef] [PubMed]
- Scarlett, J. On the dispersion of dirty paper coding. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2282–2286. [Google Scholar]

| ⋯ | |||||
|---|---|---|---|---|---|
| ⋯ | |||||
| ⋯ | |||||
| ⋯ | |||||
| ⋯ | |||||
| ⋮ |
| Slots | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ⋯ | |||
| ⋯ | ||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| 2 | ⋯ | |||||
| 1 | ⋯ | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorce, J.-M.; Mary, P.; Anade, D.; Kélif, J.-M. Fundamental Limits of Non-Orthogonal Multiple Access (NOMA) for the Massive Gaussian Broadcast Channel in Finite Block-Length. Sensors 2021, 21, 715. https://doi.org/10.3390/s21030715
Gorce J-M, Mary P, Anade D, Kélif J-M. Fundamental Limits of Non-Orthogonal Multiple Access (NOMA) for the Massive Gaussian Broadcast Channel in Finite Block-Length. Sensors. 2021; 21(3):715. https://doi.org/10.3390/s21030715
Chicago/Turabian StyleGorce, Jean-Marie, Philippe Mary, Dadja Anade, and Jean-Marc Kélif. 2021. "Fundamental Limits of Non-Orthogonal Multiple Access (NOMA) for the Massive Gaussian Broadcast Channel in Finite Block-Length" Sensors 21, no. 3: 715. https://doi.org/10.3390/s21030715
APA StyleGorce, J.-M., Mary, P., Anade, D., & Kélif, J.-M. (2021). Fundamental Limits of Non-Orthogonal Multiple Access (NOMA) for the Massive Gaussian Broadcast Channel in Finite Block-Length. Sensors, 21(3), 715. https://doi.org/10.3390/s21030715






