Efficient Online Object Tracking Scheme for Challenging Scenarios
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contributions
- We introduce novel criteria for detecting occlusion by utilizing APCE, model update rules, and previous history of the modified response map to prevent the tracking model from wrong updates.
- We introduce an effective occlusion handling mechanism by incorporating a modified feedback-based fractional-gain Kalman filter in the spatiotemporal context framework to track an object’s motion.
- We incorporate a max-pooling-based scale scheme by maximizing over posterior probability in the STC framework’s detection stage. We applied a combination of STC and max-pooling to attain higher accuracy.
- We introduce an APCE-based adaptive learning rate mechanism that utilizes information of current frame and previous history to reduce error accumulation and correctly updates from the wrong appearance of the target.
1.3. Organization
2. Review of STC and Fractional Calculus
2.1. STC Tracking
2.2. Fractional Calculus
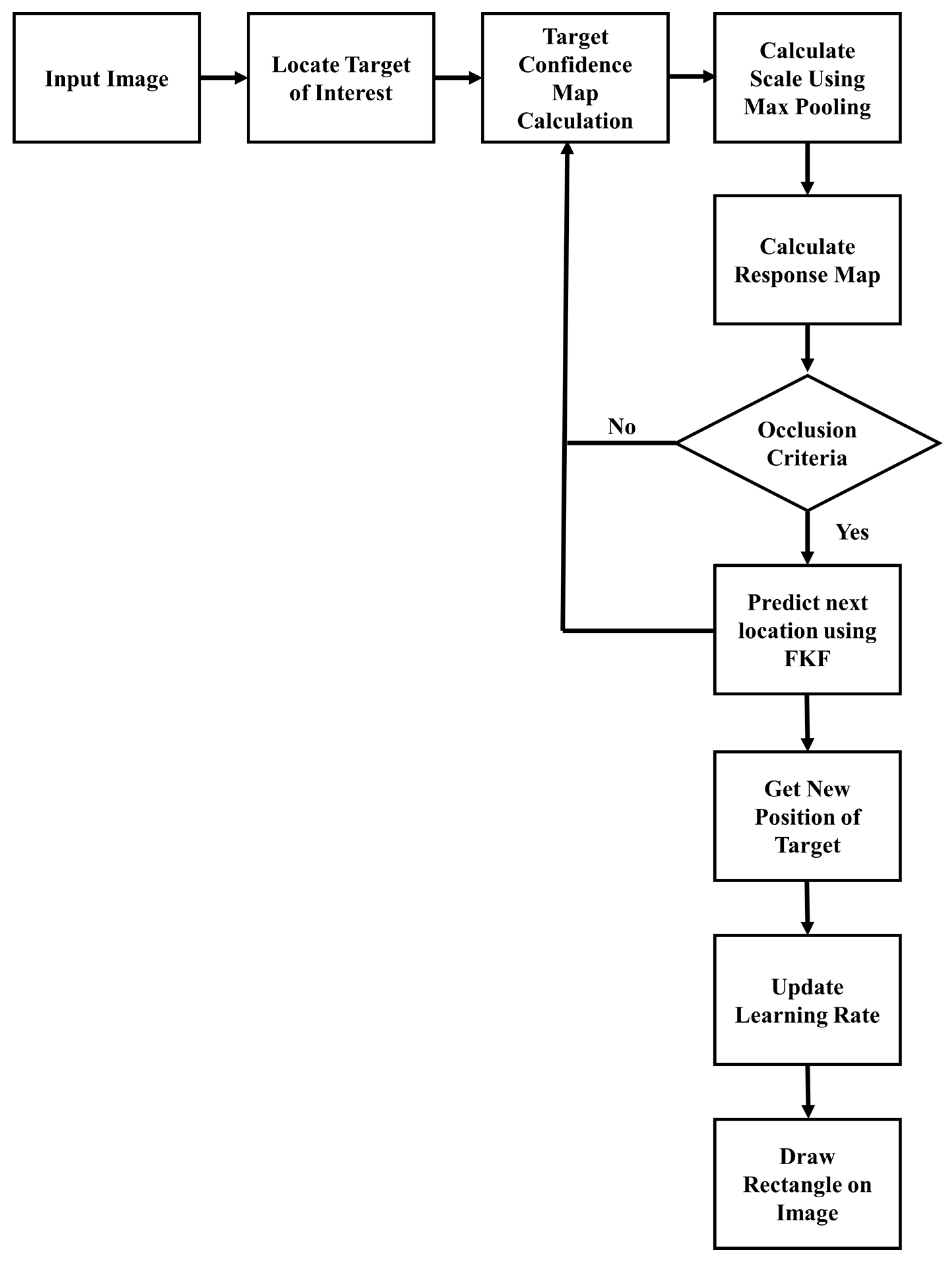
3. Proposed Solution
3.1. Scale Integration Scheme
3.2. Occlusion Detection Mechanism
- When or, it indicates that the target is coming out of the shelter, and both the tracking and model updates are based on STC.
- When and, it indicates that the target is in the occlusion state and tracking is based on the fractional-gain Kalman filter. The tracking model is also updated based on the Kalman filter prediction.
- When or, it indicates that the target occludes, and both the tracking and model update are based on STC.
- When or, it indicates that the target tracking is good and that both the tracking and model update are based on STC.
3.3. Fractional-Gain Kalman Filter
3.4. Adaptive Learning Rate
| Algorithm 1: Proposed Tracking Method |
| Input: Video with initialized ground truth on frame 1. Output: Rectangle on each frame. for 1st to the last frame. Compute context prior model by using (3). Compute confidence map by using (11). Compute center of target location. Estimate scale by using (15). Compute APCE by using (16). Determine occlusion detection using (17) and (18). Check four rules of occlusion detection given in Section 3.2. if rule 2 occurs Activate fractional-gain Kalman filter Compute fractional Kalman gain by using (30). Predict position by using (22). Compute error covariance by using (28). end Calculate occlusion indicator using (31). Calculate learning rate using (32) Update context prior model by using (3). Update spatial context model by using (9). Update STC model by using (12). Estimate the position of target. End |
4. Performance Analysis
4.1. Evaluation Criteria
4.2. Quantitative Analysis
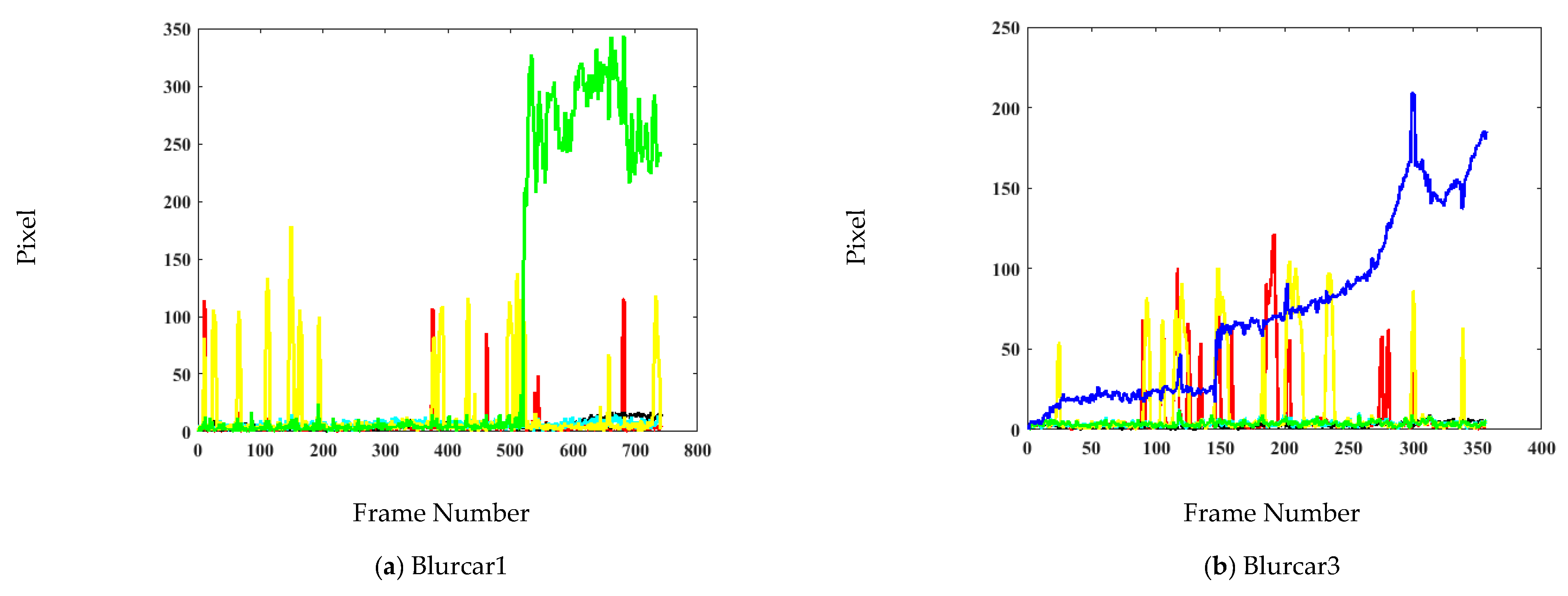
4.3. Qualitative Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pantrigo, J.J.; Hernández, J.; Sánchez, A. Multiple and variable target visual tracking for video-surveillance applications. Pattern Recognit. Lett. 2010, 31, 1577–1590. [Google Scholar] [CrossRef]
- Ahmed, I.; Jeon, G. A real-time person tracking system based on SiamMask network for intelligent video surveillance. J. Real-Time Image Process 2021, 18, 1803–1814. [Google Scholar] [CrossRef]
- Carcagnì, P.; Mazzeo, P.L.; Distante, C.; Spagnolo, P.; Adamo, F.; Indiveri, G. A UAV-Based Visual Tracking Algorithm for Sensible Areas Surveillance. In Proceedings of the International Workshop on Modelling and Simulation for Autonomous Systems, Rome, Italy, 5–6 May 2014; Springer: New York, NY, USA, 2014; pp. 12–19. [Google Scholar]
- Geiger, A.; Lauer, M.; Wojek, C.; Stiller, C.; Urtasun, R. 3d traffic scene understanding from movable platforms. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1012–1025. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Shi, J.; Yeung, D.-Y.; Jia, J. Understanding and diagnosing visual tracking systems. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3101–3109. [Google Scholar]
- Bonatti, R.; Ho, C.; Wang, W.; Choudhury, S.; Scherer, S. Towards a robust aerial cinematography platform: Localizing and tracking moving targets in unstructured environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 229–236. [Google Scholar]
- Petitti, A.; di Paola, D.; Milella, A.; Mazzeo, P.L.; Spagnolo, P.; Cicirelli, G.; Attolico, G. A distributed heterogeneous sensor network for tracking and monitoring. In Proceedings of the 2013 10th IEEE International Conference on Advanced Video and Signal Based Surveillance, Krakow, Poland, 27–30 August 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 426–431. [Google Scholar]
- Wu, Y.; Lim, J.; Yang, M.-H. Online object tracking: A benchmark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2411–2418. [Google Scholar]
- Danelljan, M.; Khan, F.S.; Felsberg, M.; Granström, K.; Heintz, F.; Rudol, P.; Wzorek, M.; Kvarnström, J.; Doherty, P. A low-level active vision framework for collaborative unmanned aircraft systems. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: New York, NY, USA, 2014; pp. 223–237. [Google Scholar]
- Petitti, A.; di Paola, D.; Milella, A.; Mazzeo, P.L.; Spagnolo, P.; Cicirelli, G.; Attolico, G. A heterogeneous robotic network for distributed ambient assisted living. In Human Behavior Understanding in Networked Sensing; Springer: Cham, Switzerland, 2014; pp. 321–338. [Google Scholar]
- Amorim, T.G.S.; Souto, L.A.; Nascimento, T.P.D.; Saska, M. Multi-Robot Sensor Fusion Target Tracking with Observation Constraints. IEEE Access 2021, 9, 52557–52568. [Google Scholar] [CrossRef]
- Ali, A.; Kausar, H.; Muhammad, I.K. Automatic visual tracking and firing system for anti aircraft machine gun. In Proceedings of the 6th International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, 19–22 January 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 253–257. [Google Scholar]
- Cao, J.; Song, C.; Song, S.; Xiao, F.; Zhang, X.; Liu, Z.; Ang, M.H., Jr. Robust Object Tracking Algorithm for Autonomous Vehicles in Complex Scenes. Remote Sens. 2021, 13, 3234. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Yoo, J.; Kwon, S. Efficient Single-Shot Multi-Object Tracking for Vehicles in Traffic Scenarios. Sensors 2021, 21, 6358. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Jalil, A.; Niu, J.; Zhao, X.; Rathore, S.; Ahmed, J.; Iftikhar, M.A. Visual object tracking—Classical and contemporary approaches. Front. Comput. Sci. 2016, 10, 167–188. [Google Scholar] [CrossRef]
- Mazzeo, P.L.; Spagnolo, P.; Distante, C. Visual Tracking by using dense local descriptors. In Adaptive Optics: Analysis, Methods & Systems; Optical Society of America: Washington, DC, USA, 2015; p. JT5A-16. [Google Scholar]
- Ali, A.; Jalil, A.; Ahmed, J. A new template updating method for correlation tracking. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Abbasi, S.; Rezaeian, M. Visual object tracking using similarity transformation and adaptive optical flow. Multimed. Tools Appl. 2021, 80, 33455–33473. [Google Scholar] [CrossRef]
- Adamo, F.; Mazzeo, P.L.; Spagnolo, P.; Distante, C. A FragTrack algorithm enhancement for total occlusion management in visual object tracking. In Automated Visual Inspection and Machine Vision; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9530, p. 95300R. [Google Scholar]
- Yang, L.; Zhong-li, W.; Bai-gen, C. An intelligent vehicle tracking technology based on SURF feature and Mean-shift algorithm. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1224–1228. [Google Scholar]
- Matsushita, Y.; Yamaguchi, T.; Harada, H. Object tracking using virtual particles driven by optical flow and Kalman filter. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 15–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1064–1069. [Google Scholar]
- Mei, X.; Ling, H. Robust visual tracking and vehicle classification via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2259–2272. [Google Scholar] [PubMed] [Green Version]
- Judy, M.; Poore, N.C.; Liu, P.; Yang, T.; Britton, C.; Bolme, D.S.; Mikkilineni, A.K.; Holleman, J. A digitally interfaced analog correlation filter system for object tracking applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2764–2773. [Google Scholar] [CrossRef]
- Adamo, F.; Carcagnì, P.; Mazzeo, P.L.; Distante, C.; Spagnolo, P. TLD and Struck: A Feature Descriptors Comparative Study. In International Workshop on Activity Monitoring by Multiple Distributed Sensing; Springer: Cham, Switzerland, 2014; pp. 52–63. [Google Scholar]
- Dong, E.; Deng, M.; Tong, J.; Jia, C.; Du, S. Moving vehicle tracking based on improved tracking–learning–detection algorithm. IET Comput. Vis. 2019, 13, 730–741. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Zhang, L.; Liu, Q.; Zhang, D.; Yang, M.H. Fast visual tracking via dense spatio-temporal context learning. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: New York, NY, USA, 2014; Volume 8693, pp. 127–141. [Google Scholar] [CrossRef] [Green Version]
- Die, J.; Li, N.; Liu, Y.; Wu, Y. Correlation Filter Tracking Algorithm Based on Spatio-Temporal Context. In Proceedings of the International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Kunming, China, 20–22 July 2019; Springer: Cham, Switzerland, 2019; pp. 279–289. [Google Scholar]
- Yang, X.; Zhu, S.; Zhou, D.; Zhang, Y. An improved target tracking algorithm based on spatio-temporal context under occlusions. Multidimens. Syst. Signal Process. 2020, 31, 329–344. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Qin, J. Adaptive spatio-temporal context learning for visual tracking. Imaging Sci. J. 2019, 67, 136–147. [Google Scholar] [CrossRef]
- Zhang, D.; Dong, E.; Yu, H.; Jia, C. An Improved Object Tracking Algorithm Combining Spatio-Temporal Context and Selection Update. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4822–4827. [Google Scholar]
- Song, H.; Wu, Y.; Zhou, G. Design of bio-inspired binocular UAV detection system based on improved STC algorithm of scale transformation and occlusion detection. Int. J. Micro Air Veh. 2021, 13, 17568293211004846. [Google Scholar] [CrossRef]
- Feng, F.; Shen, B.; Liu, H. Visual object tracking: In the simultaneous presence of scale variation and occlusion. Syst. Sci. Control Eng. 2018, 6, 456–466. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhou, X.; Chan, S.; Chen, S. Robust object tracking via large margin and scale-adaptive correlation filter. IEEE Access 2017, 6, 12642–12655. [Google Scholar] [CrossRef]
- Zhang, M.; Xing, J.; Gao, J.; Hu, W. Robust visual tracking using joint scale-spatial correlation filters. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1468–1472. [Google Scholar]
- Nguyen, A.H.; Mai, L.; Do, H.N. Visual Object Tracking Method of Spatio-temporal Context Learning with Scale Variation. In Proceedings of the International Conference on the Development of Biomedical Engineering in Vietnam, Ho Chi Minh City, Vietnam, 20–22 July 2020; Springer: Cham, Switzerland, 2020; pp. 733–742. [Google Scholar]
- Wang, X.; Hou, Z.; Yu, W.; Pu, L.; Jin, Z.; Qin, X. Robust occlusion-aware part-based visual tracking with object scale adaptation. Pattern Recognit. 2018, 81, 456–470. [Google Scholar] [CrossRef]
- Ma, H.; Lin, Z.; Acton, S.T. FAST: Fast and Accurate Scale Estimation for Tracking. IEEE Signal Process. Lett. 2019, 27, 161–165. [Google Scholar] [CrossRef]
- Danelljan, M.; Häger, G.; Khan, F.; Felsberg, M. Accurate scale estimation for robust visual tracking. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014; BMVA Press: Durham, UK, 2014. [Google Scholar]
- Li, Y.; Zhu, J. A scale adaptive kernel correlation filter tracker with feature integration. In Proceedings of the European conference on computer vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 254–265. [Google Scholar]
- Bibi, A.; Ghanem, B. Multi-template scale-adaptive kernelized correlation filters. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 50–57. [Google Scholar]
- Lu, H.; Xiong, D.; Xiao, J.; Zheng, Z. Robust long-term object tracking with adaptive scale and rotation estimation. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420909736. [Google Scholar] [CrossRef]
- Yin, X.; Liu, G.; Ma, X. Fast Scale Estimation Method in Object Tracking. IEEE Access 2020, 8, 31057–31068. [Google Scholar] [CrossRef]
- Ma, H.; Acton, S.T.; Lin, Z. SITUP: Scale invariant tracking using average peak-to-correlation energy. IEEE Trans. Image Process. 2020, 29, 3546–3557. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehmood, K.; Jalil, A.; Ali, A.; Khan, B.; Murad, M.; Khan, W.U.; He, Y. Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking. Electronics 2021, 10, 43. [Google Scholar] [CrossRef]
- Khan, B.; Ali, A.; Jalil, A.; Mehmood, K.; Murad, M.; Awan, H. AFAM-PEC: Adaptive Failure Avoidance Tracking Mechanism Using Prediction-Estimation Collaboration. IEEE Access 2020, 8, 149077–149092. [Google Scholar] [CrossRef]
- Mehmood, K.; Jalil, A.; Ali, A.; Khan, B.; Murad, M.; Cheema, K.M.; Milyani, A.H. Spatio-Temporal Context, Correlation Filter and Measurement Estimation Collaboration Based Visual Object Tracking. Sensors 2021, 21, 2841. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Wang, J.; Miao, Y.; Yang, Y.; Zhao, Z.; Wang, Z.; Sun, Q.; Wu, D.O. Combining Spatio-Temporal Context and Kalman Filtering for Visual Tracking. Mathematics 2019, 7, 1059. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Mirza, S.M. Object tracking using correlation, Kalman filter and fast means shift algorithms. In Proceedings of the 2006 International Conference on Emerging Technologies, Peshawar, Pakistan, 13–14 November 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 174–178. [Google Scholar]
- Kaur, H.; Sahambi, J.S. Vehicle tracking using fractional order Kalman filter for non-linear system. In Proceedings of the International Conference on Computing, Communication & Automation, Greater Noida, India, 15–16 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 474–479. [Google Scholar]
- Soleh, M.; Jati, G.; Hilman, M.H. Multi Object Detection and Tracking Using Optical Flow Density–Hungarian Kalman Filter (Ofd-Hkf) Algorithm for Vehicle Counting. J. Ilmu Komput. dan Inf. 2018, 11, 17–26. [Google Scholar] [CrossRef]
- Farahi, F.; Yazdi, H.S. Probabilistic Kalman filter for moving object tracking. Signal Process. Image Commun. 2020, 82, 115751. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Gunjal, B.R.; Shinde, H.A.; Vanam, S.M.; Aher, S.S. Moving object tracking using kalman filter. In Proceedings of the 2018 International Conference on Advances in Communication and Computing Technology (ICACCT), Sangamner, India, 8–9 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 544–547. [Google Scholar]
- Ali, A.; Jalil, A.; Ahmed, J.; Iftikhar, M.A.; Hussain, M. Correlation, Kalman filter and adaptive fast mean shift based heuristic approach for robust visual tracking. Signal Image Video Process. 2015, 9, 1567–1585. [Google Scholar] [CrossRef]
- Kaur, H.; Sahambi, J.S. Vehicle tracking in video using fractional feedback Kalman filter. IEEE Trans. Comput. Imaging 2016, 2, 550–561. [Google Scholar] [CrossRef]
- Zhou, X.; Fu, D.; Shi, Y.; Wu, C. Adaptive Learning Compressive Tracking Based on Kalman Filter. In Proceedings of the International Conference on Image and Graphics, Shanghai, China, 13–15 September 2017; Springer: Cham, Switzerland, 2017; pp. 243–253. [Google Scholar]
- Zhang, Y.; Yang, Y.; Zhou, W.; Shi, L.; Li, D. Motion-aware correlation filters for online visual tracking. Sensors 2018, 18, 3937. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mueller, M.; Smith, N.; Ghanem, B. Context-aware correlation filter tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1396–1404. [Google Scholar]
- Shin, J.; Kim, H.; Kim, D.; Paik, J. Fast and robust object tracking using tracking failure detection in kernelized correlation filter. Appl. Sci. 2020, 10, 713. [Google Scholar] [CrossRef] [Green Version]
- Sierociuk, D.; Dzieliński, A. Fractional Kalman filter algorithm for the states, parameters and order of fractional system estimation. Int. J. Appl. Math. Comput. Sci. 2006, 16, 129–140. [Google Scholar]
- Wang, M.; Liu, Y.; Huang, Z. Large margin object tracking with circulant feature maps. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4021–4029. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative scale space tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2544–2550. [Google Scholar]




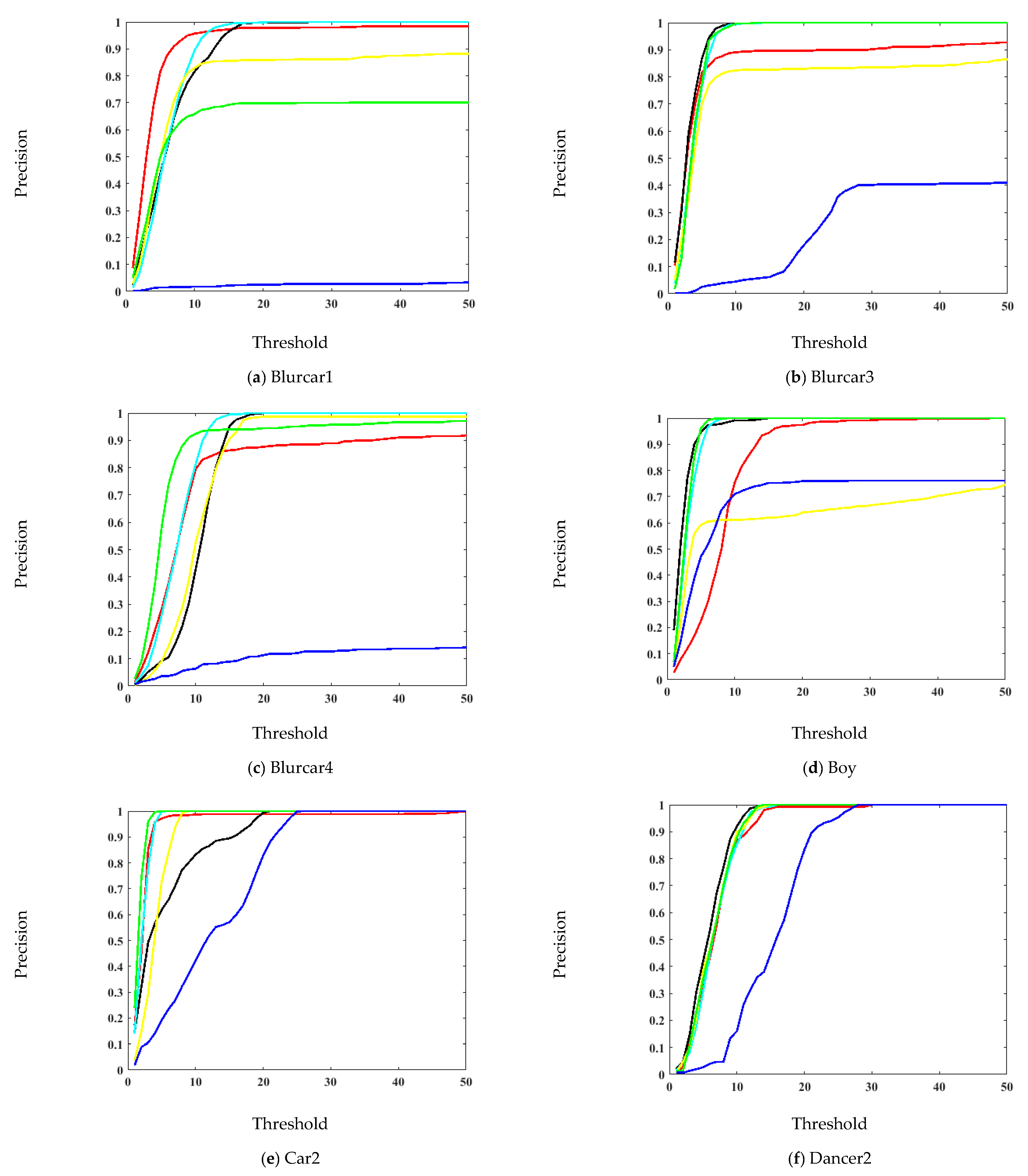
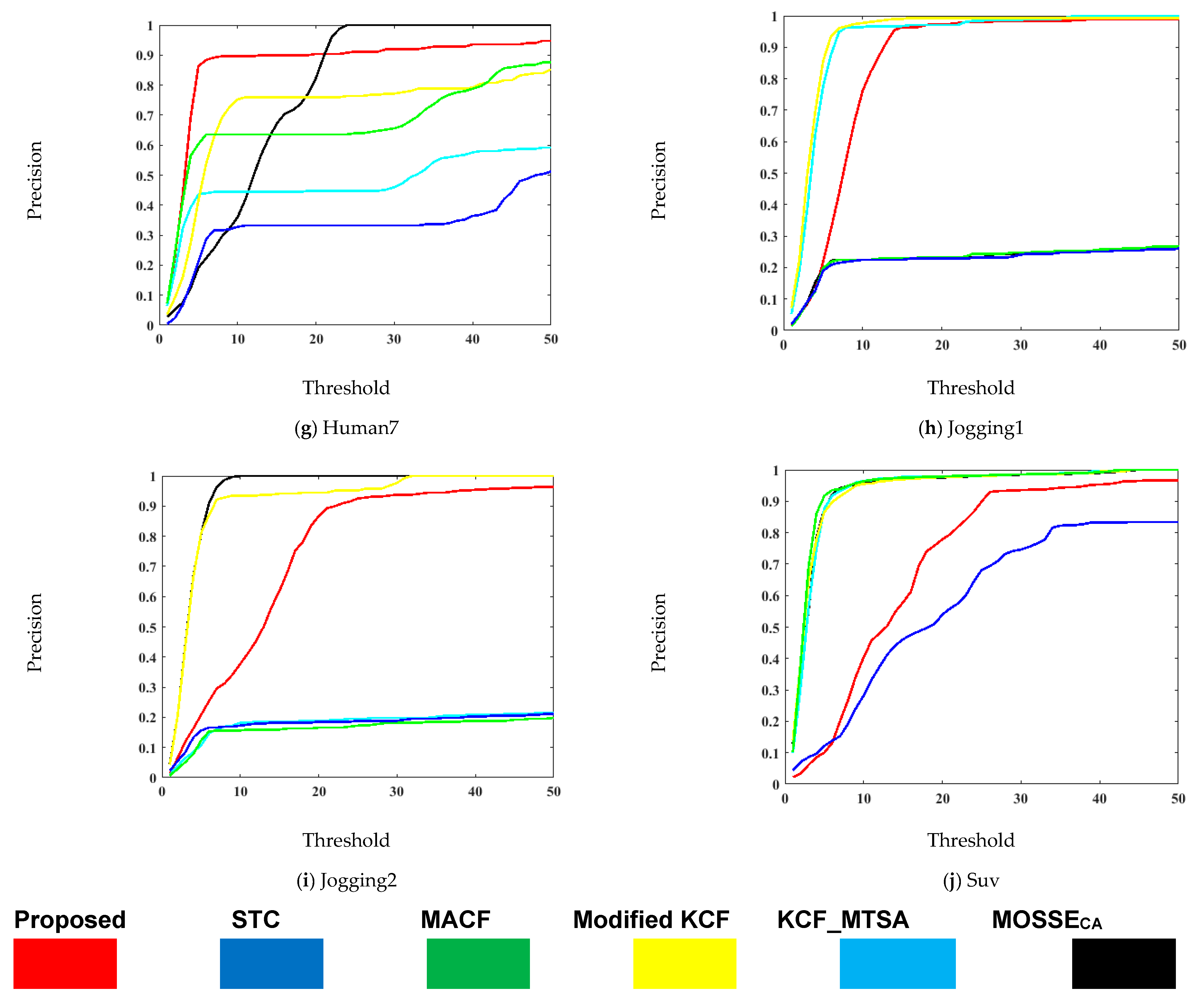
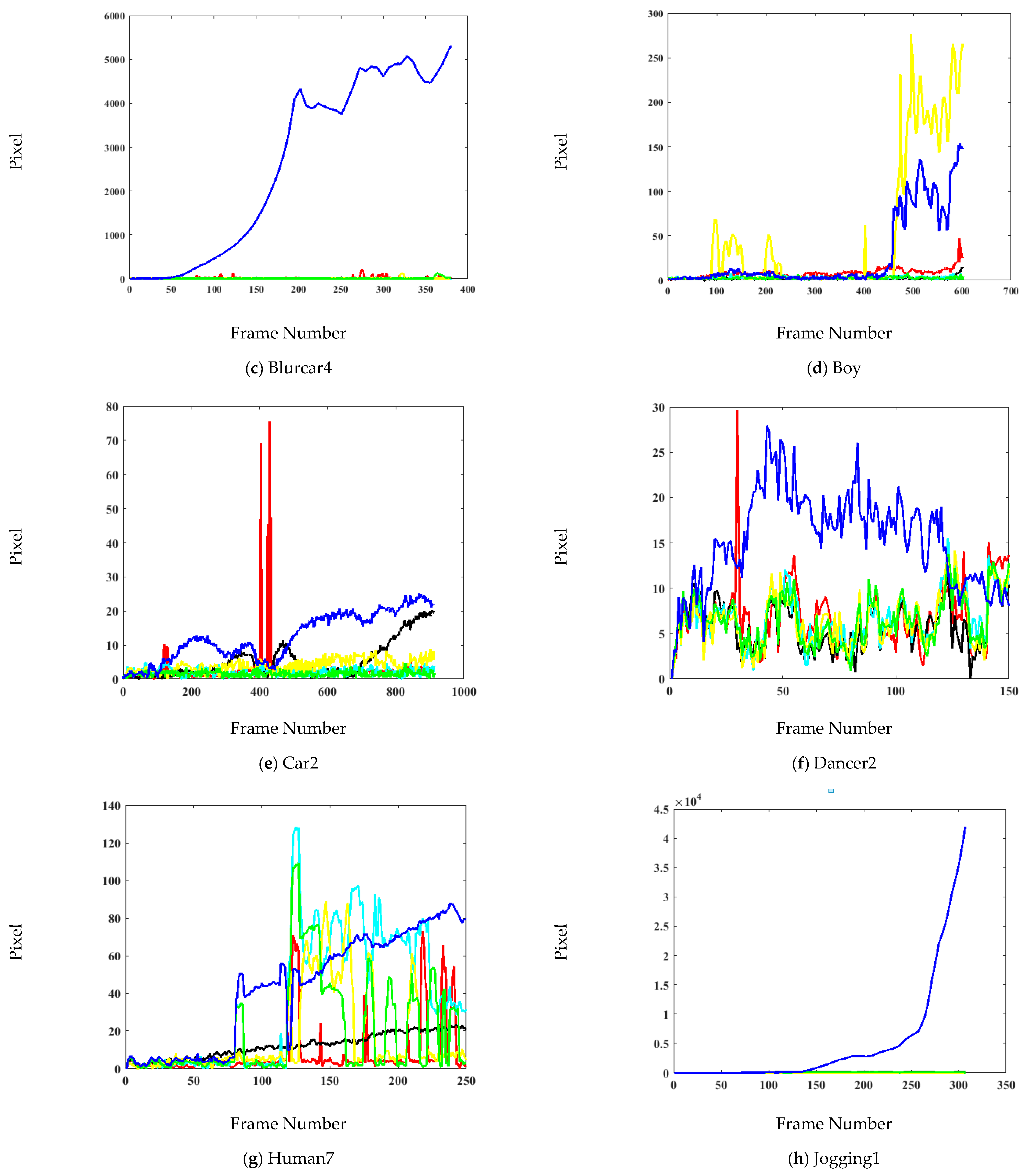
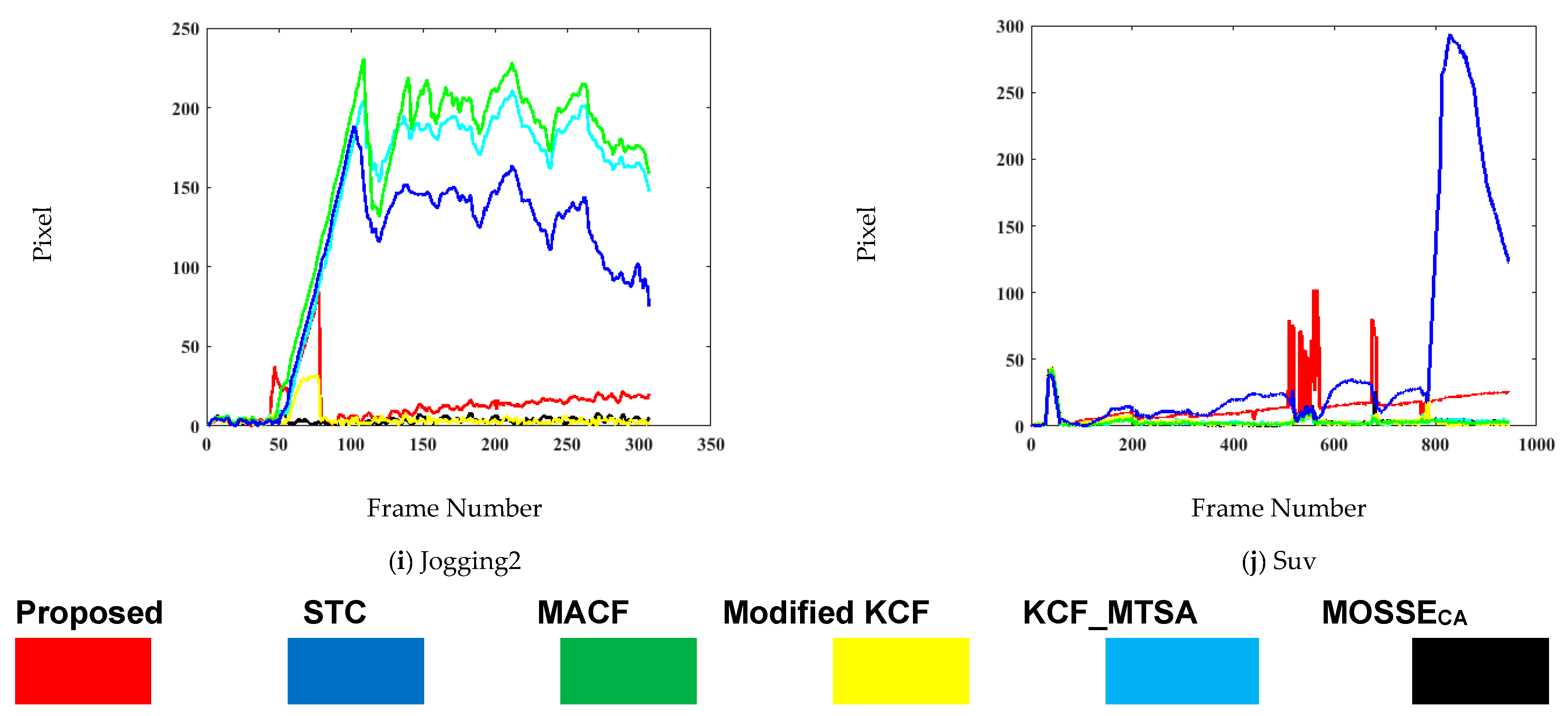



| Sequence | Proposed | Modified KCF [59] | STC [27] | MACF [57] | MOSSECA [58] | KCF_MTSA [41] |
|---|---|---|---|---|---|---|
| Blurcar1 | 0.978 | 0.858 | 0.024 | 0.698 | 0.999 | 0.999 |
| Blurcar3 | 0.896 | 0.829 | 0.406 | 1 | 1 | 1 |
| Blurcar4 | 0.876 | 0.987 | 0.113 | 0.944 | 1 | 1 |
| Boy | 0.973 | 0.64 | 0.761 | 1 | 1 | 1 |
| Car2 | 0.988 | 1 | 1 | 1 | 0.993 | 1 |
| Dancer2 | 0.993 | 1 | 1 | 1 | 1 | 1 |
| Human7 | 0.904 | 0.76 | 0.332 | 0.636 | 0.824 | 0.448 |
| Jogging1 | 0.973 | 0.993 | 0.228 | 0.231 | 0.231 | 0.964 |
| Jogging2 | 0.866 | 0.945 | 0.186 | 0.166 | 1 | 0.189 |
| Suv | 0.778 | 0.978 | 0.805 | 0.978 | 0.976 | 0.98 |
| Mean Precision | 0.923 | 0.899 | 0.486 | 0.765 | 0.902 | 0.858 |
| Sequence | Proposed | Modified KCF [59] | STC [27] | MACF [57] | MOSSECA [58] | KCF_MTSA [41] |
|---|---|---|---|---|---|---|
| Blurcar1 | 4.86 | 16.05 | 1.31 × 106 | 85.16 | 6.34 | 6.01 |
| Blurcar3 | 9.12 | 14.46 | 71.37 | 3.69 | 2.98 | 3.7 |
| Blurcar4 | 15.01 | 11.19 | 2.61 × 103 | 8.04 | 10.15 | 7.15 |
| Boy | 8.09 | 50.34 | 27.4 | 2.65 | 2.31 | 2.91 |
| Car2 | 2.68 | 3.96 | 12.43 | 1.55 | 5.39 | 2.13 |
| Dancer2 | 6.82 | 6.41 | 15.3 | 6.48 | 5.8 | 6.68 |
| Human7 | 7.59 | 16.74 | 42.98 | 19.62 | 12.14 | 36.63 |
| Jogging1 | 8.39 | 3.72 | 5010 | 94.97 | 115.98 | 4.27 |
| Jogging2 | 14.2 | 4.74 | 104.02 | 147.77 | 3.47 | 136.4 |
| Suv | 15.36 | 3.65 | 48 | 3.34 | 3.73 | 3.71 |
| Mean Error | 9.212 | 13.126 | 1.3 × 106 | 37.327 | 16.829 | 20.959 |
| Sequence | Proposed | Modified KCF [59] | STC [27] | MACF [57] | MOSSECA [58] | KCF_MTSA [41] |
|---|---|---|---|---|---|---|
| Blurcar1 | 10.78 | 66.29 | 27.75 | 18.5 | 53.06 | 15.35 |
| Blurcar3 | 18.04 | 33.62 | 28.87 | 32.7 | 51.74 | 6.08 |
| Blurcar4 | 5.7 | 21.42 | 20.07 | 8.64 | 27.65 | 5.83 |
| Boy | 26.67 | 85.51 | 33.48 | 58.7 | 157.17 | 22.02 |
| Car2 | 57.18 | 90.7 | 94.08 | 55.3 | 95.38 | 11.2 |
| Dancer2 | 29.66 | 29.65 | 65.1 | 29.2 | 38.87 | 6.26 |
| Human7 | 25.17 | 34.44 | 59.66 | 40.5 | 26.11 | 11.48 |
| Jogging1 | 42.71 | 95.45 | 61.75 | 49 | 36.59 | 12.55 |
| Jogging2 | 22.77 | 33.01 | 56.92 | 34.6 | 33.97 | 11 |
| Suv | 69.61 | 76.32 | 98.03 | 50.9 | 79.7 | 8.44 |
| Sequence | Frame Size | Number of Frames | Time |
|---|---|---|---|
| Blurcar1 | 640 × 480 | 742 | 0.011 |
| Blurcar3 | 640 × 480 | 357 | 0.008 |
| Blurcar4 | 640 × 480 | 380 | 0.009 |
| Boy | 640 × 480 | 602 | 0.009 |
| Car2 | 320 × 240 | 913 | 0.018 |
| Dancer2 | 320 × 262 | 150 | 0.006 |
| Human7 | 320 × 240 | 250 | 0.007 |
| Jogging1 | 352 × 288 | 307 | 0.012 |
| Jogging2 | 352 × 288 | 307 | 0.008 |
| Suv | 320 × 240 | 945 | 0.017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, K.; Ali, A.; Jalil, A.; Khan, B.; Cheema, K.M.; Murad, M.; Milyani, A.H. Efficient Online Object Tracking Scheme for Challenging Scenarios. Sensors 2021, 21, 8481. https://doi.org/10.3390/s21248481
Mehmood K, Ali A, Jalil A, Khan B, Cheema KM, Murad M, Milyani AH. Efficient Online Object Tracking Scheme for Challenging Scenarios. Sensors. 2021; 21(24):8481. https://doi.org/10.3390/s21248481
Chicago/Turabian StyleMehmood, Khizer, Ahmad Ali, Abdul Jalil, Baber Khan, Khalid Mehmood Cheema, Maria Murad, and Ahmad H. Milyani. 2021. "Efficient Online Object Tracking Scheme for Challenging Scenarios" Sensors 21, no. 24: 8481. https://doi.org/10.3390/s21248481
APA StyleMehmood, K., Ali, A., Jalil, A., Khan, B., Cheema, K. M., Murad, M., & Milyani, A. H. (2021). Efficient Online Object Tracking Scheme for Challenging Scenarios. Sensors, 21(24), 8481. https://doi.org/10.3390/s21248481







