A Multi-Step CNN-Based Estimation of Aircraft Landing Gear Angles
Abstract
:1. Introduction
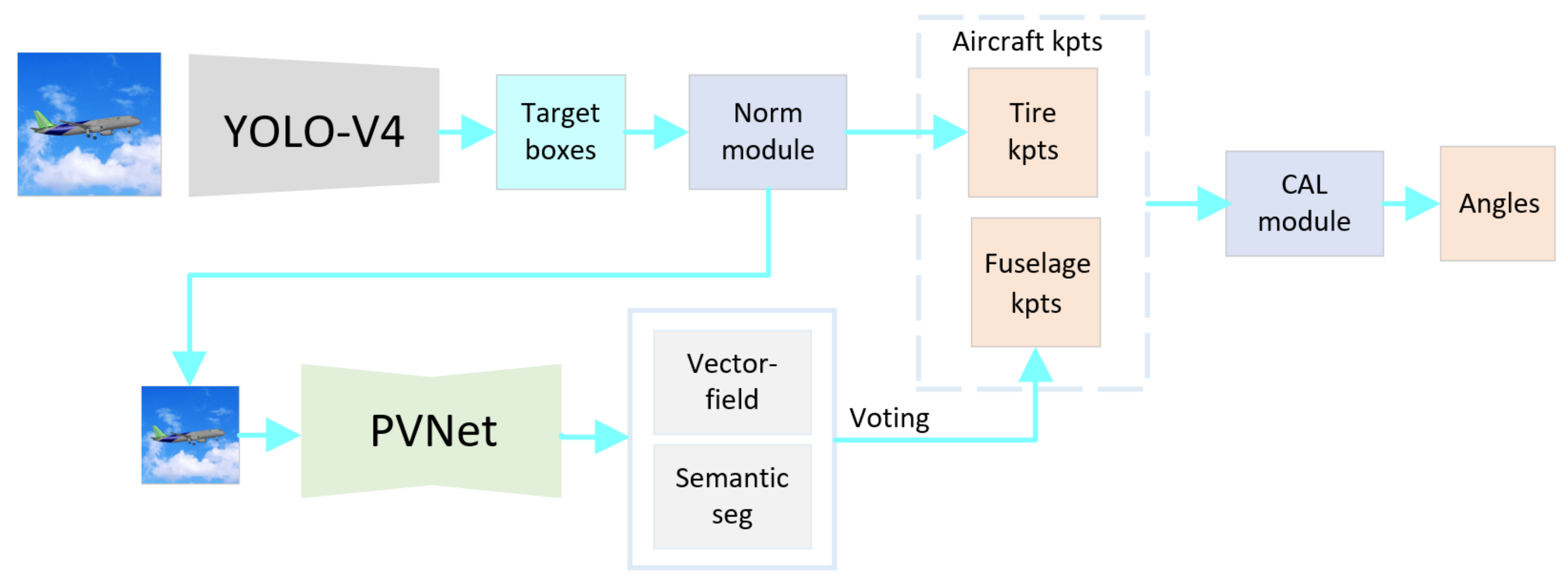
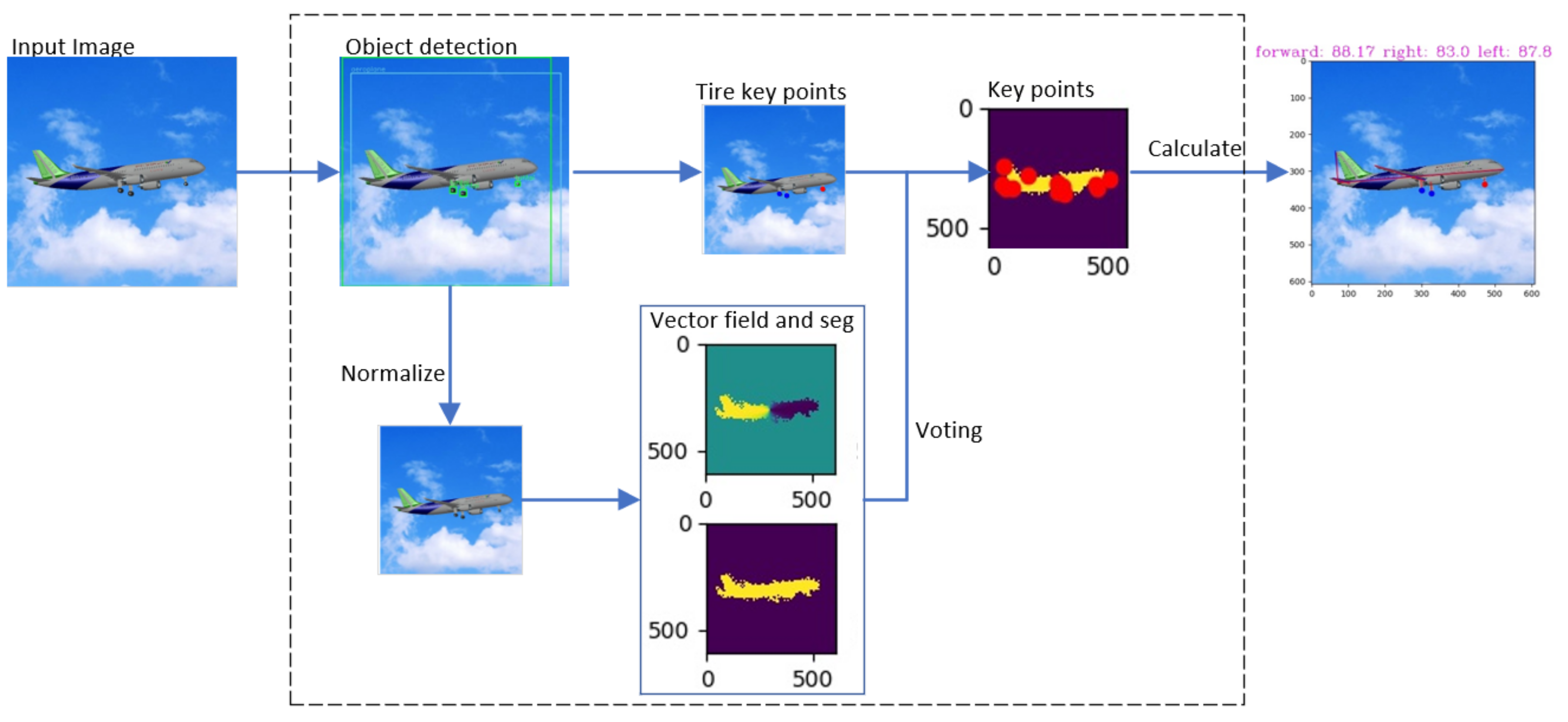
- Object extraction and normalization modules are added to adapt to the change in aircraft target scale. The target detection module extracts the area of the aircraft, and the normalization module normalizes the area size. Then, the normalized area is inputted into the subsequent vector field regression network, voting for the key points of the fuselage. The normalization module could effectively avoid the error of the vector field network, which is caused by dramatic changes in the input image. The target detection module adopts an efficient YOLO-V4 model.
- The aircraft is divided into the landing gear and the fuselage to detect key points. The landing gears are movable, and the shape of the aircraft without the landing gear changes very little and can be regarded as a rigid body. Therefore, the aircraft as a whole can be divided into the landing gear and the two parts of the fuselage. Aircraft key points consist of landing gear key points and fuselage key points. The target detection module obtains the key points of the landing gears. The key points of the fuselage are acquired by a robust pixel-level voting network, which requires the model to be a rigid body. In addition, the distance-based coefficients are multiplied by the loss function to optimize the vector field;
- To resolve the difficulty of obtaining depth information, we propose a method to directly calculate the absolute angle between the landing gears and fuselage plane by using key positions in 2D images according to the constraints of aircraft, omitting the step of regaining 3D spatial coordinates;
- This article contributes a synthetic aircraft dataset of different camera views containing landing gears with different angles to verify the algorithm performance.
2. Related Works
3. Proposed Methods
3.1. Norm Module
3.2. Vector Field Loss Function Optimization
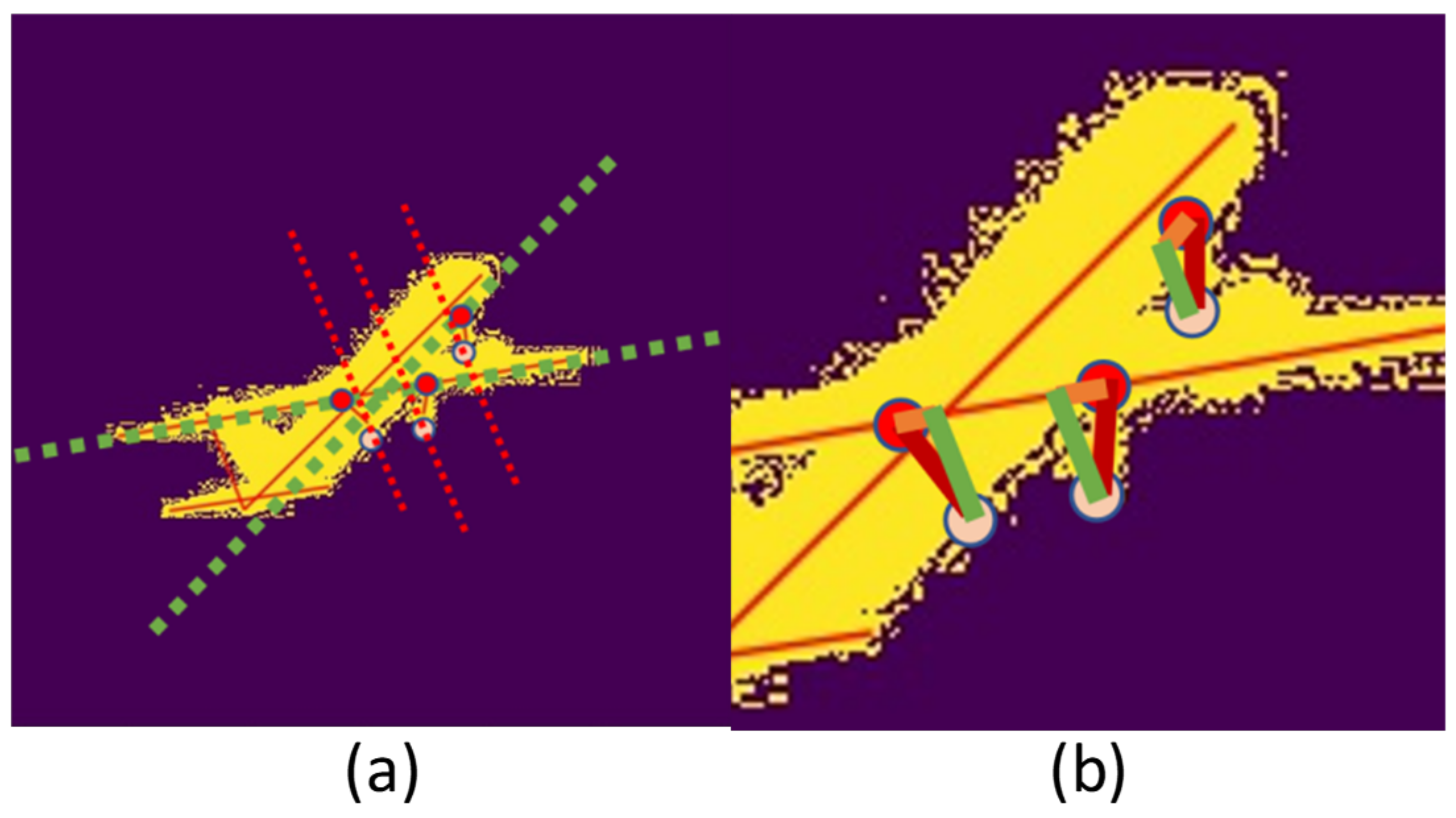
3.3. CAL Module
- Find the right triangle between the landing gear and fuselage shown in Figure 3b. Because the aircraft’s vertical tail is perpendicular to the fuselage plane, in Figure 3a, the line that is parallel to the aircraft’s vertical line is perpendicular to the fuselage plane. Considering the rotating direction of the landing gear, the vertical foot of the nose landing gear is on the fuselage line, and the vertical foot of the rear landing gear is on the wing belonging to the fuselage plane.
- Given the aircraft model, the true length in the triangle is calculated from the ratio of the length of each side to the length of the fuselage, wing, and tail respectively.
- Then the sines and cosines is used to calculate the angle between the landing gears and fuselage plane.
3.4. Synthetic Aircraft Datasets
4. Experiments
4.1. Angle Measurement Results
4.2. Normalized Module
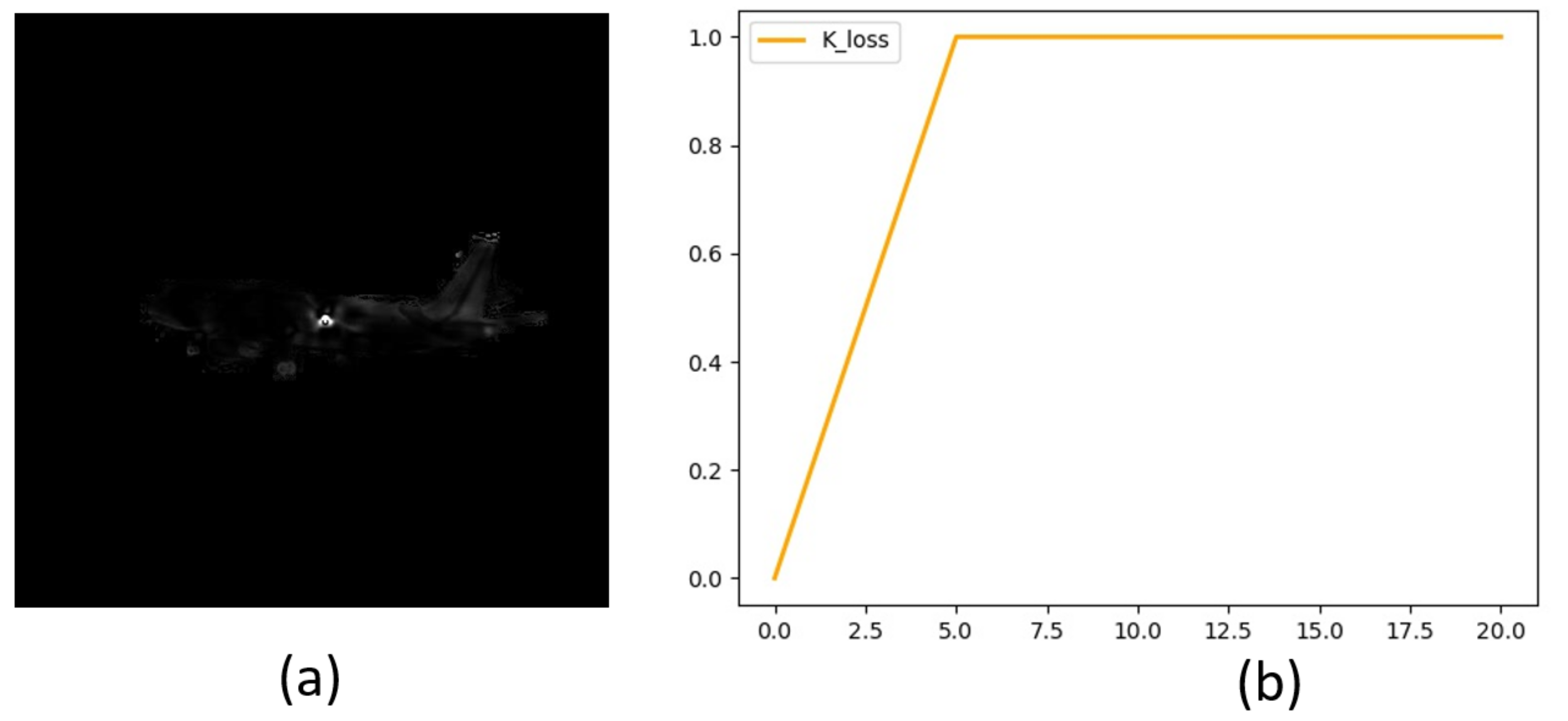
4.3. K Loss Function
4.4. Experiment on Different Datasets
4.5. Robustness
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.L. Video Monitoring Method Based on Multi-Camera Collaboration for Aircraft Landing Process. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. (In Chinese). [Google Scholar]
- Peng, S.; Liu, Y.; Huang, Q.; Zhou, X.; Bao, H. PVNet: Pixel-wise Voting Network for 6DoF Object Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4556–4565. [Google Scholar]
- Murthy, K.; Shearn, M.; Smiley, B.D.; Chau, A.H.; Levine, J.; Robinson, M.D. Sky Sat-1: Very High-Resolution Imagery from a Small Satellite. In Proceedings of the SPIE Remote Sensing, Amsterdam, The Netherlands, 22–25 September 2014. [Google Scholar]
- Khodambashi, S.; Moghaddam, M. An Impulse Noise Fading Technique Based On Local Histogram Processing. In Proceedings of the 2009 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 14–17 December 2009; pp. 95–100. [Google Scholar]
- Kim, Y.T. Contrast enhancement using brightness preserving bi-histogram equalization. IEEE Trans. Consum. Electron. 1997, 43, 1–8. [Google Scholar]
- Chen, S.D.; Ramli, R. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 2003, 49, 1310–1319. [Google Scholar] [CrossRef]
- Qian, G. Detecting Transformer Winding Deformation Fault Types Based on Continuous Wavelet Transform. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 1886–1891. [Google Scholar]
- Best, S. A discussion on the significance of geometry in determining the resonant behavior of fractal and other non-Euclidean wire antennas. IEEE Antennas Propag. Mag. 2003, 45, 9–28. [Google Scholar] [CrossRef]
- Jiao, T.; Wang, M.; Zhang, J.; Wang, Y. Wheel image enhancement based on wavelet analysis and pseudo-color processing. Autom. Instrum. 2020, 1, 47–51. [Google Scholar]
- Wang, Z.; Wang, F.; Chi, G. A research on defect image enhancement based on partial differential equation of quantum mechanics. Int. J. Comput. Sci. Math. 2018, 9, 122–132. [Google Scholar] [CrossRef]
- Li, J.; Liang, X.; Shen, S.M.; Xu, T.; Yan, S. Scale-aware Fast R-CNN for Pedestrian Detection. IEEE Trans. Multimed. 2018, 20, 985–996. [Google Scholar] [CrossRef] [Green Version]
- Razavian, A.S.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN Features off-the-shelf: An Astounding Baseline for Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR Workshops 2014, Columbus, OH, USA, 23–28 June 2014; pp. 512–519. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018. Available online: http://timmurphy.org/2009/07/22/line-spacing-in-latex-documents/ (accessed on 8 April 2018).
- Bochkovskiy, A.; Wang, C.Y.; Liao, H. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Ali, W.; Abdelkarim, S.; Zahran, M.; Zidan, M.; Sallab, A.E. YOLO3D: End-to-end real-time 3D Oriented Object Bounding Box Detection from LiDAR Point Cloud. In Proceedings of the ECCV 2018 Workshops, Munich, Germany, 8–14 September 2019; pp. 716–728. [Google Scholar]
- Beltran, J.; Guindel, C.; Moreno, F.M.; Cruzado, D.; Garcia, F.; Arturo, D. BirdNet: A 3D Object Detection Framework from LiDAR information. In Proceedings of the 21st International Conference on Intelligent Transportation Systems, ITSC 2018, Maui, HI, USA, 4–7 November 2018; pp. 3517–3523. [Google Scholar]
- Zhou, Y.; Sun, P.; Zhang, Y.; Anguelov, D.; Gao, J.; Ouyang, T.; Guo, J.; Ngiam, J.; Vasudevan, V. End-to-End Multi-View Fusion for 3D Object Detection in LiDAR Point Clouds. arXiv 2019, arXiv:1910.06528. [Google Scholar]
- Wu, D.; Zhuang, Z.; Xiang, C.; Zou, W.; Li, X. 6D-VNet: End-to-end 6DoF Vehicle Pose Estimation from Monocular RGB Images. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 1238–1247. [Google Scholar]
- Kehl, W.; Manhardt, F.; Tombari, F.; Ilic, S.; Navab, N. SSD-6D: Making RGB-Based 3D Detection and 6D Pose Estimation Great Again. In Proceedings of the IEEE International Conference on Computer Vision, ICCV 2017, Venice, Italy, 22–29 October 2017; pp. 1530–1538. [Google Scholar]
- Chabot, F.; Chaouch, M.; Rabarisoa, J.; Teulière, C.; Chateau, T. Deep MANTA: A Coarse-to-Fine Many-Task Network for Joint 2D and 3D Vehicle Analysis from Monocular Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1827–1836. [Google Scholar]
- Tekin, B.; Sinha, S.N.; Fua, P. Real-Time Seamless Single Shot 6D Object Pose Prediction. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 292–301. [Google Scholar]
- Wang, H.; Sridhar, S.; Huang, J.; Valentin, J.; Song, S.; Guibas, L.J. Normalized Object Coordinate Space for Category-Level 6D Object Pose and Size Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 2637–2646. [Google Scholar]
- Lee, T.; Lee, B.; Kim, M.; Kweon, I. Category-Level Metric Scale Object Shape and Pose Estimation. IEEE Robot. Autom. Lett. 2021, 6, 8575–8582. [Google Scholar] [CrossRef]
- Brachmann, E.; Michel, F.; Krull, A.; Yang, M.Y.; Gumhold, S.; Rother, C. Uncertainty-Driven 6D Pose Estimation of Objects and Scenes from a Single RGB Image. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 3364–3372. [Google Scholar]
- Desingh, K.; Lu, S.; Opipari, A.; Jenkins, O. Factored Pose Estimation of Articulated Objects using Efficient Nonparametric Belief Propagation. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7221–7227. [Google Scholar]
- Mao, Y.; Yang, S.; Chao, D.; Pan, Z.; Yang, R. Real-Time Simultaneous Pose and Shape Estimation for Articulated Objects Using a Single Depth Camera. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1517–1532. [Google Scholar]
- Martín-Martín, R.; Höfer, S.; Brock, O. An Integrated Approach to Visual Perception of Articulated Objects. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5091–5097. [Google Scholar]
- Kumar, S.; Dhiman, V.; Ganesh, M.R.; Corso, J.J. Spatiotemporal Articulated Models for Dynamic SLAM. arXiv 2016, arXiv:1604.03526. [Google Scholar]
- Schmidt, T.; Hertkorn, K.; Newcombe, R.; Marton, Z.C.; Fox, D. Depth-based tracking with physical constraints for robot manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA 2015, Seattle, WA, USA, 26–30 May 2015; pp. 119–126. [Google Scholar]
- Schmidt, T.; Newcombe, R.; Fox, D. Self-Supervised Visual Descriptor Learning for Dense Correspondence. IEEE Robot. Autom. Lett. 2017, 2, 420–427. [Google Scholar] [CrossRef]
- Daniele, A.; Howard, T.; Walter, M.A.; Howard, T.; Walter, M. A Multiview Approach to Learning Articulated Motion Models. In Robotics Research, Proceedings of the 18th International Symposium, ISRR 2017, Puerto Varas, Chile, 11–14 December 2017; Springer: Cham, Switzerland, 2019; pp. 371–386. [Google Scholar]
- Ranjan, A.; Hoffmann, D.T.; Tzionas, D.; Tang, S.; Romero, J.; Black, M.J. Learning Multi-Human Optical Flow. Int. J. Comput. Vis. 2020, 128, 873–890. [Google Scholar] [CrossRef] [Green Version]
- Tkach, A.; Tagliasacchi, A.; Remelli, E.; Pauly, M.; Fitzgibbon, A. Online generative model personalization for hand tracking. ACM Trans. Graph. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Guo, H.; Zhang, C. Pose guided structured region ensemble network for cascaded hand pose estimation. Neurocomputing 2020, 395, 138–149. [Google Scholar] [CrossRef] [Green Version]
- Ge, L.; Ren, Z.; Yuan, J. Point-to-Point Regression PointNet for 3D Hand Pose Estimation. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018; pp. 489–505. [Google Scholar]
- Chang, J.Y.; Moon, G.; Lee, K.M. V2V-PoseNet: Voxel-to-Voxel Prediction Network for Accurate 3D Hand and Human Pose Estimation from a Single Depth Map. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5079–5088. [Google Scholar]
- Wan, C.; Probst, T.; Gool, L.V.; Yao, A. Dense 3D Regression for Hand Pose Estimation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5147–5156. [Google Scholar]
- Li, W.; Lei, H.; Zhang, J.; Wang, X. 3D hand pose estimation based on label distribution learning. J. Comput. Appl. 2021, 41, 550–555. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1302–1310. [Google Scholar]
- Newell, A.; Huang, Z.; Deng, J. Associative Embedding: End-to-End Learning for Joint Detection and Grouping. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kocabas, M.; Karagoz, S.; Akbas, E. MultiPoseNet: Fast Multi-Person Pose Estimation using Pose Residual Network. In Proceedings of the ECCV 2018, 15th European Conference, Munich, Germany, 8–14 September 2018; pp. 437–453. [Google Scholar]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Jian, S. Cascaded Pyramid Network for Multi-person Pose Estimation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7103–7112. [Google Scholar]
- Xiao, B.; Wu, H.; Wei, Y. Simple Baselines for Human Pose Estimation and Tracking. In Proceedings of the ECCV 2018, 15th European Conference, Munich, Germany, 8–14 September 2018; pp. 472–487. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 3364–3372. [Google Scholar]
- Misra, D. Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Kim, H.; Park, S.; Wang, J.; Kim, Y.; Jeong, J. Advanced Bilinear Image Interpolation Based On Edge Features. In Proceedings of the First International Conference on Advances in Multimedia, Colmar, France, 20–25 July 2009; pp. 33–36. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. PoseCNN: A Convolutional Neural Network for 6D Object Pose Estimation in Cluttered Scenes. In Proceedings of the Robotics: Science and Systems XIV, Pittsburgh, PA, USA, 26–30 June 2018. [Google Scholar]
- Girshick, R. Fast R-CNN. arXiv 2015, arXiv:1504.08083. [Google Scholar]
- Xu, L.; Fu, Q.; Tao, W.; Zhao, H. Monocular vehicle pose estimation based on 3D model. Opt. Precis. Eng. 2021, 29, 1346–1355. [Google Scholar] [CrossRef]
- Best, S.R. Operating band comparison of the perturbed Sierpinski and modified Parany Gasket antennas. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 35–38. [Google Scholar] [CrossRef]
- Guariglia, E. Harmonic Sierpinski Gasket and Applications. Entropy 2018, 20, 714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krzysztofik, W.J. Fractal Geometry in Electromagnetics Applications- from Antenna to Metamaterials. Microw. Rev. 2013, 19, 3–14. [Google Scholar]
- Hohlfeld, R.G.; Cohen, N. Self-similarity and the geometric requirements for frequency independence in antennae. Fractals 1999, 7, 79–84. [Google Scholar] [CrossRef]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Webb, R. Learning from Simulated and Unsupervised Images through Adversarial Training. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2242–2251. [Google Scholar]
- Bousmalis, K.; Silberman, N.; Dohan, D.; Erhan, D.; Krishnan, D. Unsupervised Pixel-Level Domain Adaptation with Generative Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 95–104. [Google Scholar]
- Tremblay, J.; Prakash, A.; Acuna, D.; Brophy, M.; Jampani, V.; Anil, C.; To, T.; Cameracci, E.; Boochoon, S.; Birchfield, S. Training Deep Networks with Synthetic Data: Bridging the Reality Gap by Domain Randomization. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 23–30. [Google Scholar]

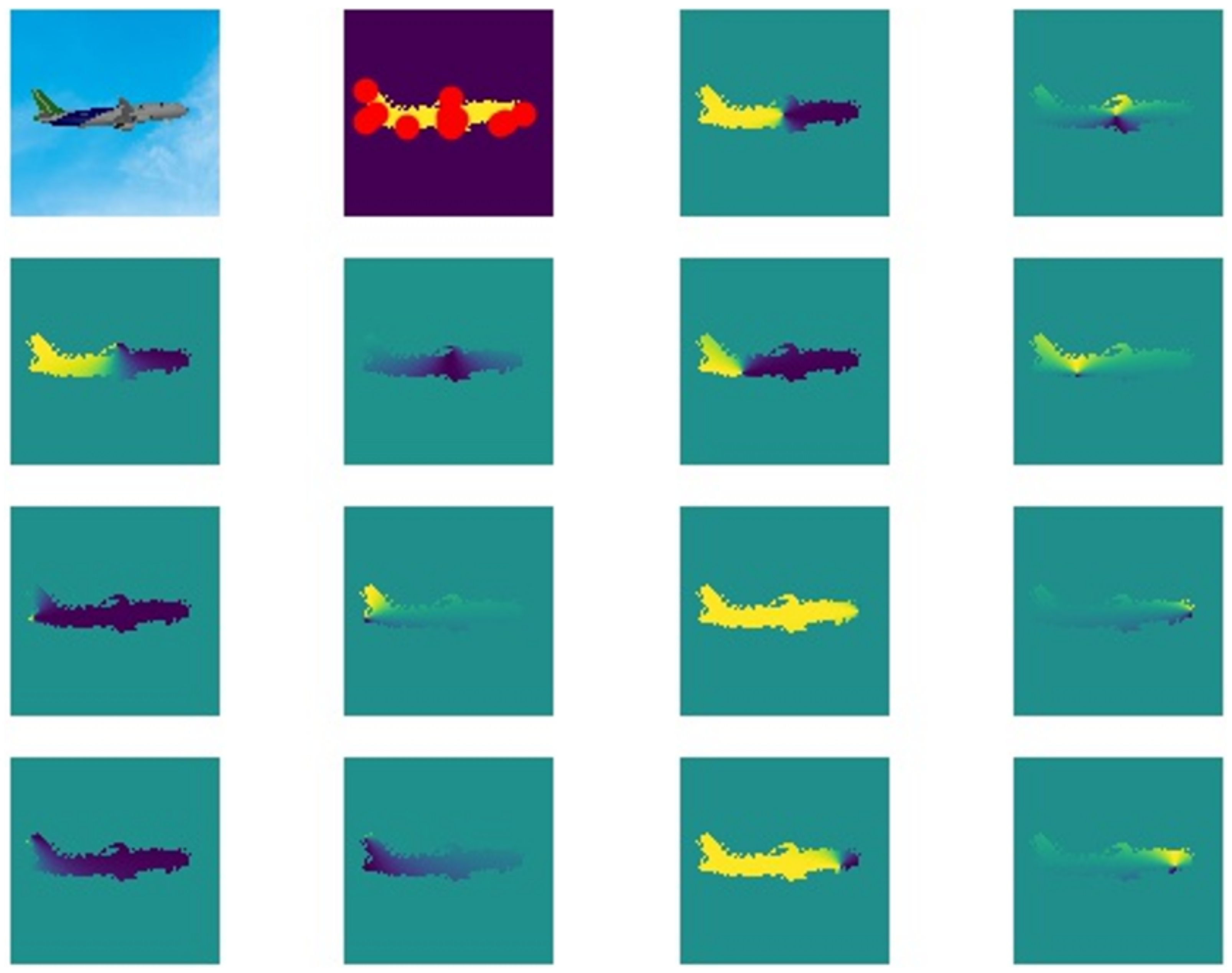
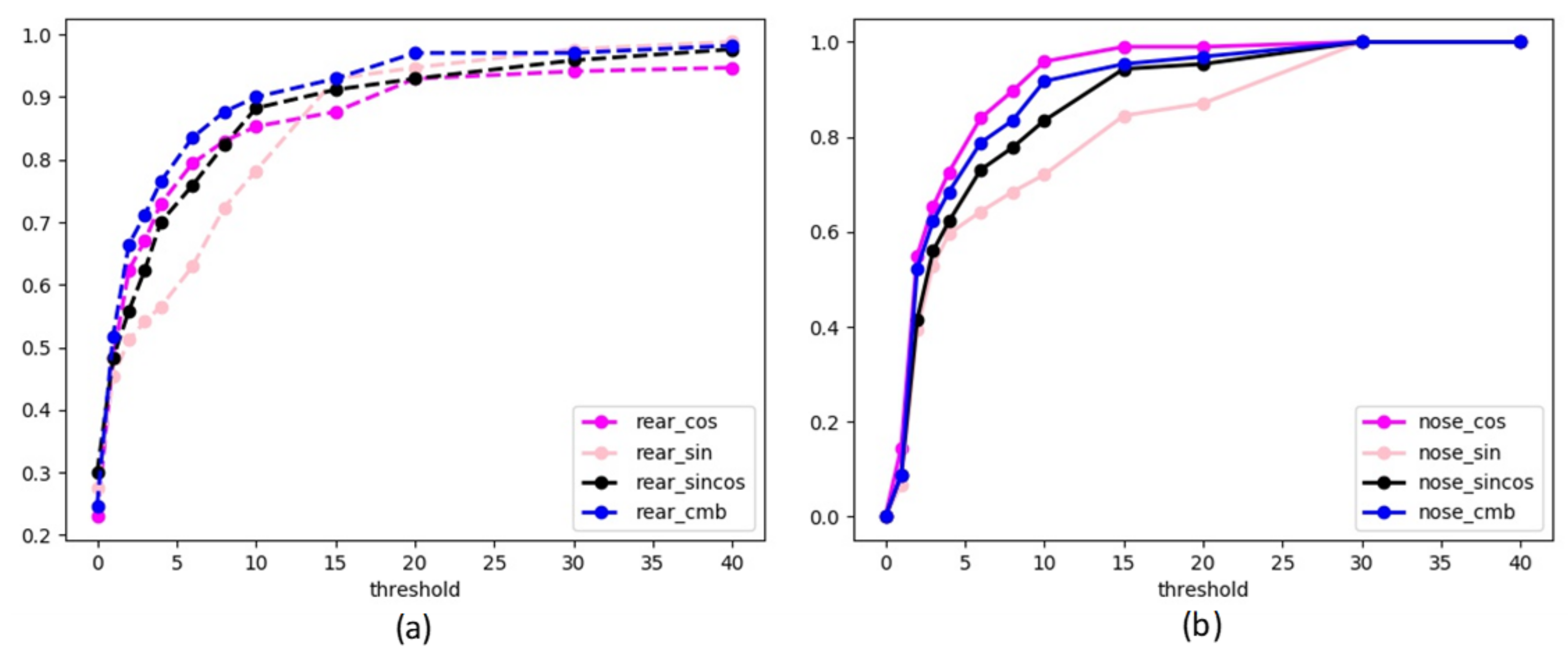
| Method | The Nose Error | The Rear Error | Mean Angle Error | The Nose Accuracy | The Rear Accuracy |
|---|---|---|---|---|---|
| Sine | 18.7 | 12.4 | 12.2 | 33.8% | 52.5% |
| Cosine | 15.8 | 10.2 | 11.8 | 71.2% | 77.5% |
| Sine and cosine | 16.6 | 11.2 | 11.6 | 45.8% | 62.0% |
| Combined method | 11.5 | 8.7 | 9.1 | 68.9% | 77.8% |
| Normalize | The Nose Angle | The Rear Angle | Mean Angle Error | Kpt Fuselage | Kpt Landing Gear | The Nose Accuracy | The Rear Accuracy |
|---|---|---|---|---|---|---|---|
| F | 30.6 | 16.6 | 17.7 | 10.9 | 3.8 | 27.9% | 58.1% |
| T | 11.5 | 8.7 | 9.1 | 3.6 | 3.7 | 68.7% | 78.0% |
| K Loss | The Nose Angle | The Rear Angle | Mean Angle Error | Kpt Fuselage | Kpt Landing Gear | The Nose Accuracy | The Rear Accuracy |
|---|---|---|---|---|---|---|---|
| F | 11.8 | 8.1 | 8.9 | 4.5 | 3.8 | 66.7% | 79.9% |
| T | 11.9 | 7.9 | 8.8 | 3.3 | 3.7 | 67.4% | 81.0% |
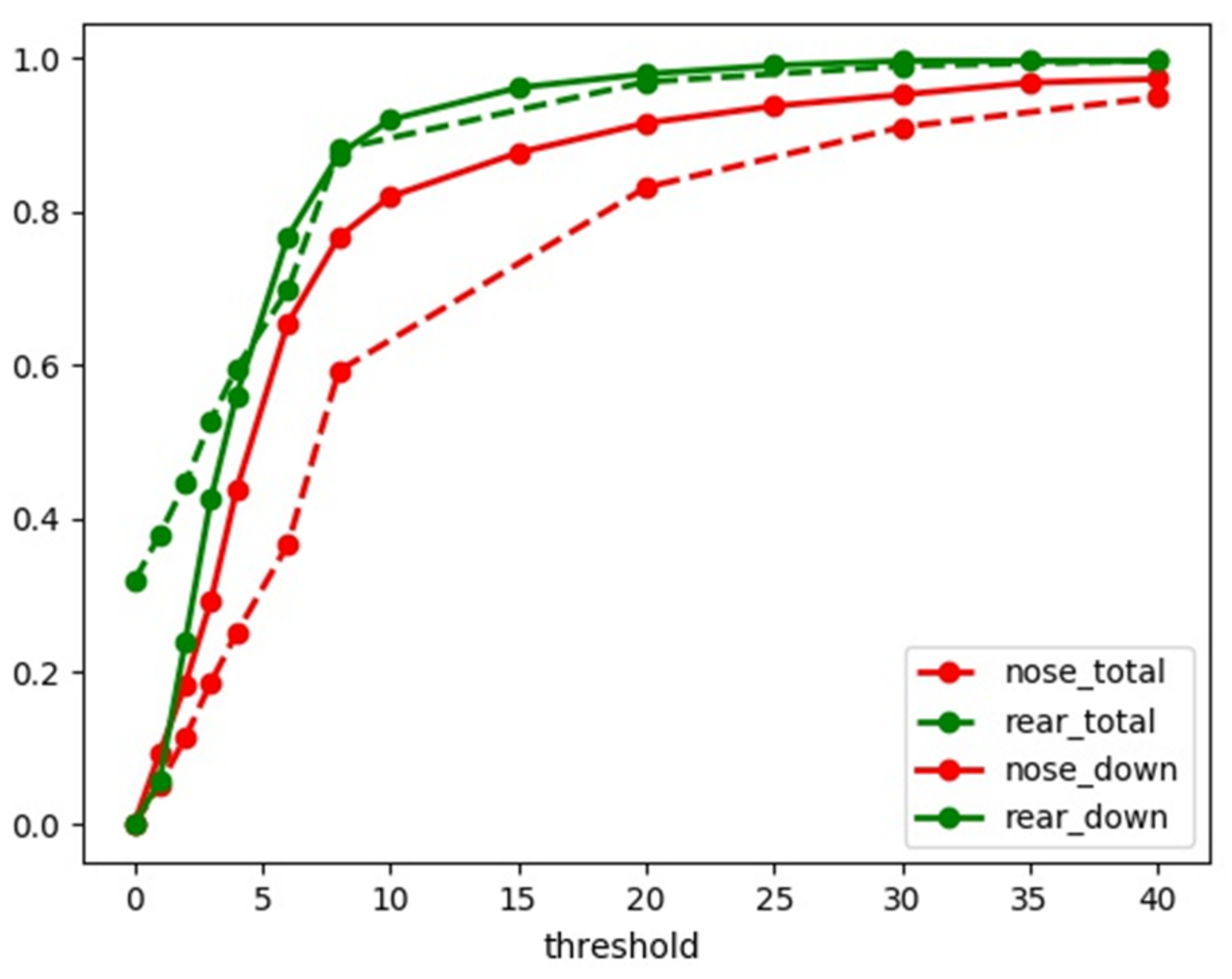
| Datasets | The Nose Angle | The Rear Angle | Mean Angle Error | Kpt Fuselage | Kpt Landing Gear | The Nose Accuracy | The Rear Accuracy |
|---|---|---|---|---|---|---|---|
| Total | 18.3 | 8 | 11.7 | 5 | 4.6 | 49.0% | 82.2% |
| Parallel | 11.5 | 8.7 | 9.1 | 3.6 | 3.7 | 68.9% | 77.8% |
| Undercart down | 12.0 | 8.5 | 10.2 | 2.8 | 3.0 | 70.4% | 77.1% |
| Within 10 degrees | 11.5 | 5.1 | 9.6 | 5 | 4.6 | 66.0% | 92.1% |
| All meet | 8.3 | 4.8 | 7.2 | 3 | 3.1 | 81.9% | 91.9% |
| Datasets | The Nose Angle | The Rear Angle | Mean Angle Error | Kpt Fuselage | Kpt Landing Gear | The Nose Accuracy | The Rear Accuracy |
|---|---|---|---|---|---|---|---|
| Overall | 64.0 | 59.9 | 60.8 | 54.8 | 13.5 | 9.4% | 5.3% |
| Varying light | 6.7 | 4.5 | 4.6 | 3.7 | 3.3 | 84.8% | 91.4% |
| Low resolution | 9.1 | 5.2 | 5.6 | 1.9 | 1.4 | 64.9% | 88.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Wu, Z.; Li, J.; Lai, Z.; Zhao, B.; Min, C. A Multi-Step CNN-Based Estimation of Aircraft Landing Gear Angles. Sensors 2021, 21, 8440. https://doi.org/10.3390/s21248440
Li F, Wu Z, Li J, Lai Z, Zhao B, Min C. A Multi-Step CNN-Based Estimation of Aircraft Landing Gear Angles. Sensors. 2021; 21(24):8440. https://doi.org/10.3390/s21248440
Chicago/Turabian StyleLi, Fuyang, Zhiguo Wu, Jingyu Li, Zhitong Lai, Botong Zhao, and Chen Min. 2021. "A Multi-Step CNN-Based Estimation of Aircraft Landing Gear Angles" Sensors 21, no. 24: 8440. https://doi.org/10.3390/s21248440
APA StyleLi, F., Wu, Z., Li, J., Lai, Z., Zhao, B., & Min, C. (2021). A Multi-Step CNN-Based Estimation of Aircraft Landing Gear Angles. Sensors, 21(24), 8440. https://doi.org/10.3390/s21248440







