A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm
Abstract
:1. Introduction
2. Methodology
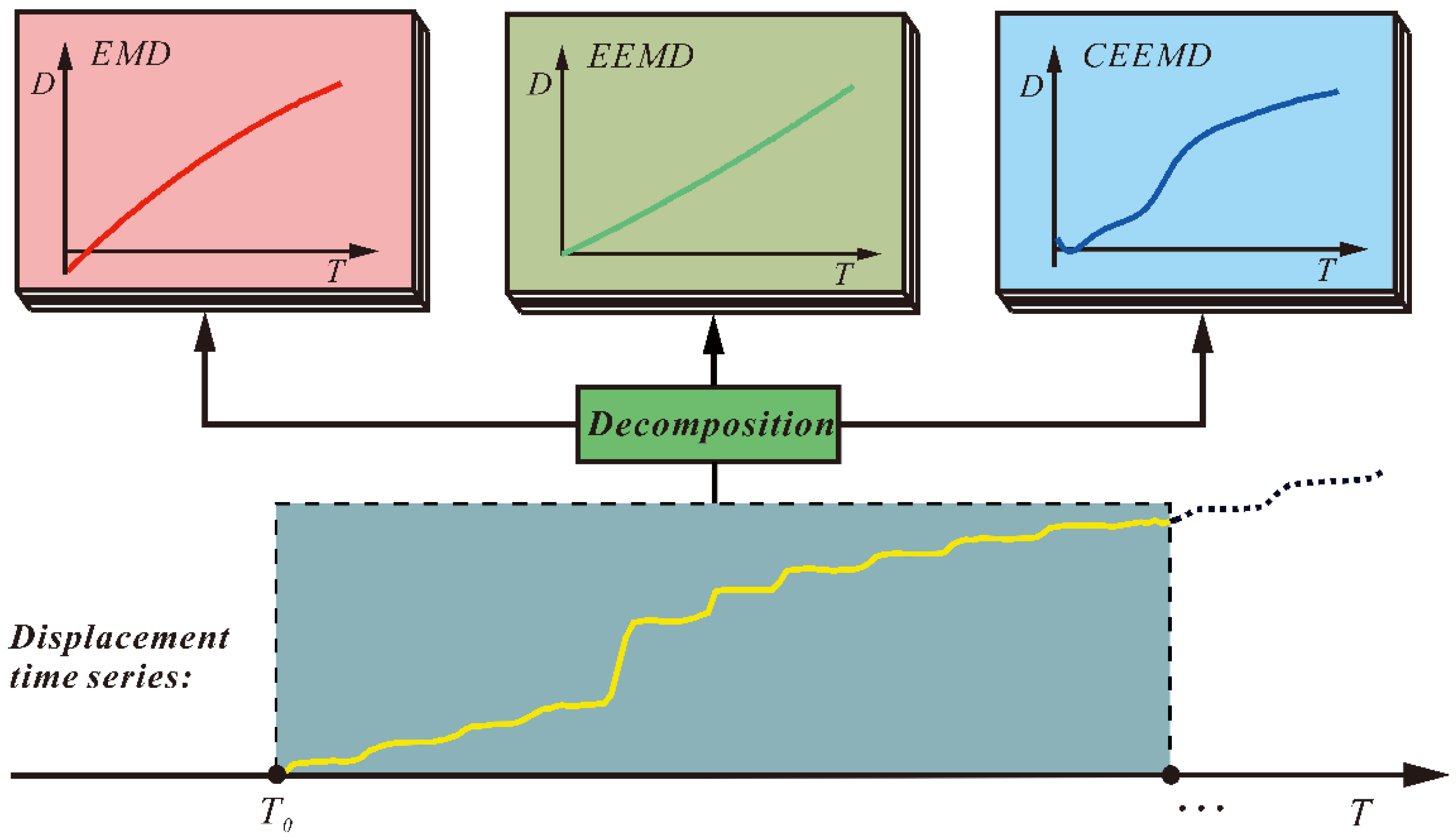
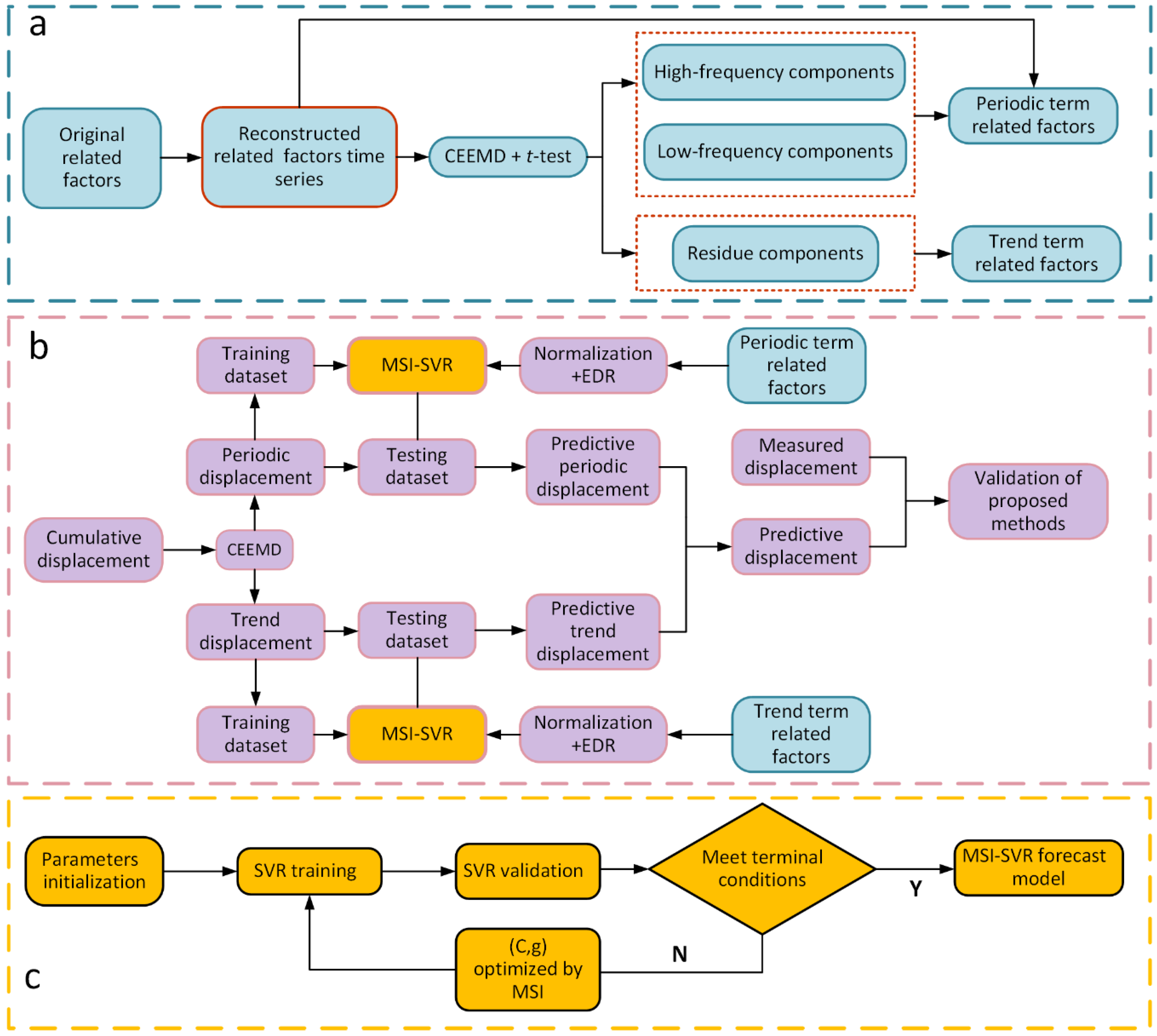
2.1. Data Preprocessing with CEEMD
2.2. Selection of Optimal Related Factors via EDR
2.3. Support Vector Regression (SVR)
2.4. Multiple Swarm Intelligence
2.4.1. Bat Algorithm (BA)
2.4.2. Grey Wolf Optimization (GWO)
2.4.3. Dragonfly Algorithm (DA)
2.4.4. Whale Optimization Algorithm (WOA)
2.4.5. Grasshopper Optimization Algorithm (GOA)
2.4.6. Sparrow Search Algorithm (SSA)
2.5. Procedure of the Proposed Hybrid Algorithm
2.6. Performance Evaluation Formula
3. Cases Study
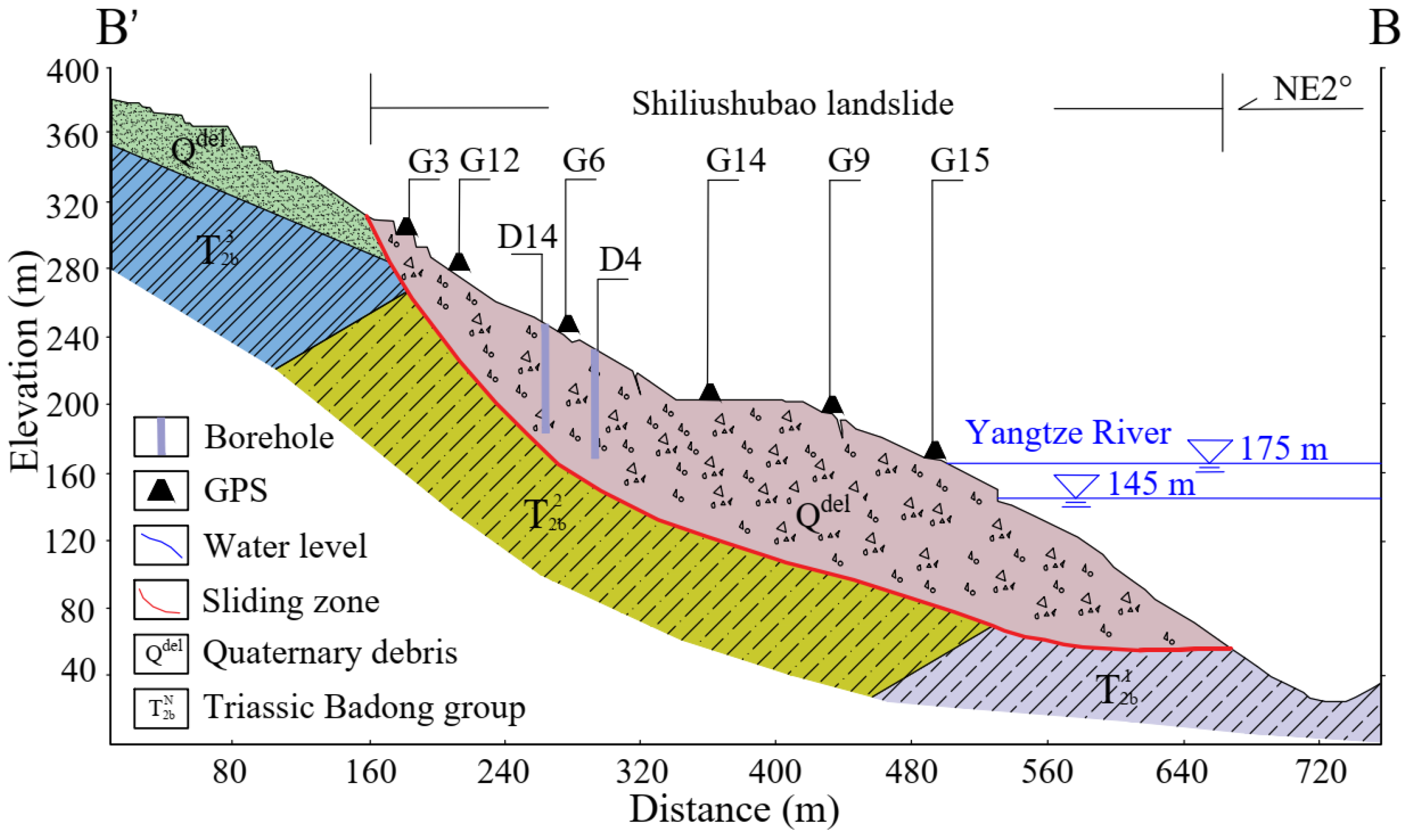
3.1. Geological Conditions
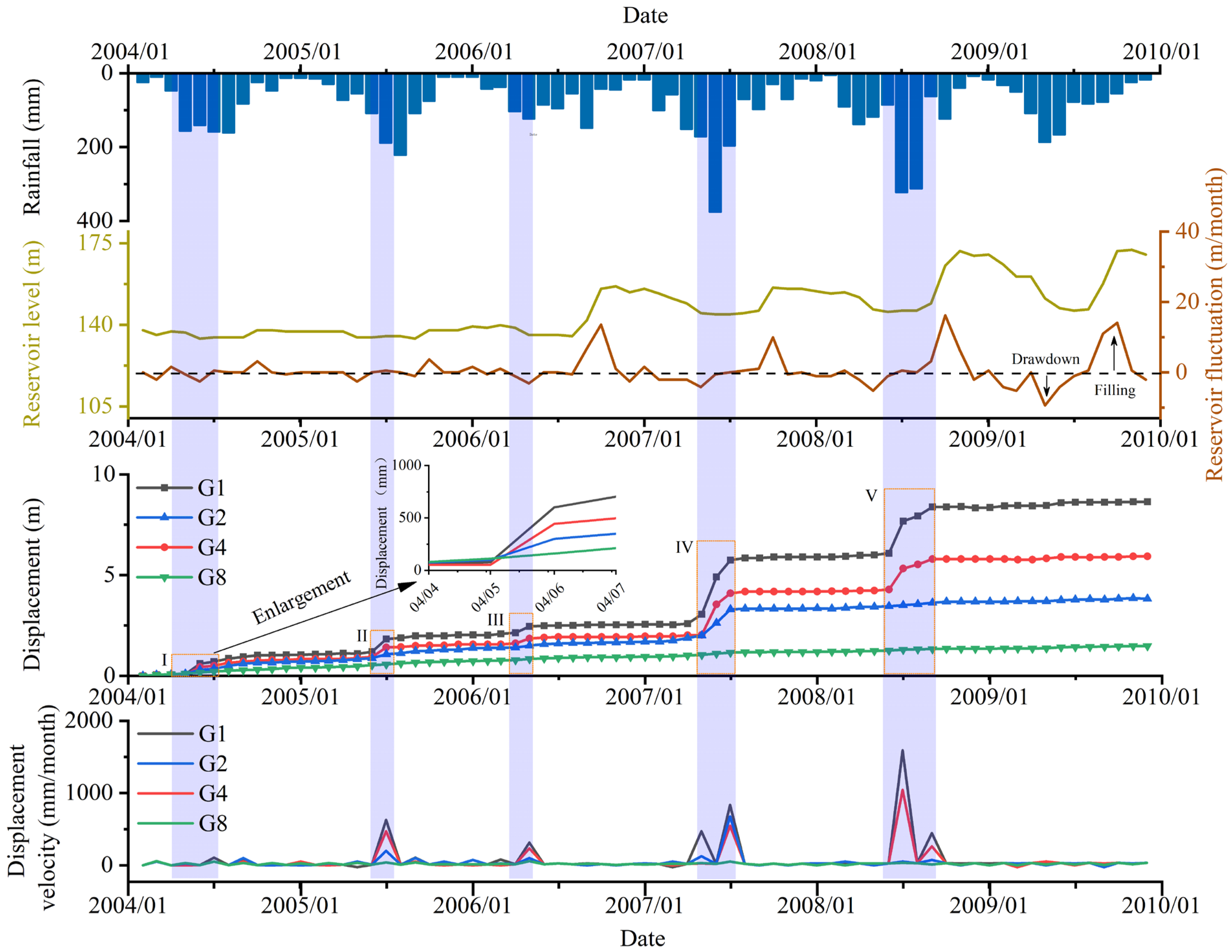
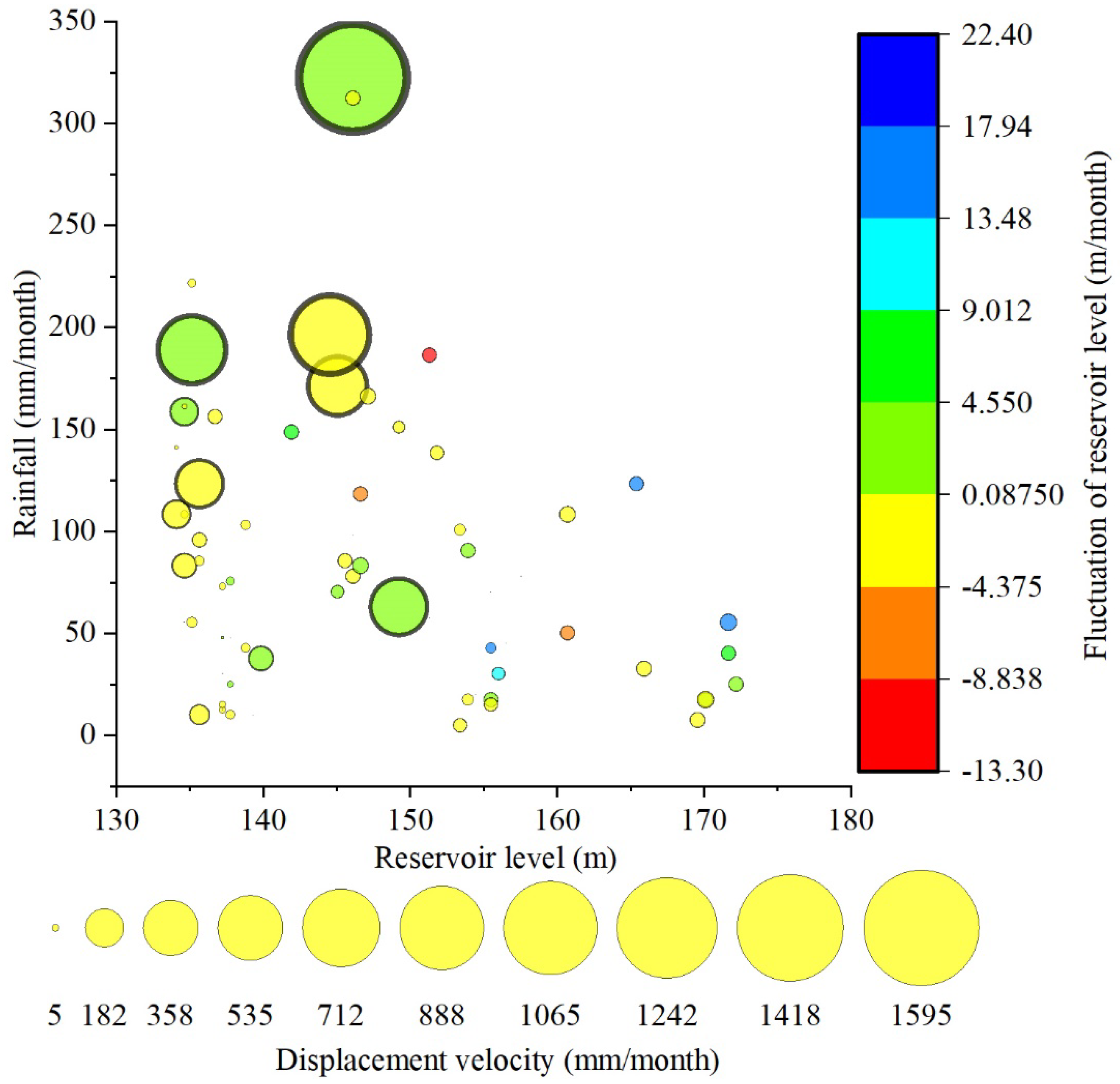
3.2. Rainfall and Reservoir Levels
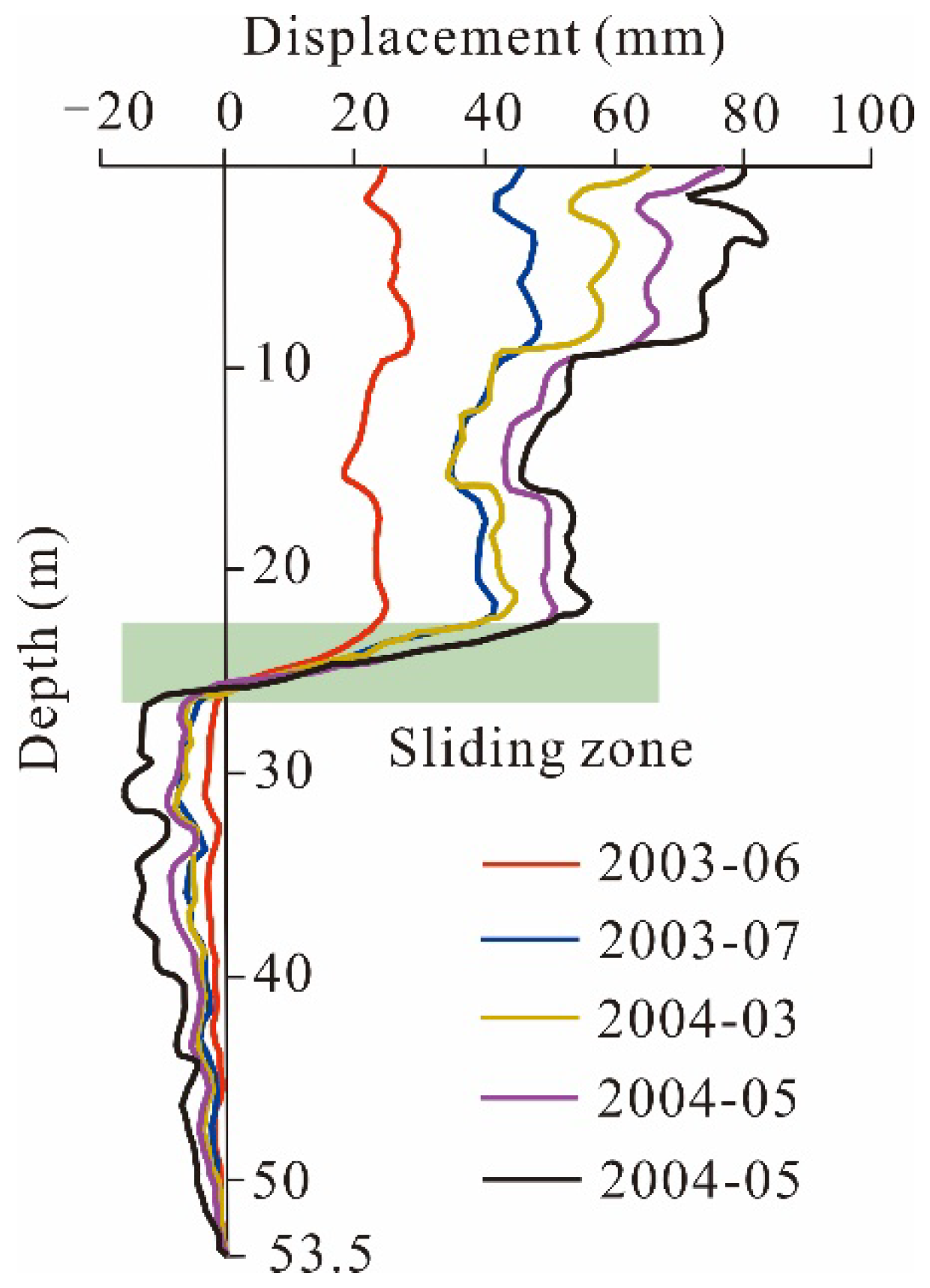
3.3. Deformation Characteristics
3.4. Landslide Monitoring
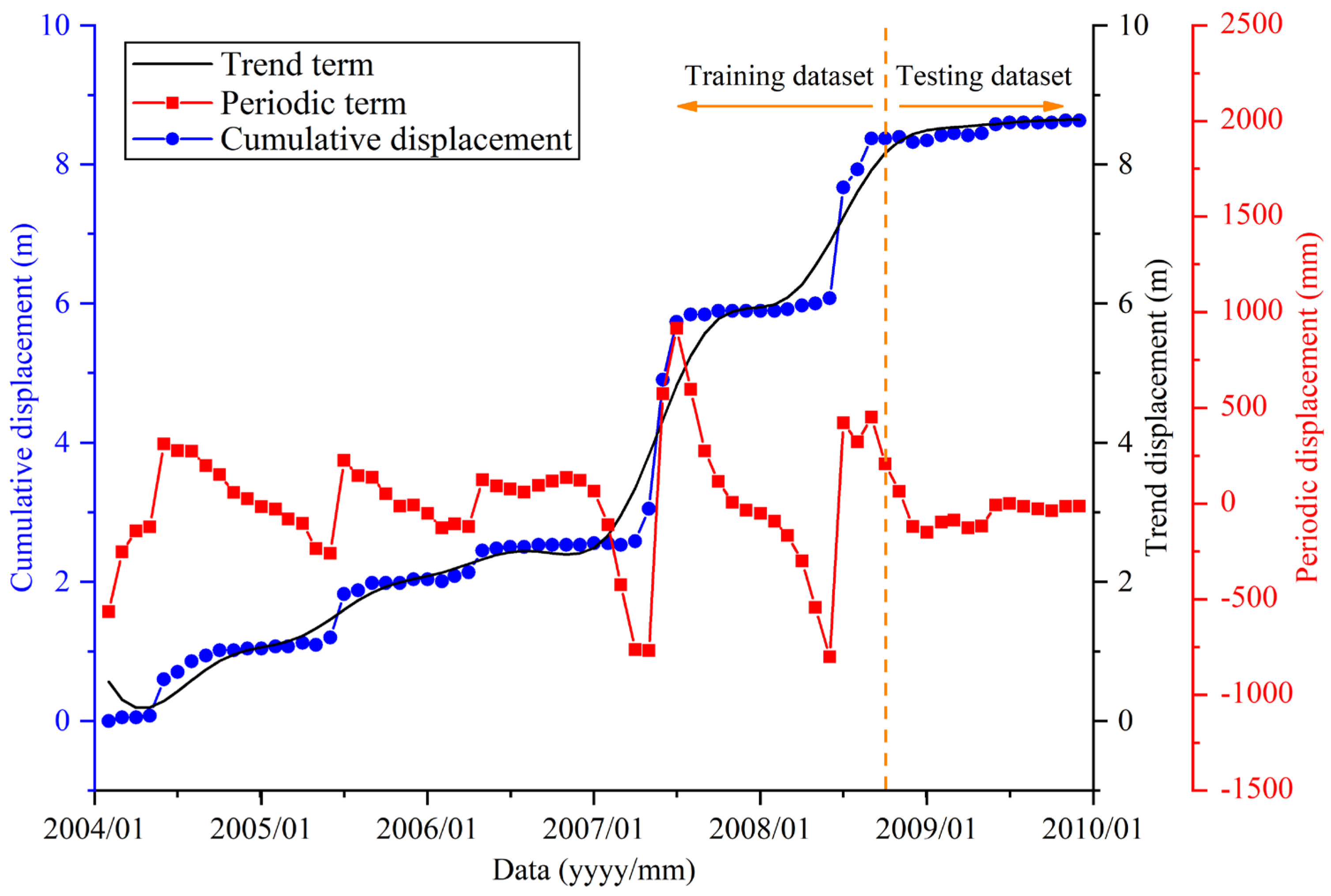
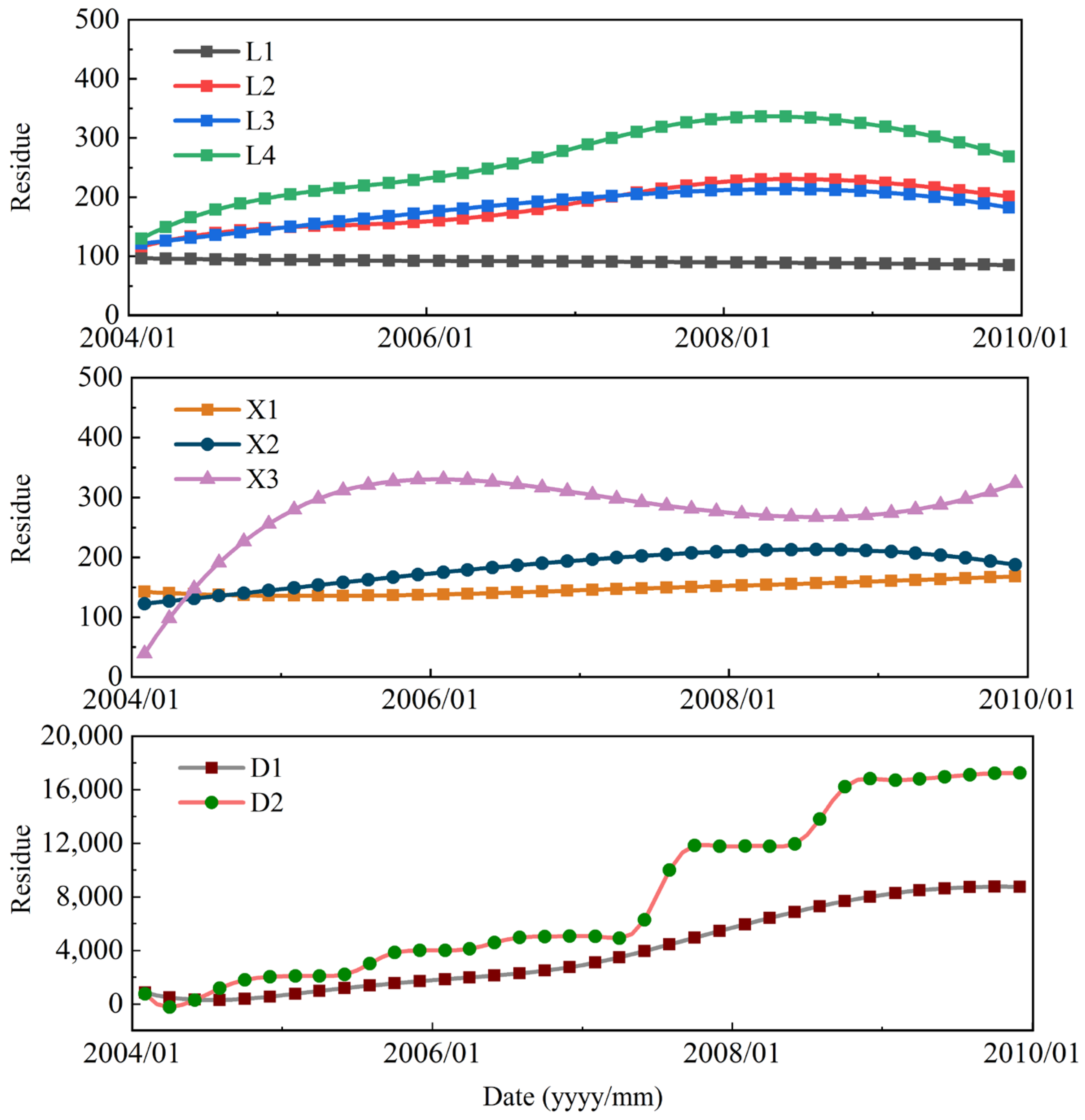
3.5. Analysis of Monitoring Data
4. Data Processing and Statistical Analysis
4.1. CEEMD Decomposition of Landslide Displacement Versus Time Data
- ensemble member = 200
- standard deviation of added white noise in each ensemble member = 0.2
- threshold variance = 0.2
- threshold for first iteration = 4
4.2. CEEMD Decomposition of Related Factors
4.3. Factors Affecting Landslide Displacement Selected by EDR
5. Prediction Results and Comparison
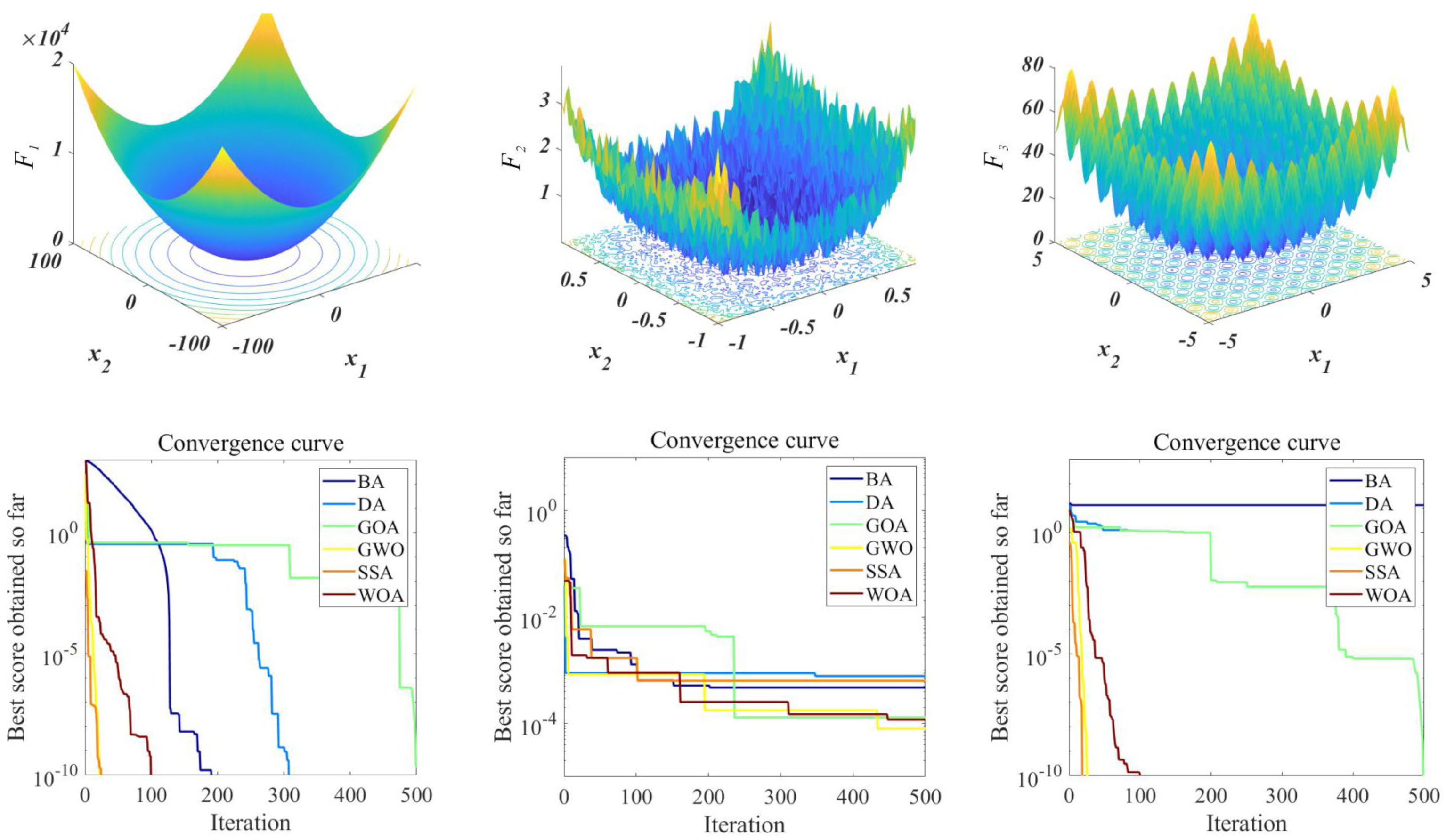
5.1. Parameter Optimization
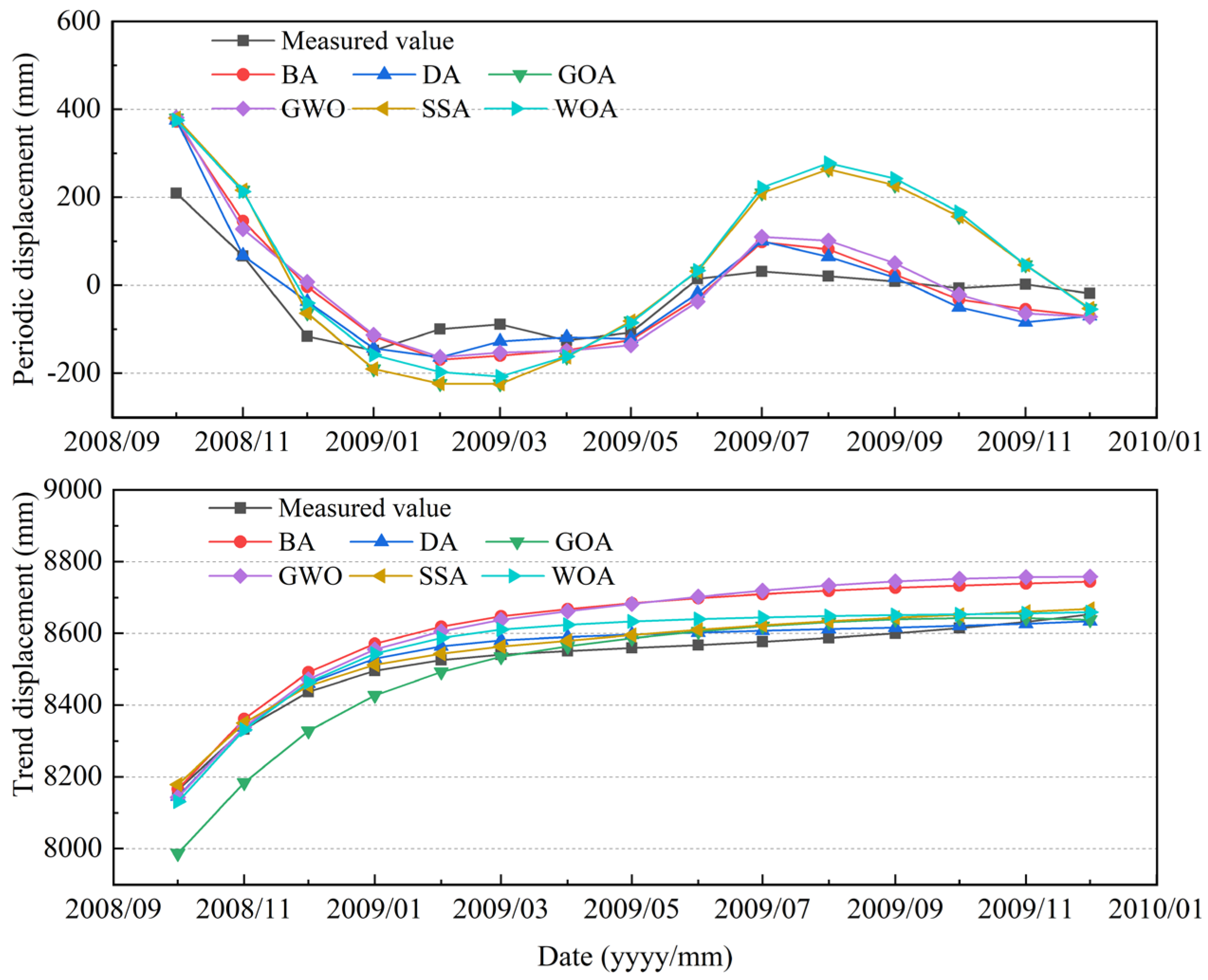
5.2. Prediction of Periodic and Trend Displacements
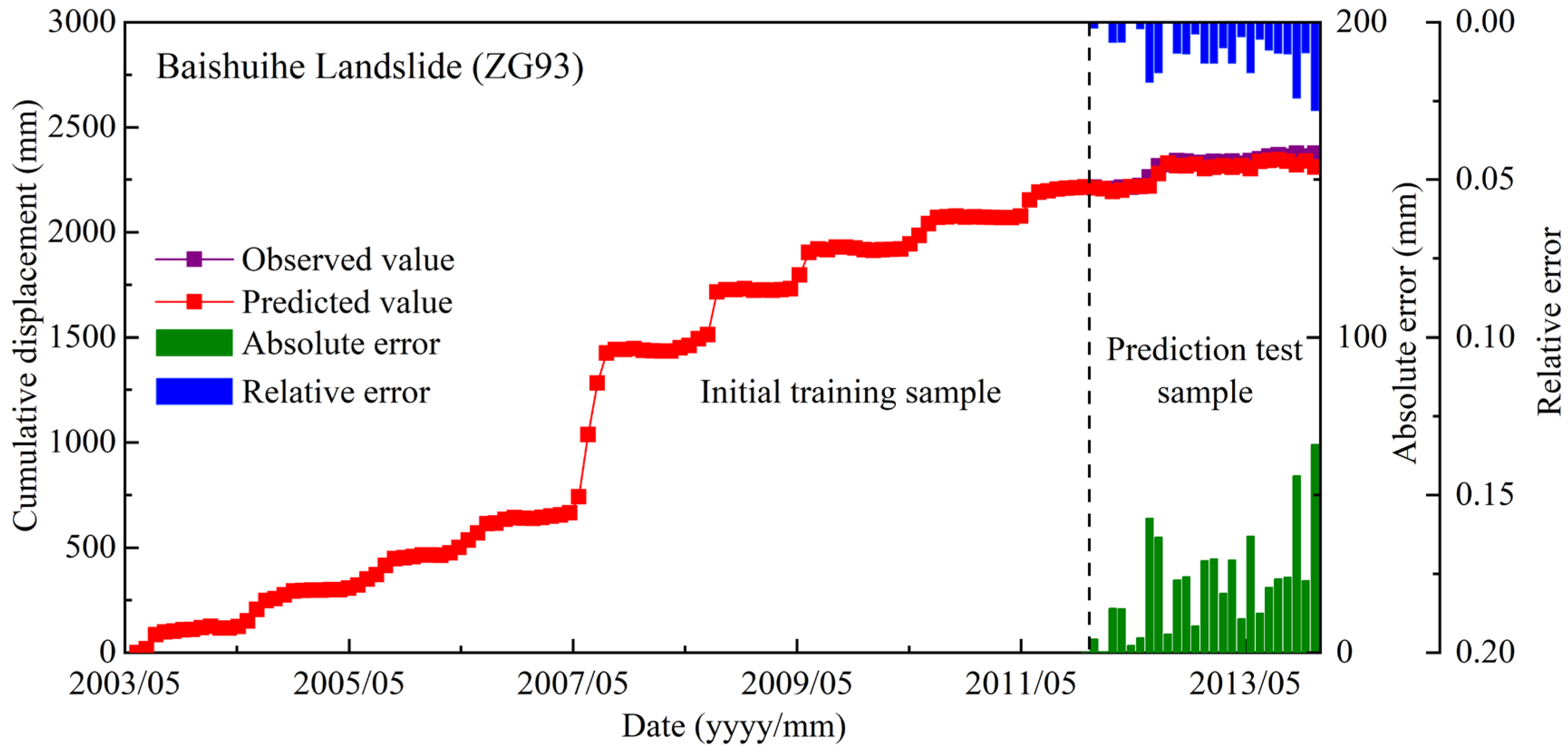
5.3. Prediction of Cumulative Displacements
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tang, H.; Wasowski, J.; Juang, C.H. Geohazards in the three Gorges Reservoir Area, China–Lessons learned from decades of research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Wang, J.; Schweizer, D.; Liu, Q.; Su, A.; Hu, X.; Blum, P. Three-dimensional landslide evolution model at the Yangtze River. Eng. Geol. 2021, 292, 106275. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, H.; Wen, T.; Ma, J. A hybrid intelligent approach for constructing landslide displacement prediction intervals. Appl. Soft Comput. 2019, 81, 105506. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Tang, J.; He, Z.Y.; Tan, J.; Li, C. A novel displacement prediction method using gated recurrent unit model with time series analysis in the Erdaohe landslide. Nat. Hazards 2020, 105, 783–813. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Liu, X.; Zhang, Y.; Ma, J. Combined forecasting model with CEEMD-LCSS reconstruction and the ABC-SVR method for landslide displacement prediction. J. Clean. Prod. 2021, 293, 126205. [Google Scholar] [CrossRef]
- Yin, Y.P.; Huang, B.L.; Wang, W.P.; Wei, Y.J.; Ma, X.H.; Ma, F.; Zhao, C.J. Reservoir-induced landslides and risk control in Three Gorges Project on Yangtze River, China. J. Rock Mech. Geotech. Eng. 2016, 8, 577–595. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Yin, K.; Cao, Y.; Intrieri, E.; Ahmed, B.; Catani, F. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 2018, 15, 2211–2225. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Niu, X.; Tang, H.; Wang, Y.; Wen, T.; Zhang, J. Displacement Prediction of a Complex Landslide in the Three Gorges Reservoir Area (China) Using a Hybrid Computational Intelligence Approach. Complexity 2020, 2020, 2624547. [Google Scholar] [CrossRef]
- Saito, M. Forecasting the time of occurrence of a slope failure. In Proceedings of the 6th International Congress on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; pp. 537–541. [Google Scholar]
- Crosta, G.B.; Agliardi, F. Failure forecast for large rock slides by surface displacement measurements. Can. Geotech. J. 2003, 40, 176–191. [Google Scholar] [CrossRef]
- Ma, J.W.; Tang, H.M.; Liu, X.; Hu, X.L.; Sun, M.J.; Song, Y.J. Establishment of a deformation forecasting model for a step-like landslide based on decision tree C5.0 and two-step cluster algorithms: A case study in the Three Gorges Reservoir area, China. Landslides 2017, 14, 1275–1281. [Google Scholar] [CrossRef]
- Zou, Z.; Yang, Y.; Fan, Z.; Tang, H.; Zou, M.; Hu, X.; Xiong, C.; Ma, J. Suitability of data preprocessing methods for landslide displacement forecasting. Stoch. Environ. Res. Risk Assess. 2020, 34, 1105–1119. [Google Scholar] [CrossRef]
- Ma, J.; Liu, X.; Niu, X.; Wang, Y.; Wen, T.; Zhang, J.; Zou, Z. Forecasting of landslide displacement using a probability-scheme combination ensemble prediction technique. Int. J. Environ. Res. Public Health 2020, 17, 4788. [Google Scholar] [CrossRef]
- Tharwat, A.; Gabel, T. Parameters optimization of support vector machines for imbalanced data using social ski driver algorithm. Neural. Comput. Appl. 2019, 32, 6925–6938. [Google Scholar] [CrossRef]
- Cai, Z.; Xu, W.; Meng, Y.; Shi, C.; Wang, R. Prediction of landslide displacement based on GA-LSSVM with multiple factors. Bull. Eng. Geol. Environ. 2015, 75, 637–646. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, K.; Wang, J.; Huang, F. Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model. Chin. J. Rock Mech. Eng. 2015, 34, 382–391. [Google Scholar]
- Peng, L.; Niu, R.; Wu, T. Time series analysis and support vector machine for landslide displacement prediction. J. Zhejiang Univ. (Eng. Sci.) 2013, 47, 1672–1679. [Google Scholar]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Fu, X. A novel method for landslide displacement prediction by integrating advanced computational intelligence algorithms. Sci. Rep. 2018, 8, 7287. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Lv, J.; Li, X.; Li, L. Support vector regression and ant colony optimization for HVAC cooling load prediction. In Proceedings of the 2010 International Symposium on Computer, Communication, Control and Automation (3CA), IEEE, Tainan, Taiwan, 5–7 May 2010; Volume 1, pp. 537–541. [Google Scholar]
- Balogun, A.L.; Rezaie, F.; Pham, Q.B.; Gigović, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, S.T.; Lee, S. Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
- Li, L.W.; Wu, Y.P.; Miao, F.S.; Liao, K.; Zhang, F.L. Displacement prediction of landslides based on variational mode decomposition and GWO-MIC-SVR model. Chin. J. Rock Mech. Eng. 2018, 37, 1395–1406. (In Chinese) [Google Scholar]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Wen, T.; Ma, J.; Tan, Q.; Xia, D.; Liu, X.; Zhang, Y. A Hybrid Landslide Displacement Prediction Method Based on CEEMD and DTW-ACO-SVR—Cases Studied in the Three Gorges Reservoir Area. Sensors 2020, 20, 4287. [Google Scholar] [CrossRef]
- Zhang, Y.; Agarwal, P.; Bhatnagar, V.; Balochian, S.; Yan, J. Swarm Intelligence and Its Applications. Sci. World J. 2013, 2013, 528069. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef]
- Kişi, Ö. Streamflow Forecasting Using Different Artificial Neural Network Algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Beni, G. From Swarm Intelligence to Swarm Robotics. In Swarm Robotics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–9. [Google Scholar]
- Liu, Y.; Wang, R. Study on network traffic forecast model of SVR optimized by GAFSA. Chaos Solitons Fractals 2016, 89, 153–159. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd Elazim, S.M.; Abdelaziz, A.Y. Ant Lion Optimization Algorithm for Renewable Distributed Generations. Energy 2016, 116, 445–458. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, Y.; Ping, W.; Dong, Y. A Novel Hybrid Classification Method Based on the Opposition-Based Seagull Optimization Algorithm. IEEE Access 2020, 8, 100778–100790. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspir. Comput. 2013, 5, 141. [Google Scholar] [CrossRef] [Green Version]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2015, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.Z.; Mirjalili, S.; Saremi, S.; Faris, H.; Aljarah, I. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2017, 48, 805–820. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Du, H.; Song, D.; Chen, Z.; Shu, H.; Guo, Z. Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method. J. Clean. Prod. 2020, 270, 122248. [Google Scholar] [CrossRef]
- Li, Y.; Sun, R.; Yin, K.; Xu, Y.; Chai, B.; Xiao, L. Forecasting of landslide displacements using a chaos theory based wavelet analysis-Volterra filter model. Sci. Rep. 2019, 9, 19853. [Google Scholar] [CrossRef]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
- Ren, F.; Wu, X.; Zhang, K.; Niu, R. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China. Environ. Earth Sci. 2014, 73, 4791–4804. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Huang, H.F.; Wu, Y.I.; Yi-Liang, L. Study on variables selection using SVR-MIV method in displacement prediction of landslides. Chin. J. Undergr. Space Eng. 2016, 12, 213–219. (In Chinese) [Google Scholar]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In SIGMOD ’05, Proceedings of the 24th ACM International Conference on Management of Data, New York, NY, USA, 13–15 June 2005; ACM Press: New York, NY, USA, 2005; pp. 491–502. [Google Scholar] [CrossRef]
- Mai, S.T.; Goebl, S.; Plant, C. A Similarity Model and Segmentation Algorithm for White Matter Fiber Tracts. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, IEEE, Washington, DC, USA, 10–13 December 2012. [Google Scholar]
- Xu, Y.; Zhang, M.; Zhu, Q.; He, Y. An improved multi-kernel RVM integrated with CEEMD for high-quality intervals prediction construction and its intelligent modeling application. Chemometr. Intell. Lab. Syst. 2017, 171, 151–160. [Google Scholar] [CrossRef]
- Ranacher, P.; Tzavella, K. How to compare movement? A review of physical movement similarity measures in geographic information science and beyond. Cartogr. Geogr. Inf. Sci. 2014, 41, 286–307. [Google Scholar] [CrossRef]
- Moayedi, A.; Abbaspour, R.A.; Chehreghan, A. An evaluation of the efficiency of similarity functions in density-based clustering of spatial trajectories. Ann. GIS 2019, 25, 313–327. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Mi, X.; Li, Y.; Duan, Z.; Xu, Y. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional Gated Recurrent Unit network and Support Vector Regression. Renew. Energy 2019, 143, 842–854. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Xie, Y.; Li, X.; Zhao, W. Prediction and application of porosity based on support vector regression model optimized by adaptive dragonfly algorithm. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 43, 1073–1086. [Google Scholar] [CrossRef]
- Barman, M.; Dev Choudhury, N.B. Hybrid GOA-SVR technique for short term load forecasting during periods with substantial weather changes in North-East India. Procedia Comput. Sci. 2018, 143, 124–132. [Google Scholar] [CrossRef]
- Deng, D.; Liang, Y.; Wang, L.; Wang, C.-S.; Sun, Z.-H.; Wang, C.; Dong, M.-M. Displacement prediction method based on ensemble empirical mode decomposition and support vector machine regression—A case of landslides in Three Gorges Reservoir area. Rock Soil Mech. 2017, 38, 3660–3669. [Google Scholar]
- Hongtao, N. Smart safety early warning model of landslide geological hazard based on BP neural network. Saf. Sci. 2020, 123, 104572. [Google Scholar] [CrossRef]
- Adnan, M.S.G.; Rahman, M.S.; Ahmed, N.; Ahmed, B.; Rabbi, M.F.; Rahman, R.M. Improving Spatial Agreement in Machine Learning-Based Landslide Susceptibility Mapping. Remote. Sens. 2020, 12, 3347. [Google Scholar] [CrossRef]
- Ahmad, H.; Ningsheng, C.; Rahman, M.; Islam, M.M.; Pourghasemi, H.R.; Hussain, S.F.; Habumugisha, J.M.; Liu, E.; Zheng, H.; Ni, H.; et al. Geohazards Susceptibility Assessment along the Upper Indus Basin Using Four Machine Learning and Statistical Models. ISPRS Int. J. Geo-Inf. 2021, 10, 315. [Google Scholar] [CrossRef]



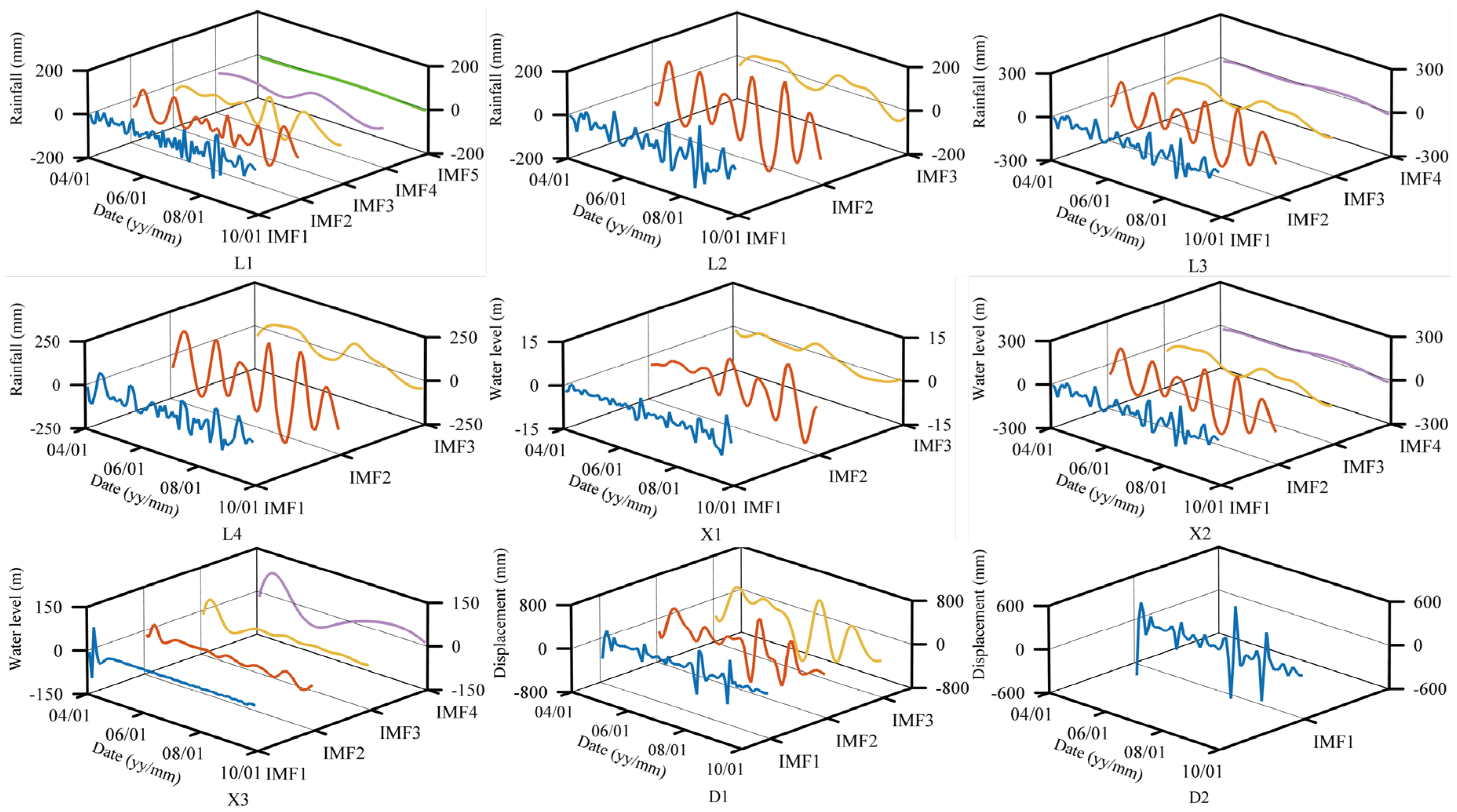
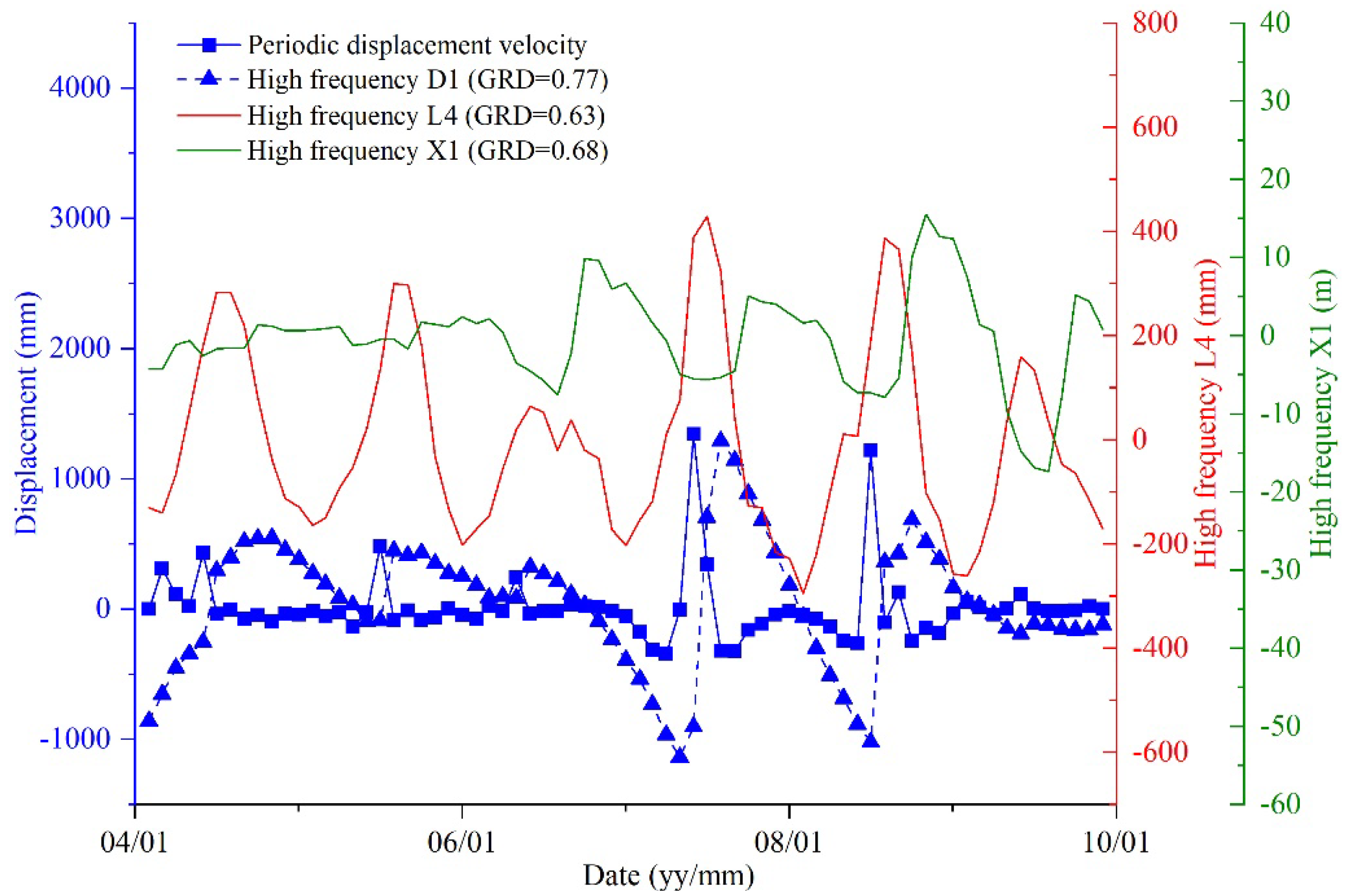


| Groups | Restructured Factor | Component | t | Sig. | Mean (mm) | Std. Deviation (mm) |
|---|---|---|---|---|---|---|
| Rainfall | L1 | IMF2 | 0.22 | 0.83 | 1.50 | 56.92 |
| IMF3 | −0.20 | 0.84 | −1.23 | 50.75 | ||
| IMF4 | 0.60 | 0.55 | 3.02 | 42.24 | ||
| IMF5 | 0.10 | 0.92 | 0.41 | 36.49 | ||
| L2 | IMF2 | 0.47 | 0.64 | 6.16 | 110.1 | |
| IMF3 | −1.34 | 0.18 | −10.09 | 63.28 | ||
| L3 | IMF2 | 0.23 | 0.82 | 3.05 | 111.1 | |
| IMF3 | −1.70 | 0.09 | −12.42 | 61.56 | ||
| IMF4 | −1.08 | 0.28 | −6.75 | 52.48 | ||
| L4 | IMF2 | 0.38 | 0.70 | 5.43 | 120.1 | |
| IMF3 | −0.61 | 0.54 | −5.02 | 69.11 | ||
| Reservoir water level | X1 | IMF2 | 0.47 | 0.64 | 0.26 | 4.73 |
| IMF3 | 2.07 | 0.04 | 0.66 | 2.70 | ||
| X2 | IMF2 | 0.22 | 0.83 | 2.91 | 111.6 | |
| IMF3 | −1.58 | 0.12 | −11.65 | 62.23 | ||
| IMF4 | −0.98 | 0.33 | −6.13 | 52.64 | ||
| X3 | IMF2 | −0.17 | 0.86 | −0.37 | 18.16 | |
| IMF3 | −0.52 | 0.61 | −1.49 | 24.30 | ||
| IMF4 | −2.19 | 0.03 | −10.94 | 42.05 | ||
| Displacement | D1 | IMF2 | −0.04 | 0.97 | −1.16 | 229.4 |
| IMF3 | −1.07 | 0.29 | −40.82 | 320.5 |
| Groups | Component | Periodic Displacement | Trend Displacement | ||
|---|---|---|---|---|---|
| Origin | High | Low | |||
| Rainfall | L1 | 61 | 60 | / | 68 |
| L2 | 56 | 53 | / | 24 | |
| L3 | 56 | 53 | / | 42 | |
| L4 | 54 | 49 | / | 42 | |
| Reservoir level | X1 | 53 | 33 | 44 | 22 |
| X2 | 56 | 53 | / | 41 | |
| X3 | 69 | 41 | 58 | 60 | |
| Displacement | D1 | 67 | 21 | / | 3 |
| D2 | 66 | 32 | / | 2 | |
| Function | Range | Theoretical Minimum Value |
|---|---|---|
| 0 | ||
| 0 | ||
| 0 |
| Algorithm | Parameters | Periodic | Trend | ||||
|---|---|---|---|---|---|---|---|
| C | g | C | g | ||||
| BA-SVR | Sizepop = 20 | Max_iter. = 200 | A = 0.2 | 220.67 | 0.00109 | 657.16 | 0.00106 |
| Lb = 1 × 10−2 | Ub =1 × 102 | r = 0.5 | |||||
| Freq_min = 0.1 | Freq_min = 0.2 | Alpha = 0.2 | |||||
| DA-SVR | Sizepop = 30 | Max_iter. = 200 | e = f = 0.1 | 66506 | 0.00001 | 83702 | 0.00001 |
| lb = 1 × 10−5 | ub = 1 × 105 | c = 0.7 | |||||
| w = 0.5 | s = 0.1 | a = 0.1 | |||||
| GOA-SVR | Sizepop = 30 | Max_iter. = 200 | l = 1.5 | 16.13 | 0.00100 | 29.68 | 0.01000 |
| lb = 1 × 10−3 | ub = 1 × 103 | f = 0.5 | |||||
| GWO-SVR | Sizepop = 30 | Max_iter. = 200 | dim = 2 | 474.94 | 0.00100 | 706.29 | 0.00100 |
| lb = 1 × 10−3 | ub = 1 × 103 | / | |||||
| SSA-SVR | Sizepop = 30 | Max_iter. = 200 | pNum = 20% | 16.17 | 0.00100 | 9677.9 | 0.00014 |
| lb = 1 × 10−4 | ub = 1 × 104 | sNum = 20% | |||||
| OA-SVR | Sizepop = 20 | Max_iter. = 200 | dim = 2 | 1.74 | 0.01000 | 48277.4 | 0.00001 |
| lb = 1 × 10−5 | ub = 1 × 105 | b = 1 | |||||
| Optimization Algorithm | Periodic Displacement | Trend Displacement | ||||||
|---|---|---|---|---|---|---|---|---|
| MAPE | RMSE | MAE | R2 | MAPE | RMSE | MAE | R2 | |
| BA | 0.688 | 13.691 | 30.118 | 0.757 | 0.395 | 1065.132 | 926.683 | 0.8621 |
| DA | 0.788 | 13.652 | 30.367 | 0.761 | 0.008 | 20.448 | 66.336 | 0.9997 |
| GOA | 0.692 | 13.663 | 30.110 | 0.758 | 0.008 | 19.649 | 66.214 | 0.9997 |
| GWO | 0.680 | 13.592 | 29.558 | 0.751 | 0.008 | 20.448 | 66.336 | 0.9997 |
| SSA | 0.786 | 13.589 | 30.307 | 0.762 | 0.009 | 22.766 | 64.733 | 0.9998 |
| WOA | 0.788 | 13.629 | 30.329 | 0.761 | 0.008 | 20.448 | 66.336 | 0.9997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Wang, Y.; Wang, Q. A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm. Sensors 2021, 21, 8352. https://doi.org/10.3390/s21248352
Zhang J, Tang H, Tannant DD, Lin C, Xia D, Wang Y, Wang Q. A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm. Sensors. 2021; 21(24):8352. https://doi.org/10.3390/s21248352
Chicago/Turabian StyleZhang, Junrong, Huiming Tang, Dwayne D. Tannant, Chengyuan Lin, Ding Xia, Yankun Wang, and Qianyun Wang. 2021. "A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm" Sensors 21, no. 24: 8352. https://doi.org/10.3390/s21248352
APA StyleZhang, J., Tang, H., Tannant, D. D., Lin, C., Xia, D., Wang, Y., & Wang, Q. (2021). A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm. Sensors, 21(24), 8352. https://doi.org/10.3390/s21248352









