Voxelisation Algorithms and Data Structures: A Review
Abstract
:1. Introduction
2. Voxelisation Properties
2.1. Common Voxelisation Properties
2.2. Binary and Non-Binary Voxelisation
3. Voxelisation of 3D Geometric Primitives
3.1. Point Voxelisation
3.2. Line Voxelisation
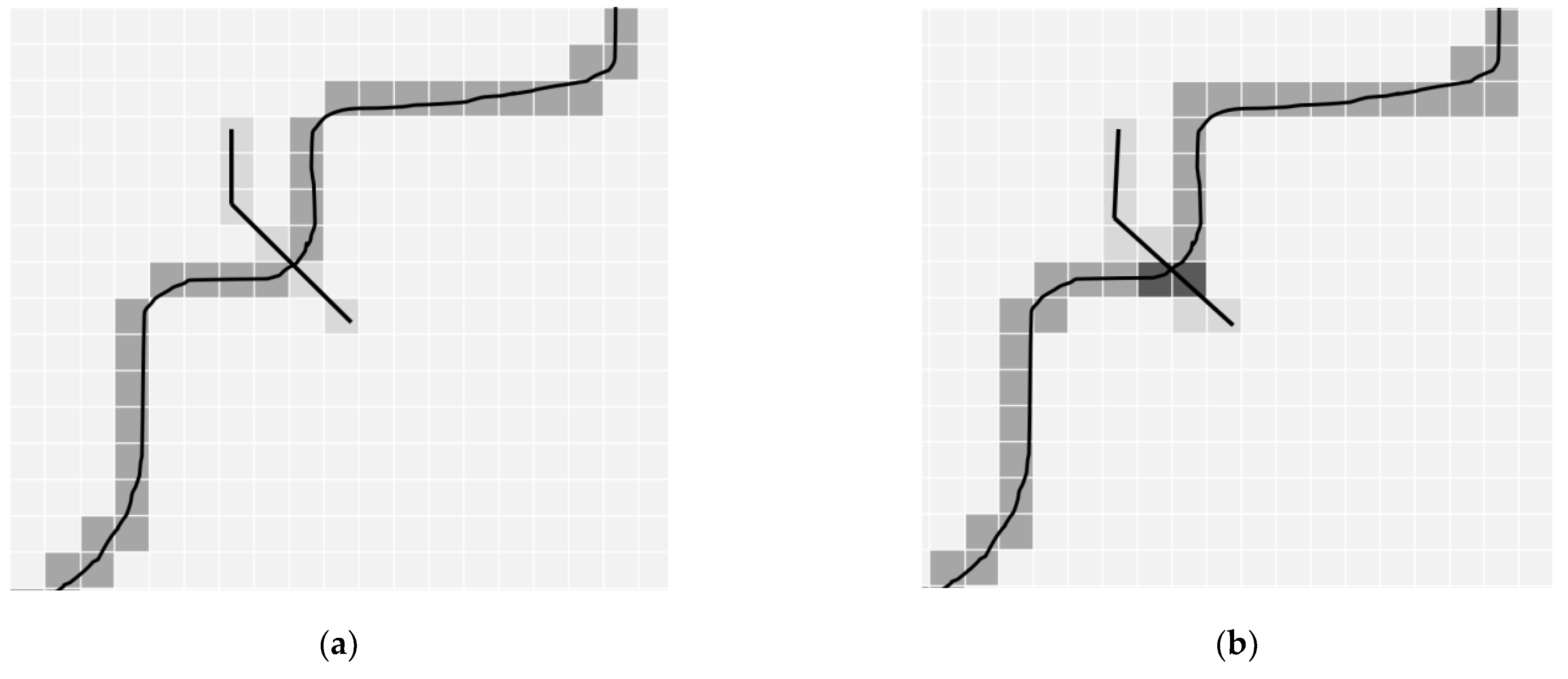
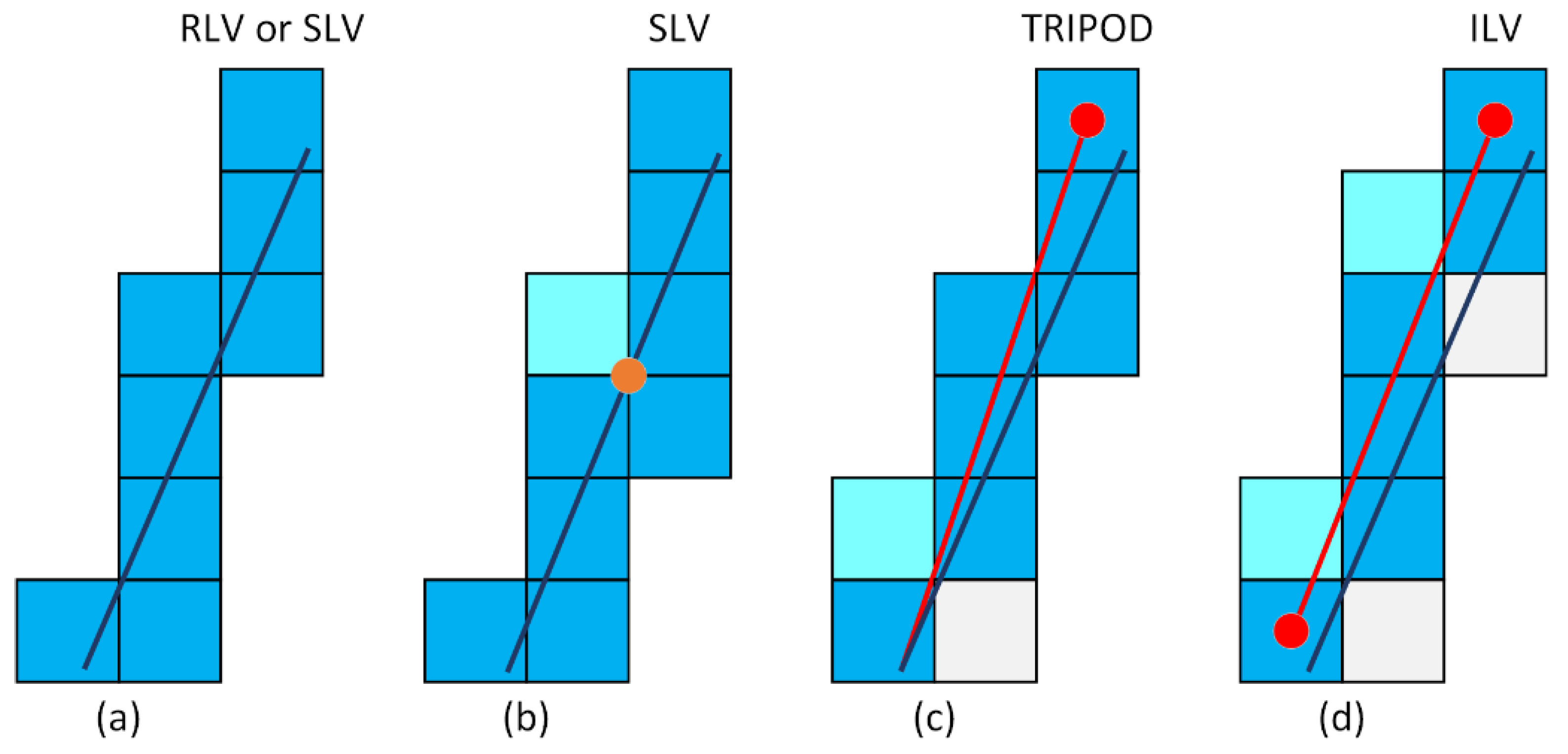
3.2.1. 6-Connected Voxelisation Algorithms
3.2.2. 26-Connected Voxelisation Algorithms
3.2.3. Spline Voxelisation Algorithms
3.2.4. Comparison of Line Voxelisation Algorithms
3.3. Triangle Voxelisation
3.3.1. Rasterisation
3.3.2. Raycasting
3.3.3. Comparison of Triangle Voxelisation Algorithms
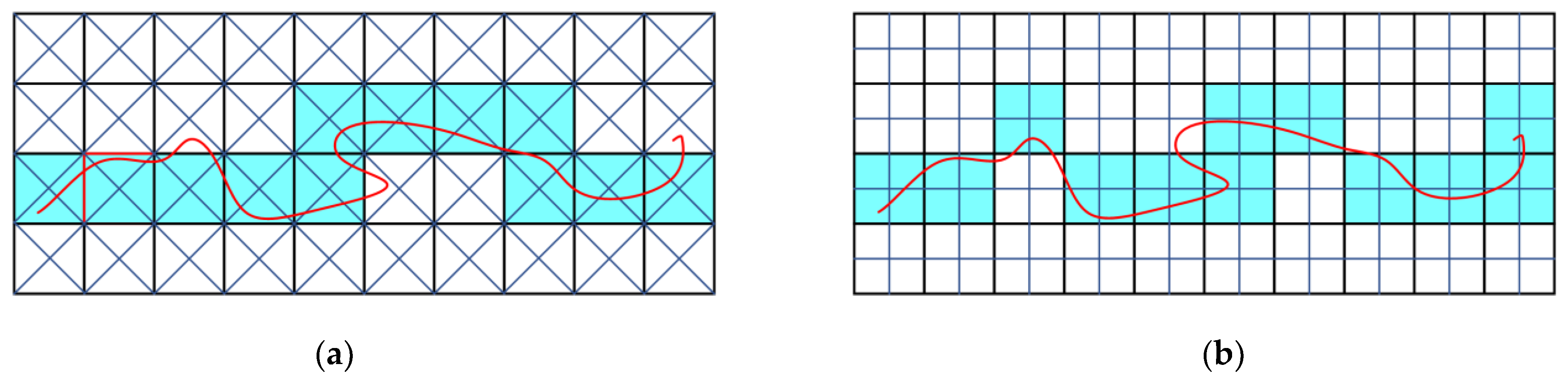
3.4. Surface Voxelisation
3.4.1. Slice-Based
3.4.2. Rasterisation
3.4.3. Comparison of Surface Voxelisation Algorithms
3.5. Solid Voxelisation
3.5.1. Slice-Based
3.5.2. Rasterisation
3.5.3. Comparison of Solid Voxelisation Algorithms
4. Voxel Data Technology and Structures
4.1. Voxel Hardware Technology
4.2. Voxel Data Structures
4.2.1. Static Grids
4.2.2. Dynamic Grids
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amanatides, J.; Woo, A. A Fast Voxel Traversal Algorithm for Ray Tracing; Eurographic: Goslar, Germany, 1987; Volume 87, pp. 3–10. [Google Scholar]
- Eisemann, E.; Décoret, X. Fast scene voxelization and applications. In Proceedings of the 2006 Symposium on Interactive 3D Graphics and Games, Redwood City, CA, USA, 14–17 March 2006; pp. 71–78. [Google Scholar]
- Schwarz, M.; Seidel, H.-P. Fast parallel surface and solid voxelization on GPUs. ACM Trans. Graph. 2010, 29, 1–10. [Google Scholar] [CrossRef]
- Gorte, B.G.H.; Zhou, K.; van der Sande, C.J.; Valk, C. A computationally cheap trick to determine shadow in a voxel model. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Reinbothe, C.K.; Boubekeur, T.; Alexa, M. Hybrid Ambient Occlusion; Eurographics: Goslar, Germany, 2009; pp. 51–57. [Google Scholar]
- Nichols, G.; Penmatsa, R.; Wyman, C. Interactive, multiresolution image-space rendering for dynamic area lighting. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2010; Volume 29, pp. 1279–1288. [Google Scholar]
- Aleksandrov, M.; Zlatanova, S.; Kimmel, L.; Barton, J.; Gorte, B. Voxel-based visibility analysis for safety assessment of urban environments. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Singapore, 24–27 September 2019; Volume 4. [Google Scholar] [CrossRef] [Green Version]
- Petoussi-Henss, N.; Zankl, M.; Fill, U.; Regulla, D. The GSF family of voxel phantoms. Phys. Med. Biol. 2001, 47, 89–106. [Google Scholar] [CrossRef]
- Caon, M. Voxel-based computational models of real human anatomy: A review. Radiat. Environ. Biophys. 2004, 42, 229–235. [Google Scholar] [CrossRef]
- Nießner, M.; Zollhöfer, M.; Izadi, S.; Stamminger, M. Real-time 3D reconstruction at scale using voxel hashing. ACM Trans. Graph. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Beckhaus, S.; Wind, J.; Strothotte, T. Hardware-based voxelization for 3D spatial analysis. In Proceedings of the 5th International Conference on Computer Graphics and Imaging, Athens, Greece, 8–10 July 2002; Volume 20. [Google Scholar]
- Jørgensen, F.; Møller, R.R.; Nebel, L.; Jensen, N.-P.; Christiansen, A.V.; Sandersen, P.B.E. A method for cognitive 3D geological voxel modelling of AEM data. Bull. Eng. Geol. Environ. 2013, 72, 421–432. [Google Scholar] [CrossRef] [Green Version]
- Stafleu, J.; Dubelaar, C.W. Product specification subsurface model GeoTOP. TNO Rep. 2016, R10133. [Google Scholar] [CrossRef]
- Li, W.; Fan, Z.; Wei, X.; Kaufman, A. GPU-based flow simulation with complex boundaries. GPU Gems 2003, 2, 747–764. [Google Scholar]
- Huang, M.; Wei, P.; Liu, X. An efficient encoding voxel-based segmentation (EVBS) algorithm based on fast adjacent voxel search for point cloud plane segmentation. Remote Sens. 2019, 11, 2727. [Google Scholar] [CrossRef] [Green Version]
- Poux, F.; Billen, R. Voxel-based 3D point cloud semantic segmentation: Unsupervised geometric and relationship featuring vs deep learning methods. ISPRS Int. J. Geo-Inf. 2019, 8, 213. [Google Scholar] [CrossRef] [Green Version]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Kyaw, A.S. Unity 4. X Game AI Programming; Packt Publishing Ltd.: Birmingham, UK, 2013. [Google Scholar]
- Gorte, B.; Aleksandrov, M.; Zlatanova, S. Towards egress modelling in voxel building models. ISPRS annals of the photogrammetry, remote sensing and spatial information sciences. In Proceedings of the 4th International Conference on Smart Data and Smart Cities, Kuala Lumpur, Malaysia, 1–3 October 2019; Volume 4. [Google Scholar] [CrossRef] [Green Version]
- Gorte, B.; Zlatanova, S.; Fadli, F. Navigation in indoor voxel models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 279–283. [Google Scholar] [CrossRef] [Green Version]
- Boyles, M.; Fang, S. Slicing-based volumetric collision detection. J. Graph. Tools 1999, 4, 23–32. [Google Scholar] [CrossRef]
- Silver, D.; Gagvani, N. Shape-based volumetric collision detection. In Proceedings of the 2000 IEEE Symposium on Volume Visualization (VV 2000), Salt Lake City, UT, USA, 9–10 October 2000; pp. 57–61. [Google Scholar]
- Cohen-Or, D.; Kaufman, A. 3D line voxelization and connectivity control. IEEE Comput. Graph. Appl. 1997, 17, 80–87. [Google Scholar]
- Dachille, F., IX; Kaufman, A. Incremental triangle voxelization. In Proceedings of the Graphics Interface, Montreal, QC, Canada, 15–17 May 2000; pp. 205–212. [Google Scholar]
- Kaufman, A.; Shimony, E. 3D scan-conversion algorithms for voxel-based graphics. In Proceedings of the 1986 workshop on Interactive 3D graphics, New York, NY, USA, 1 January 1987; pp. 45–75. [Google Scholar]
- Pantaleoni, J. VoxelPipe: A programmable pipeline for 3D voxelization. In Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics, Vancouver, BC, Canada, 5–7 August 2011; pp. 99–106. [Google Scholar]
- Cohen-Or, D.; Kaufman, A. Fundamentals of surface voxelization. Graph. Model. Image Process. 1995, 57, 453–461. [Google Scholar] [CrossRef]
- Liao, D. GPU-accelerated multi-valued solid voxelization by slice functions in real time. In Proceedings of the 24th Spring Conference on Computer Graphics, Budmerice, Slovakia, 21–23 April 2008; pp. 113–120. [Google Scholar]
- Wang, S.W.; Kaufman, A.E. Volume sampled voxelization of geometric primitives. In Proceedings Visualization’93, San Jose, CA, USA, 25–29 October 1993; IEEE: New York, NY, USA, 1999; pp. 78–84. [Google Scholar]
- Bridson, R.E. Computational Aspects of Dynamic Surfaces; Stanford University: Stanford, CA, USA, 2003. [Google Scholar]
- Houston, B.; Nielsen, M.B.; Batty, C.; Nilsson, O.; Museth, K. Hierarchical RLE level set: A compact and versatile deformable surface representation. ACM Trans. Graph. 2006, 25, 151–175. [Google Scholar] [CrossRef]
- Nielsen, M.B.; Museth, K. Dynamic Tubular Grid: An efficient data structure and algorithms for high resolution level sets. J. Sci. Comput. 2006, 26, 261–299. [Google Scholar] [CrossRef] [Green Version]
- Museth, K. VDB: High-resolution sparse volumes with dynamic topology. ACM Trans. Graph. 2013, 32, 1–22. [Google Scholar] [CrossRef]
- Setaluri, R.; Aanjaneya, M.; Bauer, S.; Sifakis, E. SPGrid: A sparse paged grid structure applied to adaptive smoke simulation. ACM Trans. Graph. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Crassin, C.; Green, S. Octree-based sparse voxelization using the GPU hardware rasterizer. OpenGL Insights 2012, 303–318. Available online: https://research.nvidia.com/publication/octree-based-sparse-voxelization-using-gpu-hardware-rasterizer (accessed on 30 November 2021).
- Janßen, C.F.; Koliha, N.; Rung, T. A fast and rigorously parallel surface voxelization technique for GPU-accelerated CFD simulations. Commun. Comput. Phys. 2015, 17, 1246–1270. [Google Scholar] [CrossRef]
- Hasselgren, J.; Akenine-Möller, T.; Ohlsson, L. Conservative rasterization. In GPU Gems 2; Nvidia Developer: Santa Clara, CA, USA, 2005; pp. 677–690. [Google Scholar]
- Zhang, L.; Chen, W.; Ebert, D.S.; Peng, Q. Conservative voxelization. Vis. Comput. 2007, 23, 783–792. [Google Scholar] [CrossRef]
- Eisemann, E.; Décoret, X. Single-pass gpu solid voxelization and applications. In Proceedings of the GI’08: Proceedings of the Graphics Interface, Windsor, ON, Canada, 28–30 May 2008. [Google Scholar]
- Fei, Y.; Wang, B.; Chen, J. Point-tessellated voxelization. In Proceedings of the Graphics Interface 2012, Toronto, ON, Canada, 28–30 May 2012; pp. 9–18. [Google Scholar]
- Zhang, Y.; Garcia, S.; Xu, W.; Shao, T.; Yang, Y. Efficient voxelization using projected optimal scanline. Graph. Models 2018, 100, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Sramek, M.; Kaufman, A.E. Alias-free voxelization of geometric objects. IEEE Trans. Vis. Comput. Graph. 1999, 5, 251–267. [Google Scholar] [CrossRef]
- Fang, S.; Chen, H. Hardware accelerated voxelization. Comput. Graph. 2000, 24, 433–442. [Google Scholar] [CrossRef]
- Heidelberger, B.; Teschner, M.; Gross, M.H. Volumetric collision detection for derformable objects. CS Tech. Rep. 2003, 395, 9. [Google Scholar] [CrossRef]
- Young, G.; Krishnamurthy, A. GPU-accelerated generation and rendering of multi-level voxel representations of solid models. Comput. Graph. 2018, 75, 11–24. [Google Scholar] [CrossRef]
- Zhang, Z.; Morishima, S.; Wang, C. Thickness-aware voxelization. Comput. Animat. Virtual Worlds 2018, 29, e1832. [Google Scholar] [CrossRef]
- Sigg, C.; Peikert, R.; Gross, M. Signed distance transform using graphics hardware. In Proceedings of the IEEE Visualization, Seattle, WA, USA, 22–24 October 2003; IEEE: Manhattan, NY, USA, 2003; pp. 83–90. [Google Scholar]
- Varadhan, G.; Krishnan, S.; Kim, Y.J.; Diggavi, S.; Manocha, D. Efficient max-norm distance computation and reliable voxelization. In Symposium on Geometry Processing; ACM Digital Library: New York, NY, USA, 2003; pp. 116–126. [Google Scholar]
- Jones, M.W.; Baerentzen, J.A.; Sramek, M. 3D distance fields: A survey of techniques and applications. IEEE Trans. Vis. Comput. Graph. 2006, 12, 581–599. [Google Scholar] [CrossRef]
- Novotny, P.; Dimitrov, L.I.; Sramek, M. Enhanced voxelization and representation of objects with sharp details in truncated distance fields. IEEE Trans. Vis. Comput. Graph. 2009, 16, 484–498. [Google Scholar] [CrossRef]
- Sramek, M.; Kaufman, A. Object voxelization by filtering. In Proceedings of the IEEE Symposium on Volume Visualization (Cat. No. 989EX300), Research Triangle Park, NC, USA, 19–20 October 1998; pp. 111–118. [Google Scholar]
- Stolte, N. Robust Voxelization of Surfaces; Center for Visual Computing and Computer Science Department, State University of New York at Stony Brook: Stony Brook, NY, USA, 1997; Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.22.1047&rep=rep1&type=pdf (accessed on 30 November 2021).
- Liao, D.; Fang, S. Fast CSG voxelization by frame buffer pixel mapping. In Proceedings of the 2000 IEEE Symposium on Volume Visualization (VV 2000), Salt Lake City, UT, USA, 9–10 October 2000; IEEE: Manhattan, NY, USA, 2000; pp. 43–48. [Google Scholar]
- Gorte, B.; Zlatanova, S. Rasterization and Voxelization of Two- and Three-dimensional Space Partitionings. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 283–288. [Google Scholar] [CrossRef] [Green Version]
- Nourian, P.; Gonçalves, R.; Zlatanova, S.; Ohori, K.A.; Vo, A.V. Voxelization Algorithms for Geospatial Applications: Computational Methods for Voxelating Spatial Datasets of 3D City Models Containing 3D Surface, Curve and Point Data Models. MethodsX 2016, 3, 69–86. [Google Scholar] [CrossRef]
- Birdsall, C.K. Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms, PIC-MCC. IEEE Trans. Plasma Sci. 1991, 19, 65–85. [Google Scholar] [CrossRef]
- Wu, X. An efficient antialiasing technique. ACM Siggraph Comput. Graph. 1991, 25, 143–152. [Google Scholar] [CrossRef]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- Fujimoto, A.; Tanaka, T.; Iwata, K. Arts: Accelerated ray-tracing system. IEEE Comput. Graph. Appl. 1986, 6, 16–26. [Google Scholar] [CrossRef]
- Liu, X.W.; Cheng, K. Three-dimensional extension of Bresenham’s algorithm and its application in straight-line interpolation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 459–463. [Google Scholar] [CrossRef]
- Laine, S. A topological approach to voxelization. Comput. Graph. Forum 2013, 32, 77–86. [Google Scholar] [CrossRef]
- Håkansson, T. A Comparison of Optimal Scanline Voxelization Algorithms. Master’s Thesis, Computer Science and Software Engineering, Linköping University, Linköping, Sweden, 2020. [Google Scholar]
- Pineda, J. A parallel algorithm for polygon rasterization. In Proceedings of the 15th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1–5 August 1988; pp. 17–20. [Google Scholar]
- Akenine-Möller, T.; Aila, T. Conservative and tiled rasterization using a modified triangle set-up. J. Graph. Tools 2005, 10, 1–8. [Google Scholar] [CrossRef]
- Woo, R.; Choi, S.; Sohn, J.-H.; Song, S.-J.; Bae, Y.-D.; Yoo, H.-J. A low-power 3D rendering engine with two texture units and 29-Mb embedded DRAM for 3G multimedia terminals. IEEE J. Solid-State Circuits 2004, 39, 1101–1109. [Google Scholar] [CrossRef]
- Akenine-Möller, T.; Ström, J. Graphics for the masses: A hardware rasterization architecture for mobile phones. In ACM SIGGRAPH 2003 Papers; Association for Computing Machinery: New York, NY, USA, 2003; pp. 801–808. [Google Scholar]
- Ma, Y.; Wang, X.; Zhu, M.; Wan, W. Rasterization of geometric primitive in graphics based on FPGA. In Proceedings of the 2010 International Conference on Audio, Language and Image Processing, Shanghai, China, 23–25 November 2010; IEEE: Manhattan, NY, USA, 2010; pp. 1211–1216. [Google Scholar]
- McCormack, J.; McNamara, R. Tiled polygon traversal using half-plane edge functions. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Workshop on Graphics Hardware, Interlaken, Switzerland, 21–22 August 2000; Association for Computing Machinery: New York, NY, USA, 2000; pp. 15–21. [Google Scholar]
- Abrash, M. Rasterization on Larrabee. Dr. Dobbs J. 1 May 2009. Available online: http://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/15869-f11/www/readings/abrash09_lrbrast.pdf (accessed on 30 November 2021).
- Sun, C.-H.; Tsao, Y.-M.; Lok, K.-H.; Chien, S.-Y. Universal Rasterizer with edge equations and tile-scan triangle traversal algorithm for graphics processing units. In Proceedings of the 2009 IEEE International Conference on Multimedia and Expo, New York, NY, USA, 28 June–3 July 2009; IEEE: New York, NY, USA, 2009; pp. 1358–1361. [Google Scholar]
- Wang, X.; Guo, F.; Zhu, M. A more efficient triangle rasterization algorithm implemented in FPGA. In Proceedings of the 2012 International Conference on Audio, Language and Image Processing, Shanghai, China, 16–18 July 2012; pp. 1108–1113. [Google Scholar]
- Fatahalian, K.; Luong, E.; Boulos, S.; Akeley, K.; Mark, W.R.; Hanrahan, P. Data-parallel rasterization of micropolygons with defocus and motion blur. In Proceedings of the Conference on High Performance Graphics 2009, New York, NY, USA, 1–3 August 2009; pp. 59–68. [Google Scholar]
- Möller, T.; Trumbore, B. Fast, minimum storage ray-triangle intersection. J. Graph. Tools 1997, 2, 21–28. [Google Scholar] [CrossRef]
- Shevtsov, M.; Soupikov, A.; Kapustin, A.; Novorod, N. Ray-triangle intersection algorithm for modern CPU architectures. In Proceedings of the GraphiCon, Moscow, Russia, 30 October 2007; Volume 2007, pp. 33–39. [Google Scholar]
- Assarsson, U.; Moller, T. Optimized view frustum culling algorithms for bounding boxes. J. Graph. Tools 2000, 5, 9–22. [Google Scholar] [CrossRef]
- Badouel, D. An efficient ray-polygon intersection. In Graphics Gems; Academic Press Professional: San Diego, CA, USA, 1990; pp. 390–393. [Google Scholar]
- Haines, E. Point in Polygon Strategies. Graph. Gems 1994, 4, 24–46. [Google Scholar]
- Rauwendaal, R. Hybrid Computational Voxelization Using the Graphics Pipeline. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2012. [Google Scholar]
- Liu, F.; Huang, M.-C.; Liu, X.-H.; Wu, E.-H. Freepipe: A programmable parallel rendering architecture for efficient multi-fragment effects. In Proceedings of the 2010 ACM SIGGRAPH symposium on Interactive 3D Graphics and Games, Washington, DC, USA, 19–21 February 2010; pp. 75–82. [Google Scholar]
- Seiler, L.; Carmean, D.; Sprangle, E.; Forsyth, T.; Dubey, P.; Junkins, S.; Lake, A.; Cavin, R.; Espasa, R.; Grochowski, E.; et al. Larrabee: A many-core x86 architecture for visual computing. ACM Trans. Graph. 2009, 29, 10–21. [Google Scholar] [CrossRef] [Green Version]
- Eisenacher, C.; Loop, C.T. Data-parallel micropolygon rasterization. In Eurographics (Short Papers); European Association for Computer Graphics: Norrköping, Sweden, 2010; pp. 53–56. [Google Scholar]
- Faieghi, M.; Tutunea-Fatan, O.R.; Eagleson, R. Fast and cross-vendor OpenCL-based implementation for voxelization of triangular mesh models. Comput. Aided. Des. Appl. 2018, 15, 852–862. [Google Scholar] [CrossRef]
- Kalojanov, J.; Billeter, M.; Slusallek, P. Two-level grids for ray tracing on GPUs. Comput. Graph. Forum 2011, 30, 307–314. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, W.; Bao, H.; Zhang, H.; Peng, Q. Real-time voxelization for complex polygonal models. In Proceedings of the 12th Pacific Conference on Computer Graphics and Applications, Seoul, Korea, 6–8 October 2004; IEEE: Manhattan, NY, USA, 2004; pp. 43–50. [Google Scholar]
- Reitinger, B.; Bornik, A.; Beichel, R. Efficient volume measurement using voxelization. In Proceedings of the 19th Spring Conference on Computer Graphics, New York, NY, USA, 24–26 April 2003; pp. 47–54. [Google Scholar]
- Nooruddin, F.S.; Turk, G. Simplification and repair of polygonal models using volumetric techniques. IEEE Trans. Vis. Comput. Graph. 2003, 9, 191–205. [Google Scholar] [CrossRef] [Green Version]
- Forest, V.; Barthe, L.; Paulin, M. Real-time hierarchical binary-scene voxelization. J. Graph. Gpu Game Tools 2009, 14, 21–34. [Google Scholar] [CrossRef]
- Lopez-Moreno, J.; Miraut, D.; Cirio, G.; Otaduy, M.A. Sparse GPU Voxelization of Yarn-Level Cloth. Comput. Graph. Forum 2017, 36, 22–34. [Google Scholar] [CrossRef]
- Wang, S.W.; Kaufman, A.E. Volume-sampled 3D modeling. IEEE Comput. Graph. Appl. 1994, 14, 26–32. [Google Scholar] [CrossRef]
- Widjaya, H.; Moller, T.; Entezari, A. Voxelization in common sampling lattices. In Proceedings of the 11th Pacific Conference on Computer Graphics and Applications, Canmore, AB, Canada, 8–10 October 2003; IEEE: New York, NY, USA, 2003; pp. 497–501. [Google Scholar]
- Bergs, T.; Henrichs, O.; Wilms, M.; Prümmer, M.; Arntz, K. Development of a voxelization tool for the calculation of vector-based workpiece representations. Procedia CIRP 2021, 100, 7–12. [Google Scholar] [CrossRef]
- Baumann, P.; Dehmel, A.; Furtado, P.; Ritsch, R.; Widmann, N. The multidimensional database system RasDaMan. In Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 1–4 June 1998; pp. 575–577. [Google Scholar]
- Laine, S.; Karras, T. Efficient sparse voxel octrees. IEEE Trans. Vis. Comput. Graph. 2010, 17, 1048–1059. [Google Scholar] [CrossRef] [Green Version]
- Laine, S.; Karras, T. Efficient Sparse Voxel Octrees–Analysis, Extensions, and Implementation; NVIDIA Research: Santa Clara, CA, USA, 2010; Volume 2, Available online: https://research.nvidia.com/publication/efficient-sparse-voxel-octrees-analysis-extensions-and-implementation (accessed on 30 November 2021).
- Villanueva, A.J.; Marton, F.; Gobbetti, E. SSVDAGs: Symmetry-aware sparse voxel DAGs. In Proceedings of the 20th ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, New York, NY, USA, 27–28 February 2016; pp. 7–14. [Google Scholar]
- Baert, J.; Lagae, A.; Dutré, P. Out-of-core construction of sparse voxel octrees. In Proceedings of the 5th high-performance graphics conference, New York, NY, USA, 19–21 July 2013; pp. 27–32. [Google Scholar]
- Rodríguez, M.B.; Gobbetti, E.; Guitián, J.A.I.; Makhinya, M.; Marton, F.; Pajarola, R.; Suter, K.S. State-of-the-art in compressed GPU-based direct volume rendering. Comput. Graph. Forum 2014, 33, 77–100. [Google Scholar] [CrossRef]
- Kämpe, V.; Sintorn, E.; Assarsson, U. High resolution sparse voxel dags. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Villanueva, A.J.; Marton, F.; Gobbetti, E. Symmetry-aware Sparse Voxel DAGs (SSVDAGs) for compression-domain tracing of high-resolution geometric scenes. J. Comput. Graph. Tech. Vol. 2017, 6, 1–30. [Google Scholar]
- Dado, B.; Kol, T.R.; Bauszat, P.; Thiery, J.; Eisemann, E. Geometry and attribute compression for voxel scenes. Comput. Graph. Forum 2016, 35, 397–407. [Google Scholar] [CrossRef] [Green Version]
- Dolonius, D.; Sintorn, E.; Kämpe, V.; Assarsson, U. Compressing color data for voxelized surface geometry. IEEE Trans. Vis. Comput. Graph. 2017, 25, 1270–1282. [Google Scholar] [CrossRef] [PubMed]
- Careil, V.; Billeter, M.; Eisemann, E. Interactively Modifying Compressed Sparse Voxel Representations scenes. Comput. Graph. Forum 2020, 39, 111–119. [Google Scholar] [CrossRef]
- Loop, C.; Zhang, C.; Zhang, Z. Real-time high-resolution sparse voxelization with application to image-based modeling. In Proceedings of the 5th High-performance Graphics Conference, New York, NY, USA, 19–21 July 2013; pp. 73–79. [Google Scholar]
- Pätzold, M.; Kolb, A. Grid-free out-of-core voxelization to sparse voxel octrees on GPU. In Proceedings of the 7th Conference on High-Performance Graphics, Los Angeles, CA, USA, 7–9 August 2015; pp. 95–103. [Google Scholar]
- Museth, K. NanoVDB: A GPU-friendly and portable VDB data structure for real-time rendering and simulation. In Proceedings of the ACM SIGGRAPH 2021 Talks, New York, NY, USA, 2021, 9–13 August; pp. 1–2.
- Houston, B.; Wiebe, M.; Batty, C. RLE sparse level sets. In Proceedings of the ACM SIGGRAPH 2004 Sketches, New York, NY, USA, 8–12 August 2004; p. 137. [Google Scholar]
- Nielsen, M.B. Efficient and High Resolution Level Set Simulations. Ph.D. Thesis, Aarhus University, Aarhus, Denmark, 2006. [Google Scholar]
- Hoetzlein, R.K. GVDB: Raytracing sparse voxel database structures on the GPU. In Proceedings of the High Performance Graphics, Dublin, Ireland, 20–22 June 2016; pp. 109–117. [Google Scholar]
- Wu, K.; Truong, N.; Yuksel, C.; Hoetzlein, R. Fast fluid simulations with sparse volumes on the GPU. Comput. Graph. Forum 2018, 37, 157–167. [Google Scholar] [CrossRef]
- Gao, M.; Wang, X.; Wu, K.; Pradhana, A.; Sifakis, E.; Yuksel, C.; Jiang, C. GPU optimization of material point methods. ACM Trans. Graph. 2019, 37, 1–12. [Google Scholar] [CrossRef]
- Hu, Y.; Li, T.; Anderson, L.; Ragan-Kelley, J.; Durand, F. Taichi: A language for high-performance computation on spatially sparse data structures. ACM Trans. Graph. 2019, 38, 1–16. [Google Scholar] [CrossRef] [Green Version]





| Method | Type | Property | General Purpose |
|---|---|---|---|
| 2D Bresenham’s line algorithm [58] | Integer-only | 8-connected | Line primitives rasterisation |
| 2D-DDA | Floating-point or integer | 8-connected | Line primitives rasterisation |
| 3D-DDA [59] | Floating-point or integer | 26-connected | Line primitives voxelisation |
| RLV & SLV [1] | Floating-point | Conservative | Line primitives voxelisation |
| Xiaolin Wu’s line algorithm [57] | Floating-point | Conservative | Antialiasing |
| Tripod [23] | Integer | 6-connected | Line primitives voxelisation |
| 3D Bresenham’s line algorithm [60] | Integer-only | 26-connected | Line primitives voxelisation |
| Targets-based approaches [61] | Floating-point | 6/26-connected | Irregular line primitives voxelisation |
| ILV [41] | Integer-only | 6-connected | Surface voxelisation |
| Method | Type | Property | Main Technique |
|---|---|---|---|
| [3,63,65,66,67,71] | Rasterisation | 6/26-connected & conservative | Bounding box, backtrack, zigzag, central-line, and midpoint traversal |
| [3,26,68,69,70] | Rasterisation | 6/26-connected & conservative | Tile-based |
| [55,73,74,75,77] | Raycasting | 6/26-connected | Ray-triangle and ray-polygon intersection |
| [41,62] | Rasterisation | 6/26-connected & conservative | Line rasterisation |
| Method | Type | Property | Main Technique | General Purpose |
|---|---|---|---|---|
| [43] | Slice-based | ‘26-connected’ | Plane slicing | Rendering |
| [14] | Slice-based | ‘26-connected’ | Depth peeling | Rendering |
| [38] | Slice-based | Conservative | Bounding box | Collision detection |
| [72] | Rasterisation | 26-connected | Bounding box | Rendering |
| [79] | Rasterisation | 26-connected | Bounding box | Rendering |
| [81] | Rasterisation | 26-connected | Tile-based | Voxelisation |
| [3] | Rasterisation | Conservative & 26-connected | Bounding box | Voxelisation |
| [83] | Rasterisation | ‘Conservative’ | Two level grids | Rendering |
| [26] | Rasterisation | Conservative & 26-connected | Tile-based & bucketing | Voxelisation & rendering |
| [40] | Rasterisation | 26-connected | Point tessellation | Voxelisation |
| [55] | Raycasting | 6/26-connected | Intersecting targets | Voxelisation |
| [41] | Rasterisation | 6/26-connected | ILV | Voxelisation |
| [45] | Rasterisation & raycasting | Conservative | Tile-based + ray-triangle intersection | Voxelisation & rendering |
| Method | Type | Property | Main Technique | General Purpose |
|---|---|---|---|---|
| [43] | Slice-based | Interior only | Plane slicing | Voxelisation |
| [84] | Slice-based | Interior only | Surface voxelisation + 2D scan-filling | Voxelisation |
| [2] | Slice-based | Interior only | Bitwise OR operation | Rendering |
| [28] | Slice-based | Interior only | Mask creation | Voxelisation |
| [39] | Slice-based | Interior only & conservative | Single pass & bitwise OR operation | Voxelisation |
| [3] | Rasterisation | Interior only | Tile-based, bounding box, sparse octree | Voxelisation & storage |
| Method | Geometry Voxelisation Type | GPU API/CPU | Voxel Data Structure | Attribute Conservation | Out-of-Core |
|---|---|---|---|---|---|
| [92] | Any | CPU | Regular grid | x | x |
| [39] | Solid | OpenGL & DirectX 10 | Regular grid | x | - |
| [28] | Solid | OpenGL 2 | Regular grid | x | - |
| [3] | Solid | CUDA | SVO | - | - |
| [93,94] | Surface | CUDA | SVO | x | - |
| [26] | Surface | CUDA | Regular grid | x | - |
| [40] | Surface | OpenGL 4 & DirectX 11 | Regular grid | x | - |
| [103] | Surface | DirectX 11 | SVO | x | - |
| [96] | Surface | CPU | SVO | - | x |
| [98] | Surface | CUDA | SVDAG | - | x |
| [104] | Surface | CUDA | SVO | x | x |
| [95,99] | Surface | OpenGL | SSVDAG | - | x |
| [100] | Surface | GPU | SVDAG | x | x |
| [101,102] | Surface | CUDA | SVDAG | x | x |
| Method | GPU API/CPU | Voxel Data Structure | Out-of-Core | Maximum Tested Grid Size | General Purpose |
|---|---|---|---|---|---|
| [30] | CPU | SBG | - | 2000 3 | Simulation and rendering |
| [106] | CPU | RLE | - | 624 × 554 × 488 | Rendering |
| [32] | CPU | DT-Grid | - | 1024 3 | Fluid simulation |
| [31] | CPU | H-RLE | - | 5K × 3K × 3K | Fluid simulation |
| [33] | CPU | VDB | x | 15K × 900 × 500 | Simulation and rendering |
| [34] | CPU | SPGrid | - | 2K × 2K × 4K | Fluid simulation |
| [108] | CUDA | GVDB | - | 2048 3 | Simulation and rendering |
| [109] | CUDA | GVDB | - | 1056 × 288 × 768 | Fluid simulation |
| [110] | CUDA | GSPGrid | - | 512 3 | MPM simulation |
| [111] | CUDA, OpenGL, Apple Metal | GVDB, GSPGrid, custom | - | 4096 3 | Simulation, rendering, and 3D deep learning |
| [105] | CUDA, OpenCL, OptiX OpenGL, DirectX12, WebGL, HLSL & GLSL | NanoVDB | x | / | Simulation and rendering |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleksandrov, M.; Zlatanova, S.; Heslop, D.J. Voxelisation Algorithms and Data Structures: A Review. Sensors 2021, 21, 8241. https://doi.org/10.3390/s21248241
Aleksandrov M, Zlatanova S, Heslop DJ. Voxelisation Algorithms and Data Structures: A Review. Sensors. 2021; 21(24):8241. https://doi.org/10.3390/s21248241
Chicago/Turabian StyleAleksandrov, Mitko, Sisi Zlatanova, and David J. Heslop. 2021. "Voxelisation Algorithms and Data Structures: A Review" Sensors 21, no. 24: 8241. https://doi.org/10.3390/s21248241
APA StyleAleksandrov, M., Zlatanova, S., & Heslop, D. J. (2021). Voxelisation Algorithms and Data Structures: A Review. Sensors, 21(24), 8241. https://doi.org/10.3390/s21248241







