Specific Radar Recognition Based on Characteristics of Emitted Radio Waveforms Using Convolutional Neural Networks
Abstract
:1. Introduction
2. Description of the Database
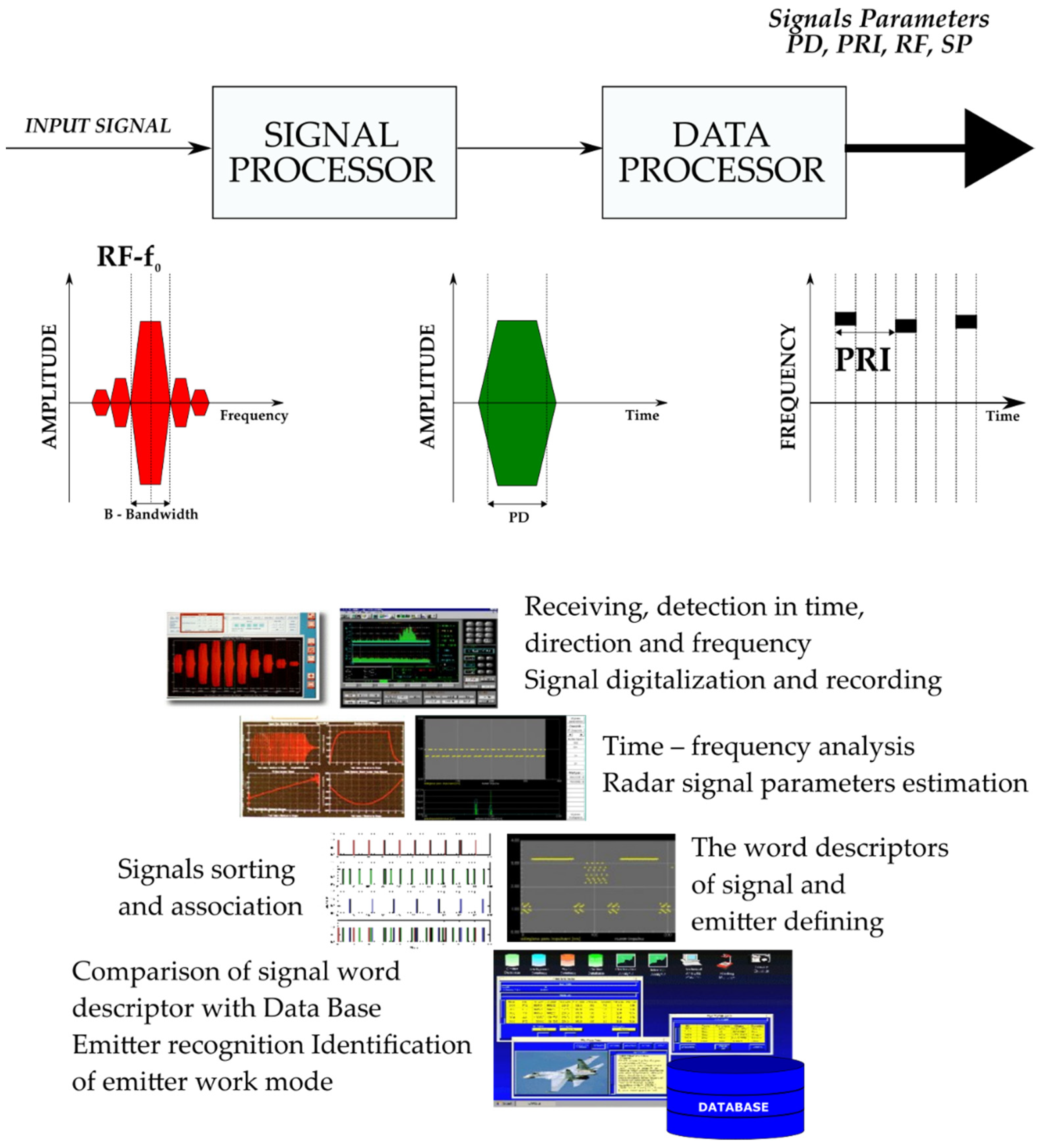
2.1. Description of Radar Signal Parameters
- -
- Automatic detection direction that finds and monitors the emission sources with a frequency ranging from 500 MHz to 18 GHz;
- -
- Signal parameters measured: frequency, pulse width, amplitude, direction of arrival, pulse repetition frequency, antenna rotation period;
- -
- Deinterleaving;
- -
- Acousto-optical channel of spectrum analyzer 500 MHz and channel of compression spectrum analyzer 40 MHz;
- -
- Radio frequency measurement with 1 MHz accuracy;
- -
- Instantaneous time parameters measurement with 25 ns accuracy.
2.2. Constructing a Set of Data for Training a Neural Network
- (a)
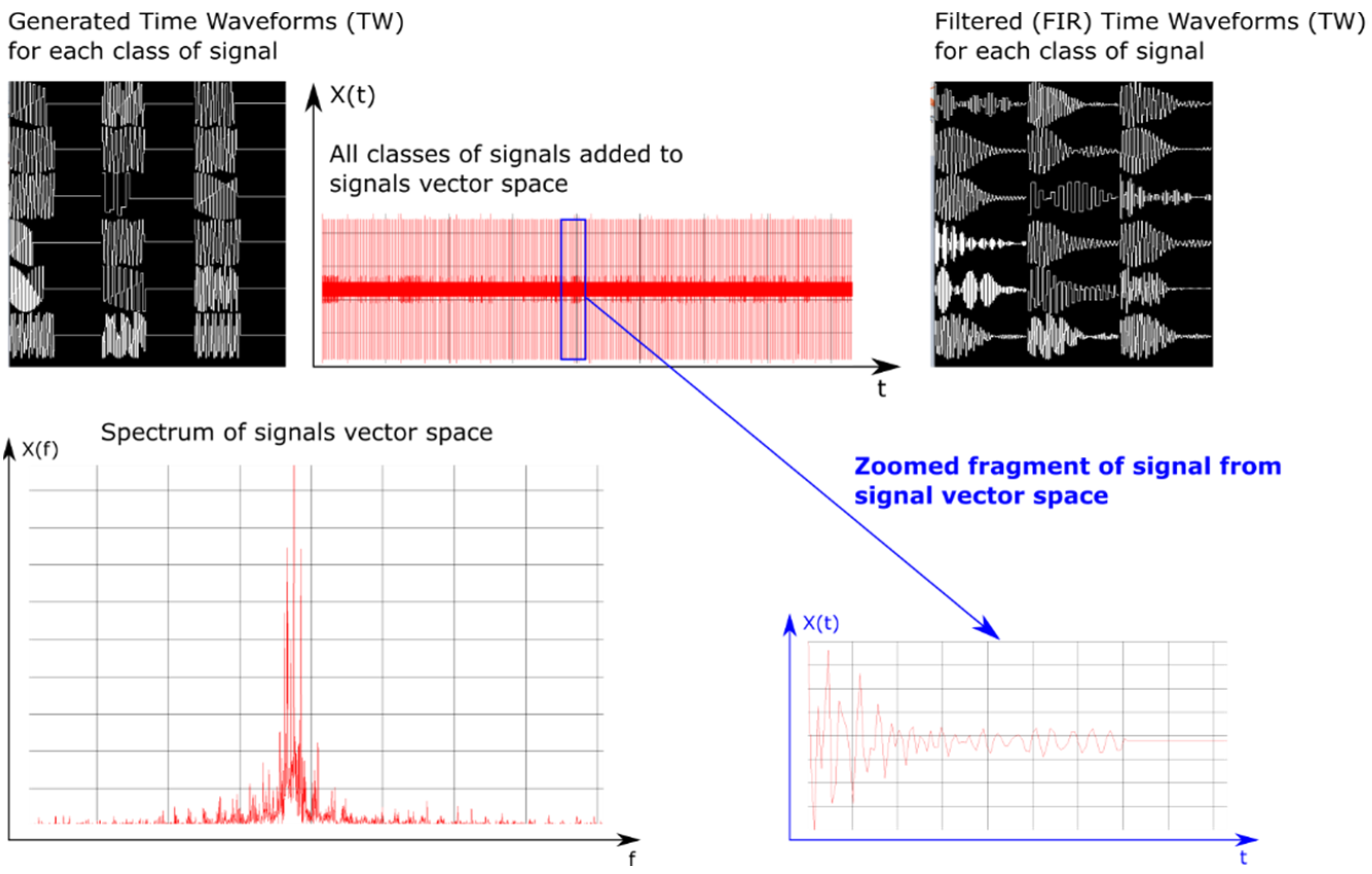
- The first training dataset consists of time waveforms (TW) of the signals with variable PD, RF and intra-pulse modulation. An example of the time waveforms of a signal simulated with the use of a simulation environment (which is described in more detail in Section 5), based on the parameters presented in Table 1, is depicted in Figure 4.
- (b)
- The second training dataset consists of variable PRI waveforms which change depending on the applied inter-pulse modulation. Below, in Figure 5, these changes of PRI are shown.
- (c)
- The third training dataset consists of variable PD waveforms changing from pulse to pulse.
2.3. The Similarity between the Classes of Signals
3. Proposed Model
4. CNN Learning
| Algorithm 1 Batch normalization procedure | |
| Input: X[N] |
|
| N, |
|
| , , |
|
| |
| Output: |
|
| 1: initialize: | |
| 2: for in do |
|
| 3: | |
| 4: end for | |
| 5: | |
| 6: for in do |
|
| 7: | |
| 8: | |
| 9: end for | |
| 10: | |
| 11: for in do |
|
| 12: | |
| 13: | |
| 14: end for | |
5. Simulation Environment
| Algorithm 2 Add signals to vector space (Random PRI, PD, RF Modulation) | |
| Input: |
|
| |
| |
| |
| |
| Output: |
|
| 1: initialize: |
|
| 2: for in (L − 1) do | |
| 3: |
|
| 4: |
|
| 5: |
|
| 6: |
|
| 7: | |
| 8: |
|
| 9: while do | |
| 10: |
|
| 11: |
|
| 12: |
|
| 13: |
|
| 14: |
|
| 15: |
|
| 16: |
|
| 17: end while | |
| 18: end for | |
| Algorithm 3 Add signal to vector space (random PRI modulation) | |
| Input: |
|
| |
| |
| shift |
|
| Output: |
|
| 1: initialize: | |
| 2: for in (currentWaveformLength − 1) do | |
| 3: |
|
| 11: end for | |
| Algorithm 4 Filter all signals | |
| Input: |
|
| |
| |
| 1: initialize: |
|
| 2: for in (L − 1) do | |
| 3: |
|
| 4: |
|
| 5: |
|
| 11: end for | |
6. Experiment Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adamy, D.L. EW 102. A Second Course in Electronic Warfare; Horizon House Publications: London, UK, 2004. [Google Scholar]
- Vakin, S.A.; Shustov, L.N.; Dunwell, R.H. Fundamentals of Electronic Warfare; Artech House: Boston, MA, USA, 2001. [Google Scholar]
- Willey, R.G. ELINT: The Interception and Analysis of Radar Signals; Horizon House Publications: London, UK, 2006. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, G.; et al. TensorFlow. A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; USENIX Association: Berkeley, CA, USA, 2016; pp. 265–283. [Google Scholar]
- Anitha, U.; Malarkkan, S. Underwater object identification and recognition with sonar images using soft computing techniques. Indian J. Geo Mar. Sci. 2018, 47, 665–673. [Google Scholar]
- Ding, J.; Liu, Z.C. A study of radar emitter recognition based on characteristic parameter matching method. Mod. Radar 2011, 33, 29–33. [Google Scholar]
- Kirichenko, L.; Radivilova, T.; Bulakh, V. Machine learning in classification time series with fractal properties. Data 2019, 4, 5. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.A.P.; Masse, N. Neural Networks for Classification of Radar Signals; Defence Research Establishment: Ottawa, ON, Canada, 1993; Technical Note 93–33. [Google Scholar]
- Matuszewski, J.; Pietrow, D. Recognition of electromagnetic sources with the use of deep neural networks. In Proceedings of the XII Conference on Reconnaissance and Electronic Warfare Systems, Ołtarzew, Poland, 19–21 November 2018; Volume 11055, pp. 100–114. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, G.; Chen, H.; Gao, J. Automatic radar waveform recognition based on deep convolutional denoising auto-encoders. Circuits Syst. Signal Process. 2018, 37, 4034–4048. [Google Scholar] [CrossRef]
- Kechagias-Stamatis, O.; Aouf, N.; Belloni, C. SAR automatic target recognition based on convolutional neural networks. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, Ireland, 23–26 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D.; et al. HOG-ShipCLSNet: A novel deep learning network with hog feature fusion for SAR ship classification. IEEE Trans. Geosci. Remote Sens. 2021, 1–22. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. A polarization fusion network with geometric feature embedding for SAR ship classification. Pattern Recognit. 2021, 123, 108365. [Google Scholar] [CrossRef]
- Nishizaki, H.; Makino, K. Signal classification using deep learning. In Proceedings of the 2019 IEEE International Conference on Sensors and Nanotechnology, Penang, Malaysia, 24–25 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, G.; Rong, H.; Jin, W.; Hu, L. Radar emitter signal recognition based on resemblance coefficient features. In Rough Sets & Current Trends in Computing, International Conference; Rsctc: Uppsala, Sweden, 2014. [Google Scholar]
- Wu, X.; Shi, Y.; Meng, W.; Ma, X.; Fang, N. Specific emitter identification for satellite communication using probabilistic neural networks. Int. J. Satell. Commun. Netw. 2019, 37, 283–291. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, F.; Tang, B.; Yin, Q.; Sun, X. Slim and efficient neural network design for resource-constrained SAR target recognition. Remote Sens. 2018, 10, 1618. [Google Scholar] [CrossRef] [Green Version]
- Shieh, C.S.; Lin, C.T. A vector neural network for emitter identification. IEEE Trans. Antennas Propag. 2002, 50, 1120–1127. [Google Scholar] [CrossRef] [Green Version]
- Pietkiewicz, T.; Sikorska-Łukasiewicz, K. Comparison of two classifiers based on neural networks and the DTW method of comparing time series to recognize maritime objects upon FLIR images. In Proceedings of the XII Conference on Reconnaissance and Electronic Warfare Systems, Ołtarzew, Poland, 19–21 November 2018; Volumn 110550V. [Google Scholar] [CrossRef]
- Tachibana, K.; Otsuka, K. Wind prediction performance of complex neural network with ReLU activation function. In Proceedings of the 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018; pp. 1029–1034. [Google Scholar] [CrossRef]
- Yun, L.; Jing-Chao, L. Radar signal recognition algorithms based on neural network and grey relation theory. In Proceedings of the 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, Harbin, China, 26–30 July 2011; Volume 2, pp. 1482–1485. [Google Scholar] [CrossRef]
- Zhang, M.; Diao, M.; Gao, L.; Liu, L. Neural networks for radar waveform recognition. Symmetry 2017, 9, 75. [Google Scholar] [CrossRef] [Green Version]
- Mussab Elamien Abd Elmaggeed, A.J.A. Neural network algorithm for radar signal recognition. J. Eng. Res. Appl. 2015, 5, 123–125. [Google Scholar]
- Petrov, N.; Jordanov, I.; Roe, J. Radar emitter signals recognition and classification with feedforward networks. In Proceedings of the 17th International Conference in Knowledge Based and Intelligent Information and Engineering Systems—KES2013, Kitakyushu, Japan, 9–11 September 2013; Volume 22, pp. 1192–1200. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zheng, T.; Lei, P.; Bai, X. A hierarchical convolution neural network (CNN)-based ship target detection method in spaceborne SAR imagery. Remote Sens. 2019, 11, 620. [Google Scholar] [CrossRef] [Green Version]
- Chi, Z.; Li, Y.; Chen, C. Deep convolutional neural network combined with concatenated spectrogram for environmental sound classification. In Proceedings of the 2019 IEEE 7th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 19–20 October 2019; pp. 251–254. [Google Scholar] [CrossRef]
- Kong, M.; Zhang, J.; Liu, W.; Zhang, G. Radar emitter identification based on deep convolutional neural network. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; pp. 309–314. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Squeeze-and-excitation Laplacian pyramid network with dual-polarization feature fusion for ship classification in sar images. IEEE Geosci. Remote Sens. Lett. 2021, 751–755. [Google Scholar] [CrossRef]
- Cruz-López, J.A.; Boyer, V.; El-Baz, D. Training many neural networks in parallel via back-propagation. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lake Buena Vista, FL, USA, 29 May–2 June 2017; pp. 501–509. [Google Scholar] [CrossRef] [Green Version]
- Aida-Zade, K.; Mustafayev, E.; Rustamov, S. Comparison of deep learning in neural networks on CPU and GPU-based frameworks. In Proceedings of the 2017 IEEE 11th International Conference on Application of Information and Communication Technologies (AICT), Moscow, Russia, 20–22 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Furukawa, M.; Itsubo, T.; Matsutani, H. An in-network parameter aggregation using DPDK for multi-GPU deep learning. In Proceedings of the 2020 Eighth International Symposium on Computing and Networking (CANDAR), Naha, Japan, 24–27 November 2020; pp. 108–114. [Google Scholar] [CrossRef]
- Hoskote, Y.; Vangal, S.; Dighe, S.; Borkar, N.; Borkar, S. Teraflops prototype processor with 80 cores. In Proceedings of the 2007 IEEE Hot Chips 19 Symposium (HCS), Stanford, CA, USA, 19–21 August 2007; pp. 1–15. [Google Scholar] [CrossRef]
- Clark, D. Breaking the teraFLOPS barrier. Computer 1997, 30, 12–14. [Google Scholar] [CrossRef]
- Dhabe, P.; Vyas, P.; Ganeriwal, D.; Pathak, A. Pattern classification using updated fuzzy hyper-line segment neural network and it’s GPU parallel implementation for large datasets using CUDA. In Proceedings of the 2016 International Conference on Computing, Analytics and Security Trends (CAST), Pune, India, 19–21 December 2016; pp. 24–29. [Google Scholar] [CrossRef]
- Dumin, O.; Prishchenko, O.; Pochanin, G.; Plakhtii, V.; Shyrokorad, D. Subsurface object identification by artificial neural networks and impulse radiolocation. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 434–437. [Google Scholar] [CrossRef]
- Jurado-Lucena, A.; Montiel-Sanchez, I.; Escot Bocanegra, D.; Fernandez-Recio, R.; Poyatos Martinez, D. Class identification of aircrafts by means of artificial neural networks trained with simulated radar signatures. Prog. Electromagn. Res. 2011, 21, 243–255. [Google Scholar] [CrossRef]
- Li, P.; Chen, M.; Hu, F.; Xu, Y. A spectrogram-based voiceprint recognition using deep neural network. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 2923–2927. [Google Scholar] [CrossRef]
- ŞEN, S.Y.; ÖZKURT, N. ECG arrhythmia classification by using convolutional neural network and spectrogram. In Proceedings of the 2019 Innovations in Intelligent Systems and Applications Conference (ASYU), Izmir, Turkey, 31 October–2 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kılıç, A.; Babaoğlu, S.; Babalik, A.; Arslan, A. Through-wall radar classification of human posture using convolutional neural networks. Int. J. Antennas Propag. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Yonel, B.; Mason, E.; Yazıcı, B. Deep learning for passive synthetic aperture radar. IEEE J. Sel. Top. Signal Process. 2018, 12, 90–103. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matuszewski, J.; Pietrow, D. Artificial neural networks in the filtration of radiolocation information. In Proceedings of the 2020 IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 25–29 February 2020; pp. 680–685. [Google Scholar] [CrossRef]
- Wang, L.; Tang, J.; Liao, Q. A study on radar target detection based on deep neural networks. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Nalini, M.K.; Radhika, K.R. Comparative analysis of deep network models through transfer learning. In Proceedings of the 2020 Fourth International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, 7–9 October 2020; pp. 1007–1012. [Google Scholar] [CrossRef]
- Yang, X.; Denis, L.; Tupin, F.; Yang, W. SAR image despeckling using pre-trained convolutional neural network models. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, D.Y.; Jeong, J.H.; Shim, K.H.; Lee, S.W. Decoding movement imagination and execution from eeg signals using bci-transfer learning method based on relation network. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1354–1358. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Chen, S.; Wei, S.; Chen, J. A data-efficient training model for signal integrity analysis based on transfer learning. In Proceedings of the 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Bangkok, Thailand, 11–14 November 2019; pp. 186–189. [Google Scholar] [CrossRef]
- Darzikolaei, M.A.; Ebrahimzade, A.; Gholami, E. Classification of radar clutters with artificial neural network. In Proceedings of the 2015 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 5–6 November 2015; pp. 577–581. [Google Scholar] [CrossRef]
- Matuszewski, J.; Pietrow, D. Deep learning neural networks with using pseudo-random 3D patterns generator. In Proceedings of the 2019 IEEE International Scientific-Practical Conference Problems of Infocommunications, Science and Technology (PIC S&T), Kiev, Ukraine, 8–11 October 2019; pp. 262–267. [Google Scholar] [CrossRef]
- Du, X.; Liao, K.; Shen, X. Secondary radar signal processing based on deep residual separable neural network. In Proceedings of the 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 12–16. [Google Scholar] [CrossRef]
- Hannun, A.; Case, C.; Casper, J.; Catanzaro, B.; Diamos, G.; Elsen, E.; Prenger, R.; Satheesh, S.; Sengupta, S.; Coates, A.; et al. Deep Speech: Scaling up end-to-end speech recognition. arXiv 2014, arXiv:1412.5567. [Google Scholar]
- Hwang, M.-J.; Soong, F.; Song, E.; Wang, X.; Kang, H.; Kang, H.G. LP-wavenet: Linear prediction-based wavenet speech synthesis. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 810–814. [Google Scholar]
- Matuszewski, J.; Sikorska-Łukasiewicz, K. Neural network application for emitter identification. In Proceedings of the 2017 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Matuszewski, J. Identification of radar signals using discriminant vectors. In Proceedings of the MIKON 2008–17th International Conference on Microwaves, Radar and Wireless Communications, Wroclaw, Poland, 19–21 May 2008; pp. 433–436. [Google Scholar]
- Lin, W.; Hasenstab, K.; Moura Cunha, G.; Schwartzman, A. Comparison of handcrafted features and convolutional neural networks for liver MR image adequacy assessment. Sci. Rep. 2020, 10, 20336. [Google Scholar] [CrossRef] [PubMed]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep Learning vs. Traditional Computer Vision; ImaR Technology Gateway, Institute of Technology Tralee: Trale, Ireland, 2019. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167v3. [Google Scholar]
- Giusti, A.; Cireşan, D.C.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Fast image scanning with deep max-pooling convolutional neural networks. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 4034–4038. [Google Scholar] [CrossRef] [Green Version]
- Özgür, A.; Nar, F. Effect of Dropout layer on Classical Regression Problems. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Asgher, U.; Muhammad, H.; Hamza, M.M.; Ahmad, R.; Butt, S.I.; Jamil, M. Robust hybrid normalized convolution and forward error correction in image reconstruction. In Proceedings of the 2014 10th International Conference on Innovations in Information Technology (IIT), Abu Dhabi, United Arab Emirates, 9–11 November 2014; pp. 54–59. [Google Scholar] [CrossRef]
- Zhang, L.; Borggreve, D.; Vanselow, F.; Brederlow, R. Quantization considerations of dense layers in convolutional neural Networks for resistive crossbar implementation. In Proceedings of the 2020 9th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Marcu, D.C.; Grava, C. The impact of activation functions on training and performance of a deep neural network. In Proceedings of the 16th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, 10–11 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, J.-C.; Chung, K. Hybrid multi-modal deep learning using collaborative concat layer in health bigdata. IEEE Access 2020, 8, 192469–192480. [Google Scholar] [CrossRef]
- Hong, S.; Song, S. Kick: Shift-N-Overlap cascades of transposed convolutional layer for better autoencoding reconstruction on remote sensing imagery. IEEE Access 2020, 8, 107244–107259. [Google Scholar] [CrossRef]
- Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Tseng, C.; Lee, S. Design of digital differentiator using supervised learning on keras framework. In Proceedings of the 2019 IEEE 8th Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; pp. 162–163. [Google Scholar] [CrossRef]
- Al-Abri, S.; Lin, T.X.; Tao, M.; Zhang, F. A derivative-free optimization method with application to functions with exploding and vanishing gradients. IEEE Control Syst. Lett. 2021, 5, 587–592. [Google Scholar] [CrossRef]
- Masters, T. Practical Neural Network Recipes in C++; Academic Press: London, UK, 1993; ISBN 0124790402, 9780124790407. [Google Scholar]
- Stroustrup, B. The C++ Programming Language, 4th ed.; Addison-Wesley Professional: Boston, MA, USA, 2013. [Google Scholar]
- Bantle, M.; Bayerl, P.; Funken, S.; Thoma, M. Radar signal processing with openCL on integrated graphic processors. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S.G. The design and implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef] [Green Version]
- Visweswar, C.; Mitra, S.K. New linearly tapered window and its application to FIR filter design. In Proceedings of the 2005 European Conference on Circuit Theory and Design, Cork, Ireland, 29 August–1 September 2005; Volume 3, pp. III/445–III/448. [Google Scholar] [CrossRef]
- Ichige, K.; Iwaki, M.; Ishii, R. Accurate estimation of minimum filter length for optimum FIR digital filters. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2000, 47, 1008–1016. [Google Scholar] [CrossRef]
- Shimauchi, S.; Ohmuro, H. Accurate adaptive filtering in square-root Hann windowed short-time Fourier transform domain. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1305–1309. [Google Scholar] [CrossRef]














| Class Number | PRI | PD | RF | SP [s] |
|---|---|---|---|---|
| 0 | 0.877–0.878 | 0.929–1.725 | 2.800–2.832 | 3.97–4.00 |
| 1 | 1.229–1.230 | 3.958–4.492 | 1.255–1.368 | 2.85–2.87 |
| 2 | 1.223–1.223 | 2.512–2.863 | 1.221–1.339 | 5.80–5.96 |
| 3 | 1.223–1.223 | 3.277–3.277 | 1.228–1.330 | 2.86–2.88 |
| 4 | 1.248–1.250 | 2.512–3.015 | 1.215–1.351 | 2.86–2.87 |
| 5 | 1.247–1.250 | 3.216–3.571 | 1.248–1.303 | 2.85–2.88 |
| 6 | 1.250–1.252 | 3.727–3.885 | 1.308–1.365 | 2.87–2.88 |
| 7 | 1.751–1.752 | 0.431–0.705 | 3.144–3.162 | 2.81–2.92 |
| 8 | 1.251–1.252 | 2.018–2.379 | 2.816–2.842 | 5.04–5.08 |
| 9 | 0.768–0.768 | 1.308–3.384 | 2.832–2.854 | 3.96–3.99 |
| 10 | 1.738–1.739 | 2.811–3.514 | 1.203–1.254 | 6.02–6.07 |
| 11 | 1.775–1.778 | 3.482–3.482 | 1.220–1.240 | 9.72–9.76 |
| 12 | 1.856–1.858 | 1.727–4.592 | 3.040–3.092 | 6.03–6.09 |
| 13 | 1.905–1.905 | 0.888–1.466 | 2.219–2.235 | 9.85–9.91 |
| 14 | 2.150–2.150 | 4.898–5.570 | 1.100–1.389 | 5.41–5.53 |
| 15 | 2.225–2.228 | 5.280–5.529 | 1.180–1.205 | 5.44–5.47 |
| 16 | 2.224–2.226 | 4.138–4.917 | 1.633–1.650 | 5.43–5.59 |
| 17 | 2.375–2.375 | 5.440–5.548 | 1.171–1.190 | 5.42–5.76 |
| Number of Signal Class | Number of Overlapping Signals in PRI | Number of Overlapping Signals in PD | Number of Overlapping Signals in the RF | Number of Overlapping Signals in the SP |
|---|---|---|---|---|
| 0 | - | 9, 13 | 8 | 9 |
| 1 | - | 12, 16 | 2, 3, 4, 5, 6, 14 | 3, 4, 5, 6, 7 |
| 2 | 3 | 4, 9, 10, 12 | 1, 3, 4, 5, 6, 10, 11, 14 | - |
| 3 | 2 | 5, 9, 10, 12 | 1, 2, 4, 5, 6, 10, 11, 14 | 1, 4, 5, 6, 7 |
| 4 | 5 | 2, 9, 10, 12 | 1, 2, 3, 5, 6, 10, 11, 14 | 1, 3, 5, 6, 7 |
| 5 | 4 | 3, 9, 10, 11, 12 | 1, 2, 3, 4, 10, 14 | 1, 3, 4, 6, 7 |
| 6 | 8 | 12 | 1, 2, 3, 4, 14 | 1, 3, 4, 5, 7 |
| 7 | - | - | - | 1, 3, 4, 5, 6 |
| 8 | 6 | 9, 12 | 0, 9 | - |
| 9 | - | 0, 2, 3, 4, 5, 8, 10, 12, 13 | 8 | 0 |
| 10 | - | 2, 3, 4, 5, 9, 11, 12 | 2, 3, 4, 5, 11, 14, 15 | 12 |
| 11 | - | 5, 10, 12 | 2, 3, 4, 10, 14 | - |
| 12 | - | 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 16 | - | 10 |
| 13 | - | 0, 9 | - | - |
| 14 | - | 15, 16, 17 | 1, 2, 3, 4, 5, 6, 10, 11, 15, 17 | 15, 16, 17 |
| 15 | 16 | 14, 17 | 10, 14, 17 | 14, 16, 17 |
| 16 | 15 | 1, 12, 14 | - | 14, 15, 17 |
| 17 | - | 14, 15 | 14, 15 | 14, 15, 16 |
| Layer Number | Layer Type | Layer Dimension | Activation Function |
|---|---|---|---|
| 0 | B | - | - |
| 1 | R 1 | - | - |
| 2 | C_1D 2 | [KS 3: 5, NK 4: 5, SS 5: 1] | ReLU [20,62] |
| 3 | B 6 | - | - |
| 4 | MP_1D 7 | [SS: 2] | - |
| 5 | C_1D | [KS: 3, NK: 9, SS: 1] | ReLU |
| 6 | B | - | - |
| 7 | MP_1D | [SS: 2] | - |
| 8 | C_1D | [KS: 2, NK: 6, SS: 1] | ReLU |
| 9 | B | - | - |
| 10 | MP_1D | [SS: 2] | - |
| 11 | F | - | - |
| 12 | D 8 | - | ReLU |
| 13 | B | - | - |
| 14 | Dropout | - | - |
| 15 | D | - | Softmax [20] |
| 16 | B | - | - |
| Input Vectors: | |||
|---|---|---|---|
| PD Samples (Post-Processing) | PRI Samples (Post-Processing) | TW Samples (Raw Acquired Signal Samples) | |
| Structure CNN for PD parameter 9 | Structure CNN for PRI parameter | Structure CNN for TW parameter | |
| Associated Outputs in CNN for PD, PRI and TW Parameters | |||
| Layer number | Layer type | Dimensions of layer | Activation function |
| 0 | D | - | ReLU |
| 1 | B | - | - |
| 2 | D | - | Softmax |
| 3 | B | - | - |
| Layer Number | Layer Type | Dimensions of Layer | Activation Function |
|---|---|---|---|
| 0 | R | - | - |
| 1 | C_1D | [KS: 5, NK: 30, SS: 1] | ReLU |
| 2 | B | - | - |
| 3 | MP_1D | [SS: 2] | - |
| 4 | C_1D | [KS: 4, NK: 30, SS: 2] | ReLU |
| 5 | B | - | - |
| 6 | MP_1D | [SS: 2] | - |
| 7 | C_1D | [KS: 3, NK: 30, SS: 3] | ReLU |
| 8 | B | - | - |
| 9 | MP_1D | [SS: 2] | - |
| 10 | C_1D | [KS: 4, NK: 30, SS: 2] | ReLU |
| 11 | B | - | - |
| 12 | C_1D | [KS: 5, NK: 30, SS: 1] | ReLU |
| 13 | B | - | - |
| 14 | MP_1D | [SS: 2] | - |
| 15 | F | - | - |
| 16 | D | - | Softmax |
| Processing Network | Input Tensor Size | Number of Layers | Number of Weights | Size on Disk | Processing Time for a Single Tensor [s] | GPU Processor |
|---|---|---|---|---|---|---|
| TW or PD or PRI | (1, 128) | 17 | 2248 | 63 kB | 0.015 | Geforce 1060 GTX 6GB |
| TW + PRI + PD | (3, 128) | 3 × 17 (In parallel) + 3 (Output) = 54 | 2248 × 3 + 1332 = 8076 | (63 × 3 + 18) kB = 207 kB | 0.046 |
| Input Size of ANN: | 512 | ||||
|---|---|---|---|---|---|
| Number of Samples 10: | 190 | Number of Tests 11: | 1900 | 12: | 0.0001 |
| Epochs 13 [B:S:E] 14 | Batch Size [B:S:E] | Prediction 15 [Min–Max] | |||
| 60 | 10:10:90 | 0.056–0.111 | |||
| 70 | 10:10:90 | 0.055–0.111 | |||
| 80 | 10:10:90 | 0.056–0.056 | |||
| 90 | 10:10:90 | 0.056–0.111 | |||
| 100 | 10:10:90 | 0.056–0.056 | |||
| 110 | 10:10:90 | 0.056–0.056 | |||
| 110:10:240 | 90 | 0.056–0.167 | |||
| Input Size of ANN: | 512 | ||||
|---|---|---|---|---|---|
| Number of Samples: | 190 | Number of Tests: | 1900 | : | 0.0001 |
| Number of Epochs | Batch Size [B:S:E] | Prediction [Min–Max] | |||
| 60 | 10:10:90 | 0.000–0.333 | |||
| 70 | 10:10:90 | 0.056–0.500 | |||
| 80 | 10:10:90 | 0.056–0.333 | |||
| 90 | 10:10:90 | 0.056–0.556 | |||
| 100 | 20:10:90 | 0.056–0.611 | |||
| 110 | 20:10:90 | 0.056–0.778 | |||
| 120 | 20:10:90 | 0.056–0.500 | |||
| 130 | 20:10:90 | 0.111–0.722 | |||
| 140 | 20:10:90 | 0.056–0.667 | |||
| 150 | 20:10:90 | 0.111–0.556 | |||
| Input Size of ANN: | 93 | ||||
|---|---|---|---|---|---|
| Number of Samples: | 190 | Number of Tests: | 1900 | : | 0.0001 |
| Number of Epochs [B:S:E] | Batch Size [B:S:E] | Prediction [Min–Max] | |||
| 60 | 10:10:90 | 0.294–0.584 | |||
| 70 | 10:10:90 | 0.334–0.538 | |||
| 80 | 10:10:90 | 0.343–0.607 | |||
| 90 | 10:10:90 | 0.392–0.589 | |||
| 100 | 10:10:90 | 0.363–0.633 | |||
| 110 | 10:10:90 | 0.447–0.664 | |||
| 120 | 10:10:90 | 0.440–0.672 | |||
| 130 | 10:10:90 | 0.474–0.667 | |||
| 140 | 10:10:90 | 0.467–0.717 | |||
| 150 | 10:10:90 | 0.463–0.652 | |||
| Input Size of ANN (TW): | 93 | ||||
|---|---|---|---|---|---|
| Number of Samples: | 190 | Number of Tests: | 1900 | : | 0.0001 |
| Number of Epochs [B:S:E] | Input Size (PRI, PD) [B:S:E] | Prediction [Min–Max] | |||
| 128 | 128:32:288 | 0.774–0.889 | |||
| 128 | 320:32:480 | 0.776–0.944 | |||
| 128 | 512:32:672 | 0.808–0.944 | |||
| 128 | 704:32:864 | 0.670–0.889 | |||
| 128:32:160 | 896:32:928 | 0.778–0.889 | |||
| 160:32:224 | 960:32:992 | 0.832–0.923 | |||
| 256 | 128:32:288 | 0.722–0.944 | |||
| 256 | 320:32:480 | 0.722–1.000 | |||
| Input Size of ANN: | |||||||
|---|---|---|---|---|---|---|---|
| Number of Samples | 80 | Number of Tests | 80 | Batch Size: | 40 | : | |
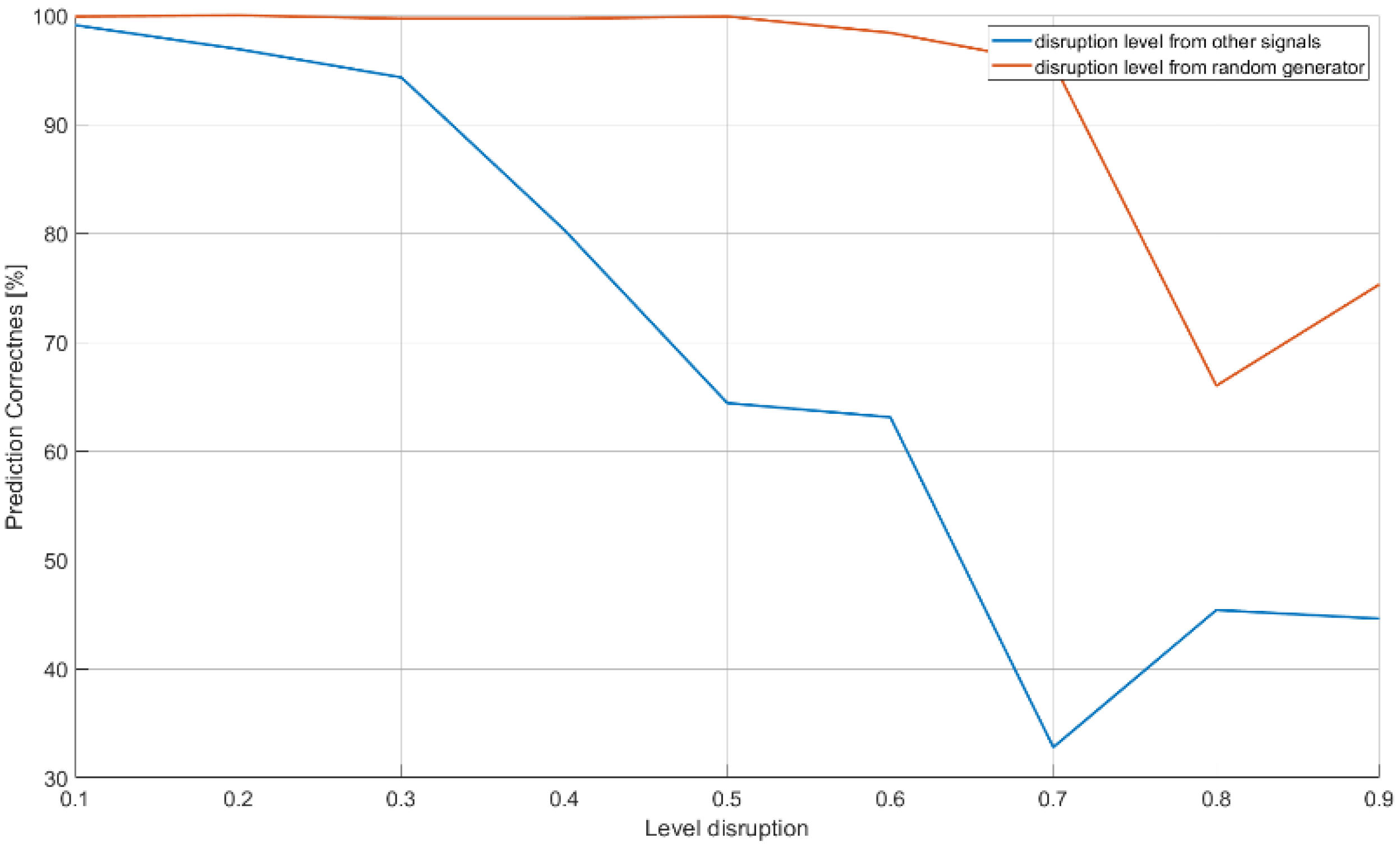
| Number of Epochs | Prediction | Disruption Level | |||||
| 256 | 0.991 | 0.1 | |||||
| 0.969 | 0.2 | ||||||
| 0.943 | 0.3 | ||||||
| 0.803 | 0.4 | ||||||
| 0.644 | 0.5 | ||||||
| 0.631 | 0.6 | ||||||
| 0.328 | 0.7 | ||||||
| 0.454 | 0.8 | ||||||
| 0.446 | 0.9 | ||||||
| Input Size of ANN: | |||||||
| 499 | 0.922 | 0.9 | |||||
| Input Size of ANN: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Epochs: | 256 | Number of Samples: | 80 | Number of Tests | 80 | Batch Size | 40 | : | |
| Prediction | Disruption Level | ||||||||
| 0.999 | 0.1 | ||||||||
| 1.000 | 0.2 | ||||||||
| 0.997 | 0.3 | ||||||||
| 0.997 | 0.4 | ||||||||
| 0.999 | 0.5 | ||||||||
| 0.984 | 0.6 | ||||||||
| 0.956 | 0.7 | ||||||||
| 0.660 | 0.8 | ||||||||
| 0.753 | 0.9 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matuszewski, J.; Pietrow, D. Specific Radar Recognition Based on Characteristics of Emitted Radio Waveforms Using Convolutional Neural Networks. Sensors 2021, 21, 8237. https://doi.org/10.3390/s21248237
Matuszewski J, Pietrow D. Specific Radar Recognition Based on Characteristics of Emitted Radio Waveforms Using Convolutional Neural Networks. Sensors. 2021; 21(24):8237. https://doi.org/10.3390/s21248237
Chicago/Turabian StyleMatuszewski, Jan, and Dymitr Pietrow. 2021. "Specific Radar Recognition Based on Characteristics of Emitted Radio Waveforms Using Convolutional Neural Networks" Sensors 21, no. 24: 8237. https://doi.org/10.3390/s21248237
APA StyleMatuszewski, J., & Pietrow, D. (2021). Specific Radar Recognition Based on Characteristics of Emitted Radio Waveforms Using Convolutional Neural Networks. Sensors, 21(24), 8237. https://doi.org/10.3390/s21248237






