Vital Signs Prediction for COVID-19 Patients in ICU
Abstract
:1. Introduction
2. Material and Methods
2.1. Data
2.2. Methods
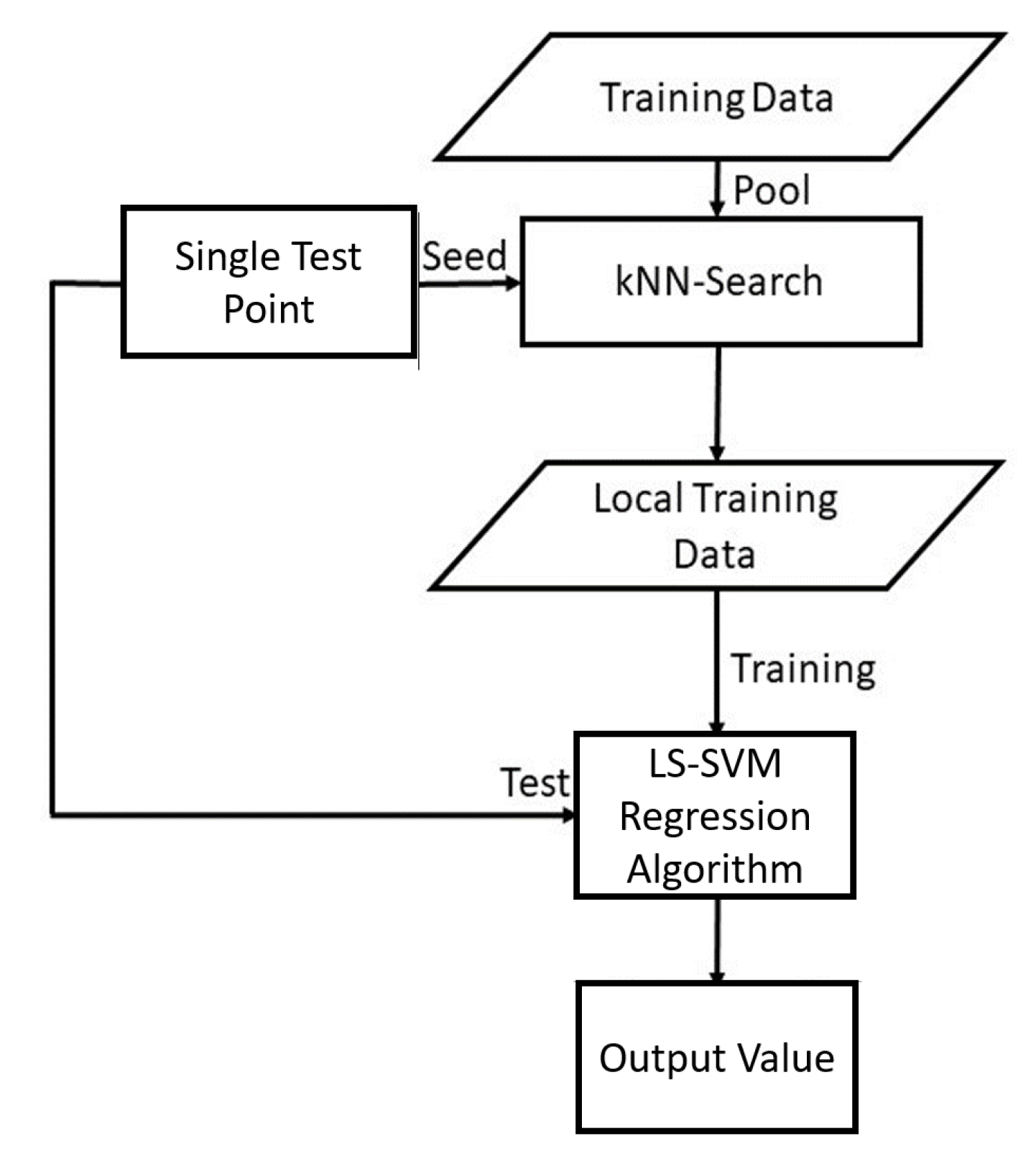
Local Learning of SVMs
- Given a test example , compute distances to all training examples and pick the nearest K neighbours.
- Train the LS-SVM model with the K nearest neighbours.
- Use the resulting regressor to estimate the output of .
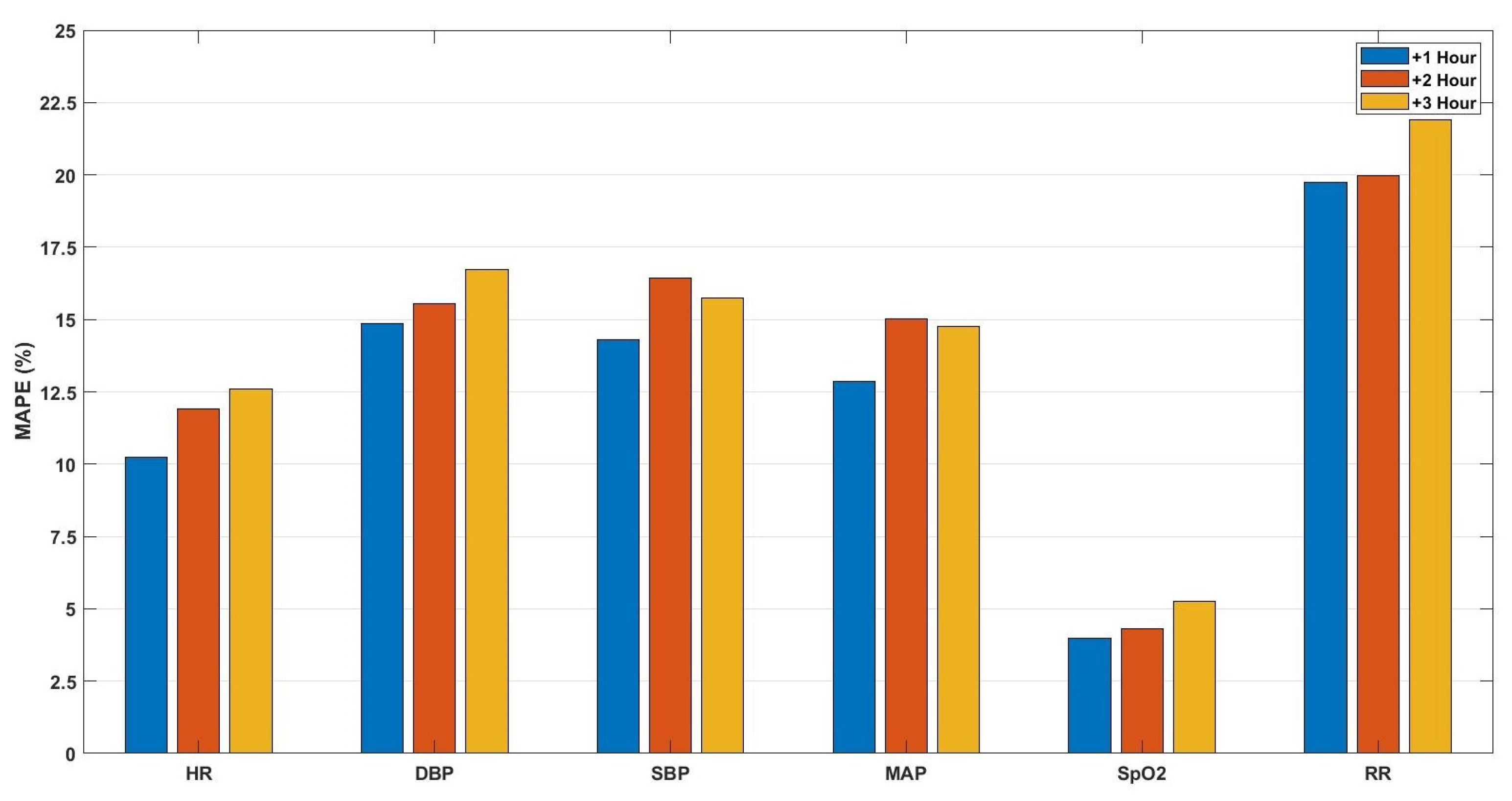
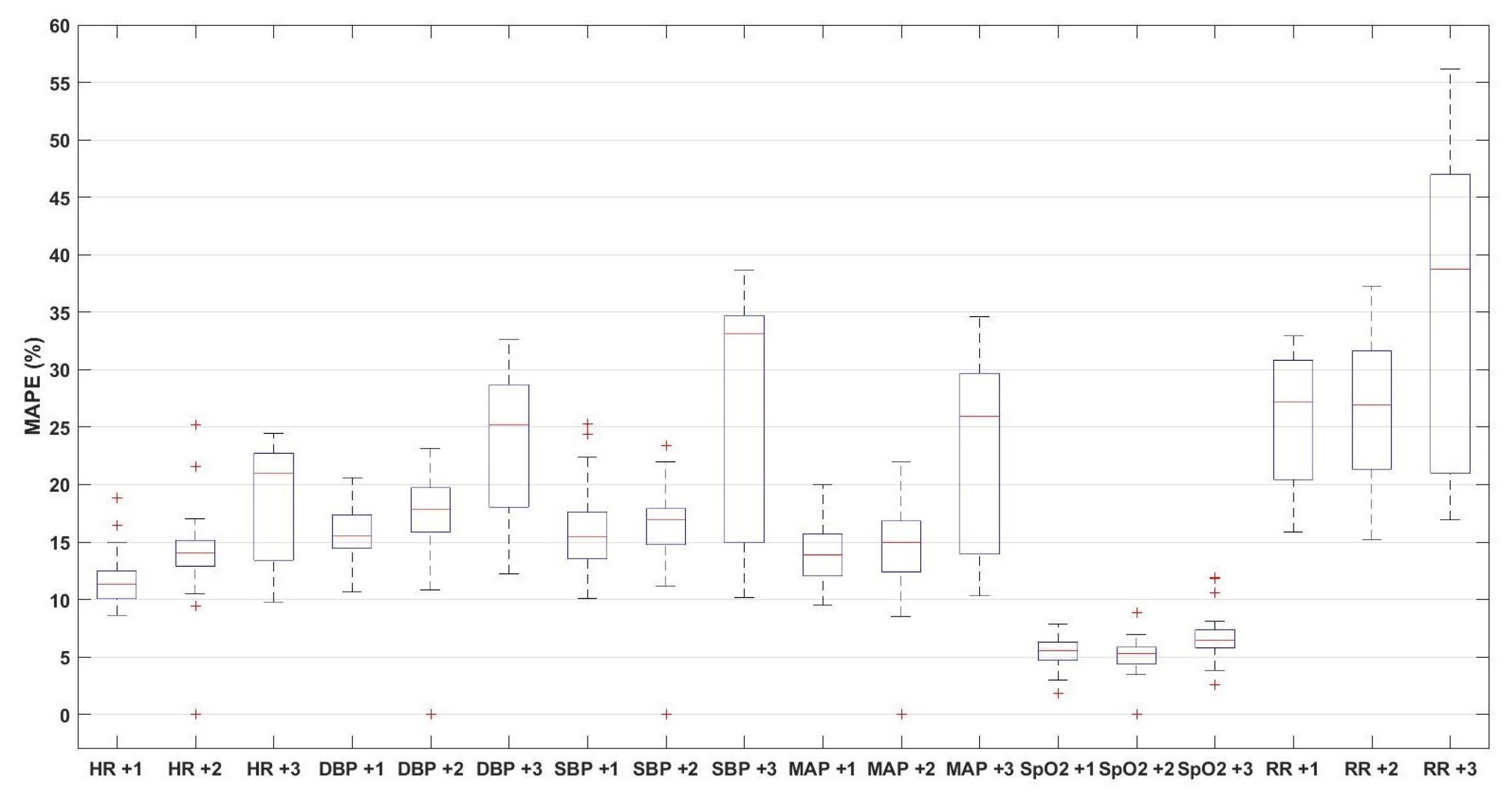
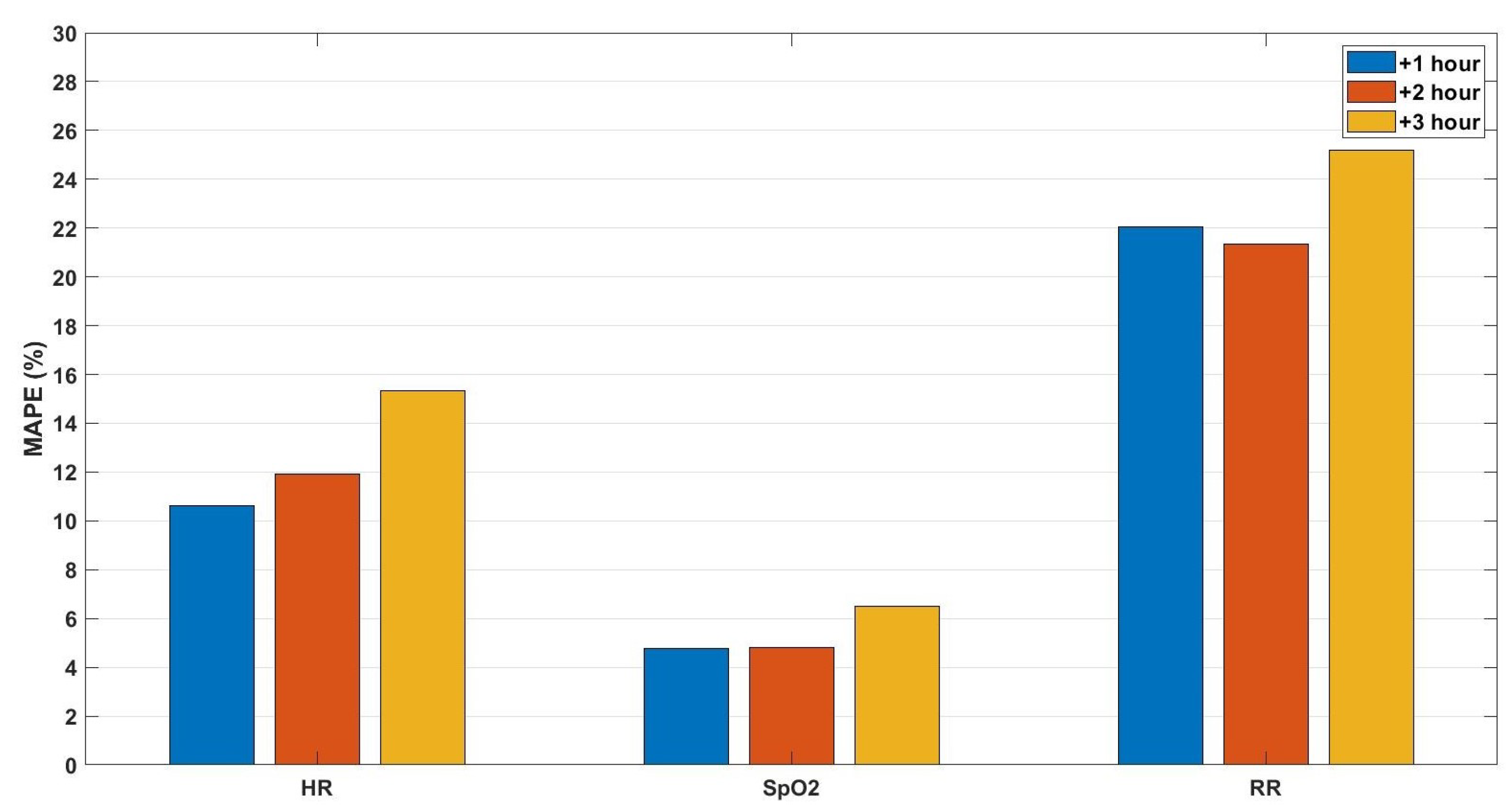
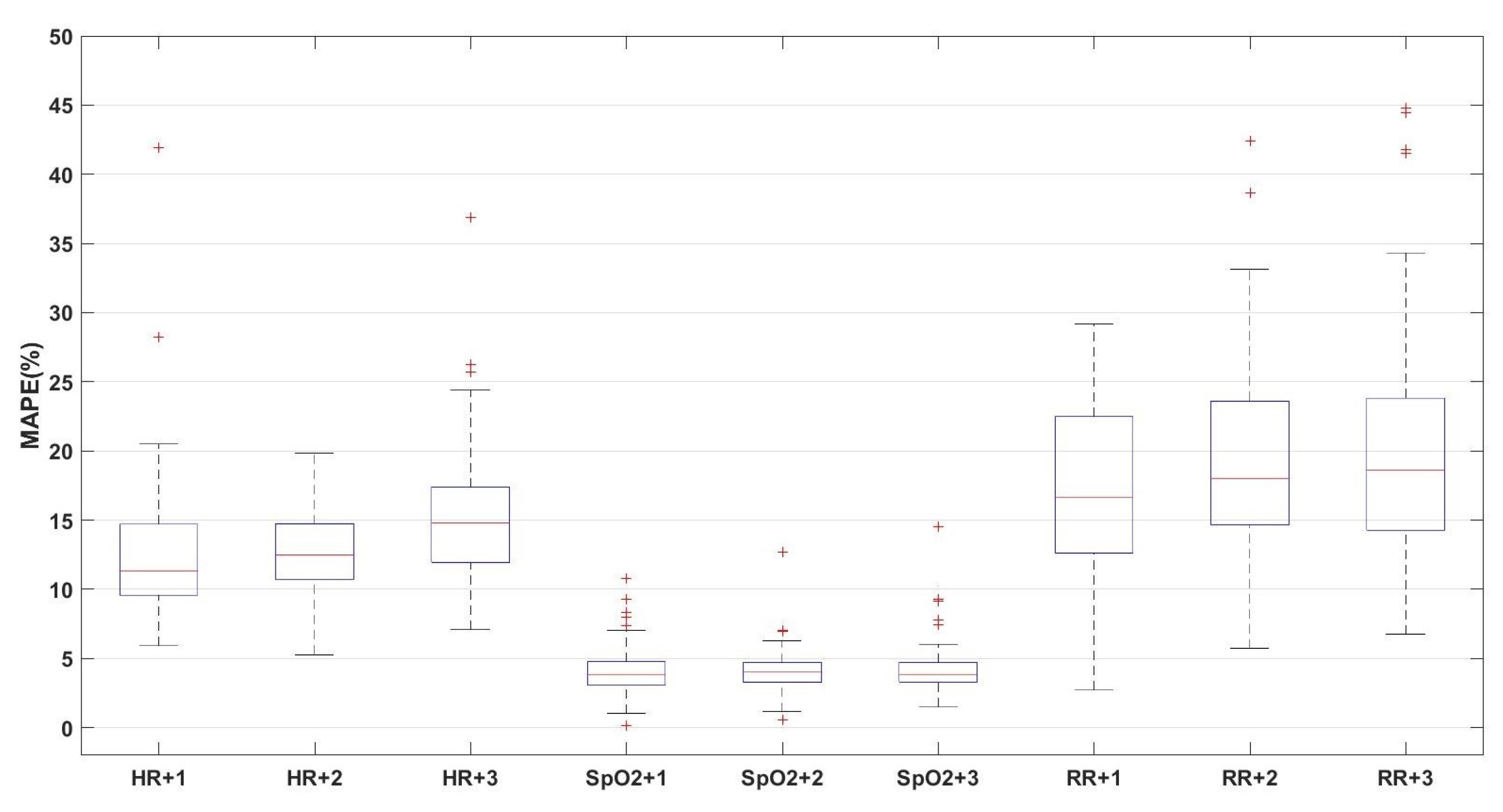
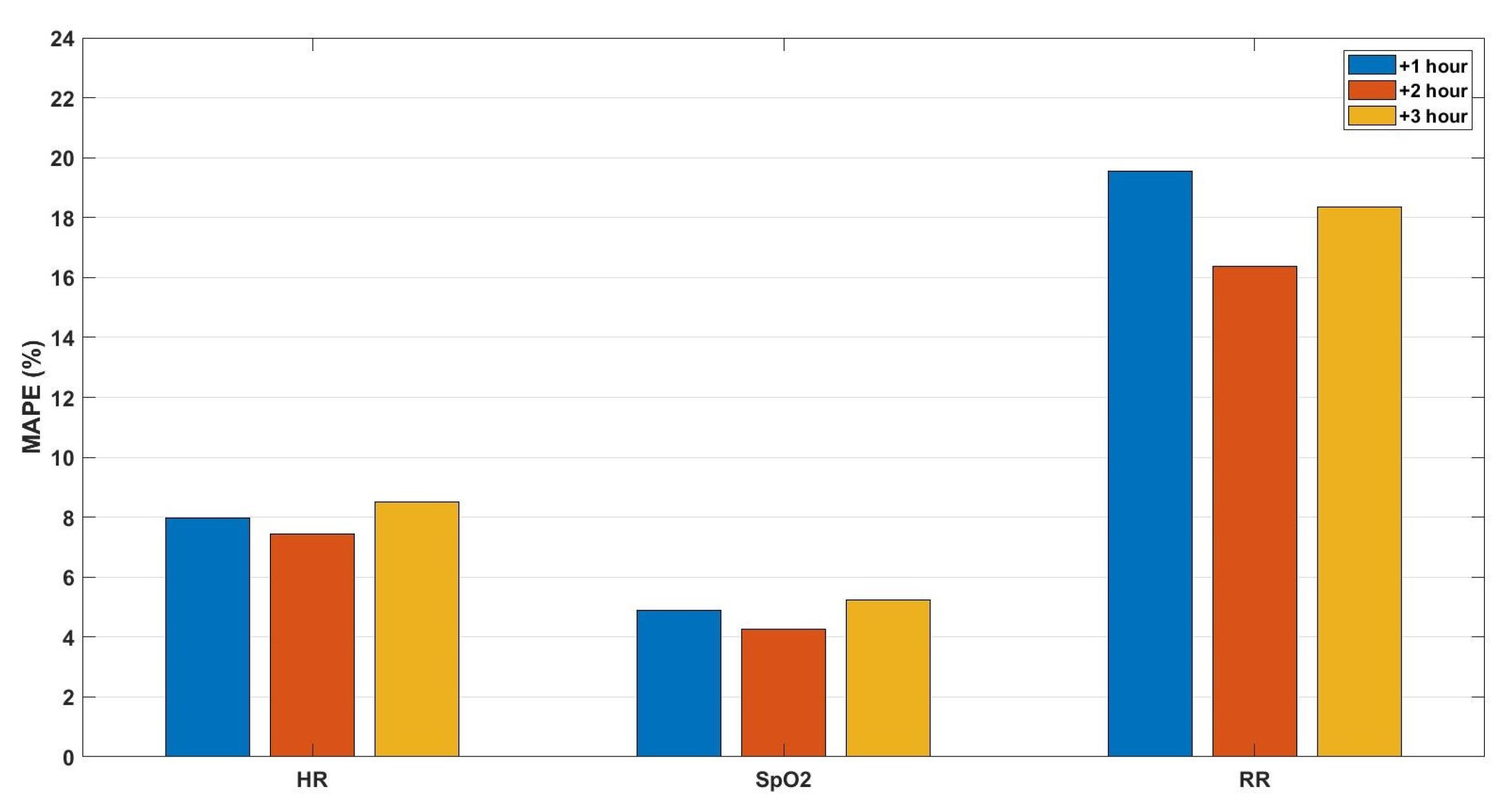
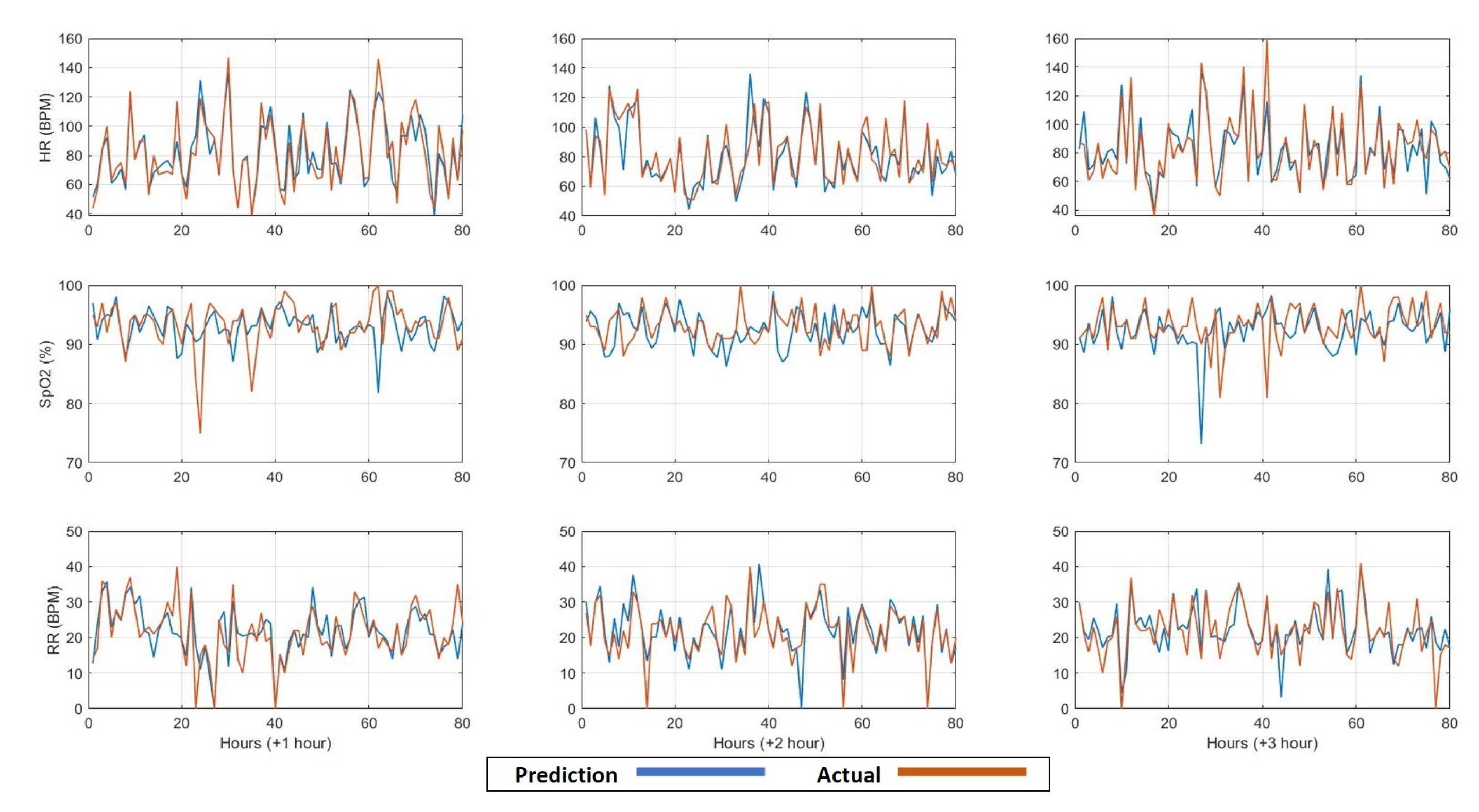
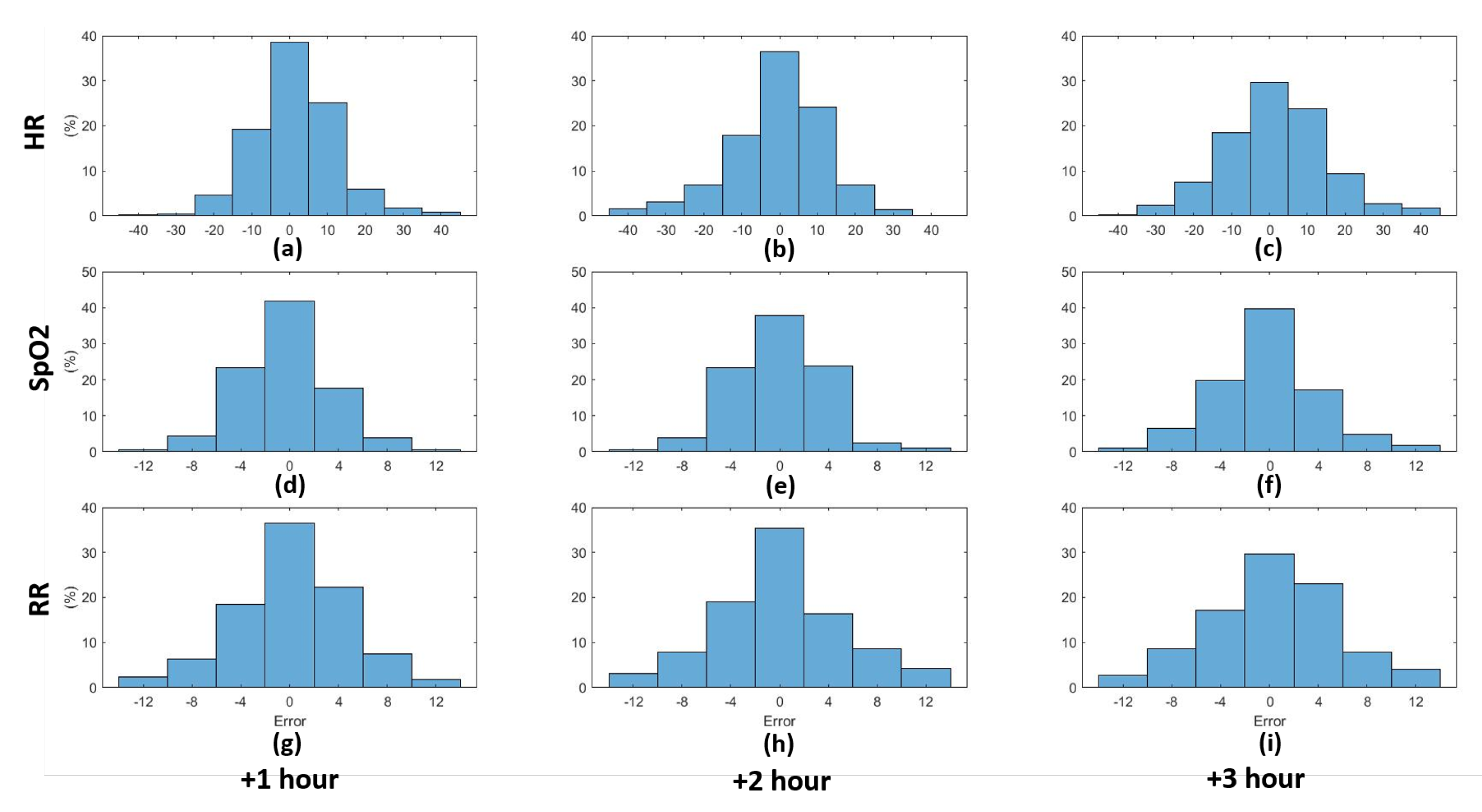
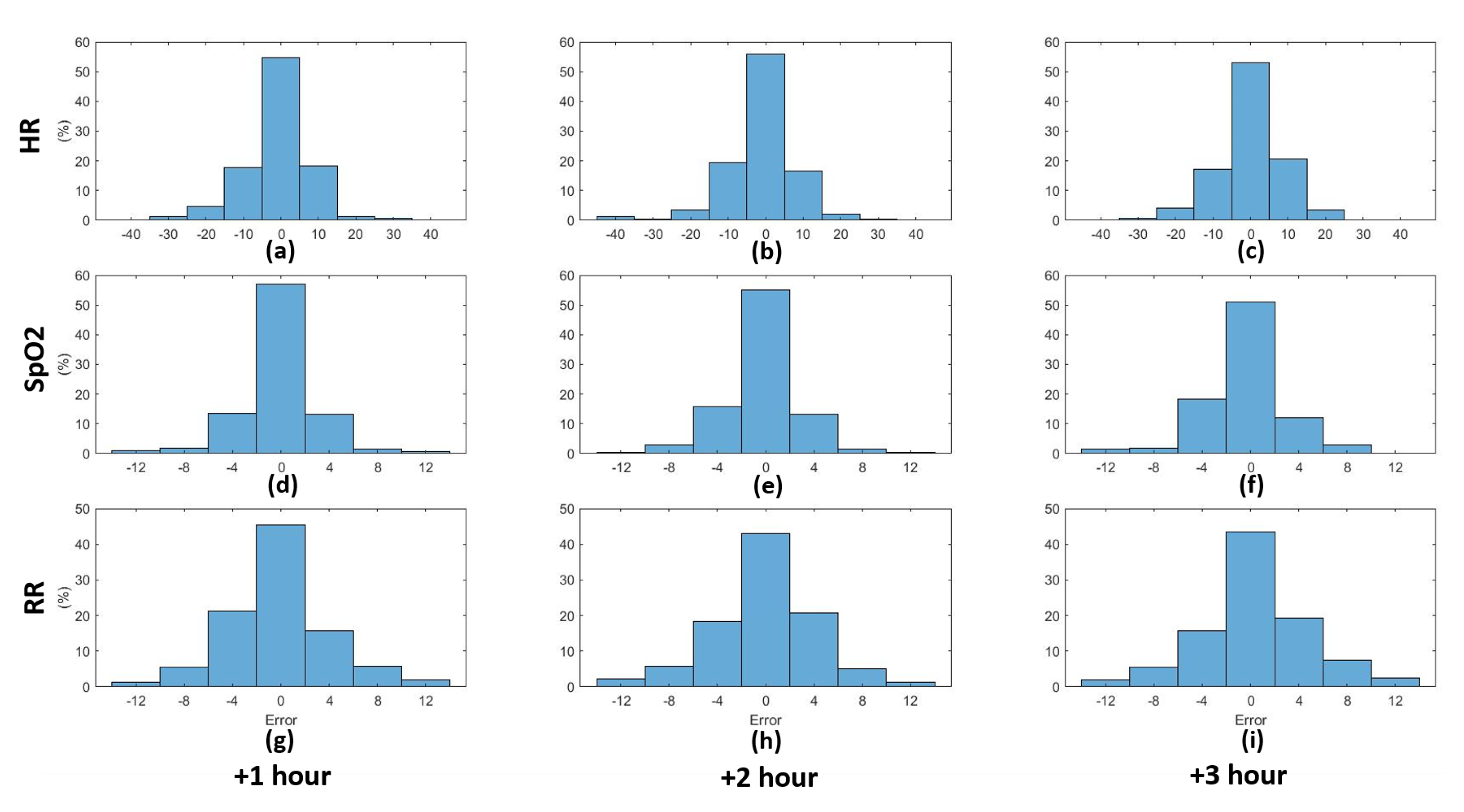
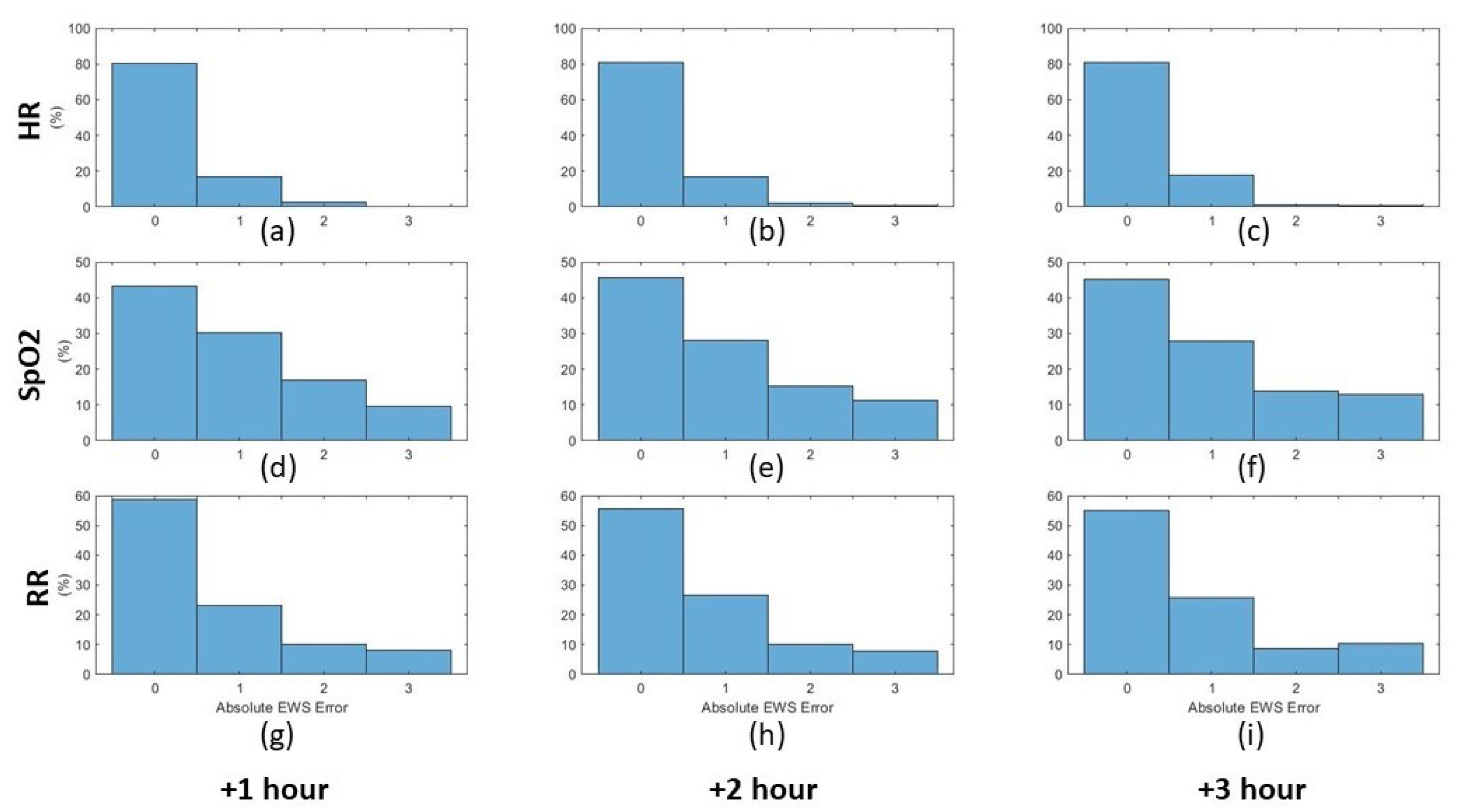
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brekke, I.J.; Puntervoll, L.H.; Pedersen, P.B.; Kellett, J.; Brabr, M. The value of vital sign trends in predicting and monitoring clinical deterioration: A systematic review. PLoS ONE 2019, 14, e0210875. [Google Scholar] [CrossRef] [PubMed]
- Kause, J.; Smith, G.; Prytherch, D.; Parr, M.; Flabouris, A.; Hillman, K. A comparison of Antecedents to Cardiac Arrests, Deaths and Emergency Intensive care Admissions in Australia and New Zealand, and the United Kingdom—The ACADEMIA study. Resuscitation 2004, 62, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Barfod, C.; Lauritzen, M.M.P.; Danker, J.K.; Sölétormos, G.; Forberg, J.L.; Berlac, P.A.; Lippert, F.; Lundstrøm, L.H.; Antonsen, K.; Lange, K.H.W. Abnormal vital signs are strong predictors for intensive care unit admission and in-hospital mortality in adults triaged in the emergency department—A prospective cohort study. Scand. Trauma Resusc. Emerg. Med. 2012, 10, 20–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Youssef Ali Amer, A.; Vranken, J.; Wouters, F.; Mesotten, D.; Vandervoort, P.; Storms, V.; Luca, S.; Vanrumste, B.; Aerts, J.-M. Feature engineering for ICU mortality prediction based on hourly to bi-hourly measurements. Appl. Sci. 2019, 9, 3525. [Google Scholar] [CrossRef] [Green Version]
- Redfern Oliver, C.; Pimentel, M.A.F.; David, P.; Meredith, P. Predicting in-hospital mortality and unanticipated admissions to the intensive care unit using routinely collected blood tests and vital signs: Development and validation of a multivariable model. Resuscitation 2018, 133, 75–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahdavi, M.; Choubdar, H.; Zabeh, E.; Rieder, M.; Safavi-Naeini, S. A machine learning based exploration of COVID-19 mortality risk. PLoS ONE 2021, 16, e0252384. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yao, J.; Motani, M. Early Prediction of Vital Signs Using Generative Boosting via LSTM Networks. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), San Diego, CA, USA, 18–21 November 2019. [Google Scholar]
- Youssef Ali Amer, A.; Wouters, F.; Vranken, J.; de Korte-de Boer, D.; Smit-Fun, V.; Duflot, P.; Beaupain, M.-H.; Vandervoort, P.; Luca, S.; Aerts, J.-M.; et al. Vital Signs Prediction and Early Warning Score Calculation Based on Continuous Monitoring of Hospitalised Patients Using Wearable Technology. Sensors 2020, 20, 6593. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
- Youssef Ali Amer, A.; Aerts, J.; Vanrumste, B.; Luca, S. A Localised Learning Approach Applied to Human Activity Recognition. IEEE Intell. Syst. 2020, 99, 58–71. [Google Scholar]
- Youssef Ali Amer, A. Localised Least Squares Support Vector Machines with Application to Weather Forecasting. Master’s Thesis, KU Leuven, Leuven, Belgium, 2016. [Google Scholar]
- Cheng, H.; Tan, P.-N.; Jin, R. Localized support vector machine and its efficient algorithm. In Proceedings of the SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007. [Google Scholar]
- Cheng, H.; Tan, P.; Jin, R. Efficient algorithm for localized support vector machine. IEEE Trans. Knowl. Data Eng. 2010, 22, 537–549. [Google Scholar] [CrossRef]
- Bottou, L.; Vapnik, V. Local Learning Algorithms. Neural Comput. 1992, 4, 888–900. [Google Scholar] [CrossRef]
- Yang, H.; Huang, K.; King, I.; Lyu, M.R. Localized support vector regression for time series prediction. Neurocomputing 2009, 72, 10–12. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Cayton, L. Fast nearest neighbor retrieval for bregman divergences. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 112–119, ISBN 9781605582054. [Google Scholar] [CrossRef] [Green Version]


| ZOL (51 Patients) | MUMC+ (50 Patients) | CHU de Liège (84 Patients) | |
|---|---|---|---|
| Demographic and comorbidity parameters | Descriptive statistics | ||
| Age (mean ± std) | 65.84 ± 12.44 | 67.02 ± 1.28 | 69 ± 12.16 |
| Gender (male, %) | 62.7% | 80.0% | 68% |
| Height (cm; mean ± std) | 166.63 ± 12.11 | 176.3 ± 8.3 | 168 ± 26.53 |
| Weight (kg; mean ± std) | 83.76 ± 16.34 | 85.91 ± 13.68 | 81.45 ± 20.01 |
| Smoking status (%) | Never: 66% Smoker: 6.4% Former smoker: 27.7% | Never: 90% Smoker: 6.0% Former smoker: 4.0% | Never: 50% Smoker: 6% Former Smoker: 12% |
| Cardiovascular disease (%) | 17.6% | 4.0% | 23% (yes) 22% (no) 55% (unknown) |
| Diabetes (%) | 27.5% | 18.0% | 51% (yes) 21% (no) 28% (unknown) |
| Arterial hypertension (%) | 43.1% | 16.0% | 61% (yes) 14% (no) 25% (unknown) |
| Cerebrovascular accident or transient ischaemic attack (%) | 5.9% | 2.0% | (unknown) |
| Kidney insufficiency (%) | 60.8% | 0.0% | (unknown) |
| Heart Failure (%) | 29.4% | 4.0% | (unknown) |
| NYHA classification | II: 8.3% III: 8.3% | 6.0% | (unknown) |
| Myocardial infarction (%) | 9.8% | 42% | (unknown) |
| PCI/PTCA | 9.8% | 67.02 ± 1.28 | (unknown) |
| COPD | 11.8 % | 80.0 % | 24% (yes) 29% (no) 47% (unknown) |
| Asthma (%) | 7.8% | 176.3 ± 8.3 | 9% (yes) 38% (no) 53% (unknown) |
| Intubated | 23 (46%) | 50 (100%) | 38 (46%) |
| O Mask/Nasal Cannula | 40 (78%) | (Unknown) | 71 (86%) |
| SCORE | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| Temperature (C) | <35.1 | 35.1–36.5 | 36.6–37.5 | >37.5 | |||
| Heart Rate (BPM) | <40 | 40–50 | 51–100 | 101–110 | 111–130 | >130 | |
| Respiration Rate (BPM) | <9 | 9–14 | 15–20 | 21–30 | >30 | ||
| Oxygen Saturation (%) | <91 | 91–93 | 94–95 | >95 | |||
| Systolic Blood Pressure (mmHg) | <70 | 70–80 | 81–100 | 101–180 | 180–200 | >200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssef Ali Amer, A.; Wouters, F.; Vranken, J.; Dreesen, P.; de Korte-de Boer, D.; van Rosmalen, F.; van Bussel, B.C.T.; Smit-Fun, V.; Duflot, P.; Guiot, J.; et al. Vital Signs Prediction for COVID-19 Patients in ICU. Sensors 2021, 21, 8131. https://doi.org/10.3390/s21238131
Youssef Ali Amer A, Wouters F, Vranken J, Dreesen P, de Korte-de Boer D, van Rosmalen F, van Bussel BCT, Smit-Fun V, Duflot P, Guiot J, et al. Vital Signs Prediction for COVID-19 Patients in ICU. Sensors. 2021; 21(23):8131. https://doi.org/10.3390/s21238131
Chicago/Turabian StyleYoussef Ali Amer, Ahmed, Femke Wouters, Julie Vranken, Pauline Dreesen, Dianne de Korte-de Boer, Frank van Rosmalen, Bas C. T. van Bussel, Valérie Smit-Fun, Patrick Duflot, Julien Guiot, and et al. 2021. "Vital Signs Prediction for COVID-19 Patients in ICU" Sensors 21, no. 23: 8131. https://doi.org/10.3390/s21238131
APA StyleYoussef Ali Amer, A., Wouters, F., Vranken, J., Dreesen, P., de Korte-de Boer, D., van Rosmalen, F., van Bussel, B. C. T., Smit-Fun, V., Duflot, P., Guiot, J., van der Horst, I. C. C., Mesotten, D., Vandervoort, P., Aerts, J.-M., & Vanrumste, B. (2021). Vital Signs Prediction for COVID-19 Patients in ICU. Sensors, 21(23), 8131. https://doi.org/10.3390/s21238131








