A Method for Identification and Assessment of Radioxenon Plumes by Absorption in Polycarbonates
Abstract
:1. Introduction
2. Materials and Methods
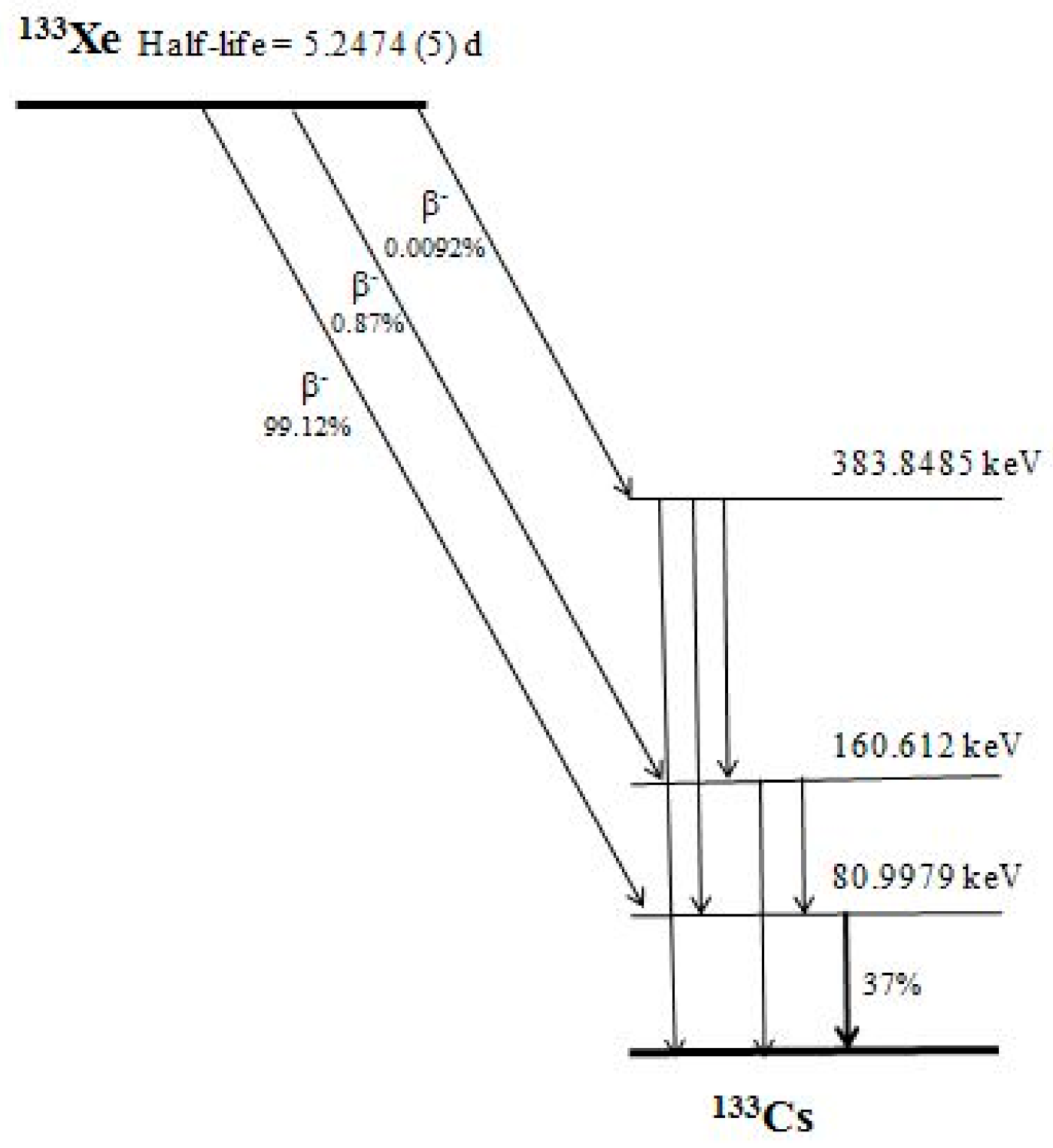
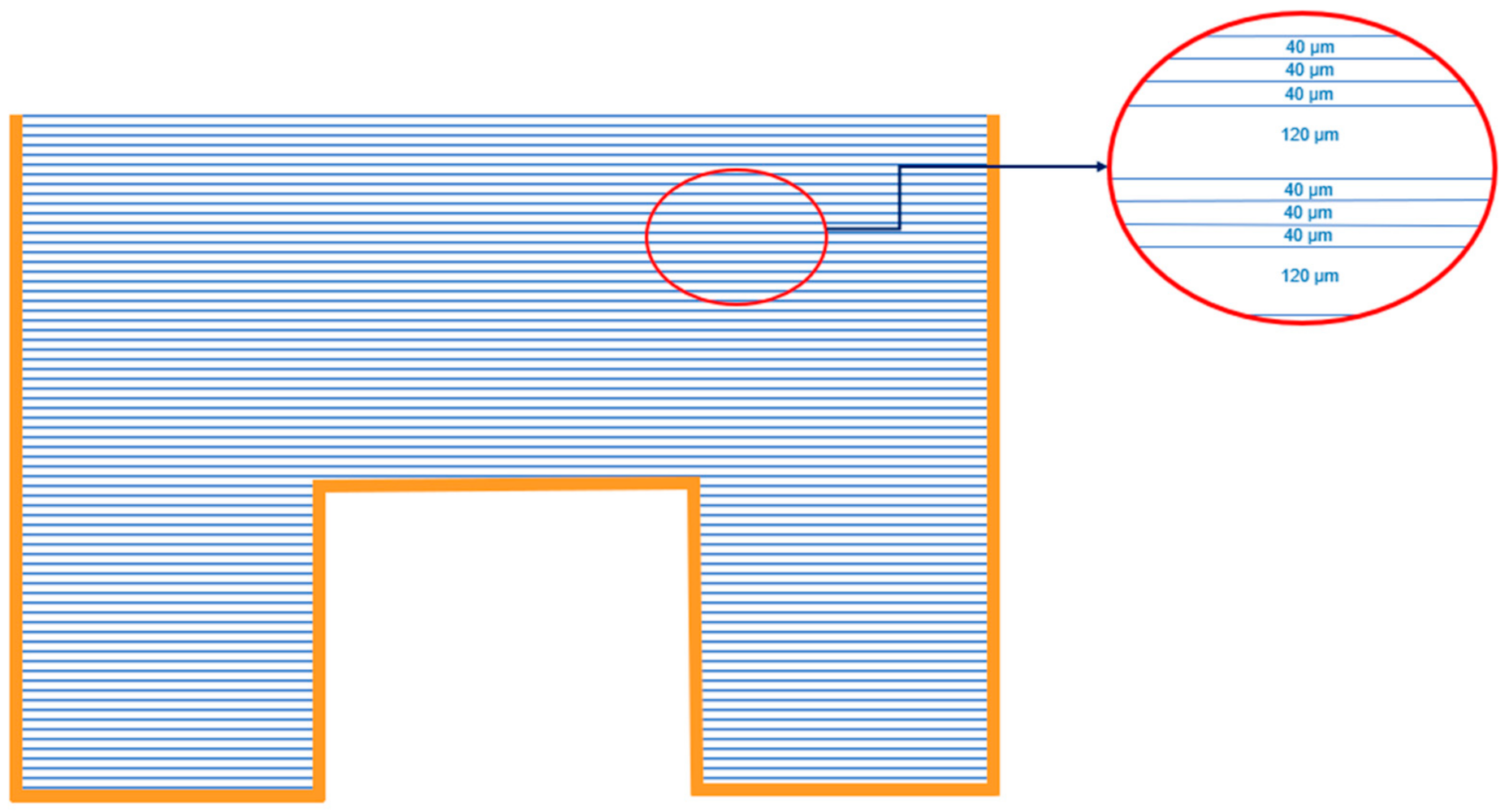
2.1. The Concept and Basics of the Method
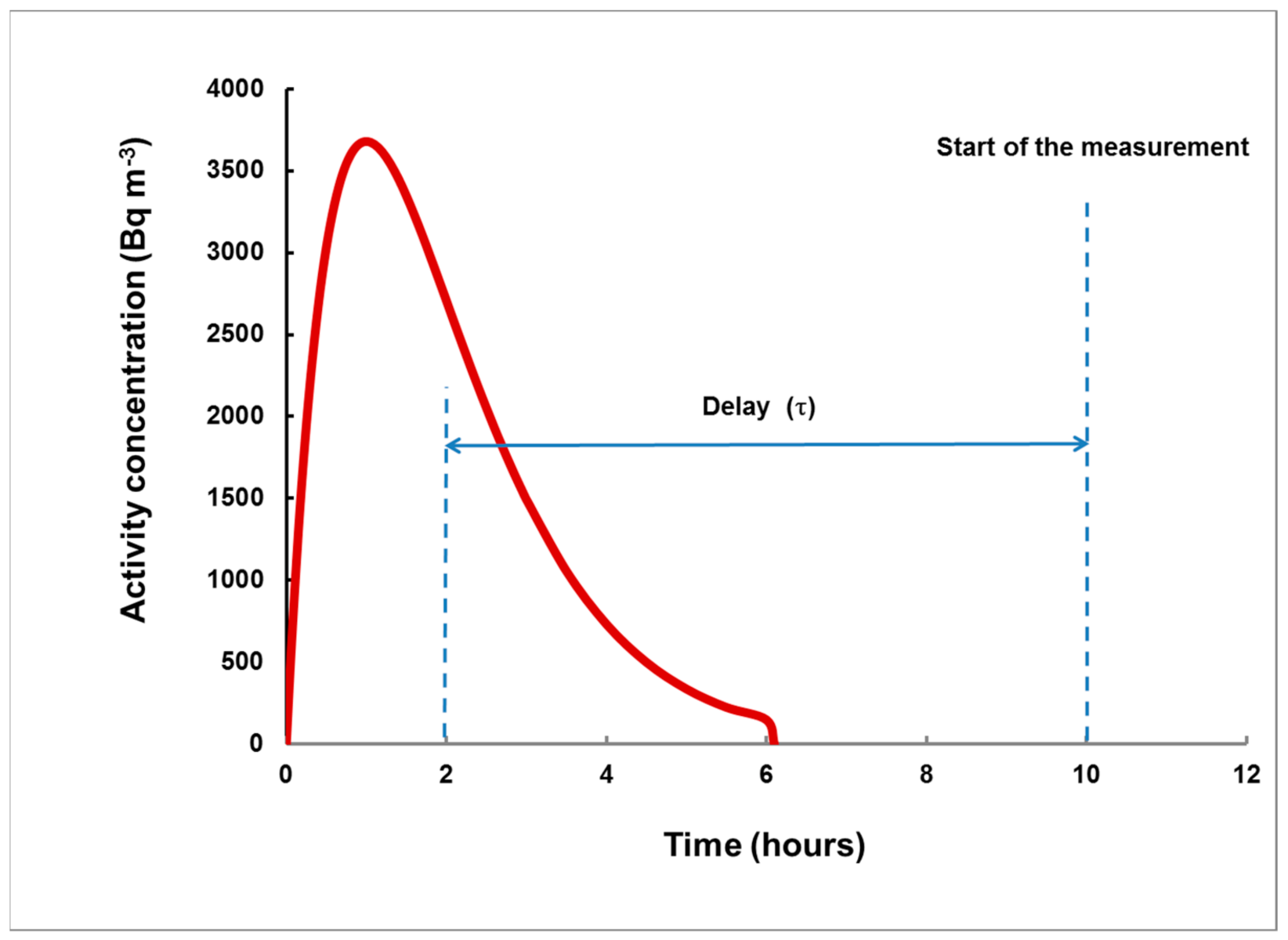
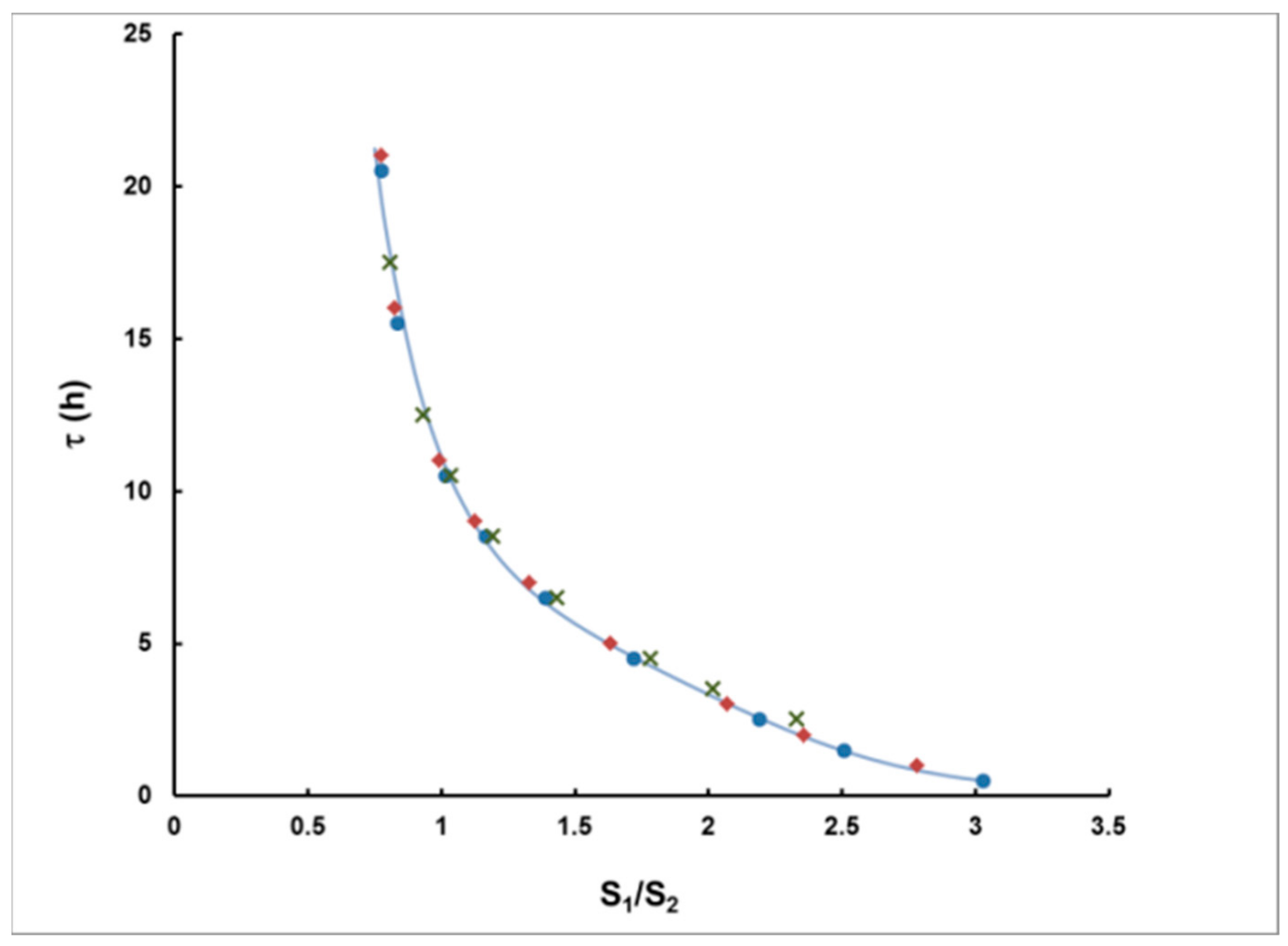
- For measurement in two consecutive time intervals, (0–8 h) and (8–24 h), the observed ratio S1/S2 can be correlated with the delay τ, measured from the center of the plume, and the dependence τ = τ(S1/S2) can be used to assess the delay τ of a plume of any shape.
- The signal S2 may be expressed as:
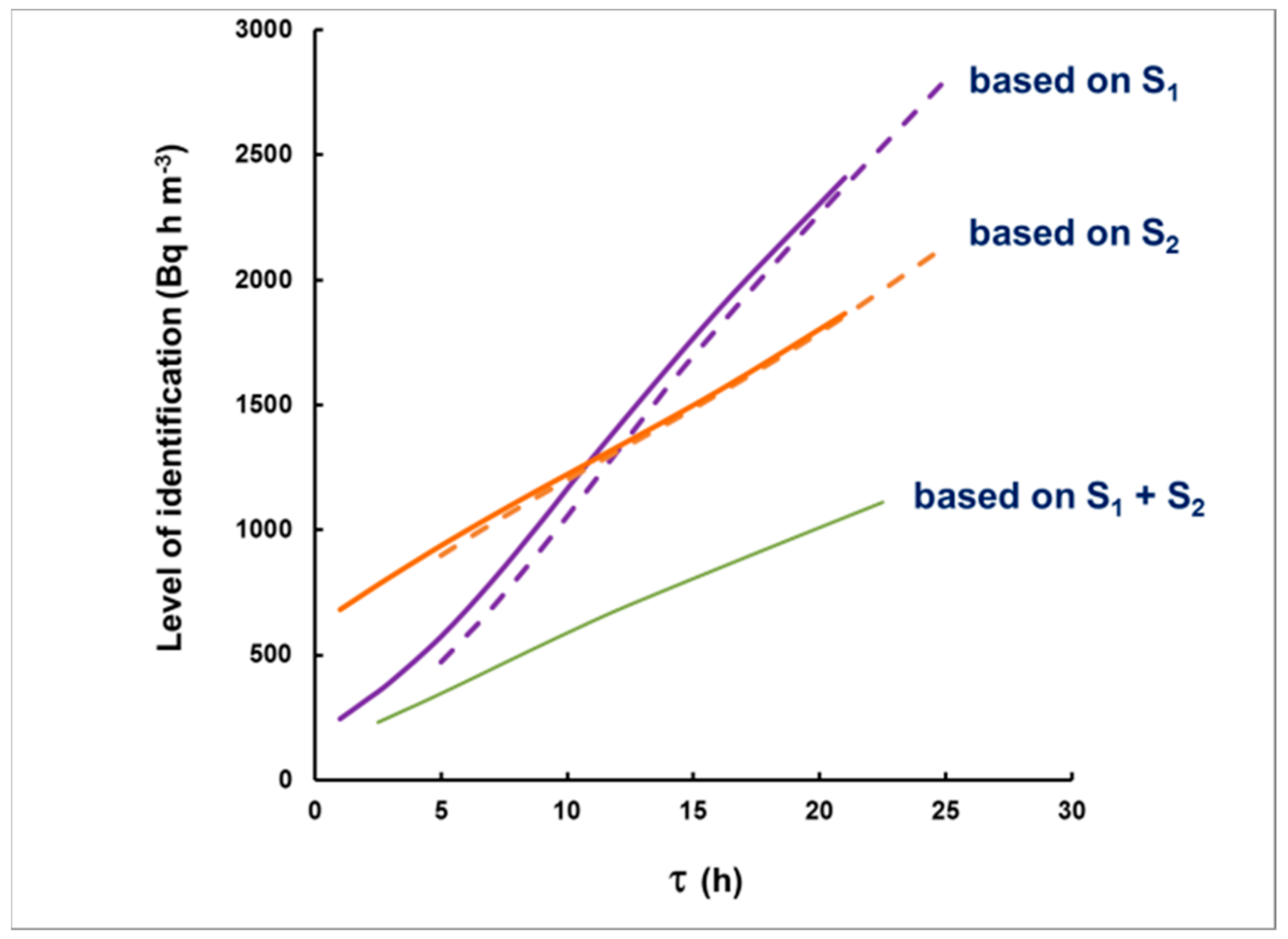
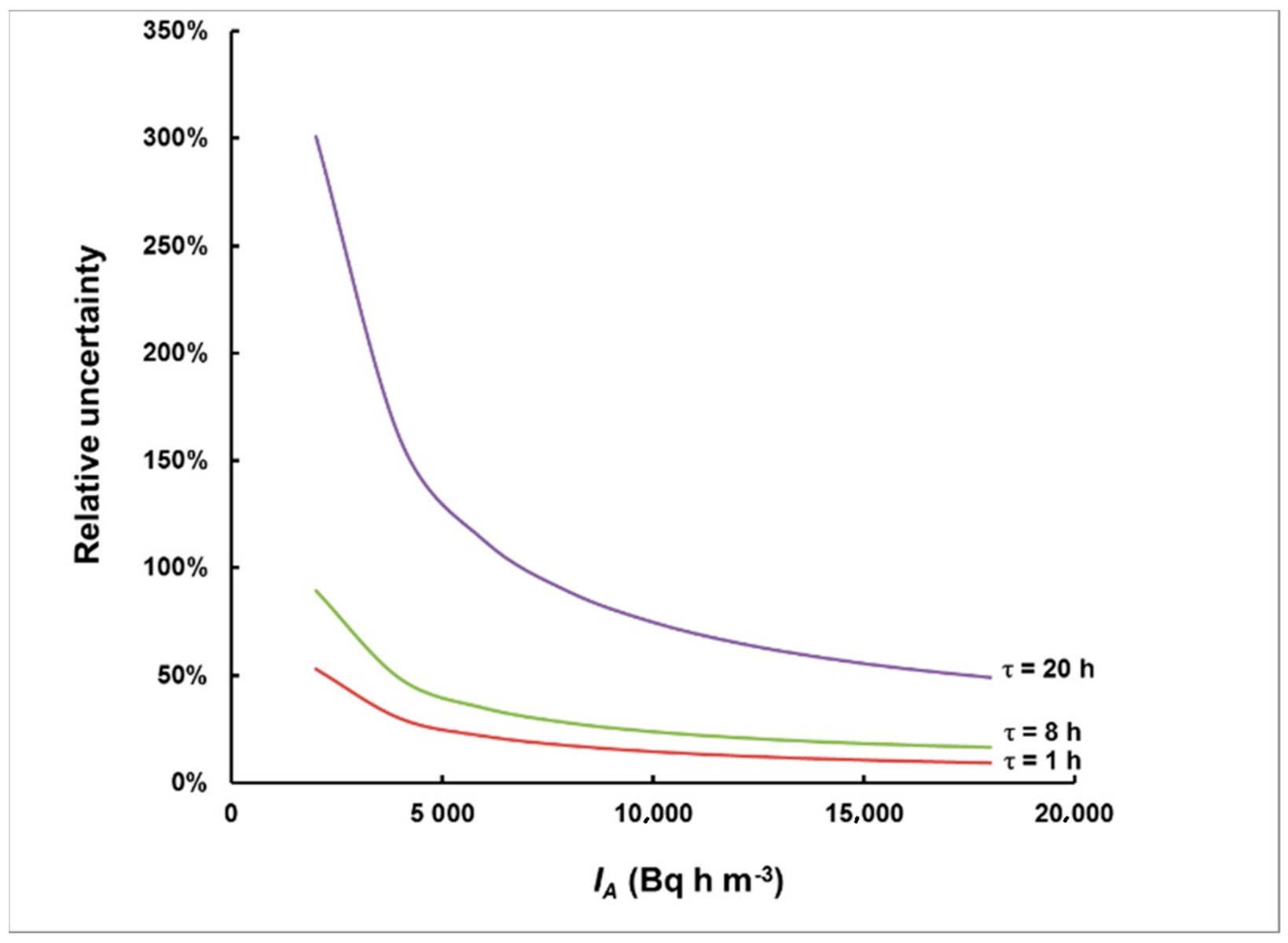
2.2. Estimating the Uncertainty and the Level of Plume Identification
3. Results
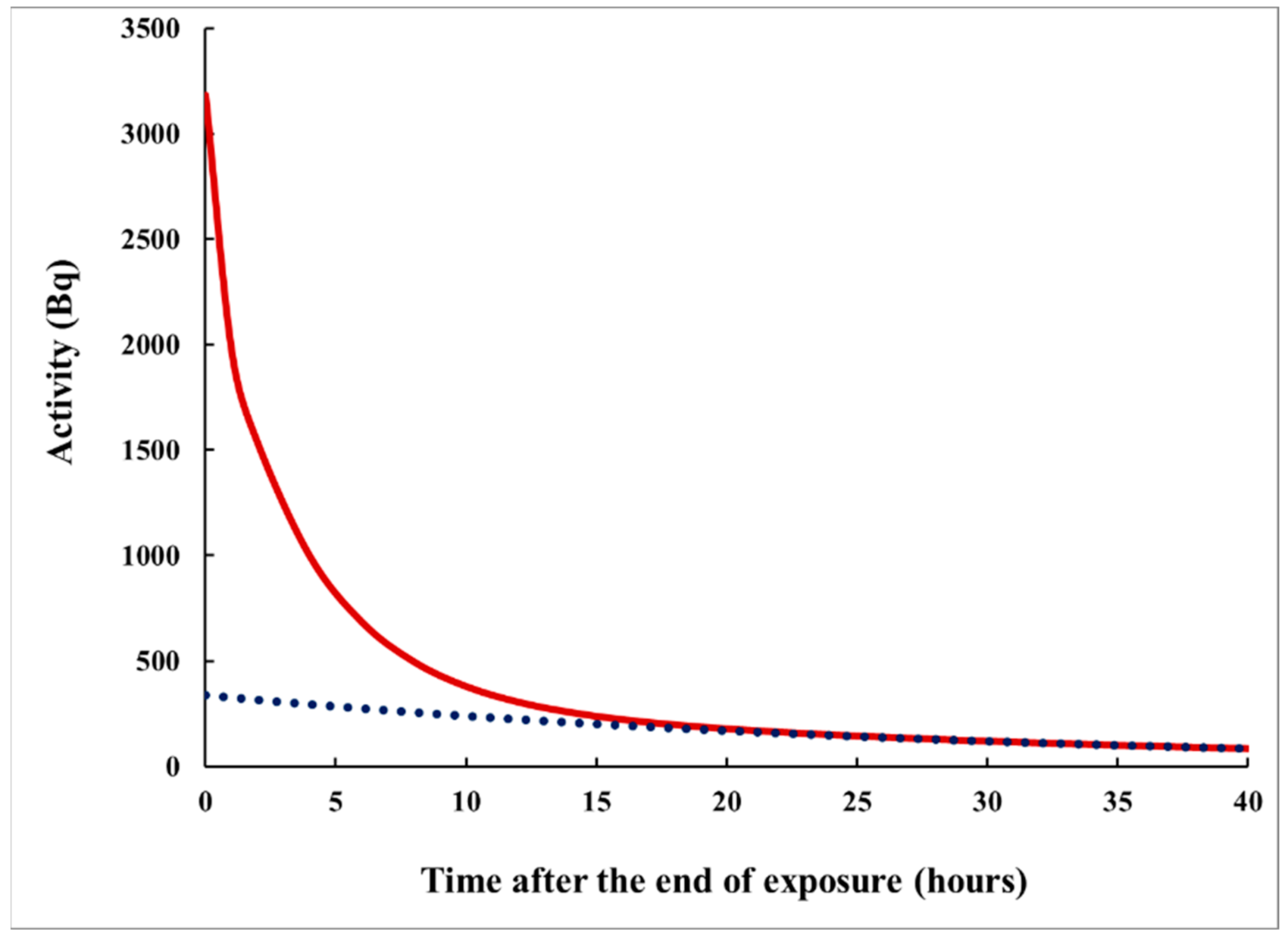
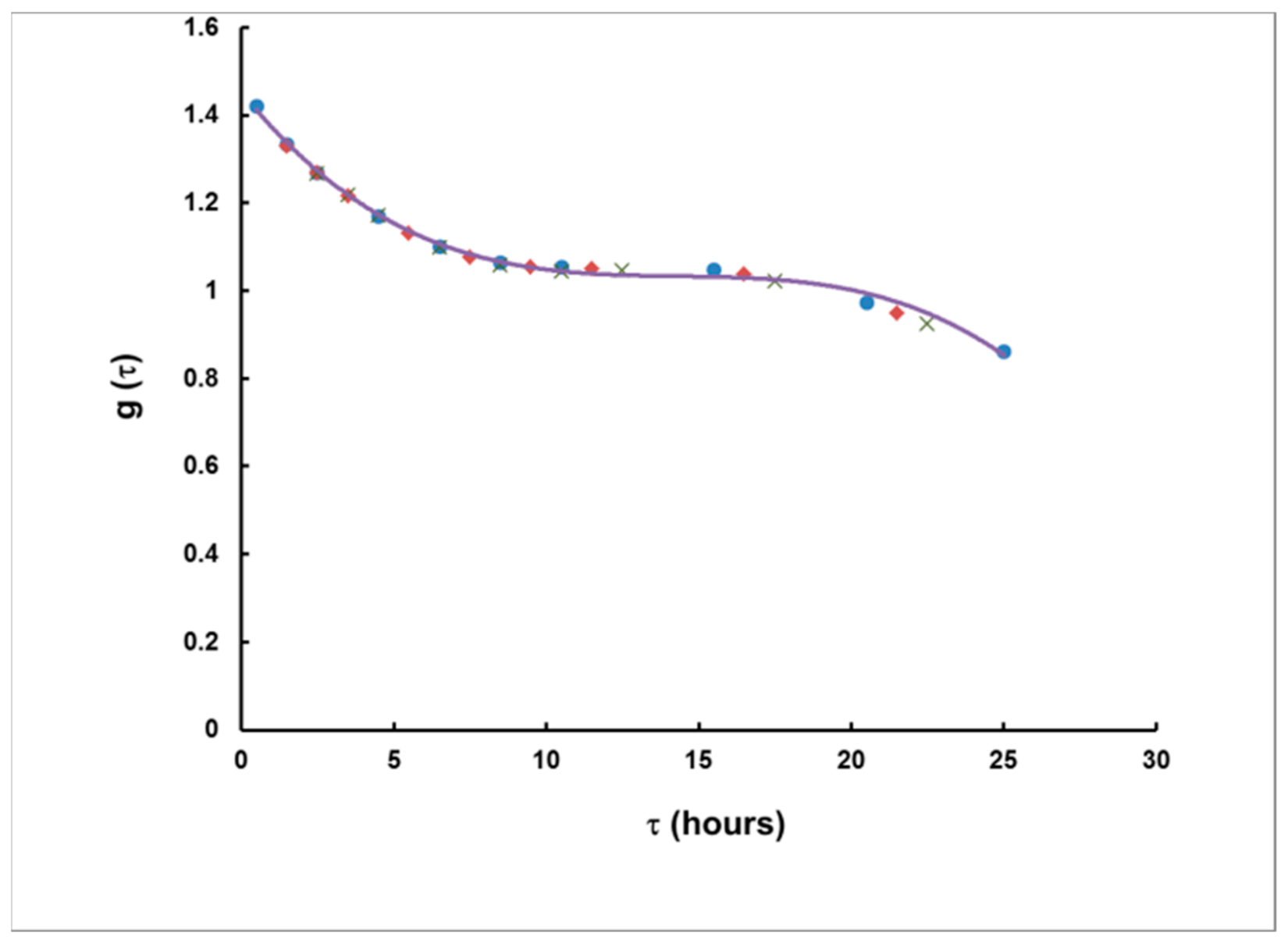
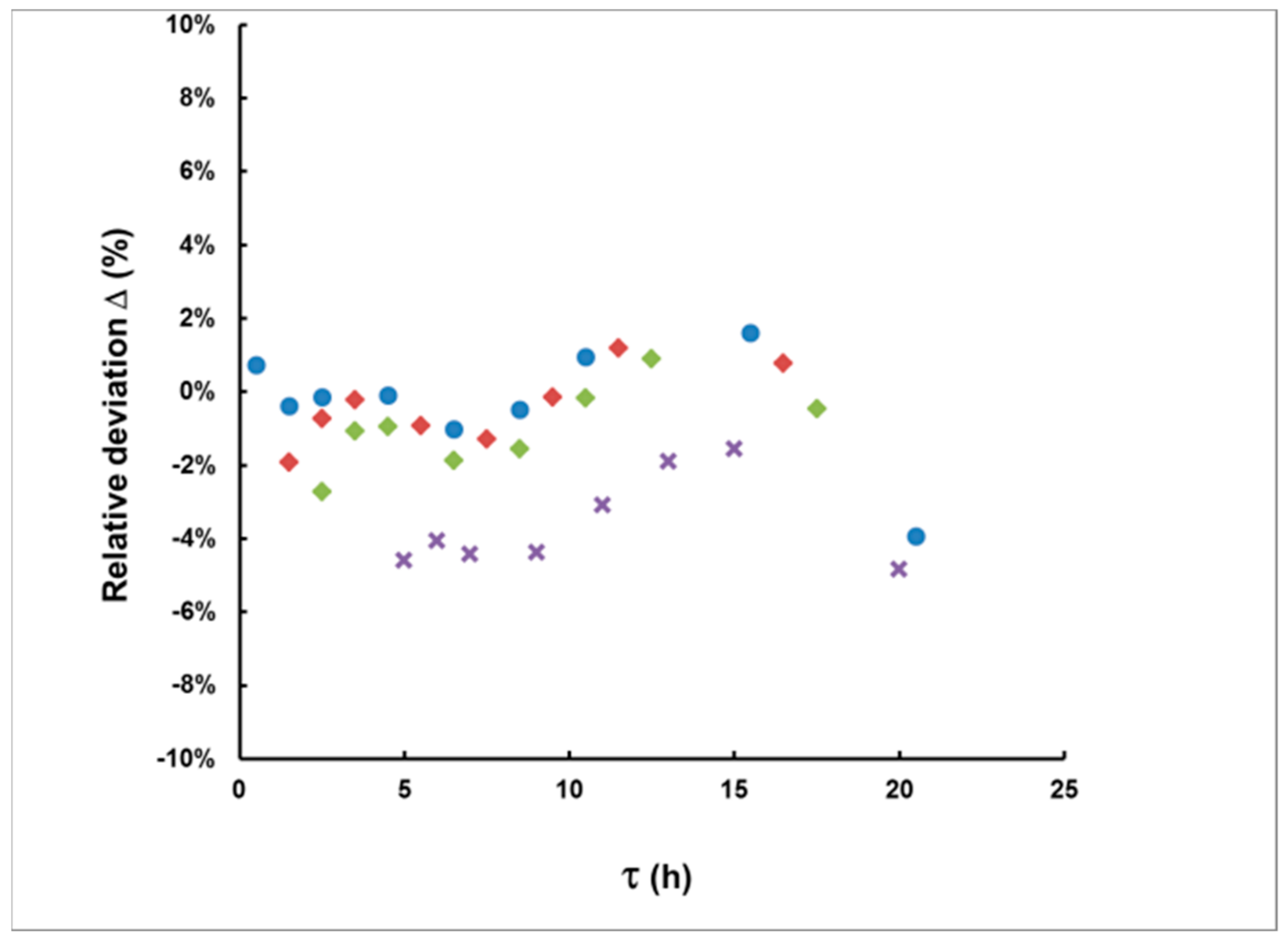
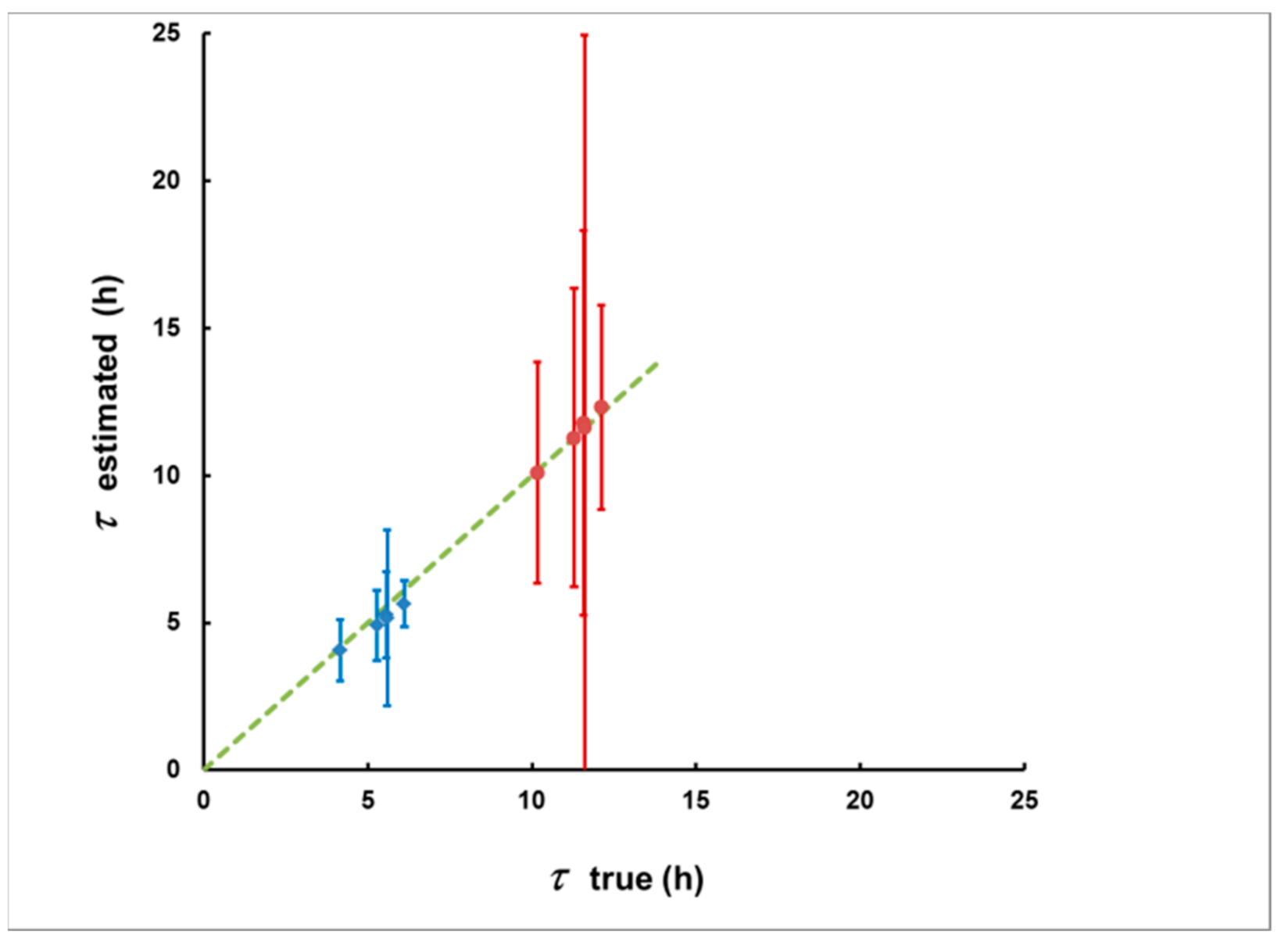
3.1. Methodological Bias in the Estimates of the of Delay and the Integrated Concentration
3.2. Simulation of Levels of Identification and Instrumental Uncertainty
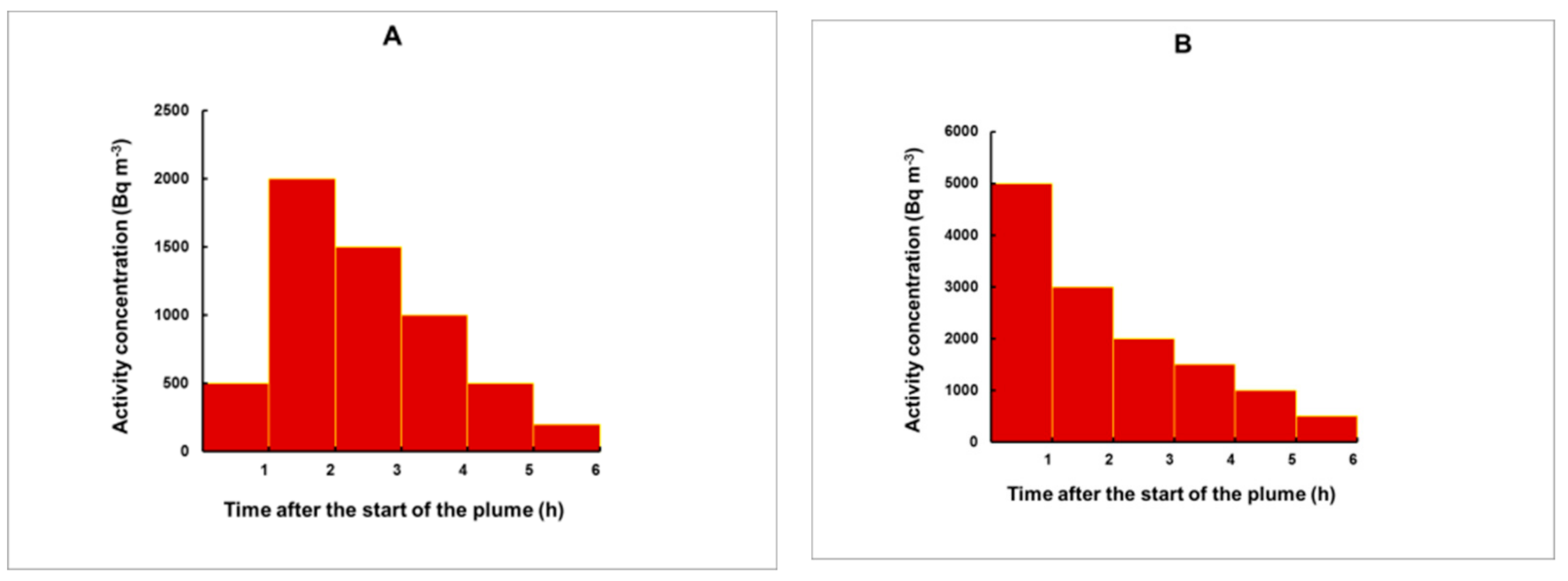
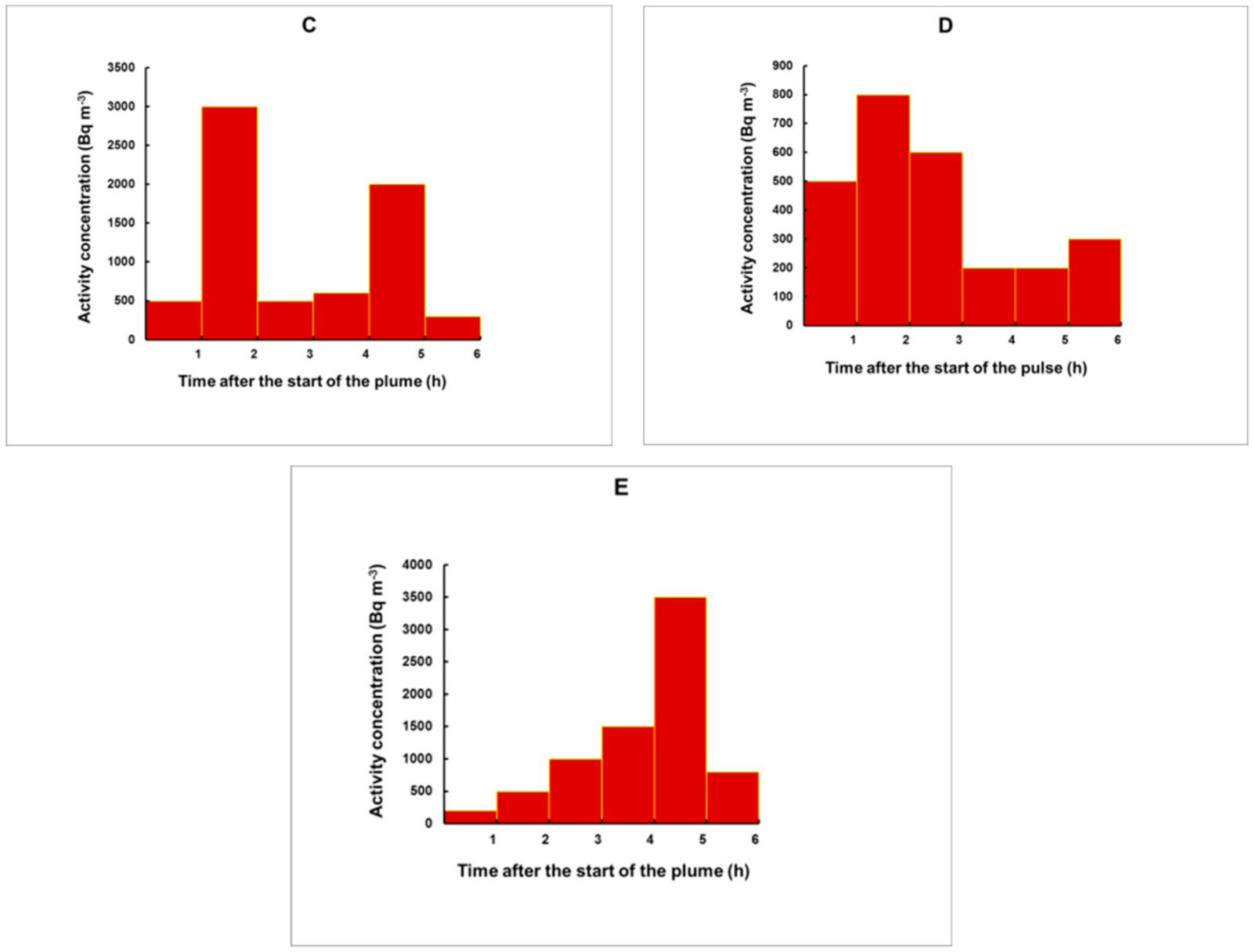
3.3. Simulation of Plumes for an Arbitrary Shape
4. Discussion and Conclusions
- The time (before the start of the gamma spectrometry measurement) at which the center of the plume was situated;
- The 133Xe activity concentration, integrated over the total duration of the plume, provided that the plume ended before the specimen was taken from the place of exposure. Otherwise, IA will refer to the time from the start of the plume until the moment when the specimen was removed for analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Commission of the European Communities. Commission recommendation of 18 December 2003 on standardised information on radioactive airborne and liquid discharges into the environment from nuclear power reactors and reprocessing plants in normal operation (notified under document No: C(2003) 4832). Off. J. Eur. Union 2004, L2, 36–46. [Google Scholar]
- Stohl, A.; Seibert, P.; Wotawa, G.; Arnold, D.; Burkhart, J.F.; Eckhardt, S.; Tapia, C.; Vargas, A.; Yasunari, T.J. Xenon-133 and caesium-137 releases into the atmosphere from the Fukushima Dai-ichi nuclear power plant: Determination of the source term, atmospheric dispersion, and deposition. Atmos. Chem. Phys. 2012, 12, 2313–2343. [Google Scholar] [CrossRef] [Green Version]
- Comprehensive Nuclear-Test-Ban Treaty Organization. Available online: https://www.ctbto.org (accessed on 15 September 2021).
- Stocki, T.J.; Armand, P.; Heinrich, P.; Ungar, R.K.; D’Amours, R.; Korpach, E.P.; Bellivier, A.; Taffary, T.; Malo, A.; Bean, M.; et al. Measurement and modelling of radioxenon plumes in the Ottawa Valley. J. Environ. Radioact. 2008, 99, 1775–1788. [Google Scholar] [CrossRef] [PubMed]
- Mitev, K.; Cassette, P. Radioactive noble gas detection and measurement with plastic scintillators. In Plastic Scintillators; Hamel, M., Ed.; Springer: Basel, Switzerland, 2021; pp. 385–423. [Google Scholar]
- Kalinowski, M.B.; Tatlisu, H. Global Radioxenon Emission Inventory from Nuclear Power Plants for the Calendar Year. Pure Appl. Geophys. 2014, 178, 2695–2708. [Google Scholar] [CrossRef]
- Saey, P.R.J.; Bean, M.; Becker, A.; Coyne, J.; D’Amours, R.; De Geer, L.-E.; Hogue, R.; Stocki, T.J.; Ungar, R.K.; Wotawa, G. A long distance measurement of radioxenon in Yellowknife, Canada, in late October 2006. Geophys. Res. Lett. 2007, 34, L20802. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Chernobyl’s Legacy: Health, Environmental and Socio-Economic Impacts and Recommendations to the Governments of Belarus, the Russian Federation and Ukraine; Kinly, D., III, Ed.; IAEA: Vienna, Austria, 2005. [Google Scholar]
- Stohl, A.; Seibert, P.; Wotawa, G. The total release of xenon-133 from the Fukushima Dai-ichi nuclear power plant accident. J. Environ. Radioact. 2012, 112, 155–159. [Google Scholar] [CrossRef] [Green Version]
- Perkins, R.W.; Casey, L.A. Radioxenons: Their Role in Monitoring a Comprehensive Test Ban Treaty; Rep. DOE/RL-96-1; Pac. Northwest Natl. Lab.: Richland, WA, USA, 1996. [Google Scholar]
- Leith, W. Geologic and Engineering Constraints on the Feasibility of Clandestine Nuclear Testing by Decoupling in Large Underground Cavities; U.S. Geol. Surv. Open File Rep.: Reston, Virginia, 2001; pp. 1–28. [Google Scholar]
- Bowyer, T.W.; Biegalski, S.R.; Cooper, M.; Eslinger, P.W.; Haas, D.; Hayes, J.C.; Miley, H.S.; Strom, D.J.; Woods, V. Elevated radioxenon detected remotely following the Fukushima nuclear accident. J. Environ. Radioact. 2011, 102, 681–687. [Google Scholar] [CrossRef]
- Sinclair, L.E.; Seywerd, H.C.J.; Fortin, R.; Carson, J.M.; Saull, P.R.B.; Coyle, M.J.; Van Brabant, R.A.; Buckle, J.L.; Desjardins, S.M.; Hall, R.M. Aerial measurement of radioxenon concentration off the west coast of Vancouver Island following the Fukushima reactor accident. J. Environ. Radioact. 2011, 102, 1018–1023. [Google Scholar] [CrossRef] [Green Version]
- Möre, H.; Hubbard, L.M. 222Rn absorption in plastic holders for alpha track detectors: A source of error. Radiat. Prot. Dosim. 1997, 74, 85–91. [Google Scholar] [CrossRef]
- Pressyanov, D.; Van Deynse, A.; Buysse, J.; Poffijn, A.; Meesen, G. Polycarbonates: A new retrospective radon monitor. In Proceedings of the IRPA Regional Congress on Radiation Protection in Central Europe, Budapest, Hungary, 23–27 August 1999; pp. 716–722. [Google Scholar]
- Pressyanov, D.S.; Mitev, K.K.; Stefanov, V.H. Measurements of 85Kr and 133Xe by absorption in Makrofol. Nucl. Instrum. Methods Phys. Res. 2004, 527, 657–659. [Google Scholar] [CrossRef]
- Pressyanov, D. Modeling a 222Rn measurement technique based on absorption in polycarbonates and track-etch counting. Health Phys. 2009, 97, 604–612. [Google Scholar] [CrossRef]
- Pressyanov, D.; Mitev, K.; Georgiev, S.; Dimitrova, I. Sorption and desorption of radioactive noble gases in polycarbonates. Nucl. Instrum. Methods Phys. Res. 2009, 598, 620–627. [Google Scholar] [CrossRef]
- Georgiev, S.; Mitev, K.; Pressyanov, D.; Boshkova, T.; Dimitrova, I. Measurement of Xe-133 in Air by Absorption in Polycarbonates—Detection Limits and Potential Applications. In Proceedings of the 2011 IEEE Nuclear Science Symposium Conference Record NP1.M-85, Valencia, Spain, 23–29 October 2011. [Google Scholar]
- Mitev, K.; Zhivkova, V.; Pressyanov, D.; Georgiev, S.; Dimitrova, I.; Gerganov, G.; Boshkova, T.; Pressyanov, D. Liquid scintillation counting of polycarbonates: A sensitive technique for measurement of activity concentration of some radioactive noble gases. Appl. Radiat. Isot. 2014, 93, 87–95. [Google Scholar] [CrossRef]
- Pressyanov, D.; Mitev, K.; Dimitrova, I.; Georgiev, S. Solubility of krypton, xenon and radon in polycarbonates. Application for measurement of their radioactive isotopes. Nucl. Instrum. Methods Phys. Res. 2011, 629, 323–328. [Google Scholar] [CrossRef]
- Tommasino, L.; Tommasino, M.C.; Viola, P. Radon-film-badges by solid radiators to complement track detector-based radon monitors. Radiat. Meas. 2009, 44, 719–723. [Google Scholar] [CrossRef]
- Mitev, K.; Cassette, P.; Georgiev, S.; Dimitrova, I.; Sabot, B.; Boshkova, T.; Tartès, I.; Pressyanov, D. Determination of 222Rn absorption properties of polycarbonate foils by liquid scintillation counting. Application to 222Rn measurements. Appl. Radiat. Isot. 2016, 109, 270–275. [Google Scholar] [CrossRef]
- Mitev, K.; Cassette, P.; Tartès, I.; Georgiev, S.; Dimitrova, I.; Pressyanov, D. Diffusion lengths and partition coefficients of 131mXe and 85Kr in Makrofol N and Makrofol DE polycarbonates. Appl. Radiat. Isot. 2018, 134, 269–274. [Google Scholar] [CrossRef]
- Laboratoire National Henri Becquerel. Available online: https://lnhb.br/donnees-nucleaires/donnees-nucleaires-tableau (accessed on 16 November 2021).
- Tommasino, L. Radon film-badges versus existing passive monitors based on track etch detectors. Nukleonika 2010, 55, 549–553. [Google Scholar]
- Tommasino, L.; Tomasino, M.C.; Espinosa, G. Radon film badges based on radon-sorption in solids. A new field for solving long-lasting problems. Rev. Mex. Fis. 2010, S56, 1–4. [Google Scholar]
- Pressyanov, D. Modeling response of radon track detectors with solid absorbers as radiators. Radiat. Meas. 2011, 46, 357–361. [Google Scholar] [CrossRef]
- Pressyanov, D.; Georgiev, S.; Dimitrova, I.; Mitev, K. Experimental study of the response of radon track detectors with solid absorbers as radiators. Radiat. Meas. 2013, 50, 141–144. [Google Scholar] [CrossRef]
- Pressyanov, D.; Georgiev, S.; Dimitrova, I.; Mitev, K.; Boshkova, T. Determination of the diffusion coefficient and solubility of radon in plastics. Radiat. Prot. Dosim. 2011, 145, 123–126. [Google Scholar] [CrossRef]
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. In NIST Technical Note 1297; 1994. Available online: https://emtoolbox.nist.gov/Publications/NISTTechnicalNote1297s.pdf (accessed on 20 September 2021).
- Currie, L.A. Limits for Qualitative Detection and Quantitative Determination. Anal. Chem. 1968, 40, 586–593. [Google Scholar] [CrossRef]
- Pressyanov, D.; Buysse, J.; Poffijn, A.; Van Deynse, A.; Meesen, G. Integrated measurements of 222Rn by absorption in Makrofol. Nucl. Instrum. Methods Phys. Res. 2004, 516, 203–208. [Google Scholar] [CrossRef]
- Dimitrov, D.; Pressyanov, D. The CD/DVD method as a tool for the health physics service and ventilation diagnostics in underground mines. Radiat. Prot. Dosim. 2018, 181, 30–33. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pressyanov, D.; Stavrev, P. A Method for Identification and Assessment of Radioxenon Plumes by Absorption in Polycarbonates. Sensors 2021, 21, 8107. https://doi.org/10.3390/s21238107
Pressyanov D, Stavrev P. A Method for Identification and Assessment of Radioxenon Plumes by Absorption in Polycarbonates. Sensors. 2021; 21(23):8107. https://doi.org/10.3390/s21238107
Chicago/Turabian StylePressyanov, Dobromir, and Pavel Stavrev. 2021. "A Method for Identification and Assessment of Radioxenon Plumes by Absorption in Polycarbonates" Sensors 21, no. 23: 8107. https://doi.org/10.3390/s21238107
APA StylePressyanov, D., & Stavrev, P. (2021). A Method for Identification and Assessment of Radioxenon Plumes by Absorption in Polycarbonates. Sensors, 21(23), 8107. https://doi.org/10.3390/s21238107





