1. Introduction
In recent years, the concept of the internet of things (IoT) has developed rapidly in various fields [
1,
2,
3]. The main concept is to enable the interconnection of physical infrastructures and devices in order to obtain valuable information typically generated by sensors. In such a system, the monitoring and communication can be achieved via distributed sensor networks. These networks not only monitor and record real-time information regarding the connected devices, but also forward the collected data to a central unit for storage and further processing. Due to easier deployment and a greater level of flexibility, wireless sensor networks (WSNs) are a key technology for IoT implementation [
4]. However, one of the main challenges when dealing with wireless sensor nodes is their power supply. Wired power supplies inhibit the advantages gained by wireless connectivity, and batteries generate additional maintenance and disposal needs. To overcome these problems, energy harvesting has been identified as a power supply alternative worth investigating [
5,
6,
7].
Energy harvesting refers to the process of converting ambient energies into electrical energy to power electronic devices [
8]. Energy harvesting can be classified based on the ambient energy source, e.g., mechanical energy, thermal energy, radiant energy, and chemical energy. Since mechanical vibrations are abundant in the environment of many applications, it has attracted many investigations and research studies [
9]. Vibration energy harvesting can further be categorized into three main types based on the conversion mechanism used. These conversion mechanisms are electromagnetic [
10], piezoelectric [
11] and electrostatic transduction [
12]. Compared to electrostatic energy harvesters, electromagnetic transducers are more suitable for large-scale applications [
13]. They also do not require an external voltage bias to get started. Moreover, electromagnetic transducers are typically more robust and economical than piezoelectric transducers.
Electromagnetic energy harvesting [
14,
15] utilizes relative motion between a coil and a magnetic field, which results in the time variation of the magnetic flux. According to Faraday’s law, the changing flux will induce a voltage across the coil. We therefore believe that the investigation of the magnet and coil structure plays an important role in the design process of an electromagnetic energy harvester.
The design of the magnet and coil structure has been implemented in many different ways. In terms of material, neodymium iron boron (NdFeb) has been shown as a strong magnetic material and, thus, has been used for permanent magnets many previous works [
16,
17]. In terms of structural design, various architectures, including single magnet [
18,
19,
20] and magnet arrays [
21,
22,
23] have been proposed. Among energy harvesters with magnet arrays, Halbach arrays have been an attractive topic of investigation due to their ability to concentrate the magnetic field [
24,
25].
The effect of the coil–magnet configuration on the performance of electromagnetic energy harvesters has also been investigated in previous studies. Spreemann et al. [
26] classified different coil and magnet architectures into groups of “magnet in-line coil” and “magnet across coil”, and optimized individual structures for the output power and voltage. Zhu et al. [
27] studied the performance improvement of the Halbach array with triangular cross-sectioned magnets and the double Halbach array compared to the standard Halbach array. Li et al. [
28] investigated the effect of magnet shape and their arrangement on the harvester performance through four types of configurations. These are cubic-Halbach, cubic-alternative, triangle-Halbach, and triangle-alternative. Moreover, Kim et al. [
29] optimized harvesters with cylindrical shape and compared the output voltage and output power according to various aspect ratios. These studies have shown that the coil–magnet topology has a great impact on the electromagnetic energy harvester’s performance.
Although the use of cylindrical shaped structures in electromagnetic harvester prototype has been popular [
18,
30,
31], and there exist many previous studies on Halbach arrays, only few research studies have concentrated on the effect of the magnetic structure with cylindrical Halbach arrays [
32,
33]. Shahosseini et al. [
32] presented two cylindrical magnetic structures with Halbach arrays and compared their performance with single magnet configurations and configurations of two opposite polarized magnets. However, the volume of these configurations was not constant in the comparison, but increased with the increase of the number of components (e.g. number of magnets and coils). Moreover, when conducting the power comparison between all structures, only the double-concentric Halbach array structure was geometrically optimized in terms of power density. Ordoñez et al. [
33] analyzed various cylindrical configurations with Halbach arrays and compared them in terms of the magnetic flux linkage and transduction factor. However, the study lacks a comparison in terms of output power. The individual structures have also not been optimized prior to the comparison. Consequently, previous studies comparing cylindrical electromagnetic vibration energy harvesters have limitations, with respect to fair comparisons, which also limits the conclusions to be drawn from the obtained results.
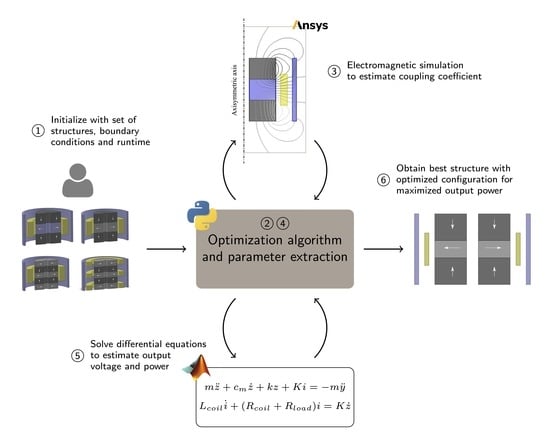
In this paper, the research objective is to investigate and compare the effect of different cylindrical magnetic structures on the harvester performance in a more systematic and fair manner. This is achieved by the introduction of a fully automatic optimization procedure, which simplifies the optimization work and provides a significant output power improvement. Specifically, the performance of different harvester configurations with cylindrical Halbach arrays are compared to each other and compared to a configuration of two opposite polarized magnets separated by a spacer. In order to conduct a fair comparison, all the structures are optimized within a given volumetric constraint. The design optimization approach is based on an expensive black-box optimization routine, with the aim to maximize the output power of the electromagnetic energy harvester. The optimization takes into consideration the magnetization directions, as well as dimensions and locations of electromagnetic components.
The remainder of the paper is organized as follows.
Section 2 presents the theoretical background of the electromagnetic energy harvester in general and the coil–magnet structure in detail.
Section 3 explains the optimization procedure used in this study. The simulation results and discussions are shown in
Section 4. Finally,
Section 5 concludes the paper.
5. Conclusions
In this paper, we investigated and compared the performance of four cylindrical coil–magnet configurations for electromagnetic vibration energy harvesters. These prototypes are based on either cylindrical Halbach arrays or opposite polarized magnets. An expensive black-box optimization algorithm was implemented to maximize the output power of these harvester configurations under a fixed volume constraint. All of the parameters regarding the dimensions and locations of the magnets and coils were under the scope of investigation. ANSYS Maxwell and MATLAB Simulink were utilized to facilitate the analysis process.
Implementing an automated optimization approach remarkably simplified the optimization procedure. Requirements for manual interference were completely eliminated. By using this approach, users no longer need to select and evaluate random sampling manually, or use intuition to find the best solution. In comparison to previous studies that investigated non-optimized structures, we demonstrated that optimization achieves a significant performance improvement.
The simulation results show that the Halbach array configuration with five magnets and three coils (H5M3C) and the Halbach array configuration with five magnets and one coil (H5M1C) tend to converge to the Halbach array configuration with three magnets and one coil (H3M1C) during the design optimization procedure. This indicates that H3M1C seems to be a better candidate for Halbach array configurations under the constraints and excitation conditions investigated in this study.
Among all configurations, the configuration with two opposite polarized magnets (DM1S1C) presents a slightly higher performance in terms of output power and volume power density than the others. However, the Halbach array with three magnets and one coil (H3M1C) provides the highest mass power density.
It is also observed that for output power optimization, where all the design parameters were under consideration, not only the coupling coefficient, but also other aspects that vary with the change of the design parameters, will affect the final performance result. Thus, the electromagnetic coupling coefficient should not be used as a metric to optimize an energy harvester if the ultimate goal is to maximize output power.
The automated optimization method, results, and conclusions of this study are significant contributions to the optimization and comparison of electromagnetic vibration energy harvesters. As such, they have the potential to result in more effective harvester implementations that lead to improved utility in a number of application scenarios.
The current study focuses on the optimization and comparison of electromagnetic energy harvesters with different cylindrical magnet–coil structures under a specific volume constraint and subjected to a specific set of vibration conditions. In addition, since the black-box optimization approach takes into account multiple parameters that can affect the output results, this method is suitable for problems that require complicated computation or are difficult to be modeled in an analytical manner. Thus, this approach can give an initial idea on the output of the complicated system in terms of a practical implementation. The lacking ability of this approach to link the result to the underlying theory, however, can be seen as a limitation of the proposed approach. With the goal of generalization, further investigations should be performed to study the optimization procedure in additional scenarios, with variations in volumetric constraints and excitation conditions. Moreover, future research on a theoretical model of the current approach could be an interesting topic.