Numerical and Experimental Evaluation and Heat Transfer Characteristics of a Soft Magnetic Transformer Built from Laminated Steel Plates
Abstract
:1. Introduction
2. Materials and Methods
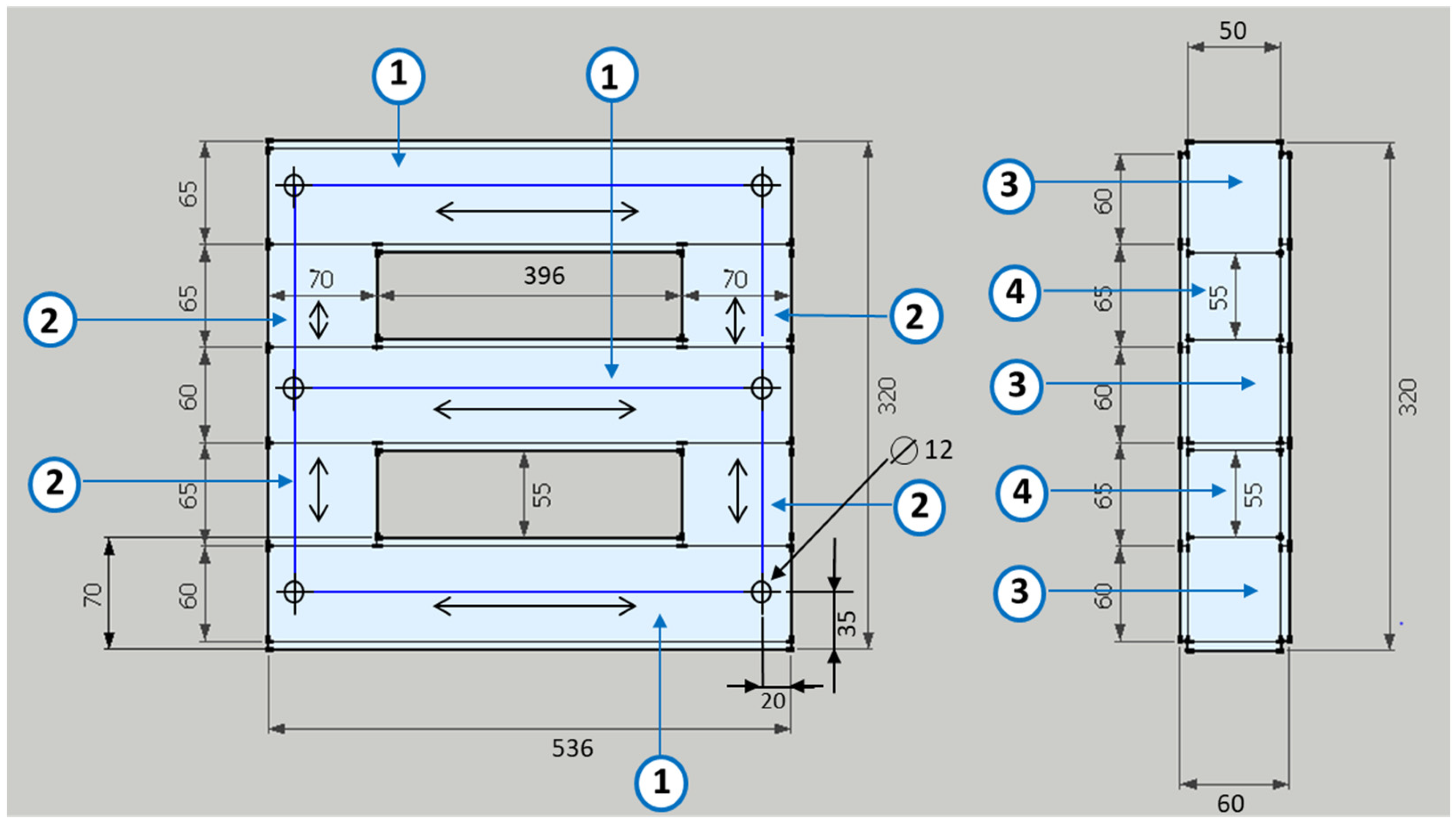
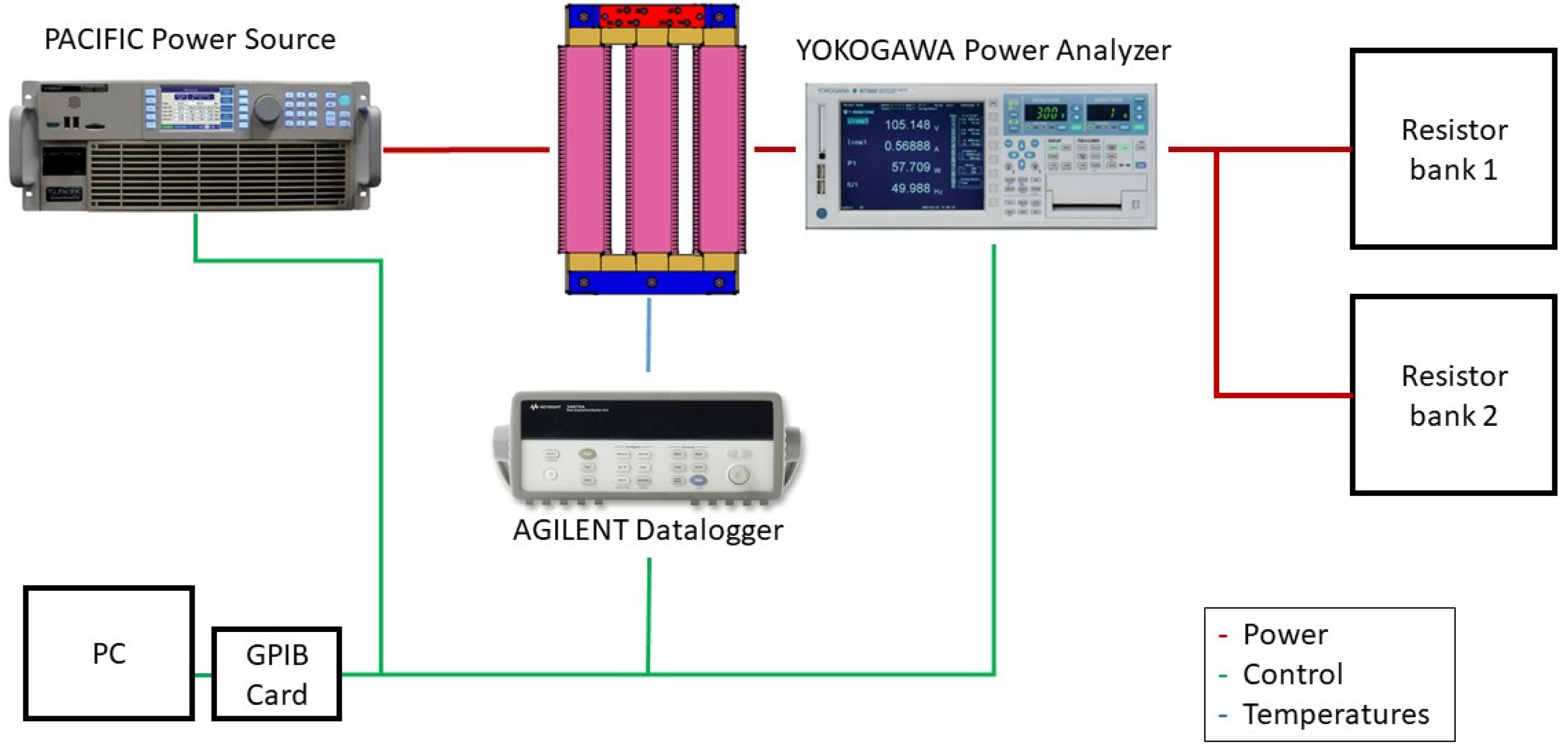
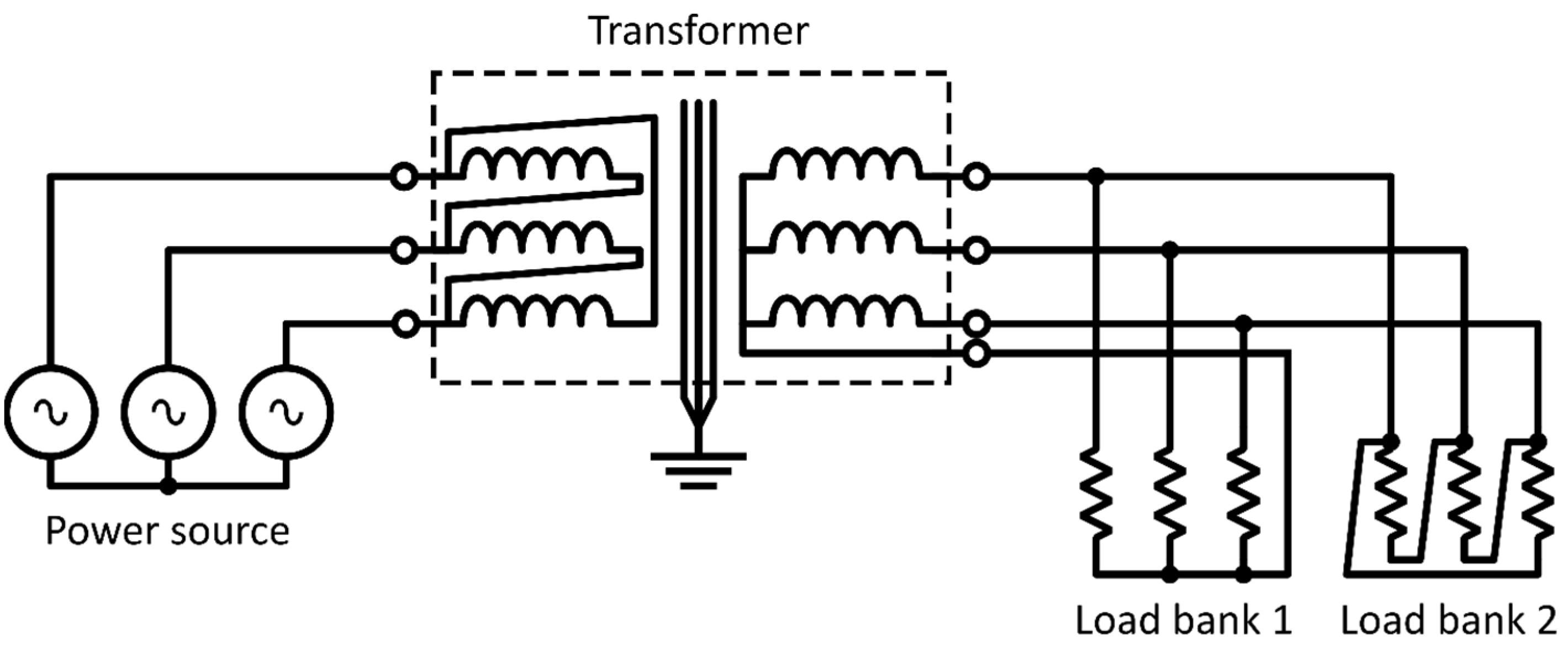
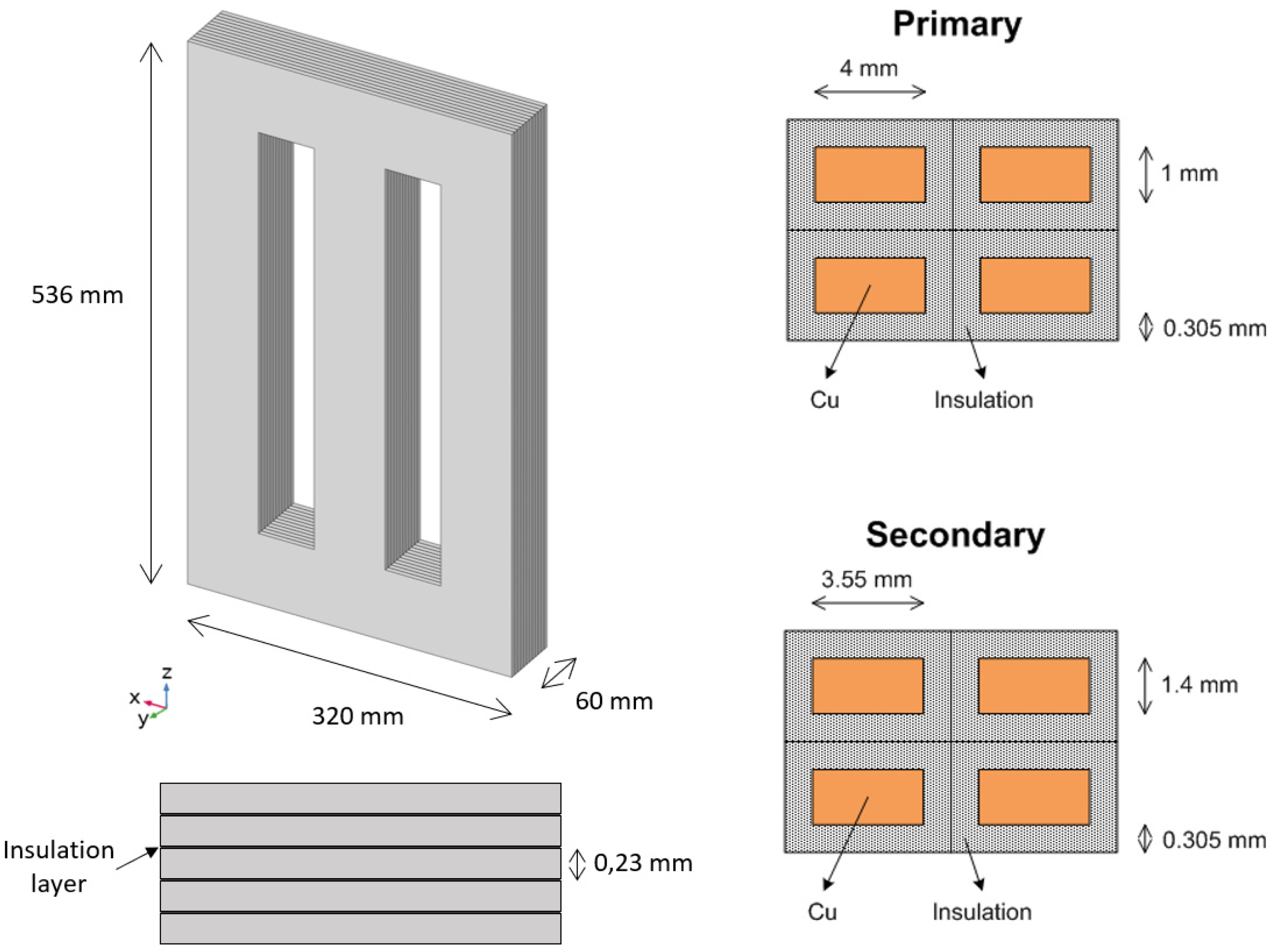
2.1. Experimental Setup
2.2. Numerical Model
2.2.1. Constitutive Equations and Boundary Conditions
2.2.2. Materials and Physical Properties
2.3. Heat Generation Due to Electromagnetic Losses
3. Results and Discussion
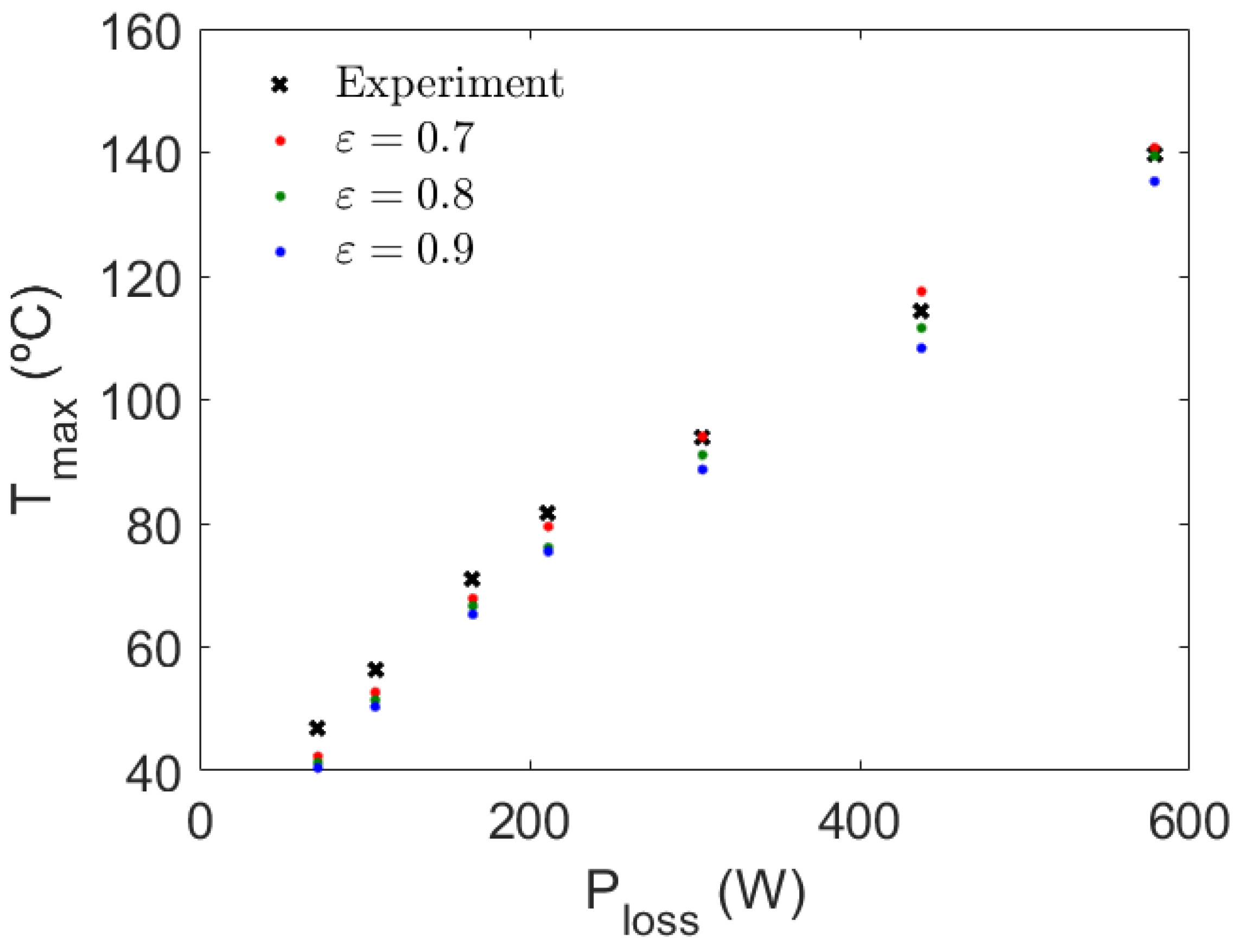
3.1. Experimental Results
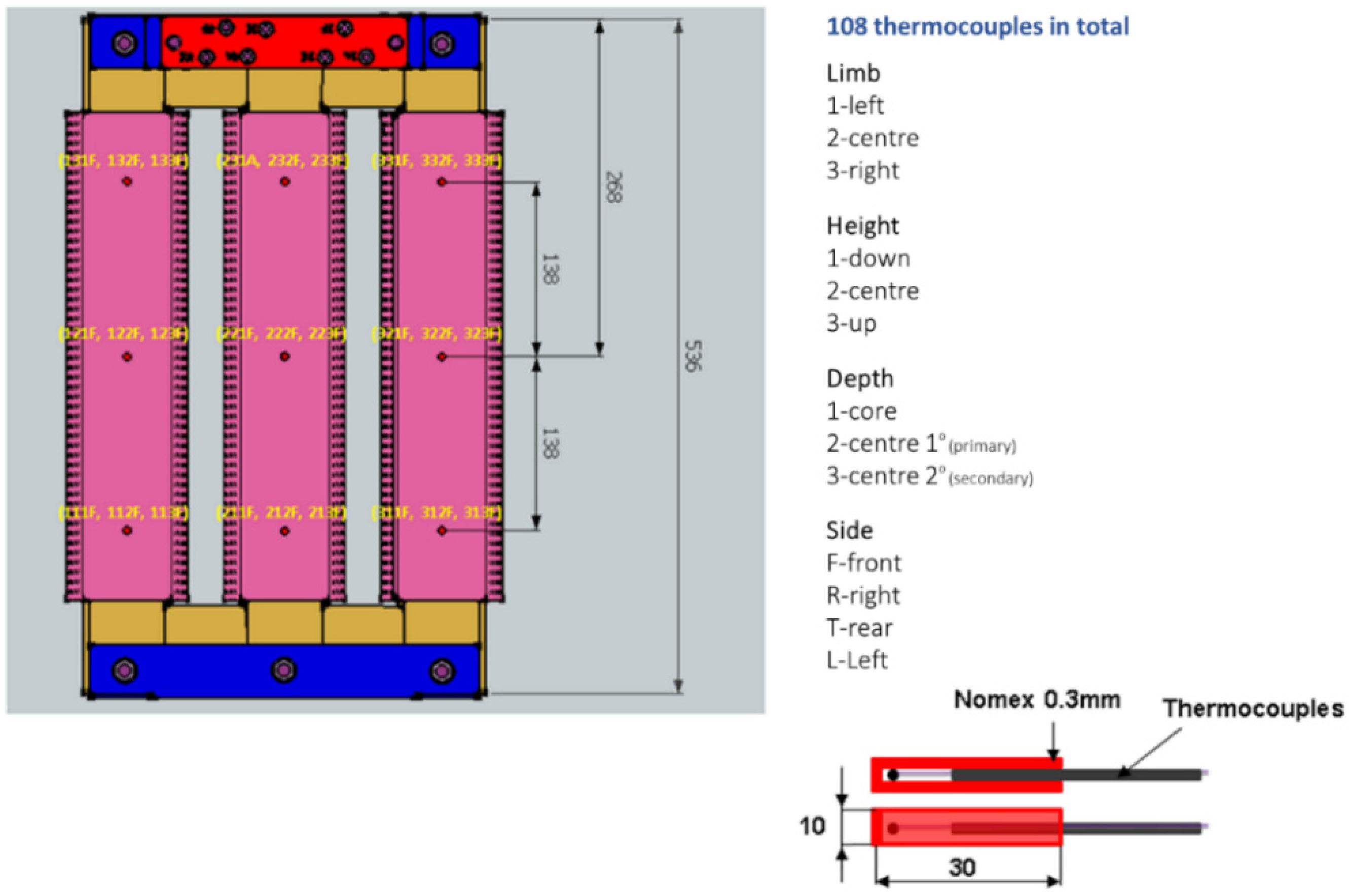
- The thermal behavior of the left and right limbs is similar. For that reason, only temperatures of the left and central limbs, i.e., T1xxx and T2xxx, were considered.
- The thermal behavior of the front and rear sides is also similar. Thus, only temperatures of the front side were evaluated (TxxxF).
- The temperature value reached at the intermediate depth (Txx2x), i.e., in the secondary winding, must be a value between the core surface and the primary winding temperatures. Hence, only temperatures on the core surface and the primary winding were selected (Txx1x and Txx3x).
- The temperature distribution in the center limb is symmetrical. Therefore, only the temperatures of the front and left of the center limb were chosen (T1xxF and T1xxL).
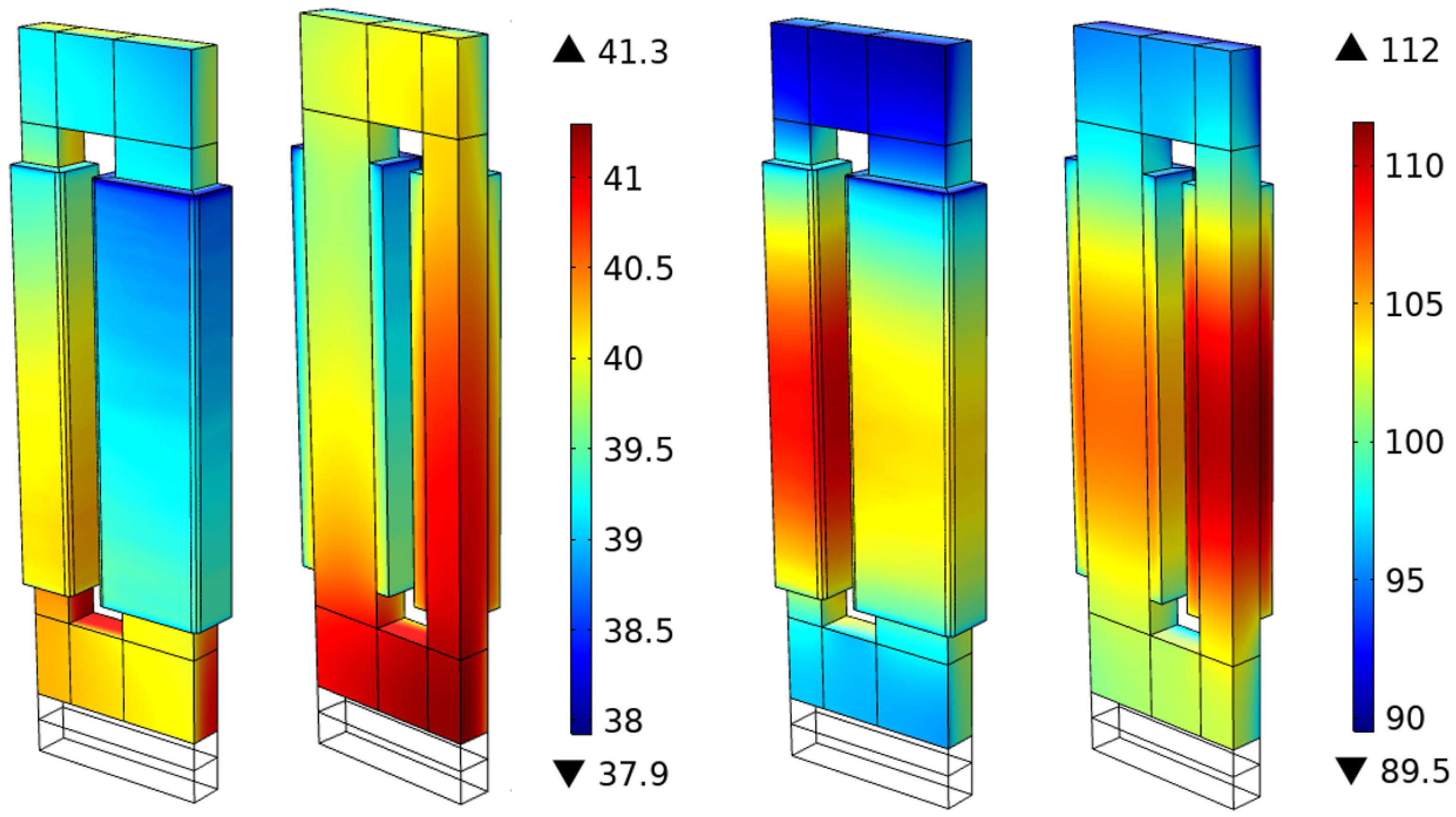
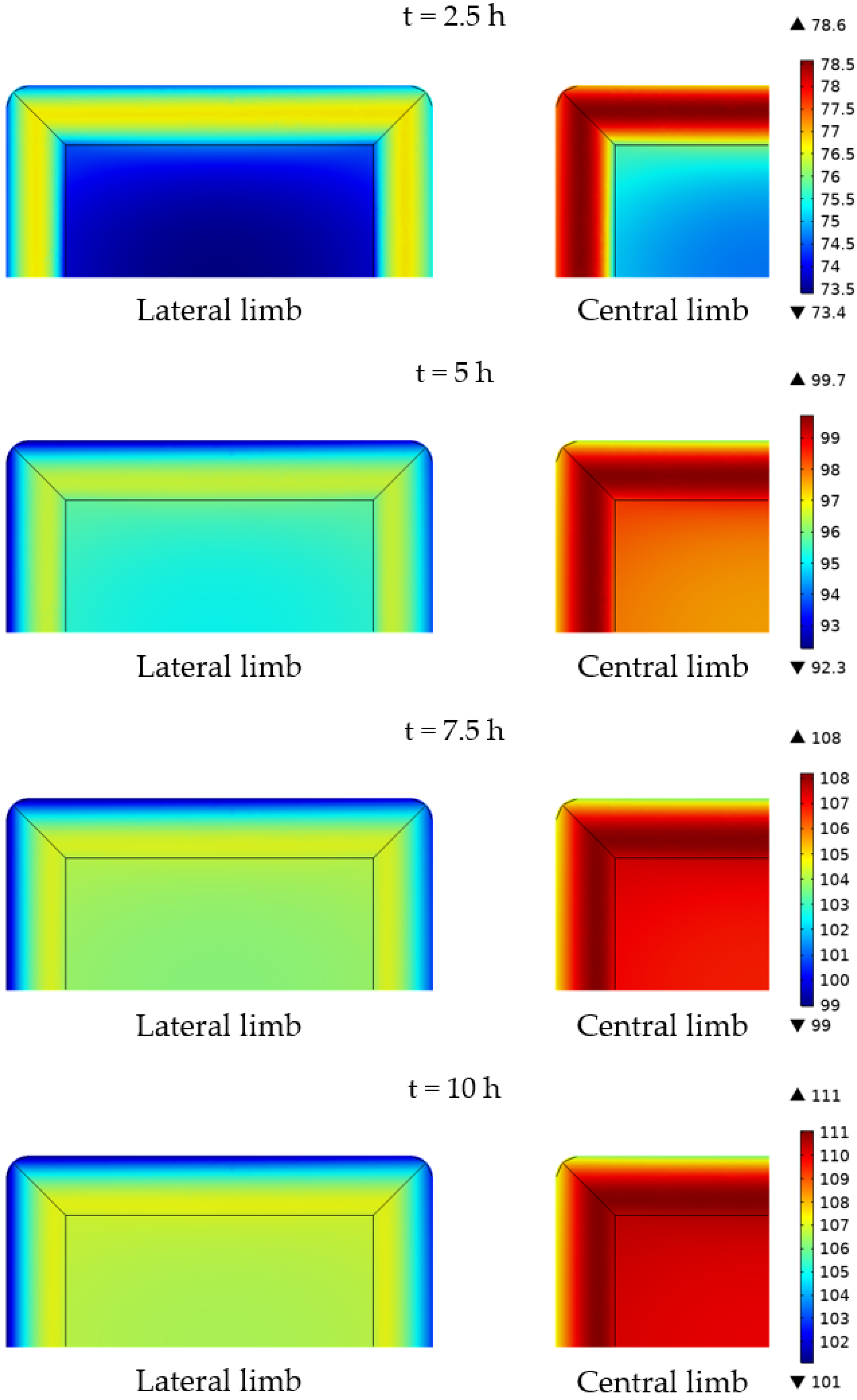
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sai Ram, B.; Paul, A.K.; Kulkarni, S.V. Soft magnetic materials and their applications in transformers. J. Magn. Magn. Mater. 2021, 537, 168210. [Google Scholar] [CrossRef]
- Petzold, J. Advantages of soft-magnetic nanocrystalline materials for modern electronic applications. J. Magn. Magn. Mater. 2002, 242–245, 84–89. [Google Scholar] [CrossRef]
- Emadi, A.; Khaligh, A.; Nie, Z.; Lee, Y. Integrated Power Electronic Converters and Digital Control; Power Electronics and Applications Series; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Rodriguez-Sotelo, D.; Rodriguez-Licea, M.A.; Soriano-Sanchez, A.G.; Espinosa-Calderon, A.; Perez-Pinal, F.J. Advanced ferromagnetic materials in power electronic converters: A state of the art. IEEE Access 2020, 8, 56238–56252. [Google Scholar] [CrossRef]
- Azuma, D.; Ito, N.; Ohta, M. Recent progress in Fe-based amorphous andnanocrystalline soft magnetic materials. J. Magn. Magn. Mater. 2020, 501, 166373. [Google Scholar] [CrossRef]
- Balci, S.; Sefa, I.; Bayram, M.B. Core Material Investigation of Medium-Frequency Power Transformers. In Proceedings of the 2014 16th International Power Electronics and Motion Control Conference and Exposition (PEMC), Antalya, Turkey, 21–24 September 2014; pp. 861–866. [Google Scholar]
- Leary, A.M.; Ohodnicki, P.R.; McHenry, M.E. Soft magnetic materials in high frequency, high-power conversion applications. JOM 2012, 64, 772–781. [Google Scholar] [CrossRef]
- Gavrila, H.; Ionita, V. Crystalline and amorphous soft magnetic materials and their applications—Status of art and challenges. J. Optoelectron. Adv. Mater. 2002, 4, 173–192. [Google Scholar]
- Salloum, E.; Maloberti, O.; Nesser, M.; Panier, S.; Dupuy, J. Identification and analysis of static and dynamic magnetization behavior sensitive to surface laser treatments within the electromagnetic field diffusion inside GO SiFe electrical steels. J. Magn. Magn. Mater. 2020, 503, 166613. [Google Scholar] [CrossRef]
- Johnson, M.J.; Chen, R.; Jiles, D.C. Reducing core losses in amorphous Fe80B12Si8 ribbons by laser-induced domain refinement. IEEE Trans. Magn. 1999, 35, 3865–3867. [Google Scholar] [CrossRef]
- Zeleňáková, A.; Kollár, P.; Kuźmiński, M.; Kollárová, M.; Vértesy, Z.; Riehemann, W. Magnetic properties and domain structure investigation of laser treated finemet. J. Magn. Magn. Mater. 2003, 254, 152–154. [Google Scholar] [CrossRef]
- Lahn, L.; Wang, C.; Allwardt, A.; Belgrand, T.; Blaszkowski, J. Improved transformer noise behavior by optimized laser domain refinement at thyssenkrupp electrical steel. IEEE Trans. Magn. 2012, 48, 1453–1456. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and Modern Approaches for Thermal Analysis of Electrical Machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef] [Green Version]
- Pierce, L.W. Predicting hottest spot temperatures in ventilated dry type transformer windings. IEEE Trans. Power Deliv. 1994, 9, 1160–1172. [Google Scholar] [CrossRef]
- Elmoudi, A.; Palola, J.; Lehtonen, M. A transformer thermal model for use in an on-line monitoring and diagnostic system. In Proceedings of the IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1092–1096. [Google Scholar]
- Rahimpour, E.; Azizian, D. Analysis of temperature distribution in cast-resin dry-type transformers. Electr. Eng. 2007, 89, 301–309. [Google Scholar] [CrossRef]
- Yang, X.; Ho, S.L.; Fu, W.; Zhang, Y.; Xu, G.; Yang, Q.; Deng, W.; Peng, D. An adjustable degrees-of-freedom numerical method for computing the temperature distribution of electrical devices. Electr. Eng. 2019, 101, 507–516. [Google Scholar] [CrossRef]
- Allahbakhshi, M.; Akbari, A. An improved computational approach for thermal modeling of power transformers. Int. Trans. Electr. Energy Syst. 2015, 25, 1319–1332. [Google Scholar] [CrossRef]
- Lesieutre, B.C.; Hagman, W.H.; Kirtley, J.L. An improved transformer top oil temperature model for use in an on-line monitoring and diagnostic system. IEEE Trans. Power Deliv. 1997, 12, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Terry Morris, A. Comparing Parameter Estimation Techniques for an Electrical Power Transformer Oil Temperature Prediction Model; NASA Technical Memorandum 208974; Langley Research Center: Hampton, VA, USA, 1999. [Google Scholar]
- Eteiba, M.B.; Alzahab, E.A.; Shaker, Y.O. Steady state temperature distribution of cast-resin dry type transformer based on new thermal model using finite element method. Int. J. Electrical Computer Eng. 2010, 4, 361–365. [Google Scholar]
- Akbari, M.; Rezaei-Zare, A. Transformer bushing thermal model for calculation of hot-spot temperature considering oil flow dynamics. IEEE Trans. Power Deliv. 2021, 36, 1726–1734. [Google Scholar] [CrossRef]
- Yaman, G.; Altay, R.; Taman, R. Validation of computational fluid dynamic analysis of natural convection conditions for a resin dry-type transformer with a cabin. Therm. Sci. 2019, 23, S23–S32. [Google Scholar] [CrossRef] [Green Version]
- Smolka, J.; Nowak, A.J. Experimental validation of the coupled fluid flow, heat transfer and electromagnetic numerical model of the medium-power dry-type electrical transformer. Int. J. Therm. Sci. 2008, 47, 1393–1410. [Google Scholar] [CrossRef]
- Pradhan, M.K.; Ramu, T.S. Estimation of the hottest spot temperature (HST) in power transformers considering thermal inhomogeneity of the windings. IEEE Trans. Power Deliv. 2004, 19, 1704–1712. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yan, X.; Wang, C.; Yang, Q.; Zhang, C. Eddy current loss effect in foil winding of transformer based on magneto-fluid-thermal simulation. IEEE Trans. Magn. 2019, 55, 8401705. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Li, Y.; Zhang, Z.; Ying, W.; Yang, Q. Comparison between thermal-circuit model and finite element model for dry-type transformer. In Proceedings of the 22nd International Conference on Electrical Machines and Systems, Harbin, China, 11–14 August 2019. [Google Scholar]
- COMSOL AB. Stockholm, Sweden. COMSOL Multiphysics® v. 5.6. Available online: www.comsol.com (accessed on 20 October 2021).
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw-Hilll: New York, NY, USA, 1954. [Google Scholar]
- Churchill, S.W.; Chu, H.H. Correlating equations for laminar and turbulent free convection from a vertical plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Bertin, Y. Refroidissement des Machines Electriques Tournantes. Techniques de L’ingénieur Conversion de L’énergie Electrique, Traité Génie Electrique, Editions T.I., Ref. D3460. 1999. Available online: https://www.techniques-ingenieur.fr/base-documentaire/energies-th4/generalites-sur-les-machines-electriques-tournantes-42250210/refroidissement-des-machines-electriques-tournantes-d3460/ (accessed on 20 October 2021).
- Guang-Jin, L. Contribution à la Conception des Machines Electriques à Rotor Passif pour des Applications Critiques: Modélisations Electromagnétiques et Thermiques sur Cycle de Fonctionnement, Etude du Fonctionnement en Mode Dégradé. Ph.D. Thesis, École Normale Supérieure de Cachan, Cachan, France, 2011. [Google Scholar]



| Case | Power Input, Transformer (W) | Total Power Losses (W) | Percentage of Power Losses in the Core (%) | Power Losses per Unit Volume—Core (kW/m3) | Power Losses per Unit Volume—Winding (kW/m3) |
|---|---|---|---|---|---|
| 1 | 1205.5 | 71.8 | 94.3 | 8.8 | 0.96 |
| 2 | 4202.1 | 106.6 | 62.0 | 8.6 | 9.5 |
| 3 | 6547.3 | 165.7 | 39.4 | 8.5 | 23.6 |
| 4 | 7647.5 | 211.4 | 32.4 | 8.9 | 33.6 |
| 5 | 9399.7 | 304.8 | 27.0 | 10.7 | 52.3 |
| 6 | 11,160.3 | 437.5 | 24.3 | 13.9 | 77.9 |
| 7 | 12,534.2 | 578.7 | 23.1 | 17.4 | 104.7 |
| Left Limb | Centre Limb | |||||
|---|---|---|---|---|---|---|
| Front | Left | Right | Front | Left | ||
| Down | Core | T111F | T111L | T111R | T211F | T211L |
| Centre2 | T113F | T113L | T113R | T213F | T213L | |
| Centre | Core | T121F | T121L | T121R | T221F | T221L |
| Centre2 | T123F | T123L | T123R | T223F | T223L | |
| Up | Core | T131F | T131L | T131R | T231F | T231L |
| Centre2 | T133F | T133L | T133R | T233F | T233L | |
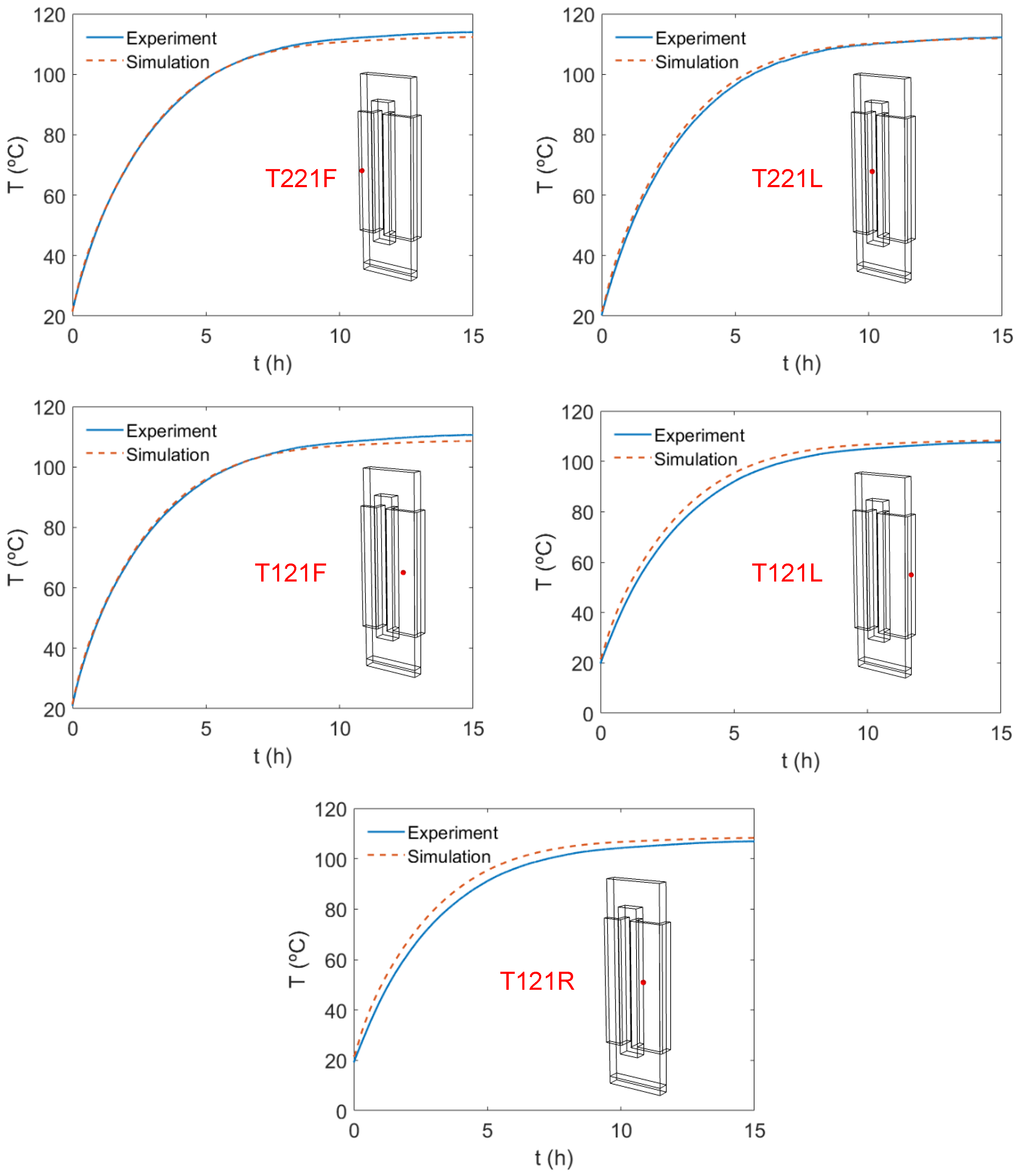
| Position | Tsim (°C) | Texp (°C) | Deviation (°C) |
|---|---|---|---|
| 231F | 103.3 | 104.0 | 0.7 |
| 221F | 111.2 | 114.2 | 3.0 |
| 211F | 106.7 | 104.0 | 2.7 |
| 231L | 103.3 | 104.2 | 0.9 |
| 221L | 111.2 | 112.5 | 1.3 |
| 211L | 106.7 | 100.1 | 6.6 |
| 131F | 100.6 | 100.4 | 0.2 |
| 121F | 107.0 | 110.9 | 3.9 |
| 111F | 103.8 | 100.6 | 3.2 |
| 131L | 100.7 | 99.2 | 1.5 |
| 121L | 106.8 | 107.9 | 1.1 |
| 111L | 103.9 | 101.4 | 2.5 |
| 131R | 100.7 | 99.8 | 0.9 |
| 121R | 106.8 | 107.2 | 0.4 |
| 111R | 103.9 | 98.2 | 5.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cano-Pleite, E.; Barrado, A.; Garcia-Hernando, N.; Olías, E.; Soria-Verdugo, A. Numerical and Experimental Evaluation and Heat Transfer Characteristics of a Soft Magnetic Transformer Built from Laminated Steel Plates. Sensors 2021, 21, 7939. https://doi.org/10.3390/s21237939
Cano-Pleite E, Barrado A, Garcia-Hernando N, Olías E, Soria-Verdugo A. Numerical and Experimental Evaluation and Heat Transfer Characteristics of a Soft Magnetic Transformer Built from Laminated Steel Plates. Sensors. 2021; 21(23):7939. https://doi.org/10.3390/s21237939
Chicago/Turabian StyleCano-Pleite, Eduardo, Andrés Barrado, Néstor Garcia-Hernando, Emilio Olías, and Antonio Soria-Verdugo. 2021. "Numerical and Experimental Evaluation and Heat Transfer Characteristics of a Soft Magnetic Transformer Built from Laminated Steel Plates" Sensors 21, no. 23: 7939. https://doi.org/10.3390/s21237939
APA StyleCano-Pleite, E., Barrado, A., Garcia-Hernando, N., Olías, E., & Soria-Verdugo, A. (2021). Numerical and Experimental Evaluation and Heat Transfer Characteristics of a Soft Magnetic Transformer Built from Laminated Steel Plates. Sensors, 21(23), 7939. https://doi.org/10.3390/s21237939








