Evolving Deep Architecture Generation with Residual Connections for Image Classification Using Particle Swarm Optimization
Abstract
:1. Introduction
1.1. Research Problems
1.2. Contributions
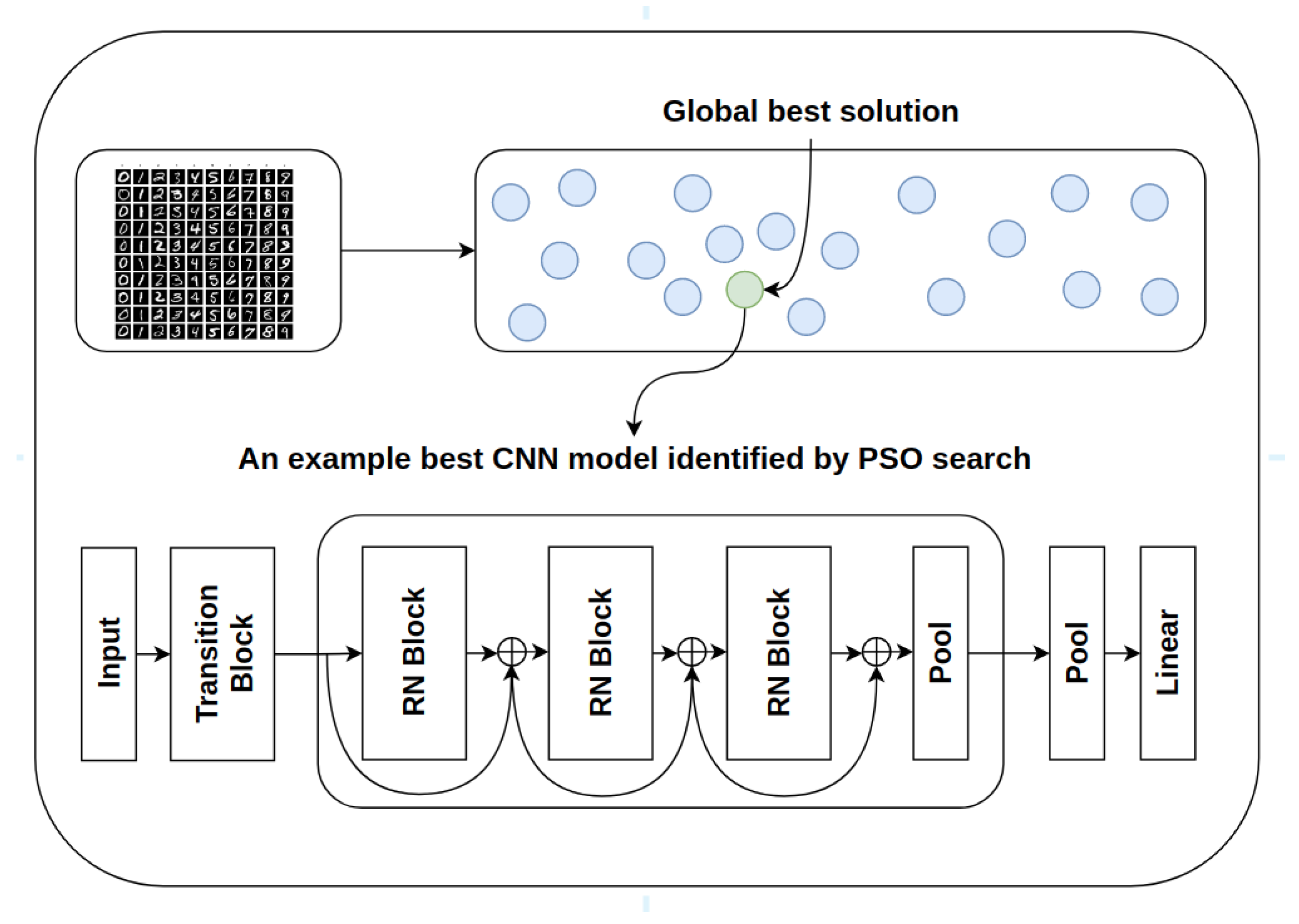
- A new PSO algorithm, namely resPsoCnn, is proposed for residual deep architecture generation. The novel aspects of the resPsoCnn model include (1) a new residual group-based encoding scheme and (2) a new search mechanism guided by neighboring and global promising solutions for deep architecture search. Specifically, the new group-based encoding scheme is able to describe network configurations with residual connections. In the encoding scheme, candidate models are firstly converted into groups. Each group contains one or more convolutional blocks and an optional pooling layer. The number of filters in the convolutional layers in each group, which controls the network width, is also optimized. The kernel sizes of convolutional layers are individually encoded, giving fine-grained control over the receptive field of each block. The number of blocks within each group can vary to increase or decrease the model depth, while different pooling layer types are embedded to control downsampling.
- We propose an optimization strategy that exploits the advantages of skip connections to avoid the vanishing gradient problem. Such a strategy addresses the weaknesses in related studies. As an example, (1) existing studies either perform optimization tasks only on fixed skeleton models (e.g., fixed numbers of blocks with fixed kernel sizes) that exploit skip connections but restrict model diversity, (2) or they optimize a range of hyperparameter settings, capable of producing diverse but shallow networks, without residual connections. Our proposed strategy undertakes both weaknesses by providing the ability to leverage skip connections in establishing deep network architectures, whilst optimizing a range of network settings to improve diversity.
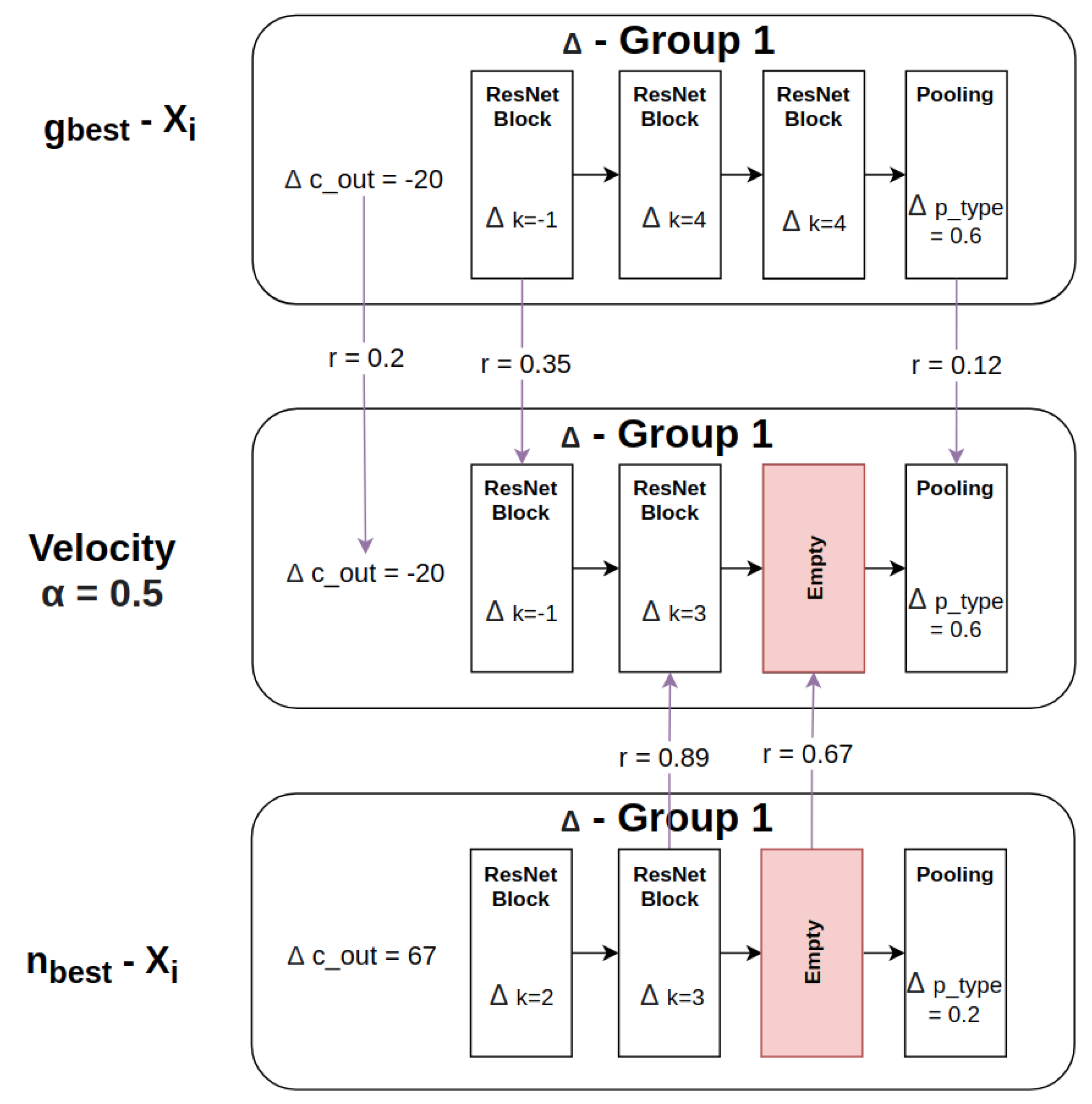
- We propose a new velocity updating mechanism that adds randomness to the updating of both the group and block hyperparameters. Specifically, it employs multiple elite signals, i.e., the swarm leader and the non-uniformly randomly selected neighboring best solutions, for searching optimal hyperparameters. Such a search process guided by multiple promising signals escalates social communication and is more likely to overcome stagnation. The hyperparameter updating procedure at the group and block levels is conducted by either selecting from the difference between the current particle and global best solution, or the difference between the current particle and a neighboring best solution, to increase search diversity. The proposed search mechanism optimizes the number of groups, network width and depth, kernel sizes and pooling layer choices to produce a rich assortment of optimal residual deep architectures. Owing to the guidance of multiple elite signals, our search process achieves a better balance between exploration and exploitation to overcome weaknesses such as the local optimum traps of existing search methods led by only single leader. Evaluated using a number of benchmark datasets, our devised networks produce superior performances in respect to those yielded by several state-of-the-art existing methods.
2. Related Studies
2.1. Deep Architecture Generation Using PSO Methods
2.2. Deep Architecture Generation Using Other Search Methods
3. The Proposed PSO-Based Deep Architecture Generation
3.1. Encoding Strategy and Initialization
- A model contains at least one group. We optimize the number of groups between 1 and .
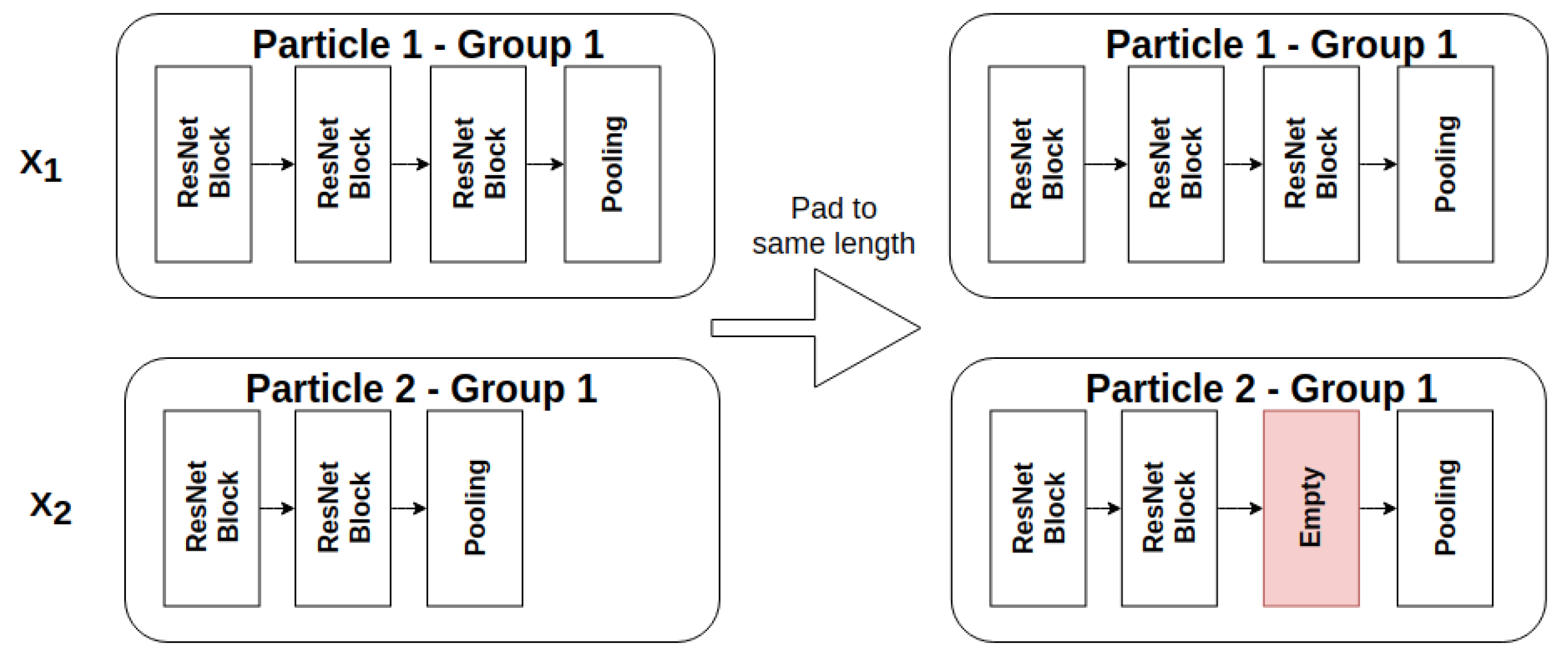
- A group contains at least one residual block. The number of blocks the model can contain during initialization is set between 1 and . We optimize the number of residual blocks in each group.
- All blocks within a group share the same number of channels for compatibility. We optimize the number of channels used by a group between and .
- A group contains an optional pooling layer, which can be of the following types: max pooling, average pooling or no pooling. We optimize the pooling type by dividing a search range between 0 and 1 into three regions and attribute a pooling type to each region.
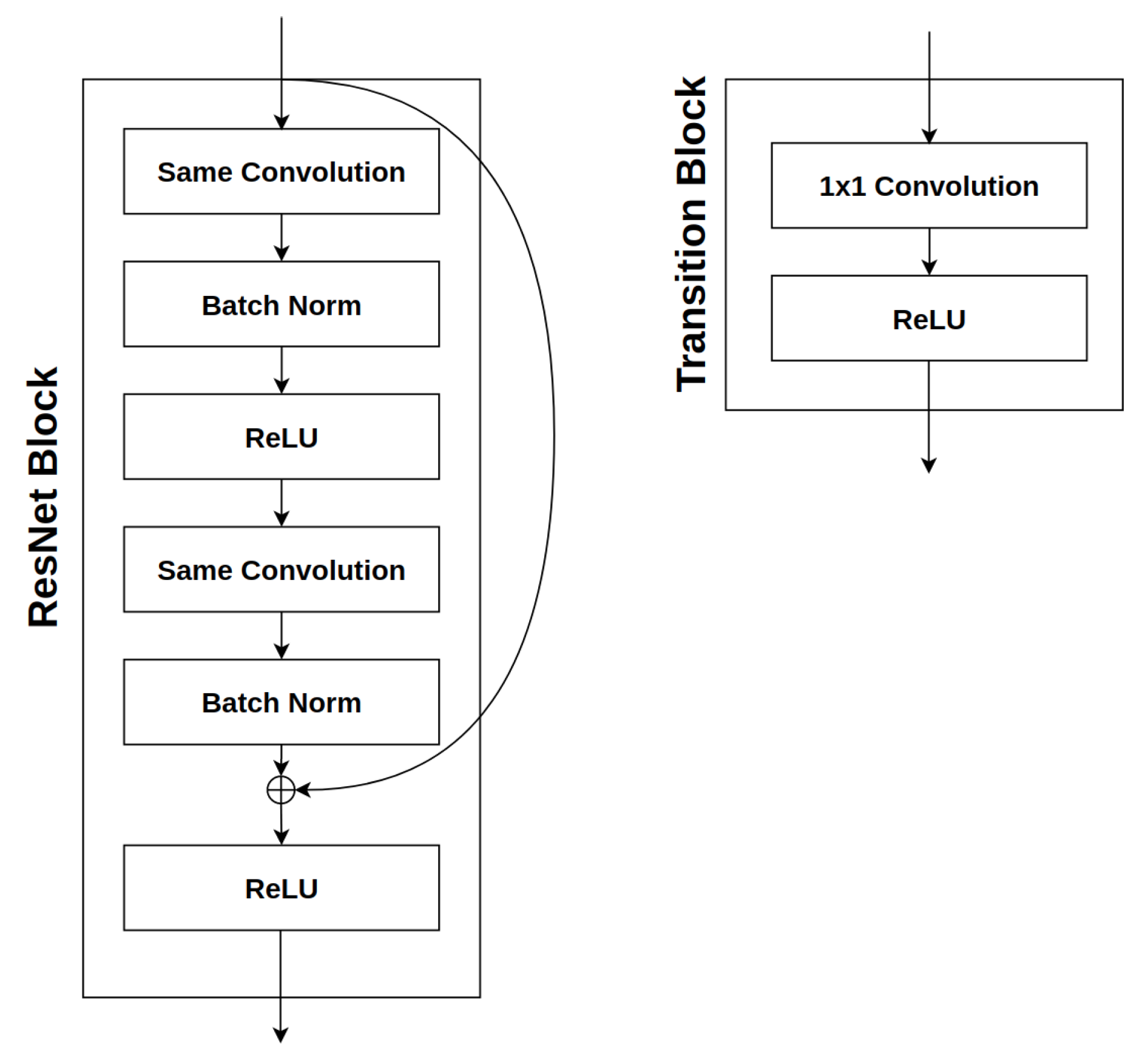
- A block contains a stack of convolutions layers, performing the same convolutions, i.e., the appropriate padding is used to ensure the dimensions of the output match those of the input volume. The degree of padding depends on the kernel size. The kernel size of a convolutional layer is optimized on a block-by-block basis between and . This is necessary, as the kernel size controls the receptive field, which, in turn, controls the visibility degree of an image with respect to one filter, at one time [1].
3.2. Decoding Strategy
3.3. The Optimization Strategy
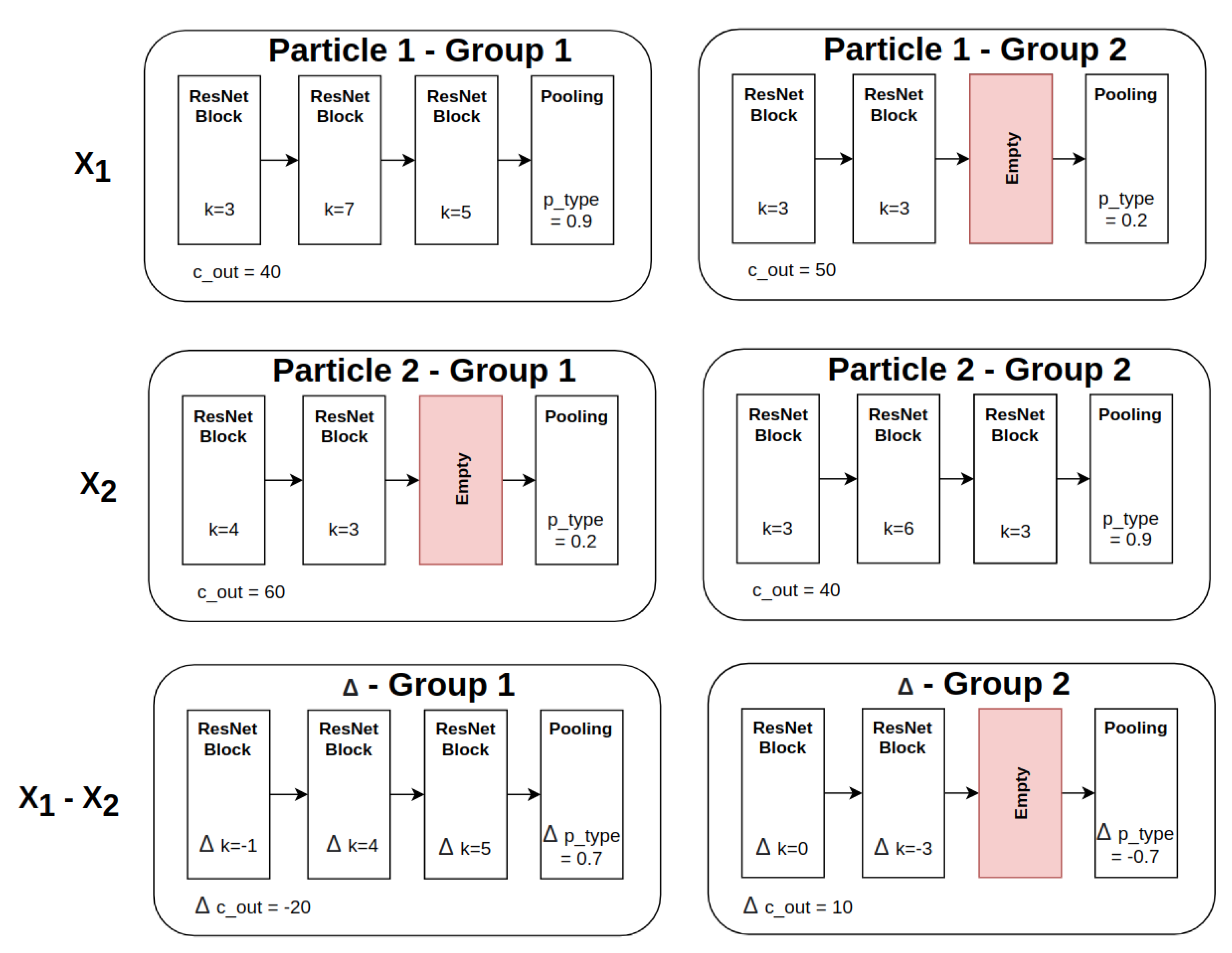
3.4. Particle Difference Calculation
3.4.1. Particle Difference Calculation between Groups with Respect to the Number of Channels
3.4.2. Particle Difference Calculation between Groups with Respect to the Number of Blocks
3.4.3. Particle Difference Calculation with Respect to the Block Kernel Size k
3.4.4. Particle Difference Calculation with Respect to the Pooling Type
3.5. Velocity Calculation
3.6. Position Updating
3.7. Fitness Evaluation
4. Experimental Studies
4.1. Datasets
4.2. Parameter Settings
4.3. Benchmark Models
4.4. Results
4.4.1. Performance Comparison with Existing Studies
4.4.2. Evaluation of the Proposed Encoding and Search Strategies
4.5. Theoretical Justification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the effective receptive field in deep convolutional neural networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 4905–4913. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In British Machine Vision Conference (BMVC); BMVA Press: Durham, UK, 2016; Volume 87, pp. 1–12. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf (accessed on 15 November 2021).
- Zeng, M.; Xiao, N. Effective Combination of DenseNet and BiLSTM for Keyword Spotting. IEEE Access 2019, 7, 10767–10775. [Google Scholar] [CrossRef]
- Ayyachamy, S.; Alex, V.; Khened, M.; Krishnamurthi, G. Medical image retrieval using Resnet-18. In Medical Imaging 2019: Imaging Informatics for Healthcare, Research, and Applications; Chen, P.H., Bak, P.R., Eds.; International Society for Optics and Photonics, SPIE: Washington, DC, USA, 2019; Volume 10954, pp. 233–241. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient inference. arXiv 2016, arXiv:1611.06440. [Google Scholar]
- Rezende, E.; Ruppert, G.; Carvalho, T.; Ramos, F.; De Geus, P. Malicious software classification using transfer learning of resnet-50 deep neural network. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 1011–1014. [Google Scholar]
- Miao, F.; Yao, L.; Zhao, X. Evolving convolutional neural networks by symbiotic organisms search algorithm for image classification. Appl. Soft Comput. 2021, 109, 107537. [Google Scholar] [CrossRef]
- Junior, F.E.F.; Yen, G.G. Particle swarm optimization of deep neural networks architectures for image classification. Swarm Evol. Comput. 2019, 49, 62–74. [Google Scholar] [CrossRef]
- Xie, L.; Yuille, A. Genetic CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1388–1397. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Caruana, R.; Lawrence, S.; Giles, C.L. Overfitting in neural nets: Backpropagation, conjugate gradient, and early stopping. In Proceedings of the 13th International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; pp. 402–408. [Google Scholar]
- Fielding, B.; Zhang, L. Evolving Deep DenseBlock Architecture Ensembles for Image Classification. Electronics 2020, 9, 1880. [Google Scholar] [CrossRef]
- Wang, B.; Xue, B.; Zhang, M. Particle Swarm optimisation for Evolving Deep Neural Networks for Image Classification by Evolving and Stacking Transferable Blocks. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y.; Xue, B.; Zhang, M. Evolving deep convolutional neural networks by variable-length particle swarm optimization for image classification. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Wang, B.; Sun, Y.; Xue, B.; Zhang, M. Evolving Deep Neural Networks by Multi-Objective Particle Swarm Optimization for Image Classification. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO’19, Prague, Czech Republic, 13–17 July 2019; pp. 490–498. [Google Scholar] [CrossRef] [Green Version]
- Dutta, T.; Dey, S.; Bhattacharyya, S.; Mukhopadhyay, S. Quantum fractional order darwinian particle swarm optimization for hyperspectral multi-level image thresholding. Appl. Soft Comput. 2021, 2021, 107976. [Google Scholar] [CrossRef]
- Szwarcman, D.; Civitarese, D.; Vellasco, M. Quantum-Inspired Neural Architecture Search. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, L.; Lim, C.P.; Yu, Y. Intelligent human action recognition using an ensemble model of evolving deep networks with swarm-based optimization. Knowl.-Based Syst. 2021, 220, 106918. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Cai, Z.; Yang, J.; Zhou, Z.; Gong, X. Continuous Particle Swarm Optimization-Based Deep Learning Architecture Search for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1082. [Google Scholar] [CrossRef]
- Juang, C.F.; Chang, Y.C.; Chung, I.F. Optimization of recurrent neural networks using evolutionary group-based particle swarm optimization for hexapod robot gait generation. Hybrid Metaheuristics Res. Appl. 2018, 84, 227. [Google Scholar]
- Tan, T.Y.; Zhang, L.; Lim, C.P. Intelligent skin cancer diagnosis using improved particle swarm optimization and deep learning models. Appl. Soft Comput. 2019, 84, 105725. [Google Scholar] [CrossRef]
- Zhang, L.; Lim, C.P. Intelligent optic disc segmentation using improved particle swarm optimization and evolving ensemble models. Appl. Soft Comput. 2020, 92, 106328. [Google Scholar] [CrossRef]
- Tan, T.Y.; Zhang, L.; Lim, C.P. Adaptive melanoma diagnosis using evolving clustering, ensemble and deep neural networks. Knowl.-Based Syst. 2020, 187, 104807. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, L. High-quality face image generation using particle swarm optimization-based generative adversarial networks. Future Gener. Comput. Syst. 2021, 122, 98–104. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef] [Green Version]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Monarch Butterfly Optimization Based Convolutional Neural Network Design. Mathematics 2020, 8, 936. [Google Scholar] [CrossRef]
- Strumberger, I.; Tuba, E.; Bacanin, N.; Beko, M.; Tuba, M. Modified and Hybridized Monarch Butterfly Algorithms for Multi-Objective Optimization. In Hybrid Intelligent Systems; Madureira, A.M., Abraham, A., Gandhi, N., Varela, M.L., Eds.; Springer: Cham, Switzerland, 2020; pp. 449–458. [Google Scholar]
- Bacanin, N.; Tuba, M. Artificial Bee Colony (ABC) Algorithm for Constrained Optimization Improved with Genetic Operators. Stud. Inform. Control 2012, 21, 137–146. [Google Scholar] [CrossRef]
- Yang, X. Firefly Algorithm, Nature Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010. [Google Scholar]
- Chen, D.; Li, X.; Li, S. A Novel Convolutional Neural Network Model Based on Beetle Antennae Search Optimization Algorithm for Computerized Tomography Diagnosis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Chen, H. BSAS: Beetle swarm antennae search algorithm for optimization problems. arXiv 2018, arXiv:1807.10470. [Google Scholar]
- Lee, C.H.; Lai, W.Y.; Lin, Y.C. A TSK-type fuzzy neural network (TFNN) systems for dynamic systems identification. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 4, pp. 4002–4007. [Google Scholar]
- Li, M.; Hsu, W.; Xie, X.; Cong, J.; Gao, W. SACNN: Self-attention convolutional neural network for low-dose CT denoising with self-supervised perceptual loss network. IEEE Trans. Med. Imaging 2020, 39, 2289–2301. [Google Scholar] [CrossRef]
- Tirumala, S.S. Evolving deep neural networks using coevolutionary algorithms with multi-population strategy. Neural Comput. Appl. 2020, 32, 13051–13064. [Google Scholar] [CrossRef]
- Calisto, M.G.B.; Lai-Yuen, S.K. Self-adaptive 2D-3D ensemble of fully convolutional networks for medical image segmentation. In Medical Imaging 2020: Image Processing; Išgum, I., Landman, B.A., Eds.; International Society for Optics and Photonics, SPIE: Washington, DC, USA, 2020; Volume 11313, pp. 459–469. 2020. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Litjens, G.; Toth, R.; van de Ven, W.; Hoeks, C.; Kerkstra, S.; van Ginneken, B.; Vincent, G.; Guillard, G.; Birbeck, N.; Zhang, J.; et al. Evaluation of prostate segmentation algorithms for MRI: The PROMISE12 challenge. Med. Image Anal. 2014, 18, 359–373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ortego, P.; Diez-Olivan, A.; Del Ser, J.; Veiga, F.; Penalva, M.; Sierra, B. Evolutionary LSTM-FCN networks for pattern classification in industrial processes. Swarm Evol. Comput. 2020, 54, 100650. [Google Scholar] [CrossRef]
- Xie, H.; Zhang, L.; Lim, C.P. Evolving CNN-LSTM models for time series prediction using enhanced grey wolf optimizer. IEEE Access 2020, 8, 161519–161541. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In International Conference on Learning Representations; Banff National Park: Banff, AB, Canada, 2014. [Google Scholar]
- Lawrence, T.; Zhang, L.; Lim, C.P.; Phillips, E.J. Particle Swarm Optimization for Automatically Evolving Convolutional Neural Networks for Image Classification. IEEE Access 2021, 9, 14369–14386. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C. The MNIST Database. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 21 November 2021).
- Larochelle, H.; Erhan, D.; Courville, A.; Bergstra, J.; Bengio, Y. An Empirical Evaluation of Deep Architectures on Problems with Many Factors of Variation. In Proceedings of the 24th International Conference on MACHINE Learning, ICML’07, Corvalis, OR, USA, 20–24 June 2007; pp. 473–480. [Google Scholar] [CrossRef]
- Larochelle, H.; Erhan, D.; Courville, A. icml2007data. 2007. Available online: http://www.iro.umontreal.ca/~lisa/icml2007data/ (accessed on 21 November 2021).
- Kinghorn, P.; Zhang, L.; Shao, L. A region-based image caption generator with refined descriptions. Neurocomputing 2018, 272, 416–424. [Google Scholar] [CrossRef] [Green Version]

| Domain | Parameter | Range |
|---|---|---|
| Model | Number of groups | from 1 to |
| Group | Number of residual blocks | from 1 to |
| Group | The number of channels for all blocks in a group | from to |
| Convolution | Kernel size k | from to |
| Pooling | Pooling type | from 0 to 1 |
| Notation | Description |
|---|---|
| The position X of the ith particle in the swarm | |
| The nth group | |
| The mth block | |
| Kernel size for the mth block of the nth group of the ith particle in position X |
| Dataset | Description | Classes | Train/Test Samples |
|---|---|---|---|
| MNIST [3,52] | Handwritten digits | 10 | 60,000/10,000 |
| MNIST-RD [53,54] | Rotated MNIST digits | 10 | 12,000/50,000 |
| MNIST-RB [53,54] | MNIST digits with random background noise | 10 | 12,000/50,000 |
| MNIST-BI [53,54] | MNIST digits with background images | 10 | 12,000/50,000 |
| MNIST-RD+BI [53,54] | Rotated MNIST digits with background images | 10 | 12,000/50,000 |
| Rectangles-I [53,54] | Rectangle border shapes with background images | 2 | 12,000/50,000 |
| Name | Description | Value Used |
|---|---|---|
| Minimum kernel size | 3 | |
| Maximum kernel size | 7 | |
| Minimum number of channels | 16 | |
| Maximum number of channels | 256 | |
| Maximum number of blocks | 15 | |
| Maximum number of groups | 2 | |
| Layer selection boundary threshold | 0.5 | |
| Velocity weighting factor | 0.5 |
| Model | MNIST | MNIST-RD | MNIST-RB | MNIST-BI | MNIST-RD+BI | Rectangles-I |
|---|---|---|---|---|---|---|
| Hand-crafted architectures | ||||||
| LeNet-1 [3] | 1.70% | 19.3% | 7.50% | 9.80% | 40.06% | 16.92% |
| LeNet-4 [3] | 1.10% | 11.79% | 6.18% | 8.96% | 33.83% | 16.09% |
| LeNet-5 [3] | 0.95% | 11.10% | 5.99% | 8.70% | 34.64% | 12.48% |
| Evolutionary algorithms for architecture generation | ||||||
| IPPSO (best) [21] | 1.13% | - | - | - | 33% | - |
| IPPSO (mean) [21] | 1.21% | - | - | - | 34.50% | - |
| MBO-ABCFE (best) [35] | 0.34% | - | - | - | - | - |
| GeNET (best) [16] | 0.34% | - | - | - | - | - |
| DNN-COCA (mean) [43] | 1.30% | - | - | - | - | - |
| psoCNN (best) [15] | 0.32% | 3.58% | 1.79% | 1.90% | 14.28% | 2.22% |
| psoCNN (mean) [15] | 0.44% | 6.42% | 2.53% | 2.40% | 20.98% | 3.94% |
| sosCNN (best) [14] | 0.30% | 3.01% | 1.49% | 1.68% | 10.65% | 1.57% |
| sosCNN (mean) [14] | 0.40% | 3.78% | 1.89% | 1.98% | 13.61% | 2.37% |
| resPsoCnn (best) | 0.31% | 2.67% | 1.70% | 1.74% | 8.76% | 1.19% |
| resPsoCnn (mean) | 0.33% | 3.02% | 1.76% | 1.90% | 9.27% | 1.47% |
| Model | MNIST | MNIST-RD | MNIST-RB | MNIST-BI | MNIST-RD+BI | Rectangles-I |
|---|---|---|---|---|---|---|
| resPsoCnn (best) | 0.31% | 2.67% | 1.70% | 1.74% | 8.76% | 1.19% |
| resPsoCnn (mean) | 0.33% | 3.02% | 1.76% | 1.90% | 9.27% | 1.47% |
| sosCNN (best) [14] | 0.30% | 3.01% | 1.49% | 1.68% | 10.65% | 1.57% |
| sosCNN (mean) [14] | 0.40% | 3.78% | 1.89% | 1.98% | 13.61% | 2.37% |
| error difference (best) | 0.01%(+) | −0.34%(−) | 0.21%(+) | 0.06%(+) | −1.89%(−) | −0.38%(−) |
| error difference (mean) | −0.07%(−) | −0.76%(−) | −0.13%(−) | −0.08%(−) | −4.34%(−) | −0.90%(−) |
| Model | MNIST | MNIST-RD | MNIST-RB | MNIST-BI | MNIST-RD+BI | Rectangles-I |
|---|---|---|---|---|---|---|
| sosCNN (best) [14] | 0.30% | 3.01% | 1.49% | 1.68% | 10.65% | 1.57% |
| sosCNN (mean) [14] | 0.40% | 3.78% | 1.89% | 1.98% | 13.61% | 2.37% |
| resPsoCnn-PB-GB (best) | 0.30% | 2.84% | 1.51% | 1.79% | 9.20% | 0.89% |
| resPsoCnn-PB-GB (mean) | 0.40% | 3.23% | 1.76% | 2.02% | 9.74% | 1.66% |
| resPsoCnn (best) | 0.31%(+) | 2.67%(−) | 1.70%(+) | 1.74%(+) | 8.76%(−) | 1.19%(+) |
| resPsoCnn (mean) | 0.33%(−) | 3.02%(−) | 1.76%(−) | 1.90%(−) | 9.27%(−) | 1.47%(−) |
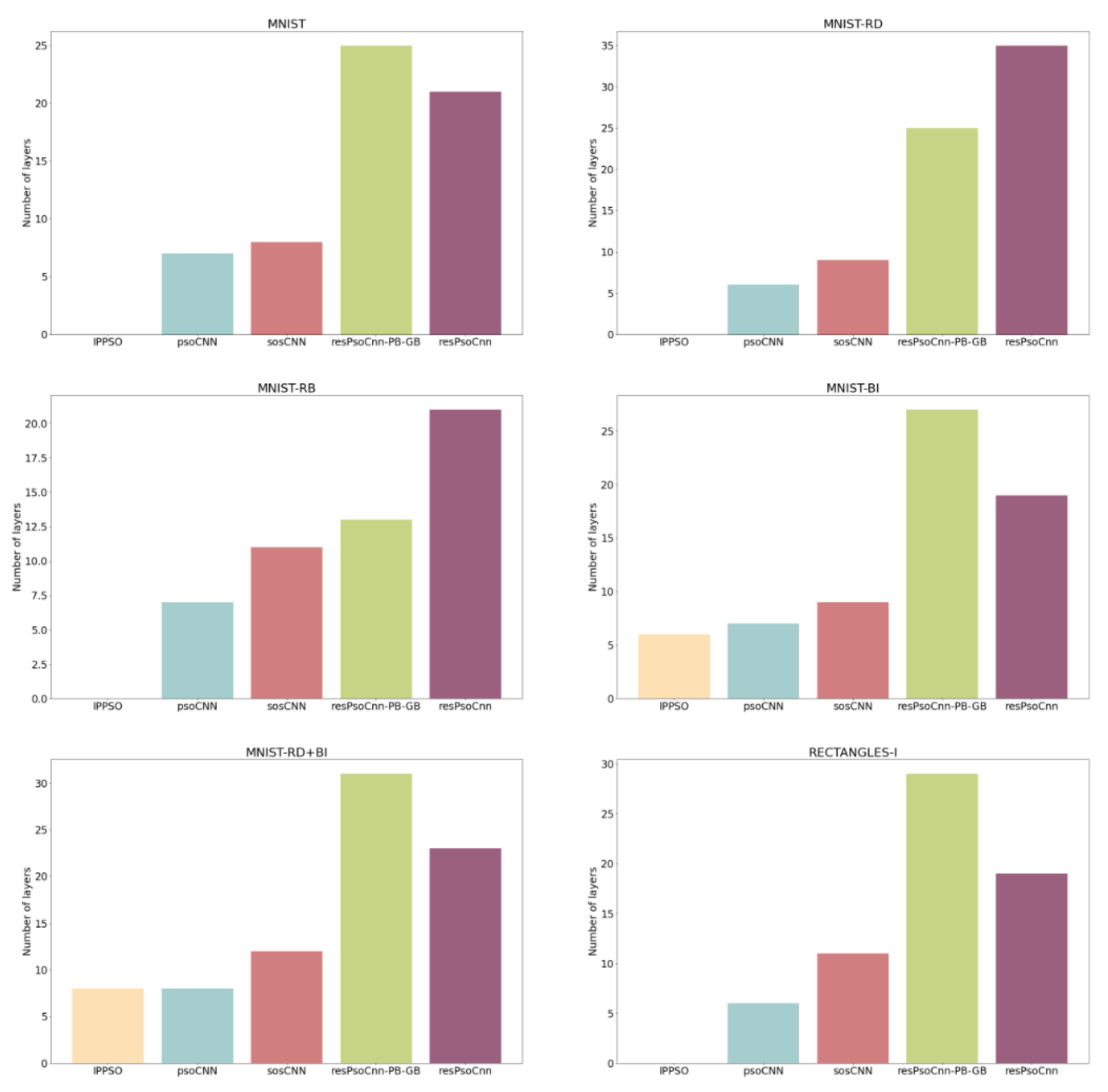
| Dataset | Structure |
|---|---|
| MNIST [3,52] | TB( ) + RB(177 × 4 × 4) + RB(177 × 4 × 4) + RB(177 × 6 × 6) + AveragePool + TB( ) + RB(175 × 6 × 6) + RB(175 × 6 × 6) + RB(175 × 5 × 5) + RB(175 × 3 × 3) + AveragePool + FC |
| MNIST-RD [53,54] | TB( ) + RB(161 × 5 × 5) + RB(161 × 7 × 7) + RB(161 × 6 × 6) + RB(161 × 6 × 6) + RB(161 × 4 × 4) + RB(161 × 5 × 5) + RB(161 × 7 × 7) + TB( ) + RB(115 × 5 × 5) + RB(115 × 7 × 7) + RB(115 × 5 × 5) + RB(115 × 6 × 6) + RB(115 × 3 × 3) + RB(115 × 7 × 7) + RB(115 × 4 × 4) + AveragePool + FC |
| MNIST-RB [53,54] | TB( ) + RB(153 × 4 × 4) + RB(153 × 6 × 6) + + RB(153 × 4 × 4) + RB(153 × 3 × 3) AveragePool + TB( ) + RB(183 × 4 × 4) + RB(183 × 6 × 6) + RB(183 × 7 × 7) + AveragePool + FC |
| MNIST-BI [53,54] | TB( ) + RB(136 × 4 × 4) + RB(136 × 3 × 3) + RB(136 × 5 × 5) + RB(136 × 3 × 3) + AveragePool + TB( ) + RB(136 × 6 × 6) + RB(136 × 5 × 5) + RB(136 × 5 × 5) + RB(136 × 3 × 3) + RB(136 × 3 × 3) + RB(136 × 3 × 3) + AveragePool + FC |
| MNIST-RD+BI [53,54] | TB( ) + RB(231 × 5 × 5) + RB(231 × 5 × 5) + RB(231 × 7 × 7) + RB(231 × 3 × 3) + AveragePool + TB( ) + RB(120 × 4 × 4) + RB(120 × 6 × 6) + RB(120 × 6 × 6) + RB(120 × 5 × 5) + AveragePool + FC |
| RECTANGLES-I [53,54] | TB( ) + RB(195 × 3 × 3) + RB(195 × 6 × 6) + RB(195 × 3 × 3) + AveragePool + TB( ) + RB(85 × 7 × 7) + RB(85 × 5 × 5) + RB(85 × 3 × 3) + AveragePool + FC |
| Dataset | Structure |
|---|---|
| MNIST [3,52] | TB( ) + RB(176 × 4 × 4) + RB(176 × 5 × 5) + RB(176 × 5 × 5) + RB(176 × 4 × 4) + RB(176 × 5 × 5) + RB(176 × 3 × 3) + AveragePool + TB( ) + RB(198 × 5 × 5) + RB(198 × 6 × 6) + RB(198 × 4 × 4) + RB(198 × 4 × 4) + AveragePool + FC |
| MNIST-RD [53,54] | TB( ) + RB(184 × 4 × 4) + RB(184 × 4 × 4) + RB(184 × 5 × 5) + RB(184 × 4 × 4) + RB(184 × 3 × 3) + RB(184 × 3 × 3) + AveragePool + TB( ) + RB(146 × 4 × 4) + RB(146 × 4 × 4) + RB(146 × 5 × 5) + RB(146 × 3 × 3) + AveragePool + FC |
| MNIST-RB [53,54] | TB( ) + RB(216 × 5 × 5) + RB(216 × 6 × 6) + AveragePool + TB( ) + RB(158 × 7 × 7) + RB(158 × 4 × 4) + Ma × Pool + FC |
| MNIST-BI [53,54] | TB( ) + RB(188 × 4 × 4) + RB(188 × 5 × 5) + RB(188 × 5 × 5) + RB(188 × 4 × 4) + RB(188 × 4 × 4) + RB(188 × 3 × 3) + RB(188 × 3 × 3) + AveragePool + TB( ) + RB(177 × 5 × 5) + RB(177 × 3 × 3) + RB(177 × 3 × 3) + RB(177 × 3 × 3) + Ma × Pool + FC |
| MNIST-RD+BI [53,54] | TB( ) + RB(231 × 4 × 4) + RB(231 × 5 × 5) + RB(231 × 5 × 5) + RB(231 × 4 × 4) + RB(231 × 3 × 3) + RB(231 × 4 × 4) + AveragePool + TB( ) + RB(120 × 5 × 5) + RB(120 × 5 × 5) + RB(120 × 3 × 3) + RB(120 × 4 × 4) + RB(120 × 4 × 4) + RB(120 × 3 × 3) + RB(120 × 3 × 3) + AveragePool + FC |
| RECTANGLES-I [53,54] | TB( ) + RB(71 × 4 × 4) + RB(71 × 3 × 3) + RB(71 × 7 × 7) + RB(71 × 6 × 6) + RB(71 × 6 × 6) + RB(71 × 6 × 6) + TB( ) + RB(21 × 5 × 5) + RB(21 × 4 × 4) + RB(21 × 6 × 6) + RB(21 × 6 × 6) + RB(21 × 7 × 7) + RB(21 × 4 × 4) + FC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawrence, T.; Zhang, L.; Rogage, K.; Lim, C.P. Evolving Deep Architecture Generation with Residual Connections for Image Classification Using Particle Swarm Optimization. Sensors 2021, 21, 7936. https://doi.org/10.3390/s21237936
Lawrence T, Zhang L, Rogage K, Lim CP. Evolving Deep Architecture Generation with Residual Connections for Image Classification Using Particle Swarm Optimization. Sensors. 2021; 21(23):7936. https://doi.org/10.3390/s21237936
Chicago/Turabian StyleLawrence, Tom, Li Zhang, Kay Rogage, and Chee Peng Lim. 2021. "Evolving Deep Architecture Generation with Residual Connections for Image Classification Using Particle Swarm Optimization" Sensors 21, no. 23: 7936. https://doi.org/10.3390/s21237936
APA StyleLawrence, T., Zhang, L., Rogage, K., & Lim, C. P. (2021). Evolving Deep Architecture Generation with Residual Connections for Image Classification Using Particle Swarm Optimization. Sensors, 21(23), 7936. https://doi.org/10.3390/s21237936







