Hybrid FSK-PSK Waveform Optimization for Radar Based on Alternating Direction Method of Multiplier (ADMM)
Abstract
:1. Introduction
- (1)
- The low sidelobe waveform (LSW) optimization algorithm based on ADMM, i.e., LSW-ADMM, is proposed. Distinctive phase encoding sequences are used for different sub-pulses, which are optimized with the LSW-ADMM algorithm for sidelobe reduction. Compared with the conventional FSK-PSK signals modulated by the classical code sequences, a higher-order of randomness is achieved, which guarantees enhanced anti-jamming capability of the radar system.
- (2)
- To encounter the intra-pulse slice repeater jamming, the ASRJ-ADMM algorithm is proposed. Each sub-pulse of the FSK-PSK signal, which is coded with a distinctive set of phases, performs frequency hopping according to the optimized sequence. By ensuring the orthogonality of the sub-pulses of the FSK-PSK signal, the intra-pulse slice repeater jamming is effectively suppressed.
2. FSK-PSK Hybrid Modulated Signal Model
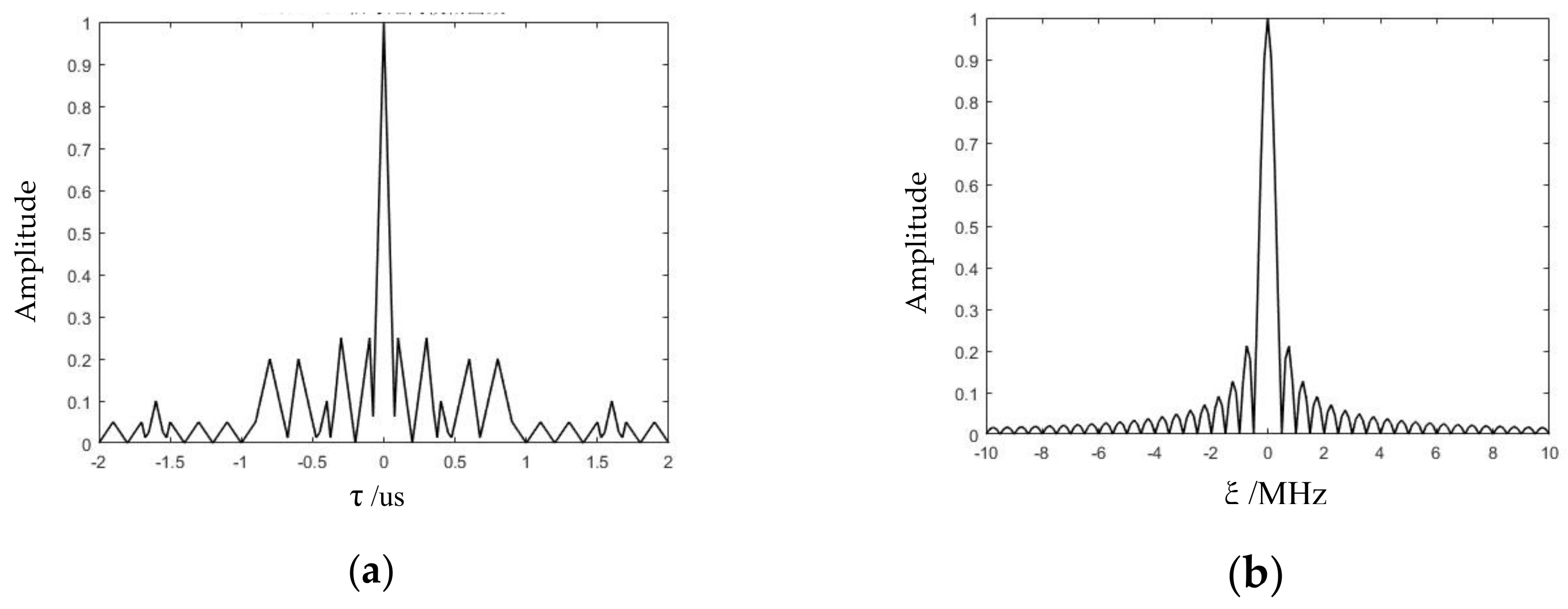
2.1. Ambiguity Function of the FSK-PSK Hybrid Modulated Signal
2.2. Autocorrelation Function of FSK-PSK Hybrid Modulated Signal
3. Low Sidelobe Waveform Optimization Algorithm Based on ADMM (LSW-ADMM)
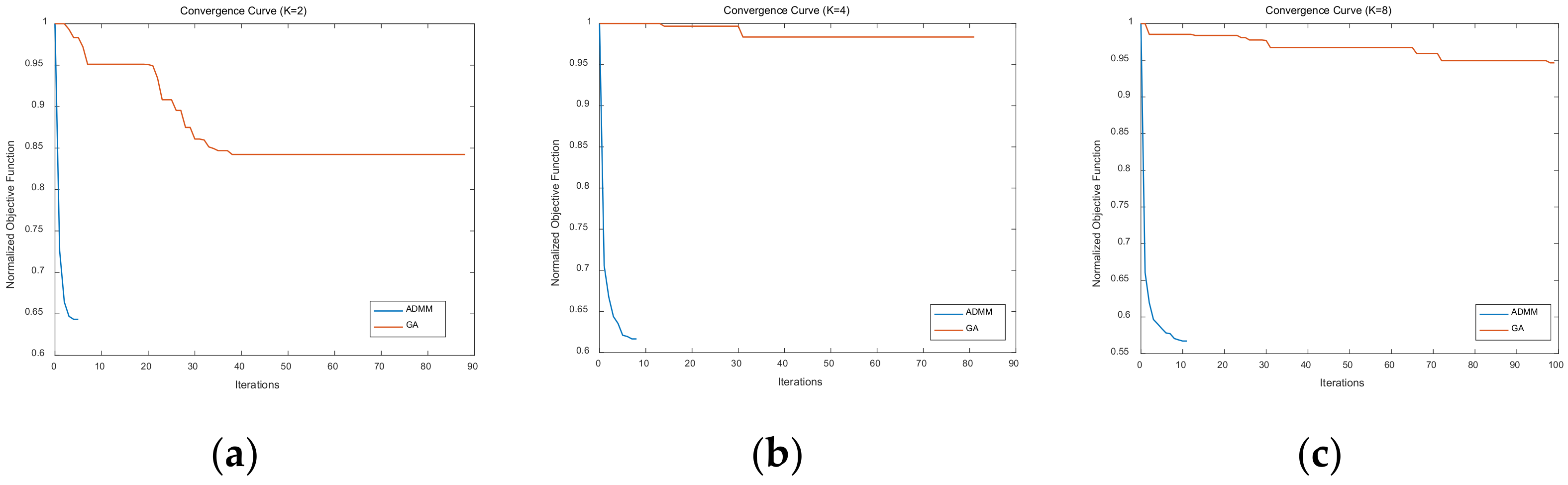
3.1. ADMM Algorithm
3.2. LSW-ADMM Optimization Method
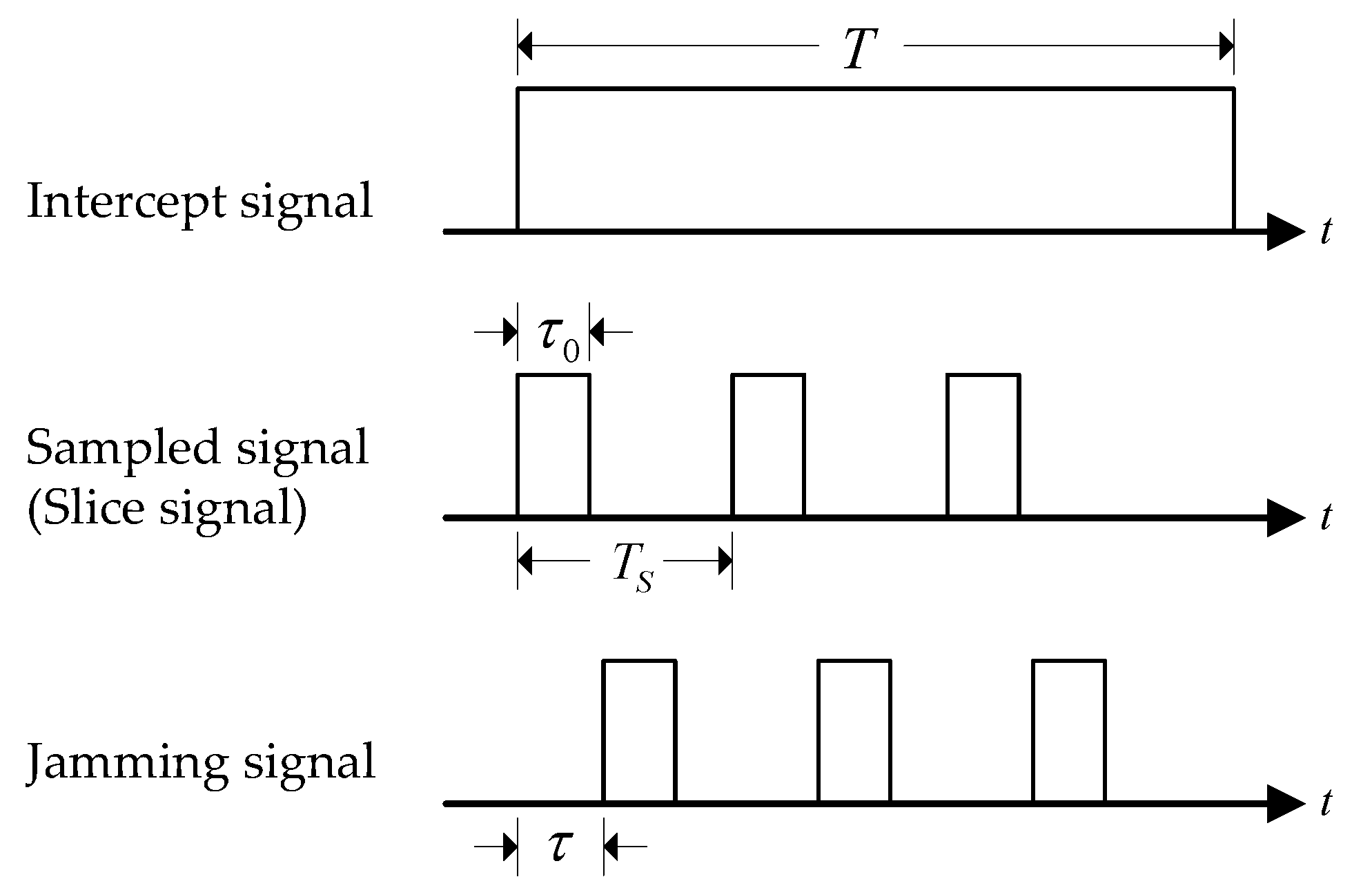
4. Anti-Slice-Repeater-Jamming Algorithm Based on ADMM (ASRJ-ADMM)
4.1. Intra-Pulse Slice Repeater Model
4.2. Intra-Pulse Slice Repeater Jamming Suppression Model
4.3. ASRJ-ADMM Optimization Method
5. Computational Complexity Analysis
6. Numerical Experiments
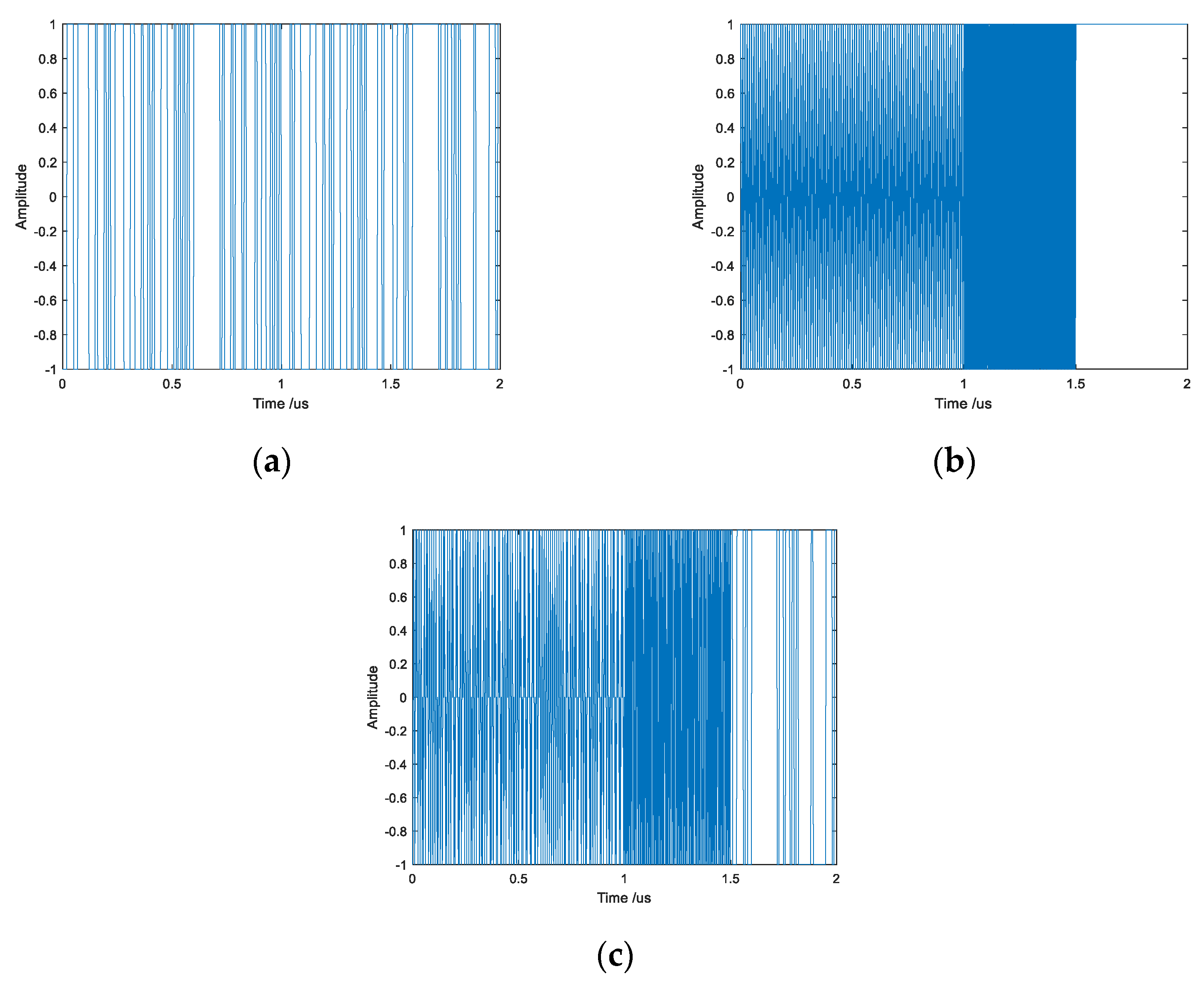
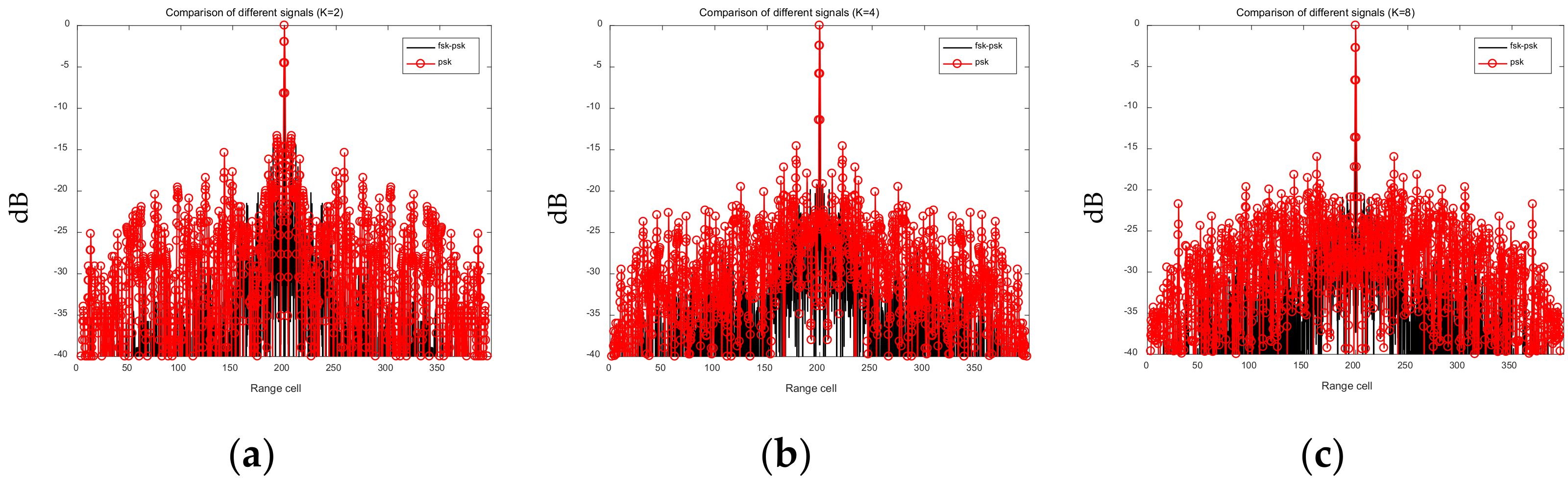
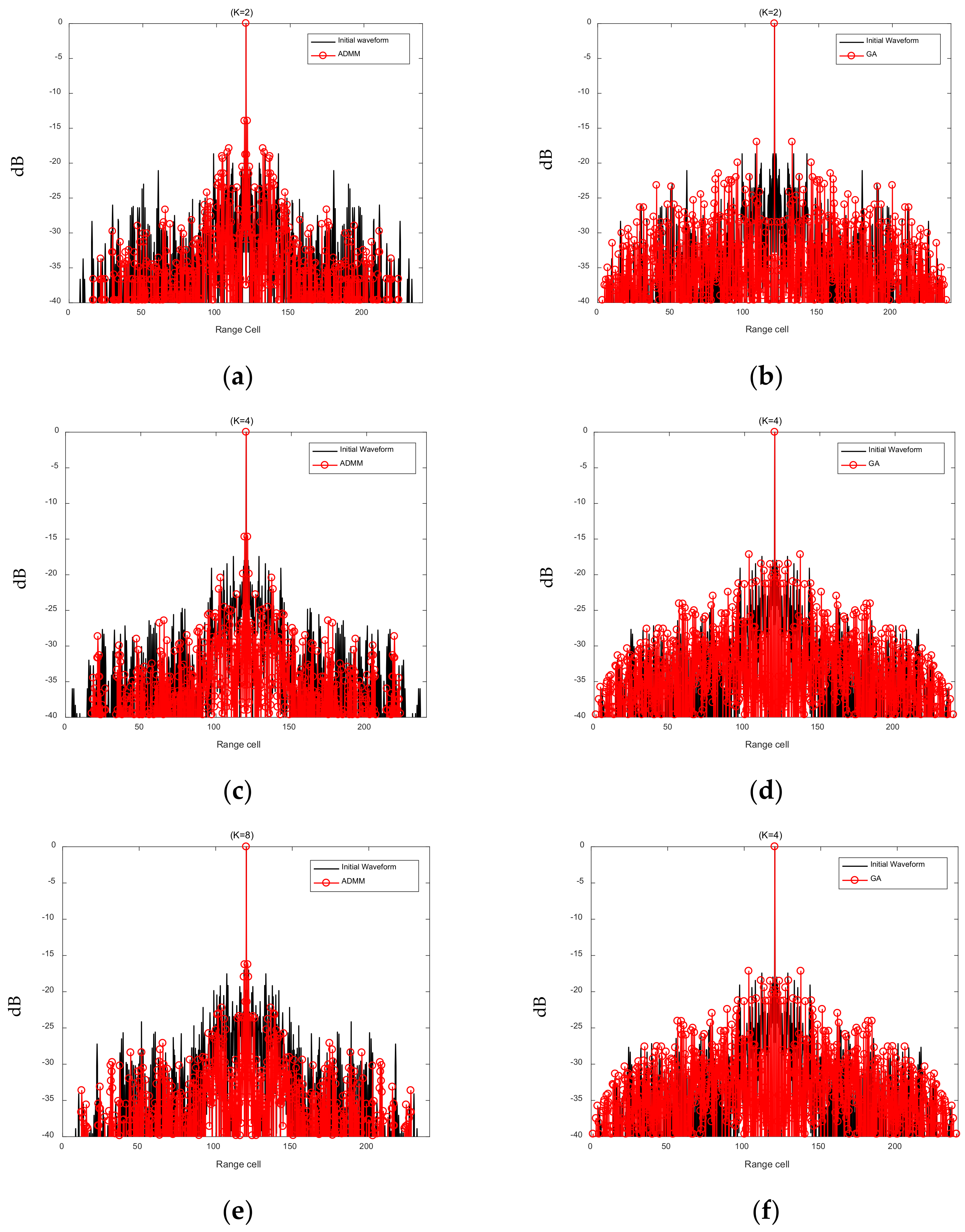
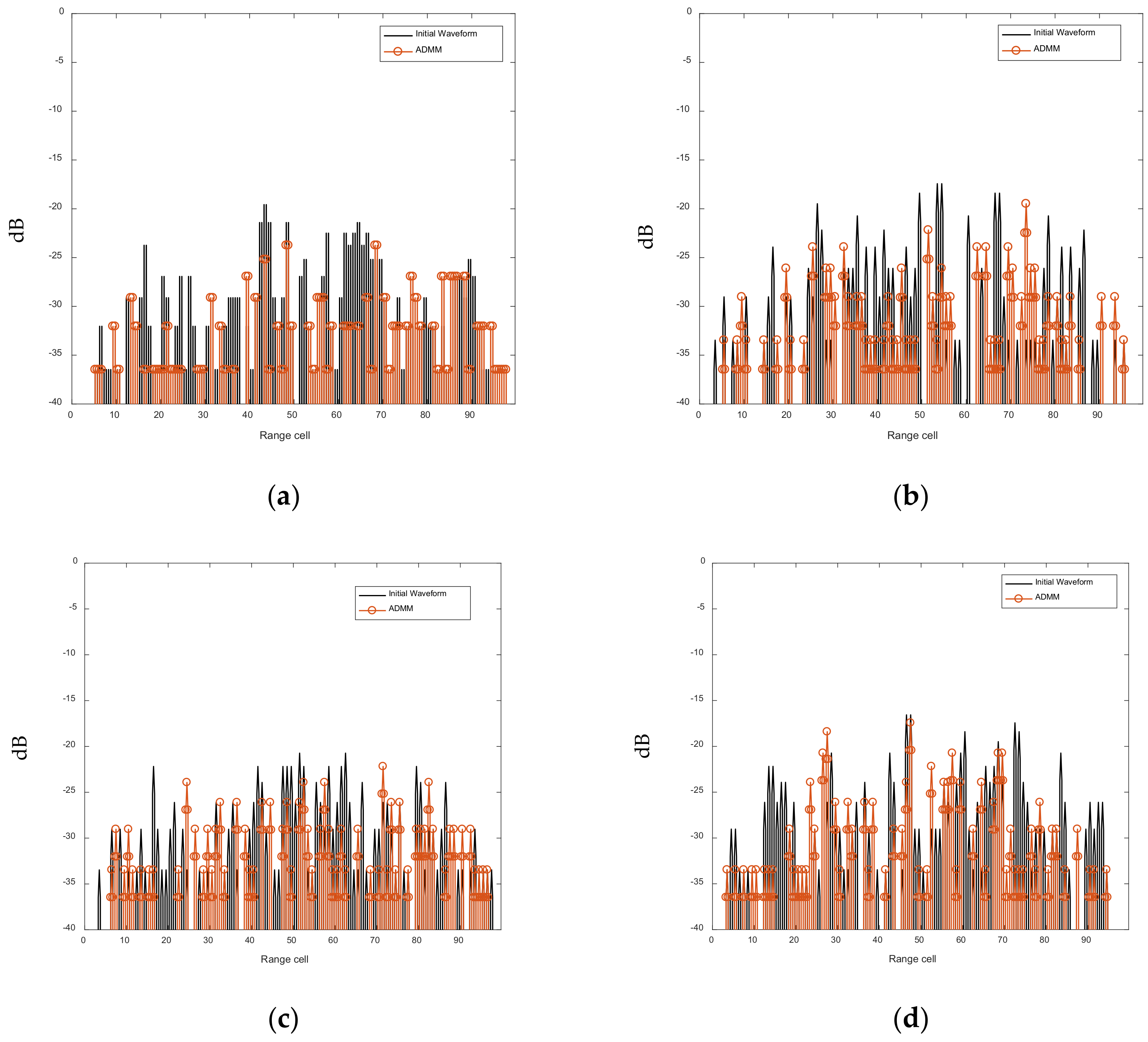
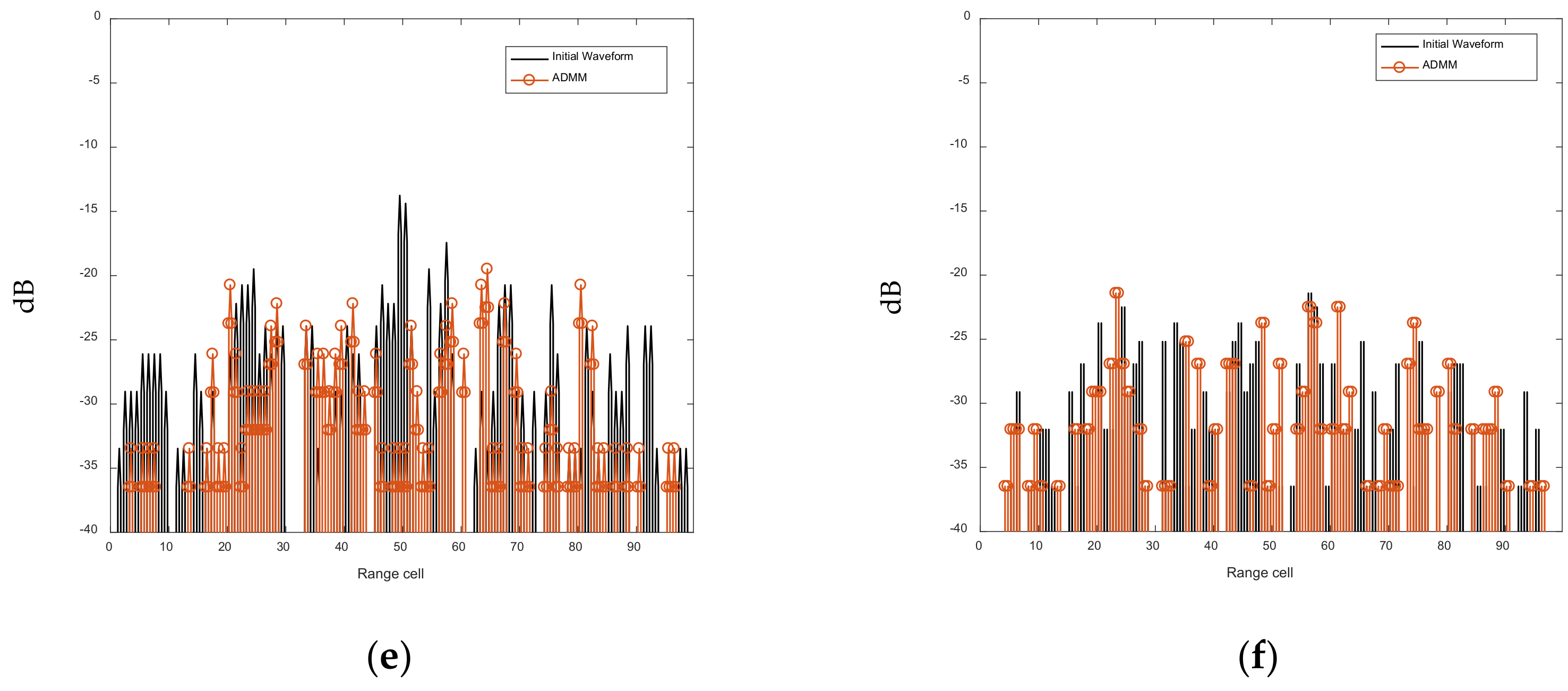
6.1. Optimization of the AF of the FSK-PSK Signal
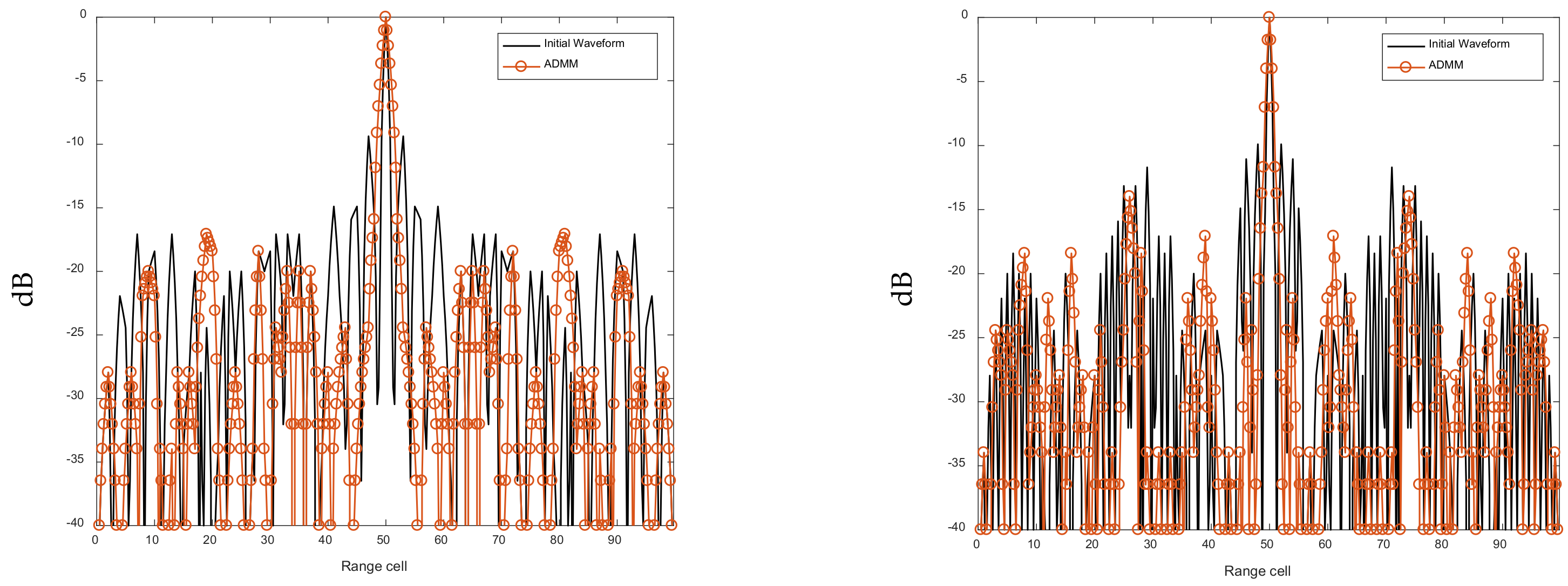
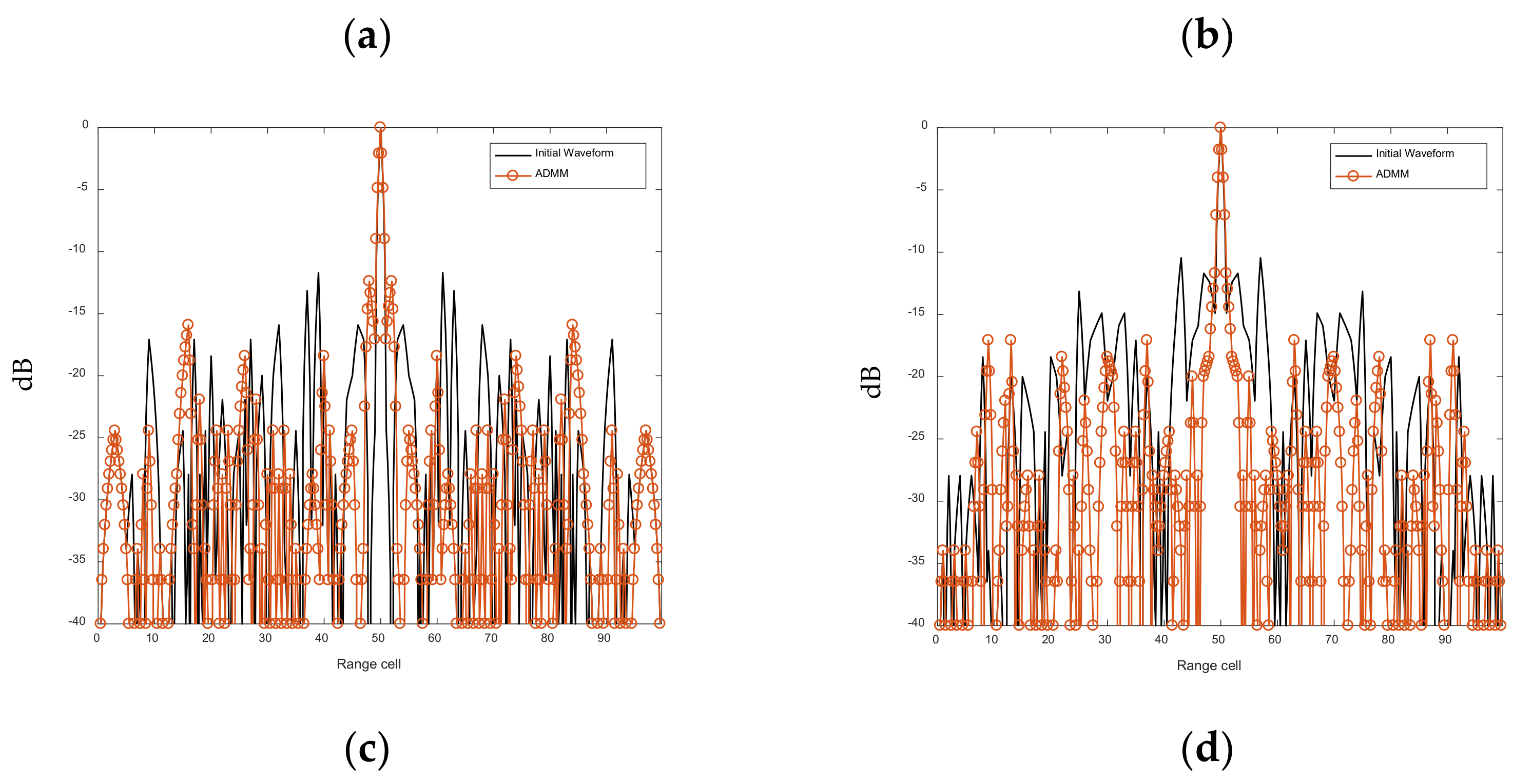
6.2. Joint Optimization of Intra-Pulse Sub-Pulse Correlation Function
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karbasi, S.M.; Radmard, M.; Nayebi, M.M.; Bastani, M.H. Design of multiple-input multiple-output transmit waveform and receive filter for extended target detection. IET Radar Sonar Navig. 2015, 9, 1345–1353. [Google Scholar] [CrossRef]
- Abergel, R.; Denis, L.; Ladjal, S.; Tupin, F. Subpixellic Methods for Sidelobes Suppression and Strong Targets Extraction in Single Look Complex SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 759–776. [Google Scholar] [CrossRef] [Green Version]
- Galati, G.; Pavan, G.; de Palo, F. Noise radar technology: Pseudorandom waveforms and their information rate. In Proceedings of the 2014 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Meikle, H. Modern Radar System, 2nd ed.; Artech House Inc.: Boston, MA, USA; London, UK, 2008; ISBN 13:978-1-59693-242-5. [Google Scholar]
- Cao, S.; Zheng, K.; Meng, X.; Pan, C.; He, Z. Detection performance analysis on a new multi-cycle FSK/PSK signal. In Proceedings of the 2012 International Conference on Computational Problem-Solving (ICCP), Leshan, China, 19–21 October 2012; pp. 55–58. [Google Scholar] [CrossRef]
- Jing, Y.; Liang, J.; Tang, B.; Li, J. Designing Unimodular Sequence With Low Peak of Sidelobe Level of Local Ambiguity Function. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1393–1406. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, H.; Leung, H.; Moo, P.W. Unimodular Waveform Design with Desired Ambiguity Function for Cognitive Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2489–2496. [Google Scholar] [CrossRef]
- Wu, Z.-J.; Zhou, Z.-Q.; Wang, C.-X.; Li, Y.-C.; Zhao, Z.-F. Doppler Resilient Complementary Waveform Design for Active Sensing. IEEE Sens. J. 2020, 20, 9963–9976. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Yang, J.; Kong, L. Finite Alphabet Unimodular Sequence Design with Low WISL via an Inexact ADPM Framework. In Proceedings of the Radar Conference (RadarConf20) 2020 IEEE, Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Jing, Y.; Liang, J.; Vorobyov, S.A.; Fan, X.; Zhou, D. Joint Design of Radar Transmit Waveform and Mismatched Filter with Low Sidelobes. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 1936–1940. [Google Scholar] [CrossRef]
- Neuberger, N.; Vehmas, R. A Costas-Based Waveform for Local Range-Doppler Sidelobe Level Reduction. IEEE Signal Process. Lett. 2021, 28, 673–677. [Google Scholar] [CrossRef]
- Najafabadi, H.E.; Leung, H.; Moo, P.W. Designing Sequences with Minimized Mean Sidelobe Level for Cognitive Radars. IEEE Access 2021, 9, 101643–101654. [Google Scholar] [CrossRef]
- Hague, D.A. Adaptive Transmit Waveform Design Using Multitone Sinusoidal Frequency Modulation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1274–1287. [Google Scholar] [CrossRef]
- Alhujaili, K.; Monga, V.; Rangaswamy, M. Quartic Gradient Descent for Tractable Radar Slow-Time Ambiguity Function Shaping. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1474–1489. [Google Scholar] [CrossRef]
- Fan, T.; Kong, Y.; Wang, M.; Yu, X.; Cui, G.; Zhang, L. Doppler Filter Bank Design for Non-Uniform PRI Radar in Signal-Dependent Clutter. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Alhujaili, K.; Yu, X.; Cui, G.; Monga, V. Spectrally Compatible MIMO Radar Beampattern Design under Constant Modulus Constraints. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4749–4766. [Google Scholar] [CrossRef]
- Raei, E.; Alaee-Kerahroodi, M.; Bhavani Shankar, M.R. ADMM Based Transmit Waveform and Receive Filter Design in Cognitive Radar Systems. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, W.; Naghsh, M.M.; Lin, R.; Li, J. Doppler Sensitive Discrete-Phase Sequence Set Design for MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4209–4223. [Google Scholar] [CrossRef]
- Arriaga-Trejo, A. Design of Constant Modulus Sequences with Doppler Shift Tolerance and Good Complete Second Order Statistics. In Proceedings of the Radar Conference (RADAR) 2020 IEEE International, Washington, DC, USA, 28–30 April 2020; pp. 274–279. [Google Scholar] [CrossRef]
- Huang, W.; Lin, R. Efficient Design of Doppler Sensitive Long Discrete-Phase Periodic Sequence Sets for Automotive Radars. In Proceedings of the 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wei, X.; Yuan, W.; Zhu, X. Research on suppression of slicing jamming with digital array radar. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1580–1584. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, Z.; Dai, Y.; Li, X. Anti-intermittent sampling repeater jamming method based on convex optimization techniques. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, K.; Li, D.; Quan, S.; Liu, T.; Su, Y.; He, F. SAR Waveform and Mismatched Filter Design for Countering Interrupted-Sampling Repeater Jamming. IEEE Trans. Geosci. Remote. Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, T.; Li, S.; Yuan, T.; Wang, F. SAR Anti-Jamming Technique Using Orthogonal LFM-PC Hybrid Modulated Signal. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhong, S.; Huang, X.; Wang, H.; Xiong, X. Anti-Intermittent Sampling Repeater Jamming Waveform Design based on Immune Genetics. In Proceedings of the 2019 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 12–14 July 2019; pp. 553–559. [Google Scholar] [CrossRef]
- Hanbali, S.B.S. Technique to Counter Improved Active Echo Cancellation Based on ISRJ With Frequency Shifting. IEEE Sens. J. 2019, 19, 9194–9199. [Google Scholar] [CrossRef]
- Zhou, K.; Li, D.; Su, Y.; Liu, T. Joint Design of Transmit Waveform and Mismatch Filter in the Presence of Interrupted Sampling Repeater Jamming. IEEE Signal Process. Lett. 2020, 27, 1610–1614. [Google Scholar] [CrossRef]
- Skinner, B.J.; Donohoe, J.P.; Ingels, F.M. Correlation properties of Gaussian FSK/PSK radar signals. In Proceedings of the Southeastcon’93, Charlotte, NC, USA, 4–7 April 1993. [Google Scholar] [CrossRef]
- Donohoe, J.P.; Ingels, F.M. The ambiguity properties of FSK/PSK signals. In Proceedings of the IEEE International Conference on Radar, Arlington, VA, USA, 7–10 May 1990; pp. 268–273. [Google Scholar] [CrossRef]
- LeMieux, J.A.; Ingels, F.M. Analysis of FSK/PSK modulated radar signals using Costas arrays and complementary Welti codes. In Proceedings of the IEEE International Conference on Radar, Arlington, VA, USA, 7–10 May 1990; pp. 589–594. [Google Scholar] [CrossRef]
- Wong, K.T.; Chung, W.K. Pulse-diverse radar/sonar FSK-PSK waveform design to emphasize/deemphasize designated Doppler-delay sectors. In Proceedings of the Record of the IEEE 2000 International Radar Conference, Alexandria, VA, USA, 12 May 2000; pp. 745–749. [Google Scholar] [CrossRef]
- Chung, W.K.; Wong, K.T. Pulse-diverse radar waveform design for accurate joint estimation of time delay and Doppler shift. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; pp. 3037–3040. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, C. Interrupted Sampling Repeater Jamming Suppression Method based on Hybrid Modulated Radar Signal. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A.; Owczarek, R. An application of iterated function system attractor for specific radar source identification. In Proceedings of the MIKON 2008—17th International Conference on Microwaves, Radar and Wireless Communications, Wroclaw, Poland, 19–21 May 2008. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Cheng, Z.; Liao, B.; He, Z.; Li, J.; Han, C. A Nonlinear-ADMM Method for Designing MIMO Radar Constant Modulus Waveform With Low Correlation Sidelobes. Signal Process. 2019, 159, 93–103. [Google Scholar] [CrossRef]
- Cheng, Z.; Liao, B.; Shi, S.; He, Z.; Li, J. Co-Design for Overlaid MIMO Radar and Downlink MISO Communication Systems via Cramér–Rao Bound Minimization. IEEE Trans. Signal Process. 2019, 67, 6227–6240. [Google Scholar] [CrossRef]
- Tang, B.; Li, J.; Liang, J. Alternating Direction Method of Multipliers for Radar Waveform Design in Spectrally Crowded Environments. Signal Process. 2018, 142, 398–402. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J. Constant Modulus Probing Waveform Design for Mimo Radar via Admm Algorithm. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3305–3309. [Google Scholar] [CrossRef]
- Eisen, M.; Mokhtari, A.; Ribeiro, A. Decentralized Quasi-Newton Methods. IEEE Trans. Signal Process. 2017, 65, 2613–2628. [Google Scholar] [CrossRef]
- Li, J.; Luo, X.; Duan, X.; Wang, W.; Ou, J. A Novel Radar Waveform Design for Anti-Interrupted Sampling Repeater Jamming via Time-Frequency Random Coded Method. Prog. Electromagn. Res. M 2020, 98, 89–99. [Google Scholar] [CrossRef]
- Ge, M.; Yu, X.; Yan, Z.; Cui, G.; Kong, L. Joint cognitive optimization of transmit waveform and receive filter against deceptive interference. Signal Process. 2021, 185. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Zou, J.; Chen, Z. Interrupted-Sampling Repeater Jamming Suppression Based on Stacked Bidirectional Gated Recurrent Unit Network and Infinite Training. IEEE Access 2019, 7, 107428–107437. [Google Scholar] [CrossRef]



| LSW-ADMM |
|---|
|
|
|
|
|
|
| ASRJ-ADMM |
|---|
|
|
|
|
|
|
| K = 2 | K = 4 | K = 8 | |
|---|---|---|---|
| FSK-PSK signal | −36.3435 | −35.4542 | −35.2794 |
| PSK signal | −28.8652 | −29.2404 | −29.0089 |
| K = 2 | K = 4 | K = 8 | |
|---|---|---|---|
| Not optimized | −36.3435 | −35.4542 | −35.2794 |
| LSW-ADMM | −39.8323 | −39.2367 | −40.2767 |
| GA | −36.9693 | −35.7298 | −35.8229 |
| Discrete Phase | K = 2 AC-ASL CC-AL | K = 4 AC-ASL CC-AL | K = 8 AC-ASL CC-AL |
|---|---|---|---|
| Not optimized | −23.4898 −34.3268 | −23.5395 −33.2408 | −23.0620 −32.9777 |
| LSW-ADMM | −27.6087 −37.5398 | −26.8966 −37.0582 | −28.5616 −37.6952 |
| LSW-ADMM | 589 s | 647 s | 790 s |
| ASRJ-ADMM | 623 s | 765 s | 810 s |
| GA | 2305 s | 2465 s | 2725 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Z.; Zhao, J.; Geng, Z.; Zhu, X.; Zhang, J. Hybrid FSK-PSK Waveform Optimization for Radar Based on Alternating Direction Method of Multiplier (ADMM). Sensors 2021, 21, 7915. https://doi.org/10.3390/s21237915
Fei Z, Zhao J, Geng Z, Zhu X, Zhang J. Hybrid FSK-PSK Waveform Optimization for Radar Based on Alternating Direction Method of Multiplier (ADMM). Sensors. 2021; 21(23):7915. https://doi.org/10.3390/s21237915
Chicago/Turabian StyleFei, Zhiting, Jiachen Zhao, Zhe Geng, Xiaohua Zhu, and Jindong Zhang. 2021. "Hybrid FSK-PSK Waveform Optimization for Radar Based on Alternating Direction Method of Multiplier (ADMM)" Sensors 21, no. 23: 7915. https://doi.org/10.3390/s21237915
APA StyleFei, Z., Zhao, J., Geng, Z., Zhu, X., & Zhang, J. (2021). Hybrid FSK-PSK Waveform Optimization for Radar Based on Alternating Direction Method of Multiplier (ADMM). Sensors, 21(23), 7915. https://doi.org/10.3390/s21237915







