Study of Intra-Chamber Processes in Solid Rocket Motors by Fiber Optic Sensors
Abstract
:1. Introduction
2. Theory
3. Experiment
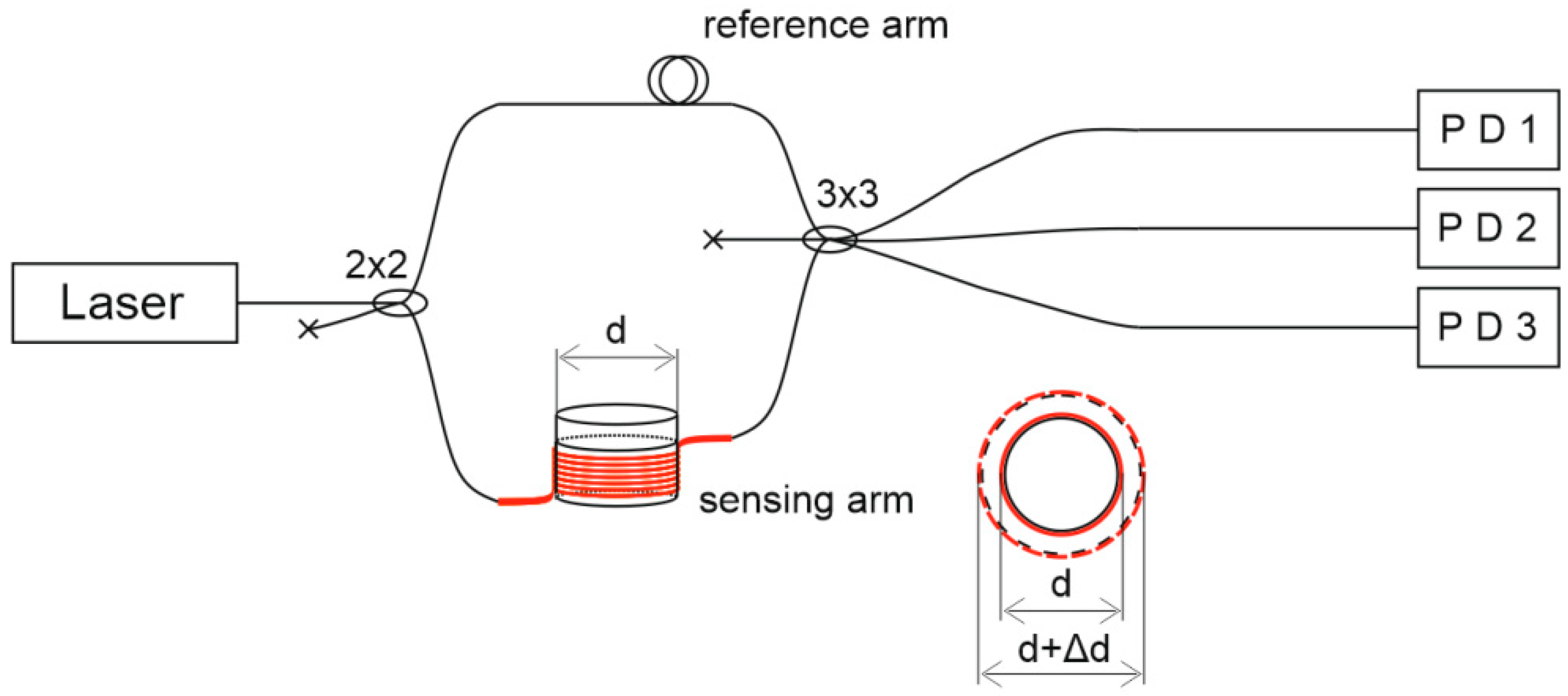
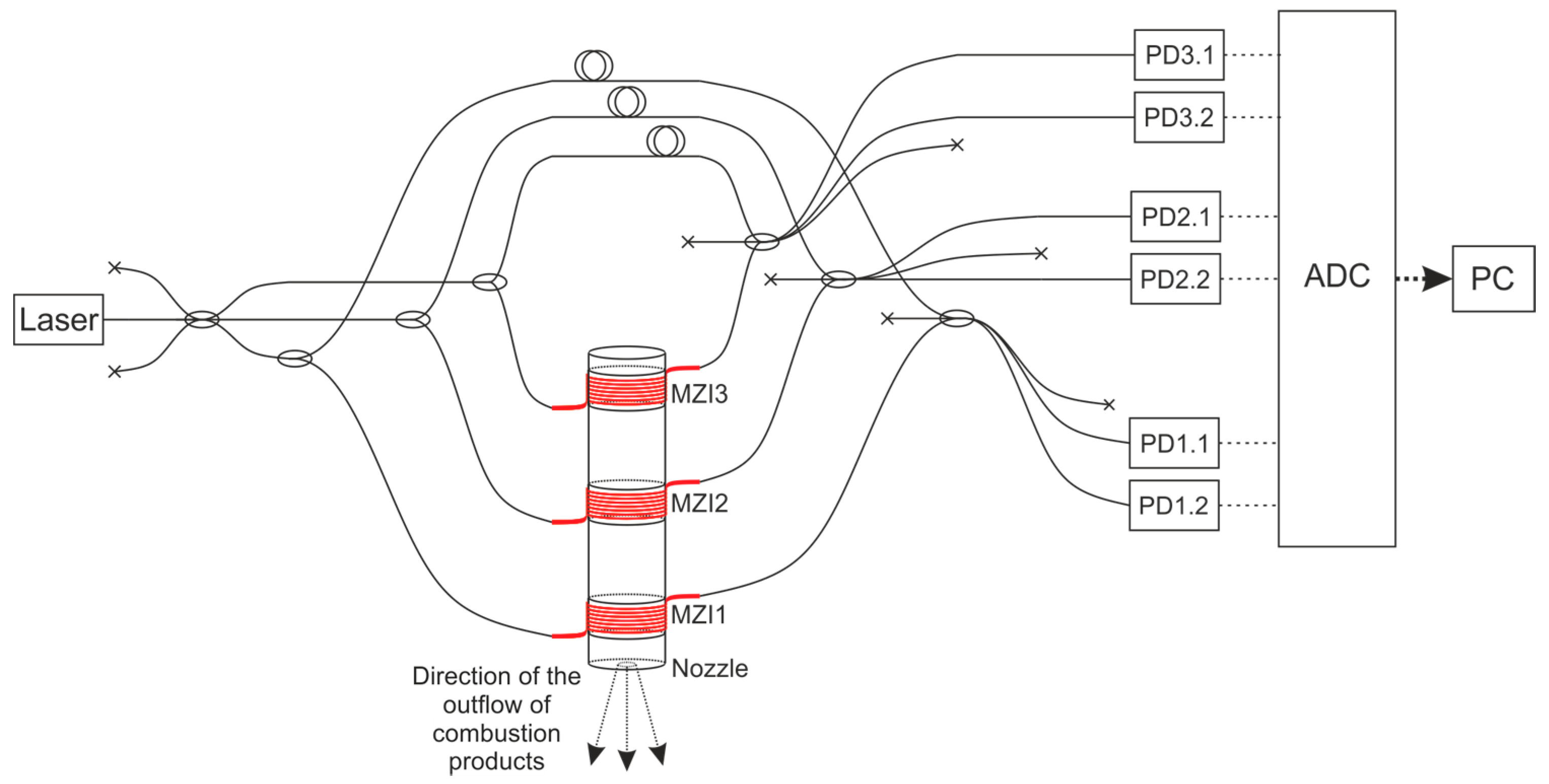
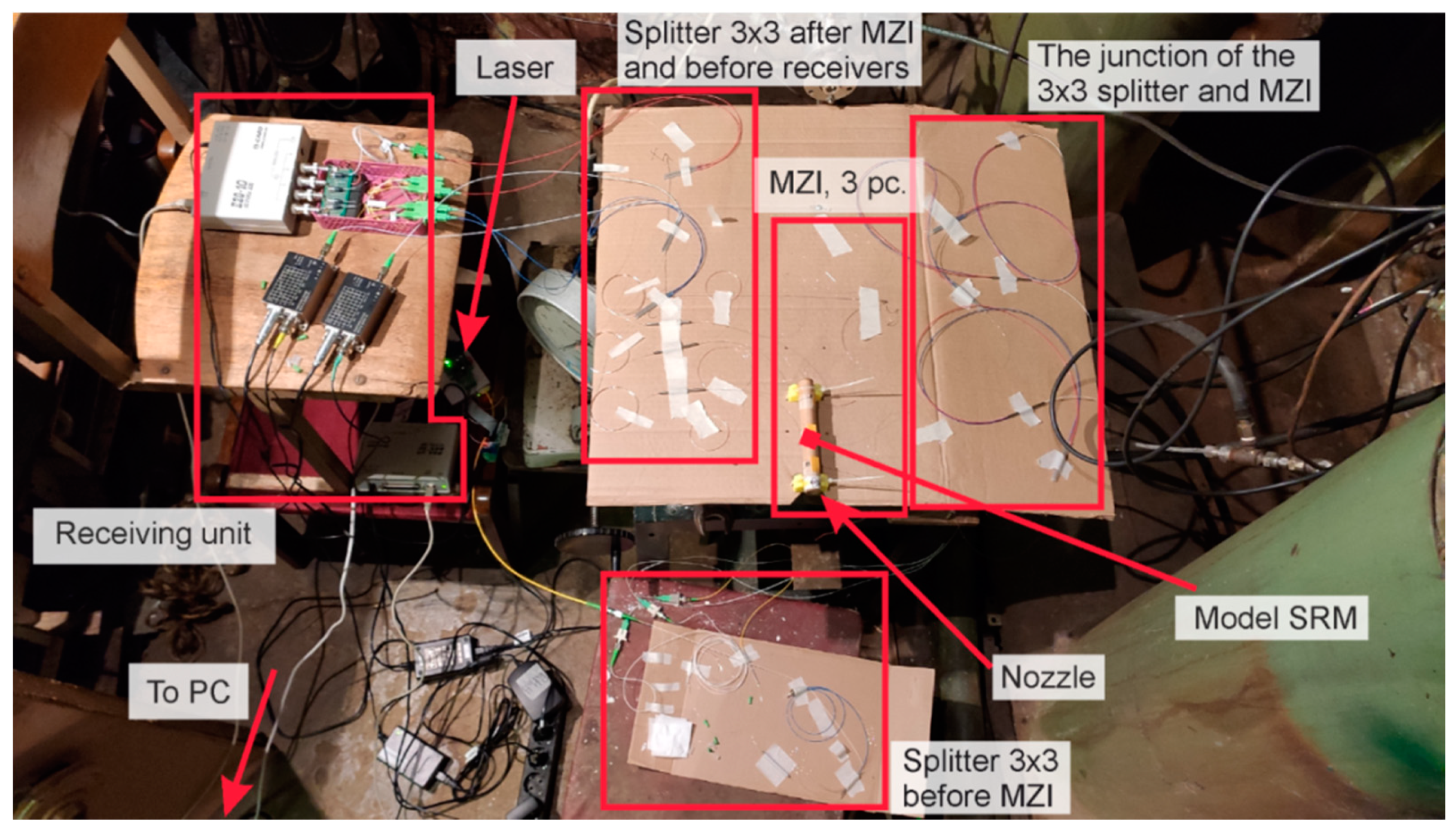
3.1. Description of the Experimental Setup and Methods for Recording the Characteristics of Intra-Chamber Processes
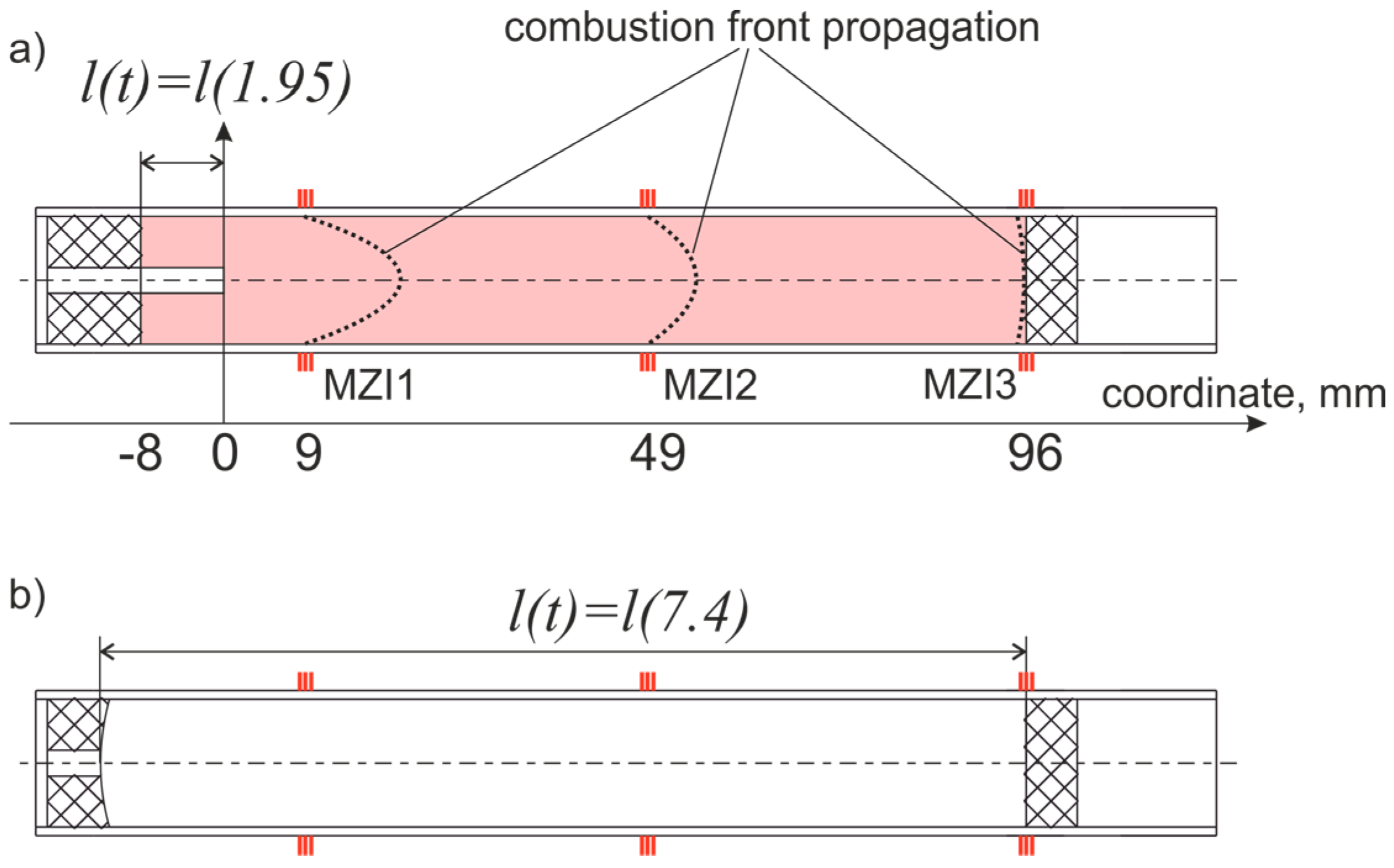
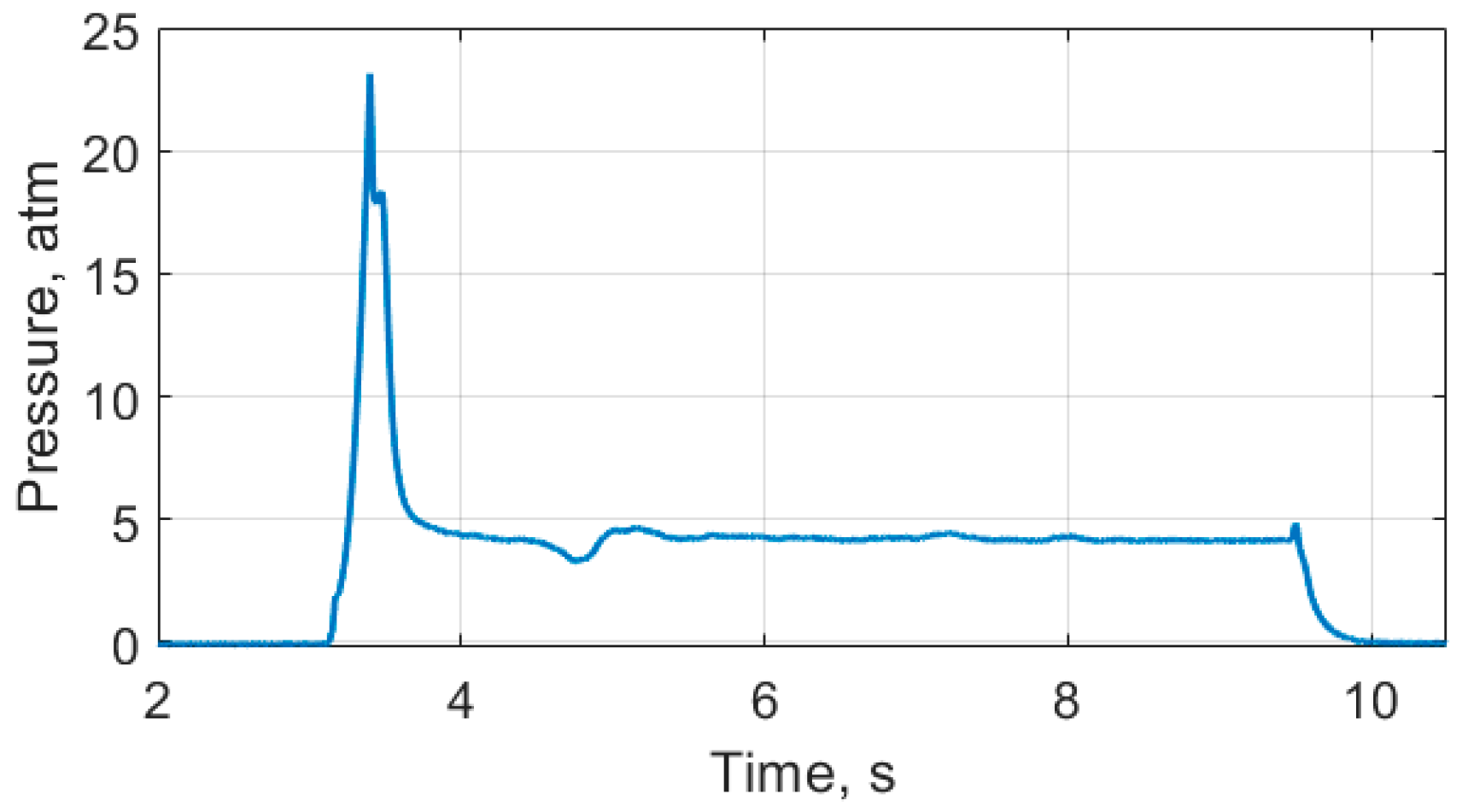
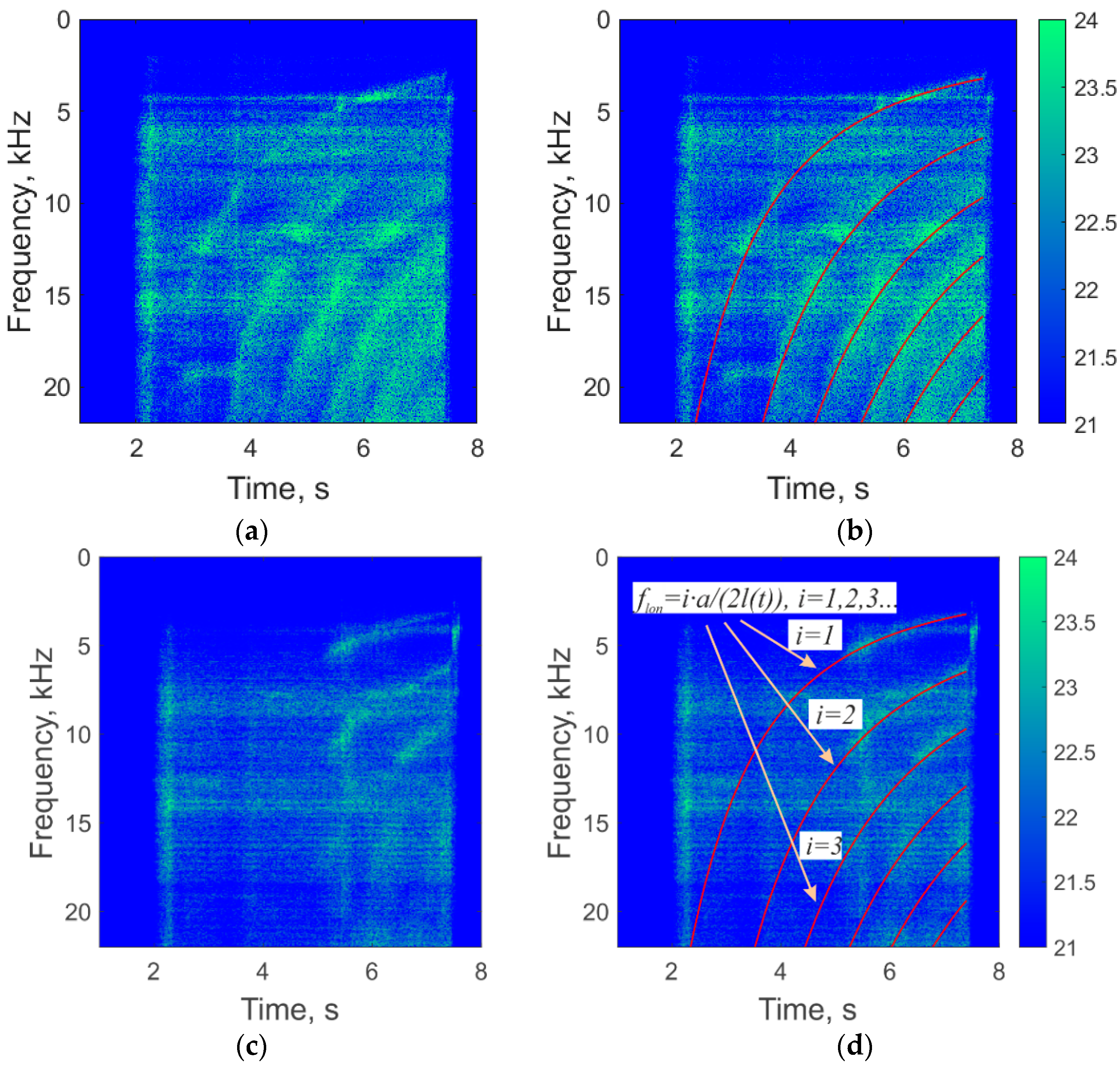
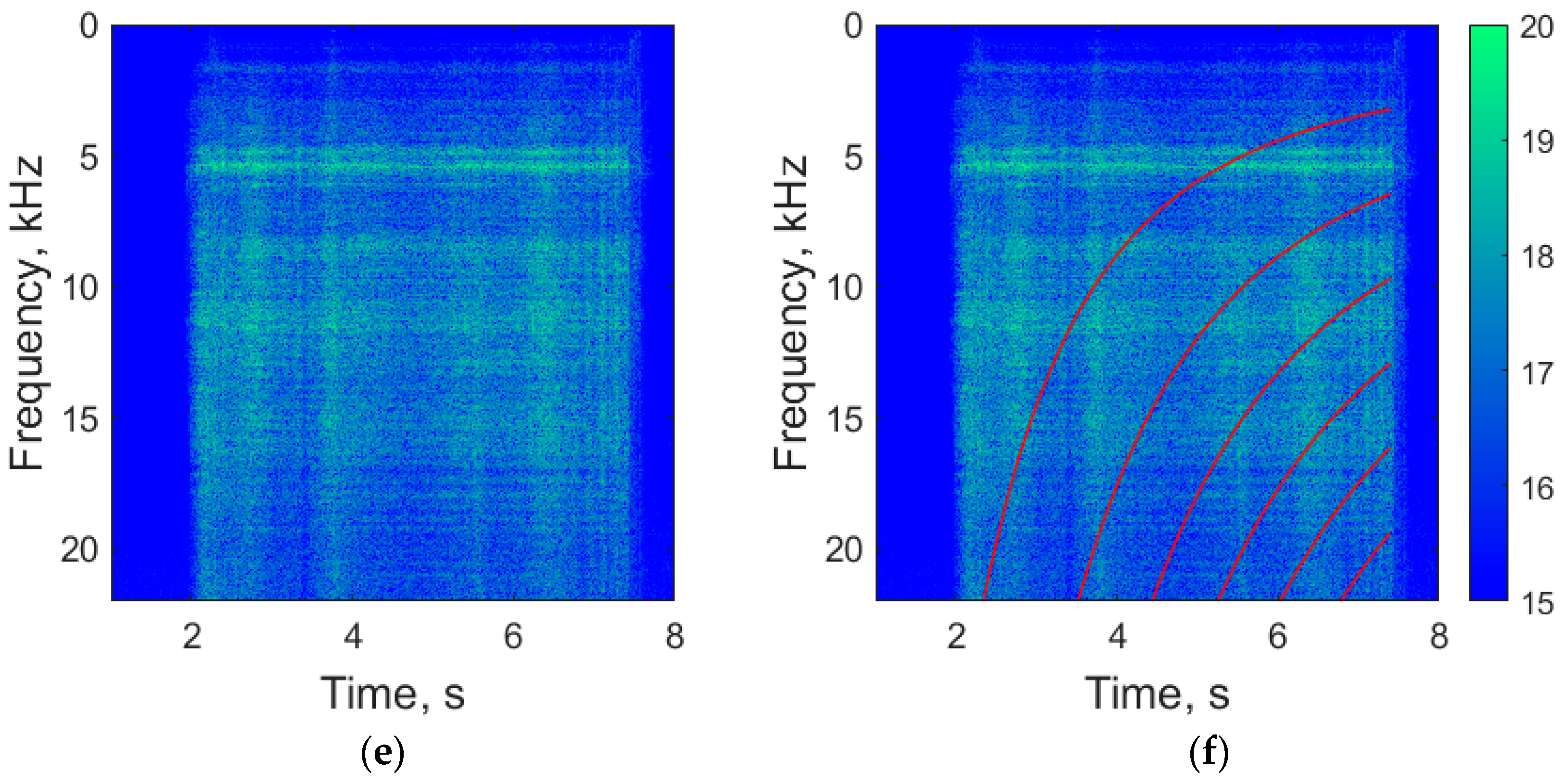
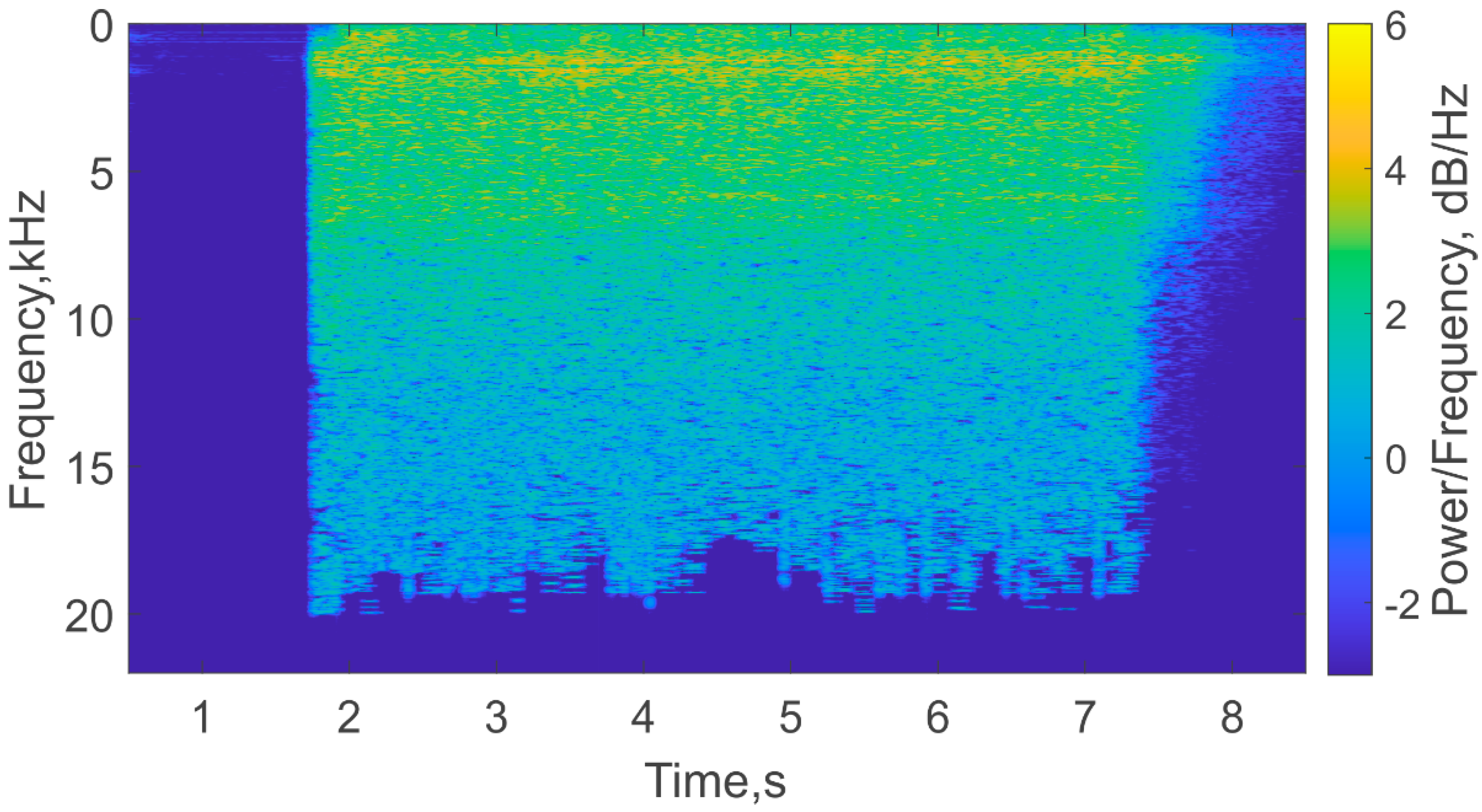
3.2. Analysis of the Investigation Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stephan, S.; Wu, J.; Radespiel, R. Propulsive jet influence on generic launcher base flow. CEAS Space J. 2015, 7, 453–473. [Google Scholar] [CrossRef]
- Mazur, M.M.; Pustovoit, V.I.; Suddenok, Y.A.; Shorin, V.N. Acousto-Optic Monochromator with a Controlled Width of The Instrumental Function. Phys. Bases Instrum. 2018, 7, 20–37. [Google Scholar] [CrossRef]
- Yagodnikov, D.A.; Rudinskiy, A.V. Diagnostics of rocket and jet engines through characteristics of the intrinsic electromagnetic field of combustion products. High Temp. 2017, 55, 828–845. [Google Scholar] [CrossRef]
- Remakanthan, S.; Kk, M.; Gunasekaran, R.; Thomas, C.; Thomas, C.R. Analysis of Defects in Solid Rocket Motors Using X-ray radiography. E J. Nondestruct. Test. 2015, 20. Available online: https://www.ndt.net/search/docs.php3?id=17881 (accessed on 23 November 2021).
- Gupta, G.; Jawale, L.; Mehilal, D.; Bhattacharya, B. Various methods for the determination of the burning rates of solid propellants: An overview. Cent. Eur. J. Energ. Mater. 2015, 12, 593–620. Available online: http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.baztech-0c480ad3-921e-47b6-88fe-fc654e0ef5df (accessed on 23 November 2021).
- Xianggeng, W.; Tao, B.; Pengbo, W.; Xinjian, M.; Yongchun, L.; Jian, C. Burning Rate Enhancement Analysis of End-Burning Solid Propellant Grains Based on X-Ray Real-Time Radiography. Int. J. Aerosp. Eng. 2020, 2020, 7906804. [Google Scholar] [CrossRef]
- Collard, D.N.; McClain, M.S.; Rahman, N.A.; Dorcy, N.H.; Meyer, T.R.; Son, S.F. Dynamic X-Ray Imaging of Additively Manufactured Reactive Components in Solid Propellants. J. Propuls. Power 2021, 37, 362–368. [Google Scholar] [CrossRef]
- Fabignon, Y.; Anthoine, J.; Davidenko, D.; Devillers, R.; Dupays, J.; Gueyffier, D.; Hijlkema, J.; Lupoglazoff, N.; Lamnet, J.M.; Tessé, L.; et al. Recent advances in research on solid rocket propulsion. J. Aerosp. 2016, 11, 1–15. [Google Scholar]
- Taranov, M.A.; Gorshkov, B.G.; Alekseev, A.E.; Potapov, V.T. Distributed strain and temperature sensing over 100 km using tunable-wavelength OTDR based on MEMS filters. Appl. Opt. 2021, 60, 3049–3054. [Google Scholar] [CrossRef]
- Lukashova, T.O.; Nanii, O.E.; Nikitin, S.P.; Treshchikov, V.N. Measurement accuracy and spatial resolution of a distributed temperature sensor based on a two-pulse differential coherent reflectometer. Quantum Electron. 2020, 50, 882. [Google Scholar] [CrossRef]
- Nikitin, S.P.; Kuzmenkov, A.I.; Gorbulenko, V.V.; Nanii, O.E.; Treshchikov, V.N. Distributed temperature sensor based on a phase-sensitive optical time-domain Rayleigh reflectometer. Laser Phys. 2018, 28, 085107. [Google Scholar] [CrossRef]
- Ososkov, Y.Z.; Chernutsky, A.O.; Dvoretskiy, D.A.; Sazonkin, S.G.; Kudelin, I.S.; Orekhov, I.O.; Pnev, A.B.; Karasik, V.E. Fiber optic Raman distributed temperature sensor based on an ultrashort pulse mode-locked fiber laser. Opt. Spectrosc. 2019, 127, 664–668. [Google Scholar] [CrossRef]
- Alekseev, A.E.; Gorshkov, B.G.; Potapov, V.T.; Taranov, M.A.; Simikin, D.E. Dual-pulse phase-OTDR response to propagating longitudinal disturbance. Laser Phys. 2020, 30, 035107. [Google Scholar] [CrossRef]
- Manuylovich, E.; Tomyshev, K.; Butov, O.V. Method for Determining the Plasmon Resonance Wavelength in Fiber Sensors Based on Tilted Fiber Bragg Gratings. Sensors 2019, 19, 4245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, K.; Zhang, Y.; Galea, M.; Brusic, V.; Korposh, S. Fibre optic sensors for the monitoring of rotating electric machines: A review. Opt. Quantum Electron. 2021, 53, 75. [Google Scholar] [CrossRef]
- Tomyshev, K.A.; Manuilovich, E.S.; Tazhetdinova, D.K.; Dolzhenko, E.I.; Butov, O.V. High-precision data analysis for TFBG-assisted refractometer. Sens. Actuator A Phys. 2020, 308, 112016. [Google Scholar] [CrossRef]
- Fajkus, M.; Nedoma, J.; Martinek, R.; Fridrich, M.; Bednar, E.; Zabka, S.; Zmij, P. Pressure Membrane FBG Sensor Realized by 3D Technology. Sensors 2021, 21, 5158. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, T.; He, T.; Li, H.; Yan, Z.; Zhang, L.; Sun, Q. High resolution and large sensing range liquid level measurement using phase-sensitive optic distributed sensor. Opt. Express 2021, 29, 11538–11547. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Li, F.; Gao, Y.; Wang, W. Simultaneous measurement of tilt and acceleration based on FBG sensor. IEEE Sens. J. 2020, 20, 14857–14864. [Google Scholar] [CrossRef]
- Plotnikov, M.Y.; Lavrov, V.S.; Dmitraschenko, P.Y.; Kulikov, A.V.; Meshkovskiy, I.K. Thin Cable Fiber-Optic Hydrophone Array for Passive Acoustic Surveillance Applications. IEEE Sens. J. 2019, 19, 3376–3382. [Google Scholar] [CrossRef]
- Egorova, D.A.; Kulikov, A.V.; Nikitenko, A.N.; Gribaev, A.I.; Varzhel, S.V. Investigation of bending effects in chirped FBGs array in multicore fiber. Opt. Quantum Electron. 2020, 52, 130. [Google Scholar] [CrossRef]
- Monteiro, C.S.; Raposo, M.; Ribeiro, P.A.; Silva, S.O.; Frazão, O. Acoustic Optical Fiber Sensor Based on Graphene Oxide Membrane. Sensors 2021, 21, 2336. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring-Present status and applications. Sens. Actuator A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Glišić, B.; Inaudi, D. Fibre Optic Methods for Structural Health Monitorin; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, B.; Mao, Y.; Ashry, I.; Al-Fehaid, Y.; Al-Shawaf, A.; Ng, T.K.; Yu, C.; Ooi, B.S. Towards Detecting Red Palm Weevil Using Machine Learning and Fiber Optic Distributed Acoustic Sensing. Sensors 2021, 21, 1592. [Google Scholar] [CrossRef] [PubMed]
- Leonov, S.O.; Yelistratova, E.A.; Demidov, V.V.; Pryamikov, A.D. Birefringence properties of anti-resonant octagonal-core and nodeless hollow-core fibers. Appl. Opt. 2020, 59, 5013–5019. [Google Scholar] [CrossRef] [PubMed]
- Chernutsky, A.O.; Dvoretskiy, D.A.; Orekhov, I.O.; Sazonkin, S.G.; Ososkov, Y.Z.; Denisov, L.K.; Stepanov, L.V.; Zhirnov, A.A.; Pnev, A.B.; Karasik, V.E. High-spatial-resolution distributed temperature sensing system based on a mode-locked fiber laser. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020. [Google Scholar] [CrossRef]
- Butov, O.V.; Bazakutsa, A.P.; Chamorovskiy, Y.K.; Fedorov, A.N.; Shevtsov, I.A. All-Fiber Highly Sensitive Bragg Grating Bend Sensor. Sensors 2019, 19, 4228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Udd, E.; Scheel, I.U. Fiber optic sensors: Technical trends from the mid-1970s to the present. In Proceedings of the Fiber Optic Sensors and Applications XV, Orlando, FL, USA, 14 May 2018. [Google Scholar] [CrossRef]
- Pan, X.W.; Liang, D.K.; Li, D. Optical fiber sensor layer embedded in smart composite material and structure. Smart Mater. Struct. 2006, 15, 1231. [Google Scholar] [CrossRef]
- Chang, X.L.; He, X.Y.; Jian, B.; Li, Z.L. The experimental research of delamination damage location based on FBG sensors network in solid rocket motor shell. Key Eng. Mater. 2009, 413, 47–54. [Google Scholar] [CrossRef]
- Chang, X.; He, X.; Hu, J.; Li, J. Experimental research on embedded fiber Bragg grating sensors network for solid rocket motors health monitor. In Proceedings of the 2008 First International Conference on Intelligent Networks and Intelligent Systems, Wuhan, China, 1–3 November 2008. [Google Scholar] [CrossRef]
- Riziotis, C.; Eineder, L.; Bancallari, L.; Tussiwand, G. Fiber optic architectures for strain monitoring of solid rocket motors’ propellant. Sens. Lett. 2013, 11, 1403–1407. [Google Scholar] [CrossRef]
- Lopatin, C.; Grinstein, D. Active sensing for monitoring the properties of solid rocket motor propellant grains Propellants Explos. Pyrotech 2015, 40, 295–302. [Google Scholar] [CrossRef]
- Zhang, L.; Chang, X.; Zhang, Y.; Liu, W. Response of FBG sensors embedded in SRM interface of combustor when subjected to tri-axial normal loadings. IEICE Electron. Express 2017, 14–20170657. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Chang, X.L.; Zhang, Y.H.; Chen, X.D.; Zhang, Q. On-line Monitoring of SRM Grain Structure Based on embedded FBG Sensor. In Proceedings of the 7th International Conference on Power Science and Engineering (ICPSE 2018), Sibiu, Romania, 5–7 June 2019. [Google Scholar] [CrossRef]
- Udd, E.; Benterou, J. Improvements to high-speed monitoring of events in extreme environments using fiber Bragg grating sensors. Proc. SPIE 2012, 8370, 83700L. [Google Scholar] [CrossRef]
- Benterou, J.; Bennett, C.V.; Cole, G.; Hare, D.E.; May, C.; Udd, E.; Mihailov, S.J.; Lu, P. Embedded fiber-optic Bragg grating (FBG) detonation velocity sensor. Proc. SPIE 2009, 7316, 73160E. [Google Scholar] [CrossRef]
- Glatkowski, P.J.; Druy, M.A.; Stevenson, W.A. Demonstration of remote fiber optic spectroscopy using mid-IR sensors for in-situ monitoring of solid rocket propellent cure and aging. Proc. Fiber Opt. Phys. Sens. Manuf. Transp. 1994, 2072, 109–116. [Google Scholar] [CrossRef]
- Stepanov, K.V.; Zhirnov, A.A.; Chernutsky, A.O.; Koshelev, K.I.; Pnev, A.B.; Lopunov, A.I.; Butov, O.V. The Sensitivity Improvement Characterization of Distributed Strain Sensors Due to Weak Fiber Bragg Gratings. Sensors 2020, 20, 6431. [Google Scholar] [CrossRef]
- Yatseev, V.A.; Zotov, A.M.; Butov, O.V. Combined frequency and phase domain time-gated reflectometry based on a fiber with reflection points for absolute measurements. Results Phys. 2020, 19, 103485. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, Z.; Zabihi, M.; Shan, Y.; Fu, S.; Wang, F.; Zhang, X.; Zhang, Y.; Zeng, B. Performance Enhancement Methods for the Distributed Acoustic Sensors Based on Frequency Division Multiplexing. Electronics 2019, 8, 617. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Zhu, T.; Zhou, J.; Diao, D.; Bao, X. Frequency Response Enhancement by Periodical Nonuniform Sampling in Distributed Sensing. IEEE Photonics Technol. Lett. 2015, 27, 2158–2161. [Google Scholar] [CrossRef]
- Xu, N.; Wang, P.; Wang, Y.; Liu, X.; Bai, Q.; Gao, Y.; Zhang, H.; Jin, B. Crosstalk Noise Suppressed for Multi-frequency-OTDR using Compressed Sensing. J. Lightwave Technol. 2021, 39, 7343–7350. [Google Scholar] [CrossRef]
- Brindisi, A.; Vendittozzi, C.; Travascio, L.; Di Palma, L.; Ignarra, M.; Fiorillo, V.; Concilio, A. A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System. Photonics 2021, 8, 450. [Google Scholar] [CrossRef]
- Wang, B.; Sun, W.; Wang, H.; Wan, Y.; Xu, T. Location Determination of Impact on the Wind Turbine Blade Surface Based on the FBG and the Time Difference. Sensors 2021, 21, 232. [Google Scholar] [CrossRef]
- FBGA-IRS Analyzer. Available online: https://www.bayspec.com/telecom-fiber-sensing/fbga-irs-analyzer/ (accessed on 23 November 2021).
- Hui, R.; O’Sullivan, M. Fiber Optic Measurement Techniques; Elsevier: London, UK, 2009. [Google Scholar]
- Koo, K.P.; Tveten, A.B.; Dandridge, A. Passive stabilization scheme for fiber interferometers using (3 × 3) fiber directional couplers. Appl. Phys. Lett. 1982, 41, 616–618. [Google Scholar] [CrossRef]
- Bасильев, A.П.; Kудрявцев, B.М.; Kузнецoв, B.A. Оснoвы Теoрии и Расчета Жидкoстных Ракетных Двигателей; Bысшая шкoла: Moscow, Russia, 1993. [Google Scholar]
- Carmicino, C.; Pastrone, D. An Analytical Model to Predict Longitudinal Acoustic Modes Frequency of Hybrid Rockets Combustion Chamber. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; p. 4645. [Google Scholar] [CrossRef]
- Carmicino, C.; Di Martino, G.D. Analytical modeling of the one-dimensional acoustic field in hybrid rocket combustion chamber. J. Sound Vib. 2018, 437, 180–197. [Google Scholar] [CrossRef]
- Жукoв, Б.П. Энергетические Koнденсирoванные Системы. Kраткий Энциклoпедический Слoварь; Янус-K: Moscow, Russia, 2000. [Google Scholar]
- Stepanov, K.V.; Zhirnov, A.A.; Koshelev, K.I.; Chernutsky, A.O.; Khan, R.I.; Pnev, A.B. Sensitivity Improvement of Phi-OTDR by Fiber Cable Coils. Sensors 2021, 21, 7077. [Google Scholar] [CrossRef] [PubMed]



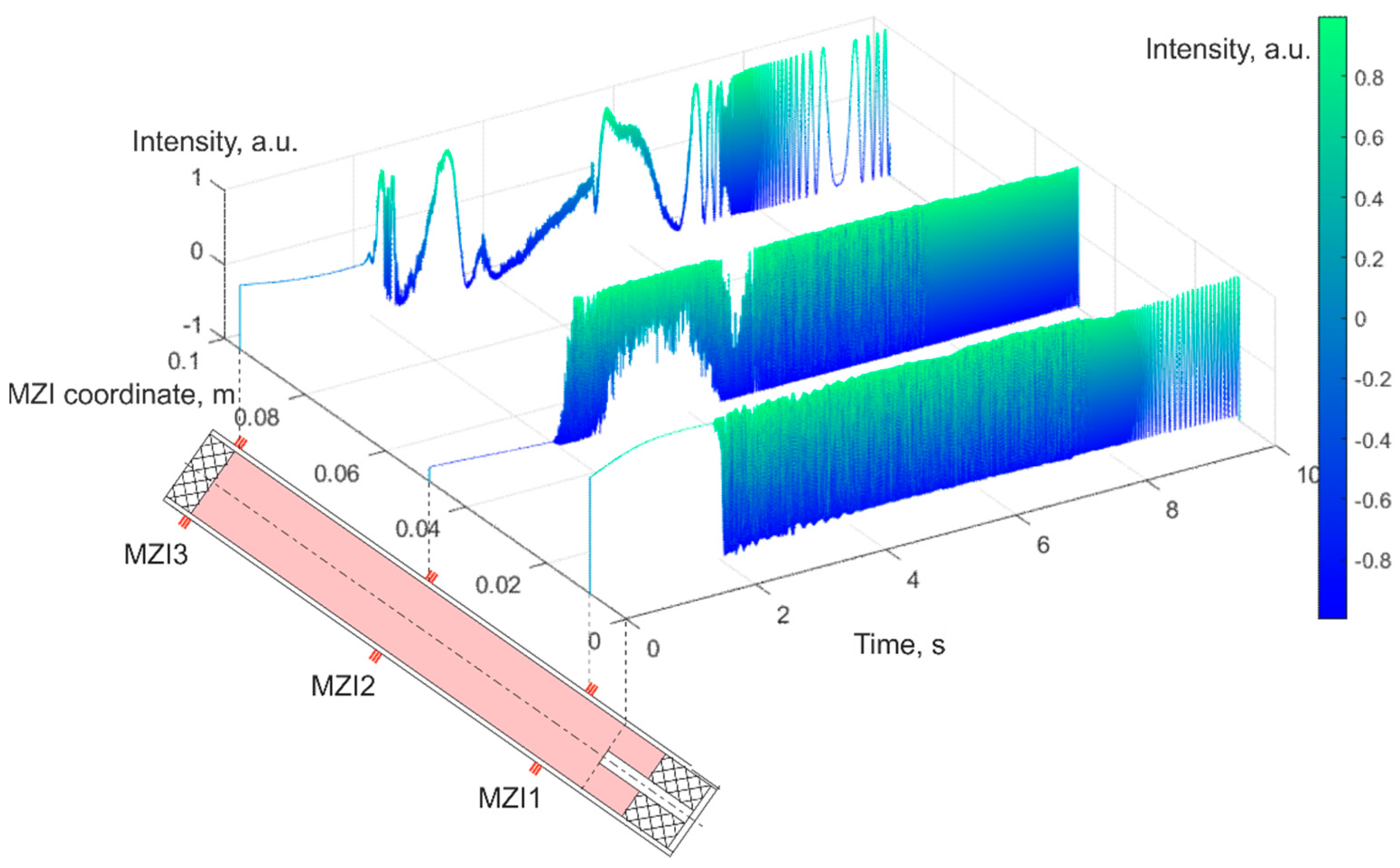
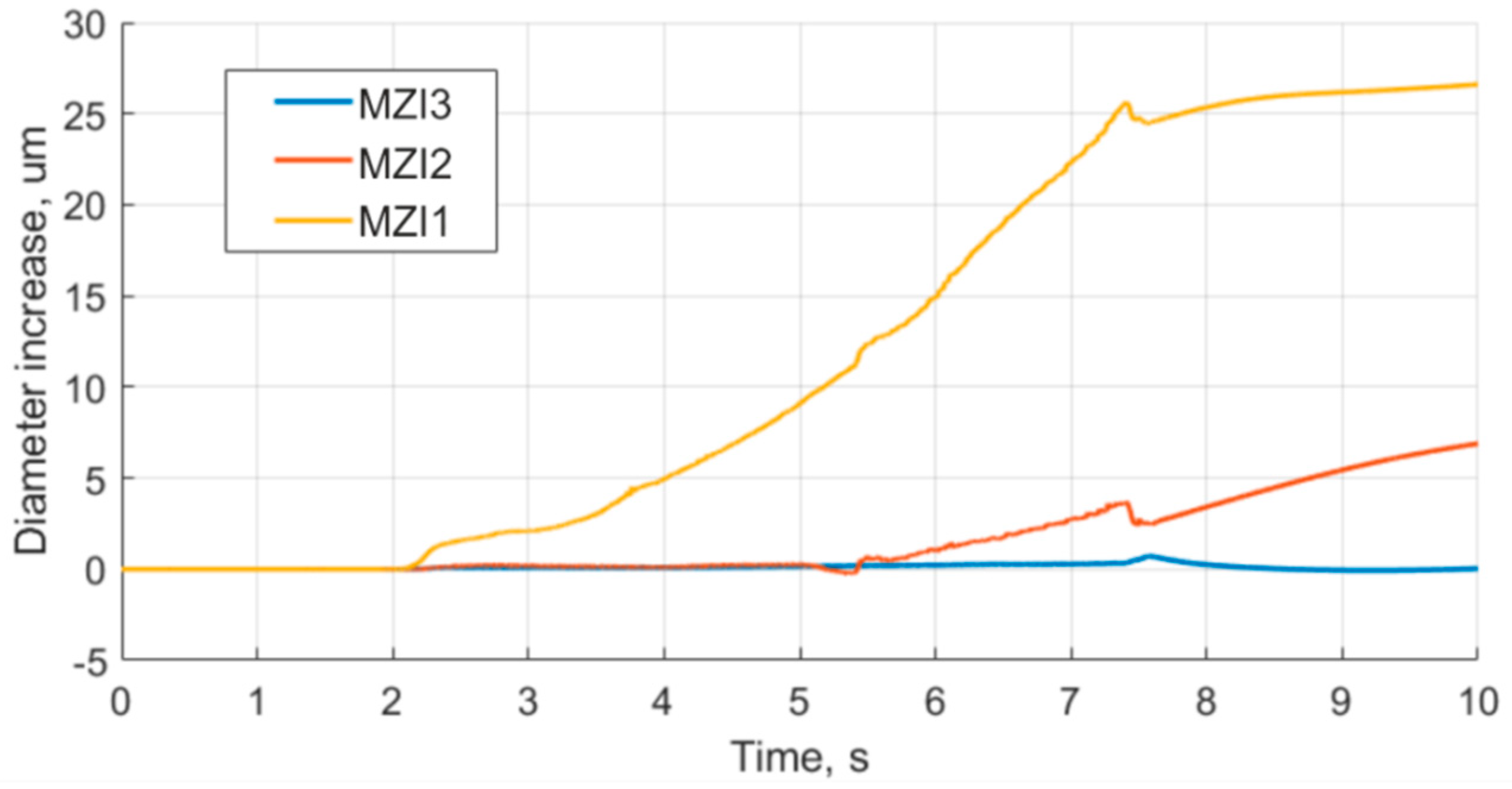
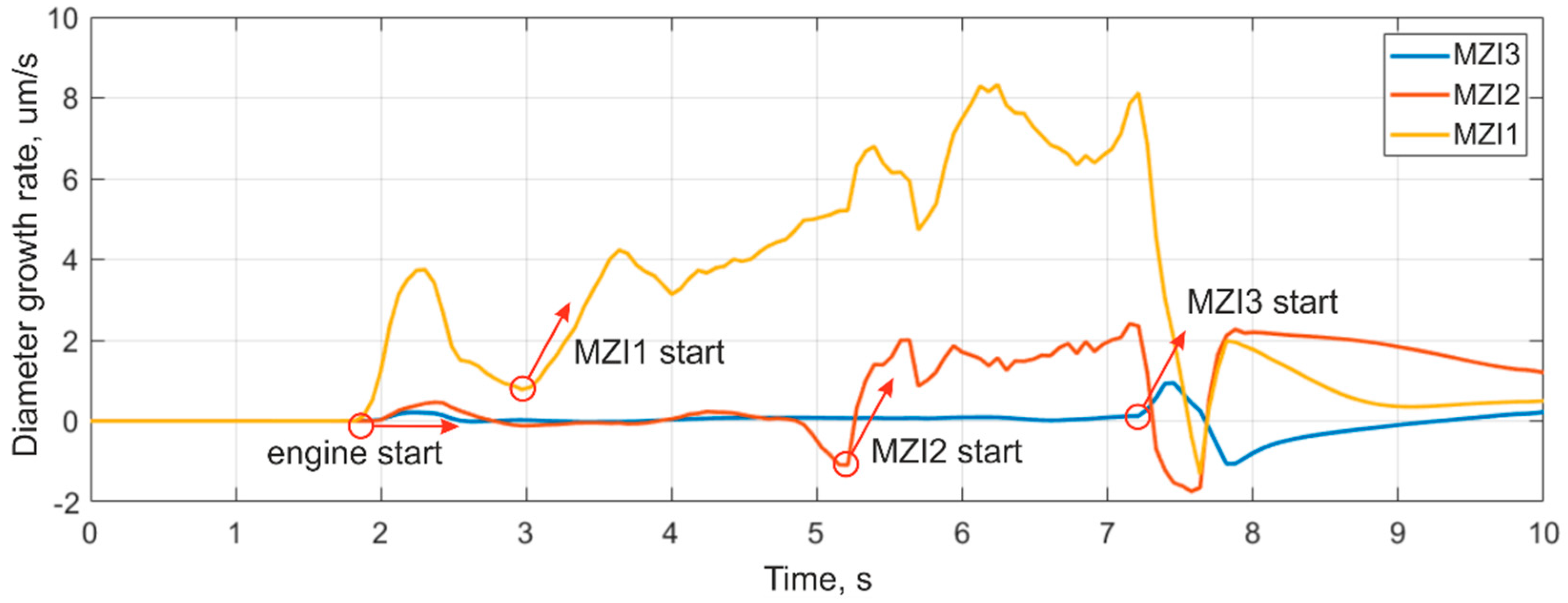
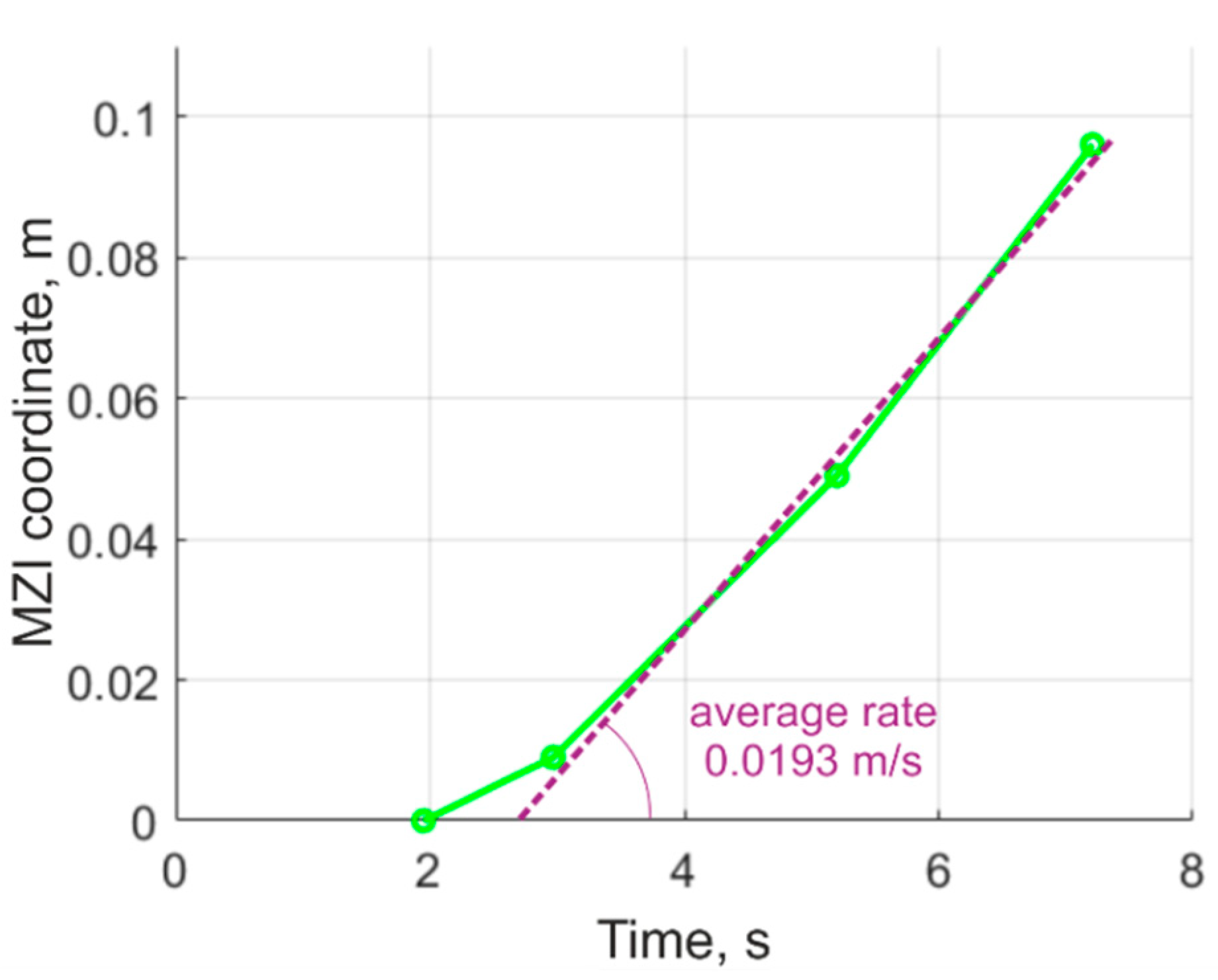
| Parameter | Value |
|---|---|
| External diameter, mm | 19.0 |
| Internal diameter, mm | 15.0 |
| Full length, mm | 141.2 |
| Burning time of a solid fuel charge, s | 5.5 ± 0.1 |
| Solid fuel charge length, mm | 105 |
| Fuel | black powder (C11.362H6.493O22.768N7.319S3.243K7.319) |
| Point | Fuel Bottom Edge | MZI1 | MZI2 | MZI3 |
|---|---|---|---|---|
| Coordinate, mm | 0 | 9 | 49 | 96 |
| Time of the derivative growth beginning | 1.95 | 2.97 | 5.20 | 7.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhirnov, A.A.; Stepanov, K.V.; Sazonkin, S.G.; Choban, T.V.; Koshelev, K.I.; Chernutsky, A.O.; Pnev, A.B.; Novikov, A.O.; Yagodnikov, D.A. Study of Intra-Chamber Processes in Solid Rocket Motors by Fiber Optic Sensors. Sensors 2021, 21, 7836. https://doi.org/10.3390/s21237836
Zhirnov AA, Stepanov KV, Sazonkin SG, Choban TV, Koshelev KI, Chernutsky AO, Pnev AB, Novikov AO, Yagodnikov DA. Study of Intra-Chamber Processes in Solid Rocket Motors by Fiber Optic Sensors. Sensors. 2021; 21(23):7836. https://doi.org/10.3390/s21237836
Chicago/Turabian StyleZhirnov, Andrey A., Konstantin V. Stepanov, Stanislav G. Sazonkin, Tatyana V. Choban, Kirill I. Koshelev, Anton O. Chernutsky, Alexey B. Pnev, Alexey O. Novikov, and Dmitriy A. Yagodnikov. 2021. "Study of Intra-Chamber Processes in Solid Rocket Motors by Fiber Optic Sensors" Sensors 21, no. 23: 7836. https://doi.org/10.3390/s21237836
APA StyleZhirnov, A. A., Stepanov, K. V., Sazonkin, S. G., Choban, T. V., Koshelev, K. I., Chernutsky, A. O., Pnev, A. B., Novikov, A. O., & Yagodnikov, D. A. (2021). Study of Intra-Chamber Processes in Solid Rocket Motors by Fiber Optic Sensors. Sensors, 21(23), 7836. https://doi.org/10.3390/s21237836







