Low Discrepancy Sparse Phased Array Antennas
Abstract
:1. Introduction
- Sufficient elements to achieve a desired gain.
- Aperture size is large enough to achieve the desired beamwidth.
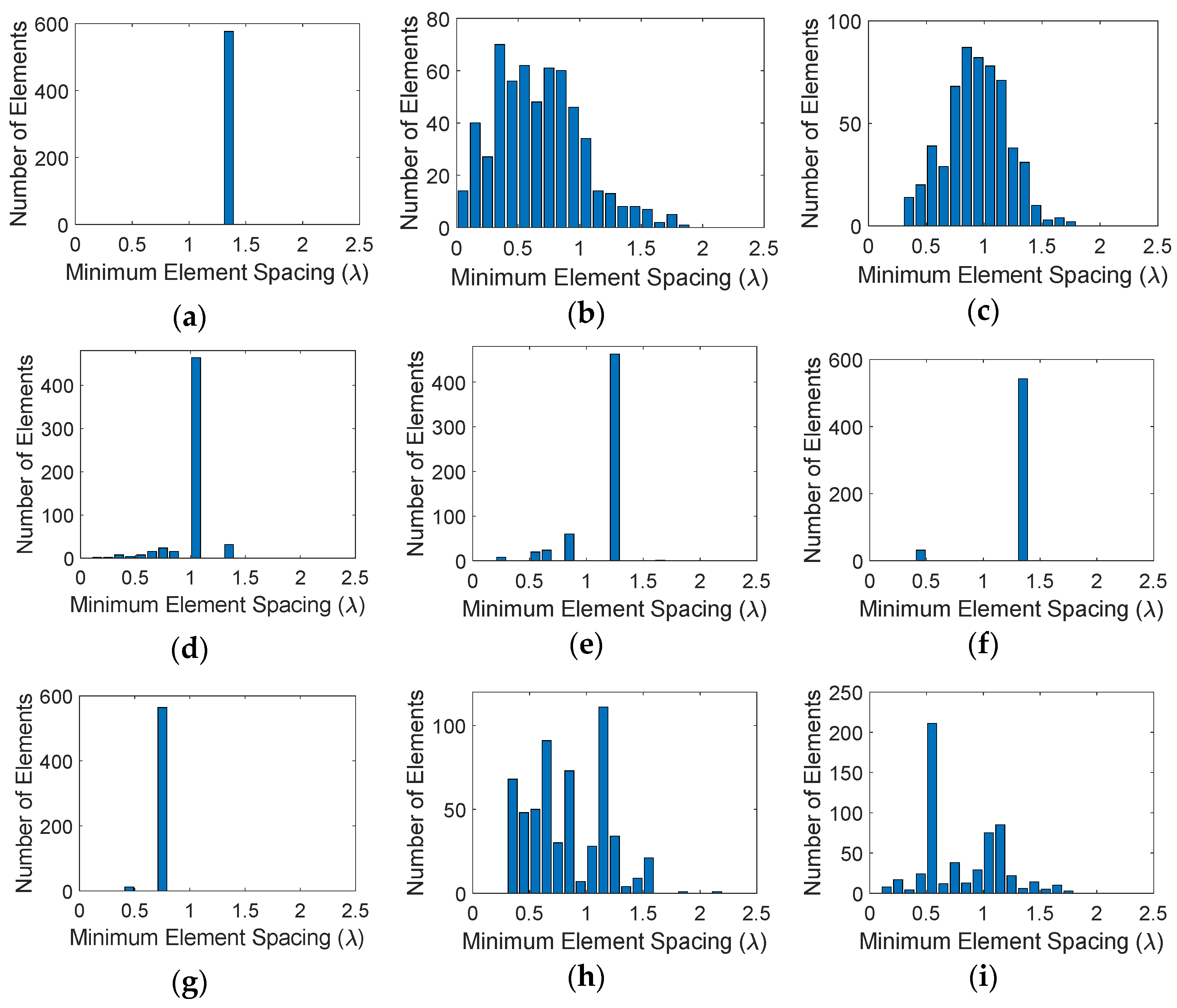
- Elements have a minimum separation distance, so they can physically fit into the aperture and mutual coupling is not a problem.
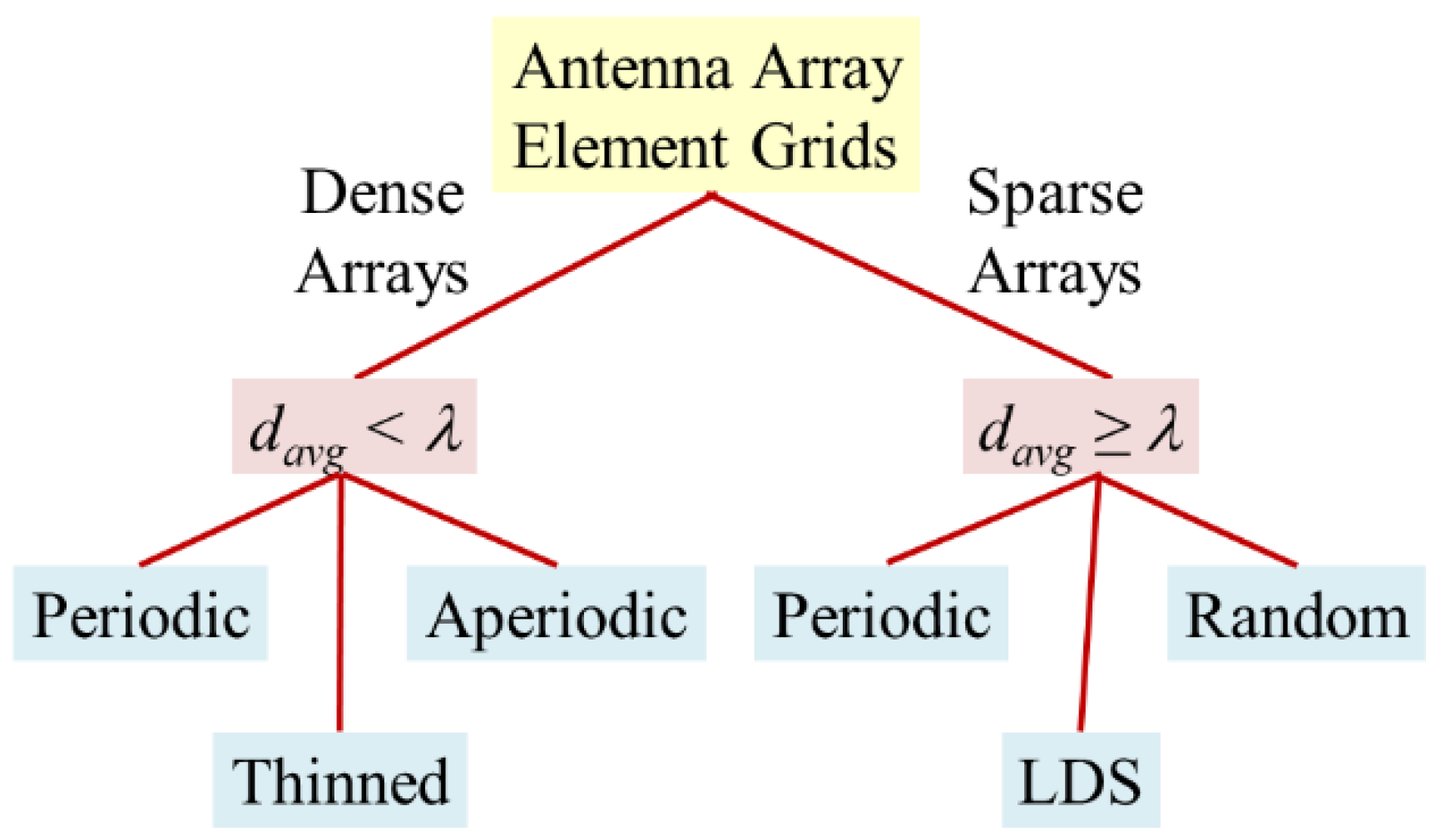
- No GLs present at maximum scan angles.
- The average element spacing is greater than .
2. Sampling Points on a Planar Aperture
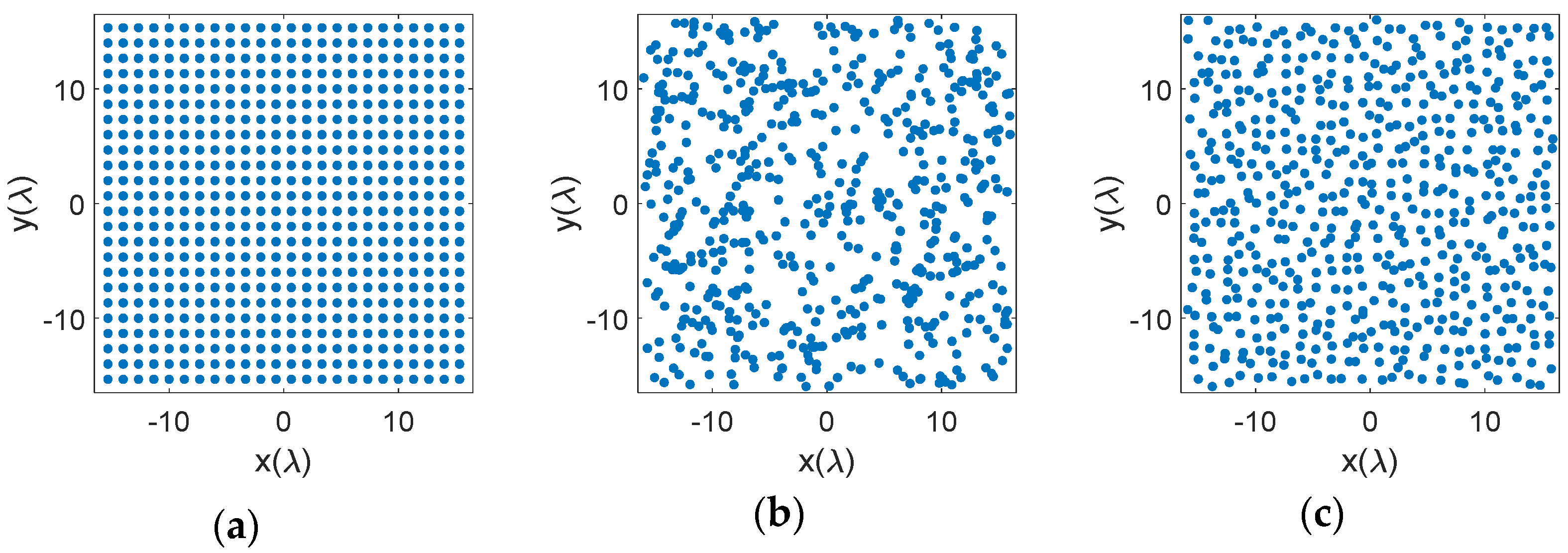
2.1. Random Sampling Approaches
2.1.1. Random Sampling
2.1.2. Random Sampling with Jitter
2.1.3. Random Hyperuniform Spatial Arrangements
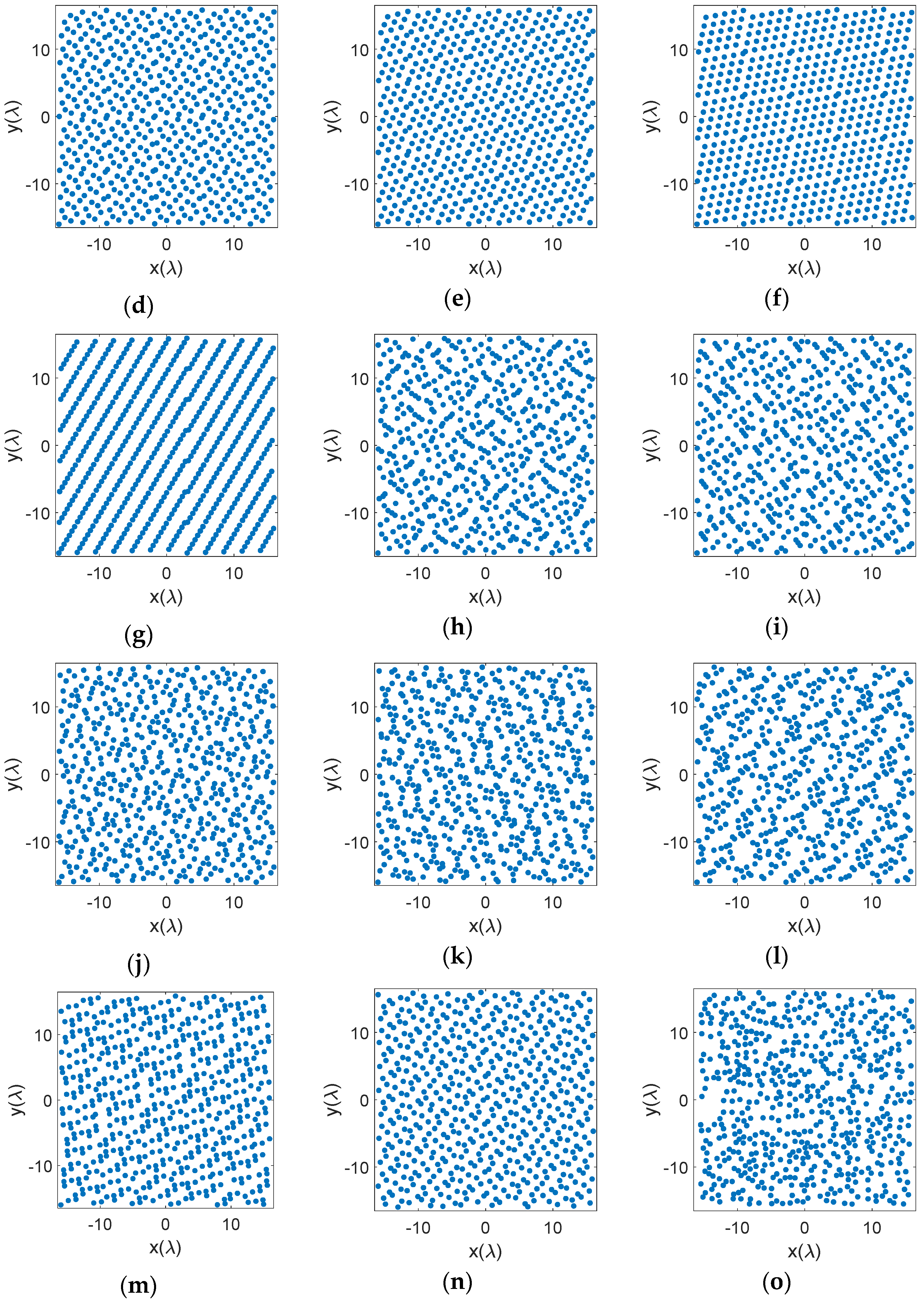
2.2. Low Discrepancy Sampling Approaches
2.2.1. Hammersley Sampling
2.2.2. Halton Sampling
2.2.3. Sobol Sampling
2.2.4. Poisson Disk Sampling
3. Sparse Planar Phased Array Antennas
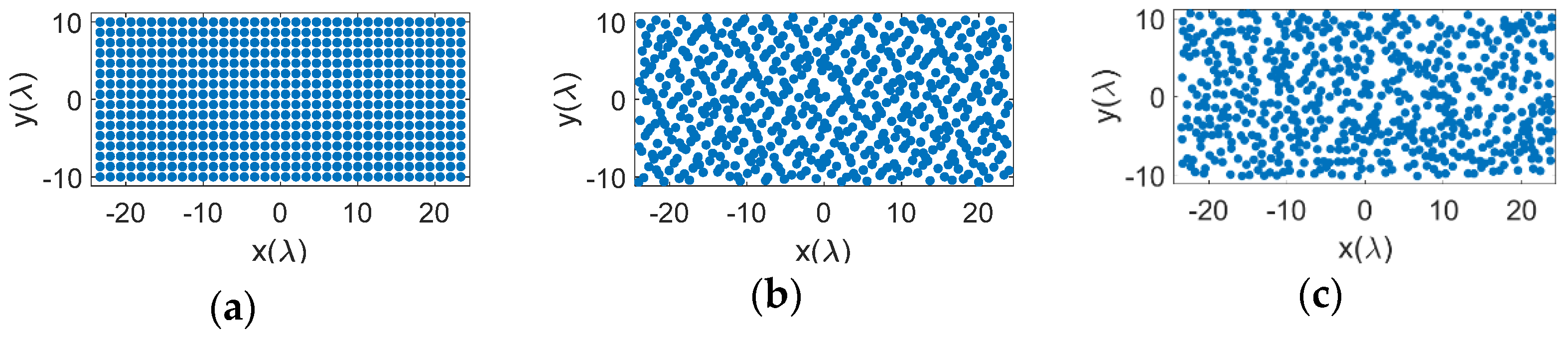
3.1. Element Distributions on the Aperture
3.2. Radiation Patterns of the Sparse Phased Array Antennas
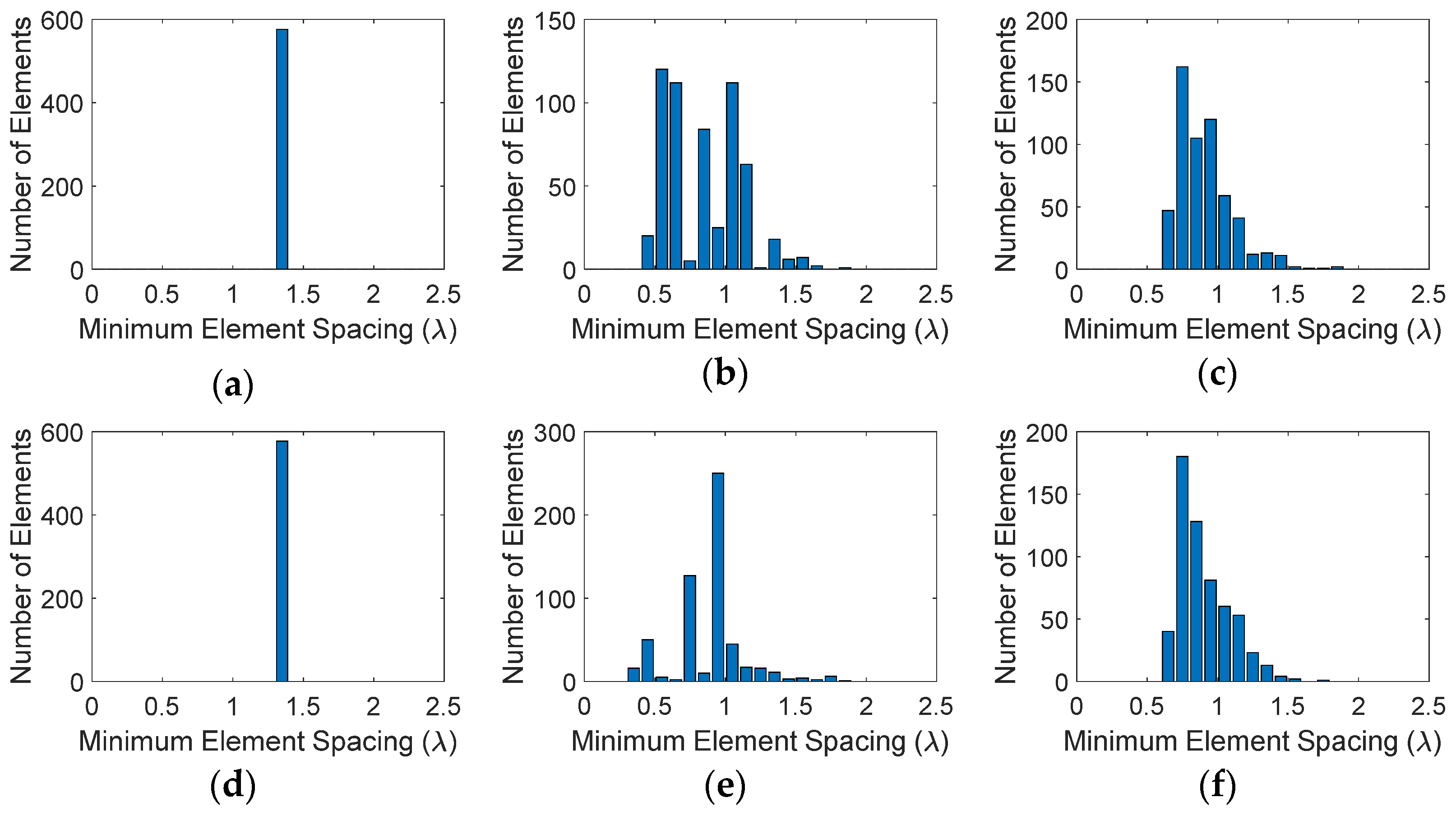
3.3. Quantitative Analysis of Sparse Array Performances
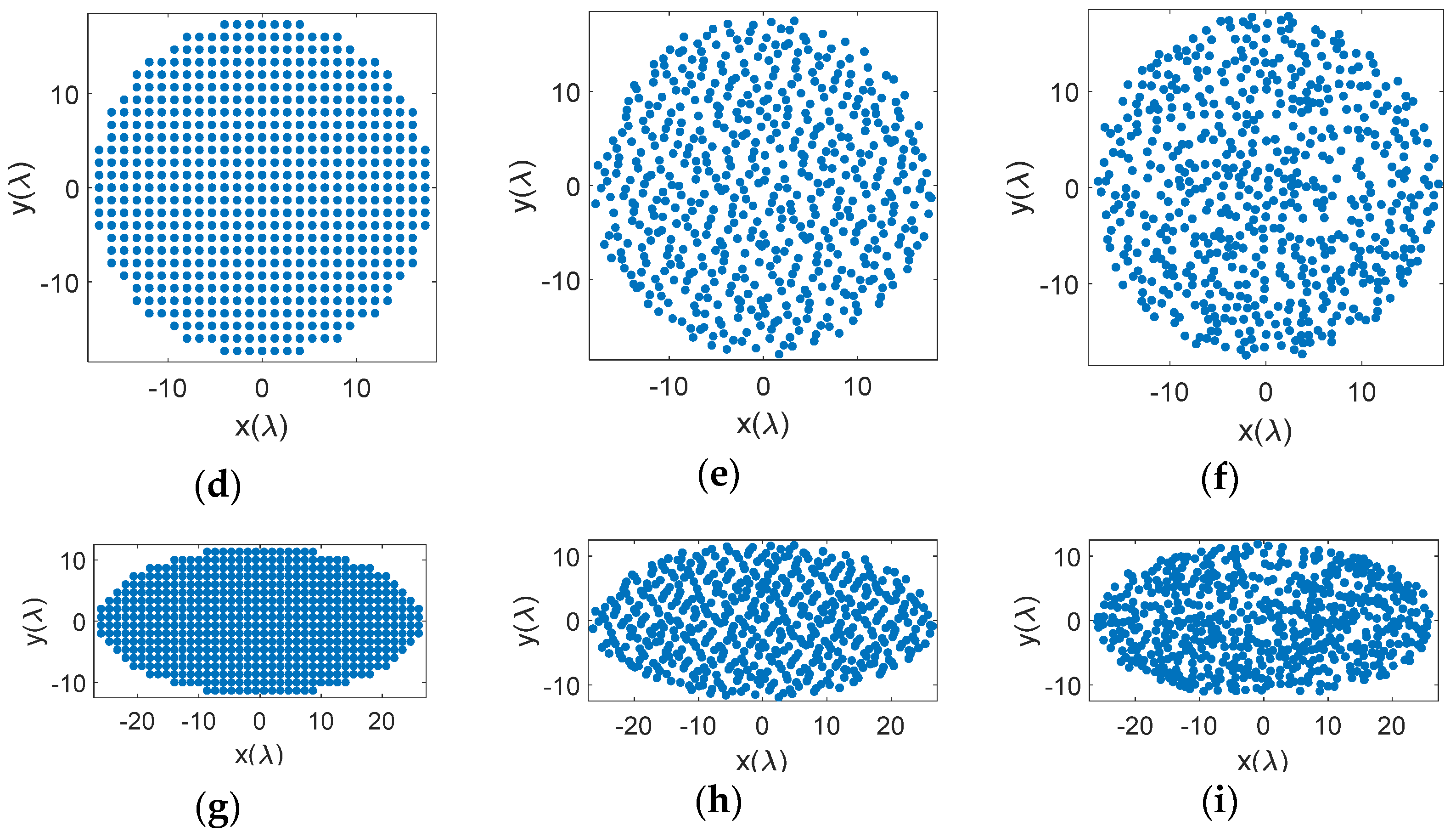
4. Aperture Shape Effects on the Performance of Sparse Phased Array Antennas
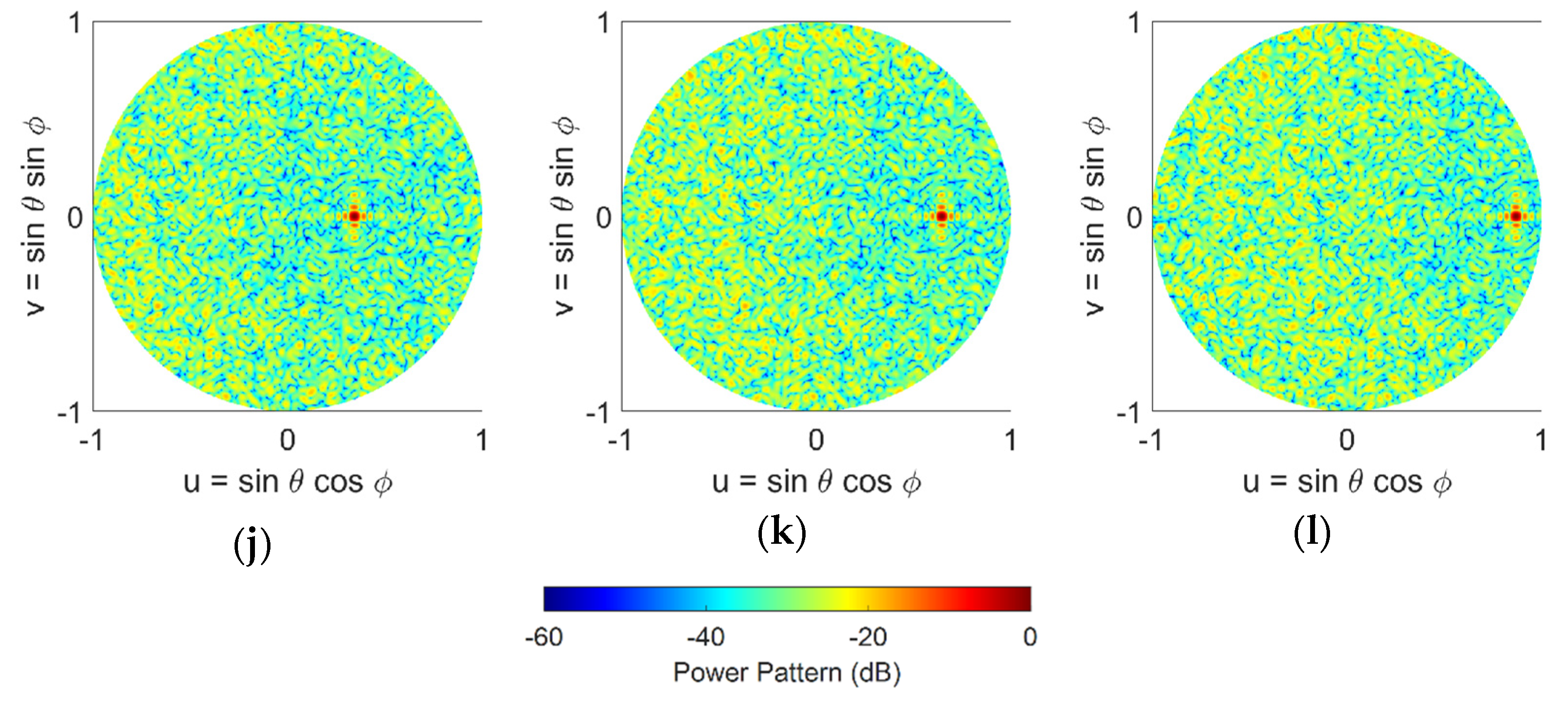
5. Beam-Scanning Performance of Sparse Phased Array Antennas
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Haupt, R.L. Timed Arrays Wideband and Time Varying Antenna Arrays; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Haupt, R.L. Antenna Arrays: A Computational Approach; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Willey, R.E. Space tapering of linear and planar arrays. IRE Trans. Antenna Propag. 1962, 10, 369–377. [Google Scholar] [CrossRef]
- Skolnik, M.; Sherman, J., III; Ogg, F., Jr. Statistically designed density-tapered arrays. IEEE AP-S Trans. 1964, 12, 408–417. [Google Scholar] [CrossRef]
- Haupt, R.L. Thinned arrays using genetic algorithms. IEEE Trans. Antennas Propag. 1997, 42, 993–999. [Google Scholar] [CrossRef]
- Kurup, D.G.; Himdi, M.; Rydberg, A. Synthesis of uniform amplitude unequally spaced antenna arrays using the differential evolution algorithm. IEEE Trans. Antennas Propag. 2003, 51, 2210–2217. [Google Scholar] [CrossRef]
- IEEE Standard for Definitions of Terms for Antennas; IEEE Std 145-2013 (Revision of IEEE Std 145-1993); IEEE: New York, NY, USA, 6 March 2014. [CrossRef]
- Available online: https://xlinux.nist.gov/dads/HTML/sparsematrix.html (accessed on 5 November 2020).
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Mailloux, R.J.; Massa, A. Unconventional Phased Array Architectures and Design Methodologies—A Review. Proc. IEEE 2016, 104, 544–560. [Google Scholar] [CrossRef]
- Oliveri, G.; Massa, A. Bayesian compressive sampling for pattern synthesis with maximaly sparse non-uniform linear arrays. IEEE Trans. Antennas Propag. 2011, 59, 467–481. [Google Scholar] [CrossRef] [Green Version]
- Oliveri, G.; Carlin, M.; Massa, A. Complex-weight sparse linear array synthesis by Bayesian compressive sampling. IEEE Trans. Antennas Propag. 2012, 60, 2309–2326. [Google Scholar] [CrossRef]
- Zhang, W.; Li, L.; Li, F. Reducing the number of elements in linear and planar antenna arrays with sparseness constrained optimization. IEEE Trans. Antennas Propag. 2011, 59, 3106–3111. [Google Scholar] [CrossRef]
- Viani, F.; Oliveri, G.; Massa, A. Compressive sensing pattern matching techniques for synthesizing planar sparse arrays. IEEE Trans. Antennas Propag. 2013, 61, 4577–4587. [Google Scholar] [CrossRef]
- Buchanan, K.; Rockway, J.; Sternberg, O.; Mai, N.N. Sum-difference beamforming for radar applications using circularly tapered random arrays. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Leeper, D.G. Isophoric arrays-massively thinned phased arrays with well-controlled sidelobes. IEEE Trans. Antennas Propag. 1999, 47, 1825–1835. [Google Scholar] [CrossRef]
- Christodoulou, C.G.; Ciaurriz, M.; Tawk, Y.; Costantine, J.; Barbin, S.E. Recent advances in randomly spaced antenna arrays. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; pp. 732–736. [Google Scholar]
- Ellingson, S.W.; Taylor, G.B.; Craig, J.; Hartman, J.; Dowell, J.; Wolfe, C.N.; Clarke, T.E.; Hicks, B.C.; Kassim, N.E.; Ray, P.S.; et al. The LWA1 Radio Telescope. IEEE Trans. Antennas Propag. 2013, 61, 2540–2549. [Google Scholar] [CrossRef]
- van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The Low-Frequency Array. Astron. Astrophys. 2013, 556, 1–54. [Google Scholar] [CrossRef] [Green Version]
- di Ninni, P.; Bolli, P.; Paonessa, F.; Pupillo, G.; Virone, G.; Wijnholds, S.J. Electromagnetic Analysis and Experimental Validation of the LOFAR Radiation Patterns. Int. J. Antennas Propag. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Available online: https://public.nrao.edu/telescopes/vlba/ (accessed on 14 November 2020).
- Available online: https://public.nrao.edu/telescopes/alma/ (accessed on 14 November 2020).
- Available online: https://public.nrao.edu/telescopes/vla/ (accessed on 14 November 2020).
- Scott, S.; Wawrzynek, J. Compressive sensing and sparse antenna arrays for indoor 3-D microwave imaging. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 1314–1318. [Google Scholar]
- Amani, N.; Maaskant, R.; van Cappellen, W.A. On the Sparsity and Aperiodicity of a Base Station Antenna Array in a Downlink MU-MIMO Scenario. In Proceedings of the 2018 International Symposium on Antennas and Propagation (ISAP), Busan, Korea, 23–26 October 2018; pp. 1–2. [Google Scholar]
- Cappellen, W.A.V.; Wijnholds, S.J.; Bregman, J.D. Sparse antenna array configurations in large aperture synthesis radio telescopes. In Proceedings of the 2006 European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 76–79. [Google Scholar]
- Hermann, W. Über die Gleichverteilung von Zahlen mod. Eins [About the equal distribution of numbers]. Math. Ann. 1916, 77, 313–352. [Google Scholar]
- Hammersley, J.M. Monte Carlo methods for solving multivariable problems. Ann. N. Y. Acad. Sci. 1960, 86, 844–874. [Google Scholar] [CrossRef]
- Sobol, I.M. The distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Faure, H. Discrépance de suites associées à un système de numération (en dimensions). Acta Arith. 1982, 41, 337–351. [Google Scholar] [CrossRef]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods, CBMS-NSF; SIAM: Philadelphia, PA, USA, 1992; Volume 63. [Google Scholar]
- Morokoff, W.J.; Caflisch, R.E. Quasi-Monte Carlo integration. J. Comput. Phys. 1995, 122, 218–230. [Google Scholar] [CrossRef] [Green Version]
- Paskov, S.H.; Traub, J.F. Faster valuation of financial derivatives. J. Portf. Manag. 1995, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Haupt, R.L. A Sparse Hammersley Element Distribution on a Spherical Antenna Array for Hemispherical Radar Coverage. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017. [Google Scholar]
- Bui, P.L.-T.; Rocca, P.; Haupt, R.L. Aperiodic planar array synthesis using pseudo-random sequences. In Proceedings of the 2018 International Applied Computational Electromagnetics Society Symposium, ACES 2018, Beijing, China, 29 July–1 August 2018; pp. 1–2. [Google Scholar]
- Torquato, S. Hyperuniform states of matter. Phys. Rep. 2018, 745, 1–95. [Google Scholar] [CrossRef] [Green Version]
- Torquato, S. Disordered hyperuniform heterogenous materials. J. Phys. Condens Matter 2016, 28, 414012. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Zheng, Y.; Xu, Y.; Jiao, Y.; Li, W. Hyperuniform flow fields resulting from hyperuniform configurations of circular disks. Phys. Rev. E 2018, 98, 063101. [Google Scholar] [CrossRef]
- Di Battista, D.; Ancora, D.; Zacharakis, G.; Ruocco, G.; Leonetti, M. Hyperuniformity in amorphous speckle patterns. Opt. Express 2018, 26, 15594–15608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DiStasio, R.A., Jr.; Zhang, G.; Stillinger, F.H.; Torquato, S. Rational design of stealthy hyperuniform two-phase media with tunable order. Phys. Rev. E 2018, 97, 023311. [Google Scholar] [CrossRef] [Green Version]
- Kocis, L.; Whiten, W.J. Computational Investigations of Low-Discrepancy Sequences. ACM Trans. Math. Softw. 1997, 23, 266–294. [Google Scholar] [CrossRef]
- van der Corput, J.G. Verteilungsfunktionen I. Akad. Van Wet. 1935, 38, 813–821. [Google Scholar]
- Wong, T.T.; Luk, W.S.; Heng, P.A. Sampling with Hammersley and Halton points. J. Graph. Tools 1997, 2, 9–24. [Google Scholar] [CrossRef]
- Sobol, I.M.; Levitan, Y.L. A pseudo-random number generator for personal computers. Comput. Math. Appl. 1999, 37, 33–40. [Google Scholar] [CrossRef] [Green Version]
- Bratley, P.; Fox, B.L. Algorithm 659 Implementing Sobol’s Quasirandom Sequence Generator. ACM Trans. Math. Softw. 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Hong, H.S.; Hickernell, F.J. Algorithm 823: Implementing Scrambled Digital Sequences. ACM Trans. Math. Softw. 2003, 29, 95–109. [Google Scholar] [CrossRef]
- Joe, S.; Kuo, F.Y. Remark on Algorithm 659: Implementing Sobol’s Quasirandom Sequence Generator. ACM Trans. Math. Softw. 2003, 29, 49–57. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/help/stats/sobolset.html (accessed on 12 October 2021).
- Gamito, M.N.; Maddock, S. Accurate multidimensional poisson disk sampling. ACM Trans. Graph. 2009, 29, 1–19. [Google Scholar] [CrossRef]
- Lagae, A.; Dutre, P. A comparison of methods for generating poisson disk distributions. Comput. Graph. Forum 2008, 27, 114–129. [Google Scholar] [CrossRef] [Green Version]







| Method | Average Minimum Element Spacing (λ) | Peak SLL (dB) | Directivity (dB) | Aperture Efficiency (%) |
|---|---|---|---|---|
| Uniform | 1.3333 | 0 | 31.5478 | 11.168 |
| Random | 0.6667 | −10.90 | 31.9619 | 12.209 |
| Random with Jitter | 0.9325 | −9.36 | 32.5775 | 14.068 |
| Hammersley (base 2) | 1.0037 | −7.0 | 32.7075 | 14.166 |
| Hammersley (base 3) | 1.1688 | −2.69 | 32.6226 | 14.215 |
| Hammersley (base 5) | 1.2624 | −0.55 | 31.6892 | 11.466 |
| Hammersley (base 7) | 0.7538 | −0.25 | 33.8949 | 19.054 |
| Halton (bases 2, 3) | 0.8436 | −10.10 | 32.4609 | 13.696 |
| Halton (bases 2, 5) | 0.8115 | −4.33 | 32.3534 | 13.361 |
| Halton (bases 2, 7) | 0.9172 | −12.35 | 32.8188 | 14.872 |
| Halton (bases 3, 5) | 0.8430 | −8.10 | 32.8611 | 15.018 |
| Halton (bases 3, 7) | 0.7663 | −5.90 | 32.2561 | 13.065 |
| Halton (bases 5, 7) | 0.8633 | −5.60 | 32.9511 | 15.332 |
| Sobol | 0.9307 | −6.58 | 32.7127 | 14.513 |
| Poisson Disk | 0.9031 | −12.28 | 32.8212 | 14.880 |
| Method/Aperture Type | Average Minimum Element Spacing (λ) | Peak SLL (dB) | Directivity (dB) | Aperture Efficiency (%) |
|---|---|---|---|---|
| Uniform/Rectangular | 1.3333 | 0 | 31.5778 | 11.175 |
| Uniform/Circular | 1.3333 | 0 | 31.5848 | 11.261 |
| Uniform/Elliptical | 1.3333 | 0 | 31.5181 | 11.228 |
| Halton/Rectangular | 0.8481 | −6.74 | 32.4857 | 13.774 |
| Halton/Circular | 0.8967 | −9.27 | 32.6474 | 14.383 |
| Halton/Elliptical | 0.7724 | −8.94 | 32.5883 | 14.365 |
| Poisson Disc/Rectangular | 0.9094 | −12.18 | 32.8062 | 14.829 |
| Poisson Disc/Circular | 0.9016 | −15.30 | 32.8643 | 15.119 |
| Poisson Disc/Elliptical | 0.9245 | −14.34 | 32.6634 | 14.616 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, T.; Anselmi, N.; Nayeri, P.; Rocca, P.; Haupt, R. Low Discrepancy Sparse Phased Array Antennas. Sensors 2021, 21, 7816. https://doi.org/10.3390/s21237816
Torres T, Anselmi N, Nayeri P, Rocca P, Haupt R. Low Discrepancy Sparse Phased Array Antennas. Sensors. 2021; 21(23):7816. https://doi.org/10.3390/s21237816
Chicago/Turabian StyleTorres, Travis, Nicola Anselmi, Payam Nayeri, Paolo Rocca, and Randy Haupt. 2021. "Low Discrepancy Sparse Phased Array Antennas" Sensors 21, no. 23: 7816. https://doi.org/10.3390/s21237816
APA StyleTorres, T., Anselmi, N., Nayeri, P., Rocca, P., & Haupt, R. (2021). Low Discrepancy Sparse Phased Array Antennas. Sensors, 21(23), 7816. https://doi.org/10.3390/s21237816







