Abstract
Epilepsy is a brain disorder disease that affects people’s quality of life. Electroencephalography (EEG) signals are used to diagnose epileptic seizures. This paper provides a computer-aided diagnosis system (CADS) for the automatic diagnosis of epileptic seizures in EEG signals. The proposed method consists of three steps, including preprocessing, feature extraction, and classification. In order to perform the simulations, the Bonn and Freiburg datasets are used. Firstly, we used a band-pass filter with 0.5–40 Hz cut-off frequency for removal artifacts of the EEG datasets. Tunable-Q Wavelet Transform (TQWT) is used for EEG signal decomposition. In the second step, various linear and nonlinear features are extracted from TQWT sub-bands. In this step, various statistical, frequency, and nonlinear features are extracted from the sub-bands. The nonlinear features used are based on fractal dimensions (FDs) and entropy theories. In the classification step, different approaches based on conventional machine learning (ML) and deep learning (DL) are discussed. In this step, a CNN–RNN-based DL method with the number of layers proposed is applied. The extracted features have been fed to the input of the proposed CNN–RNN model, and satisfactory results have been reported. In the classification step, the K-fold cross-validation with k = 10 is employed to demonstrate the effectiveness of the proposed CNN–RNN classification procedure. The results revealed that the proposed CNN–RNN method for Bonn and Freiburg datasets achieved an accuracy of 99.71% and 99.13%, respectively.
1. Introduction
Epilepsy is a noncontagious disease and one of the most prominent brain disorders. About 1% of the world’s population has been diagnosed with epilepsy [1]. Patients with epileptic seizures suffer from some temporary electric disorders [1,2,3]. About 20–30 percent of the patients diagnosed with epilepsy experience one or more strokes in a month [4,5,6]. In the epileptic seizures period, physical damages might even cause the death of the patient. The patients also suffer from lack of a good social position and experience some severe mental disorders [4,5,6].
In 2017, the International League Against Epilepsy (ILAE) presented a new classification of the epileptic seizure types: focal epilepsy, generalized epilepsy, and epilepsy with unknown symptoms [7]. In this classification, some detailed and precise information about each of the epileptic seizure types, including the types and the brain areas experiencing convulsion, are presented [7]. The early diagnosis of epileptic seizures has enormous importance and will prevent the disease progression significantly.
Many screening methods to diagnose epilepsy have been proposed until now, and the neuroimaging modalities have gained much attention from the specialized Specialist doctors [8]. Basically, the neuroimaging modalities in the diagnosis process of epileptic seizures include structural and functional methods. In the neuroimaging modalities, an epileptic seizure diagnosis based on EEG signals has remarkable popularity. EEG signal recording includes scalp EEG (sEEG) and intracranial EEG (IEEG) modalities [9]. EEG modalities include essential information from the functions of the brain in the epileptic seizures period. In comparison with other neuroimaging modalities, some benefits of EEG are a lower cost, the easiness of carrying, and suitable performance in epileptic seizure detection [9]. To diagnose epileptic seizures, doctors need to have a long record of the patient’s EEG signals. The EEG signals also usually have many various channels and artifacts, which cause some difficulties and challenges for doctors in the epileptic seizures diagnosis process [9,10].
To address these challenges, using CADS based on artificial intelligence (AI) can help to improve the speed and accuracy of the epilepsy diagnosis process [11,12,13]. AI-based CADS include ML and DL methods [14,15,16,17]. The most significant difference between CADS based on ML and DL is in the feature extraction step [9]. In CDAS based on ML, the most important feature extraction techniques include the time domain, frequency, and nonlinear features [18]. Choosing different feature extraction algorithms together to reach a high diagnosis accuracy demands a fair amount of knowledge in the field of ML [19,20].
On the other hand, the feature extraction and selection steps in CADS based on DL will be implemented on the deep layers. Many research projects are being conducted in the field of epileptic seizures diagnosis using DL and ML techniques [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76]. The purpose of these papers is to reach an authentic and accurate epileptic seizures diagnosis using EEG signals.
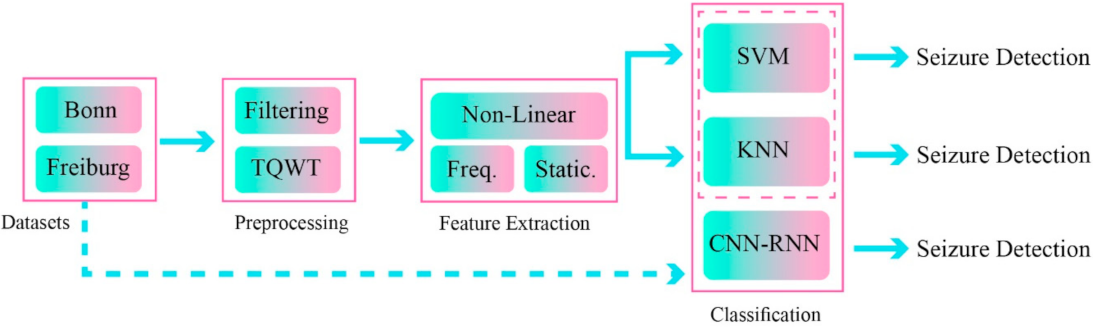
One recently developed AI field in epileptic seizures detection uses feature fusion techniques [77,78]. In these methods, a combination of features from different domains will improve the functionality and accuracy of the disease diagnosis process [77,78]. In this work, a novel epileptic seizure diagnosis method using a combination of handcrafted features and DL has been proposed; the summary of its steps is shown in Figure 1.
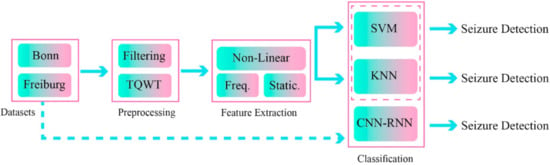
Figure 1.
Proposed method for epileptic seizure detection.
The proposed method includes the dataset, preprocessing, feature extraction, and classification steps. The two different datasets of Bonn [79] and Freiburg [80] were used to implement the proposed method. In the preprocessing step, the TQWT was used in EEG signal decomposition of different sub-bands.
Three variables are used for adjusting and reducing the search space of filter banks. The three important parameters of TQWT are the Q-factor, redundancy (r), and the number of sub-bands (J) [81]. The parameters Q = 1, r = 3, and J = 8 were chosen in this paper, similar to Reference [82]. After EEG signal decomposition using TQWT, various statistical, frequency, and nonlinear features are extracted. The EEG signals have a chaotic and nonlinear nature. Related works showed that nonlinear feature extraction methods play a significant role in improving the functionality and accuracy of the epileptic seizure diagnosis using EEG signals [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. The most important nonlinear feature extraction methods from EEG signals include various types of entropies [83], FDs [84], graphs [85], the largest Lyapunov exponent (LLE) [86], and correlation coefficients (CC) [87]. In this step, various statistical, frequency, and nonlinear features are extracted in the TQWT sub-bands.
In this paper, a novel class of entropy and fractal theory-based features was used. The combination of this class of handcrafted features was used in this paper for the first time as the first innovation. In this section, feature extraction algorithms were chosen and combined based on exploring other research papers and, also, their epileptic seizure diagnosis functionality. Fractal-based nonlinear features include Higuchi [88], Katz [88], Petrosian [88], and the detrended fluctuation analysis (DFA) [89,90]. Entropy-based feature extraction techniques also include Shannon [91,92,93], Log-Energy [93], spectral [94], Sample [95], permutation [96], Fuzzy [97], refined composite multiscale fuzzy [98], graph [99], Permutation Rényi [100], average Shannon wavelet [101], average Rényi wavelet [101], average Tsallis wavelet [101], inherent [102], fractional fuzzy [103], and average fuzzy [104]; all of these methods will be covered and fully explained in the third section.
In the classification step, a variety of classification methods based on ML methods and DL are used. Classification techniques based on ML involve the support vector machine (SVM) [105] and k-nearest neighbors (KNN) [106] methods. The DL method is a CNN–RNN with the proposed number of layers and is another the novelty of the paper.
The proposed CNN–RNN model has two inputs. In the first input, handcrafted features will be fed into the network. In the second input, raw EEG signals of each dataset will be fed into the network differently, and various features will be extracted after passing the convolutional and long short-term memory (LSTM) layers. These features will be combined afterward and will pass into the classification algorithm.
This paper is organized as follows: the proposed method for epileptic seizure detection in EEG signals is introduced in Section 2. In Section 3, the statistical metrics for the proposed method are presented. The results of the proposed method are shown in Section 4. The limitations of the study are presented in Section 5. Finally, the discussions, conclusions, and future works are introduced in Section 6.
2. Materials and Methods
2.1. Dataset
2.1.1. Bonn Dataset
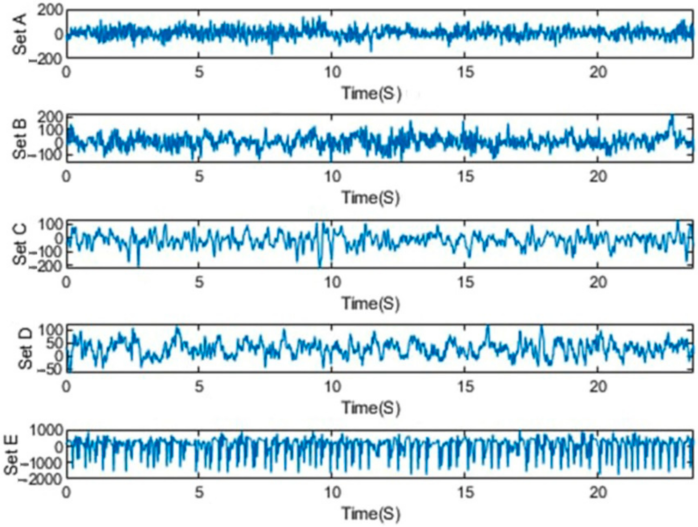
The Bonn dataset was recorded at the University of Bonn by a group of researchers, and it has been extensively used in the area of epileptic seizure analysis and detection [48]. The Bonn dataset is publicly available as 500-EEG single-channel data. It was sampled at 173.6 Hz with a 23.6 s duration. They consisted of five classes, viz., S, F, N, O, and Z, with 100 channel recordings in each class [79]. Five healthy controls in the relaxed and awake state with 10–20 standard electrode placement schemes contributed to the classes O and Z EEG surface data. Intracranial electrodes were used with five patients suffering from epilepsy to collect data of the S, F, and N classes. The hemisphere of the epileptogenic zone and the opposite hemisphere were used, respectively, for the recording of the F and S classes’ signals during the interictal (seizure-free) period. The ictal (seizure) period was taken into account in case of the recording of class S [79]. Samples of EEG signals of the dataset for each class are shown in Figure 2.
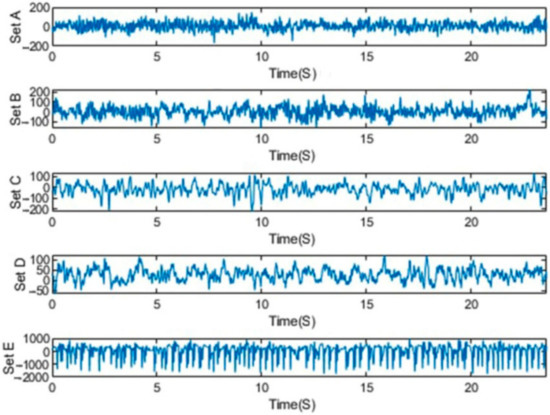
Figure 2.
Exemplary EEGs from five datasets.
Other details about the Bonn dataset are shown in Table 1.

Table 1.
A thorough explanation of the five subsets of the dataset.
To perform the experiments, 6 different classification problems are used, which are shown in Table 2.

Table 2.
More details about the six problem classifications.
2.1.2. Freiburg Dataset
The Freiburg dataset is another most frequently used resource for epileptic seizure detection [80]. It is also a freely accessible and downloadable EEG recording dataset. Twenty-one epileptic patients were considered for 24 h invasive presurgical continuous EEG signal recordings. During the time period, many seizures were recorded and occurred. This dataset includes epileptic seizure types of tonic–clonic (GTC), complex partial (CP), and simple partial (SP). Each of the cases has at least two types of epileptic seizures. The patients were from different age groups. They also differed in type and locality of seizures. The patients came to the University Hospital of Freiburg, Germany for a presurgical diagnosis. A Neurofile NT digital video EEG was used with a 256-Hz sampling rate and 128 channels [80]. The channels were numbers from 1 to 6, where the 1–3 channels were for focal recoding and 4–6 channels corresponded to extra focal ones. Interictal and ictal were the two types of signal files. The duration of the EEG signals for each patient in the ictal files was one hour. The format of the data files was ASCII. More details about this dataset is described in Table 3.

Table 3.
More details about the Fribourg dataset.
2.2. Preprocessing
Tunable-Q Wavelet Transform
The TQWT method is described in this section. TQWT is one of the newest wavelets transforms that is widely used in the processing of biological signals such as EEG signals. In TQWT, the redundancy (r), number of frequency sub-bands (J), and Q-factor (Q) can be tuned. The TQWT method consists of two low-pass and high-pass filter banks and is used to decompose EEG signals into different sub-bands. In this section, the low- and high-pass scale factors for filter banks with two channels are represented by and . The low-pass filter frequency response can be described as follows [81]:
The mathematical expression for the high-pass filter frequency response is as follows:
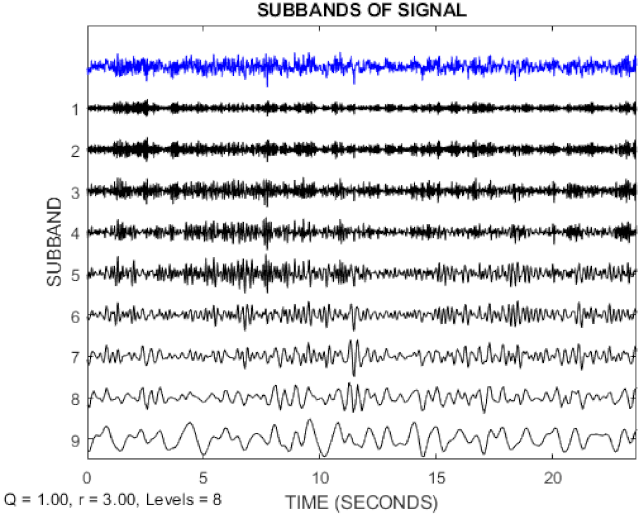
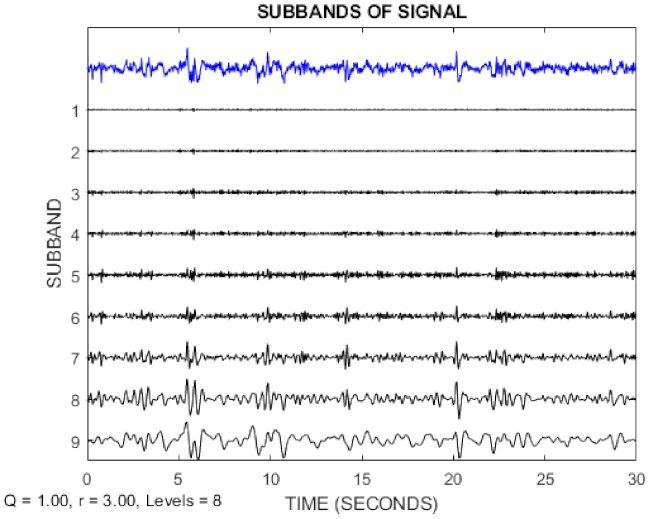
In this paper, the TQWT parameters for the two datasets are r = 3, Q = 1, and J = 8, respectively. Figure 3 and Figure 4 show the TQWT sub-bands for the Bonn and Freiburg datasets. In Figure 3 and Figure 4, EEG signals with different sub-band frequencies are shown. The selection of the EEG signal decomposition level was made similar Reference [81].
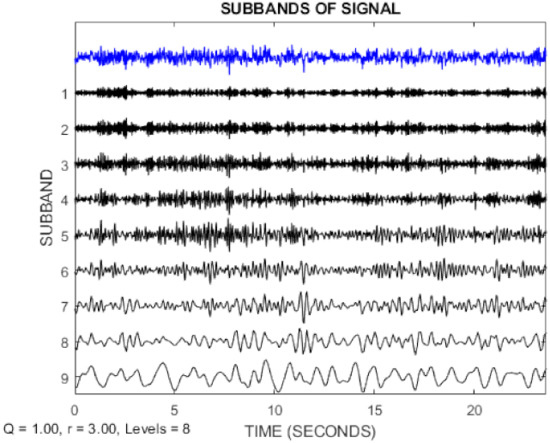
Figure 3.
EEG signal decomposition using TQWT for the Bonn dataset.
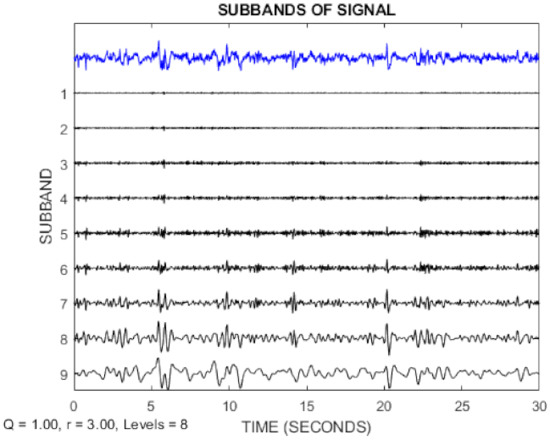
Figure 4.
EEG signal decomposition using TQWT for the Freiburg dataset.
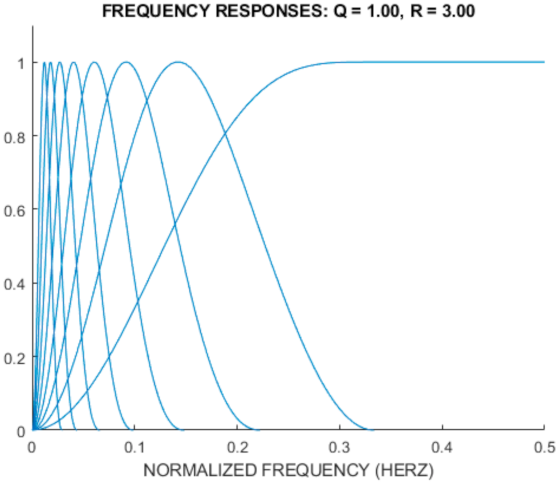
Additionally, Figure 5 shows the frequency response for TQWT based on the r = 3, Q = 1, and J = 8 parameters.
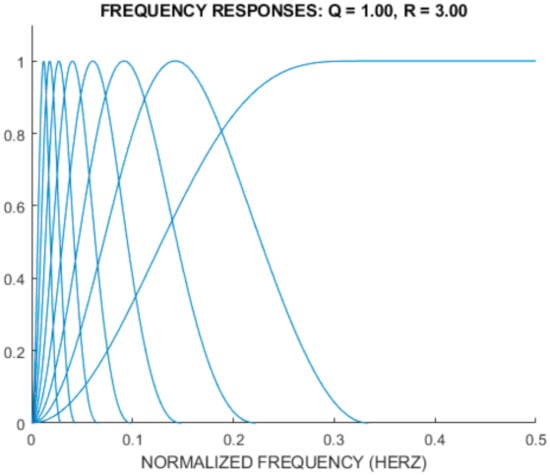
Figure 5.
The frequency response for TQWT with the R = 3, Q = 1, and J = 8 parameters.
2.3. Feature Extraction
In this section, various feature extraction methods are employed in epileptic seizure detection in the EEG signals. The feature extraction methods in the EEG signals contain the statistical, frequency domain, and nonlinear features. The nonlinear features are based on fractal theory entropy techniques. In the following section, each of these methods is discussed.
2.3.1. Statistical Features
The statistical features extract useful signal information, the most important of which are selected as shown in Table 4 [24].

Table 4.
Statistic features for epileptic seizure detection.
2.3.2. Frequency Features
- (1)
- Intensity Weighted Mean Frequency (IWMF)
The intensity weighted mean frequency (IWMF) or mean frequency is an average frequency that is calculated as the sum of the product of the normalized power spectral density (PSD) and the frequency. Consider as the normalized PSD of the signal epoch at the frequency of , and the IWMF is calculated by [107]
- (2)
- Intensity Weighted Bandwidth (IWBW)
The weighted standard deviation of the frequency and a measure of the PSD width can be obtained from [107].
where x[k] is the normalized PSD, and IMWF is the mean frequency of the input signal epoch. Whenever the PSD changes sharply, it results in a lower IWBW [107].
2.3.3. Fractal Features
The fractal dimensions (FDs) are an important class of nonlinear features and play a crucial role in the processing of EEG signals. FD-based feature extraction techniques, due to their properties, increase the accuracy of epileptic seizures detection in EEG signals. In this paper, the most important FDs, including Higuchi, Katz, Petrosian, and DFA are used to epileptic seizures detection in EEG signals. In the following, each of the FDs methods is presented along with their mathematical equations.
- (1)
- Higuchi Fractal
In this section, the theory of the Higuchi method is presented. Higuchi proposed this method in 1988, after which it has become a widely used technique for analyzing time series [88]. The Higuchi method is one of the most important FDs techniques that work well on nonlinear time series such as EEG signals. In the following, the steps of the Higuchi algorithm are proposed [88].
Consider the time sequence to be examined. The new time series is as follows [88].
In Equation (11), is means the discrete time interval between points, and is means the initial time value. For each time series , the average length is as follows [88].
In Equation (12), is a normalization factor, and is the total length of the sequence of the data . The delay is computed for all EEG data with an average length k as the mean of the lengths for . For each k ranging from 1 to , the procedure is repeated, producing the sum of the average lengths for each k as indicated below [88].
- (2)
- Katz Fractal
The FD of a curve can be termed as [88].
In Equation (14), d is the estimated diameter as the distance between the points of the sequence. Also, L parameter is the total length of the curve. The equation of the is as follows [88]:
In Equation (15), Point i is the one that maximizes the first point. The measurement units used depends on the computed FDs. The FDs are different if the units are different. Katz’s approach tries to resolve the issue by creating a general unit. The average step between successive points, a normalizes the distance [88]:
where n is the number of steps in the curve. Finally, Katz’s approach for feature extraction in EEG signals is defined as follows [88]:
- (3)
- Petrosian Fractal
This section presents the theory of the Petrosian method. In the Petrosian method, rapid FD estimation is performed, and the results show that this method has satisfactory results. The mathematical theory of the Petrosian method is shown in (18) [88]:
- (4)
- Detrended Fluctuation Analysis
The Reference [89] introduced DFA, which can be used in feature extraction from time series such as EEG signals. The RR interval of the time series is incorporated and divided into nonoverlapping and equal segments of length n for conducting such an analysis. Least squares fitting is applied to obtain the local trend in each segment and subtracted from . , the root mean square fluctuation estimates, are calculated at last, and the scaling exponents are measured as the slope of the double-log plot of F(n) against n [89,90]:
2.3.4. Entropy Features
In this paper, different entropies are exploited to extract the characteristics of EEG signals. The entropy-based features indicate the presence of signal irregularities and are also more resistant to noise than other methods. The entropy relationships used are shown below.
- (1)
- Shannon Feature
This entropy was proposed by Reference [94] and defined as
In Equation (20), Sn is the probability of the feature’s value.
- (2)
- Log-Energy Entropy
The log-energy entropy estimates the complex intensity of the signals. The log-energy entropy can be termed as [91,93]
- (3)
- Average Shannon Wavelet Entropy
In this section, the average entropy of wavelet Shannon is presented. If represents the energy of the 1st sub-band signal calculated from the wavelet coefficients, we can write the total energy of the signal as follows [101]:
where K represents the total number of EEG signals obtained from the wavelet sub-bands. The wavelet energy can be calculated as follows [101]:
The Shannon-based wavelet entropy relationship is defined as follows [101]:
Finally, the average wavelet Shannon entropy is defined based on and , which represent the Swn of the time series x and y of the EEG signal, as follows [101]:
- (4)
- Average Rényi Wavelet Entropy
The entropy of wavelet Rényi is defined in Relation (26) [101]:
Here, the parameter α is considered equal to 2. In another definition, Rényi entropy is expressed by Relation (27) [101]:
Similar to Equation (25), the average wavelet Rényi entropy is defined as follows [35]:
- (5)
- Average Tsallis Wavelet Entropy
In Reference [101], the entropy of wavelet Tsallis is studied in detail. Wavelet Tsallis entropy is defined as follows:
where parameter is called the nonextensivity index. The average wavelet Tsallis entropy is calculated as follows [101]:
- (6)
- Permutation Rényi Entropy
Consider the following time series. The vectors are constructed by selecting samples with identical distances from x, starting from the time point t [100]:
The values of are transformed in ascending order and, by generating , the modified version of , the time points are renamed [100]:
Therefore, each vector can be considered uniquely mapped on a symbol vector π = [t1, t2,…, tm]. PE can be calculated as follows [100]:
where log is a natural logarithm, and is the number of possible permutations. Since can reach ln (), PE is normalized. Then, the normalized PE relationship is defined by [100].
Here is a new definition of PE based on Rényi’s theory as follows [100]:
- (7)
- Graph Entropy
A new entropy method based on graph theory was proposed by Reference [99]. The relation of the graph entropy is described as [99].
where is the weight of the link between the ith node and the jth node, and m is the number of nodes connected to the ith node [99].
- (8)
- Fuzzy Entropy
For a time series , fuzzy entropy (FuEn) establishes vector sequences as given below [97]:
where m is the length of the sequences.
is the maximum absolute difference between and [97].
In Equations (40) and (41), parameter is the predefined gradient, and is the width of the exponential function. The function shows in the Eqation (41) [97]:
Finally, the is introduced as Equation (42) [97]:
- (9)
- Refined Composite Multiscale Fuzzy Entropy (RCMFE)
The RCMFE is computed as follows [98]:
RCMFE and RCMFE have differences that both use different equations in the first steps of their algorithms. The tolerance (r), Fuzzy entropy power (n), and the embedding dimension (m) [98].
- (10)
- Inherent Fuzzy Entropy
This section expresses inherent fuzzy entropy (IFuEn). The steps of IFuEn are as follows [102]:
Step 1. Multiple IMFs are made by breaking down the original x(t) signal and reconstructing the signal using EMD techniques, which are done as follows [102]:
- 1.
- Calculating the extremes to cover and [102].
- 2.
- Calculating the average [102]:
- 3.
- Candidates of inherent functions are derived intrinsic mode functions (IMFs) [102]:
- 4.
- Calculating the value of r(t) as follows [102]:
- 5.
- Given t = t + 1, consider d(t + 1) as the input EEG data; while iterating on the residual m(t), which continues until the final residue r that becomes a monotonic function from which no more IMF can be extracted [102].
- 6.
- The total accumulated residual IMFs are used to reconstruct the signal [102]:
Step 2: FuEn to evaluate the complexity, which is similar to Equation (42) [102].
Step 3: Multi-scale version [102]
is the coarse-grained time series, and its equation is as follows [102]:
In this regard, τ is the scale factor. Also, the length of each coarse-grained time series is N/τ [102].
- (11)
- Averaged Fuzzy Entropy
Average fuzzy entropy (AFuEn) is an improved model of FuEn. In AFuEn method, an improved m_ pattern is compared to . At this AFuEn, Equation (49) is modified as follows [104]:
In the following, four different types of operations with are defined as follows [104]:
- A translation of n samples, corresponds to .
- A reflection at the position n, corresponds to .
- An inversion at the position n, corresponds to .
- A glide reflection of n samples, corresponds to .
In this case, , , , and are obtained. The following is as follows [104]:
Finally, the is shows as Equation (51) [104]:
- (12)
- Fractional Fuzzy Entropy
In Reference [103], researchers introduced the fractional-order entropy of Shannon, which is defined as
In Equation (52), α is the fractional-order derivation. Moreover, and denote the gamma and digamma functions, respectively. The equation of fractional-order information is defined as Equation (53):
In Equation (42), FuEn is introduced. Placing Equation (53) in Equation (42), fractional fuzzy entropy (FFuEn) may be stated as
- (13)
- Spectral Entropy
This method is normalized Shannon entropy, which quantitatively defines the spectral complexity of the EEG signals as follows [94]:
- (14)
- Sample Entropy
In the equation below, the sample entropy formula is shown [95]:
where A refers to the total number of vector pairs of length m + 1, and B comprises the total number of vector pairs of length m [95].
- (15)
- Permutation Entropy
Permutation entropy estimates the complexity of biomedical signals, such as EEG signals, by measuring the couplings between two classes. The equation of permutation entropy is presented as follows [96]:
where n defines the sequence length, and illustrates the likelihood of the nth occurrence [96].
2.4. Classification
2.4.1. SVM
While these methods have been around for longer than many other machine learning algorithms, in recent decades, despite many advances in machine learning and the introduction of a wide variety of novel algorithms, support vector machines [105] have not lost their popularity and are still considered one of the most well-known and applied methods among researchers. These algorithms, which are generally based on finding hyperplanes that maximize the margin, use the kernel trick to classify data in complex and high-dimensional spaces with suitable accuracy. Linear, RBF, and polynomial are the most popular SVM kernels [105].
2.4.2. KNN
One of the simplest and, at the same time, most practical machine learning methods is the KNN algorithm [106], which is widely used for classification. There is no learning phase in this method, but in the test phase, the classifier finds the K-nearest neighbor to this data point (as the name of the method implies) and assigns the data label according to their dominant label. Nevertheless, this method works very slowly in times when the amount of training data is enormous [106].
2.4.3. CNN–RNN
In this section, the proposed DL architecture for the detection of epileptic seizures based on EEG signals is discussed. The network used in this paper has a CNN–RNN structure with the use of extracted features. Nowadays, combined deep learning models such as CNN–RNN have achieved successful results in diagnosing and predicting diseases from medical data.
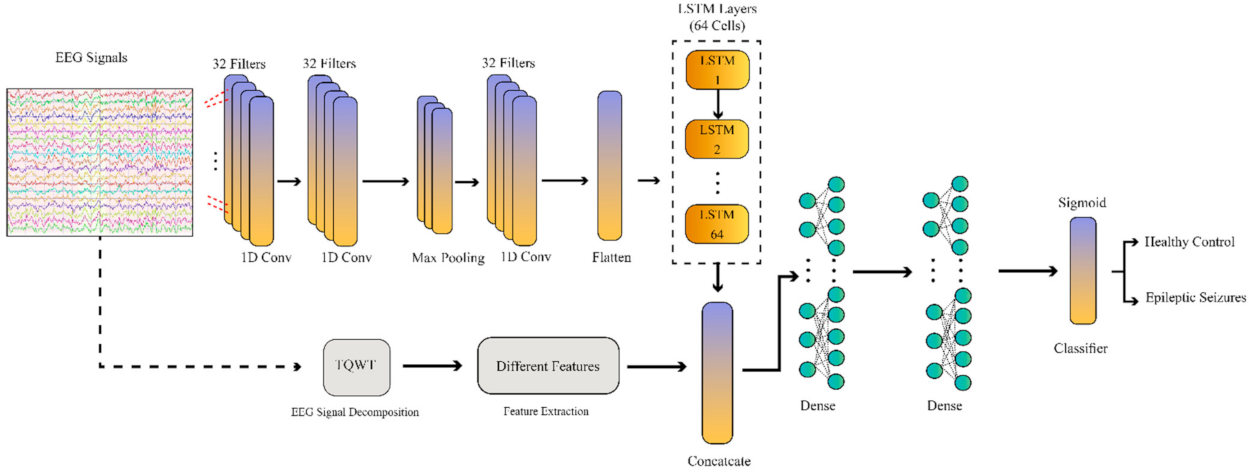
Convolutional layers are usually used in the primary layers to combine CNN models with RNN, which are responsible for extracting the features. The output of the convolutional layers is then applied to the RNN layers to use their superiority to identify the global pattern [108,109]. The purpose of this work is because the convolution layers empirically find local and spatial patterns far better than RNNs in signals [109]. Second, adding convolution layers allows the RNN to see the data faster, thus finding more distance patterns. Additionally, in this study, it has been proven that combining handcrafted features with CNN–RNN networks helps to increase the efficiency and accuracy of the CADS detection of epileptic seizures from EEG signals. In this study, the selection of the number of layers of the CNN–RNN model is presented for the first time by the researchers in this paper.
In this paper, a deep CNN–RNN network with the proposed number of layers, along with handcrafted features, is used to diagnose epileptic seizures. The proposed CNN–RNN model is applied to the Bonn and Freiburg datasets, along with the handcrafted features. The CNN–RNN model has the same structure for both datasets. Figure 6 shows the proposed CNN–RNN model. Additionally, the hyper parameters of the model are shown in Table 5.
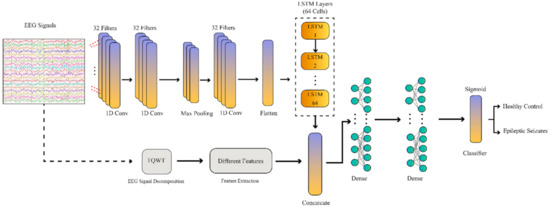
Figure 6.
Block diagram of the proposed CNN–RNN network.

Table 5.
CNN–RNN hyper-parameters.
In the proposed deep learning method, there are three convolutional layers in the convolutional section to extract features and one max-pooling layer with a feature reduction purpose. After that, there is a flatten layer to transform the extracted features into feature vectors. Then, an LSTM block with 64 neurons was used to extract the RNN features. Afterwards, a combination block was used to combine the CNN–RNN and handcrafted features. Finally, three fully connected layers were implemented to classify the data. In the proposed CNN–RNN model, each layer’s selection and its parameters were made by trial and error.
3. Statistical Metrics
In this paper, the classification results are evaluated using the 10-fold cross-validation techniques. In K-fold cross-validation, the total number of observations are split into K-folds, where the data samples are limited. Finally, the performance of the algorithm was estimated using statistical metrics include specificity (Spec), sensitivity (Sens), accuracy (Acc), and F1-score (F1-S), and precision (Prec). The true positive (TP), true negative (TN), false negative (FN), and false positive (FP) parameters are extracted from the confusion matrix [110].
4. Results
The experiments are performed on a Ryzen 1700 machine with 8-GB RAM using MATLAB for feature extraction and TensorFlow 2 and scikit-learn for the classification algorithms. In this part of the paper, we present the results of the proposed method. The proposed method includes the preprocessing, feature extraction, and classification steps. The preprocessing step includes windowing, noise removal, and decomposition of the EEG signals into various sub-bands by the TQWT. In the first step of preprocessing, the signals from the Bonn and Freiburg datasets are decomposed into different time windows. For the Bonn dataset, each EEG signal is segmented into time windows of 5 s, and for the Freiburg dataset, each EEG signal is segmented into time windows of 4 s. In the following, a Butterworth band-pass filter is used to preprocess the signals of the datasets. In the third preprocessing step, TQWT is used for EEG signal decomposition. As mentioned earlier, the important TQWT parameters are selected as Q = 1, r = 3, and J = 8 for both datasets.
In the following, various statistical, frequency, and nonlinear features are extracted from the TQWT sub-bands. The combination of these features has been done for the first time in this paper and is considered an important novelty.
In the final part of CADS, the epileptic seizure detection based on EEG signals, ML classifier algorithms, and deep learning was examined and tested. The ML classifier techniques include SVM and KNN methods. On the other hand, the DL method is a CNN–RNN model. This method of classification is another novelty of this paper. Here, the proposed CNN–RNN method has two separate inputs. In the first input, Bonn or Freiburg dataset signals are applied to one of the proposed CNN–RNN network inputs. After passing the raw signals of the datasets through the one-dimensional (1D) convolutional layers, they finally reach the flatten layer. On the other hand, handcrafted feature extraction methods are applied to the second input of the proposed CNN–RNN architecture (Figure 6). Then, the handcrafted features and the features extracted from the 1D convolutional layers are merged and passed through the RNN layers to be finally classified.
In the proposed CNN–RNN implementation on the Bonn dataset, each data is broken into 5 s windows, and after preprocessing, some features are extracted from it. At the same time, each 5 s window, which contains 868 frames of data, is broken by 25 overlaps into 33 windows, each containing 50 frames, which are used for CNN–RNN input as the raw data. In the proposed method, each 100-epoch network is trained using the categorical cross-entropy error function and Adam optimizer.
It is also important to note that the implementation and configuration of the proposed CNN–RNN model for the Freiburg dataset are similar to the Bonn dataset. As can be seen in Table 6 and Table 7, the proposed CNN–RNN model has been successful in epileptic seizure detection from the Bonn and Freiburg datasets. In Table 6, the different classifications are reviewed.

Table 6.
Results for the Bonn dataset.

Table 7.
Results for the Fribourg dataset.
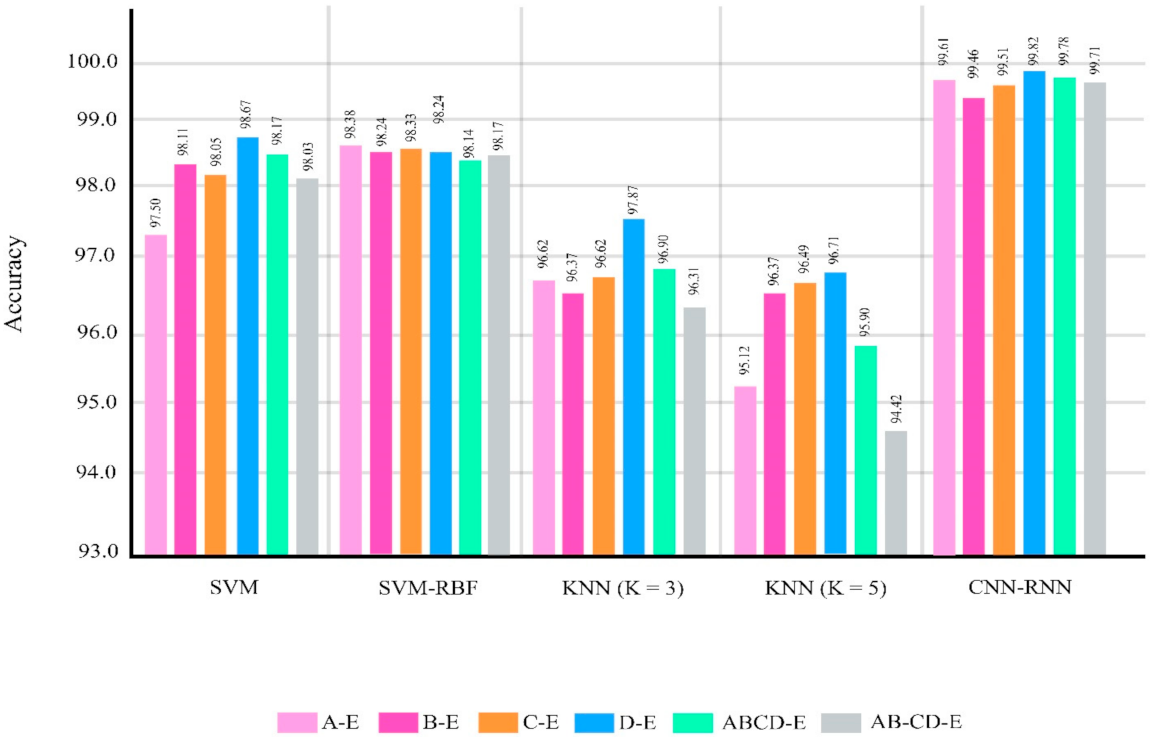
The classifications were chosen similar to the research papers about epileptic seizure diagnosis based on EEG signals using the Bonn dataset [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. Figure 7 and Table 6 show the performances of different classifier methods for the Bonn dataset.
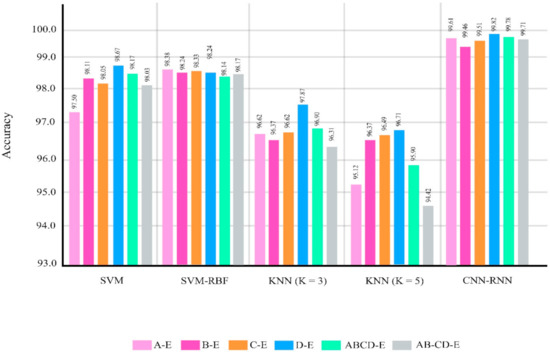
Figure 7.
Results for different methods in different classification problems of the Bonn dataset.
Additionally, the results of the Fribourg dataset are shown in Table 7.
5. Limitations of Study
In this section, the limitations of the study are discussed. As mentioned before, epileptic seizures have various types, and their on-time diagnosis has great importance. There has been no dataset on the types of epileptic seizures so far. Therefore, researchers cannot do serious research in this field. In addition, the available EEG datasets for epileptic seizure diagnosis have limited use, and achieving actual and accurate epileptic seizure detection based on AI techniques is not possible due to this limitation. Another limitation of epileptic seizure diagnosis from EEG signals is that there are no dataset of EEG signals with preictal, ictal, and interictal times being highlighted in them. In the case of addressing these limitations, it is possible to use advanced and novel DL models to diagnose various types of epileptic seizures.
6. Discussion, Conclusions, and Future Works
Epileptic seizures are defined as a group of neurological disorders, and their early diagnosis is of particular importance for specialist physicians and neurologists [82,111]. In order to epileptic seizures detection, several techniques have been proposed until now. Among the neuroimaging modalities, EEG is pivotally significant to specialist physicians compared to other modalities. EEG signals provide specialist physicians with accurate information about brain functions, which helps to accurately diagnose epileptic seizures. EEG signals, though very beneficial, are not bereft of disadvantages and always cause problems for specialist physicians. Long-term recording, multiple EEG channels, various noises in EEG signals, etc. are some of the physicians’ difficulties that pose problems for accurately and quickly diagnosing epileptic seizures.
So far, various AI methods have been proposed to epileptic seizures detection, aiming to aid specialist physicians in the rapid diagnosis of epileptic seizures based on EEG signals. Researchers in the past have mostly exploited ML methods to diagnose epileptic seizures. Inefficiency in large amounts of input data, the complexity of the methods, the need for great knowledge to use ML methods in diagnosing epileptic seizures, etc. are the most important deficiencies of these methods. To address this issue, in recent years, DL approaches have been proposed that possess appropriate efficiency and performance for diagnosing various diseases, including epileptic seizures, by using a large amount of input data.
The proposed method consisted of three parts: preprocessing, feature extraction, and classification. Two datasets, Bonn and Freiburg, were exploited for the experiments. Bonn dataset signals were selected for 5 s time windows and Freiburg dataset signals for 4 s time windows. In the preprocessing step, first, a Butterworth band-pass filter was utilized for the initial preprocessing of the two dataset signals. Following the preprocessing step, the TQWT technique was adopted to decompose the EEG signal datasets into different su-bands. The TQWT parameters were selected to be applied to the two datasets similar to Reference [82].
In the following, a variety of statistical, frequency, and nonlinear features were extracted from TQWT sub-bands. Statistical features contain statistical moments. Nonlinear features also involve two categories of FDs and entropies. FD-based nonlinear features include Higuchi, Katz, Petrosian, and DFA. Entropy-based feature extraction techniques also include Shannon, Log-Energy, spectral, Sample, permutation, Fuzzy, refined composite multiscale fuzzy, graph, Permutation Rényi, average Shannon wavelet, average Rényi wavelet, average Tsallis wavelet, inherent, fractional fuzzy, and average fuzzy. In the feature extraction section, for the first time, a combination of these features has been used to epileptic seizures detection based on EEG signals and is considered the first novelty of this article.
Finally, ML methods and a CNN–RNN based on a DL model were exploited in the classification step. Among the classification methods, the CNN–RNN was applied for the first time in this study and was carried to account for another novelty. Here, the proposed CNN–RNN approach entailed two separate inputs. In the first input, the EEG signals of the Bonn or Freiburg datasets were fed to one of the proposed CNN–RNN network inputs. After the raw signals of the datasets passing through the 1D convolutional layers, they eventually attained the flatten layer. On the other hand, handcrafted feature extraction methods were applied to the second input of the proposed CNN–RNN architecture (Figure 6). Then, the handcrafted features and the features extracted from the one-dimensional convolutional layers were combined and passed through the RNN layers to finally be classified. In the classification section, K-fold cross-validation with K = 10 was used to calculate the valid outcomes. The proposed CNN–RNN architecture is a novel feature fusion procedure. Among the advantages of the proposed architecture, its high accuracy and greater efficiency in practical applications can be meaningful. The results identified that the proposed CNN–RNN scheme was able to achieve the maximum level of accuracy among all the algorithms used.
Then, in Table 8 and Table 9, the researchers conducted on the Bonn and Freiburg datasets for the diagnosis of epileptic seizures using AI methods are presented and compared with the proposed method.

Table 8.
Comparison of the proposed method with other related works for the Bonn dataset.

Table 9.
Comparison of the proposed method with other related works on the Fribourg dataset.
According to Table 8 and Table 9, it can be perceived that the proposed CADS for the diagnosis of epileptic seizures using the handcrafted features and the proposed CNN–RNN model have achieved successful results.
As shown in Table 8 and Table 9, the proposed method could improve the performance and accuracy of an epileptic seizure diagnosis in the Bonn and Freiburg datasets. The proposed method has higher performance in comparison with other research projects. Table 8 and Table 9 shows that the results are reliable, and it is possible to use this proposed method in clinical applications to diagnose epileptic seizures. The proposed method in this paper has high efficacy in the diagnosis of epileptic seizures. In this method, different handcrafted features are used in combination with DL that improved the accuracy of diagnosing epileptic seizures based on EEG signals. The proposed method can help specialists rapidly diagnose epileptic seizures. This study shows that the proposed method can be implemented on a software platform and used in hospitals.
In future works, graph theory methods will be utilized, coupled with novel handcrafted features [112,113]. Additionally, applying new fuzzy entropies as feature extraction methods can be a future work. Additionally, another future work is to use fuzzy methods [114,115] in epileptic seizure detection. In other future works, effective connectivity techniques may be used to diagnose epileptic seizures [116,117,118]; first, EEG signals are transformed into 2D images using effective connectivity methods. Then, these 2 D images are applied to different 2D deep learning networks. Another future work is using novel DL techniques such as attention learning [119,120,121,122], transformers [123,124], and other advanced deep learning techniques [125,126,127,128,129,130,131,132,133,134] for epileptic seizure detection. Finally, adopting novel deep feature fusion techniques to epileptic seizures detection based on EEG signals can be noteworthy as one of the future works [135].
Author Contributions
Conceptualization, A.M. and A.Z.; methodology, A.Z., A.M. and M.Y.; software, A.M. and H.-R.K.; validation, R.A. and M.Y.; formal analysis, A.M., R.A., A.Z. and M.Y.; resources, A.Z. and A.M.; writing—original draft preparation, A.M., R.A. and H.-R.K.; writing—review and editing, A.M., A.Z., M.Y., R.A. and H.-R.K.; and visualization, A.Z., A.M. and R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gastaut, H. Clinical and Electroencephalographical Classification of Epileptic Seizures. Epilepsia 1970, 11, 102–112. [Google Scholar] [CrossRef]
- WHO. Improving Access to Epilepsy Care. Available online: https://www.who.int/mental_health/neurology/epilepsy/en/ (accessed on 29 August 2019).
- Arunkumar, N.; Ramkumar, K.; Venkatraman, V.; Abdulhay, E.; Fernandes, S.L.; Kadry, S.; Segal, S. Classification of focal and non focal EEG using entropies. Pattern Recognit. Lett. 2017, 94, 112–117. [Google Scholar]
- Pati, S.; Alexopoulos, A.V. Pharmacoresistant epilepsy: From pathogenesis to current and emerging therapies. Clevel. Clin. J. Med. 2010, 77, 457–467. [Google Scholar] [CrossRef]
- Newton, M.R.; Berkovic, S.; Austin, M.C.; Rowe, C.C.; McKay, W.J.; Bladin, P.F. SPECT in the localisation of extratemporal and temporal seizure foci. J. Neurol. Neurosurg. Psychiatry 1995, 59, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Seeck, M.; Lazeyras, F.; Michel, C.; Blanke, O.; Gericke, C.; Ives, J.; Delavelle, J.; Golay, X.; Haenggeli, C.; de Tribolet, N.; et al. Non-invasive epileptic focus localization using EEG-triggered functional MRI and electromagnetic tomography. Electroencephalogr. Clin. Neurophysiol. 1998, 106, 508–512. [Google Scholar] [CrossRef]
- International League against Epilepsy. Available online: https://www.ilae.org/ (accessed on 13 November 2021).
- Shoeibi, A.; Khodatars, M.; Ghassemi, N.; Jafari, M.; Moridian, P.; Alizadehsani, R.; Panahiazar, M.; Khozeimeh, F.; Zare, A.; Hosseini-Nejad, H.; et al. Epileptic Seizures Detection Using Deep Learning Techniques: A Review. Int. J. Environ. Res. Public Health 2021, 18, 5780. [Google Scholar] [CrossRef] [PubMed]
- Shoeibi, A.; Ghassemi, N.; Khodatars, M.; Jafari, M.; Moridian, P.; Alizadehsani, R.; Nahavandi, S. Applications of Epileptic Seizures Detection in Neuroimaging Modalities Using Deep Learning Techniques: Methods, Challenges, and Future Works. arXiv 2021, arXiv:2105.14278. [Google Scholar]
- Beeraka, S.M.; Kumar, A.; Sameer, M.; Ghosh, S.; Gupta, B. Accuracy Enhancement of Epileptic Seizure Detection: A Deep Learning Approach with Hardware Realization of STFT. Circuits Syst. Signal Process. 2021, 1–24. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Tsalikakis, D.G.; Karvounis, E.C.; Astrakas, L.; Konitsiotis, S.; Tzaphlidou, M. Automated Epileptic Seizure Detection Methods: A Review Study. In Epilepsy-Histological, Electroencephalographic and Psychological Aspects; IntechOpen: London, UK, 2012; pp. 75–98. [Google Scholar]
- Pediaditis, M.; Tsiknakis, M.; Leitgeb, N. Vision-based motion detection, analysis and recognition of epileptic seizures—A systematic review. Comput. Methods Programs Biomed. 2012, 108, 1133–1148. [Google Scholar] [CrossRef]
- Hussein, A.F.; Arunkumar, N.; Gomes, C.; AlZubaidi, A.K.; Habash, Q.A.; Santamaria-Granados, L.; Mendoza-Moreno, J.; Ramirez-Gonzalez, G. Focal and Non-Focal Epilepsy Localization: A Review. IEEE Access 2018, 6, 49306–49324. [Google Scholar] [CrossRef]
- Shoeibi, A.; Sadeghi, D.; Moridian, P.; Ghassemi, N.; Heras, J.; Alizadehsani, R.; Gorriz, J.M. Automatic Diagnosis of Schizophrenia using EEG Signals and CNN-LSTM Models. arXiv 2021, arXiv:2109.01120. [Google Scholar]
- Shoeibi, A.; Khodatars, M.; Jafari, M.; Moridian, P.; Rezaei, M.; Alizadehsani, R.; Khozeimeh, F.; Gorriz, J.M.; Heras, J.; Panahiazar, M.; et al. Applications of deep learning techniques for automated multiple sclerosis detection using magnetic resonance imaging: A review. Comput. Biol. Med. 2021, 136, 104697. [Google Scholar] [CrossRef] [PubMed]
- Alizadehsani, R.; Sharifrazi, D.; Izadi, N.H.; Joloudari, J.H.; Shoeibi, A.; Gorriz, J.M.; Acharya, U.R. Uncertainty-aware semi-supervised method using large unlabelled and limited labeled COVID-19 data. arXiv 2021, arXiv:2102.06388. [Google Scholar]
- Alizadehsani, R.; Roshanzamir, M.; Hussain, S.; Khosravi, A.; Koohestani, A.; Zangooei, M.H.; Abdar, M.; Beykikhoshk, A.; Shoeibi, A.; Zare, A.; et al. Handling of uncertainty in medical data using machine learning and probability theory techniques: A review of 30 years (1991–2020). Ann. Oper. Res. 2021, 1–42. [Google Scholar] [CrossRef]
- Obukhov, Y.V.; Kershner, I.A.; Tolmacheva, R.A.; Sinkin, M.V.; Zhavoronkova, L.A. Wavelet Ridges in EEG Diagnostic Features Extraction: Epilepsy Long-Time Monitoring and Rehabilitation after Traumatic Brain Injury. Sensors 2021, 21, 5989. [Google Scholar] [CrossRef]
- Akter, M.; Islam, R.; Tanaka, T.; Iimura, Y.; Mitsuhashi, T.; Sugano, H.; Wang, D.; Molla, K.I. Statistical Features in High-Frequency Bands of Interictal iEEG Work Efficiently in Identifying the Seizure Onset Zone in Patients with Focal Epilepsy. Entropy 2020, 22, 1415. [Google Scholar] [CrossRef]
- Kotiuchyi, I.; Pernice, R.; Popov, A.; Faes, L.; Kharytonov, V. A Framework to Assess the Information Dynamics of Source EEG Activity and Its Application to Epileptic Brain Networks. Brain Sci. 2020, 10, 657. [Google Scholar] [CrossRef] [PubMed]
- Patidar, S.; Pachori, R.B.; Upadhyay, A.; Acharya, U.R. An integrated alcoholic index using tunable-Q wavelet transform based features extracted from EEG signals for diagnosis of alcoholism. Appl. Soft Comput. 2017, 50, 71–78. [Google Scholar] [CrossRef]
- Sharaf, A.I.; Abu El-Soud, M.; El-Henawy, I.M. An Automated Approach for Epilepsy Detection Based on Tunable Q-Wavelet and Firefly Feature Selection Algorithm. Int. J. Biomed. Imaging 2018, 2018, 5812872. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Ghaffar, E.A. Effect of tuning TQWT parameters on epileptic seizure detection from EEG signals. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 19–20 December 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 47–51. [Google Scholar]
- Al Ghayab, H.R.; Li, Y.; Siuly, S.; Abdulla, S. A feature extraction technique based on tunable Q-factor wavelet transform for brain signal classification. J. Neurosci. Methods 2019, 312, 43–52. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B.; Upadhyay, A.; Acharya, U.R. Tunable-Q Wavelet Transform Based Multiscale Entropy Measure for Automated Classification of Epileptic EEG Signals. Appl. Sci. 2017, 7, 385. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Singh, L.; Pachori, R.B. Identification of Epileptic Seizures from Scalp EEG Signals Based on TQWT. In Machine Intelligence and Signal Analysis; Advances in Intelligent Systems and Computing; Springer International Publishing: Singapore, 2019; pp. 209–221. [Google Scholar]
- Bhattacharyya, A.; Pachori, R.B.; Acharya, U.R. Tunable-Q Wavelet Transform Based Multivariate Sub-Band Fuzzy Entropy with Application to Focal EEG Signal Analysis. Entropy 2017, 19, 99. [Google Scholar] [CrossRef]
- Gupta, V.; Bhattacharyya, A.; Pachori, R.B. Classification of seizure and non-seizure EEG signals based on EMD-TQWT method. In Proceedings of the 2017 22nd International Conference on Digital Signal Processing (DSP), London, UK, 23–25 August 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Hassan, A.R.; Siuly, S.; Zhang, Y. Epileptic seizure detection in EEG signals using tunable-Q factor wavelet transform and bootstrap aggregating. Comput. Methods Programs Biomed. 2016, 137, 247–259. [Google Scholar] [CrossRef]
- Nishad, A.; Pachori, R.B.; Acharya, U.R. Application of TQWT based filter-bank for sleep apnea screening using ECG signals. J. Ambient. Intell. Humaniz. Comput. 2018, 1–12. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, M.; Pachori, R.B.; Acharya, U.R. Decision support system for focal EEG signals using tunable-Q wavelet transform. J. Comput. Sci. 2017, 20, 52–60. [Google Scholar] [CrossRef]
- Reddy, G.R.S.; Rao, R. Automated identification system for seizure EEG signals using tunable-Q wavelet transform. Eng. Sci. Technol. Int. J. 2017, 20, 1486–1493. [Google Scholar] [CrossRef]
- Jindal, K.; Upadhyay, R.; Singh, H.S. Application of tunable-Q wavelet transform based nonlinear features in epileptic seizure detection. Analog. Integr. Circuits Signal Process. 2019, 100, 437–452. [Google Scholar] [CrossRef]
- Gupta, V.; Nishad, A.; Pachori, R.B. Focal EEG signal detection based on constant-bandwidth TQWT filter-banks. In Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 3–6 December 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 2597–2604. [Google Scholar]
- Sharma, R.R.; Pachori, R.B. Time–frequency representation using IEVDHM–HT with application to classification of epileptic EEG signals. IET Sci. Meas. Technol. 2018, 12, 72–82. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Li, M. Complex-valued distribution entropy and its application for seizure detection. Biocybern. Biomed. Eng. 2020, 40, 306–323. [Google Scholar] [CrossRef]
- Rout, S.K.; Biswal, P.K. An efficient error-minimized random vector functional link network for epileptic seizure classification using VMD. Biomed. Signal Process. Control. 2020, 57, 101787. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Akbal, E. A novel local senary pattern based epilepsy diagnosis system using EEG signals. Australas. Phys. Eng. Sci. Med. 2019, 42, 939–948. [Google Scholar] [CrossRef]
- Alturki, F.A.; Alsharabi, K.; AbdurRaqeeb, A.M.; Aljalal, M. EEG Signal Analysis for Diagnosing Neurological Disorders Using Discrete Wavelet Transform and Intelligent Techniques. Sensors 2020, 20, 2505. [Google Scholar] [CrossRef]
- Sukriti; Chakraborty, M.; Mitra, D. Epilepsy Seizure Detection using Non-linear and DWT-based Features. In Proceedings of the 2019 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 158–163. [Google Scholar]
- Houssein, E.H.; Hamad, A.; Hassanien, A.E.; Fahmy, A.A. Epileptic detection based on whale optimization enhanced support vector machine. J. Inf. Optim. Sci. 2019, 40, 699–723. [Google Scholar] [CrossRef]
- Ramanna, S.; Tirunagari, S.; Windridge, D. Epileptic seizure detection using constrained singular spectrum analysis and 1D-local binary patterns. Health Technol. 2020, 10, 699–709. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, X.; Chen, L.; Yang, Z. Automatic Diagnosis of Epileptic Seizure in Electroencephalography Signals Using Nonlinear Dynamics Features. IEEE Access 2019, 7, 61046–61056. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Li, M. Fuzzy distribution entropy and its application in automated seizure detection technique. Biomed. Signal Process. Control. 2018, 39, 360–377. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Li, M. Classification of inter-ictal and ictal EEGs using multi-basis MODWPT, dimensionality reduction algorithms and LS-SVM: A comparative study. Biomed. Signal Process. Control. 2019, 47, 240–251. [Google Scholar] [CrossRef]
- Mamli, S.; Kalbkhani, H. Gray-level co-occurrence matrix of Fourier synchro-squeezed transform for epileptic seizure detection. Biocybern. Biomed. Eng. 2019, 39, 87–99. [Google Scholar] [CrossRef]
- Aayesha; Qureshi, M.B.; Afzaal, M.; Fayaz, M. Machine learning-based EEG signals classification model for epileptic seizure detection. Multimed. Tools Appl. 2021, 80, 17849–17877. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.-D.; Luo, M.-L.; Li, K.; Yang, X.-F.; Guo, Q. Epileptic Seizure Classification of EEGs Using Time–Frequency Analysis Based Multiscale Radial Basis Functions. IEEE J. Biomed. Health Inform. 2018, 22, 386–397. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adeli, H. Deep convolutional neural network for the automated detection and diagnosis of seizure using EEG signals. Comput. Biol. Med. 2018, 100, 270–278. [Google Scholar] [CrossRef]
- Siuly, S.; Alcin, O.F.; Bajaj, V.; Sengur, A.; Zhang, Y. Exploring Hermite transformation in brain signal analysis for the detection of epileptic seizure. IET Sci. Meas. Technol. 2019, 13, 35–41. [Google Scholar] [CrossRef]
- Riaz, F.; Hassan, A.; Rehman, S.; Niazi, I.K.; Dremstrup, K. EMD-Based Temporal and Spectral Features for the Classification of EEG Signals Using Supervised Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 28–35. [Google Scholar] [CrossRef]
- Sharma, M.; Pachori, R.B.; Acharya, U.R. A new approach to characterize epileptic seizures using analytic time-frequency flexible wavelet transform and fractal dimension. Pattern Recognit. Lett. 2017, 94, 172–179. [Google Scholar] [CrossRef]
- Chandel, G.; Upadhyaya, P.; Farooq, O.; Khan, Y. Detection of Seizure Event and Its Onset/Offset Using Orthonormal Triadic Wavelet Based Features. IRBM 2019, 40, 103–112. [Google Scholar] [CrossRef]
- Chen, D.; Wan, S.; Xiang, J.; Bao, F.S. A high-performance seizure detection algorithm based on Discrete Wavelet Transform (DWT) and EEG. PLoS ONE 2017, 12, e0173138. [Google Scholar] [CrossRef]
- Sharma, R.R.; Varshney, P.; Pachori, R.B.; Vishvakarma, S.K. Automated System for Epileptic EEG Detection Using Iterative Filtering. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Pachori, R.B.; Kanhangad, V.; Panigrahi, B.K. Automated Diagnosis of Epilepsy Using Key-Point-Based Local Binary Pattern of EEG Signals. IEEE J. Biomed. Health Inform. 2016, 21, 888–896. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Li, M. Generalized Stockwell transform and SVD-based epileptic seizure detection in EEG using random forest. Biocybern. Biomed. Eng. 2018, 38, 519–534. [Google Scholar] [CrossRef]
- Abbasi, M.U.; Rashad, A.; Basalamah, A.; Tariq, M. Detection of Epilepsy Seizures in Neo-Natal EEG Using LSTM Architecture. IEEE Access 2019, 7, 179074–179085. [Google Scholar] [CrossRef]
- Karim, A.M.; Karal, Ö.; Çelebi, F.V. A new automatic epilepsy serious detection method by using deep learning based on discrete wavelet transform. In Proceedings of the 3rd International Conference on Engineering Technology and Applied Sciences (ICETAS), Skopje, Macedonia, 17–21 July 2018; pp. 15–18. [Google Scholar]
- Gao, X.; Yan, X.; Gao, P.; Gao, X.; Zhang, S. Automatic detection of epileptic seizure based on approximate entropy, recurrence quantification analysis and convolutional neural networks. Artif. Intell. Med. 2020, 102, 101711. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, S.; Murugavel, A.S.M. Epileptic seizure detection using fuzzy-rules-based sub-band specific features and layered multi-class SVM. Pattern Anal. Appl. 2018, 22, 1161–1176. [Google Scholar] [CrossRef]
- Al-Hadeethi, H.; Abdulla, S.; Diykh, M.; Deo, R.C.; Green, J. Adaptive boost LS-SVM classification approach for time-series signal classification in epileptic seizure diagnosis applications. Expert Syst. Appl. 2020, 161, 113676. [Google Scholar] [CrossRef]
- Waqar, H.; Xiang, J.; Zhou, M.; Hu, T.; Ahmed, B.; Shapor, S.H.; Iqbal, M.S.; Raheel, M. Towards Classifying Epileptic Seizures Using Entropy Variants. In Proceedings of the 2019 IEEE Fifth International Conference on Big Data Computing Service and Applications (BigDataService), Newark, CA, USA, 4–9 April 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 296–300. [Google Scholar]
- Tzimourta, K.D.; Tzallas, A.T.; Giannakeas, N.; Astrakas, L.G.; Tsalikakis, D.G.; Tsipouras, M.G. Epileptic Seizures Classification Based on Long-Term EEG Signal Wavelet Analysis. In Proceedings of the VI Latin American Congress on Biomedical Engineering CLAIB 2014, Paraná, Argentina, 29–31 October 2014; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 165–169. [Google Scholar]
- Truong, N.D.; Kavehei, O. Low Precision Electroencephalogram for Seizure Detection with Convolutional Neural Network. In Proceedings of the 2019 IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hsinchu, Taiwan, 18–20 March 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 299–301. [Google Scholar]
- Nassralla, M.; Haidar, M.; Alawieh, H.; El Hajj, A.; Dawy, Z. Patient-Aware EEG-Based Feature and Classifier Selection for e-Health Epileptic Seizure Prediction. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Yuan, Q.; Zhou, W.; Zhang, L.; Zhang, F.; Xu, F.; Leng, Y.; Wei, D.; Chen, M. Epileptic seizure detection based on imbalanced classification and wavelet packet transform. Seizure 2017, 50, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Tian, C.; Cao, R.; Wang, B.; Niu, Y.; Hu, T.; Guo, H.; Xiang, J. Epileptic Seizure Detection Based on EEG Signals and CNN. Front. Aging Neurosci. 2018, 12, 95. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodian, N.; Boese, A.; Friebe, M.; Haddadnia, J. Epileptic seizure detection using cross-bispectrum of electroencephalogram signal. Seizure 2019, 66, 4–11. [Google Scholar] [CrossRef]
- del Rincón, J.M.; Santofimia, M.J.; del Toro, X.; Barba, J.; Romero, F.; Navas, P.; López, J.C. Non-linear classifiers applied to EEG analysis for epilepsy seizure detection. Expert Syst. Appl. 2017, 86, 99–112. [Google Scholar] [CrossRef]
- Jaafar, S.T.; Mohammadi, M. Epileptic Seizure Detection using Deep Learning Approach. UHD J. Sci. Technol. 2019, 3, 41–50. [Google Scholar] [CrossRef]
- Truong, N.D.; Nguyen, A.D.; Kuhlmann, L.; Bonyadi, M.R.; Yang, J.; Ippolito, S.; Kavehei, O. Integer Convolutional Neural Network for Seizure Detection. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 849–857. [Google Scholar] [CrossRef]
- Abbaszadeh, B.; Yagoub, M. Optimum Window Size and Overlap for Robust Probabilistic Prediction of Seizures with iEEG. In Proceedings of the 2019 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Siena, Italy, 9–11 July 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Mohammadi, M.; Khan, N.A.; Pouyan, A.A. Automatic seizure detection using a highly adaptive directional time–frequency distribution. Multidimens. Syst. Signal Process. 2017, 29, 1661–1678. [Google Scholar] [CrossRef]
- Sun, C.; Cui, H.; Zhou, W.; Nie, W.; Wang, X.; Yuan, Q. Epileptic Seizure Detection with EEG Textural Features and Imbalanced Classification Based on EasyEnsemble Learning. Int. J. Neural Syst. 2019, 29, 1950021. [Google Scholar] [CrossRef] [PubMed]
- Abugabah, A.; AlZubi, A.A.; Al-Maitah, M.; Alarifi, A. Brain epilepsy seizure detection using bio-inspired krill herd and artificial alga optimized neural network approaches. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 3317–3328. [Google Scholar] [CrossRef]
- Qin, H.; Deng, B.; Wang, J.; Yi, G.; Wang, R.; Zhang, Z. Deep Multi-scale Feature Fusion Convolutional Neural Network for Automatic Epilepsy Detection Using EEG Signals. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; IEEE: Piscataway Township, NJ, USA, 2020; pp. 7061–7066. [Google Scholar]
- Amin, S.U.; Alsulaiman, M.; Muhammad, G.; Mekhtiche, M.A.; Hossain, M.S. Deep Learning for EEG motor imagery classification based on multi-layer CNNs feature fusion. Future Gener. Comput. Syst. 2019, 101, 542–554. [Google Scholar] [CrossRef]
- EEG Time Series Data (Department of Epileptology University of Bonn, Germany). Available online: http://epileptologie-bonn.de/cms/front_content.php?idcat=193&lang=3&changelang=3 (accessed on 13 November 2021).
- EEG Database. Available online: https://epilepsy.uni-freiburg.de/freiburg-seizure-prediction-project/eeg-database/ (accessed on 13 November 2021).
- Selesnick, I. Wavelet Transform with Tunable Q-Factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Ghassemi, N.; Shoeibi, A.; Rouhani, M.; Hosseini-Nejad, H. Epileptic seizures detection in EEG signals using TQWT and ensemble learning. In Proceedings of the 2019 9th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 24–25 October 2019; pp. 403–408. [Google Scholar]
- Kumar, S.P.; Sriraam, N.; Benakop, P.; Jinaga, B. Entropies based detection of epileptic seizures with artificial neural network. Expert Syst. Appl. 2010, 37, 3284–3291. [Google Scholar] [CrossRef]
- Polychronaki, G.E.; Ktonas, P.Y.; Gatzonis, S.; Siatouni, A.; Asvestas, P.A.; Tsekou, H.; Sakas, D.; Nikita, K.S. Comparison of fractal dimension estimation algorithms for epileptic seizure onset detection. J. Neural Eng. 2010, 7, 046007. [Google Scholar] [CrossRef] [PubMed]
- Supriya, S.; Siuly, S.; Wang, H.; Cao, J.; Zhang, Y. Weighted Visibility Graph with Complex Network Features in the Detection of Epilepsy. IEEE Access 2016, 4, 6554–6566. [Google Scholar] [CrossRef]
- Golovko, V.; Artsiomenka, S.; Kisten, V.; Evstigneev, V. Towards automatic epileptic seizure detection in eegs based on neural networks and largest lyapunov exponent. Int. J. Comput. 2014, 14, 36–47. [Google Scholar] [CrossRef]
- Harrison, M.A.F.; Osorio, I.; Frei, M.G.; Asuri, S.; Lai, Y.-C. Correlation dimension and integral do not predict epileptic seizures. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 033106. [Google Scholar] [CrossRef]
- Esteller, R.; Vachtsevanos, G.; Echauz, J.; Litt, B. A comparison of waveform fractal dimension algorithms. IEEE Trans. Circuits Syst. I Regul. Pap. 2001, 48, 177–183. [Google Scholar] [CrossRef]
- Márton, L.; Brassai, S.; Bakó, L.; Losonczi, L. Detrended Fluctuation Analysis of EEG Signals. Procedia Technol. 2014, 12, 125–132. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Das, A.B.; Bhuiyan, M.I.H. Discrimination and classification of focal and non-focal EEG signals using entropy-based features in the EMD-DWT domain. Biomed. Signal Process. Control. 2016, 29, 11–21. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E.W. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl.-Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Raghu, S.; Sriraam, N.; Kumar, G.P. Effect of Wavelet Packet Log Energy Entropy on Electroencephalogram (EEG) Signals. Int. J. Biomed. Clin. Eng. 2015, 4, 32–43. [Google Scholar] [CrossRef][Green Version]
- Zhang, A.; Yang, B.; Huang, L. Feature Extraction of EEG Signals Using Power Spectral Entropy. In Proceedings of the 2008 International Conference on BioMedical Engineering and Informatics, Sanya, China, 27–30 May 2008; IEEE: Piscataway Township, NJ, USA, 2008; Volume 2, pp. 435–439. [Google Scholar]
- Rizal, A.; Hadiyoso, S. Sample Entropy on Multidistance Signal Level Difference for Epileptic EEG Classification. Sci. World J. 2018, 2018, 8463256. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yan, J.; Liu, X.; Ouyang, G. Using Permutation Entropy to Measure the Changes in EEG Signals during Absence Seizures. Entropy 2014, 16, 3049–3061. [Google Scholar] [CrossRef]
- Acharya, U.R.; Hagiwara, Y.; Deshpande, S.N.; Suren, S.; Koh, J.E.W.; Oh, S.L.; Arunkumar, N.; Ciaccio, E.J.; Lim, C.M. Characterization of focal EEG signals: A review. Future Gener. Comput. Syst. 2019, 91, 290–299. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Phys. A Stat. Mech. Its Appl. 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Mohammadpoory, Z.; Nasrolahzadeh, M.; Haddadnia, J. Epileptic seizure detection in EEGs signals based on the weighted visibility graph entropy. Seizure 2017, 50, 202–208. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Duun-Henriksen, J.; Kjaer, T.W.; Morabito, F.C. Differentiating Interictal and Ictal States in Childhood Absence Epilepsy through Permutation Rényi Entropy. Entropy 2015, 17, 4627–4643. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. An Integrated Index for the Identification of Focal Electroencephalogram Signals Using Discrete Wavelet Transform and Entropy Measures. Entropy 2015, 17, 5218–5240. [Google Scholar] [CrossRef]
- Cao, Z.; Lin, C.-T. Inherent Fuzzy Entropy for the Improvement of EEG Complexity Evaluation. IEEE Trans. Fuzzy Syst. 2018, 26, 1032–1035. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, R. Fractional fuzzy entropy algorithm and the complexity analysis for nonlinear time series. Eur. Phys. J. Spéc. Top. 2018, 227, 943–957. [Google Scholar] [CrossRef]
- Girault, J.-M.; Humeau-Heurtier, A. Centered and Averaged Fuzzy Entropy to Improve Fuzzy Entropy Precision. Entropy 2018, 20, 287. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Vemuri, V.R. Use of K-Nearest Neighbor classifier for intrusion detection. Comput. Secur. 2002, 21, 439–448. [Google Scholar] [CrossRef]
- Zarjam, P.; Epps, J.; Chen, F. Spectral EEG featuresfor evaluating cognitive load. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; IEEE: Piscataway Township, NJ, USA, 2011; Volume 2011, pp. 3841–3844. [Google Scholar]
- Michielli, N.; Acharya, U.R.; Molinari, F. Cascaded LSTM recurrent neural network for automated sleep stage classification using single-channel EEG signals. Comput. Biol. Med. 2019, 106, 71–81. [Google Scholar] [CrossRef]
- Kuanar, S.; Athitsos, V.; Pradhan, N.; Mishra, A.; Rao, K. Cognitive Analysis of Working Memory Load from Eeg, by a Deep Recurrent Neural Network. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2576–2580. [Google Scholar]
- Shoeibi, A.; Ghassemi, N.; Khodatars, M.; Moridian, P.; Alizadehsani, R.; Zare, A.; Gorriz, J.M. Detection of Epileptic Seizures on EEG Signals Using ANFIS Classifier, Autoencoders and Fuzzy Entropies. arXiv 2021, arXiv:2109.04364. [Google Scholar]
- Shoeibi, A.; Ghassemi, N.; Alizadehsani, R.; Rouhani, M.; Hosseini-Nejad, H.; Khosravi, A.; Panahiazar, M.; Nahavandi, S. A comprehensive comparison of handcrafted features and convolutional autoencoders for epileptic seizures detection in EEG signals. Expert Syst. Appl. 2021, 163, 113788. [Google Scholar] [CrossRef]
- Hasanzadeh, F.; Mohebbi, M.; Rostami, R. Graph theory analysis of directed functional brain networks in major depressive disorder based on EEG signal. J. Neural Eng. 2020, 17, 026010. [Google Scholar] [CrossRef]
- Tamburro, G.; Di Fronso, S.; Robazza, C.; Bertollo, M.; Comani, S. Modulation of Brain Functional Connectivity and Efficiency During an Endurance Cycling Task: A Source-Level EEG and Graph Theory Approach. Front. Hum. Neurosci. 2020, 14, 243. [Google Scholar] [CrossRef]
- Hu, X.; Pedrycz, W.; Wang, X. Fuzzy classifiers with information granules in feature space and logic-based computing. Pattern Recognit. 2018, 80, 156–167. [Google Scholar] [CrossRef]
- Saha, A.; Konar, A.; Nagar, A.K. EEG Analysis for Cognitive Failure Detection in Driving Using Type-2 Fuzzy Classifiers. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 437–453. [Google Scholar] [CrossRef]
- Al-Ezzi, A.; Yahya, N.; Kamel, N.; Faye, I.; Alsaih, K.; Gunaseli, E. Severity Assessment of Social Anxiety Disorder Using Deep Learning Models on Brain Effective Connectivity. IEEE Access 2021, 9, 86899–86913. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, Y.; Shan, X.; Wei, H.; Guo, Y.; Chen, L.; Erkoyuncu, J.A.; Sarrigiannis, P.G. Brain functional and effective connectivity based on electroencephalography recordings: A review. Hum. Brain Mapp. 2021. [Google Scholar] [CrossRef]
- Phang, C.R.; Ting, C.M.; Noman, F.; Ombao, H. Classification of EEG-based brain connectivity networks in schizophrenia using a multi-domain connectome convolutional neural network. arXiv 2019, arXiv:1903.08858. [Google Scholar]
- Khodatars, M.; Shoeibi, A.; Sadeghi, D.; Ghaasemi, N.; Jafari, M.; Moridian, P.; Khadem, A.; Alizadehsani, R.; Zare, A.; Kong, Y.; et al. Deep learning for neuroimaging-based diagnosis and rehabilitation of Autism Spectrum Disorder: A review. Comput. Biol. Med. 2021, 139, 104949. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Davoodnia, V.; Sepas-Moghaddam, A.; Zhang, Y.; Etemad, A. Classification of Hand Movements from EEG Using a Deep Attention-Based LSTM Network. IEEE Sens. J. 2020, 20, 3113–3122. [Google Scholar] [CrossRef]
- Li, D.; Xu, J.; Wang, J.; Fang, X.; Ji, Y. A Multi-Scale Fusion Convolutional Neural Network Based on Attention Mechanism for the Visualization Analysis of EEG Signals Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2615–2626. [Google Scholar] [CrossRef] [PubMed]
- Krishna, G.; Tran, C.; Carnahan, M.; Tewfik, A.H. EEG based Continuous Speech Recognition using Transformers. arXiv 2019, arXiv:2001.00501. [Google Scholar]
- Liu, J.; Zhang, L.; Wu, H.; Zhao, H. Transformers for EEG Emotion Recognition. arXiv 2021, arXiv:2110.06553. [Google Scholar]
- Khozeimeh, F.; Sharifrazi, D.; Izadi, N.H.; Joloudari, J.H.; Shoeibi, A.; Alizadehsani, R.; Islam, S.M.S. Combining a convolutional neural network with autoencoders to predict the survival chance of COVID-19 patients. Sci. Rep. 2021, 11, 15343. [Google Scholar] [CrossRef]
- Lu, S.; Zhu, Z.; Gorriz, J.M.; Wang, S.; Zhang, Y. NAGNN: Classification of COVID-19 based on neighboring aware representation from deep graph neural network. Int. J. Intell. Syst. 2021. [Google Scholar] [CrossRef]
- Sadeghi, D.; Shoeibi, A.; Ghassemi, N.; Moridian, P.; Khadem, A.; Alizadehsani, R.; Nahavandi, S. An Overview on Artificial Intelligence Techniques for Diagnosis of Schizophrenia Based on Magnetic Resonance Imaging Modalities: Methods, Challenges, and Future Works. arXiv 2021, arXiv:2103.03081. [Google Scholar]
- Albardi, F.; Kabir, H.M.; Bhuiyan, M.M.I.; Kebria, P.M.; Khosravi, A.; Nahavandi, S. A Comprehensive Study on Torchvision Pre-trained Models for Fine-grained Inter-species Classification. arXiv 2021, arXiv:2110.07097. [Google Scholar]
- Alizadehsani, R.; Khosravi, A.; Roshanzamir, M.; Abdar, M.; Sarrafzadegan, N.; Shafie, D.; Khozeimeh, F.; Shoeibi, A.; Nahavandi, S.; Panahiazar, M.; et al. Coronary Artery Disease Detection Using Artificial Intelligence Techniques: A Survey of Trends, Geographical Differences and Diagnostic Features 1991–2020. Comput. Biol. Med. 2020, 128, 104095. [Google Scholar] [CrossRef]
- Górriz, J.M.; Ramírez, J.; Ortíz, A.; Martínez-Murcia, F.J.; Segovia, F.; Suckling, J.; Leming, M.; Zhang, Y.-D.; Álvarez-Sánchez, J.R.; Bologna, G.; et al. Artificial intelligence within the interplay between natural and artificial computation: Advances in data science, trends and applications. Neurocomputing 2020, 410, 237–270. [Google Scholar] [CrossRef]
- Sharifrazi, D.; Alizadehsani, R.; Hassannataj Joloudari, J.; Shamshirband, S.; Hussain, S.; Alizadeh Sani, Z.; Hasanzadeh, F.; Shoaibi, A.; Dehzangi, A.; Alinejad-Rokny, H. CNN-KCL: Automatic Myocarditis Diagnosis using Convolutional Neural Network Combined with K-means Clustering. Preprints 2020, 2020070650. [Google Scholar] [CrossRef]
- Yuan, Y.; Xun, G.; Suo, Q.; Jia, K.; Zhang, A. Wave2Vec: Deep representation learning for clinical temporal data. Neurocomputing 2019, 324, 31–42. [Google Scholar] [CrossRef]
- Kebria, P.M.; Alizadehsani, R.; Salaken, S.M.; Hossain, I.; Khosravi, A.; Kabir, D.; Koohestani, A.; Asadi, H.; Nahavandi, S.; Tunsel, E.; et al. Evaluating Architecture Impacts on Deep Imitation Learning Performance for Autonomous Driving. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 865–870. [Google Scholar]
- Dai, M.; Zheng, D.; Na, R.; Wang, S.; Zhang, S. EEG Classification of Motor Imagery Using a Novel Deep Learning Framework. Sensors 2019, 19, 551. [Google Scholar] [CrossRef] [PubMed]
- Ayoobi, N.; Sharifrazi, D.; Alizadehsani, R.; Shoeibi, A.; Gorriz, J.M.; Moosaei, H.; Khosravi, A.; Nahavandi, S.; Chofreh, A.G.; Goni, F.A.; et al. Time Series Forecasting of New Cases and New Deaths Rate for COVID-19 using Deep Learning Methods. arXiv 2021, arXiv:2104.15007. [Google Scholar] [CrossRef] [PubMed]
- Rajinikanth, V.; Joseph Raj, A.N.; Thanaraj, K.P.; Naik, G.R. A customized VGG19 network with concatenation of deep and handcrafted features for brain tumor detection. Appl. Sci. 2020, 10, 3429. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).