Evaluation of Deep Learning Methods in a Dual Prediction Scheme to Reduce Transmission Data in a WSN
Abstract
:1. Introduction
2. Time Series Forecasting for Energy Reduction
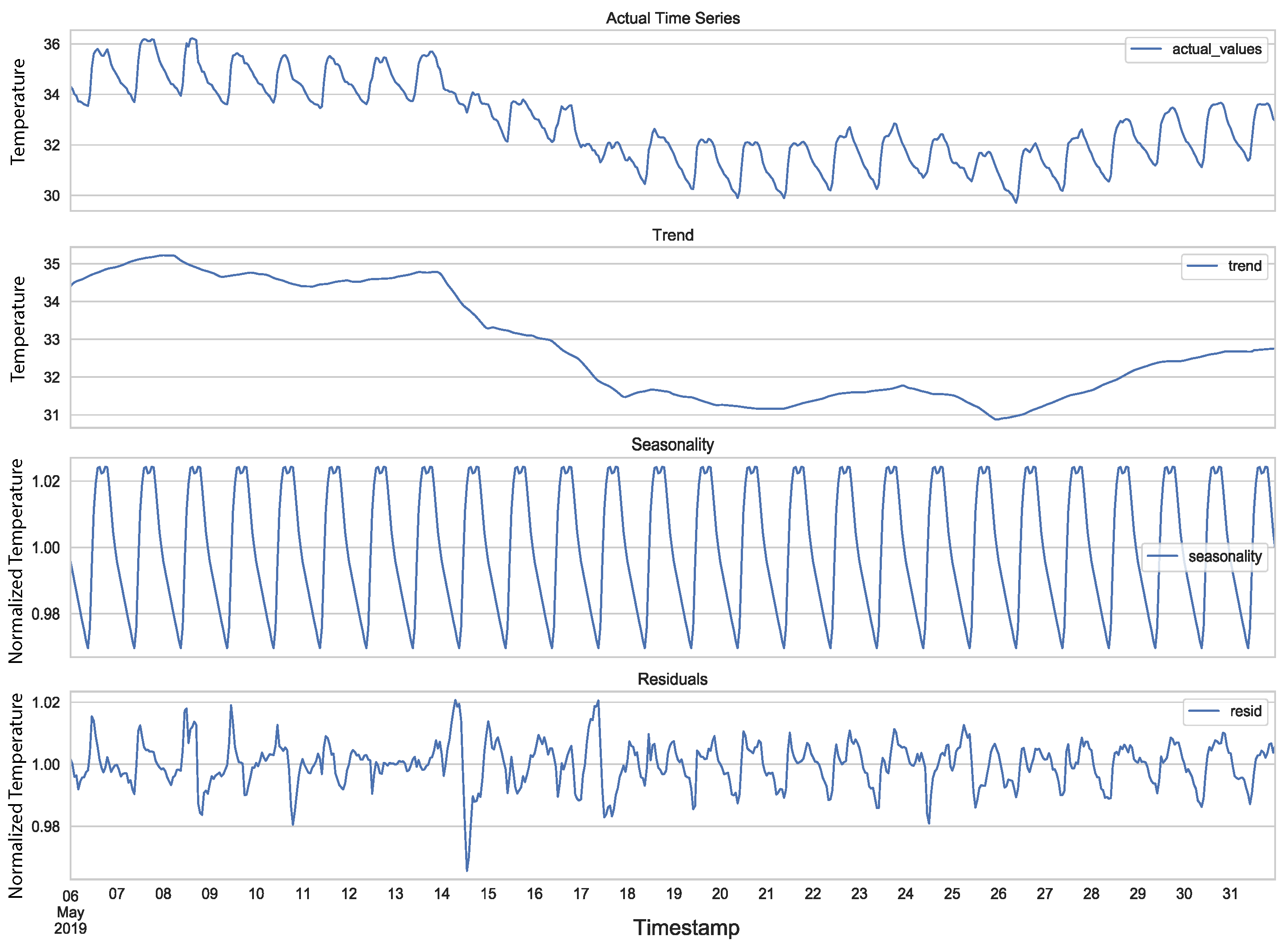
2.1. Components of a Time Series
2.2. Forecasting Time Series
2.3. Forecasting Methods
2.3.1. Statistical Methods
- Naive and sNaive: This is the most basic forecasting method. The method assumes the next value will be the same as the last one. sNaive, defined in Equation (1), is similar to the Naive method but considering the observation from one period before. Both Naive and sNaive do not provide a model, only an instantaneous forecast point.where is the actual observation, and is a point of a time period before.
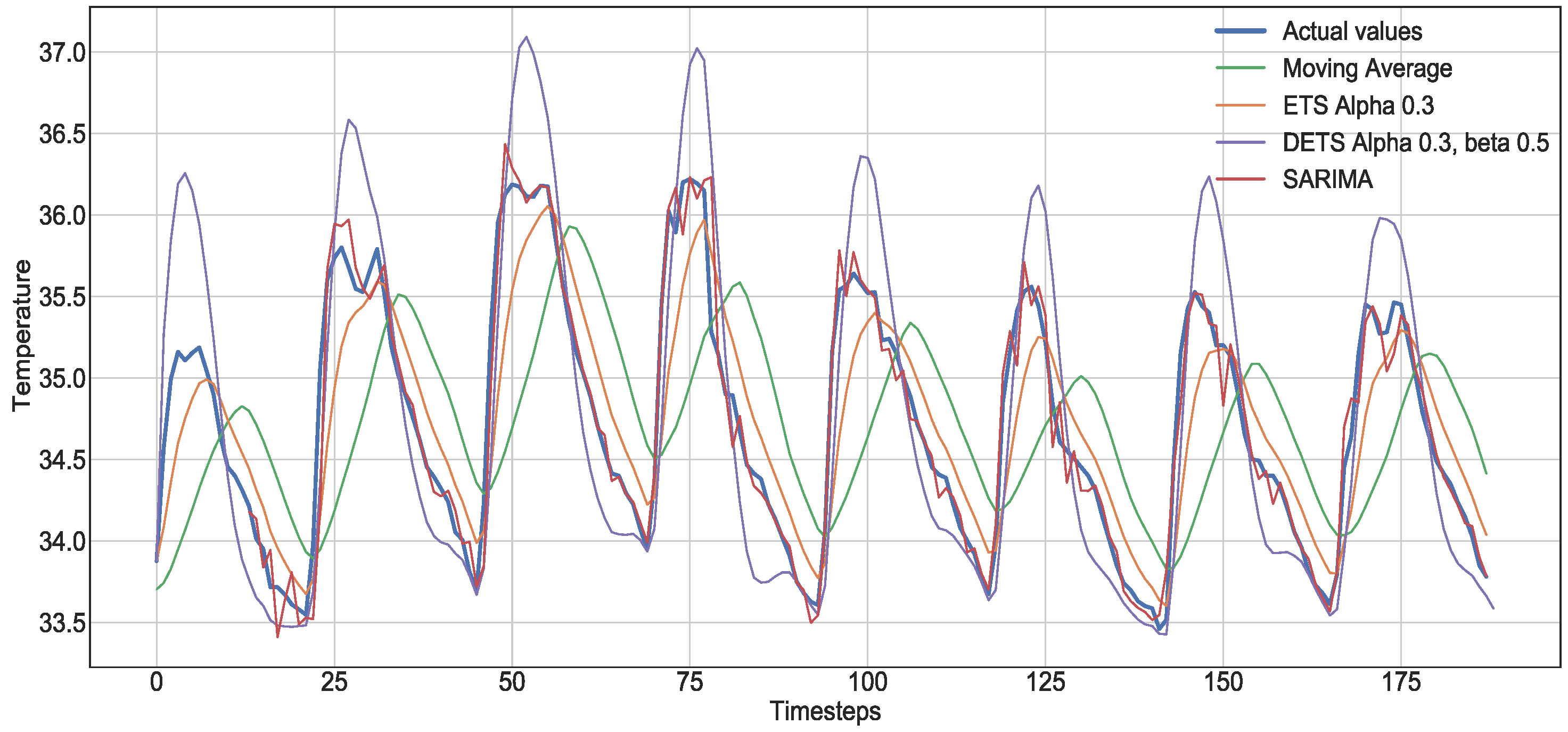
- Moving Average: This method, defined by Equation (2), takes the average of the time series over a fixed period n, called an average window. is the actual observation and the prediction. The method reduces the noise but does not anticipate trend or seasonality.
- Exponential Smoothing (ETS): This method assigns weights to the observations. The weights decay exponentially as we move back in time. It is defined by:The model is a weighted average between the most recent observation and the most recent forecast . is a smoothing factor, which defines how fast the model forgets the last available observation. The lower the , the smoother the result, and in the case of , the result is the current observation. There is no formally correct procedure for choosing , but it can be optimized.
- Double Exponential Smoothing (DETS): ETS does not perform well when the time series presents a trend. This method is a solution for such cases. It consists of dividing the time series into intercept l and trend b and applying the same exponential smoothing to the trend. The time series is divided into two functions: the first one describes the intercept that depends on the current observation, and the second function describes the trend, which depends on the intercept’s latest change and the previous values of the trend. The method is defined by the following equations:
- Seasonal Autoregressive Integrated Moving Average (SARIMA): The SARIMA model is a combination of the Integrated ARMA model (ARIMA) and a seasonal component. It is very similar to the ARIMA model but is preferable when the time series exhibits seasonality. The (AR) stands for Autoregressive, a regression of the time series onto itself. The (MA) stands for Moving Average [12]. The (I) is the order of integration, which represents the number of nonseasonal differences needed to transform the sequence to stationary. Finally, the letter (S) completes the SARIMA model, and it represents the seasonality present in the sequence, providing the model with the capacity to model seasonal components. Although this method can provide an accurate forecast, the selection and identification of the best model parameters can be very time-consuming and require many iterations.
2.3.2. Machine Learning Methods
- eXtreme Gradient Boosting (XGBoost): This method is an efficient implementation of the gradient boosting decision tree (GBDT) and can be used for both classification and regression problems [13]. Boosting is an ensemble technique that consists of introducing new models to correct the errors or optimize the existing ones. This algorithm consists of multiple decision trees generated using gradient descent with an optimization to minimize the objective function [14]. This is a fast and accurate model but requires many hyper-parameter settings to be adjusted and does not perform well with noisy data [10].
- Artificial Neural Networks (ANN): An ANN is a computational network designed to emulate the behavior of the human brain. The main unit of these structures is the neuron, which is inspired by actual human neurons. The neuron receives weighted inputs that are multiplied by an activation function to produce an output [15]. The networks consist of multiple layers of connected neurons that can learn patterns from the input data after exhausted training. The connections learn weights that represent the strength of the link between neurons.
2.4. Deep Learning for Time Series
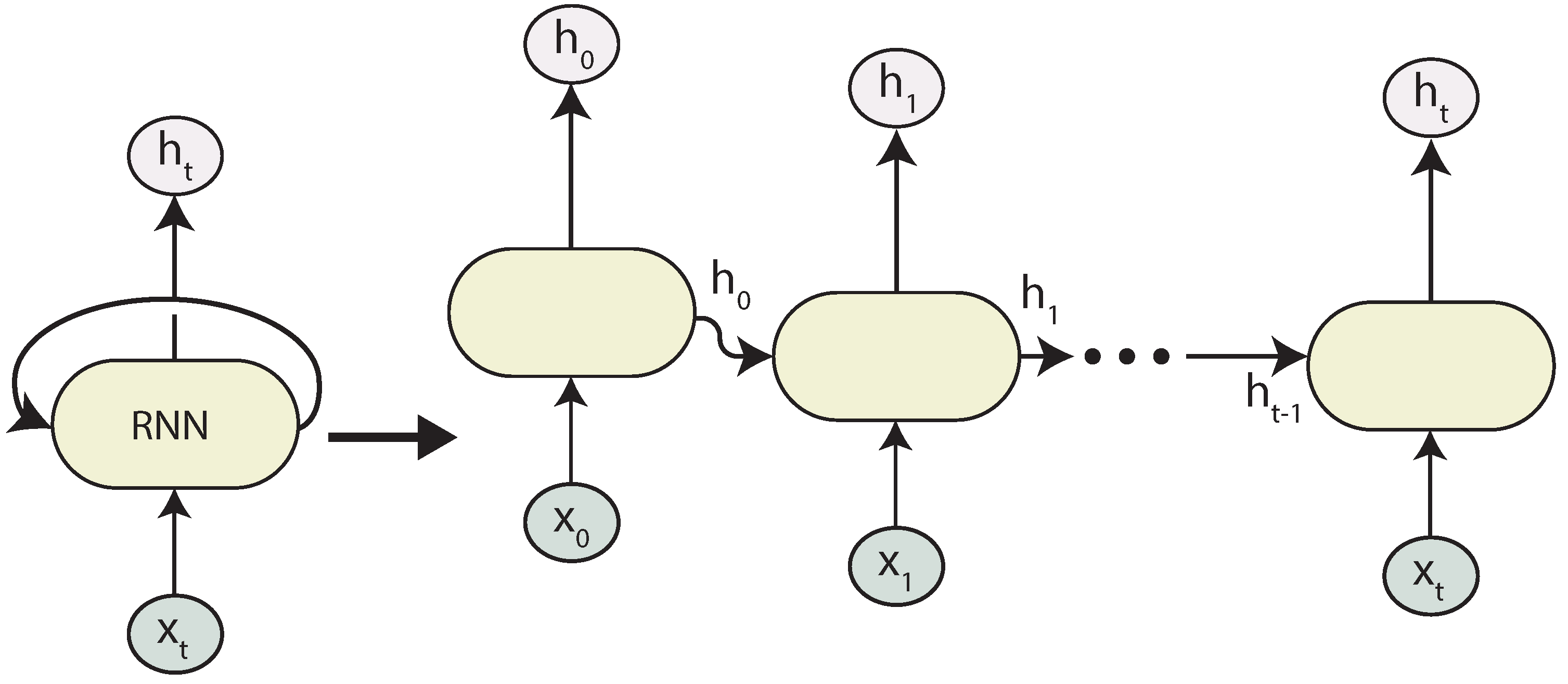
2.4.1. Recurrent Neural Networks
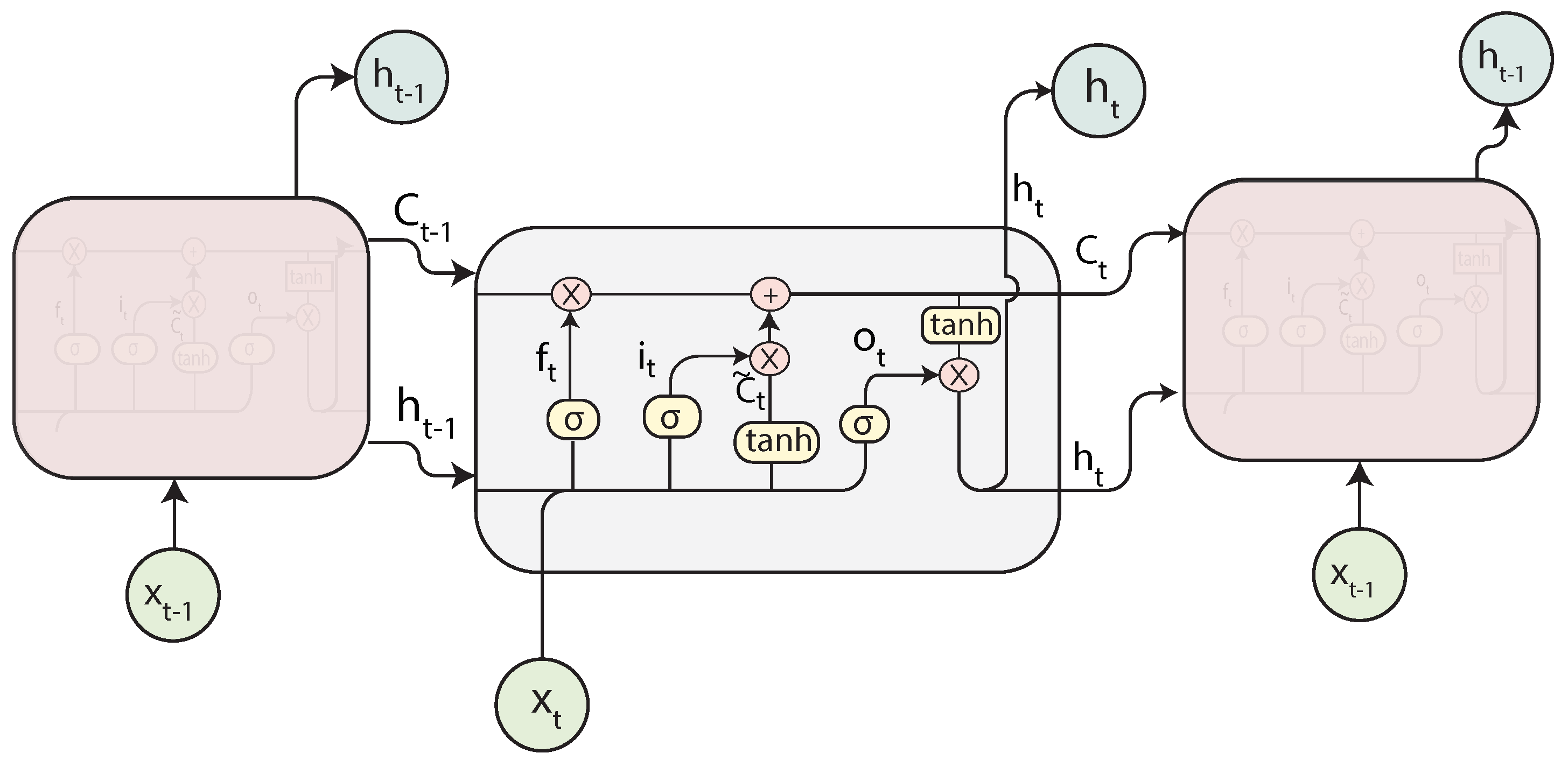
2.4.2. Long Short-Term Memory Neural Networks
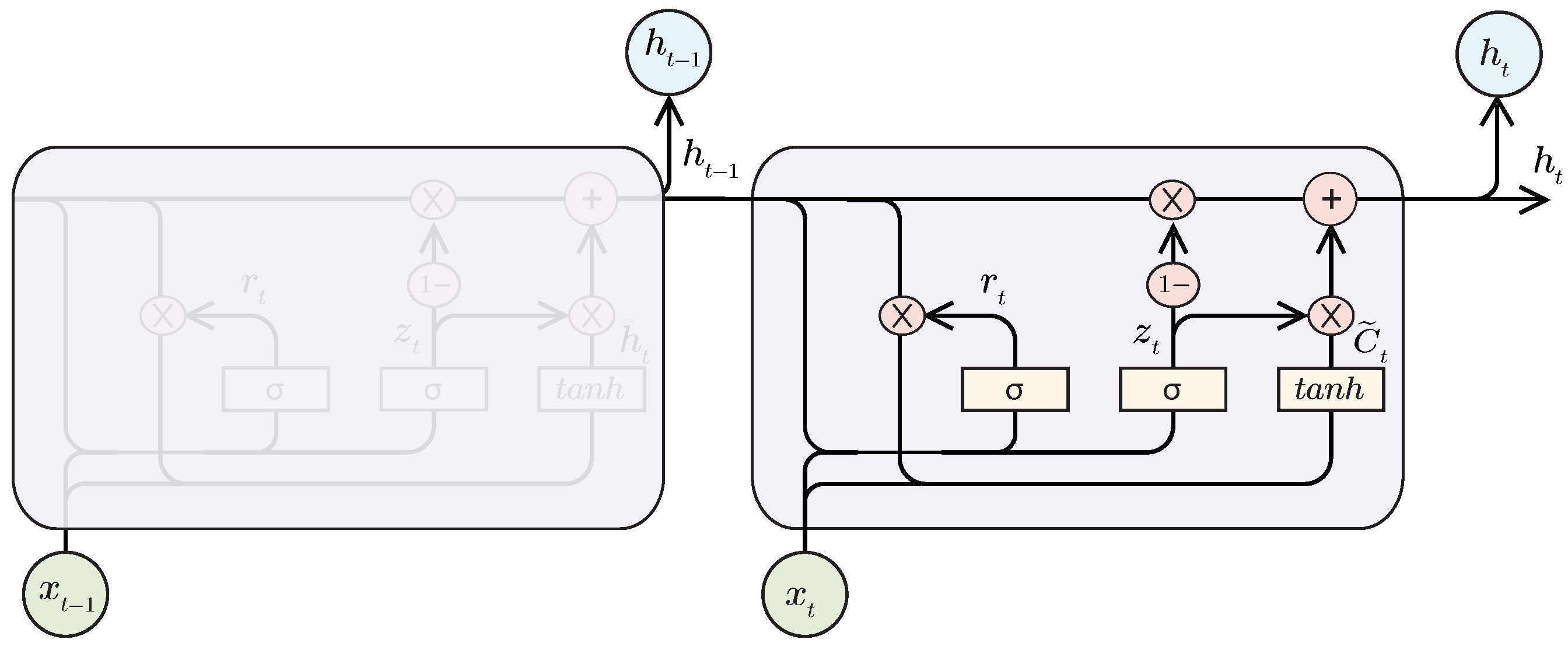
2.4.3. Gated Recurrent Unit (GRU)
2.4.4. Convolutional Neural Networks (CNN)
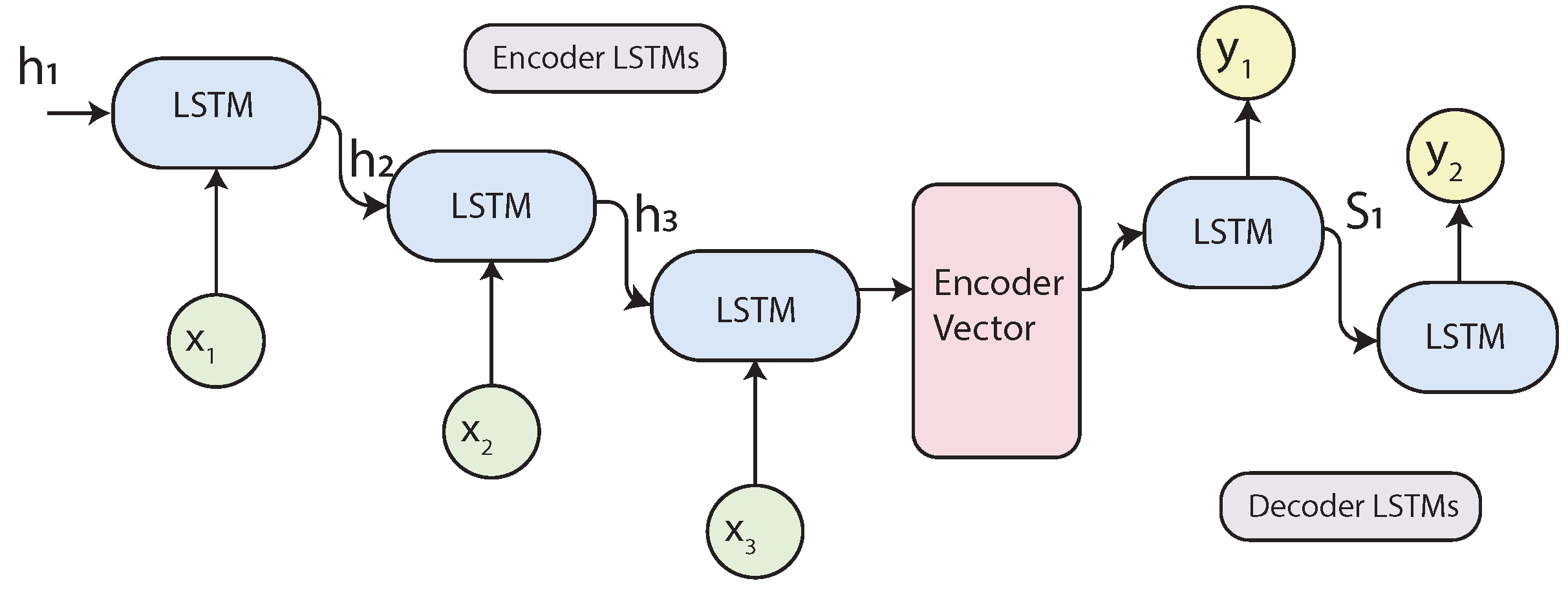
2.4.5. Sequence to Sequence (Seq2Seq) Models
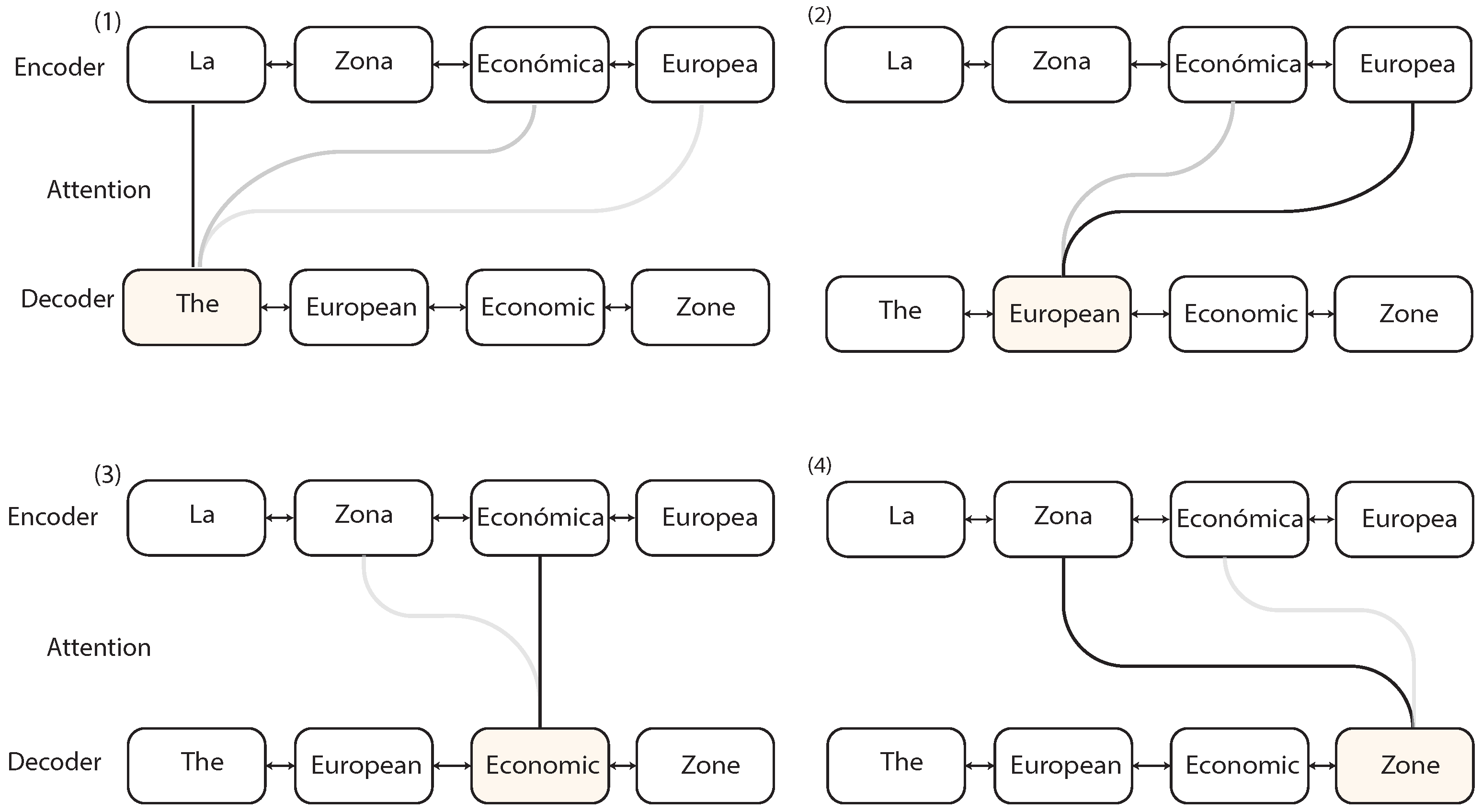
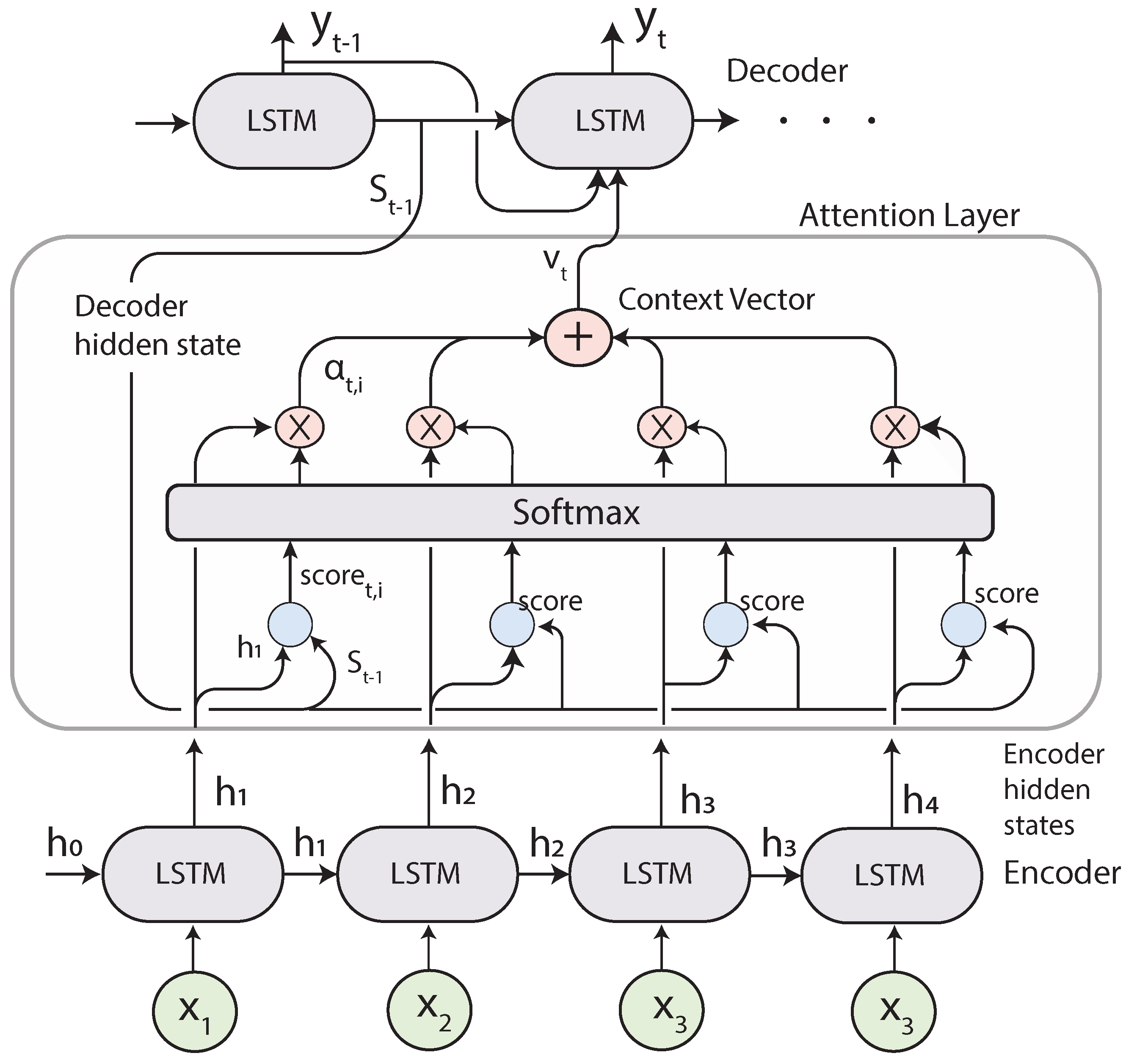
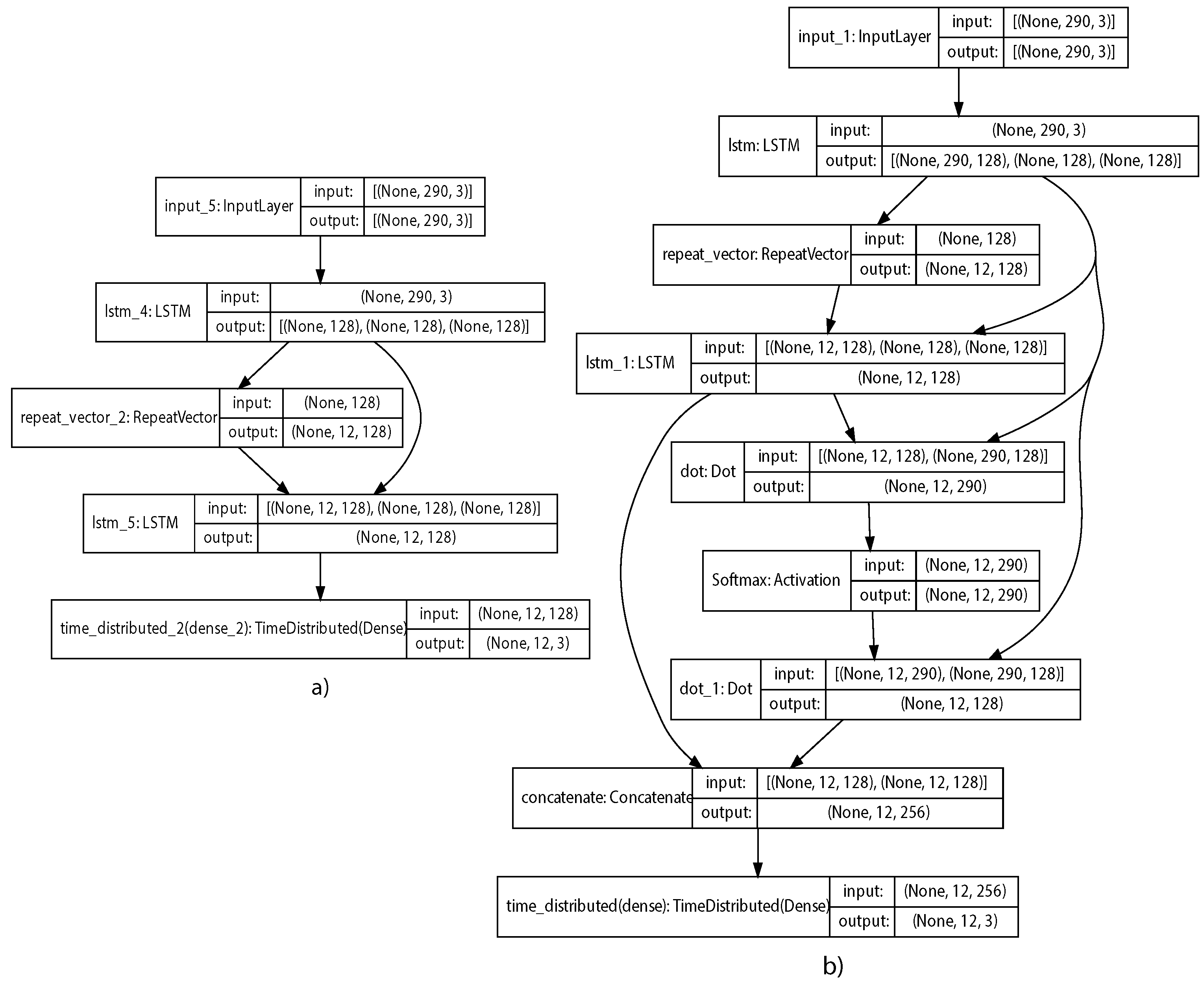
2.5. Seq2Seq with Attention
Attention Mechanism
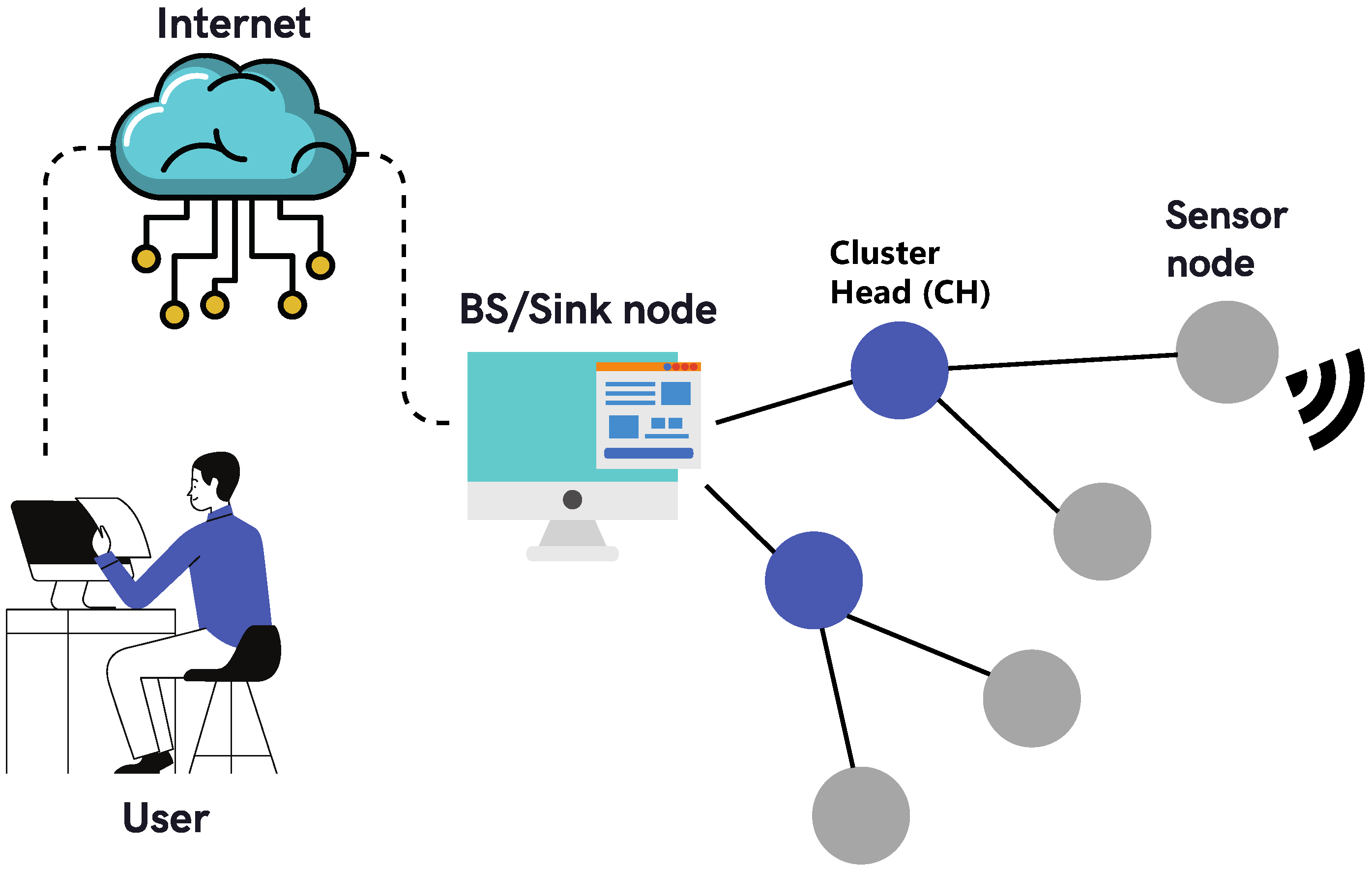
3. Data Prediction for Energy Saving in WSNs
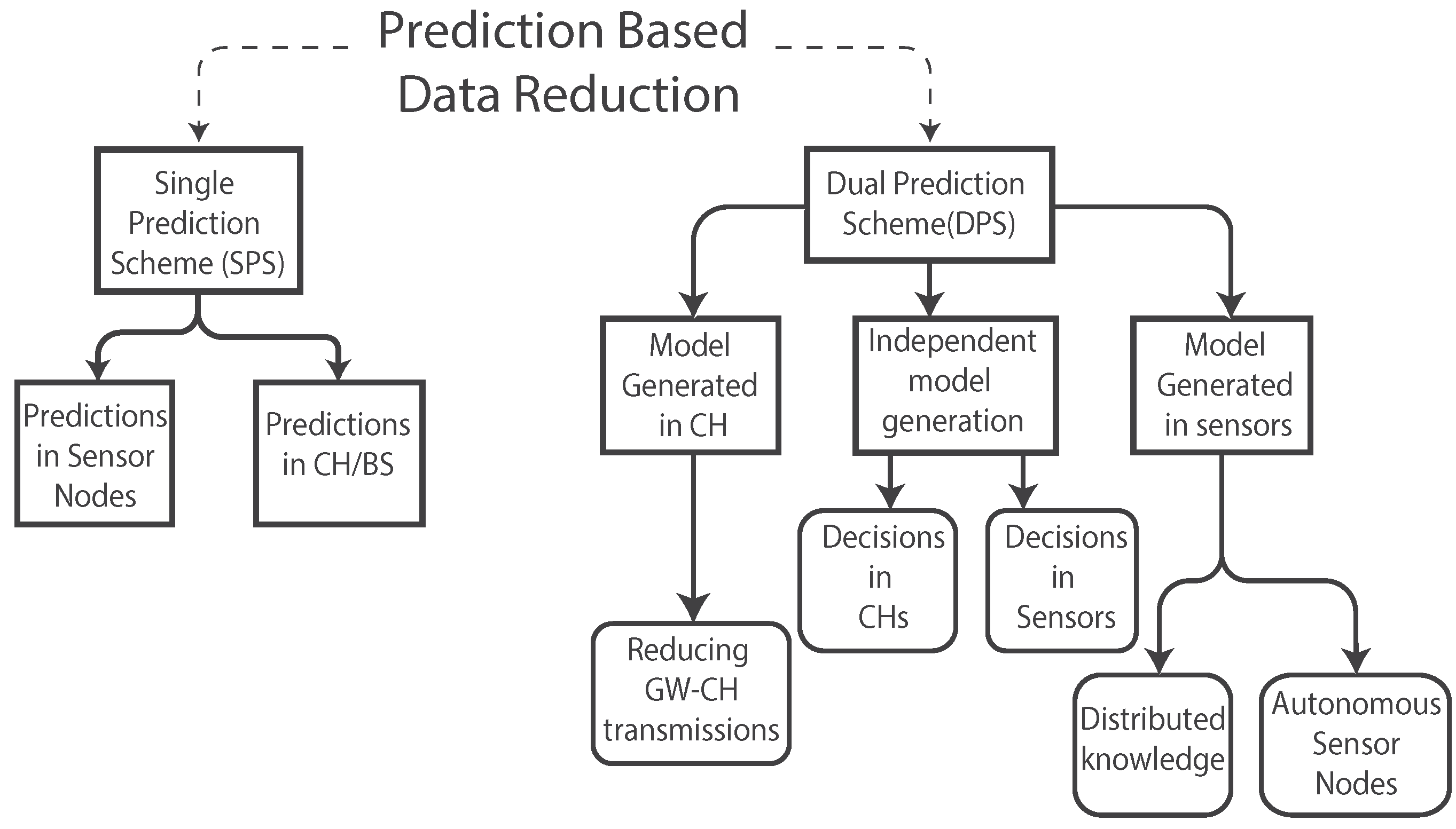
3.1. Single Prediction Scheme
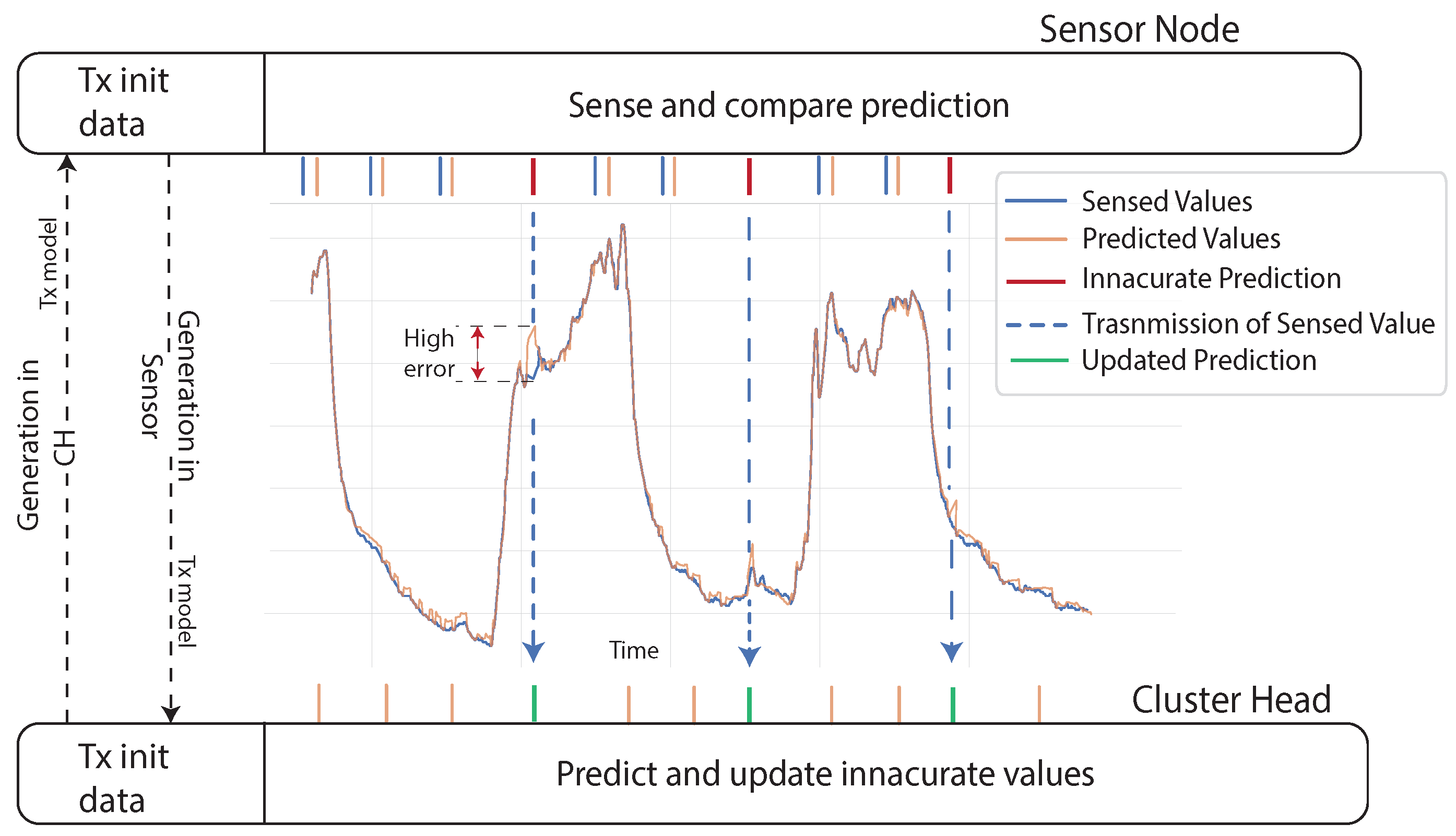
3.2. Dual Prediction Scheme
3.2.1. Model Generated in CHs
3.2.2. Independent Model Generation
3.2.3. Model Generated in Sensor Nodes
3.3. Related Works to Data Reduction for Energy Saving in WSNs
4. Problem Formulation
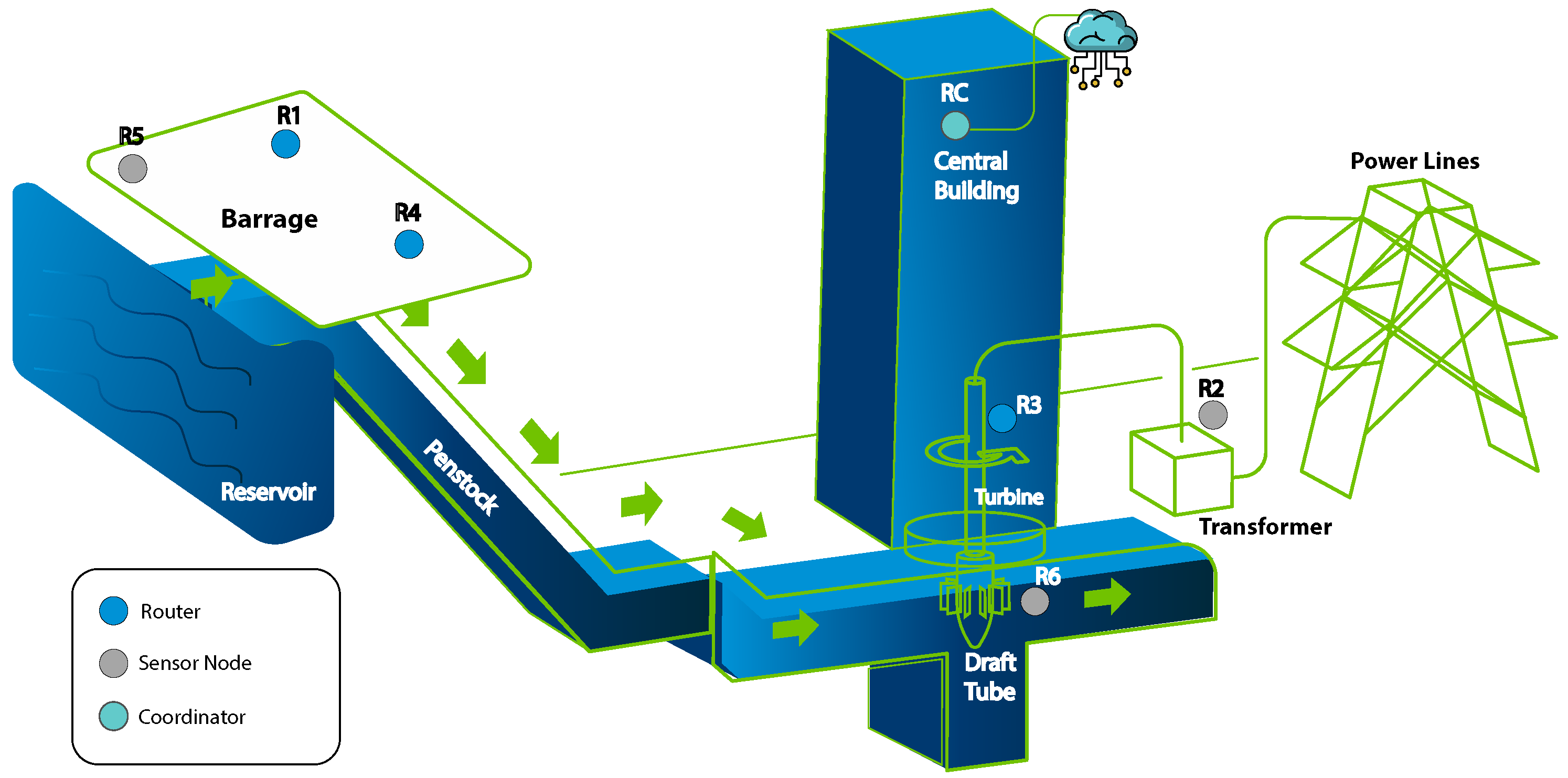
5. Materials and Methods
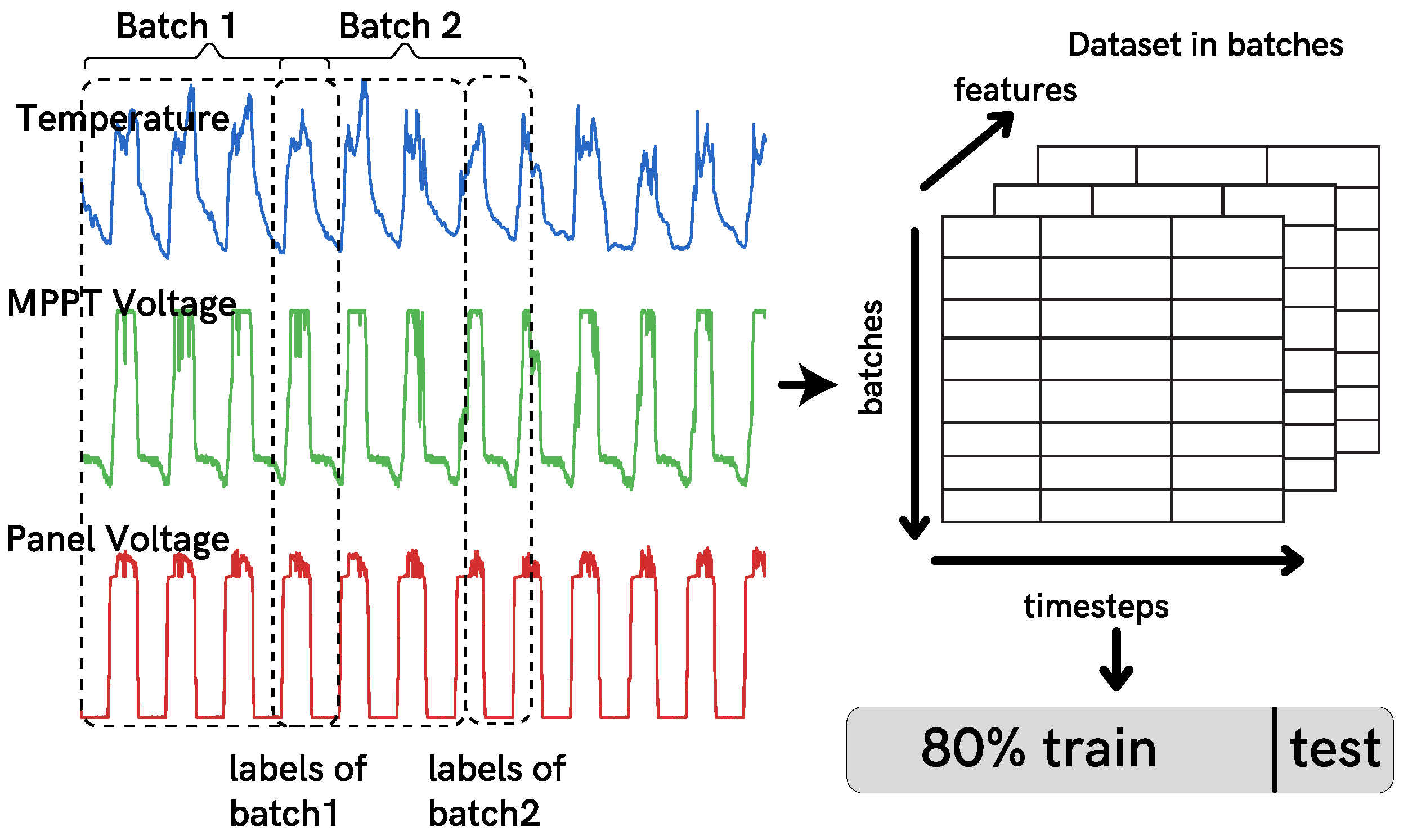
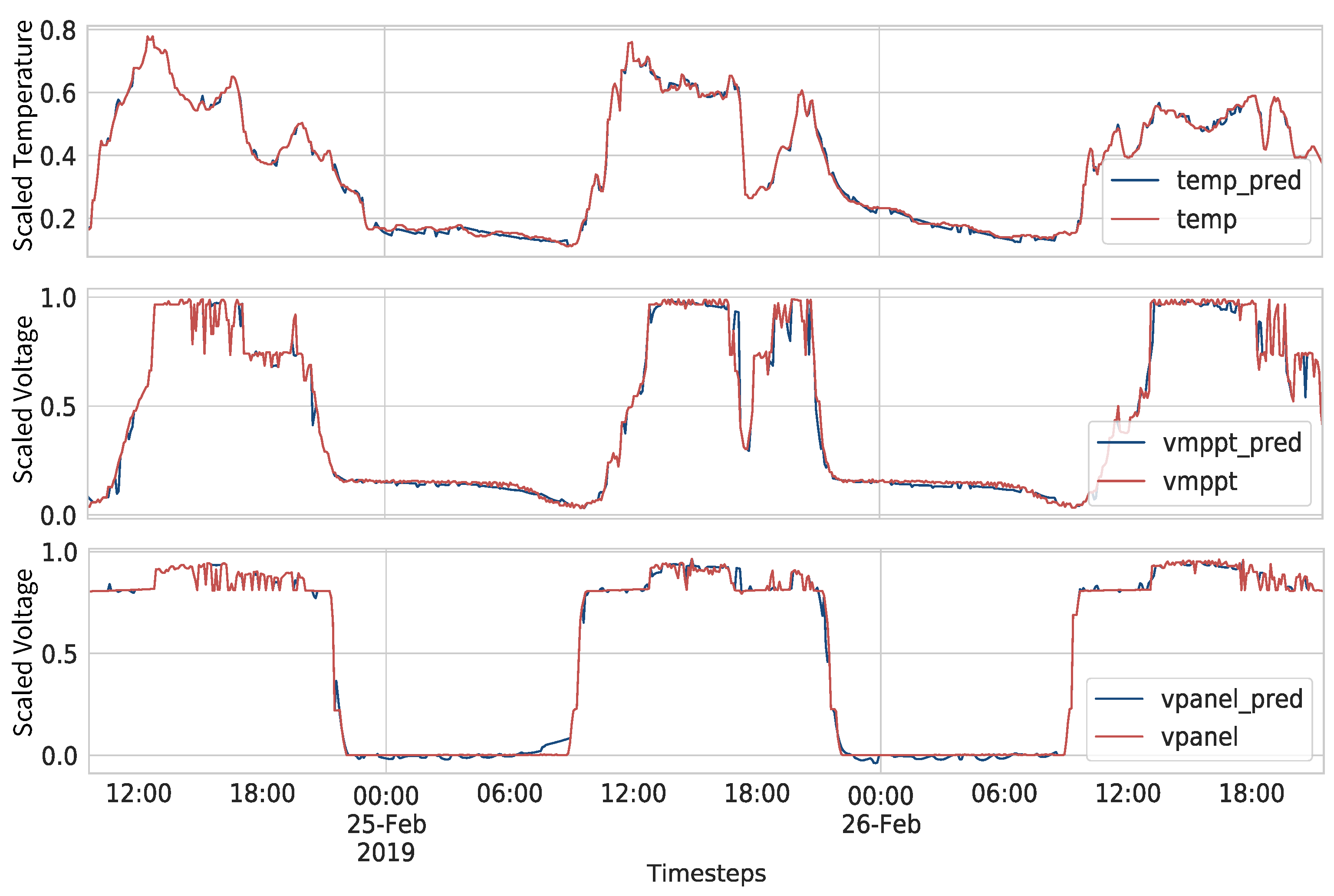
5.1. Data Preparation
5.2. Models Architecture and Parameters
6. Results and Discussion
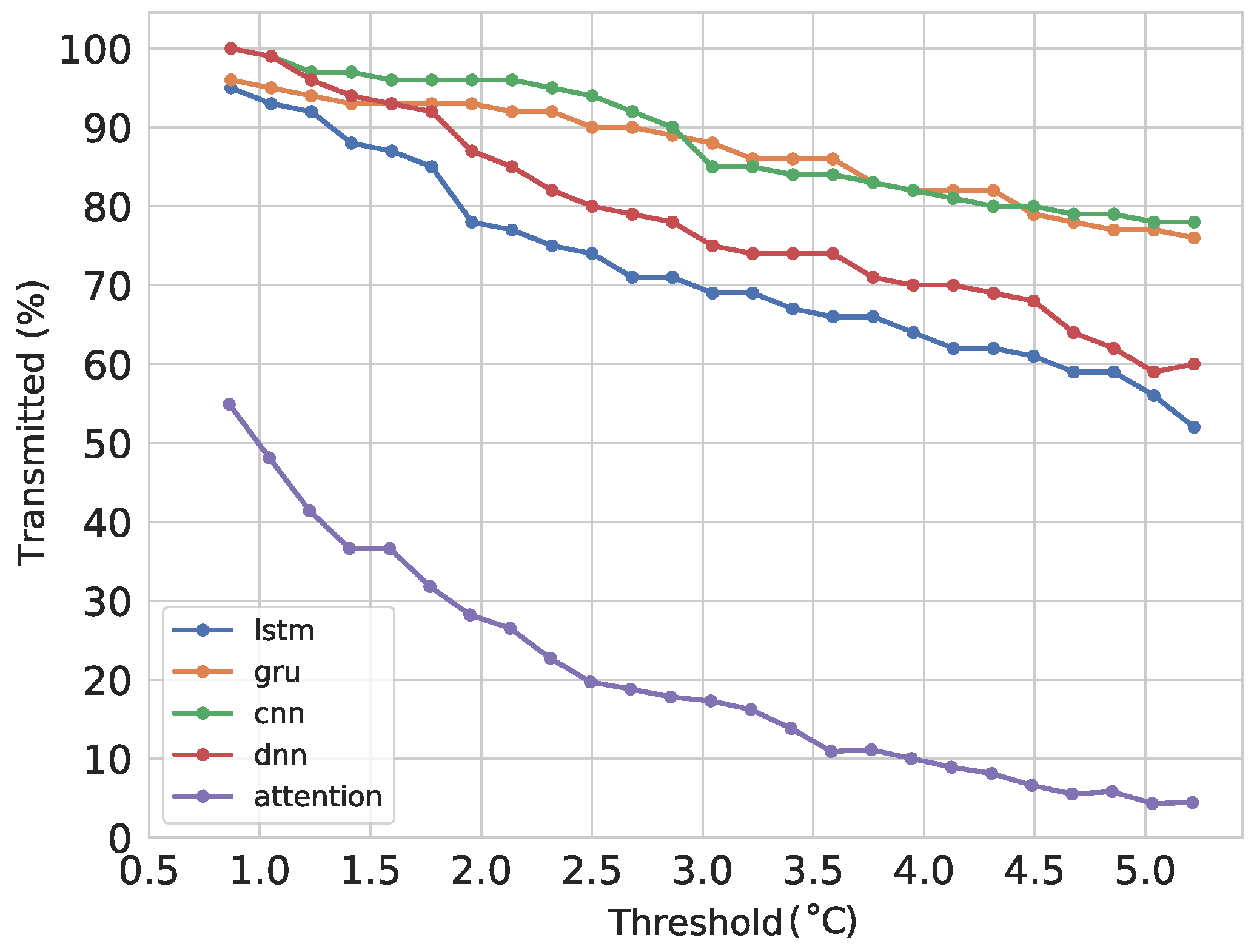
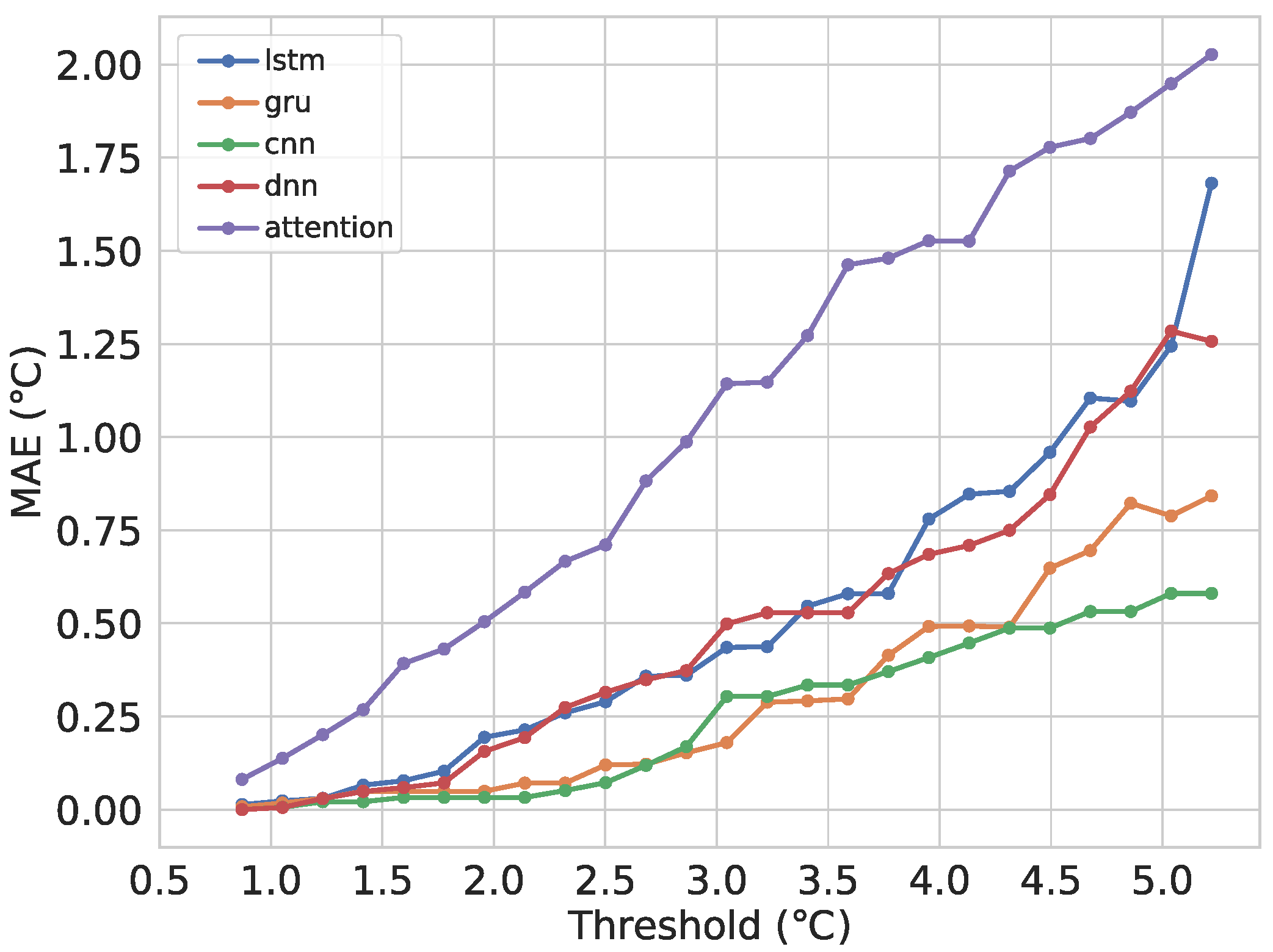
6.1. Comparison
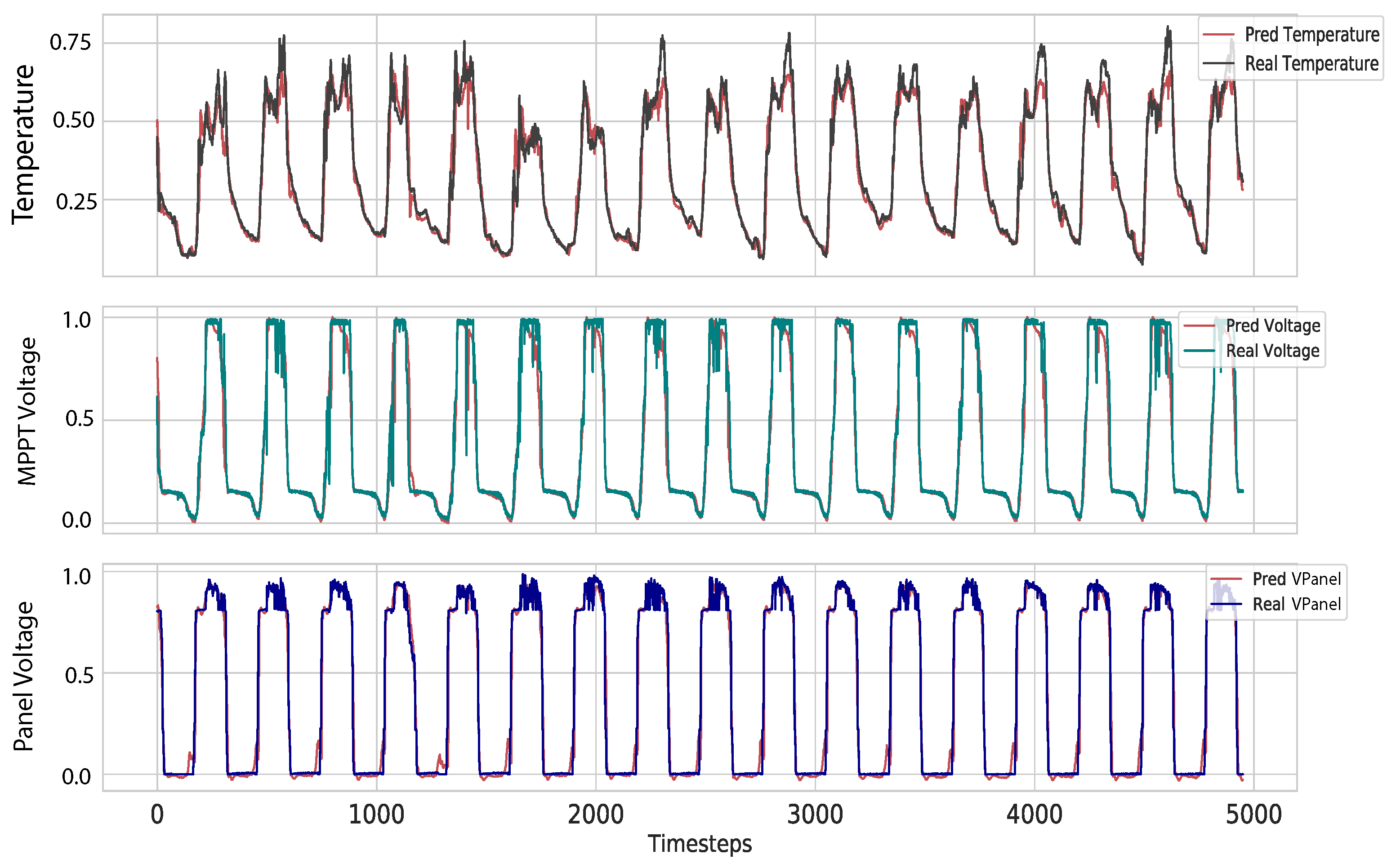
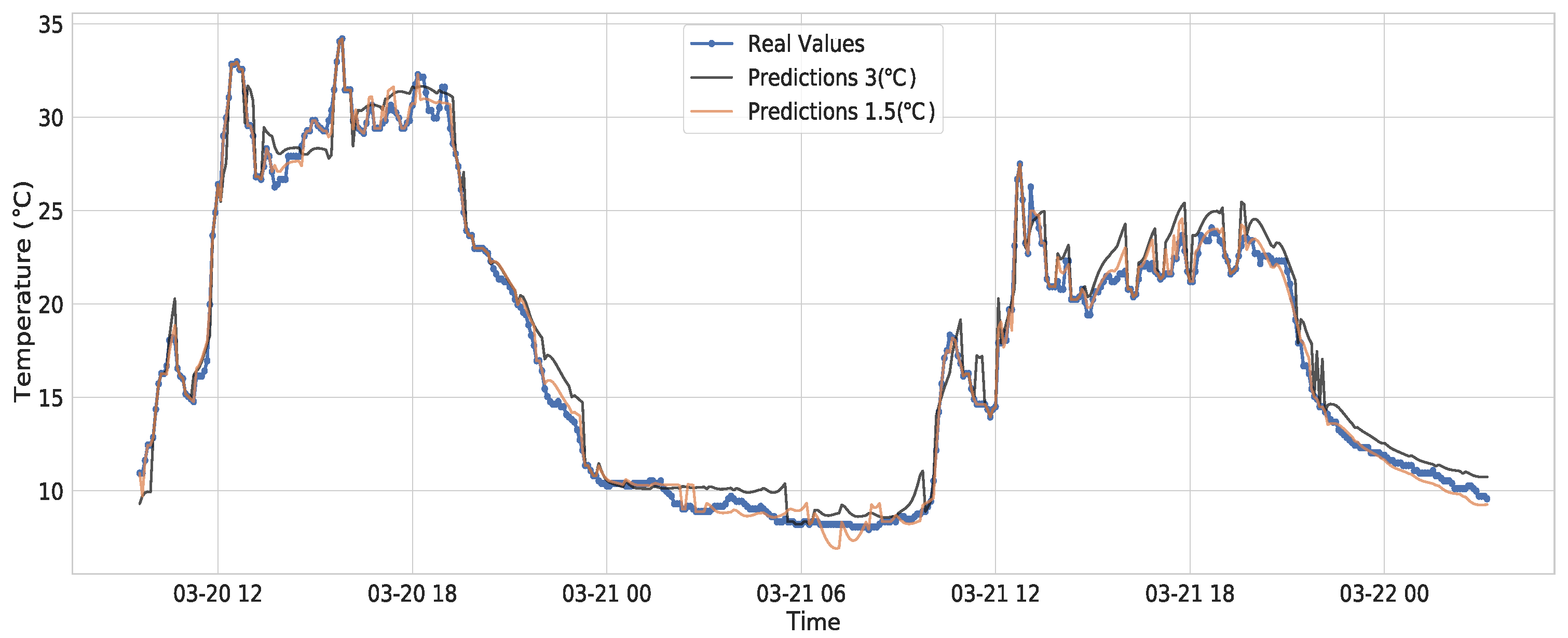
6.2. Forecasting and Transmitting
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Willig, A.; Matheus, K.; Wolisz, A. Wireless Technology in Industrial Networks. Proc. IEEE 2005, 93, 1130–1151. [Google Scholar]
- Senouci, M.R.; Mellouk, A. Wolisz. In Deploying Wireless Sensor Networks: Theory and Practice; ISTE Press Ltd.: London, UK, 2016; pp. 1–19. [Google Scholar]
- Abbasi, A.A.; Younis, M. A survey on clustering algorithms for wireless sensor networks. Comput. Commun. 2007, 30, 2826–2841. [Google Scholar] [CrossRef]
- Anastasi, G.; Conti, M.; Di Francesco, M.; Passarella, A. Energy conservation in wireless sensor networks: A survey. Ad. Hoc. Netw. 2009, 7, 537–568. [Google Scholar] [CrossRef]
- Sharma, S.; Bansal, R.K.; Bansal, S. Issues and Challenges in Wireless Sensor Networks. In Proceedings of the 2013 International Conference on Machine Intelligence and Research Advancement, Katra, India, 21–23 December 2013; pp. 58–62. [Google Scholar]
- Krishna, G.; Singh, S.K.; Singh, J.P.; Kumar, P. Energy conservation through data prediction in wireless sensor networks. In Proceedings of the 3rd International Conference on Internet of Things and Connected Technologies (ICIoTCT), Jaipur, India, 26–27 March 2018; pp. 26–27. [Google Scholar]
- Song, Y.; Luo, J.; Liu, C.; He, W. Periodicity-and-Linear-Based Data Suppression Mechanism for WSN. In Proceedings of the 2015 IEEE Trustcom/BigDataSE/ISPA, Helsinki, Finland, 20–22 August 2015; pp. 1267–1271. [Google Scholar] [CrossRef]
- Dias, G.M.; Bellalta, B.; Oechsner, S. A survey about prediction-based data reduction in wireless sensor networks. ACM Comput. Surv. (CSUR) 2016, 49, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Morales, C.R.; de Sousa, F.R.; Brusamarello, V.; Fernandes, N.C. Multivariate Data Prediction in a Wireless Sensor Network based on Sequence to Sequence Models. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar]
- Bauer, A.; Züfle, M.; Herbst, N.; Zehe, A.; Hotho, A.; Kounev, S. Time Series Forecasting for Self-Aware Systems. Proc. IEEE 2020, 108, 1068–1093. [Google Scholar] [CrossRef]
- Adhikari, R.; Agrawal, R.K. An introductory study on time series modeling and forecasting. arXiv 2013, arXiv:1302.6613. [Google Scholar]
- Samal, K.K.; Babu, K.S.; Das, S.K.; Acharaya, A. Time series based air pollution forecasting using SARIMA and prophet model. In Proceedings of the 2019 International Conference on Information Technology and Computer Communications, Singapore, 16–18 August 2019; pp. 80–85. [Google Scholar]
- Wang, L.; Wang, X.; Chen, A.; Jin, X.; Che, H. Prediction of Type 2 Diabetes Risk and Its Effect Evaluation Based on the XGBoost Model. Healthcare 2020, 8, 247. [Google Scholar] [CrossRef]
- Niu, Y. Walmart Sales Forecasting using XGBoost algorithm and Feature engineering. In Proceedings of the International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Bangkok, Thailand, 30 October–1 November 2020; pp. 458–461. [Google Scholar]
- Aliyu, F.; Umar, S.; Al-Duwaish, H. A survey of applications of artificial neural networks in wireless sensor networks. In Proceedings of the 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; pp. 1–5. [Google Scholar]
- Gamboa, J.C. Deep learning for time-series analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Shih, S.Y.; Sun, F.K.; Lee, H. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep transformer models for time series forecasting: The influenza prevalence case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Bahdanau, D.; Cho, K.H.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. In Proceedings of the Conference Proceedings EMNLP 2015: Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1412–1421. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long- and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv. Neural Inf. Process. Syst. 2019, 32, 5243–5253. [Google Scholar]
- Li, Y.; Sun, R.; Horne, R. Deep learning for well data history analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition. OnePetro, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar]
- Liazid, H.; Lehsaini, M.; Liazid, A. An improved adaptive dual prediction scheme for reducing data transmission in wireless sensor networks. Wirel. Netw. 2019, 25, 3545–3555. [Google Scholar] [CrossRef]
- López-Ardao, J.C.; Rodríguez-Rubio, R.F.; Suárez-González, A.; Rodríguez-Pérez, M.; Sousa-Vieira, M.E. Current Trends on Green Wireless Sensor Networks. Sensors 2021, 21, 4281. [Google Scholar] [CrossRef]
- Shu, T.; Chen, J.; Bhargava, V.K.; de Silva, C.W. An Energy-Efficient Dual Prediction Scheme Using LMS Filter and LSTM in Wireless Sensor Networks for Environment Monitoring. IEEE Internet Things J. 2019, 6, 6736–6747. [Google Scholar]
- Dias, G.M.; Bellalta, B.; Oechsner, S. The impact of dual prediction schemes on the reduction of the number of transmissions in sensor networks. Comput. Commun. 2017, 112, 58–72. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Li, X. Wavelet Neural Network Approach for Dynamic Power Management in Wireless Sensor Networks. In Proceedings of the International Conference on Embedded Software and Systems, Chengdu, China, 29–31 July 2008; pp. 376–381. [Google Scholar]
- Pacharaney, U.S.; Gupta, R.K. Clustering and compressive data gathering in wireless sensor network. Wirel. Pers. Commun. 2019, 109, 1311–1331. [Google Scholar]
- Tayeh, G.B.; Makhoul, A.; Perera, C.; Demerjian, J. A spatial-temporal correlation approach for data reduction in cluster-based sensor networks. IEEE Access 2019, 7, 50669–50680. [Google Scholar]
- Abboud, A.; Yazbek, A.-K.; Cances, J.-P.; Meghdadi, V. Forecasting and skipping to Reduce Transmission Energy in WSN. arXiv 2016, arXiv:1606.01937. [Google Scholar]
- Alippi, C.; Anastasi, G.; Francesco, M.D.; Roveri, M. An Adaptive Sampling Algorithm for Effective Energy Management in Wireless Sensor Networks With Energy-Hungry Sensors. IEEE Trans. Instrum. Meas. 2018, 59, 335–344. [Google Scholar] [CrossRef] [Green Version]
- Samarah, S.; Al-Hajri, M.; Boukerche, A. A Predictive Energy-Efficient Technique to Support Object-Tracking Sensor Networks. IEEE Trans. Veh. Technol. 2011, 60, 656–663. [Google Scholar]
- Fathy, Y.; Barnaghi, P.; Tafazolli, R. An adaptive method for data reduction in the Internet of Things. In Proceedings of the IEEE World Forum on Internet of Things, WF-IoT 2018—Proceedings, Singapore, 5–8 February 2018; pp. 729–735. [Google Scholar]
- Arbi, I.B.; Derbel, F.; Strakosch, F. Forecasting methods to reduce energy consumption in WSN. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Tan, L.; Wu, M. Data reduction in wireless sensor networks: A hierarchical LMS prediction approach. IEEE Sens. J. 2015, 16, 1708–1715. [Google Scholar] [CrossRef]
- Deng, H.; Guo, Z.; Lin, R.; Zou, H. Fog computing architecture-based data reduction scheme for WSN. In Proceedings of the IEEE 2019 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–27 July 2019; pp. 1–6. [Google Scholar]
- Cheng, H.; Xie, Z.; Wu, L.; Yu, Z.; Li, R. Data prediction model in wireless sensor networks based on bidirectional LSTM. Eurasip J. Wirel. Commun. Netw. 2019, 2019, 1–12. [Google Scholar]
- Cheng, H.; Xie, Z.; Shi, Y.; Xiong, N. Multi-Step Data Prediction in Wireless Sensor Networks Based on One-Dimensional CNN and Bidirectional LSTM. IEEE Access 2019, 7, 117883–117896. [Google Scholar] [CrossRef]
- Sinha, A.; Lobiyal, D.K. Prediction Models for Energy Efficient Data Aggregation in Wireless Sensor Network. Wirel. Pers. Commun. 2015, 84, 1325–1343. [Google Scholar] [CrossRef]
- Das, R.; Ghosh, S.; Mukherjee, D. Bayesian Estimator Based Weather Forecasting using WSN. In Proceedings of the 2018 3rd International Conference and Workshops on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 22–25 November 2018; pp. 1–4. [Google Scholar]
- Chreim, B.; Nassar, J.; Habib, C. Regression-based Data Reduction Algorithm for Smart Grids. In Proceedings of the 2021 IEEE 18th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2021; pp. 1–2. [Google Scholar]
- Alves, M.M.; Pirmez, L.; Rossetto, S.; Delicato, F.C.; de Farias, C.M.; Pires, P.F.; dos Santos, I.L.; Zomaya, A.Y. Damage prediction for wind turbines using wireless sensor and actuator networks. J. Netw. Comput. Appl. 2017, 80, 123–140. [Google Scholar] [CrossRef]
- Antayhua, R.A.; Pereira, M.D.; Fernandes, N.C.; Rangel de Sousa, F. Exploiting the RSSI Long-Term Data of a WSN for the RF Channel Modeling in EPS Environments. Sensors 2020, 20, 3076. [Google Scholar]
- Pereira, M.D.; Romero, R.A.; Fernandes, N.; de Sousa, F.R. Path-loss and shadowing measurements at 2.4 GHz in a power plant using a mesh network. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference. Houston, TX, USA, 14–17 May 2018. [Google Scholar]
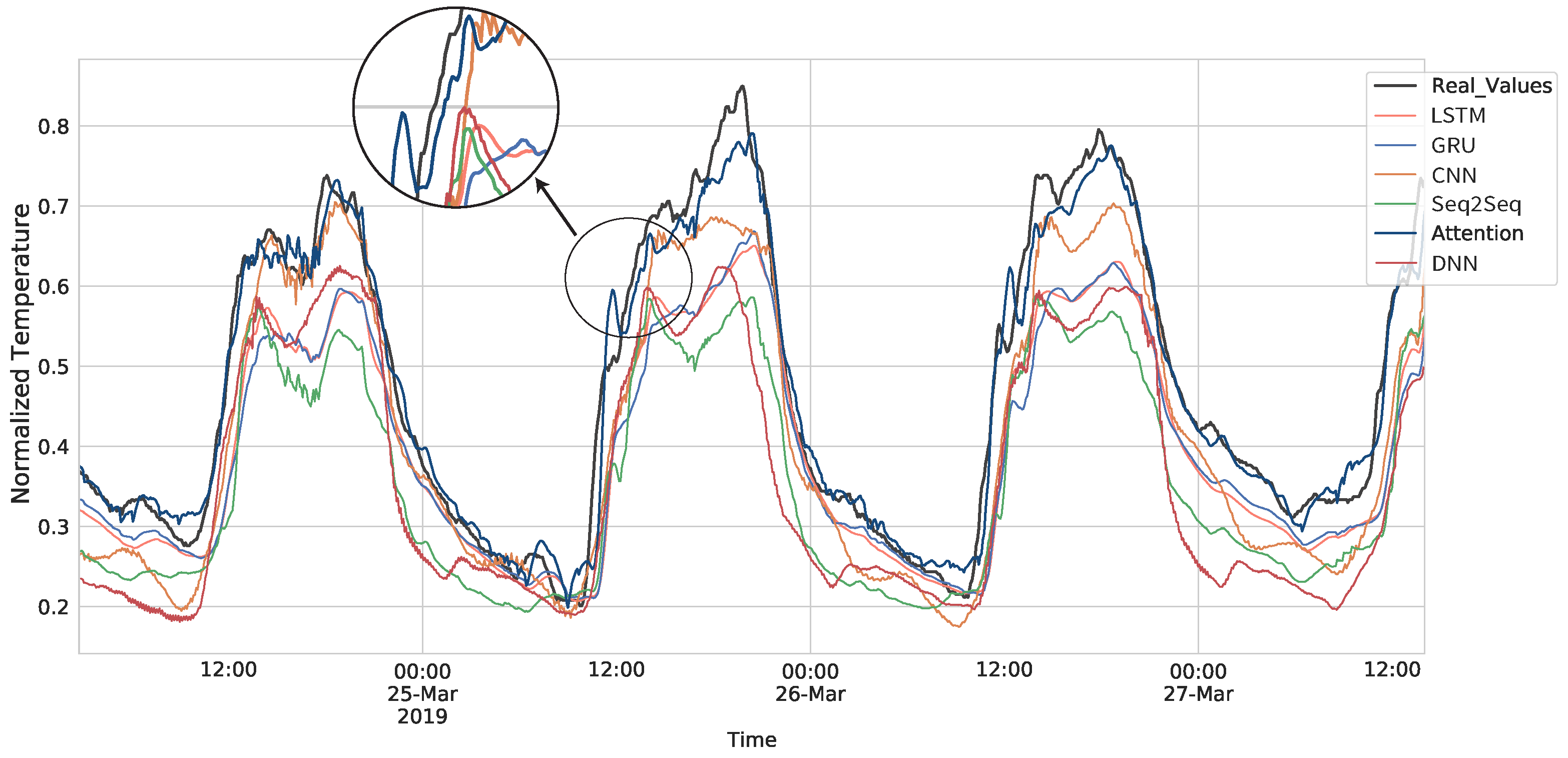
| Model | MAE | RMSE | R-Square |
|---|---|---|---|
| LSTM | 0.054004 | 0.075457 | 0.913425 |
| GRU | 0.058296 | 0.083487 | 0.851738 |
| CNN | 0.053656 | 0.08737 | 0.831054 |
| DNN | 0.072263 | 0.095527 | 0.727253 |
| Seq2Seq | 0.115742 | 0.171256 | 0.750568 |
| Seq2Seq + Attention | 0.023398 | 0.045421 | 0.958567 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, C.R.; Rangel de Sousa, F.; Brusamarello, V.; Fernandes, N.C. Evaluation of Deep Learning Methods in a Dual Prediction Scheme to Reduce Transmission Data in a WSN. Sensors 2021, 21, 7375. https://doi.org/10.3390/s21217375
Morales CR, Rangel de Sousa F, Brusamarello V, Fernandes NC. Evaluation of Deep Learning Methods in a Dual Prediction Scheme to Reduce Transmission Data in a WSN. Sensors. 2021; 21(21):7375. https://doi.org/10.3390/s21217375
Chicago/Turabian StyleMorales, Carlos R., Fernando Rangel de Sousa, Valner Brusamarello, and Nestor C. Fernandes. 2021. "Evaluation of Deep Learning Methods in a Dual Prediction Scheme to Reduce Transmission Data in a WSN" Sensors 21, no. 21: 7375. https://doi.org/10.3390/s21217375
APA StyleMorales, C. R., Rangel de Sousa, F., Brusamarello, V., & Fernandes, N. C. (2021). Evaluation of Deep Learning Methods in a Dual Prediction Scheme to Reduce Transmission Data in a WSN. Sensors, 21(21), 7375. https://doi.org/10.3390/s21217375






