The Non-Tightness of a Convex Relaxation to Rotation Recovery
Abstract
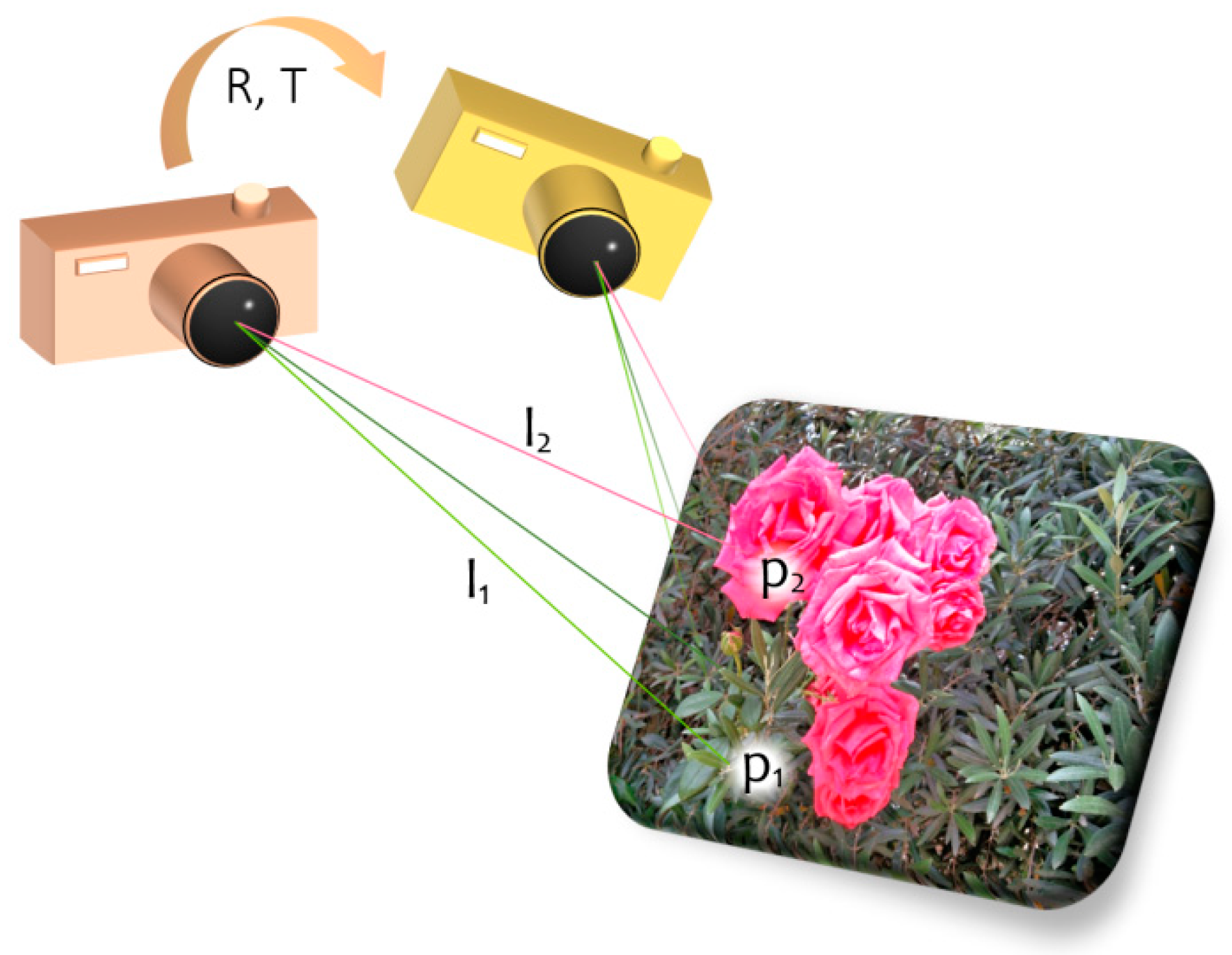
:1. Introduction
The PNP Problem: Details
2. Previous Work and Methods
Other Work on Convex Relaxation for Rotation Recovery
3. Results
3.1. Main Result: The Inadequacy of the Second Lasserre Level for Solving the PNP Problem
- (1)
- Fix a certain value of . This yields a polynomial with fixed scalar coefficients.
- (2)
- Define a distance between two polynomials as the sum of squares of differences of their coefficients. In our case, are homogenous quartics, hence there are 35 terms in this sum (the number of coefficients).
- (3)
- For any choice of , , define the function as the distance between and .
- (4)
- Find , which minimize .
- Chosen .
- Set the to fixed scalar values, by evenly distributing them over the upper half of the unit sphere.
- Minimized only over . Note that even then, no closed-form solution exists; however, the Optimization routine of the Maple© software package (Waterloo Maple Inc., 615 Kumpf Dr, Waterloo, ON N2V 1K8, Canada) was able to solve this problem with very high accuracy, obtaining a minimal value of roughly equal to .
- Empirically, it turned out that a solution exists only for values of larger than a certain threshold. Since our goal in this short submission is only to demonstrate that real PNP scenarios can fail the second Lasserre level, we did not attempt to find the smallest values of and ; however, these are interesting problems which merit further study.In order to verify the correctness of the optimization, the resulting values of , have been plugged into two packages for solving the PNP problem using SOS relaxation, and have indeed caused them to fail (see “Experimental Results”).
3.2. Some Comments on the Result
- The long running time required to produce the configuration which yields is not an issue, as our goal was to show that such a configuration exists.
- The configuration is stable, i.e small perturbations in the , still yield a polynomial which fails the relaxation. This is due to the fact that the set is open [18]. That is, the “problematic” configurations are not restricted to a low-dimensional manifold.
- Note that a rotation of and would have yielded a different polynomial, which would have also failed the relaxation; further, it would have been different from . Thus, the problem the configuration poses cannot be solved by checking whether the resulting polynomial is equal to .
- While, as proved in the following section, the third Lasserre level can solve the PNP configuration which yield , the solution did not converge due to numerical instabilities; a solution was obtained only at the fourth level. The numerical instability of solving optimization problems involving polynomials which are positive but not SOS was noticed by other researchers [9]. From the practical point of view, this indicates that there are PNP configurations at which higher Lasserre levels are required for the solution, than those indicated by Lemmas 3 and 5.
- One may wonder why the expression is added to . The reason is that we could not realize in PNP, since assumes the value of 0 at 14 points on . This means that to realize it in PNP, the matrix in Equation (2) would have had to be highly singular.
3.3. PNP and the Third Lasserre Level
- is non-negative on , and its minimum on is 0.
- is realizable in PNP for some .
- is not an SOS polynomial.
3.4. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Complexity of Solving the Optimization Problem with Lagrange Multipliers
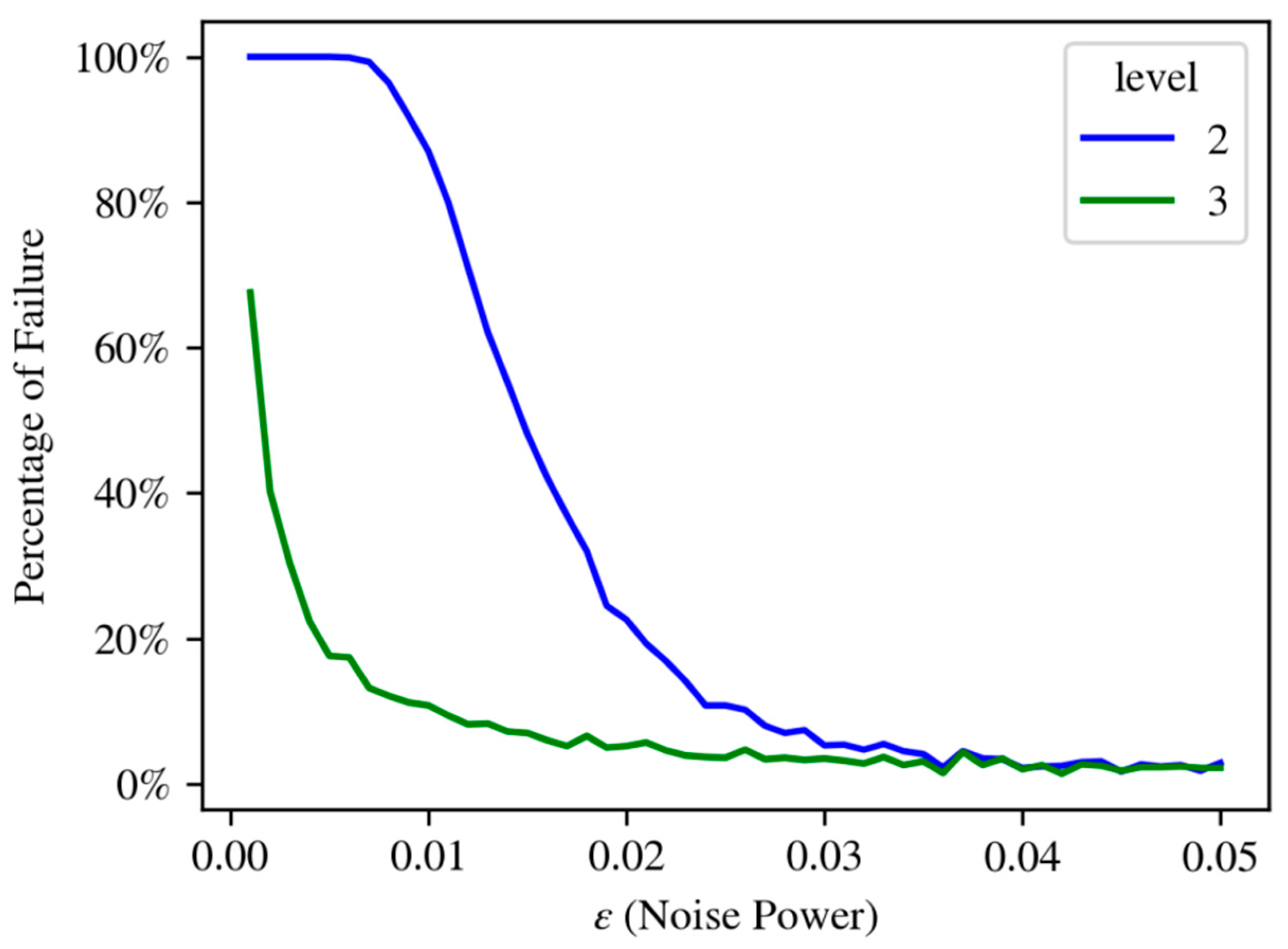
Appendix B. The Effect of the Noise Power on the Lasserre Levels
References
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. IJCV 2009, 81, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Schweighofer, G.; Pinz, A. Globally Optimal O(n) Solution to the PnP Problem for General Camera Models. In Proceedings of the British Machine Vision Conference, Leeds, UK, 20 June 2018; pp. 1–10. [Google Scholar]
- Zheng, Y.; Kuang, Y.; Sugimoto, S.; Åström, K.; Okutomi, M. Revisiting the PnP Problem: A Fast, General and Optimal Solution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2344–2351. [Google Scholar]
- Yang, H.; Antonante, P.; Tzoumas, V.; Carlone, L. Graduated Non-Convexity for Robust Spatial Perception: From Non-Minimal Solvers to Global Outlier Rejection. IEEE Robot. Autom. Lett. 2020, 5, 1127–1134. [Google Scholar] [CrossRef] [Green Version]
- Fragoso, V.; DeGol, J.; Hua, G. gDLS *: Generalized Pose-and-Scale Estimation Given Scale and Gravity Priors (CVPR). 2020. Available online: https://arxiv.org/abs/2004.02052 (accessed on 19 August 2021).
- Brynte, L.; Larsson, V.; Iglesias, J.P.; Olsson, C.; Kahl, F. On the Tightness of Semidefinite Relaxations for Rotation Estimation. arXiv 2021, arXiv:2101.020992021. [Google Scholar]
- Wikipedia Article. Available online: https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation (accessed on 19 August 2021).
- Parrilo, P.A.; Sturmfels, B. Minimizing Polynomial Functions. In Algorithmic and Quantitative Real Algebraic Geometry, DIMACS Series in Discrete Mathematics and Theoretical Computer Science; American Meteorological Society: Boston, MA, USA, 2003; Volume 60, pp. 83–99. [Google Scholar]
- Laurent, M. Sums of Squares, Moment Matrices and Optimization over Polynomials. In Emerging Applications of Algebraic Geometry; IMA: Dehradun, India, 2008; Volume 149. [Google Scholar]
- Lasserre, J.B. Global optimization with polynomials and the problem of moments. SIAM J. Optim. 2001, 11, 796–817. [Google Scholar] [CrossRef]
- Hilbert, D. Ueber die Darstellung definiter Formen als Summe von Formenquadraten. Math. Ann. 1888, 32, 342–350. [Google Scholar] [CrossRef]
- Choi, M.D.; Lam, T.Y. Extremal positive semidefinite forms. Math. Ann. 1977, 231, 1–18. [Google Scholar] [CrossRef]
- Schmüdgen, K. The K-moment Problem for Compact Semi-Algebraic Sets. Math. Ann. 1991, 289, 203–206. [Google Scholar] [CrossRef]
- Cifuentes, D.; Agarwal, S.; Parrilo, P.A.; Thomas, R.R. On the local stability of semidefinite relaxations. Math. Program. 2020. [Google Scholar] [CrossRef]
- Briales, J.; Jiménez, J.G. Convex Global 3D Registration with Lagrangian Duality. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5612–5621. [Google Scholar]
- Blekherman, G.; Smith, G.; Velasco, M. Sums of squares and varieties of minimal degree. J. Am. Math. Soc. 2016, 29, 893–913. [Google Scholar] [CrossRef] [Green Version]
- Blekherman, G. There are Significantly More Nonnegative Polynomials than Sums of Squares. Isr. J. Math. 2006, 153, 355–380. [Google Scholar] [CrossRef]
- Choi, M.D.; Lam, T.Y.; Reznick, B. Real zeros of positive semidefinite forms I. Math. Z. 1980, 171, 1–26. [Google Scholar] [CrossRef]
- Reznick, B. Department of Mathematics, University of Illinois Urbana-Champaign: Urbana, IL, USA, Unpublished work.
- Choi, M.D.; Lam, T.Y.; Reznick, B. Even symmetric sextics. Math. Z. 1987, 195, 559–580. [Google Scholar] [CrossRef]
- Choi, M.D.; Lam, T.Y.; Reznick, B. Sums of squares of real polynomials. Proc. Sympos. Pure Math. 1995, 58, 103–126. [Google Scholar]
- Didier, H.; Lasserre, J.B.; Löfberg, J. GloptiPoly 3: Moments, optimization and semidefinite programming. Optim. Methods Softw. 2009, 24, 761–779. [Google Scholar]
- Heller, J.; Pajdla, T. GpoSolver: A Matlab/C++ toolbox for global polynomial optimization. Optim. Methods Softw. 2016, 31, 405–434. [Google Scholar] [CrossRef]
- Hoeven, J.v.d.; Lecerf, G. On the Complexity Exponent of Polynomial System Solving. Found. Comput. Math. 2021, 21, 1–57. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfassi, Y.; Keren, D.; Reznick, B. The Non-Tightness of a Convex Relaxation to Rotation Recovery. Sensors 2021, 21, 7358. https://doi.org/10.3390/s21217358
Alfassi Y, Keren D, Reznick B. The Non-Tightness of a Convex Relaxation to Rotation Recovery. Sensors. 2021; 21(21):7358. https://doi.org/10.3390/s21217358
Chicago/Turabian StyleAlfassi, Yuval, Daniel Keren, and Bruce Reznick. 2021. "The Non-Tightness of a Convex Relaxation to Rotation Recovery" Sensors 21, no. 21: 7358. https://doi.org/10.3390/s21217358
APA StyleAlfassi, Y., Keren, D., & Reznick, B. (2021). The Non-Tightness of a Convex Relaxation to Rotation Recovery. Sensors, 21(21), 7358. https://doi.org/10.3390/s21217358






