Duck Eggshell Crack Detection by Nondestructive Sonic Measurement and Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Selection
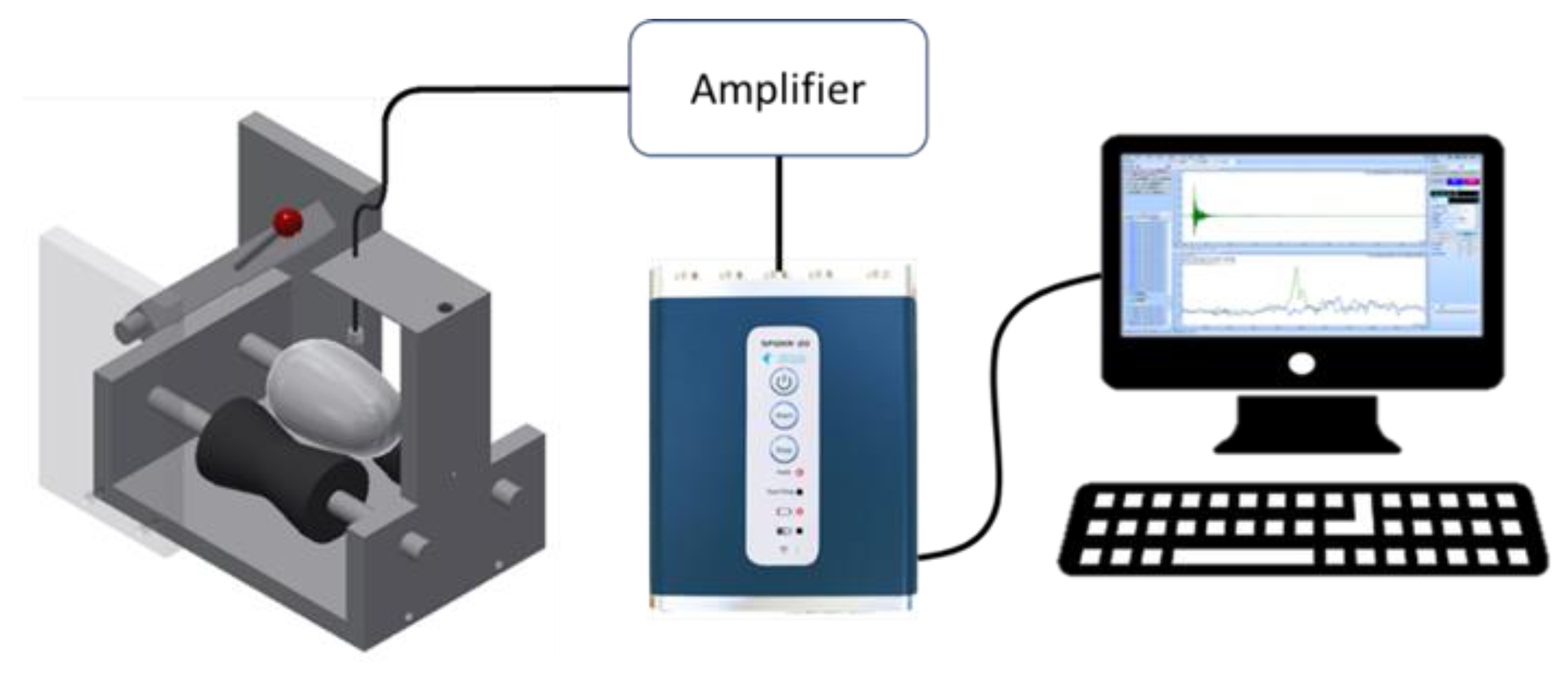
2.2. Measurement Setup
2.3. Sound Signal Sampling
2.4. Logistic Regression
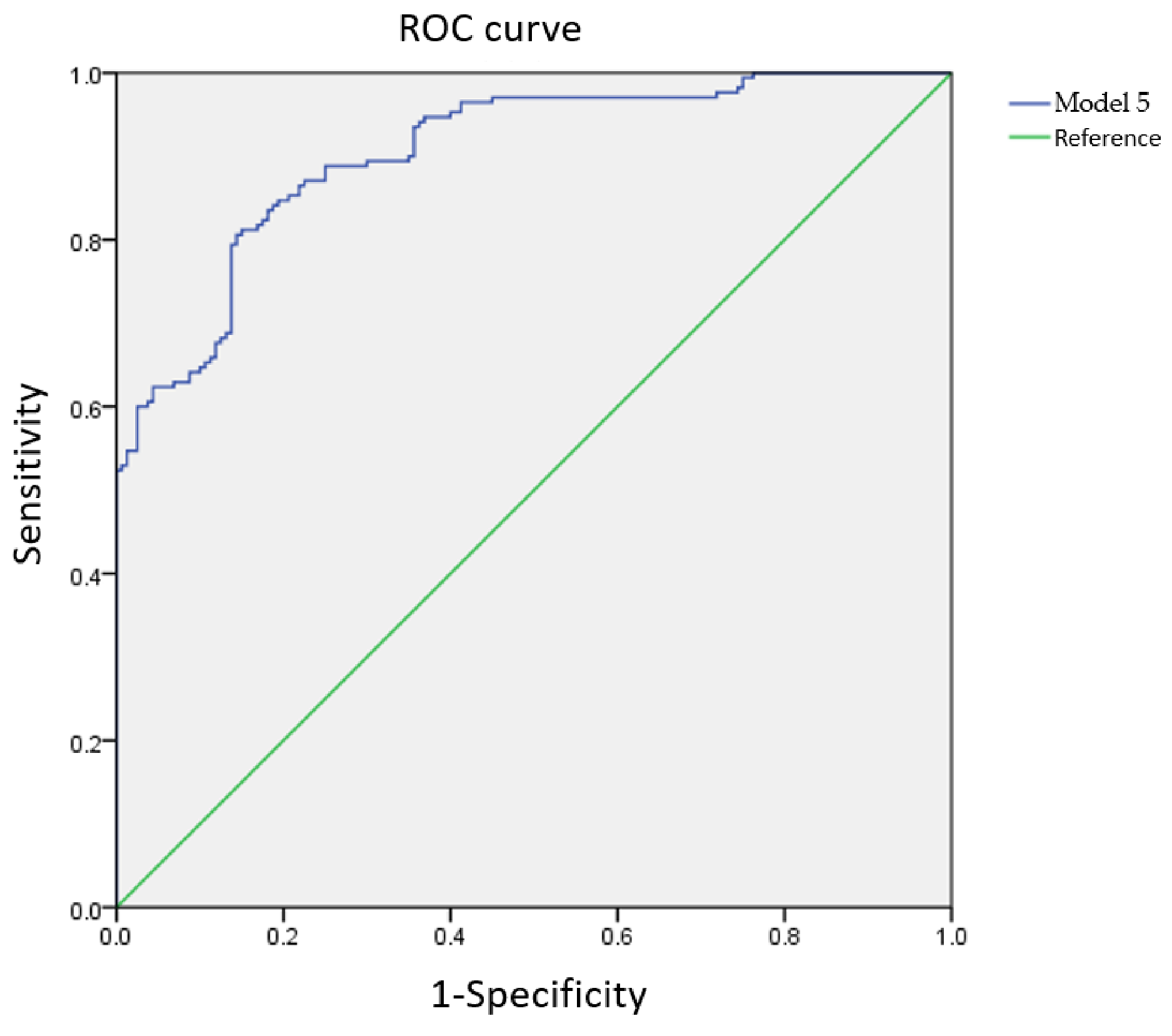
2.5. Receiver Operating Characteristic (ROC) Curve
3. Results and Discussion
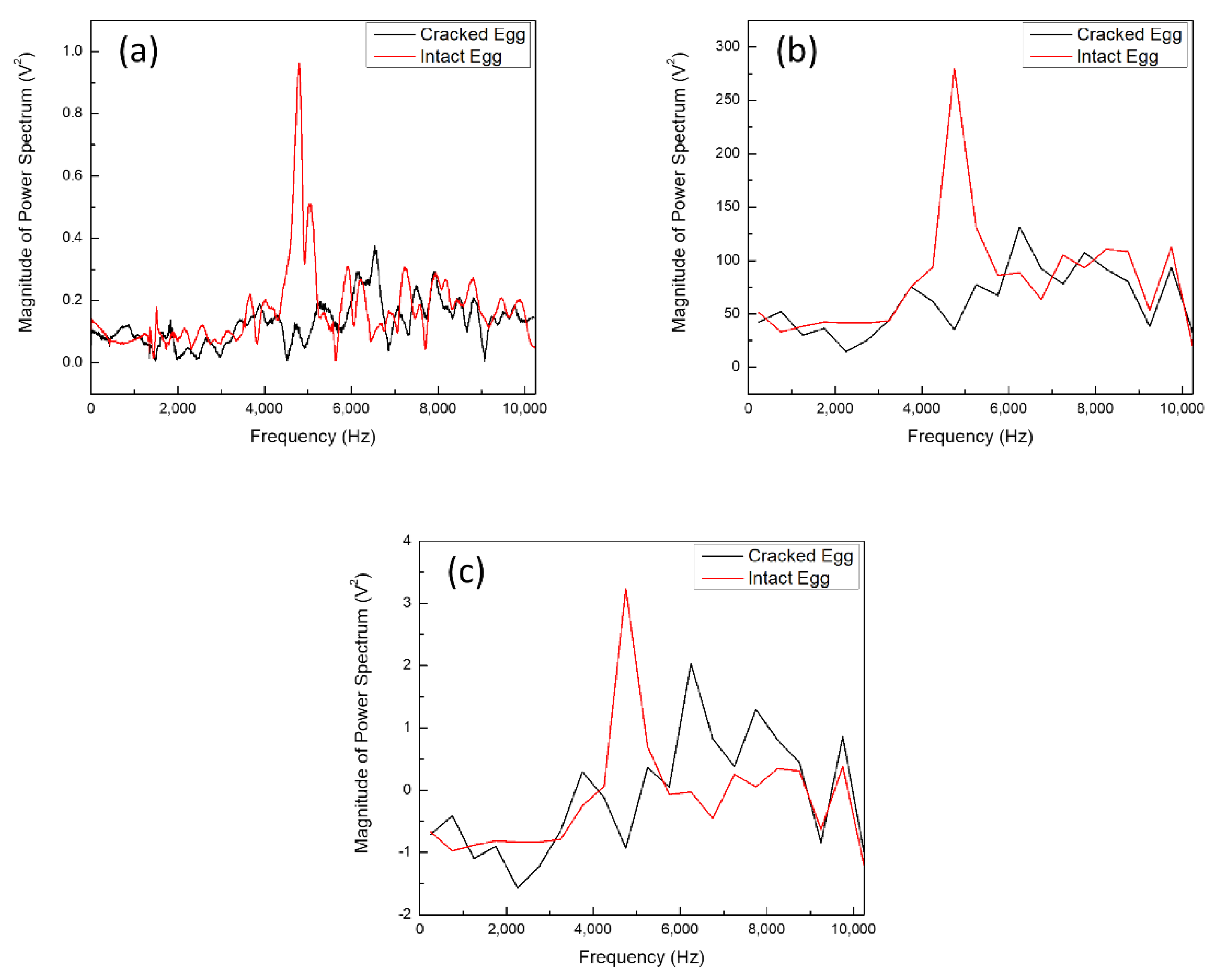
3.1. Signal Analysis
3.2. Generating Eggshell Crack Calibration Curve
| Model | Selected Frequencies Bandwidth (Hz) | Nagelkerke R2 | Intact Egg | Cracked Eggs | Overall Accuracy (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| True (units) | False (units) | Accuracy (%) | True (units) | False (units) | Accuracy(%) | ||||
| 1 | 6000 | 0.379 | 117 | 33 | 78 | 100 | 50 | 66.7 | 72.3 |
| 2 | 5000, 6000 | 0.602 | 128 | 22 | 85.3 | 124 | 26 | 82.7 | 84 |
| 3 | 1500, 5000, 6000 | 0.682 | 133 | 17 | 88.7 | 133 | 17 | 88.7 | 88.7 |
| 4 | 1500, 5000, 6000, 10,000 | 0.727 | 140 | 10 | 93.3 | 137 | 13 | 91.3 | 92.3 |
| 5 | 1500, 5000, 6000, 8500, 10,000 | 0.776 | 137 | 13 | 91.3 | 132 | 18 | 88 | 89.7 |
| i (1-n) | Frequency (Hz) | bi | Std. Error | Wald Test | Variance Inflation Factor (VIF) |
|---|---|---|---|---|---|
| 1 | 1500 | −2.461 | 0.664 | 13.721 | 1.076 |
| 2 | 5000 | 1.547 | 0.253 | 37.305 | 1.121 |
| 3 | 6000 | −2.246 | 0.326 | 47.439 | 1.074 |
| 4 | 8500 | 1.853 | 0.420 | 19.432 | 1.212 |
| 5 | 10,000 | −2.112 | 0.398 | 28.172 | 1.277 |
| c | – | −5.690 | 0.898 | 40.116 *** | – |
| Overall model fit | = 261.753 *** Hosmer–Lemeshow = 136.445 n.s. | ||||
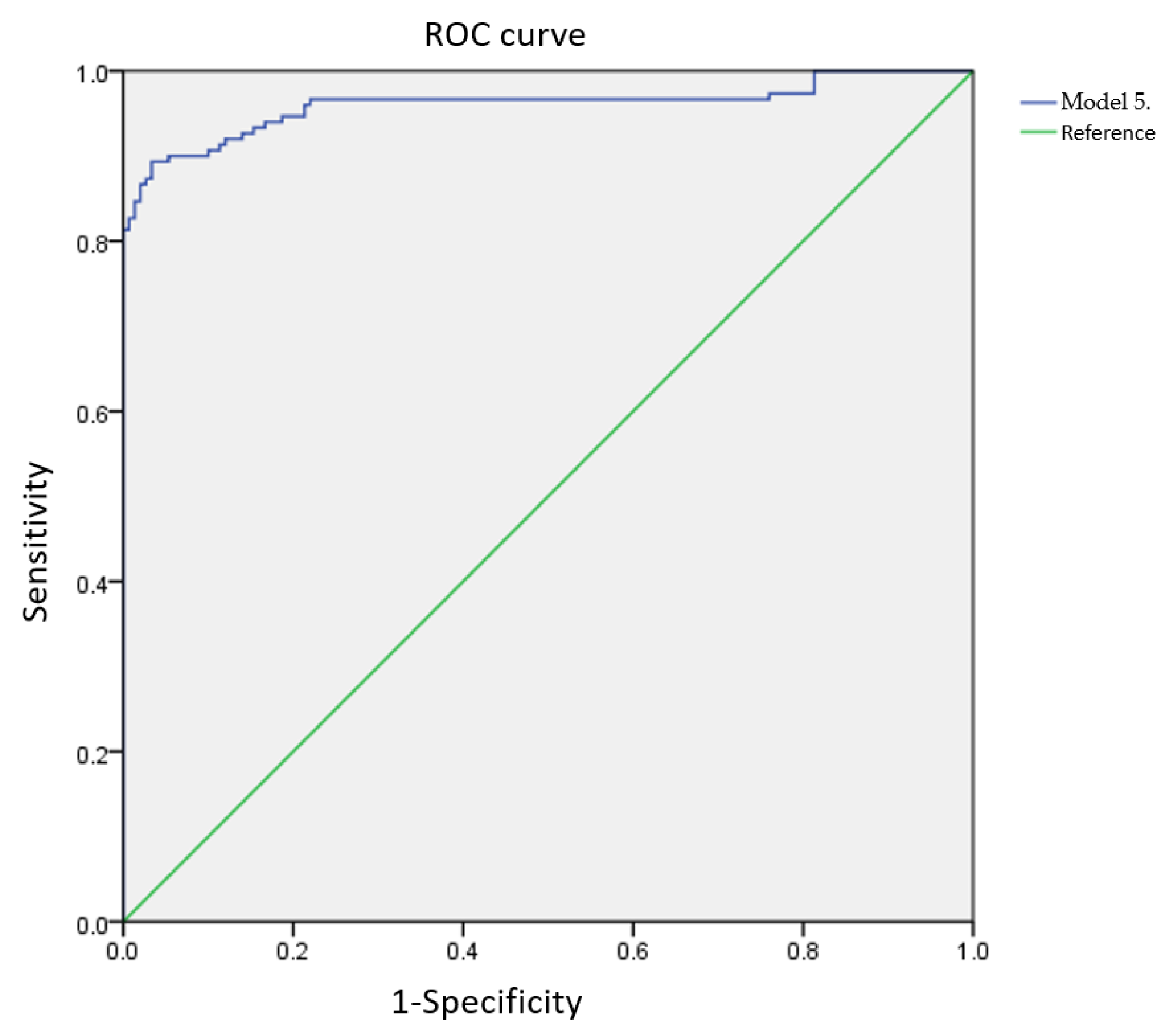
| Prediction Frequency Bandwidth (Hz) | 1500, 5000, 6000, 8500, 10,000 | |||
|---|---|---|---|---|
| State | Predicted | Accuracy | ||
| Intact | Crack | |||
| Actual | Intact | 151 | 19 | 88.8% |
| Crack | 22 | 138 | 86.3% | |
| Overall accuracy | 87.6% | |||
| Nagelkerke R2 | 0.729 | |||
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaewmanee, T.; Benjakul, S.; Visessanguan, W. Changes in chemical composition, physical properties and microstructure of duck egg as influenced by salting. Food Chem. 2009, 112, 560–569. [Google Scholar] [CrossRef]
- Yu, L.; Xue, H.; Xiong, C.; Xin, X.; Wang, P.; Feng, F.; Cao, D.; Tu, Y.; Zhao, Y. Characterization of duck egg white gel under the action of baijiu (chinese liquor). LWT 2021, 147, 111487. [Google Scholar] [CrossRef]
- Gutierrez, M.; Takahashi, H.; Juneja, L. Nutritive evaluation of hen eggs. In Hen Eggs; CRC Press: Boca Raton, FL, USA, 2018; pp. 25–35. [Google Scholar]
- Mollazade, K.; Jörissen, S.; Nüchter, A. Measuring internal quality traits in egg by 3d laser imaging. J. Food Eng. 2021, 291, 110289. [Google Scholar] [CrossRef]
- Li, C.H.; Hsieh, C.H.; Hung, C.C.; Cheng, C.W. Nondestructive detection of the gel state of preserved eggs based on dielectric impedance. Foods 2021, 10, 394. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Lu, Q.; Jiang, R. Pattern recognition of eggshell crack using pca and lda. Innov. Food Sci. Emerg. Technol. 2010, 11, 520–525. [Google Scholar] [CrossRef]
- Sharaf Eddin, A.; Ibrahim, S.A.; Tahergorabi, R. Egg quality and safety with an overview of edible coating application for egg preservation. Food Chem. 2019, 296, 29–39. [Google Scholar] [CrossRef]
- Pai, S.-Y.; Jee, W.-M.; Li, C.-W.; Cheng, C.-W. The Study of Eggshells′ Crack Detection by Acoustics. J. Agric. Food Res. 2001, 50, 79–102. [Google Scholar] [CrossRef]
- Liu, Y.C.; Chen, T.H.; Wu, Y.C.; Tan, F.J. Determination of the quality of stripe-marked and cracked eggs during storage. Asian-Aust. J. Anim. Sci 2017, 30, 1013–1020. [Google Scholar] [CrossRef]
- Priyadumkol, J.K., C.; Thainimit, S. Crack detection on unwashed eggs using image processing. J. Food Eng. 2017, 209, 76–82. [Google Scholar] [CrossRef]
- Abdullah, M.H.; Nashat, S.; Anwar, S.A.; Abdullah, M.Z. A framework for crack detection of fresh poultry eggs at visible radiation. Comput. Electron. Agric. 2017, 141, 81–95. [Google Scholar] [CrossRef]
- Cheng, C.-W.; Feng, P.H.; Xie, J.H..; Weng, Y.K. Eggshell crack detection and egg classification using resonance and support vector machine methods. Appl. Eng. Agric. 2019, 35, 23–30. [Google Scholar] [CrossRef]
- Babin, P.; Della Valle, G.; Dendievel, R.; Lourdin, D.; Salvo, L. X-Ray tomography study of the cellular structure of extruded starches and its relations with expansion phenomenon and foam mechanical properties. Carbohydr. Polym. 2007, 68, 329–340. [Google Scholar] [CrossRef]
- Chanvrier, H.J., E.; Gondek, E.; Gumy, J.-C. Insights into the texture of extruded cereals: Structure and acoustic properties. Innov. Food Sci. Emerg. Technol. 2014, 24, 61–68. [Google Scholar] [CrossRef]
- Wiktor, A.G., E.; Jakubczyk, E.; Nowacka, M.; Dadan, M.; Fijalkowska, A.; Witrowa-Rajchert, D. Acoustic emission as a tool to assess the changes induced by pulsed electric field in apple tissue. Innov. Food Sci. Emerg. Technol. 2016, 37, 375–383. [Google Scholar] [CrossRef]
- Gondek, E.W.A.; Lewicki, P.P.; Ranachowski, Z. Influence of water activity on the acoustic properties of breakfast cereals. J. Texture Stud. 2006, 37, 497–515. [Google Scholar] [CrossRef]
- Lewicki, P.P.M., A.; Kuropatwa, M.J.A.A. Influence of water activity on texture of corn flakes. Acta Agrophys. 2007, 9, 79–90. [Google Scholar]
- Wang, H.M., J.; Zhang, J.; Jiang, H.; Wang, J. Acoustic feature extraction and optimization of crack detection for eggshell. J. Food Eng. 2016, 171, 240–247. [Google Scholar] [CrossRef]
- De Ketelaere, B.C., P.; De Baerdemaeker, J. Eggshell crack detection based on acoustic resonance frequency analysis. J. Agric. Eng. Res. 2000, 76, 157–163. [Google Scholar] [CrossRef]
- Kibala, L.; Rozempolska-Rucinska, I.; Kasperek, K.; Zieba, G.; Lukaszewicz, M. Ultrasonic eggshell thickness measurement for selection of layers. Poult Sci 2015, 94, 2360–2363. [Google Scholar] [CrossRef]
- Jin, C.X., L.; Ying, Y. Eggshell crack detection based on the time-domain acoustic signal of rolling eggs on a step-plate. J. Food Eng. 2015, 153, 53–62. [Google Scholar] [CrossRef]
- Sun, C.L., J.; Yang, N.; Xu, G. Egg quality and egg albumen property of domestic chicken, duck, goose, turkey, quail, and pigeon. Poult. Sci. 2019, 98, 4516–4521. [Google Scholar] [CrossRef]
- Khaledi, A.K., F.; Esmaeili, D.; Esmaeili, S.-A.; Rostami, H.J.D.P.C. The role of hpaa protein as candidate vaccine against helicobacter pylori. Pharma Chem. 2016, 8, 235–237. [Google Scholar]
- Ghosh, A.D., P. Flood severity assessment of the coastal tract situated between muriganga and saptamukhi estuaries of sundarban delta of india using frequency ratio (fr), fuzzy logic (fl), logistic regression (lr) and random forest (rf) models. Reg. Stud. Mar. Sci. 2021, 42, 101624. [Google Scholar] [CrossRef]
- Aram-Ahmaddi, M.B.; Najafipour, H. Predicting type two diabetes and determination of effectiveness of risk factors applying logistic regression model. J. Kerman Univ. Med. Sci. 2014, 21, 103–113. [Google Scholar]
- Khandezamin, Z.N., M.; Rashti, M.J. Detection and classification of breast cancer using logistic regression feature selection and GMDH classifier. J. Biomed. Inform. 2020, 111, 103591. [Google Scholar] [CrossRef]
- Rezapour, M.M.M., A.; Ksaibati, K. Analyzing injury severity of motorcycle at-fault crashes using machine learning techniques, decision tree and logistic regression models. Int. J. Transp. Sci. Technol. 2020, 9, 89–99. [Google Scholar] [CrossRef]
- Moon, S.H.; Kim, Y.H. An Improved forecast of precipitation type using correlation-based feature selection and multinomial logistic regression. Atmos. Res. 2020, 240, 104928. [Google Scholar] [CrossRef]
- Ding, Y.C., B.; Lei, X.; Liao, B.; Wu, F.X. Predicting novel CircRNA-disease associations based on random walk and logistic regression model. Comput. Biol. Chem. 2020, 87, 107287. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Acoustical unmanned aerial vehicle detection in indoor scenarios using logistic regression model. Build. Acoust. 2021, 28, 77–96. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Horton, S.P.; Langston, C.A.; Samei, B. Seismic features and automatic discrimination of deep and shallow induced-microearthquakes using neural network and logistic regression. Geophys. J. Int. 2016, 207, 29–46. [Google Scholar] [CrossRef]
- Harakawa, R.; Ogawa, T.; Haseyama, M.; Akamatsu, T. Automatic detection of fish sounds based on multi-stage classification including logistic regression via adaptive feature weighting. J. Acoust. Soc. Am. 2018, 144, 2709–2718. [Google Scholar] [CrossRef]
- Jiang, F.G., Z.; Li, Z.; Wang, X. A Method of Predicting Visual detectability of low-velocity impact damage in composite structures based on logistic regression model. Chin. J. Aeronaut. 2021, 34, 296–308. [Google Scholar] [CrossRef]
- Fukunishi, H.N., M.; Luo, Y.; Kubo, M.; Kobayashi, Y. Alzheimer-type dementia prediction by sparse logistic regression using claim data. Comput. Methods Programs Biomed. 2020, 196, 105582. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.Z.W., Y.; Peng, J.; Sun, M.W.; Zeng, J.; Jiang, H. Comparison between logistic regression and machine learning algorithms on survival prediction of traumatic brain injuries. J. Crit. Care 2019, 54, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Zweig, M.H.; Campbell, G. Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical Medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef]
- Ma, H.; Bandos, A.I.; Gur, D. On the use of partial area under the ROC curve for comparison of two diagnostic tests. Biom. J. 2015, 57, 304–320. [Google Scholar] [CrossRef] [PubMed]
- Yesilnacar, E.T., T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Saha, S.S., M.; Mukherjee, K.; Arabameri, A.; Ngo, P.T.T.; Paul, G.C. Predicting the deforestation probability using the binary logistic regression, random forest, ensemble rotational forest, REPTree: A case study at the Gumani River basin, India. Sci. Total Environ. 2020, 730, 139197. [Google Scholar] [CrossRef]
- Smith, G. Step away from stepwise. J. Big Data 2018, 5, 32. [Google Scholar] [CrossRef]
- Botta, B.; Gattam, S.; Datta, A. Eggshell crack detection using deep convolutional neural networks. J. Food Eng. 2022, 315, 110798. [Google Scholar] [CrossRef]

| Category | Description |
|---|---|
| Minor stripe-marked egg (ME) | An egg that has a gray stripe-mark (<2 cm), but no damage has occurred to the eggshell membrane and no egg components have leaked from the egg. |
| Severe stripe-marked egg (SE) | An egg that has a single gray stripe mark or for which the sum of the lengths of individual stripe marks is more than 2 cm, but no damage has occurred to the eggshell membrane and no egg components have leaked from the egg. |
| Cracked egg (CE) | An egg that has at least one visible hair-like microcrack on the eggshell, but no damage has occurred to the eggshell membrane and no egg components have leaked from the egg. |
| Broken egg (BE) | An egg that has at least one complete eggshell crack or hole, where the eggshell and shell membrane have broken and egg components have leaked from the egg. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, C.-C.; Li, C.-H.; Huang, K.-J.; Cheng, C.-W. Duck Eggshell Crack Detection by Nondestructive Sonic Measurement and Analysis. Sensors 2021, 21, 7299. https://doi.org/10.3390/s21217299
Lai C-C, Li C-H, Huang K-J, Cheng C-W. Duck Eggshell Crack Detection by Nondestructive Sonic Measurement and Analysis. Sensors. 2021; 21(21):7299. https://doi.org/10.3390/s21217299
Chicago/Turabian StyleLai, Chia-Chun, Cheng-Han Li, Ko-Jung Huang, and Ching-Wei Cheng. 2021. "Duck Eggshell Crack Detection by Nondestructive Sonic Measurement and Analysis" Sensors 21, no. 21: 7299. https://doi.org/10.3390/s21217299
APA StyleLai, C.-C., Li, C.-H., Huang, K.-J., & Cheng, C.-W. (2021). Duck Eggshell Crack Detection by Nondestructive Sonic Measurement and Analysis. Sensors, 21(21), 7299. https://doi.org/10.3390/s21217299






