Closed-Form Pseudolinear Estimators for DRSS-AOA Localization
Abstract
:1. Introduction
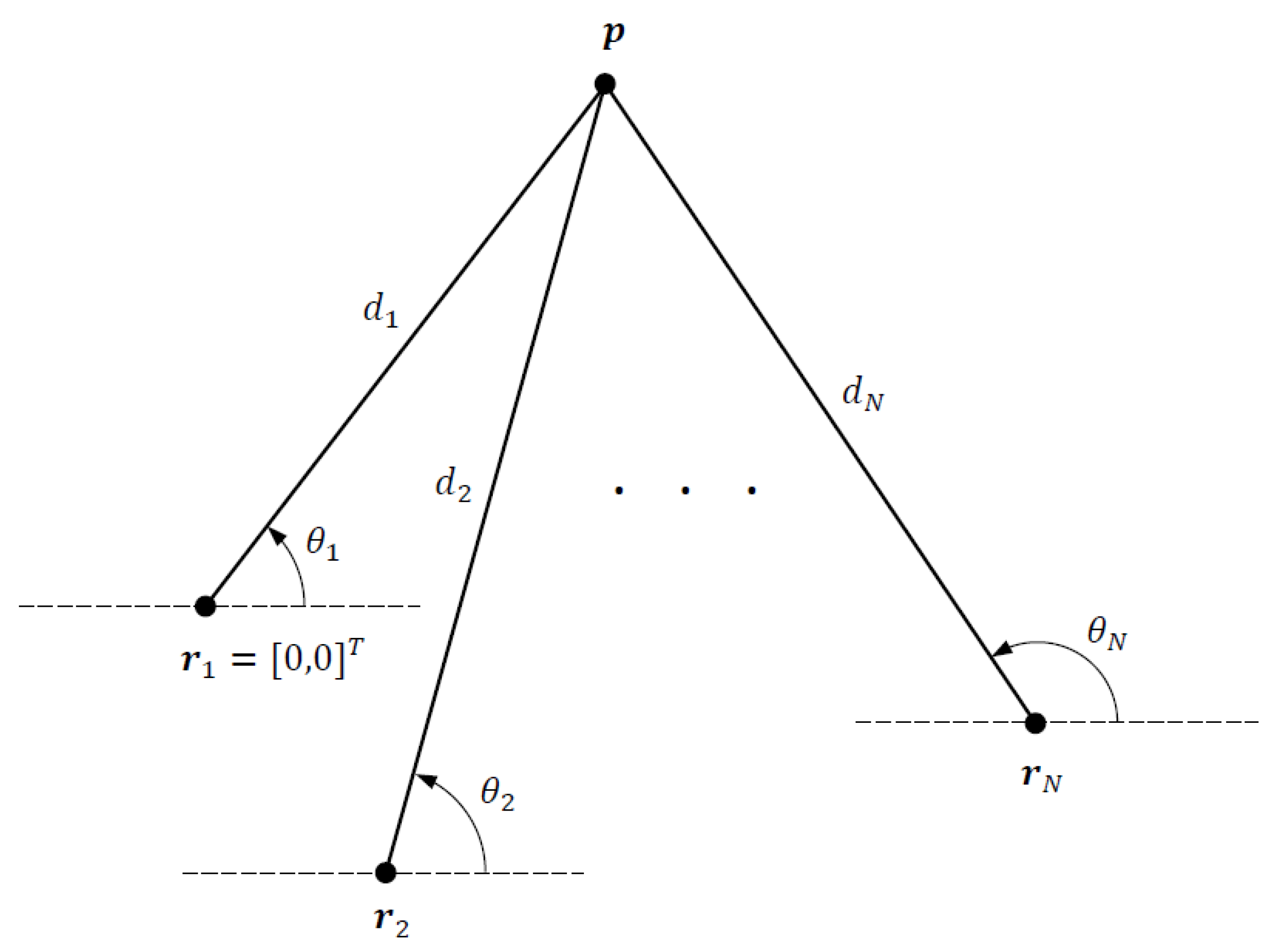
2. Problem Definition
3. Maximum Likelihood Estimator
4. Pseudolinear Equations for Hybrid Measurements
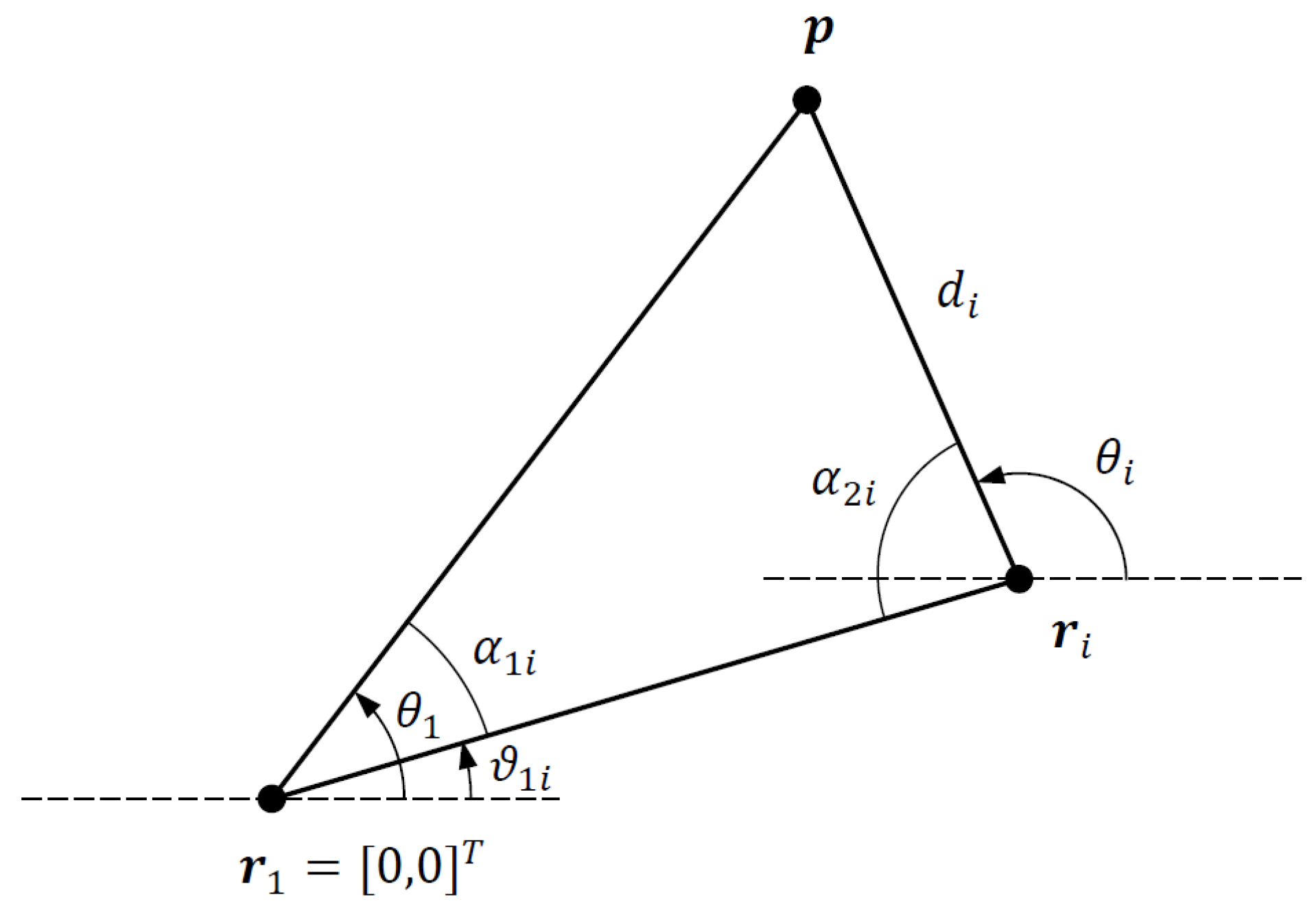
4.1. Linearized AOA Equations
4.2. Linearized DRSS Equations
4.3. Linearized DRSS-AOA Equations
5. Hybrid Pseudolinear Estimators
5.1. LS Solution and Bias Analysis
5.2. WLS Solution and Bias Analysis
5.3. WIV Solution
5.4. SHM-WIV Solution
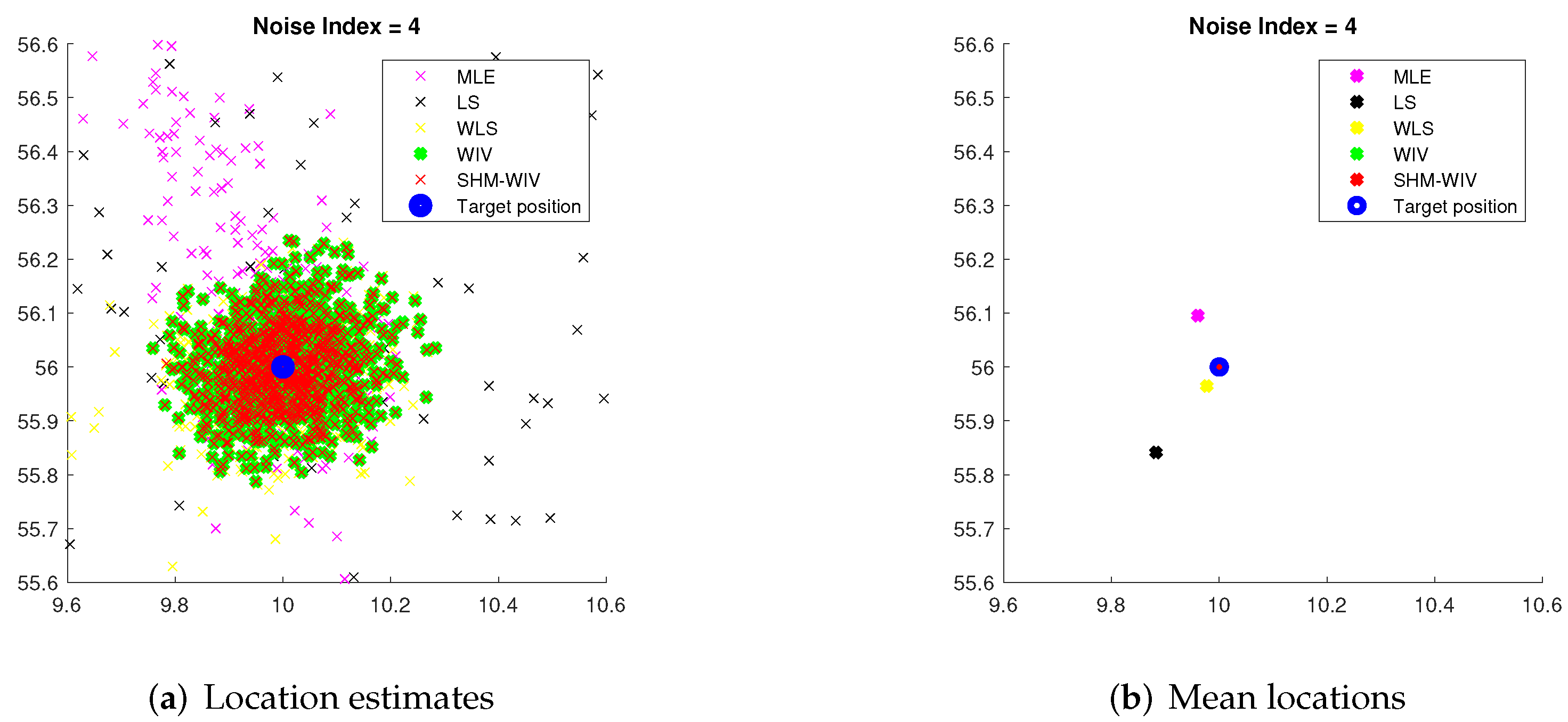
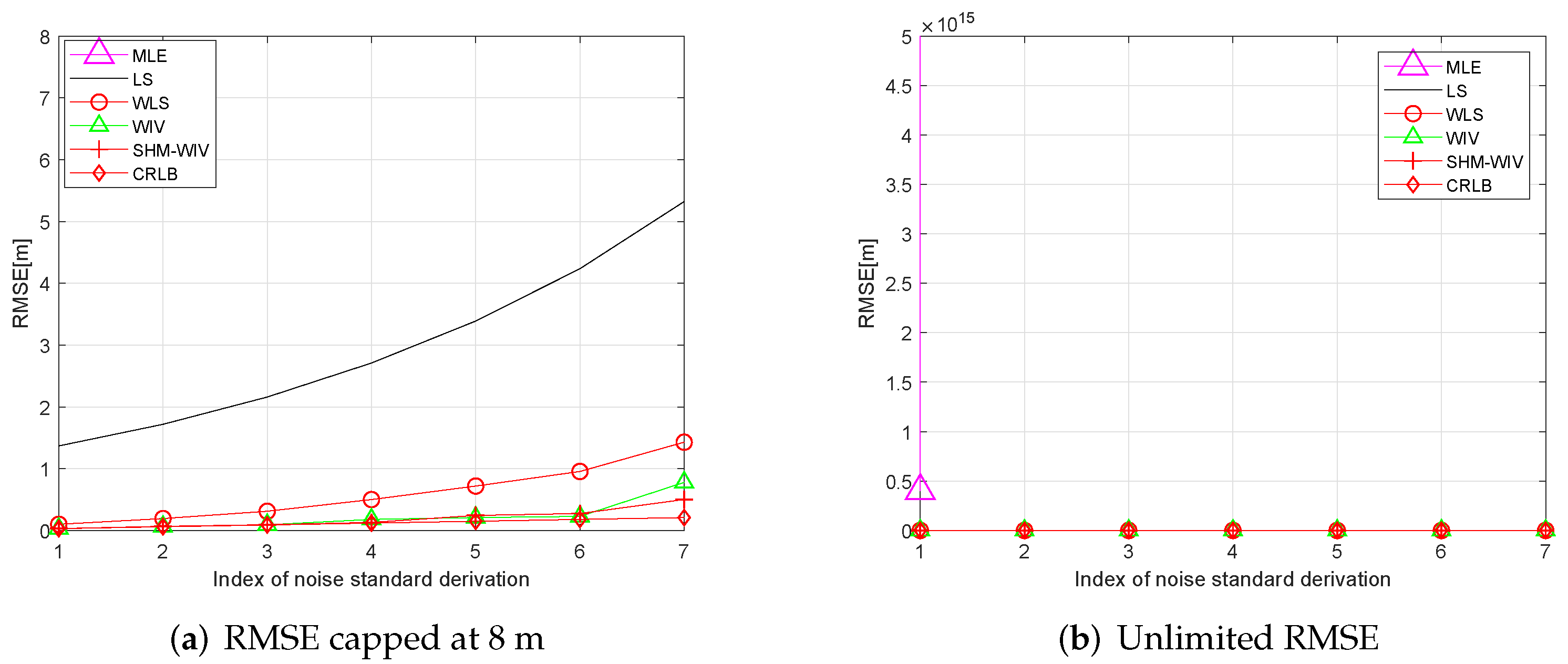
6. Simulation Results
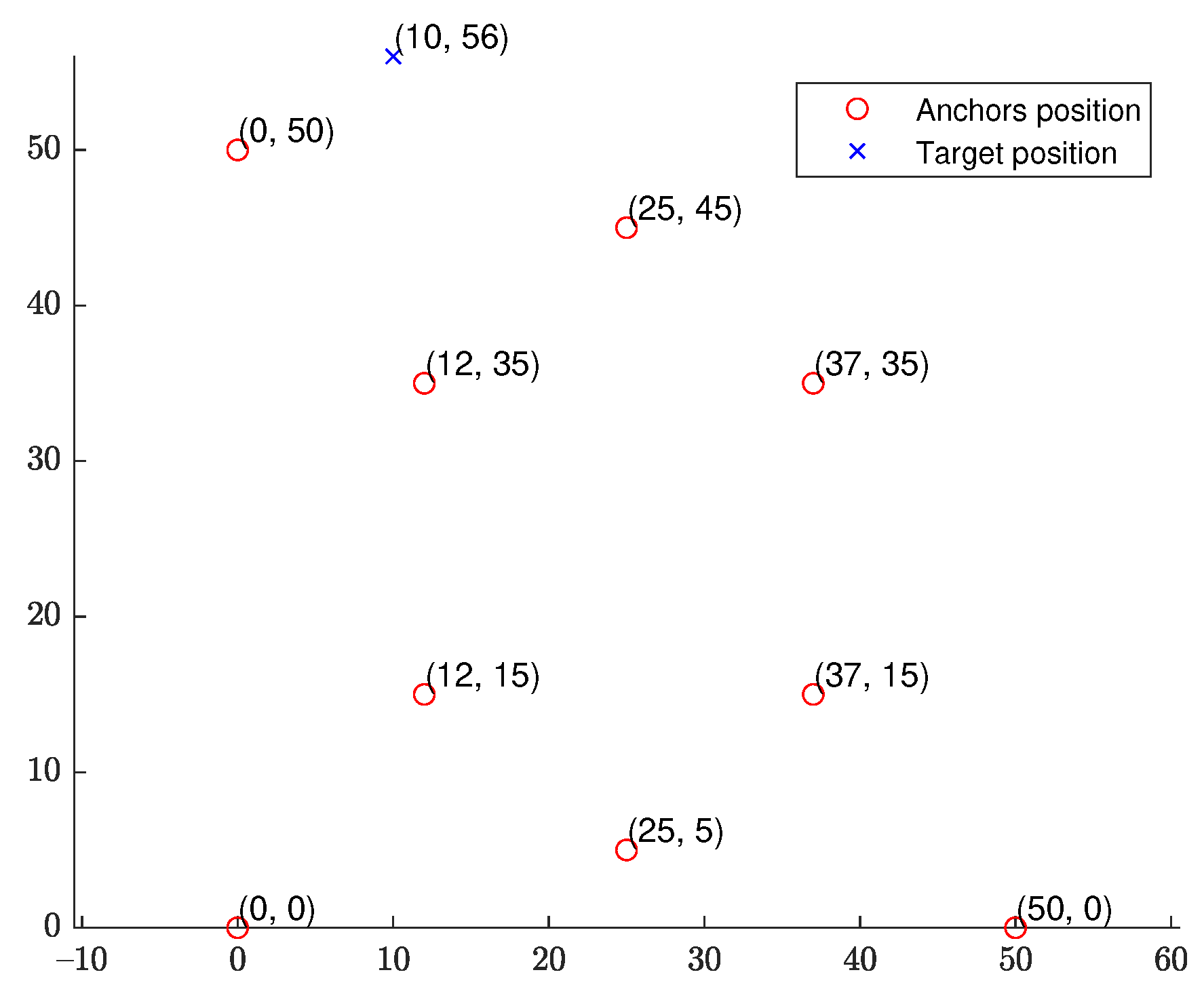
6.1. Simulation Set-Up
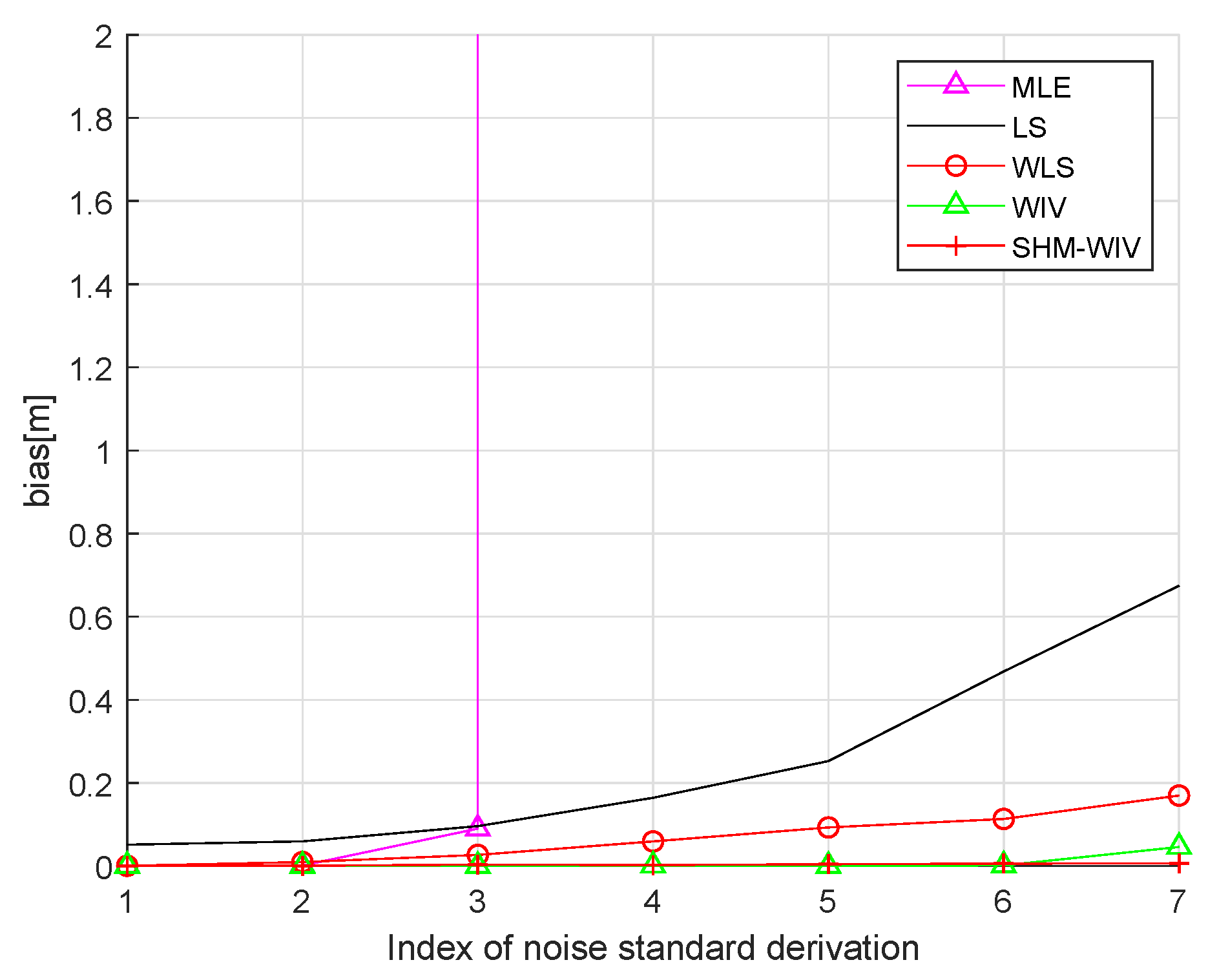
6.2. Fixed Source Location
6.3. Randomized Source Location
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Linearized DRSS Equation Noise
References
- Stansfield, R.G. Statistical theory of d.f. fixing. J. Inst. Electr. Eng. Part IIIA Radiocommun. 1947, 94, 762–770. [Google Scholar] [CrossRef]
- Torrieri, D.J. Statistical Theory of Passive Location Systems. IEEE Trans. Aerosp. Electron. Syst. 1984, AES-20, 183–198. [Google Scholar] [CrossRef] [Green Version]
- Nardone, S.; Lindgren, A.; Gong, K. Fundamental properties and performance of conventional bearings-only target motion analysis. IEEE Trans. Autom. Control 1984, 29, 775–787. [Google Scholar] [CrossRef]
- Ljung, L.; Söderström, T. Theory and Practice of Recursive Identification; MIT Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Athley, F. Threshold region performance of maximum likelihood direction of arrival estimators. IEEE Trans. Signal Process. 2005, 53, 1359–1373. [Google Scholar] [CrossRef]
- Lingren, A.G.; Gong, K.F. Position and velocity estimation via bearing observations. IEEE Trans. Aerosp. Electron. Syst. 1978, AES-14, 564–577. [Google Scholar] [CrossRef]
- Pages-Zamora, A.; Vidal, J.; Brooks, D. Closed-form solution for positioning based on angle of arrival measurements. In Proceedings of the 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Lisboa, Portugal, 15–18 September 2002; Volume 4, pp. 1522–1526. [Google Scholar] [CrossRef]
- Aidala, V.J.; Nardone, S.C. Biased Estimation Properties of the Pseudolinear Tracking Filter. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 432–441. [Google Scholar] [CrossRef]
- Chan, Y.T.; Rudnicki, S.W. Bearings-only and Doppler-bearing tracking using instrumental variables. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 1076–1083. [Google Scholar] [CrossRef]
- Holtsberg, A.; Holst, J.H. A nearly unbiased inherently stable bearings-only tracker. IEEE J. Ocean. Eng. 1993, 18, 138–141. [Google Scholar] [CrossRef]
- Pham, D.T. Some quick and efficient methods for bearing-only target motion analysis. IEEE Trans. Signal Process. 1993, 41, 2737–2751. [Google Scholar] [CrossRef]
- Nardone, S.C.; Graham, M.L. A closed-form solution to bearings-only target motion analysis. IEEE J. Ocean. Eng. 1997, 22, 168–178. [Google Scholar] [CrossRef]
- Doğançay, K. Bias compensation for the bearings-only pseudolinear target track estimator. IEEE Trans. Signal Process. 2005, 54, 59–68. [Google Scholar] [CrossRef]
- Ho, K.; Chan, Y. An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis. IEEE Trans. Signal Process. 2006, 54, 809–822. [Google Scholar] [CrossRef]
- Ho, K.C.; Chan, Y.T. Geometric-Polar Tracking From Bearings-Only and Doppler-Bearing Measurements. IEEE Trans. Signal Process. 2008, 56, 5540–5554. [Google Scholar] [CrossRef]
- Gu, G. A novel power-bearing approach and asymptotically optimum estimator for target motion analysis. IEEE Trans. Signal Process. 2011, 59, 912–922. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, G.Z. Bearings-only target motion analysis via instrumental variable estimation. IEEE Trans. Signal Process. 2010, 58, 5523–5533. [Google Scholar] [CrossRef]
- Dogancay, K. 3D Pseudolinear Target Motion Analysis From Angle Measurements. IEEE Trans. Signal Process. 2015, 63, 1570–1580. [Google Scholar] [CrossRef]
- Pang, F.; Wen, X. A Novel Closed-Form Estimator for AOA Target Localization Without Prior Knowledge of Noise Variances. Circ. Syst. Signal Process. 2021, 40, 3573–3591. [Google Scholar] [CrossRef]
- Shao, H.J.; Zhang, X.P.; Wang, Z. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Dogancay, K. Self-localization from landmark bearings using pseudolinear estimation techniques. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2361–2368. [Google Scholar] [CrossRef]
- Lee, J.H.; Buehrer, R.M. Location estimation using differential RSS with spatially correlated shadowing. In Proceedings of the Global Telecommunications Conference, 2009. GLOBECOM 2009, IEEE, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Salman, N.; Kemp, A.H.; Ghogho, M. Low complexity joint estimation of location and path-loss exponent. IEEE Wirel. Commun. Lett. 2012, 1, 364–367. [Google Scholar] [CrossRef]
- Hu, Y.; Leus, G. Robust Differential Received Signal Strength-Based Localization. IEEE Trans. Signal Process. 2017, 65, 3261–3276. [Google Scholar] [CrossRef] [Green Version]
- Ogilvy, C.S. Excursions in Geometry; Dover Publications: Mineola, NY, USA, 1990. [Google Scholar]
- Lin, L.; So, H.C.; Chan, Y.T. Accurate and Simple Source Localization Using Differential Received Signal Strength. Digit. Signal Process. 2013, 23, 736–743. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Li, X.; Huang, Z.; Tian, J. An Improved Closed-Form Solution for Differential RSS-based Localization. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Vaghefi, R.M.; Gholami, M.R.; Ström, E.G. RSS-based sensor localization with unknown transmit power. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2480–2483. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Doğançay, K.; Nguyen, N.H.; Law, Y.W. Reducing the bias in DRSS-based localization: An instrumental variable approach. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), IEEE, Coruña, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Li, J.; Doğançay, K.; Nguyen, N.H.; Law, Y.W. DRSS-Based Localisation Using Weighted Instrumental Variables and Selective Power Measurement. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, Barcelona, Spain, 4–8 May 2020; pp. 4876–4880. [Google Scholar]
- Lee, J.H.; Buehrer, R.M. Handbook of Position Location: Theory, Practice, and Advances; Chapter Fundamentals of Received Signal Strength-Based Position Location; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Wang, S.; Jackson, B.R.; Inkol, R. Hybrid RSS/AOA emitter location estimation based on least squares and maximum likelihood criteria. In Proceedings of the 2012 26th Biennial Symposium on Communications (QBSC), IEEE, Kingston, ON, Canada, 28–29 May 2012; pp. 24–29. [Google Scholar]
- Chan, Y.T.; Chan, F.; Read, W.; Jackson, B.R.; Lee, B.H. Hybrid localization of an emitter by combining angle-of-arrival and received signal strength measurements. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), IEEE, Toronto, ON, Canada, 5–8 May 2014; pp. 1–5. [Google Scholar]
- Tomic, S.; Marikj, M.; Beko, M.; Dinis, R.; Órfão, N. Hybrid RSS-AoA technique for 3-D node localization in wireless sensor networks. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), IEEE, Dubrovnik, Croatia, 24–28 August 2015; pp. 1277–1282. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A closed-form solution for RSS/AoA target localization by spherical coordinates conversion. IEEE Wirel. Commun. Lett. 2016, 5, 680–683. [Google Scholar] [CrossRef] [Green Version]
- Beko, M.; Tomic, S.; Dinis, R.; Carvalho, P. Apparatus and Method for RSS/AoA Target 3-D Localization in Wireless Networks. U.S. Patent Number 10338193, 2 July 2019. [Google Scholar]
- Nguyen, T.; D Vy, T.; Shin, Y. An efficient hybrid RSS-AoA localization for 3D wireless sensor networks. Sensors 2019, 19, 2121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, R.; Wang, D.; Yin, J.; Wu, Y. Constrained total least squares localization using angle of arrival and time difference of arrival measurements in the presence of synchronization clock bias and sensor position errors. Int. J. Distrib. Sens. Networks 2019, 15, 1550147719858591. [Google Scholar] [CrossRef] [Green Version]
- Deng, B.; Sun, Z.B.; He, Q. Efficient closed-form estimator for moving source localization using TDOA-FDOA-AOA measurements. In Proceedings of the 6th International Conference on Information Engineering, Liaoning, China, 17–18 August 2017; p. 20. [Google Scholar]
- Nguyen, N.H.; Doğançay, K. Multistatic pseudolinear target motion analysis using hybrid measurements. Signal Process. 2017, 130, 22–36. [Google Scholar] [CrossRef]
- Costa, M.S.; Tomic, S.; Beko, M. An SOCP Estimator for Hybrid RSS and AOA Target Localization in Sensor Networks. Sensors 2021, 21, 1731. [Google Scholar] [CrossRef]
- Yang, S.; Wang, G.; Hu, Y.; Chen, H. Robust Differential Received Signal Strength Based Localization With Model Parameter Errors. IEEE Signal Process. Lett. 2018, 25, 1740–1744. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; PTR Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Zekavat, R.; Buehrer, R.M. Handbook of Position Location: Theory, Practice and Advances; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 27. [Google Scholar]
- Mendel, J.M. Lessons in Estimation Theory for Signal Processing, Communications, and Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Ljung, L. System Identification: Theory for The User, 2nd ed.; Prentice-Hall: Saddle River, NJ, USA, 1999. [Google Scholar]
- Doğançay, K. Passive emitter localization using weighted instrumental variables. Signal Process. 2004, 84, 487–497. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech, Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]



| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| (degrees) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| (dBm) | 1 | 1.5 | 2 | 2.5 | 3 | 4 | 5 |
| AOA SNR (dB) | 32.95 | 26.92 | 23.40 | 20.90 | 18.96 | 17.38 | 16.04 |
| DRSS SNR (dB) |
| Noise Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| AOA | |||||||
| DRSS |
| Index | bias/RMSE | MLE | LS | WLS | WIV | SHM-WIV |
|---|---|---|---|---|---|---|
| 1 | Bias | |||||
| RMSE | ||||||
| 2 | Bias | |||||
| RMSE | ||||||
| 3 | Bias | |||||
| RMSE | ||||||
| 4 | Bias | |||||
| RMSE | ||||||
| 5 | Bias | |||||
| RMSE | ||||||
| 6 | Bias | |||||
| RMSE | ||||||
| 7 | Bias | |||||
| RMSE | 5682 |
| MLE | LS | WLS | WIV | SHM-WIV | |
|---|---|---|---|---|---|
| Time (s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Dogancay, K.; Hmam, H. Closed-Form Pseudolinear Estimators for DRSS-AOA Localization. Sensors 2021, 21, 7159. https://doi.org/10.3390/s21217159
Li J, Dogancay K, Hmam H. Closed-Form Pseudolinear Estimators for DRSS-AOA Localization. Sensors. 2021; 21(21):7159. https://doi.org/10.3390/s21217159
Chicago/Turabian StyleLi, Jun, Kutluyil Dogancay, and Hatem Hmam. 2021. "Closed-Form Pseudolinear Estimators for DRSS-AOA Localization" Sensors 21, no. 21: 7159. https://doi.org/10.3390/s21217159
APA StyleLi, J., Dogancay, K., & Hmam, H. (2021). Closed-Form Pseudolinear Estimators for DRSS-AOA Localization. Sensors, 21(21), 7159. https://doi.org/10.3390/s21217159






