Evaluation of a Concrete Slab Track with Debonding at the Interface between Track Concrete Layer and Hydraulically Stabilized Base Course Using Multi-Channel Impact-Echo Testing
Abstract
:1. Introduction
2. Background
3. Method
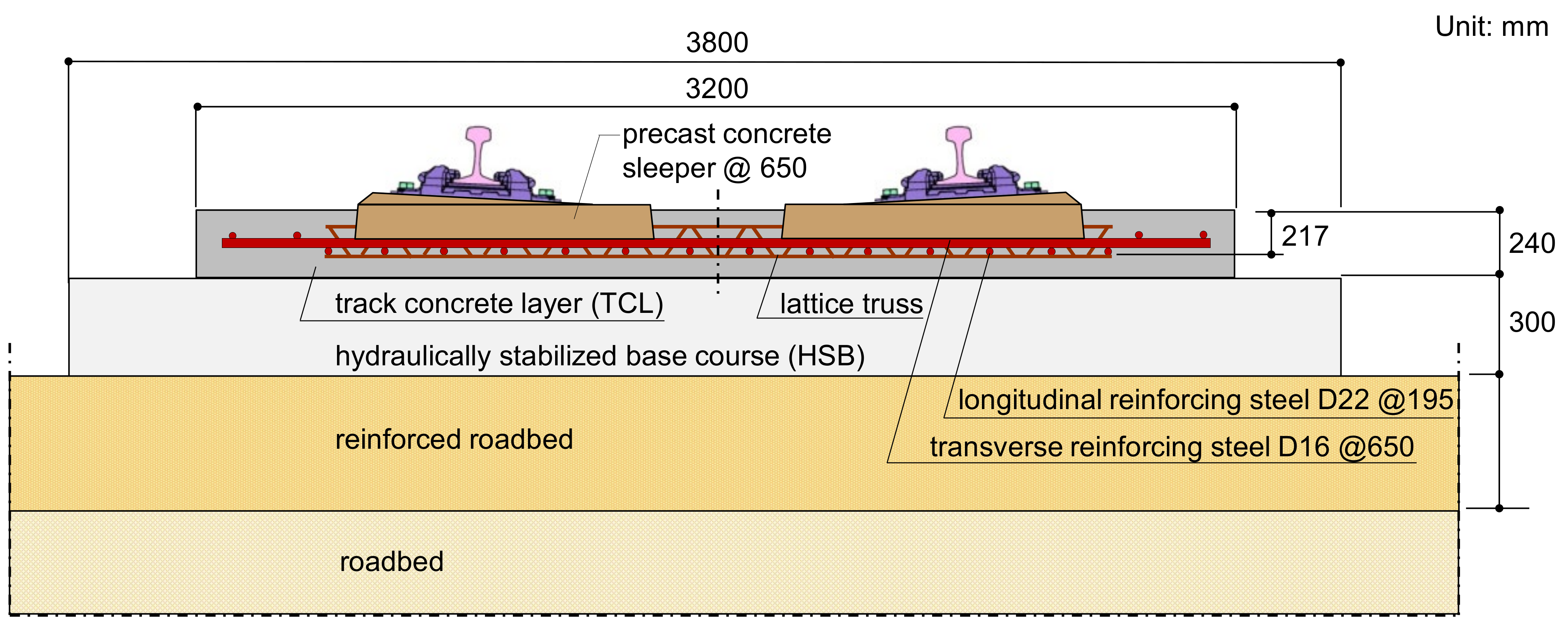
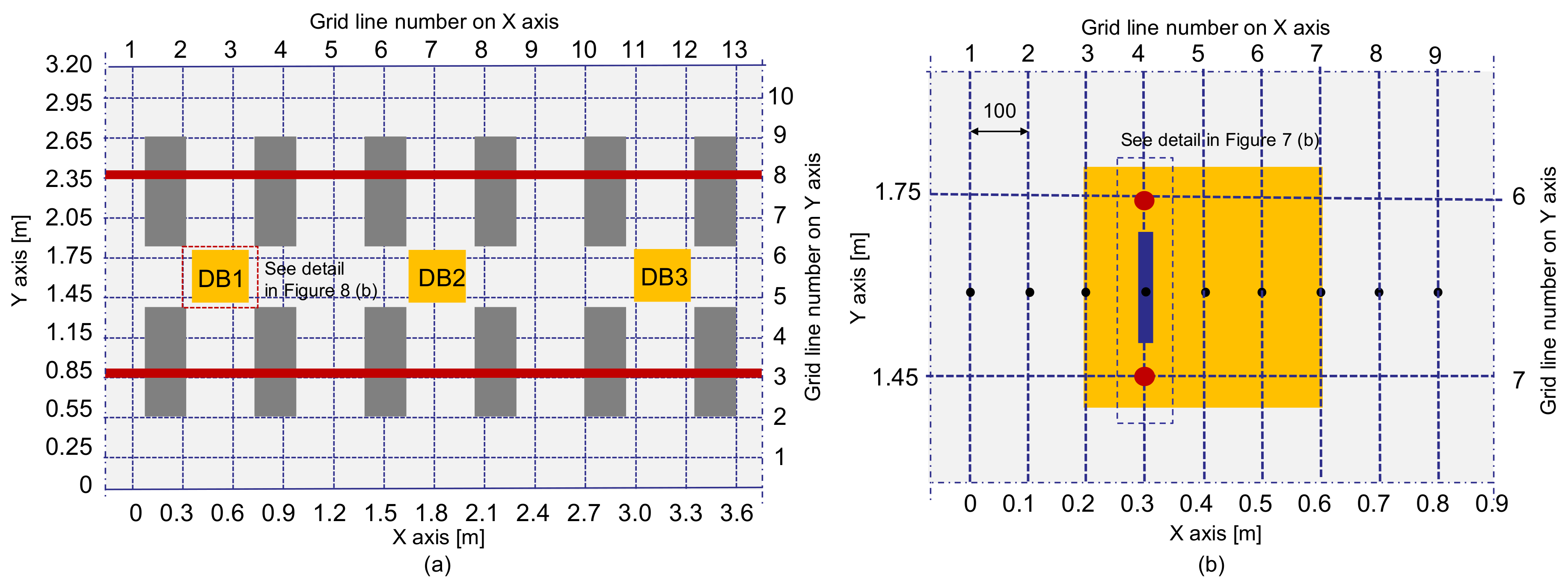
3.1. Test Specimen
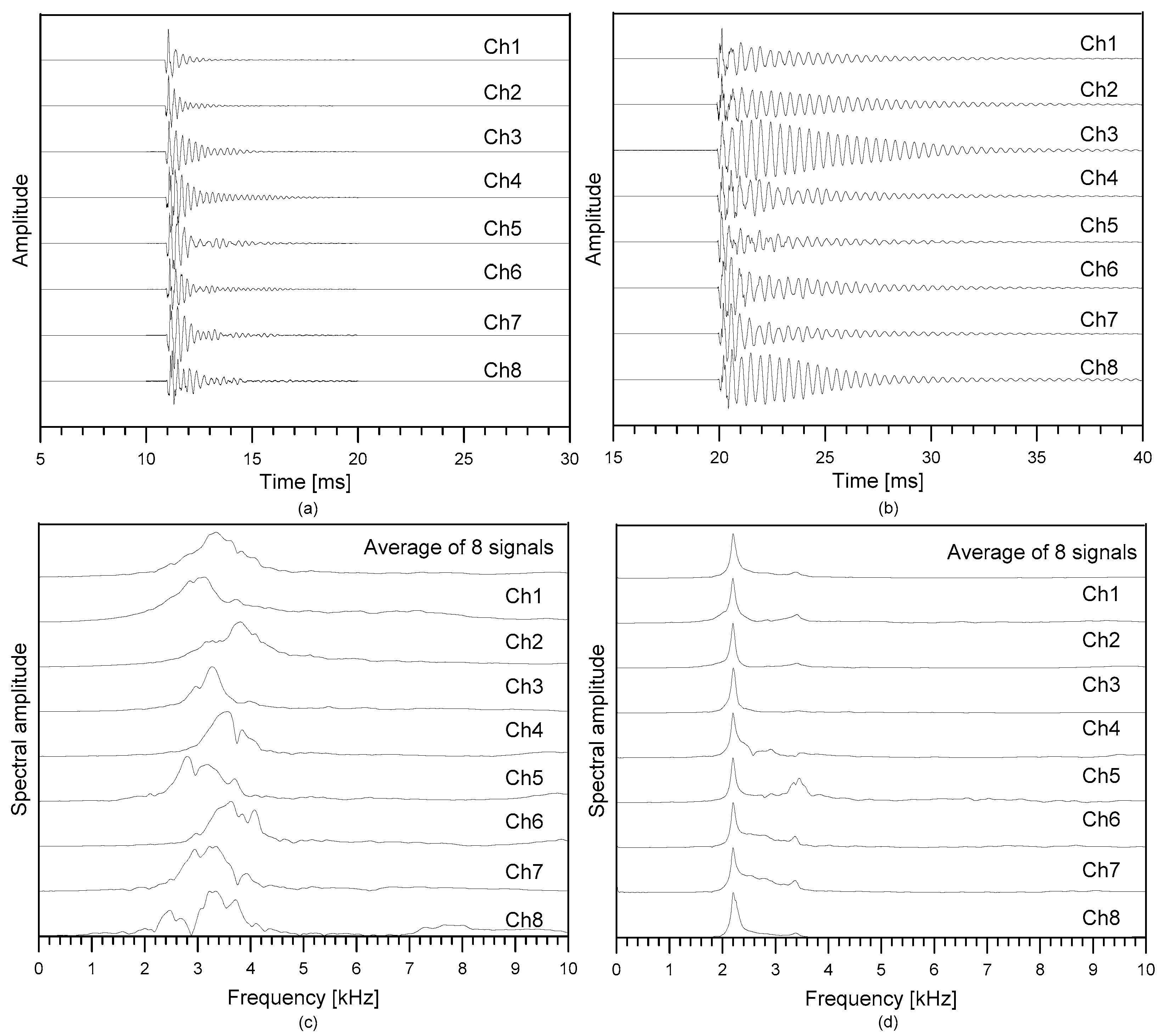
3.2. Multi-Channel IE Data Measurements
3.3. Typical Signals and IE Data Anlaysis
4. Results and Discussion
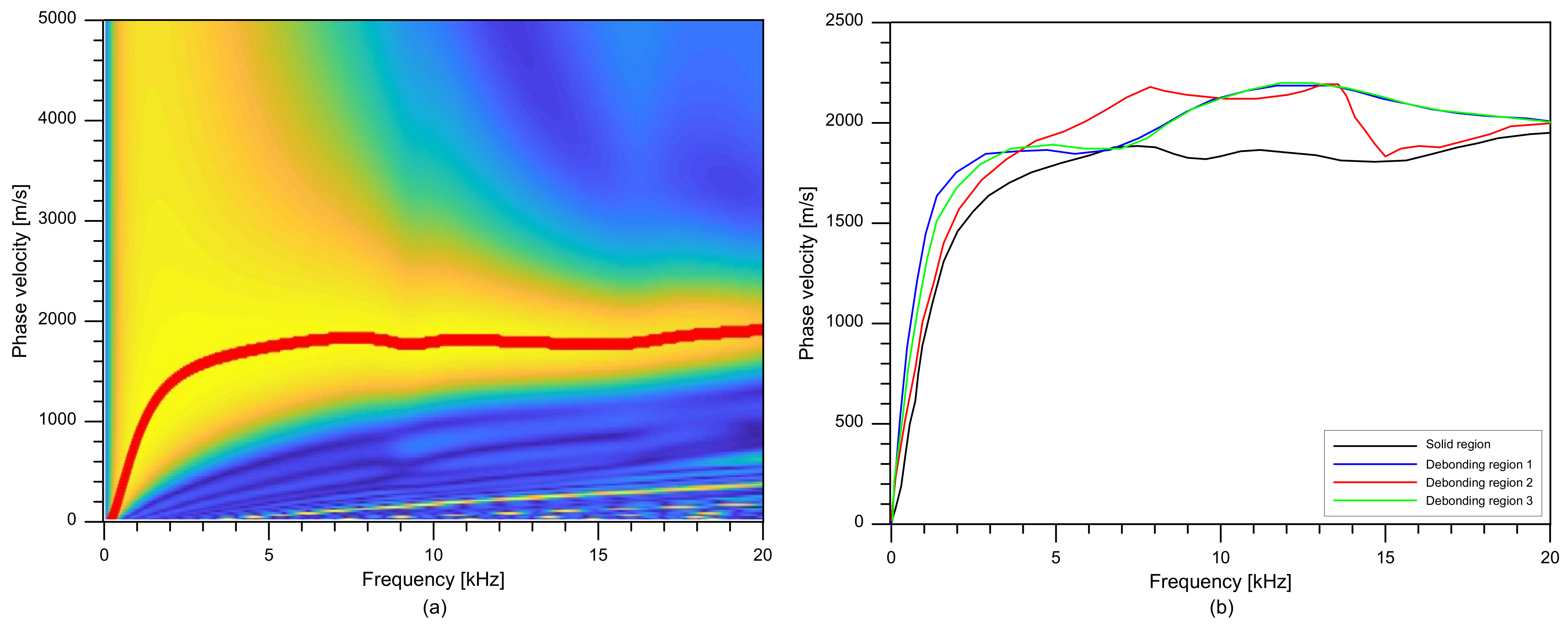
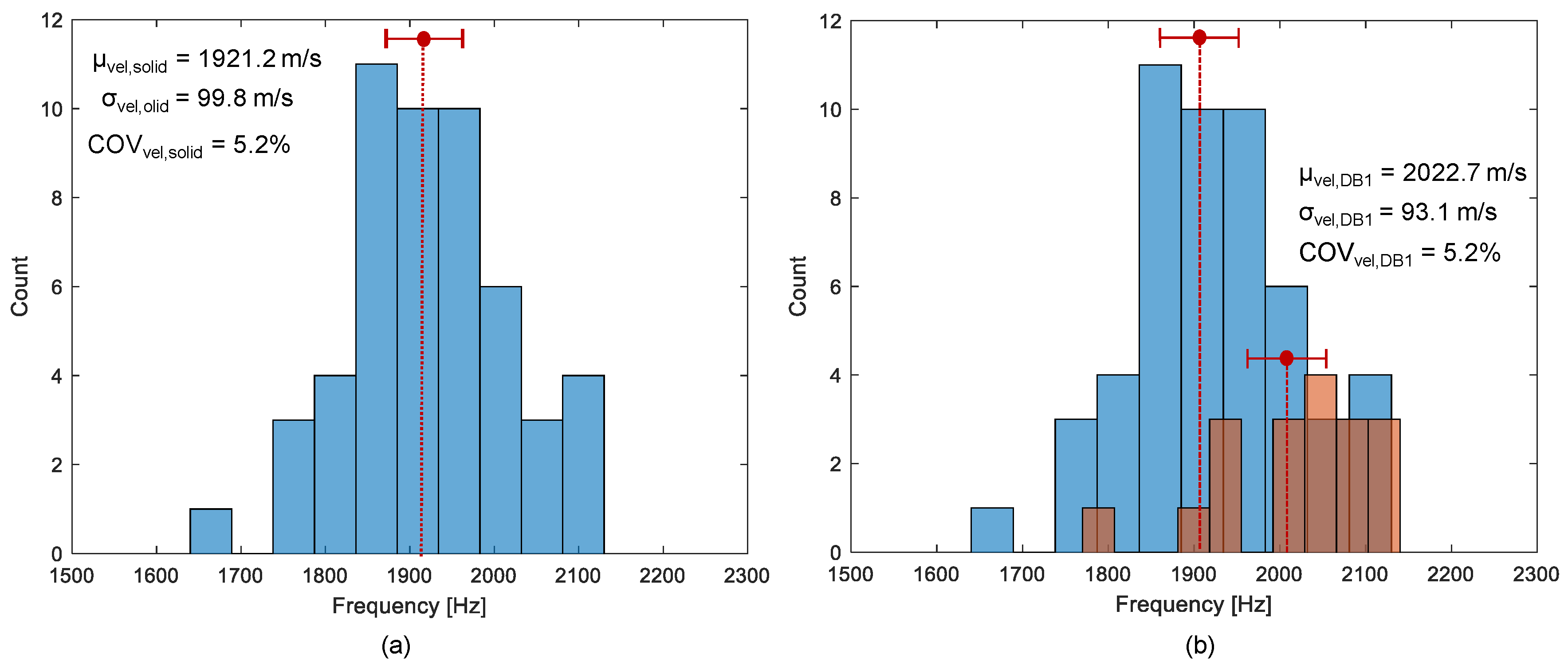
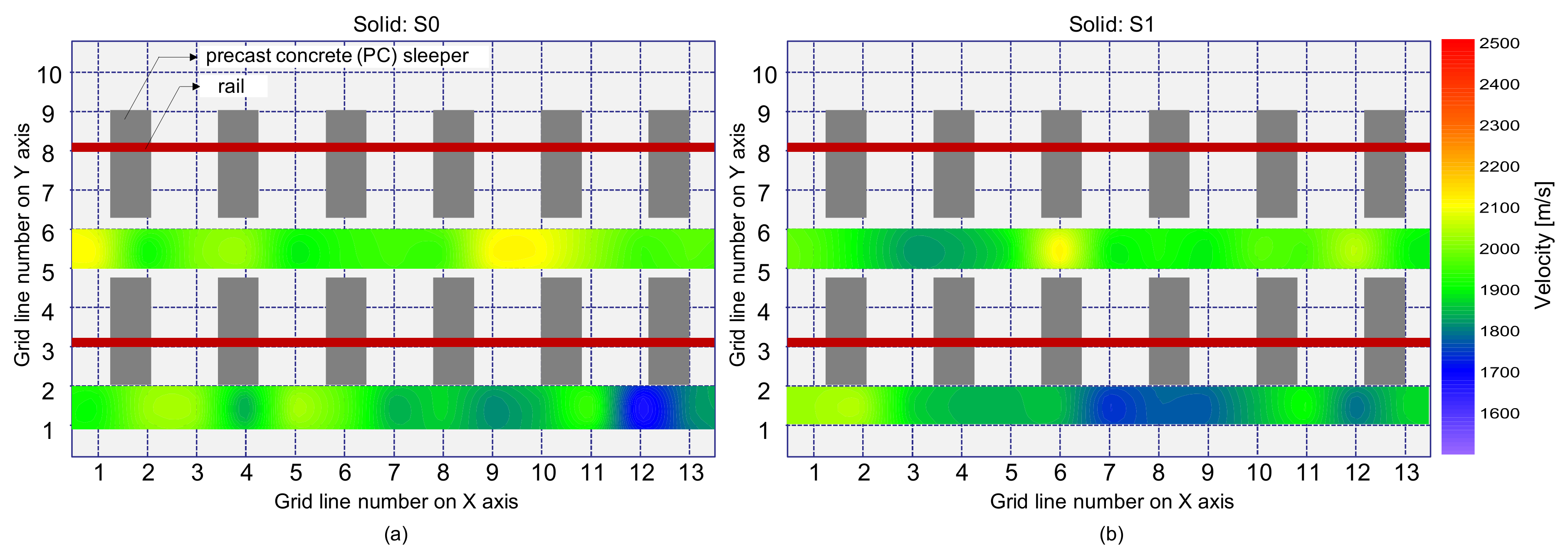
4.1. Velocity of the Propagating Waves in the Track Concrete Layer (TCL)
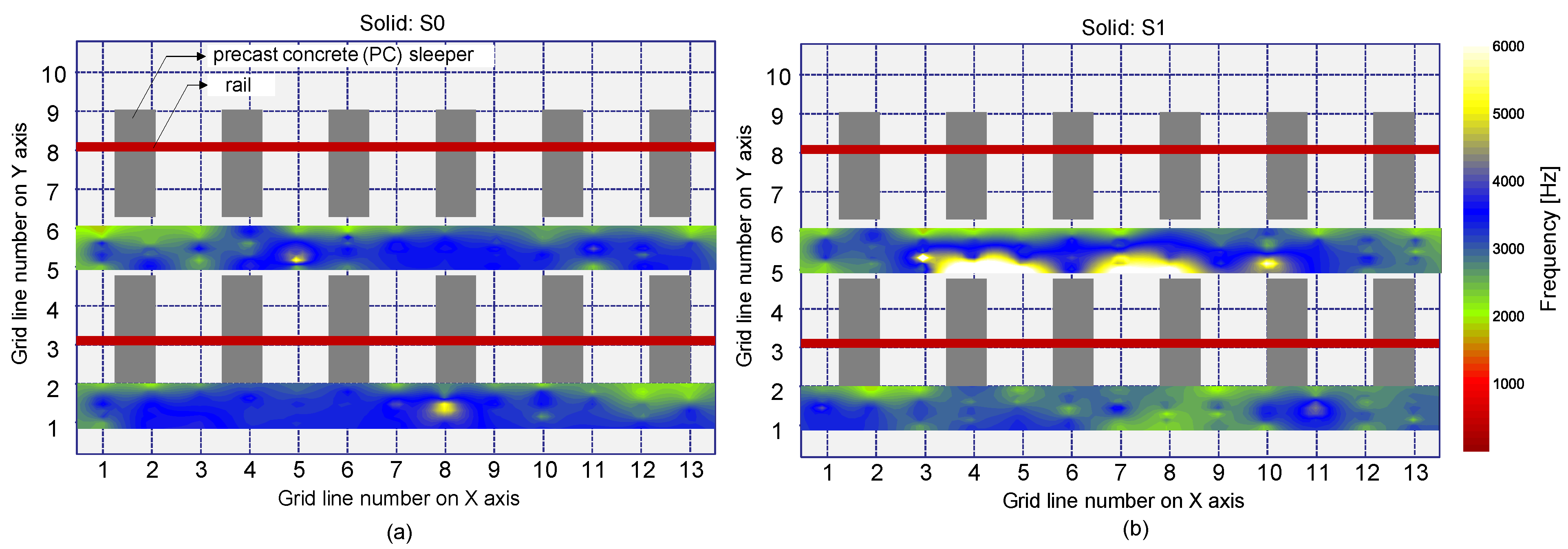
4.2. Peak Frequency Map
4.2.1. Peak Frequency Based on the Single Sensor Data Analysis
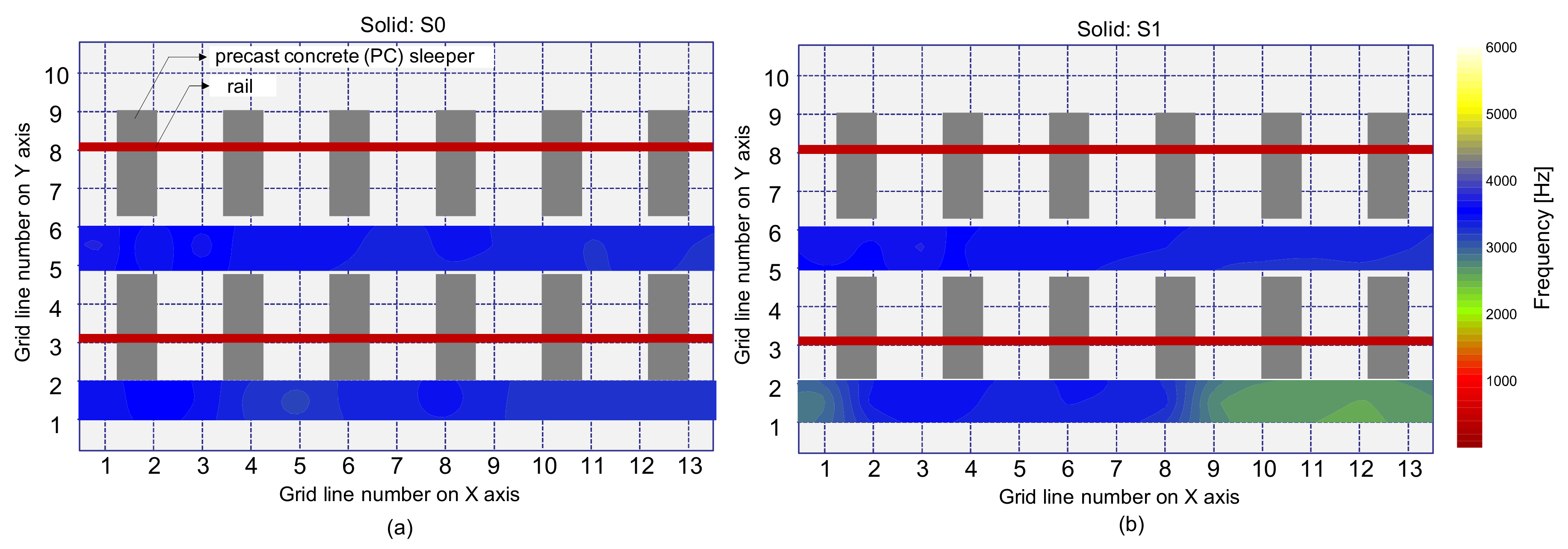
4.2.2. Peak Frequency Based on the Multi-Sensor Data Analysis
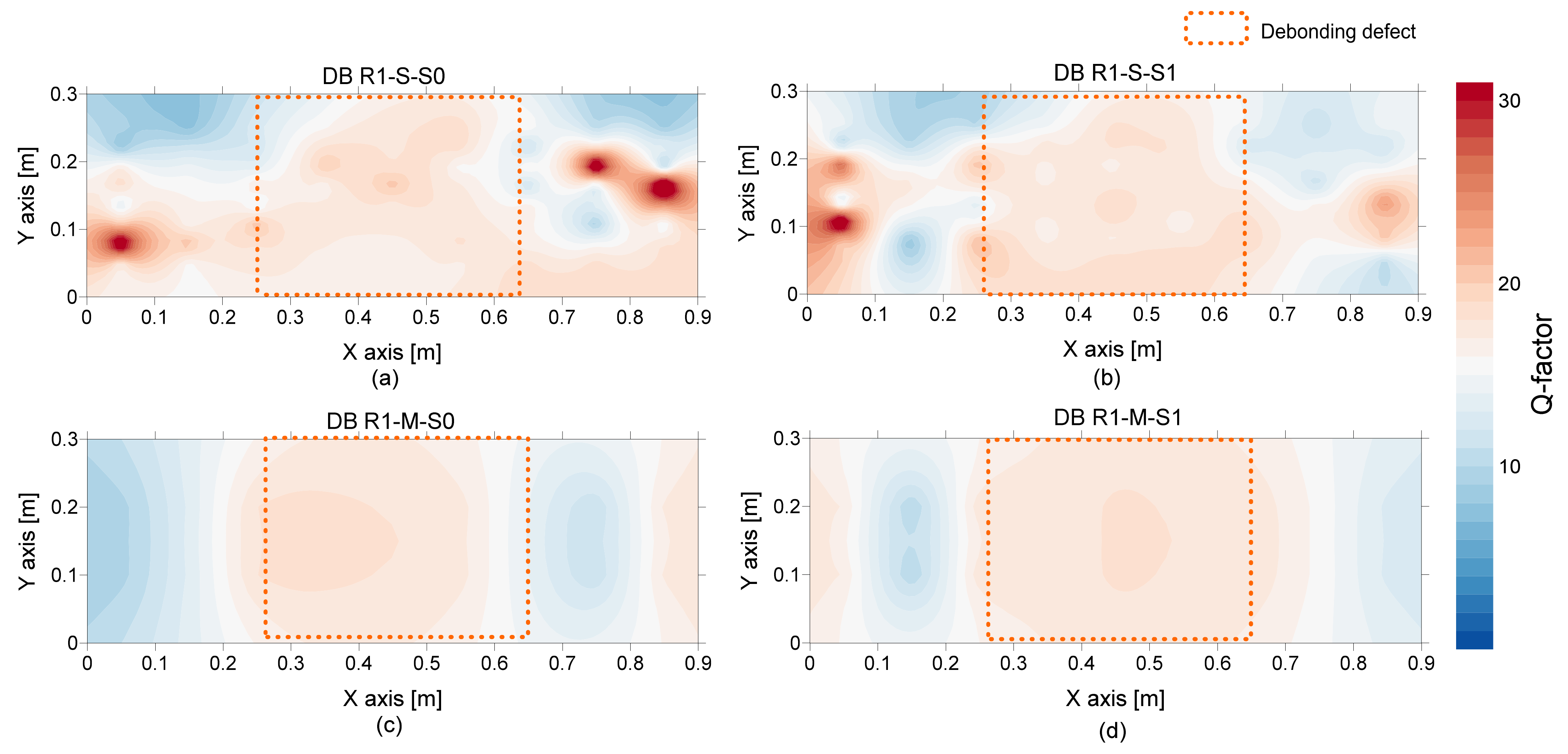
4.3. Q Factor
4.4. Evaluation of Parameters
5. Conclusions
- (1)
- It was observed that statistical results associated with the distribution of velocity could differentiate the solid regions and test regions with debonding defects. Therefore, the velocity measurement can be useful to evaluate the overall condition of the test slabs. However, special care is needed to identify the location of the debonding defect at the interface between TCL and HSB based on the single velocity value.
- (2)
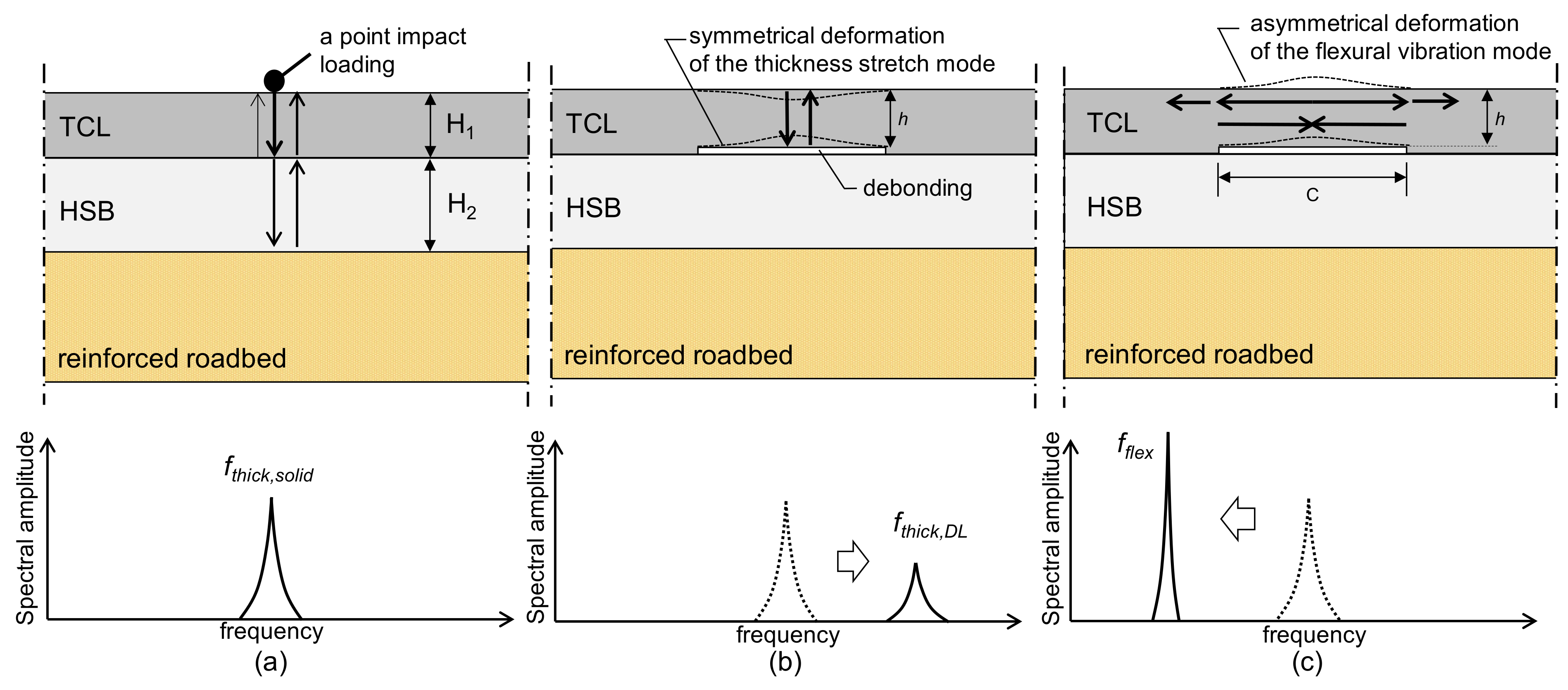
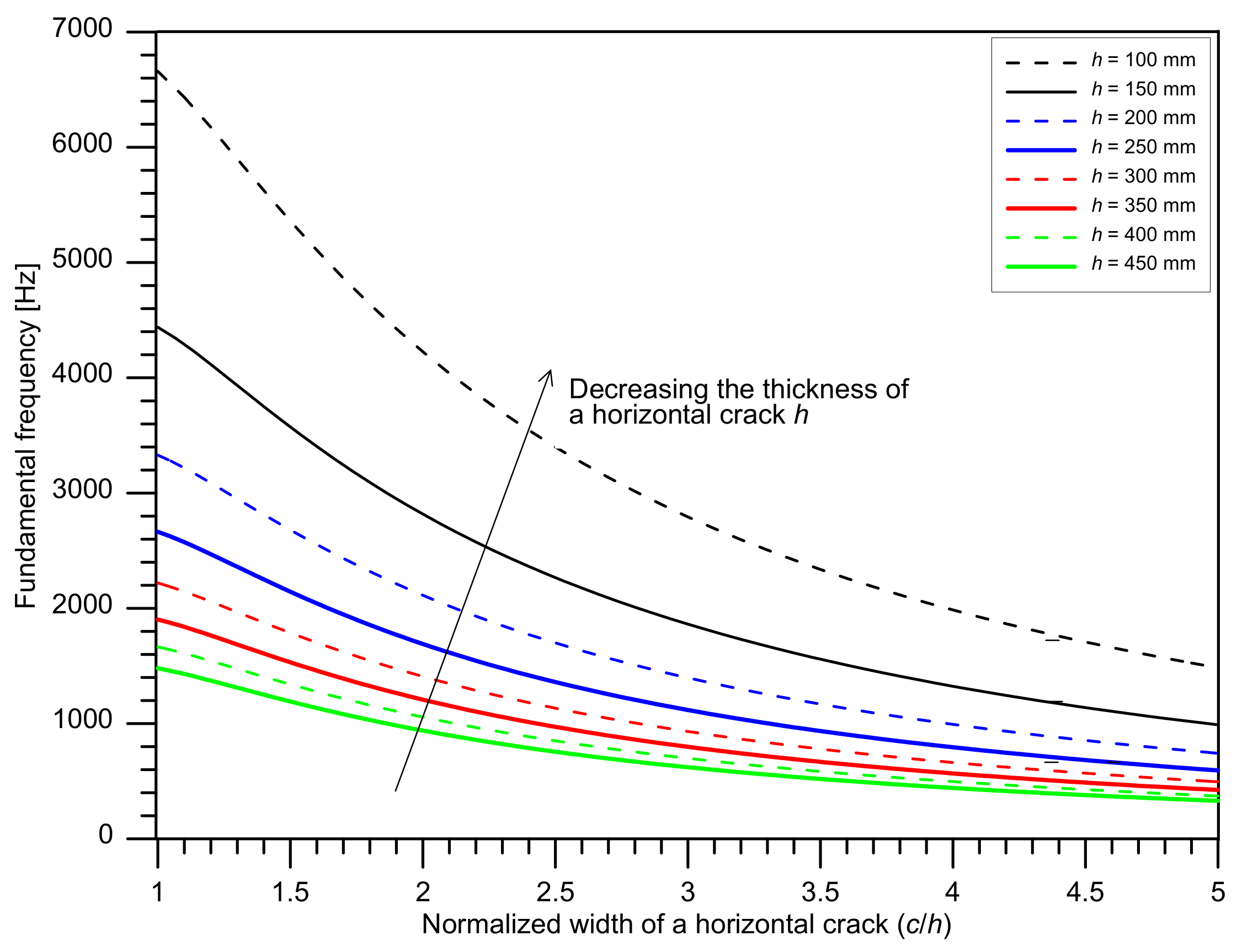
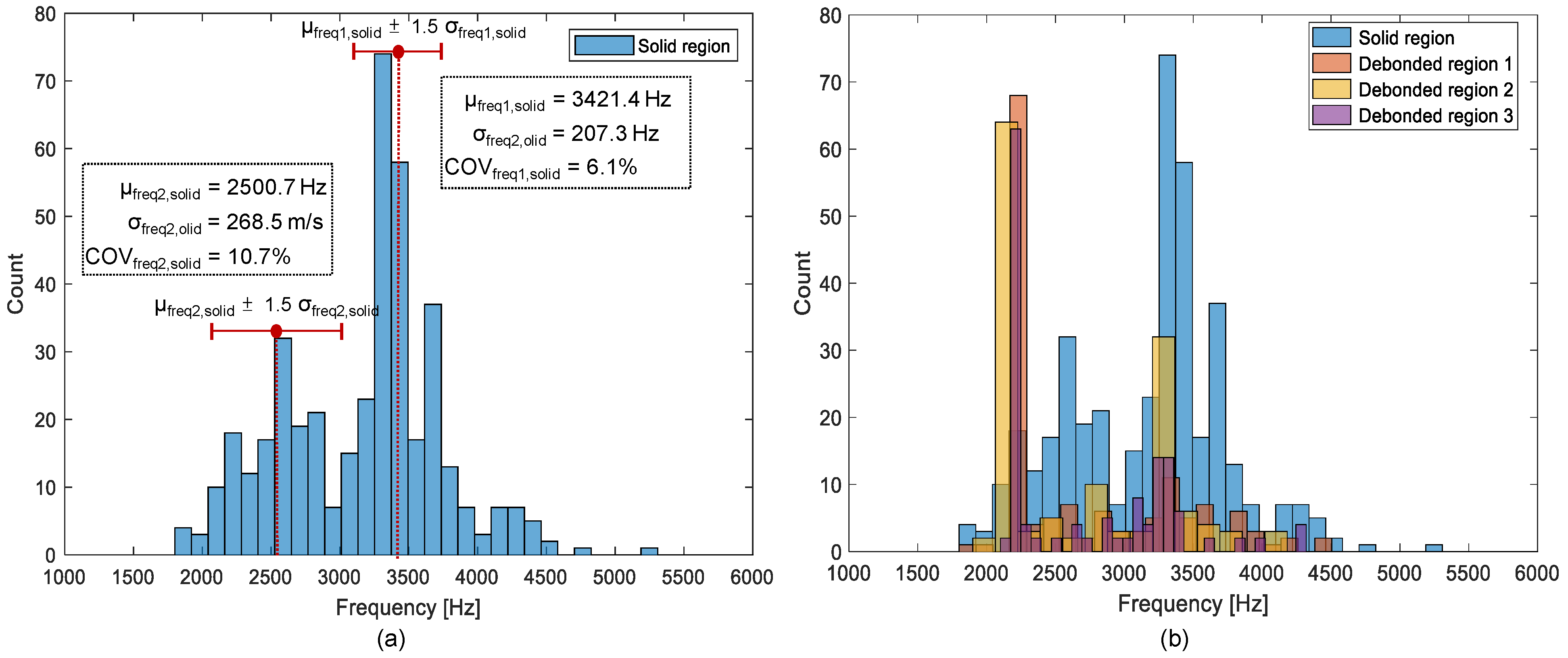
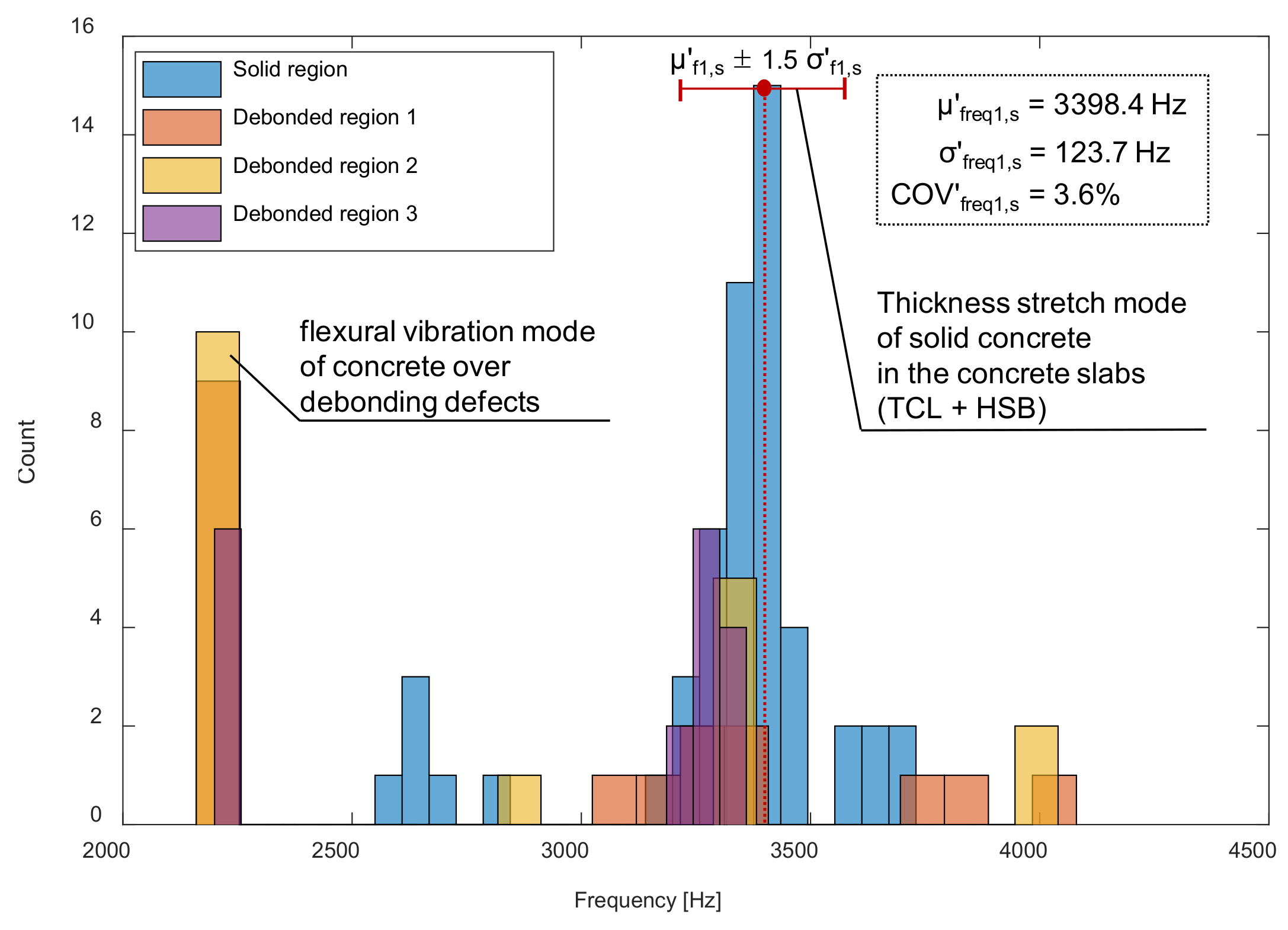
- Overall, the peak frequency map based on the single-channel IE testing is effective for differentiating solid concrete and de-bonded regions in the concrete slab track specimen. However, the presence of multiple peaks in the solid concrete region could increase difficulties in the interpretation of the IE data in actual concrete slab tracks. The primary peak (around 3300 Hz) is corresponding to the full thickness mode, which is usually interpreted as the characteristic frequency of the solid region in IE testing. The secondary peak frequency group (around 2000 Hz to 3000 Hz) is not expected by the IE theory. Dynamic response of concrete over debonding defects is characterized by flexural vibration mode with a peak frequency range of 2100 Hz to 2200 Hz. It was observed that the distribution of flexural vibration mode frequency is overlapped with the lower portion of secondary peak frequency in solid concrete, which could increase the level of error in the prediction model based on peak frequency values based on the single-channel IE testing.
- (3)
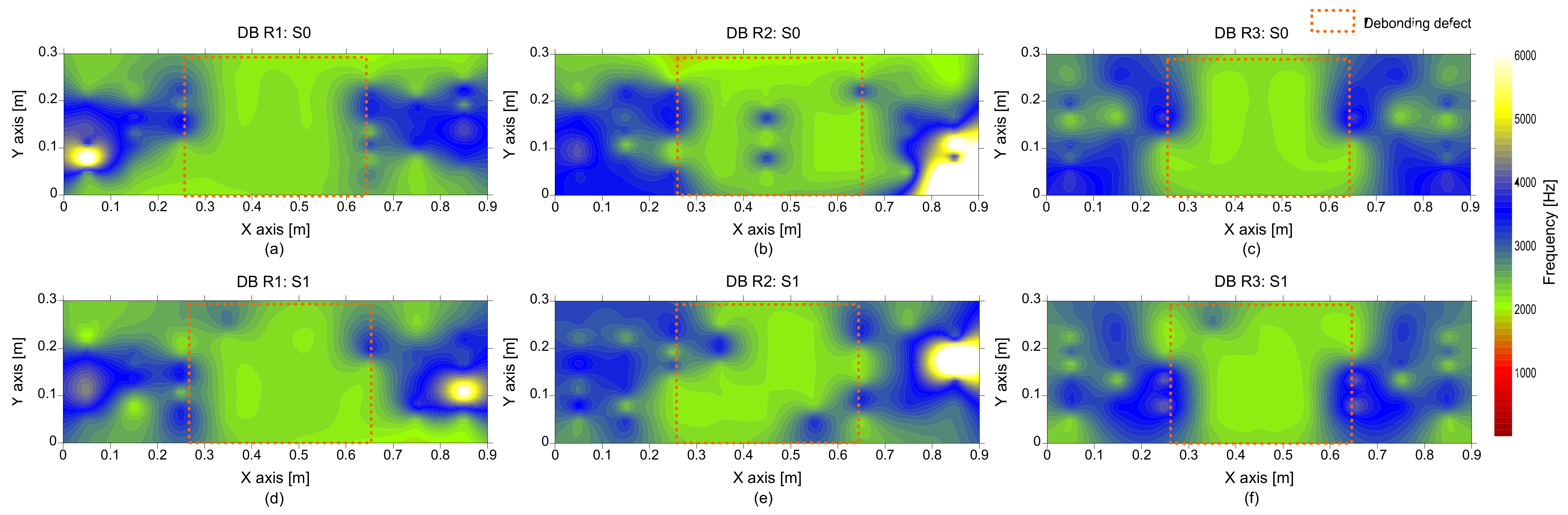
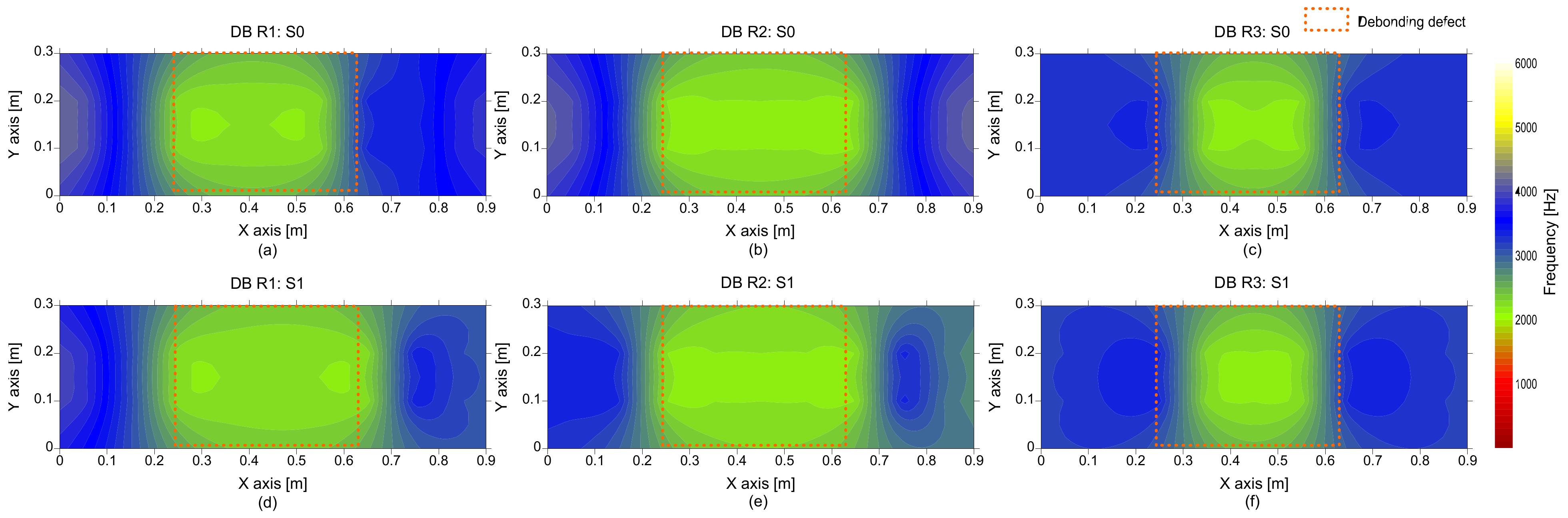
- It was demonstrated that the use of average peak frequency measured by multiple IE testing devices is effective to suppress the unknown peak frequency in the solid concrete. As a result of averaging, the peak frequency map was generally represented by blue color, representing one and half standard deviations of the average peak frequency. Three debonding defects are clearly identified as green color in the spatial distribution of the average peak frequency values in the three test regions, including debonding defects.
- (4)
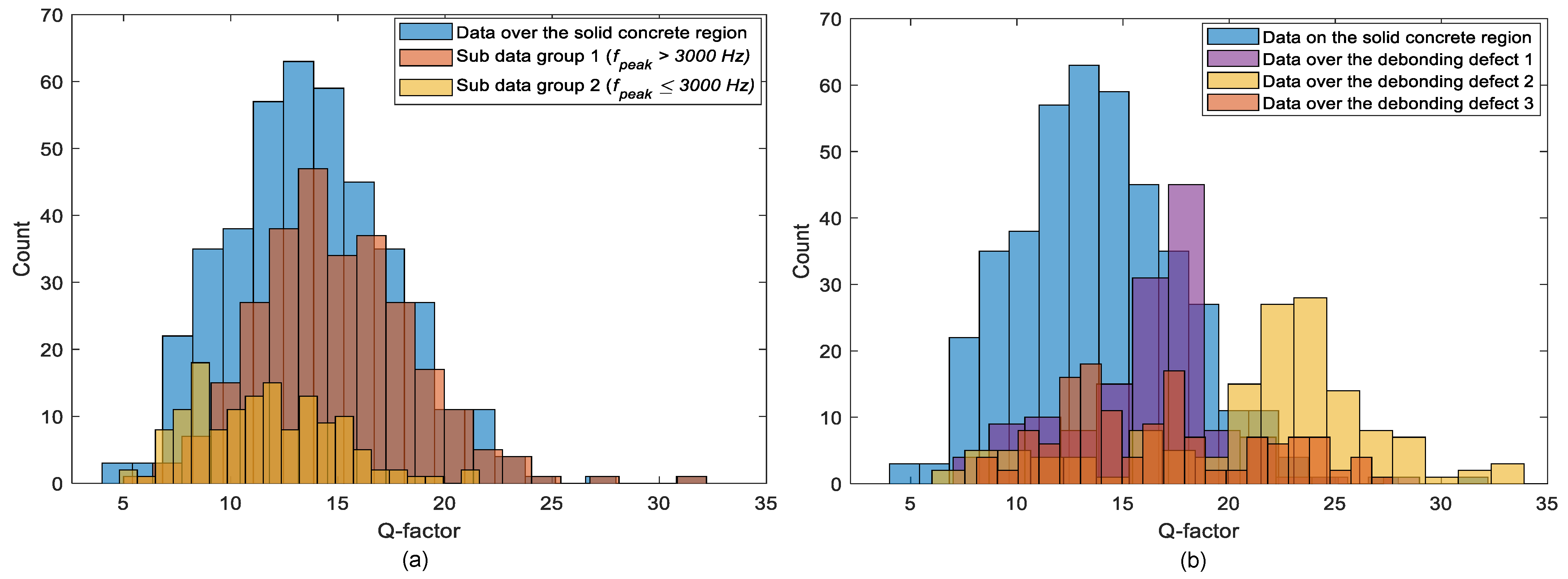
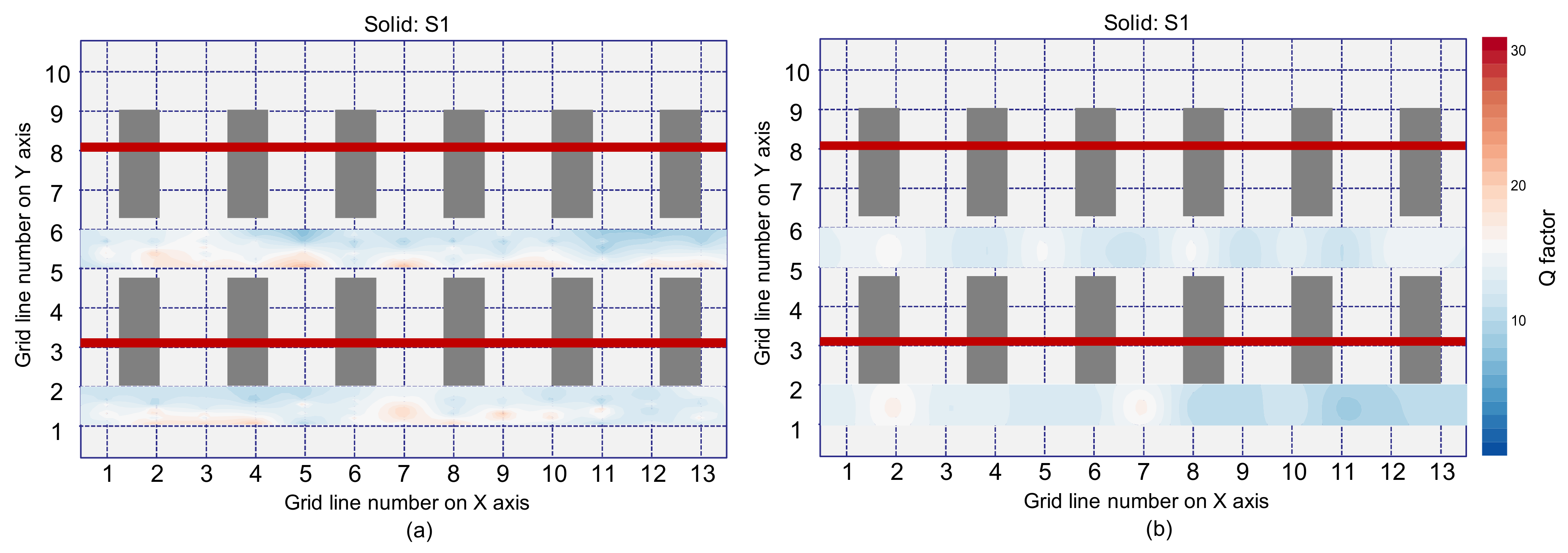
- Q factor is a potential parameter that can separate the flexural oscillation mode and the secondary peak frequency in the solid concrete when difficult to accurately classify based on differences in peak frequency values. It is noticed that the dynamic response of concrete associated with the secondary peak frequency in the solid concrete region tends to result in lower Q factor values than those associated with the first peak frequency (full-thickness mode). Furthermore, dynamic responses over debonding defects result in even greater Q factor values compared to those in full-thickness mode at solid concrete regions.
- (5)
- Overall, the prediction models based on the averaged values from multi-channel data exhibit higher AUC values than those based on single-channel data. Specifically, the equally highest AUC values (0.97) are resulted from the prediction model based on the average peak frequency () and the combined average peak frequency and averaged Q factor ( and ). The effectiveness of using the Q factor as a supplementary parameter is more clearly observed in the prediction model based on single-channel IE data. The use of dual parameters ( and ) improves the AUC value by about 5% (or 18%) compared to the model based on a single parameter of (or ).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gautier, P.-E. Slab track: Review of existing systems and optimization potentials including very high speed. Constr. Build. Mater. 2015, 92, 9–15. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, M.; Zhai, W.; Cai, C.; Zhao, C.; Zeng, D.; Zhang, J. Mechanical property and damage evolution of concrete interface of ballastless track in high-speed railway: Experiment and simulation. Constr. Build. Mater. 2018, 187, 460–473. [Google Scholar] [CrossRef]
- Vu, L.; Jang, D.D.; Kang, Y.-S. Assessment of structural dynamic response and vehicle-track interaction of precast slab track systems. Appl. Sci. 2021, 11, 3558. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, L.; Zhang, Y. Effect of daily changing temperature on the curling behavior and interface stress of slab track in construction stage. Constr. Build. Mater. 2018, 185, 638–647. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads. Int. J. Non-Linear Mech. 2014, 58, 222–232. [Google Scholar] [CrossRef]
- Ren, J.; Yang, R.; Wang, P.; Yong, P.; Wen, C. Slab Upwarping of twin-block slab track on subgrade-bridge transition section. J. Transp. Res. Board 2014, 2448, 115–124. [Google Scholar] [CrossRef]
- Korea Rail Network Authority. Concrete Railway Structures; (KR C-14040); Korea Rail Network Authority: Daejeon, Korea, 2016. [Google Scholar]
- Korea National Reailway. KR Technology: Track System of High-Speed Railway. Available online: https://english.kr.or.kr/sub/info.do?m=0303 (accessed on 15 May 2021).
- Kang, K.-D.; Kang, G.H.; Lee, B.S.; Yoo, H.S.; Jung, Y.W. Korea’s High-Speed Rail Construction and Technology Advances; The Korea Transport Institute (KOTI): Goyang-si, Korea, 2014. [Google Scholar]
- Chun, H.-K. Study of the Behavior of Concrete Slab Track of High Speed Train on Earthwork According to the Variation of Train Speed and Axle Load. In Graduate School of Railway; Seoul National University of Science and Technology: Seoul, Korea, 2016. [Google Scholar]
- Freudenstein, S. RHEDA 2000®: Ballastless track systems for high-speed rail applications. Int. J. Pavement Eng. 2010, 11, 293–300. [Google Scholar] [CrossRef]
- Bachmann, H.; Mohr, W.; Kowalski, M. The RHEDA 2000 ballastless track system. Eur. Railway Rev. 2003, 8, 45–51. [Google Scholar]
- Xu, Y.; Yan, D.; Zhu, W.; Zhou, Y. Study on the mechanical performance and interface damage of CRTS II slab track with debonding repairment. Constr. Build. Mater. 2020, 257, 119600. [Google Scholar] [CrossRef]
- Su, C.; Liu, D.; Ding, C.; Gong, C.; Zhao, P.; Liu, X. Experimental study on bond. Performances of track slab and mortar based on DIC technology. KSCE J. Civil Eng. 2018, 22, 3546–3555. [Google Scholar] [CrossRef]
- Jang, S.Y.; Choi, S.S. Crack and Damage Patterns of Concrete Track of Kyeong-Bu High-Speed Railways (KSR2014S278). In Proceedings of the 2014 Autumn Conference and Annual Meeting of the Korean Society of Railway, Jeju, Korea, 22–24 May 2014. [Google Scholar]
- ASTM. Standard Practice for Measuring Delaminations in Concrete Bridge; D4580M-12; Decks by Sounding; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Oh, T.; Popovics, J.S.; Sim, S.-H. Analysis of vibration for regions above rectangular delamination defects in solids. J. Sound Vib. 2013, 332, 1766–1776. [Google Scholar] [CrossRef]
- Oh, T.K. Defect Characterization in Concrete Elements Using Vibration Analysis and Imaging. In Civil, Environmental, and Architectural Engineering; University of Illinois at Urbana: Champaign, IL, USA, 2012; p. 129. [Google Scholar]
- Kee, S.-H.; Lee, J.-W.; Candelaria, M.D. Evaluation of delamination in concrete by IE testing using multi-channel elastic wave data. Sensors 2020, 20, 201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kee, S.-H.; Gucunski, N. Interpretation of flexural vibration modes from impact-echo testing. J. Infrastruct. Syst. 2016, 22, 3. [Google Scholar] [CrossRef]
- Oh, T.K.; Kee, S.H.; Arndt, R.W.; Popovics, J.S.; Zhu, J. Comparison of NDT methods for assessment of a concrete bridge deck. J. Eng. Mech. ASC 2013, 139, 305–314. [Google Scholar] [CrossRef]
- Gucunski, N.; National Research Council. Nondestructive Testig to Identify Concrete Bridge Deck Deterioration; SHRP 2 Report S2-R06A-RR-1; Transportation Research Board: Washington, DC, USA, 2013. [Google Scholar]
- Kee, S.-H.; Oh, T.; Popovics, J.S.; Arndt, R.W.; Zhu, J. Nondestructive bridge deck testing with air-coupled impact-echo and infrared thermography. J. Bridge Eng. ASCE 2012, 17, 928–939. [Google Scholar] [CrossRef]
- Sansalone, M.; Carino, N.J. Detecting delaminations in concrete slabs with and without overlays using the impact-echo method. ACI Mater. J. 1989, 86, 175–184. [Google Scholar]
- Sansalone, M. Impact echo: The complete story. ACI Struct. J. 1997, 94, 777–786. [Google Scholar]
- Sansalone, M.J.; Strett, W.B. Impact-Echo: Nondestructive Evaluation of Concrete and Masonry; Bullblier Press: Ithaca, NY, USA, 1997. [Google Scholar]
- Schubert, F.; Köhler, B. Ten lectures on impact-echo. J. Nondestruct. Eval. 2008, 28, 5–21. [Google Scholar] [CrossRef]
- Gibson, A.; Popovics, J.S. Lamb wave basis for impact-echo method analysis. J. Eng. Mech. ASCE 2005, 131, 438–443. [Google Scholar] [CrossRef]
- Hayashi, T.; Kawashima, K. Multiple reflections of Lamb waves at a delamination. Ultrasonics 2002, 40, 193–197. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Imaging Dispersion Curves of Surface Waves on Multichannel Record. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 1998. [Google Scholar]
- Gucunski, N.; Kee, S.; La, H.; Basily, B.; Maher, A. Delamination and concrete quality assessment of concrete bridge decks using a fully autonomous RABIT paltform. Struct. Monit. Maint. 2015, 2, 19–34. [Google Scholar]






| Prediction | Peak Frequency | Velocity or Q Factor |
|---|---|---|
| 1 (de-bonded region) | fpeak < τfreq | VR (or Q) ≥ τVel (or τQ) |
| 0 (solid region) | fpeak ≥ τfreq | VR (or Q) < τVel (or τQ) |
| Prediction | Combination of Peak Frequency and Q Factor Values |
|---|---|
| 1 (de-bonded region) | fpeak < τfreq and Q > τQ |
| 0 (solid region) | fpeak ≥ τfreq |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-W.; Lee, S.-J.; Kee, S.-H. Evaluation of a Concrete Slab Track with Debonding at the Interface between Track Concrete Layer and Hydraulically Stabilized Base Course Using Multi-Channel Impact-Echo Testing. Sensors 2021, 21, 7091. https://doi.org/10.3390/s21217091
Lee J-W, Lee S-J, Kee S-H. Evaluation of a Concrete Slab Track with Debonding at the Interface between Track Concrete Layer and Hydraulically Stabilized Base Course Using Multi-Channel Impact-Echo Testing. Sensors. 2021; 21(21):7091. https://doi.org/10.3390/s21217091
Chicago/Turabian StyleLee, Jin-Wook, Sung-Jin Lee, and Seong-Hoon Kee. 2021. "Evaluation of a Concrete Slab Track with Debonding at the Interface between Track Concrete Layer and Hydraulically Stabilized Base Course Using Multi-Channel Impact-Echo Testing" Sensors 21, no. 21: 7091. https://doi.org/10.3390/s21217091
APA StyleLee, J.-W., Lee, S.-J., & Kee, S.-H. (2021). Evaluation of a Concrete Slab Track with Debonding at the Interface between Track Concrete Layer and Hydraulically Stabilized Base Course Using Multi-Channel Impact-Echo Testing. Sensors, 21(21), 7091. https://doi.org/10.3390/s21217091






