Discrete Convolution-Based Energy Spectrum Configuring Method for the Analysis of the Intrinsic Radiation of 176Lu
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Environment
2.2. Monte Carlo Simulation
2.3. Spectra Processing
2.3.1. Definition of Source Pathway and Energy Transfer Cases
2.3.2. Data Processing with Discrete Convolution
3. Results and Discussion
3.1. Isomer Transition Spectra
3.1.1. Calculation of the Total Photo-Peak Ratio
3.1.2. Post-Processing Isomer Transition Spectra
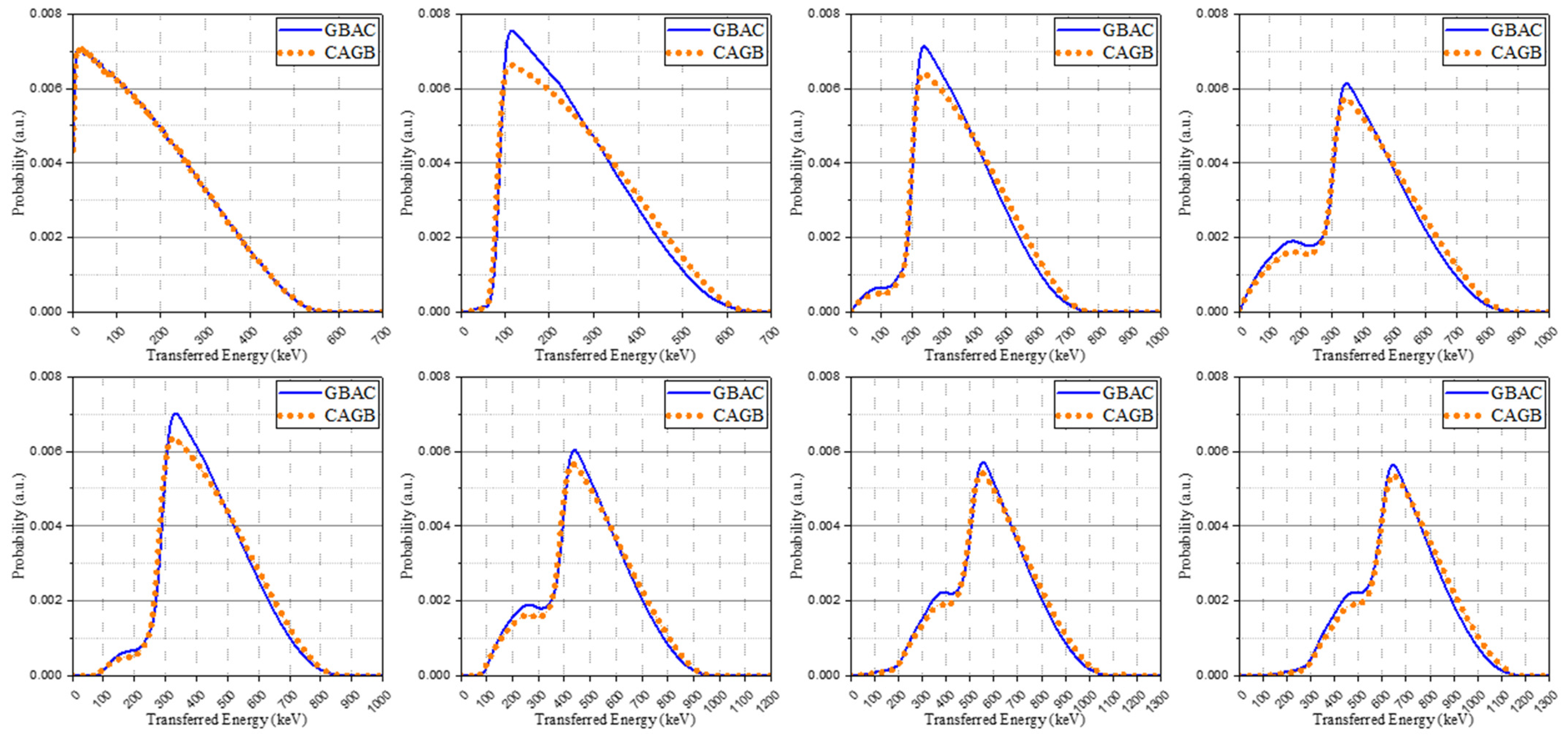
3.2. Base Spectra
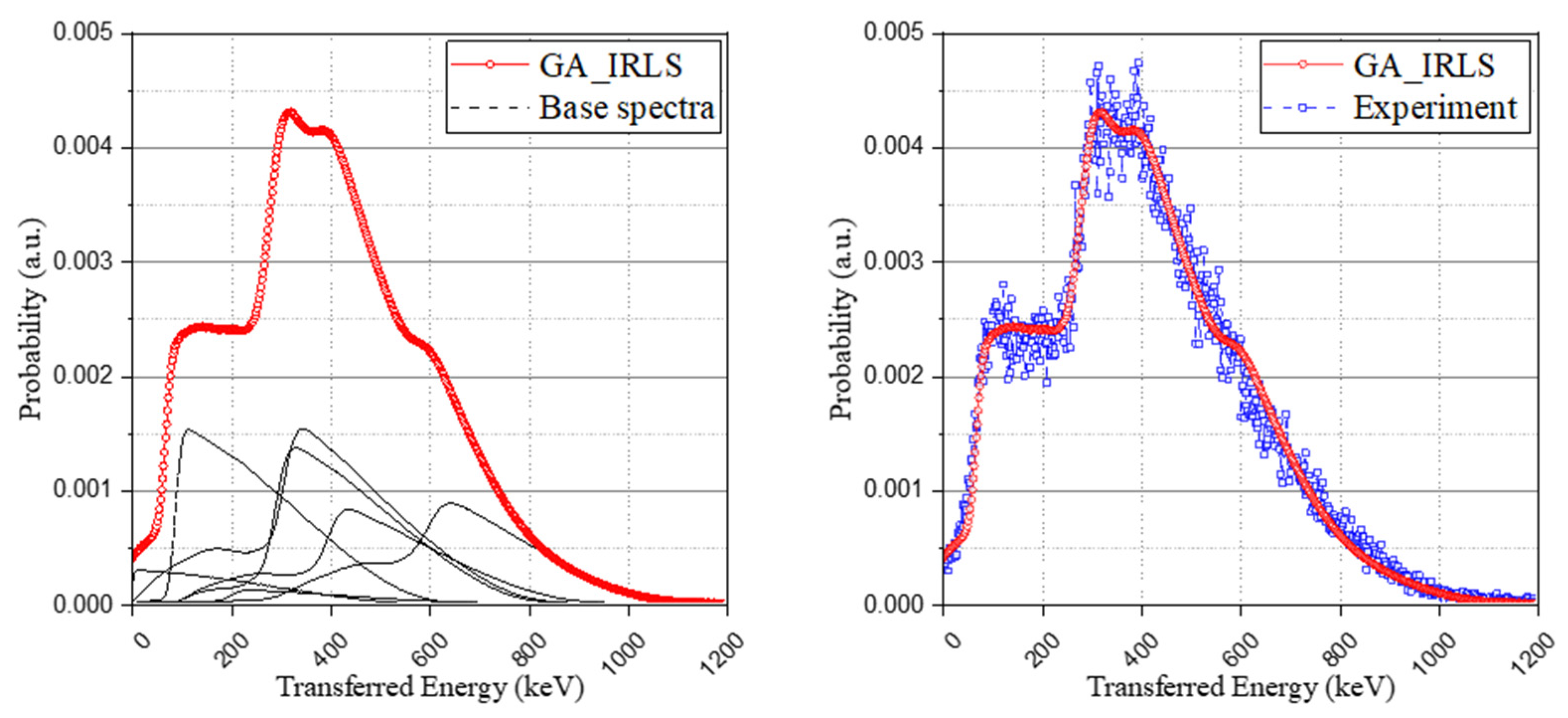
3.3. Validation of the Study
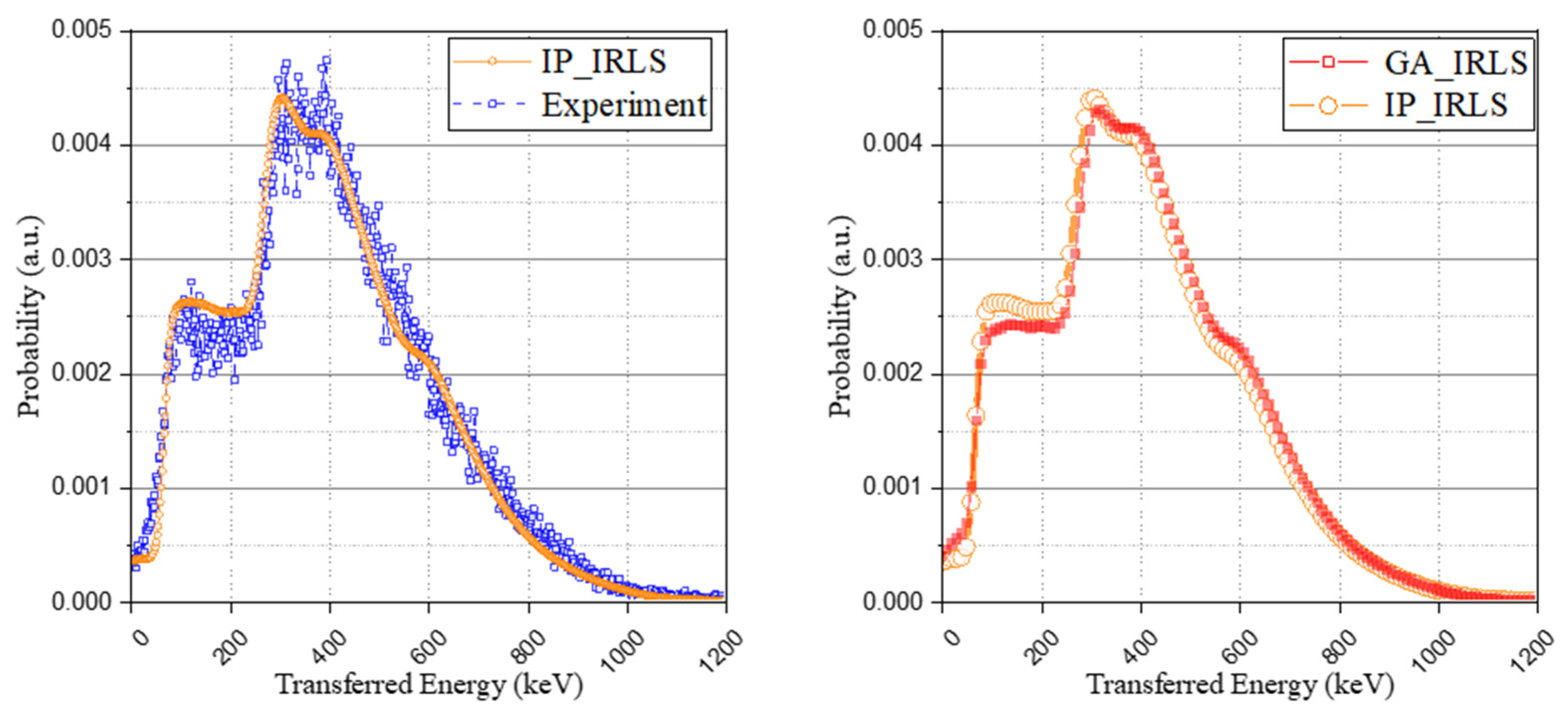
3.3.1. Genetic Algorithm-Based Spectrum Configuring
3.3.2. Interaction Probability-Based Spectrum Configuring
3.3.3. Comparison of the Proposed Method without the Compton Model and GATE Simulation Package
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Melcher, C.L.; Schweitzer, J.S. A promising new scintillator: Cerium-doped lutetium oxyorthosilicate. Nucl. Instr. Meth. A 1992, 314, 212–214. [Google Scholar] [CrossRef]
- Lee, M.S.; Cates, J.W.; Kapusta, M.; Schmand, M.; Levin, C.S. Study of Lutetium-based scintillators for PET system design with 100-ps coincidence time resolution. In Proceedings of the 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference, Manchester, UK, 26 October–2 November 2019. [Google Scholar]
- Goertzen, A.L.; Suk, J.Y.; Thompson, C.J. Imaging of Weak-Source Distributions in LSO-Based Small-Animal PET Scanners. J. Nucl. Med. 2007, 48, 1693–1698. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, E.; Tashima, H.; Nishikido, F.; Murayama, H.; Yamaya, T. Reduction method for intrinsic random coincidence events from 176Lu in low activity PET imaging. Radiol Phys. Technol. 2014, 7, 235–245. [Google Scholar] [CrossRef]
- Huber, J.S.; Moses, W.W.; Jones, W.F.; Watson, C.C. Effect of 176Lu background on singles transmission for LSO-based PET cameras. Phys. Med. Biol. 2002, 47, 3535–3541. [Google Scholar] [CrossRef]
- Basunia, M.S. Nulcear data sheets for A = 176. Nucl. Data Sheets 2006, 107, 791–1026. [Google Scholar] [CrossRef]
- Enríquez-Mier-y-Terán, F.E.; Ortega-Galindo, A.S.; Murrieta-Rodríguez, T.; Rodríguez-Villafuerte, M.; Martínez-Dávalos, A.; Alva-Sánchez, H. Coincidence energy spectra due to the intrinsic radioactivity of LYSO scintillation crystals. EJNMMI Phys. 2020, 7, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conti, M.; Eriksson, L.; Rothfuss, H.; Sjoeholm, T.; Townsend, D.; Rosenqvist, G.; Carlier, T. Characterization of 176Lu background in LSO-based PET scanners. Phys. Med. Biol. 2017, 62, 3700–3711. [Google Scholar] [CrossRef]
- Wei, Q. Intrinsic radiation in lutetium based PET detector: Advantages and disadvantages. arXiv 2015, arXiv:1501.05372. [Google Scholar]
- Grodzicka, M.; Moszynski, M.; Szczesnlak, T.; Kapusta, M.; Szawlowski, M.; Wolski, D. Energy resolution of small scintillation detectors with SiPM light readout. J. Instrum. JINST 2013, 8, P02017. [Google Scholar] [CrossRef]
- Seidel, J.; Gandler, W.R.; Green, M.V. Characteristics of a pair of small field-of-view LSO scintillation cameras. IEEE Trans. Nucl. Sci. 1996, 43, 1968–1973. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, Y.; Wang, M. Energy calibration using scintillator background radiation for high-resolution PET detectors. Nucl. Instr. Meth. A 2020, 974, 164202. [Google Scholar] [CrossRef]
- Rothfuss, H.; Panin, V.; Moor, A.; Young, J.; Hong, I.; Michel, C.; Hamill, J.; Casey, M. LSO background radiation as a transmission source using time of flight. Phys. Med. Biol. 2014, 59, 5483–5500. [Google Scholar] [CrossRef]
- Conti, M.; Eriksson, L.; Hayden, C. Monitoring energy calibration drift using the scintillator background radiation. IEEE Trans. Nucl. Sci. 2011, 58, 687–694. [Google Scholar] [CrossRef]
- Alva-Sánchez, H.; Zepeda-Barrios, A.; Díaz-Martínez, V.D.; Murrieta-Rodríguez, T.; Rodríguez-Villafuerte, A.M.M. Understanding the intrinsic radioactivity energy spectrum from 176Lu in LYSO/LSO scintillation crystals. Sci. Rep. 2018, 8, 17310. [Google Scholar] [CrossRef]
- Lara-Camacho, V.M.; Hernández-Acevedo, E.M.; Alva-Sánchez, H.; Murrieta-Rodríguez, T.; Martínez-Dávalos, A.; Moranchel, M.; Rodríguez-Villafuerte, M. Experimental validation of the ANTS2 code for modelling optical photon transport in monolithic LYSO crystals. Phys. Med. 2021, 81, 215–226. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, S.; Horii, H.; Hurutani, M.; Matsumoto, K.; Senda, M. Investigation of single, random, and true counts from natural radioactivity in LSO-based clinical PET. Ann. Nucl. Med. 2005, 19, 109–114. [Google Scholar] [CrossRef]
- Afanaciev, K.G.; Artikov, A.M.; Baranov, V.Y.; Batouritski, M.A.; Budagov, J.A.; Davydov, Y.I.; Djilkibaev, R.M.; Emeliantchik, I.F.; Fedorov, A.A.; Glagolev, V.V.; et al. Response of LYSO:Ce scintillation crystals to low energy gamma-rays. Phys. Part. Nuclei Lett. 2015, 12, 319–324. [Google Scholar] [CrossRef]
- McIntosh, B.; Stout, D.B.; Goertzen, A.L. Validation of a GATE model of 176Lu intrinsic radioactivity in LSO PET system. IEEE Trans. Nucl. Sci. 2011, 58, 682–686. [Google Scholar] [CrossRef]
- Domínguez-Jiménez, D.Y.; Alva-Sánchez, H. Energy spectra due to the intrinsic radiation of LYSO/LSO scintillators for a wide range of crystal sizes. Med. Phys. 2021, 48, 1596–1607. [Google Scholar] [CrossRef]
- Park, H.M.; Hong, H.S.; Kim, J.H.; Joo, K.S. Development of a Portable Device Based Wireless Medical Radiation Monitoring System. J. Radiat. Prot. Res. 2014, 39, 150–158. [Google Scholar] [CrossRef]
- Taheri, M.A.; Askari, M. Taghan Sasanpour, Simulation of Gaussian energy broadening in gamma response of a LYSO array detector using a semi-empirical method. Eur. Phys. J. Plus 2017, 132, 384. [Google Scholar] [CrossRef]
- Jeon, B.; Kim, J.; Moon, M.; Cho, G. Parametric optimization for energy calibration and gamma response functionof plastic scintillation detectors using a genetic algorithm. Nucl. Instr. Meth. A 2019, 930, 8–14. [Google Scholar] [CrossRef]
- Li, H.; Love, P.E.; Ogunlana, S. Genetic algorithm compared to nonlinear optimization for labour and equipment assignment. Build. Res. Inf. 1998, 26, 322–329. [Google Scholar] [CrossRef]
- Grodzicka, M.; Moszynski, M.; Szczesniak, T.; Szawlowski, M.; Baszak, J. Characterization of 4 × 4 ch MPPC array in scintillation spectrometry. In Proceedings of the 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference Record (NSS/MIC), Anaheim, CA, USA, 29 October–3 November 2012; pp. 327–330. [Google Scholar] [CrossRef]
- Moszynski, M.; Syntfeld-Kazuch, A.; Swiderski, L.; Grodzicka, M.; Wanowska, J.I.; Sibczynski, P.; Szczesniak, T. Energy resolution of scintillation detectors. Nucl. Instr. Meth. A 2016, 805, 25–35. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement, 4th ed.; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-0-470-13148-0. [Google Scholar]
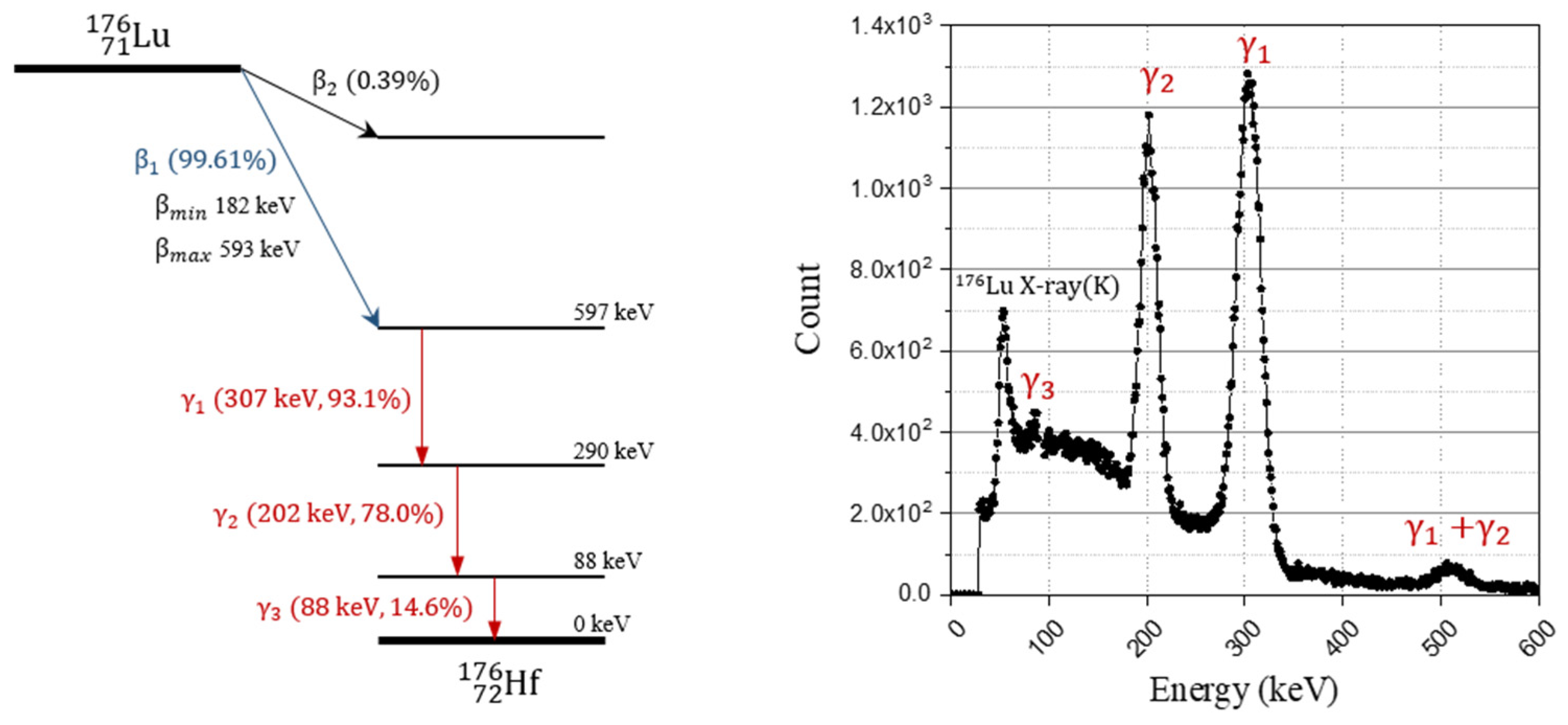

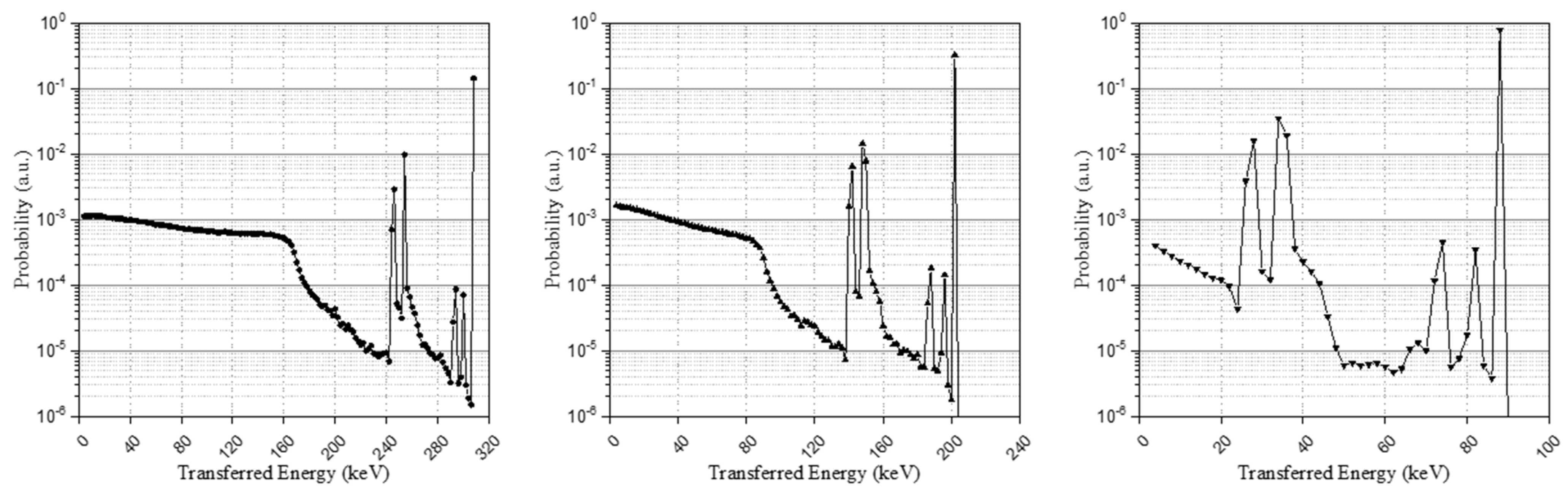



| Source Pathway | Cases of Gamma Ray Emission (γ) or Internal Conversion (IC) by Isomer Transition (IT) | ||
|---|---|---|---|
| 307 keV (ITI) | 202 keV (ITII) | 88 keV (ITIII) | |
| 1 | γ1 | γ2 | γ3 |
| 2 | γ1 | γ2 | IC3 |
| 3 | γ1 | IC2 | γ3 |
| 4 | γ1 | IC2 | IC3 |
| 5 | IC1 | γ2 | γ3 |
| 6 | IC1 | γ2 | IC3 |
| 7 | IC1 | IC2 | γ3 |
| 8 | IC1 | IC2 | IC3 |
| Energy Deposition Cases | Beta Particle | State of Ionizing Radiation | ||
|---|---|---|---|---|
| Isomer Transition I | Isomer Transition II | Isomer Transition III | ||
| 1 | Interaction | Interaction | Interaction | Escape |
| 2 | Interaction | Interaction | Interaction | Interaction |
| 3 | Interaction | Interaction | Escape | Escape |
| 4 | Interaction | Interaction | Escape | Interaction |
| 5 | Interaction | Escape | Interaction | Escape |
| 6 | Interaction | Escape | Interaction | Interaction |
| 7 | Interaction | Escape | Escape | Escape |
| 8 | Interaction | Escape | Escape | Interaction |
| Isomer Transition Pathway | Isomer Transition I | Isomer Transition II | Isomer Transition III | |||
|---|---|---|---|---|---|---|
| γ1 | IC1 | γ2 | IC2 | γ3 | IC3 | |
| Yield (Y) | 0.931 | 0.069 | 0.780 | 0.220 | 0.146 | 0.854 |
| Interaction probability (P) | 0.224 | 1.000 | 0.399 | 1.000 | 0.863 | 1.000 |
| Photo-peak efficiency (E) | 0.641 | 1.000 | 0.818 | 1.000 | 0.909 | 1.000 |
| Total photo-peak ratio (T) | 0.730 | 0.893 | 0.988 | |||
| Crystal Size | Isomer Transition I | Isomer Transition II | Isomer Transition III |
|---|---|---|---|
| 3 × 3 × 3 mm3 | 0.717 | 0.880 | 0.985 |
| 10 × 10 × 10 mm3 | 0.809 | 0.941 | 0.995 |
| 30 × 30 × 30 mm3 | 0.914 | 0.978 | 0.998 |
| Isomer Transition I | Isomer Transition II | Isomer Transition III | |
| Interaction | 0.2775 | 0.5310 | 0.9800 |
| Escape | 0.7225 | 0.4688 | 0.020 |
| Energy deposition cases | Probability | ||
| 1 | 0.00677 | ||
| 2 | 0.33182 | ||
| 3 | 0.00767 | ||
| 4 | 0.00260 | ||
| 5 | 0.37632 | ||
| 6 | 0.12745 | ||
| 7 | 0.00294 | ||
| 8 | 0.14443 | ||
| Sum | 1.00000 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, K.; Choi, H.; Yi, Y.; Kim, W.; Kim, J.; Hwang, J.; Ko, E.; Cho, G. Discrete Convolution-Based Energy Spectrum Configuring Method for the Analysis of the Intrinsic Radiation of 176Lu. Sensors 2021, 21, 7040. https://doi.org/10.3390/s21217040
Ko K, Choi H, Yi Y, Kim W, Kim J, Hwang J, Ko E, Cho G. Discrete Convolution-Based Energy Spectrum Configuring Method for the Analysis of the Intrinsic Radiation of 176Lu. Sensors. 2021; 21(21):7040. https://doi.org/10.3390/s21217040
Chicago/Turabian StyleKo, Kilyoung, Hyunwoong Choi, Yongsun Yi, Wonku Kim, Junhyeok Kim, Jisung Hwang, Eunbie Ko, and Gyuseong Cho. 2021. "Discrete Convolution-Based Energy Spectrum Configuring Method for the Analysis of the Intrinsic Radiation of 176Lu" Sensors 21, no. 21: 7040. https://doi.org/10.3390/s21217040
APA StyleKo, K., Choi, H., Yi, Y., Kim, W., Kim, J., Hwang, J., Ko, E., & Cho, G. (2021). Discrete Convolution-Based Energy Spectrum Configuring Method for the Analysis of the Intrinsic Radiation of 176Lu. Sensors, 21(21), 7040. https://doi.org/10.3390/s21217040






