Diagnosis of Pneumonia by Cough Sounds Analyzed with Statistical Features and AI
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Population and Clinical Diagnosis of Causes of Coughs
2.2. Measurement of Cough Sounds
2.3. Extraction of Acoustic Features of Cough Sounds
2.4. AI-Based Diagnostic Algorithm
2.5. Pneumonia Diagnosed by Pulmonologists Based on Cough Sounds
2.6. Statistical Analysis
3. Results
3.1. Population
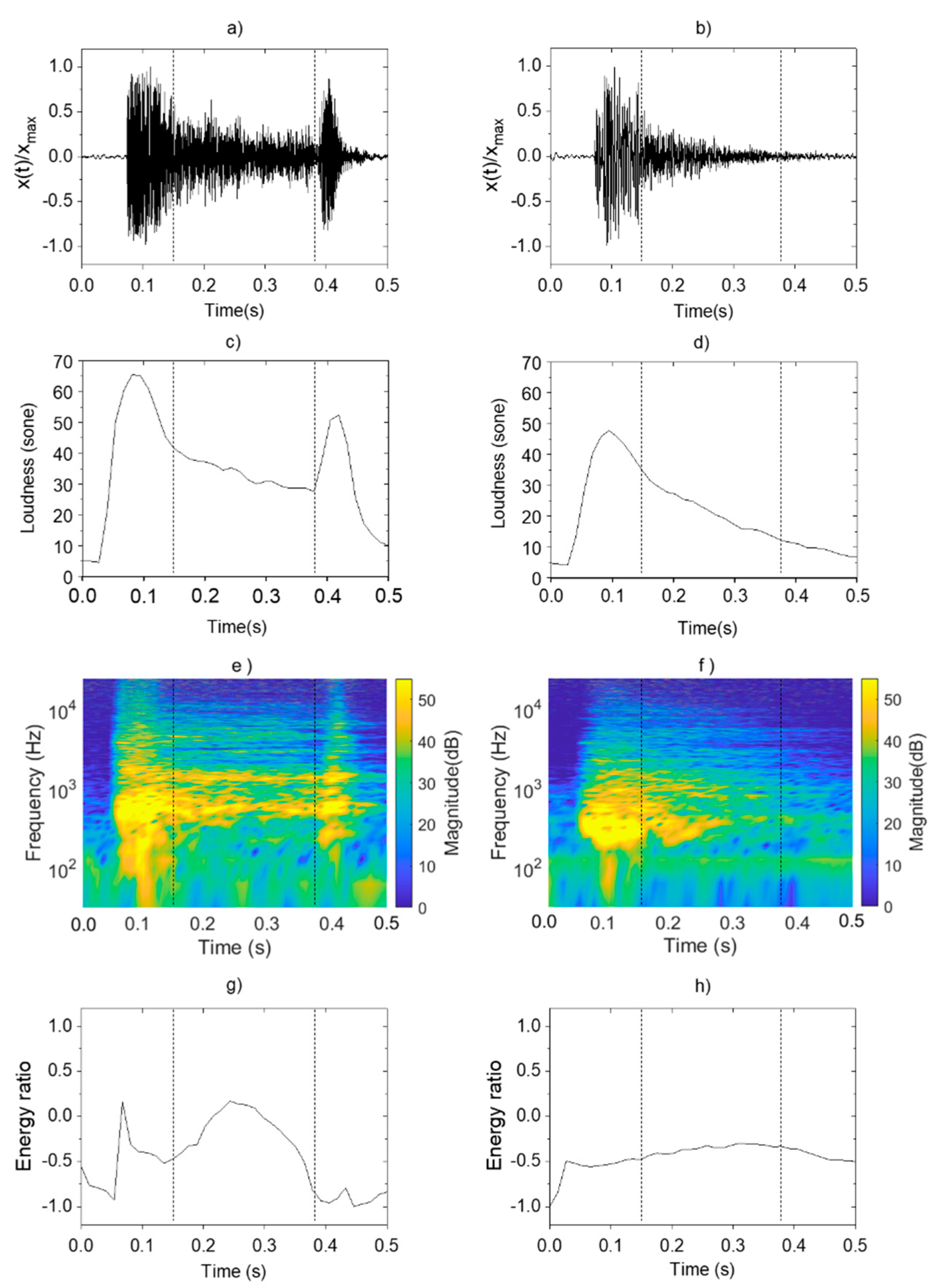
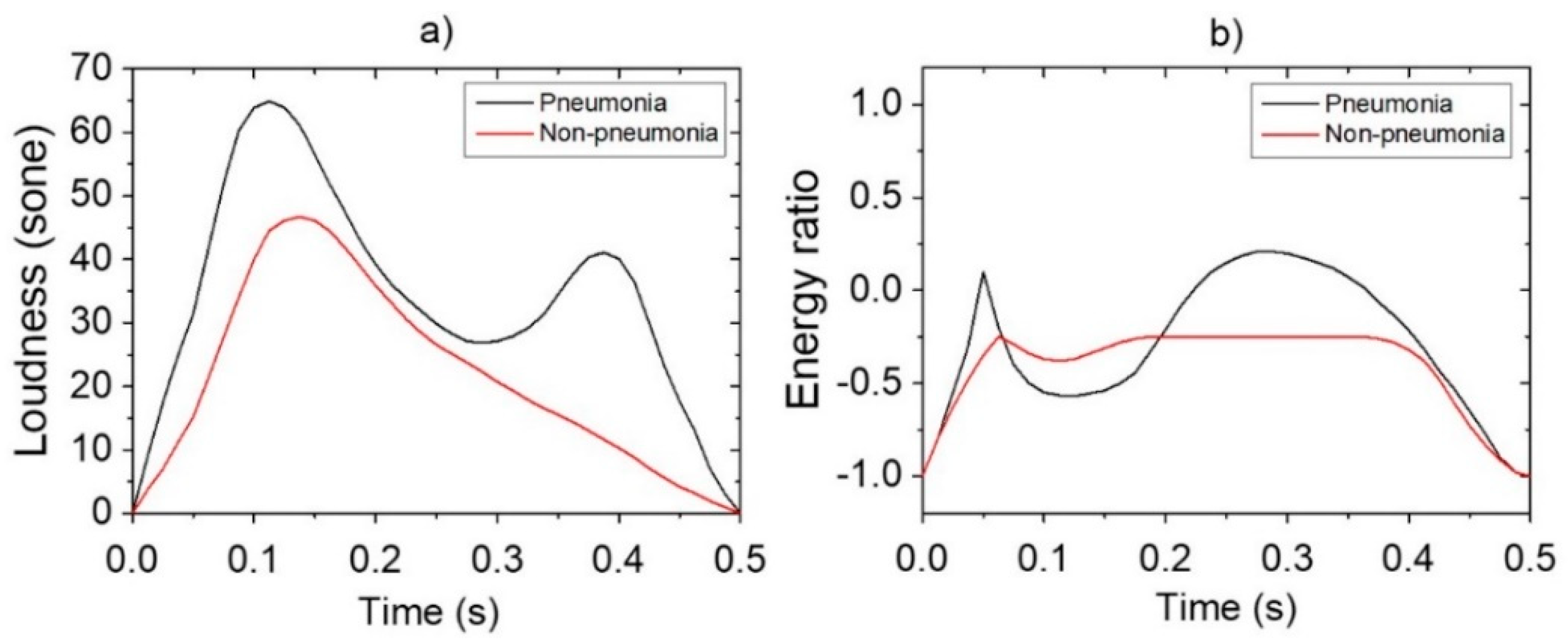
3.2. Characteristics Quantification with Psychoacoustics Aspect
3.3. Sound-Energy Distribution
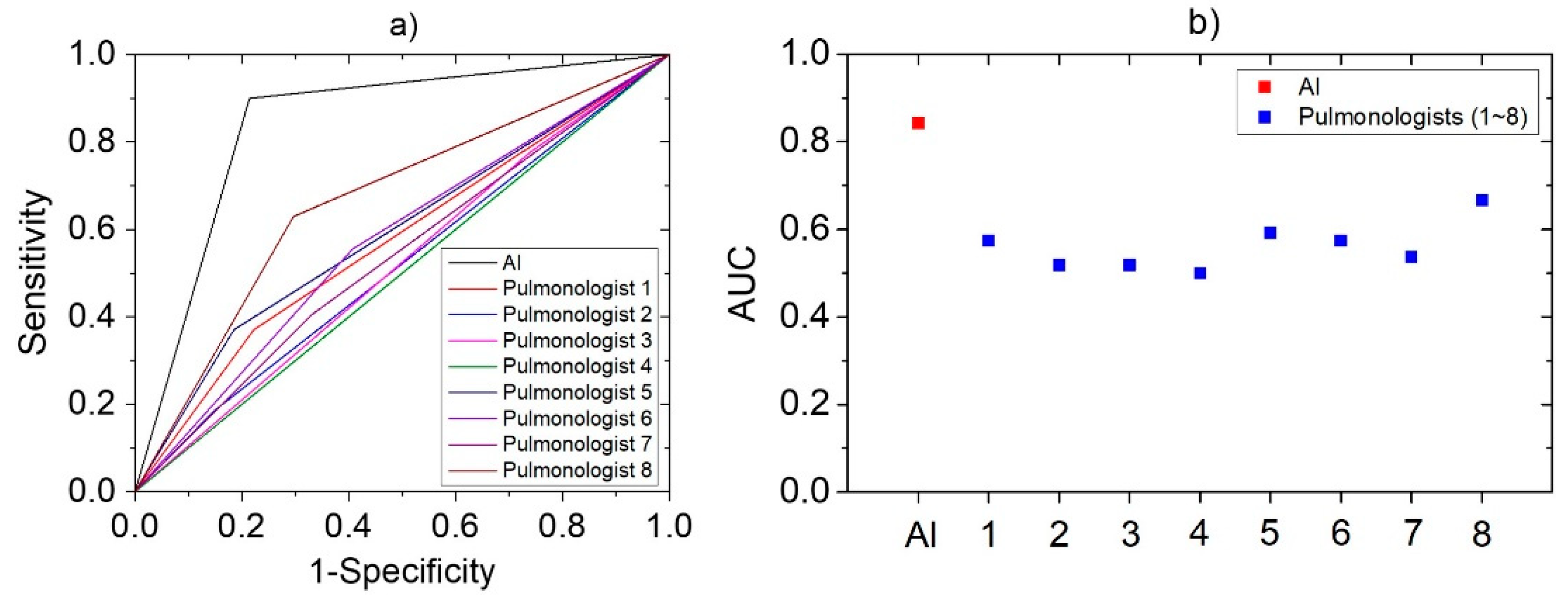
3.4. Diagnostic Accuracy of AI-Based Algorithm
3.5. Comparison with Pulmonologists
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Troeger, C.; Forouzanfar, M.; Rao, P.C.; Khalil, I.; Brown, A.; Swartz, S.; Fullman, N.; Mosser, J.; Thompson, R.L.; Reiner, R.C., Jr. Estimates of the global, regional, and national morbidity, mortality, and aetiologies of lower respiratory tract infections in 195 countries: A systematic analysis for the Global Burden of Disease Study 2015. Lancet Infect. Dis. 2017, 17, 1133–1161. [Google Scholar] [CrossRef] [Green Version]
- Lim, W.S.; Woodhead, M. British Thoracic Society adult community acquired pneumonia audit 2009/10. Thorax 2011, 66, 548–549. [Google Scholar] [CrossRef] [Green Version]
- Mandell, L.A.; Wunderink, R.G.; Anzueto, A.; Bartlett, J.G.; Campbell, G.D.; Dean, N.C.; Dowell, S.F.; File, T.M., Jr.; Musher, D.M.; Niederman, M.S. Infectious Diseases Society of America/American Thoracic Society consensus guidelines on the management of community-acquired pneumonia in adults. Clin. Infect. Dis. 2007, 44, S27–S72. [Google Scholar] [CrossRef]
- Buonsenso, D.; Pata, D.; Chiaretti, A. COVID-19 outbreak: Less stethoscope, more ultrasound. Lancet Respir. Med. 2020, 8, e27. [Google Scholar] [CrossRef] [Green Version]
- Kosasih, K.; Abeyratne, U.R.; Swarnkar, V.; Triasih, R. Wavelet augmented cough analysis for rapid childhood pneumonia diagnosis. IEEE Trans. Biomed. Eng. 2014, 62, 1185–1194. [Google Scholar] [CrossRef]
- Hee, H.I.; Balamurali, B.; Karunakaran, A.; Herremans, D.; Teoh, O.H.; Lee, K.P.; Teng, S.S.; Lui, S.; Chen, J.M. Development of Machine Learning for Asthmatic and Healthy Voluntary Cough Sounds: A Proof of Concept Study. Appl. Sci. 2019, 9, 2833. [Google Scholar] [CrossRef] [Green Version]
- Infante, C.; Chamberlain, D.; Fletcher, R.; Thorat, Y.; Kodgule, R. Use of cough sounds for diagnosis and screening of pulmonary disease. In Proceedings of 2017 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017; pp. 1–10. [Google Scholar]
- Al-khassaweneh, M.; Bani Abdelrahman, R.E. A signal processing approach for the diagnosis of asthma from cough sounds. J. Med. Eng. Technol. 2013, 37, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Enseki, M.; Nukaga, M.; Tadaki, H.; Tabata, H.; Hirai, K.; Kato, M.; Mochizuki, H. A breath sound analysis in children with cough variant asthma. Allergol. Int. 2019, 68, 33–38. [Google Scholar] [CrossRef]
- Sharan, R.V.; Abeyratne, U.R.; Swarnkar, V.R.; Porter, P. Automatic croup diagnosis using cough sound recognition. IEEE Trans. Biomed. Eng. 2018, 66, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Parker, D.; Picone, J.; Harati, A.; Lu, S.; Jenkyns, M.H.; Polgreen, P.M. Detecting paroxysmal coughing from pertussis cases using voice recognition technology. PLoS ONE 2013, 8, e82971. [Google Scholar] [CrossRef] [Green Version]
- Pramono, R.X.A.; Imtiaz, S.A.; Rodriguez-Villegas, E. A cough-based algorithm for automatic diagnosis of pertussis. PLoS ONE 2016, 11, e0162128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koehler, U.; Hildebrandt, O.; Fischer, P.; Gross, V.; Sohrabi, K.; Timmesfeld, N.; Peter, S.; Urban, C.; Steiß, J.-O.; Koelsch, S. Time course of nocturnal cough and wheezing in children with acute bronchitis monitored by lung sound analysis. Eur. J. Pediatrics 2019, 178, 1385–1394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Porter, P.; Abeyratne, U.; Swarnkar, V.; Tan, J.; Ng, T.-W.; Brisbane, J.M.; Speldewinde, D.; Choveaux, J.; Sharan, R.; Kosasih, K. A prospective multicentre study testing the diagnostic accuracy of an automated cough sound centred analytic system for the identification of common respiratory disorders in children. Respir. Res. 2019, 20, 81. [Google Scholar] [CrossRef]
- Abeyratne, U.R.; Swarnkar, V.; Setyati, A.; Triasih, R. Cough sound analysis can rapidly diagnose childhood pneumonia. Ann. Biomed. Eng. 2013, 41, 2448–2462. [Google Scholar] [CrossRef]
- Abeyratne, U.R.; Swarnkar, V.; Triasih, R.; Setyati, A. Cough Sound Analysis-A new tool for diagnosing Pneumonia. In Proceedings of 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 5216–5219. [Google Scholar]
- Sharan, R.V.; Abeyratne, U.R.; Swarnkar, V.R.; Porter, P. Cough sound analysis for diagnosing croup in pediatric patients using biologically inspired features. In Proceedings of 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 4578–4581. [Google Scholar]
- Botha, G.; Theron, G.; Warren, R.; Klopper, M.; Dheda, K.; Van Helden, P.; Niesler, T. Detection of tuberculosis by automatic cough sound analysis. Physiol. Meas. 2018, 39, 045005. [Google Scholar] [CrossRef]
- Metlay, J.P.; Waterer, G.W.; Long, A.C.; Anzueto, A.; Brozek, J.; Crothers, K.; Cooley, L.A.; Dean, N.C.; Fine, M.J.; Flanders, S.A.; et al. Diagnosis and Treatment of Adults with Community-acquired Pneumonia. An Official Clinical Practice Guideline of the American Thoracic Society and Infectious Diseases Society of America. Am. J. Respir. Crit. Care Med. 2019, 200, e45–e67. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.F.; Pavord, I.D. Prevalence, pathogenesis, and causes of chronic cough. Lancet 2008, 371, 1364–1374. [Google Scholar] [CrossRef]
- Murata, A.; Taniguchi, Y.; Hashimoto, Y.; Kaneko, Y.; Takasaki, Y.; Kudoh, S. Discrimination of productive and non-productive cough by sound analysis. Intern. Med. 1998, 37, 732–735. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, C.; Toop, L.; Dawson, K. Towards a quantitative description of asthmatic cough sounds. Eur. Respir. J. 1992, 5, 685–692. [Google Scholar] [PubMed]
- Zwicker, E.; Scharf, B. A model of loudness summation. Psychol. Rev. 1965, 72, 3. [Google Scholar] [CrossRef]
- Zwicker, E.; Fastl, H. Psychoacoustics: Facts and Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 22. [Google Scholar]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef] [Green Version]
- Lozano, M.; Fiz, J.A.; Jané, R. Automatic differentiation of normal and continuous adventitious respiratory sounds using ensemble empirical mode decomposition and instantaneous frequency. IEEE J. Biomed. Health Inform. 2015, 20, 486–497. [Google Scholar] [CrossRef] [Green Version]
- Kadambi, P.; Mohanty, A.; Ren, H.; Smith, J.; McGuinnes, K.; Holt, K.; Furtwaengler, A.; Slepetys, R.; Yang, Z.; Seo, J.; et al. Towards a wearable cough detector based on neural networks. In Proceedings of 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Hoyos-Barceló, C.; Monge-Álvarez, J.; Pervez, Z.; San-José-Revuelta, L.M.; Casaseca-de-la-Higuera, P. Efficient computation of image moments for robust cough detection using smartphones. Comput. Biol. Med. 2018, 100, 2176–2185. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wu, F.; Wei, B.; Zhang, Q.; Huang, H.; Shah, S.W.; Cheng, J. Data Augmentation and Dense-LSTM for Human Activity Recognition Using WiFi Signal. IEEE Internet Things J. 2021, 8, 4628–4641. [Google Scholar] [CrossRef]
- Teng, X.; Wang, T.; Zhang, X.; Lan, L.; Luo, Z. Enhancing Stock Price Trend Prediction via a Time-Sensitive Data Augmentation Method. Complexity 2020, 2020, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Rashid, K.M.; Louis, J. Times-series data augmentation and deep learning for construction equipment activity recognition. Adv. Eng. Inform. 2019, 42, 100944. [Google Scholar] [CrossRef]
- Pahar, M.; Niesler, T. Machine Learning based COVID-19 Detection from Smartphone Recordings: Cough, Breath and Speech. arXiv 2021, arXiv:2104.02477. [Google Scholar]
- Ciaburro, G.; Iannace, G. Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms. Informatics 2020, 7, 23. [Google Scholar] [CrossRef]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern recognition and machine learning. Mach. Learn. 2006, 128, 179–220. [Google Scholar]
- DeLong, E.; DeLong, D.; Clarke-Pearson, D. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef] [PubMed]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Jacobs, R.A. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988, 1, 295–307. [Google Scholar] [CrossRef]
- Ma, H.; Bandos, A.I.; Rockette, H.E.; Gur, D. On use of partial area under the ROC curve for evaluation of diagnostic performance. Stat. Med. 2013, 32, 3449–3458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajian-Tilaki, K. Sample size estimation in diagnostic test studies of biomedical informatics. J. Biomed. Inform. 2014, 48, 193–204. [Google Scholar] [CrossRef] [Green Version]


| PCB Piezoelectronics, 378B02 | Nominal Microphone Diameter | 12 mm |
| Frequency Response Characteristic (at 0° incidence) | Free-Field | |
| Sensitivity | 50 mV/Pa | |
| Frequency Range (±2 dB) | 3.75 to 20,000 Hz | |
| Temperature Range (Operating) | −40 to +80 °C | |
| Static Pressure Coefficient | −0.013 dB/kPa | |
| Excitation Voltage | 2 to 20 mA | |
| Recorder Settings | Sampling frequency | 48,000 Hz |
| Sampling time | 0.020833 ms | |
| Coupling type | ICP |
| Pneumonia (n = 15) | Non-Pneumonia (n = 15) | p Value | |
|---|---|---|---|
| Age, years | 49.7 ± 14.4 | 45.9 ± 13.4 | 0.469 |
| Male | 6 (40%) | 9 (60%) | 0.465 |
| BMI, kg/m2 | 25.5 ± 4.9 | 23.5 ± 4.2 | 0.258 |
| Smoking | 0.141 | ||
| Never | 7 (46.7%) | 12 (80.0%) | |
| Ex-smoker | 7 (46.7%) | 3 (20.0%) | |
| Current smoker | 1 (6.7%) | 0 (0.0%) | |
| Visual analogue scale of cough | 7.1 ± 2.2 | 7.2 ± 2.2 | 0.935 |
| Symptoms | |||
| Sputum | 15 (100.0%) | 13 (86.7%) | 0.4642 |
| Wheeze | 6 (40.0%) | 8 (53.3%) | 0.7144 |
| Dyspnea | 8 (53.3%) | 6 (40.0%) | 0.7144 |
| Accuracy (%) | Sensitivity (%) | Specificity (%) | ||
|---|---|---|---|---|
| AI | 84.9 | 90.0 | 78.6 | |
| Pulmonologist | 1 | 58.2 | 37.0 | 78.6 |
| 2 | 52.7 | 18.5 | 85.7 | |
| 3 | 49.1 | 22.2 | 75.0 | |
| 4 | 50.9 | 51.9 | 50.0 | |
| 5 | 60.0 | 37.0 | 82.1 | |
| 6 | 58.2 | 55.6 | 60.7 | |
| 7 | 54.6 | 40.7 | 67.9 | |
| 8 | 67.3 | 63.0 | 71.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, Y.; Jin, J.; Jo, H.I.; Lee, H.; Kim, S.-H.; Chung, S.J.; Yoon, H.J.; Park, J.; Jeon, J.Y. Diagnosis of Pneumonia by Cough Sounds Analyzed with Statistical Features and AI. Sensors 2021, 21, 7036. https://doi.org/10.3390/s21217036
Chung Y, Jin J, Jo HI, Lee H, Kim S-H, Chung SJ, Yoon HJ, Park J, Jeon JY. Diagnosis of Pneumonia by Cough Sounds Analyzed with Statistical Features and AI. Sensors. 2021; 21(21):7036. https://doi.org/10.3390/s21217036
Chicago/Turabian StyleChung, Youngbeen, Jie Jin, Hyun In Jo, Hyun Lee, Sang-Heon Kim, Sung Jun Chung, Ho Joo Yoon, Junhong Park, and Jin Yong Jeon. 2021. "Diagnosis of Pneumonia by Cough Sounds Analyzed with Statistical Features and AI" Sensors 21, no. 21: 7036. https://doi.org/10.3390/s21217036
APA StyleChung, Y., Jin, J., Jo, H. I., Lee, H., Kim, S.-H., Chung, S. J., Yoon, H. J., Park, J., & Jeon, J. Y. (2021). Diagnosis of Pneumonia by Cough Sounds Analyzed with Statistical Features and AI. Sensors, 21(21), 7036. https://doi.org/10.3390/s21217036








