The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes
Abstract
:1. Introduction
2. Fabrication of InAs/GaSb Superlattice Photodetectors
3. Results and Discussion
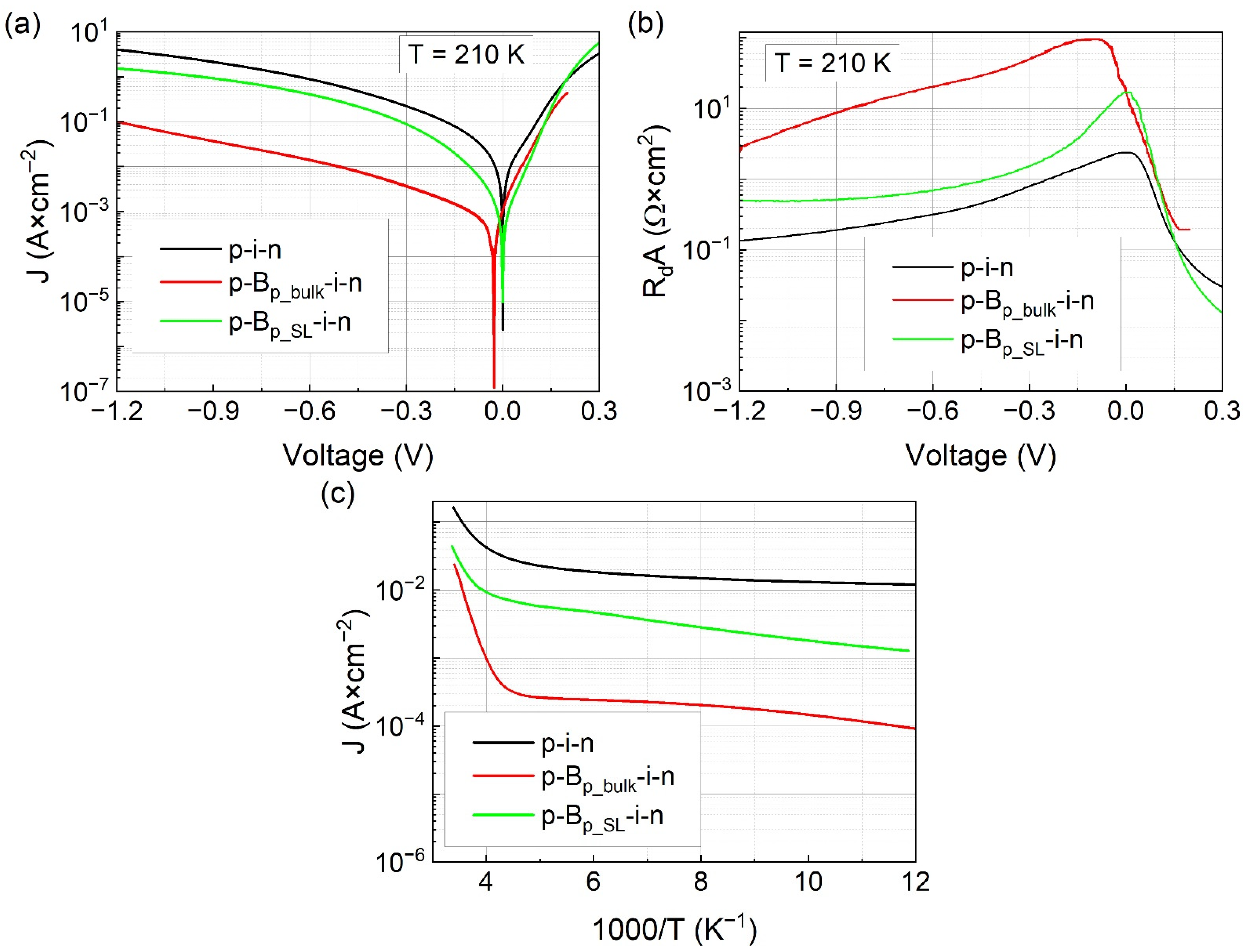
3.1. Dark Current Characteristics
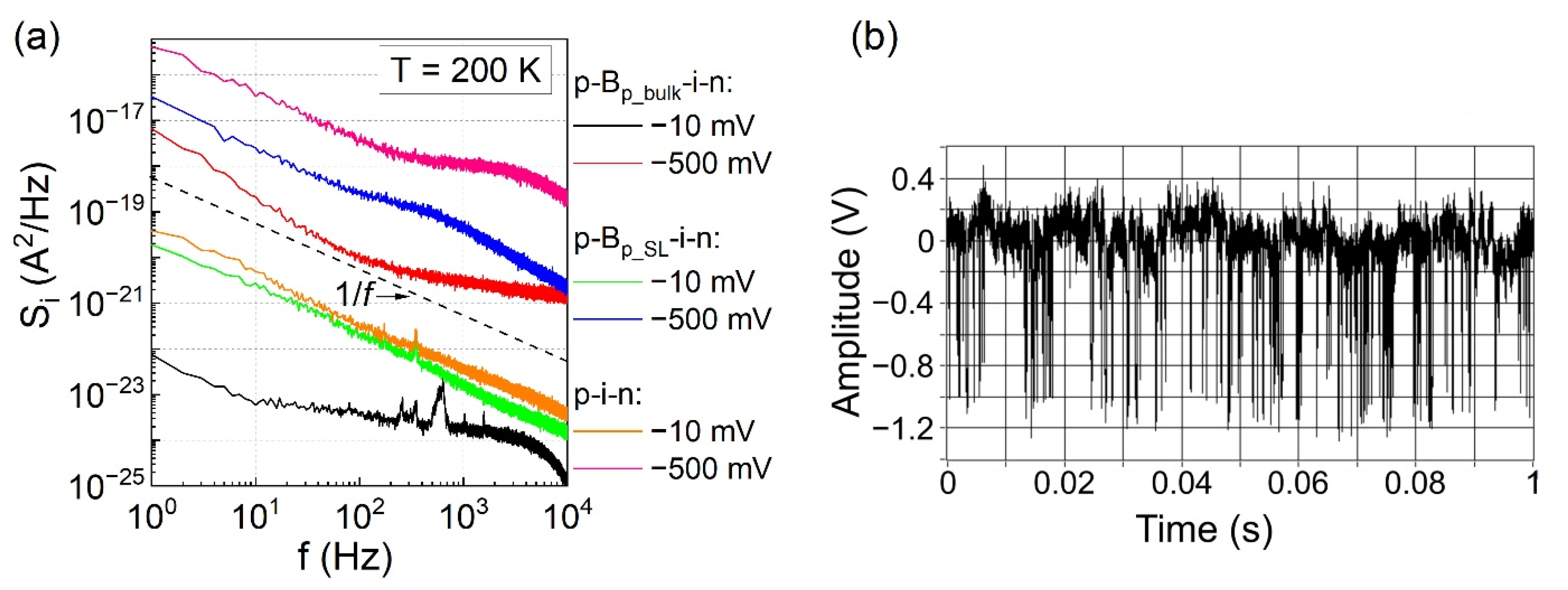
3.2. Noise Characteristics
3.3. Optical Characteristics
3.4. Specific Detectivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, B.-M.; Hoffman, D.; Wei, Y.; Delaunay, P.-Y.; Hood, A.; Razeghi, M. Very High Quantum Efficiency in Type-II InAs/GaSb Superlattice Photodiode with Cutoff of 12 μm. Appl. Phys. Lett. 2007, 90, 231108. [Google Scholar] [CrossRef]
- Jasik, A.; Sankowska, I.; Pierścińska, D.; Regiński, K.; Pierściński, K.; Kubacka-Traczyk, J. Blueshift of Bandgap Energy and Reduction of Non-Radiative Defect Density Due to Precise Control of InAs-on-GaSb Interface in Type-II InAs/GaSb Superlattice. J. Appl. Phys. 2011, 110, 123103. [Google Scholar] [CrossRef]
- Brown, G.J. Type-II InAs/GaInSb Superlattices for Infrared Detection: An Overview; Andresen, B.F., Fulop, G.F., Eds.; SPIE: Bellingham, WA, USA, 2005; pp. 65–77. [Google Scholar] [CrossRef]
- Perez, J.-P.; Durlin, Q.; Christol, P. Ga-Free InAs/InAsSb Type-II Superlattice (T2SL) Photodetector for High Operating Temperature in the Midwave Infrared Spectral Domain. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2018; Volume 11180. [Google Scholar] [CrossRef] [Green Version]
- Klipstein, P. XBn Barrier Photodetectors Based on InAsSb with High Operating Temperatures. Opt. Eng. 2011, 50, 061002. [Google Scholar] [CrossRef] [Green Version]
- Sai-Halasz, G.A.; Tsu, R.; Esaki, L. A New Semiconductor Superlattice. Appl. Phys. Lett. 1977, 30, 651–653. [Google Scholar] [CrossRef]
- Lee, H.J.; Ko, S.Y.; Kim, Y.H.; Nah, J. Strain-Induced the Dark Current Characteristics in InAs/GaSb Type-II Superlattice for Mid-Wave Detector. J. Semicond. 2020, 41, 062302. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Z.; Bai, Z.; Li, H.; Zhou, Y.; Chen, J.; He, L. Fabrication of a 1024 × 1024 Format Long Wavelength Infrared Focal Plane Array Based on Type-II Superlattice and Barrier Enhanced Structure. Infrared Phys. Technol. 2021, 115, 103700. [Google Scholar] [CrossRef]
- Bandara, S.; Tidrow, M.; Aitcheson, L.; Zeng, L.; Baril, N. III-V Material Superlattice Infrared Focal Plane Array Technology. In Proceedings of the Infrared Technology and Applications XLVII; Fulop, G.F., Kimata, M., Zheng, L., Andresen, B.F., Miller, J.L., Eds.; SPIE: Bellingham, WA, USA, 2021; p. 17. [Google Scholar] [CrossRef]
- Gautam, N.; Myers, S.; Barve, A.V.; Klein, B.; Smith, E.P.; Rhiger, D.; Plis, E.; Kutty, M.N.; Henry, N.; Schuler-Sandy, T.; et al. Band Engineered HOT Midwave Infrared Detectors Based on Type-II InAs/GaSb Strained Layer Superlattices. Infrared Phys. Technol. 2013, 59, 72–77. [Google Scholar] [CrossRef]
- Maimon, S.; Wicks, G.W. NBn Detector, an Infrared Detector with Reduced Dark Current and Higher Operating Temperature. Appl. Phys. Lett. 2006, 89, 151109. [Google Scholar] [CrossRef]
- Gautam, N.; Myers, S.; Barve, A.V.; Klein, B.; Smith, E.P.; Rhiger, D.R.; Dawson, L.R.; Krishna, S. High Operating Temperature Interband Cascade Midwave Infrared Detector Based on Type-II InAs/GaSb Strained Layer Superlattice. Appl. Phys. Lett. 2012, 101, 021106. [Google Scholar] [CrossRef]
- Tian, Z.; Cai, Z.; Yang, R.Q.; Mishima, T.D.; Santos, M.B.; Johnson, M.B.; Klem, J.F. Interband Cascade Infrared Photodetectors. In Proceedings of the Quantum Sensing and Nanophotonic Devices VII; Razeghi, M., Sudharsanan, R., Brown, G.J., Eds.; SPIE: Bellingham, WA, USA, 2010; Volume 7608, pp. 590–597. [Google Scholar] [CrossRef]
- Delga, A. 8-Quantum cascade detectors: A review. In Mid-Infrared Optoelectronics; Tournié, E., Cerutti, L., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Duxford, UK, 2020; pp. 337–377. ISBN 978-0-08-102709-7. [Google Scholar] [CrossRef]
- Savich, G.R.; Pedrazzani, J.R.; Sidor, D.E.; Maimon, S.; Wicks, G.W. Dark Current Filtering in Unipolar Barrier Infrared Detectors. Appl. Phys. Lett. 2011, 99, 121112. [Google Scholar] [CrossRef]
- Klipstein, P.; Klin, O.; Grossman, S.; Snapi, N.; Yaakobovitz, B.; Brumer, M.; Lukomsky, I.; Aronov, D.; Yassen, M.; Yofis, B.; et al. XBn Barrier Detectors for High Operating Temperatures; Razeghi, M., Sudharsanan, R., Brown, G.J., Eds.; SPIE: Bellingham, WA, USA, 2010; p. 76081V. [Google Scholar] [CrossRef]
- Ting, D.Z.-Y.; Hill, C.J.; Soibel, A.; Keo, S.A.; Mumolo, J.M.; Nguyen, J.; Gunapala, S.D. A High-Performance Long Wavelength Superlattice Complementary Barrier Infrared Detector. Appl. Phys. Lett. 2009, 95, 023508. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, L.; Zhu, L.; Deng, Z.; Huang, J.; Huang, J.; Guo, H.; Chen, L.; Lin, C.; Lin, C.; et al. Low Frequency Noise-Dark Current Correlations in HgCdTe Infrared Photodetectors. Opt. Express 2020, 28, 23660–23669. [Google Scholar] [CrossRef]
- Ramos, D.; Delmas, M.; Ivanov, R.; Höglund, L.; Costard, E.; Hellström, P.-E.; Malm, G. 1/f Noise and Dark Current Correlation in Midwave InAs/GaSb Type-II Superlattice IR Detectors. Phys. Status Solidi A 2021, 218, 2000557. [Google Scholar] [CrossRef]
- Razeghi, M.; Haddadi, A.; Chen, G.; Hoang, A.M.; Chevallier, R.; Callewaert, F. Low-Frequency Noise in Mid-Wavelength Infrared InAs/GaSb Type-II Superlattice Based Focal Plane Arrays. In Proceedings of the Infrared Technology and Applications XL; SPIE: Bellingham, WA, USA, 2014; Volume 9070, pp. 437–445. [Google Scholar] [CrossRef]
- Meng, C.; Li, J.; Yu, L.; Wang, X.; Han, P.; Yan, F.; Xu, Z.; Xu, Z.; Chen, J.; Ji, X.; et al. Investigation of a Noise Source and Its Impact on the Photocurrent Performance of Long-Wave-Infrared InAs/GaSb Type-II Superlattice Detectors. Opt. Express 2020, 28, 14753–14761. [Google Scholar] [CrossRef] [PubMed]
- Craig, A.P.; Letka, V.; Carmichael, M.; Golding, T.; Marshall, A.R. InAsSb-Based Detectors on GaSb for near-Room-Temperature Operation in the Mid-Wave Infrared. Appl. Phys. Lett. 2021, 118, 251103. [Google Scholar] [CrossRef]
- Jasik, A.; Sankowska, I.; Ratajczak, J.; Wawro, A.; Smoczyński, D.; Czuba, K.; Wzorek, M. Atomically Smooth Interfaces of Type-II InAs/GaSb Superlattice on Metamorphic GaSb Buffer Grown in 2D Mode on GaAs Substrate Using MBE. Curr. Appl. Phys. 2019, 19, 120–127. [Google Scholar] [CrossRef]
- Rehm, R.; Lemke, F.; Schmitz, J.; Wauro, M.; Walther, M. Limiting Dark Current Mechanisms in Antimony-Based Superlattice Infrared Detectors for the Long-Wavelength Infrared Regime; Andresen, B.F., Fulop, G.F., Hanson, C.M., Norton, P.R., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 94510N. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Gawron, W.; Kowalewski, A.; Stanaszek, D. Measurements of Low Frequency Noise of Infrared Photo-Detectors with Transimpedance Detection System. Metrol. Meas. Syst. 2014, 21, 461–472. [Google Scholar] [CrossRef] [Green Version]
- Brunner, A.; Rubaldo, L.; Destefanis, V.; Chabuel, F.; Kerlain, A.; Bauza, D.; Baier, N. Improvement of RTS Noise in HgCdTe MWIR Detectors. J. Electron. Mater. 2014, 43, 3060–3064. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Jureńczyk, J.; Czuba, K.; Jasik, A.; Sankowska, I.; Papis-Polakowska, E.; Kaniewski, J. Noise-Current Correlations in InAs/GaSb Type-II Superlattice Midwavelength Infrared Detectors. IEEE Trans. Electron Devices 2016, 63, 4907–4912. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kopytko, M.; Martyniuk, P. Low-Frequency Noise Limitations of InAsSb-, and HgCdTe-Based Infrared Detectors. Sens. Actuators Phys. 2020, 305, 111908. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Jureńczyk, J.; Czuba, K.; Jasik, A.; Sankowska, I.; Kaniewski, J. 1/f Noise Modeling of InAs/GaSb Superlattice Mid-Wavelength Infrared Detectors. Opt. Quantum Electron. 2017, 50, 36. [Google Scholar] [CrossRef] [Green Version]
- Klein, B.; Plis, E.; Kutty, M.N.; Gautam, N.; Albrecht, A.; Myers, S.; Krishna, S. Varshni Parameters for InAs/GaSb Strained Layer Superlattice Infrared Photodetectors. J. Phys. Appl. Phys. 2011, 44, 075102. [Google Scholar] [CrossRef]
- Czuba, K.; Sankowska, I.; Jureńczyk, J.; Jasik, A.; Papis-Polakowska, E.; Kaniewski, J. Influence of Be Doping Placement in InAs/GaSb Superlattice-Based Absorber on the Performance of MWIR Photodiodes. Semicond. Sci. Technol. 2017, 32, 055010. [Google Scholar] [CrossRef]
- Teng, Y.; Hao, X.; Zhu, H.; Zhu, H.; Liu, J.; Huai, Y.; Li, M.; Liu, M.; Xing, W.; Chen, B.; et al. Demonstration of MOCVD-Grown Long-Wavelength Infrared InAs/GaSb Superlattice Focal Plane Array. IEEE Access 2021, 9, 60689–60694. [Google Scholar] [CrossRef]
- More, V.M.; Kim, Y.; Jeon, J.; Shin, J.C.; Lee, S.J. Dual-Band Unipolar Barrier Infrared Photodetector Based on InGaAsSb Bulk and Type-II InAs/GaSb Superlattice Absorbers. J. Alloys Compd. 2021, 868, 159195. [Google Scholar] [CrossRef]
- Wu, D.; Dehzangi, A.; Razeghi, M. Demonstration of Mid-Wavelength Infrared NBn Photodetectors Based on Type-II InAs/InAs 1-x Sb x Superlattice Grown by Metal-Organic Chemical Vapor Deposition. Appl. Phys. Lett. 2019, 115, 061102. [Google Scholar] [CrossRef]
- Hao, X.; Deng, Z.; Huang, J.; Huang, Y.; Yang, H.; Teng, Y.; Zhao, Y.; Wu, Q.; Li, X.; Liu, J.; et al. Demonstration of a Dual-Band InAs/GaSb Type-II Superlattice Infrared Detector Based on a Single Heterojunction Diode. IEEE J. Quantum Electron. 2019, 56. [Google Scholar] [CrossRef]
- Wu, D.H.; Dehzangi, A.; Zhang, Y.Y.; Razeghi, M. Demonstration of Long Wavelength Infrared Type-II InAs/InAs1-XSbx Superlattices Photodiodes on GaSb Substrate Grown by Metalorganic Chemical Vapor Deposition. Appl. Phys. Lett. 2018, 112, 241103. [Google Scholar] [CrossRef]
- Martyniuk, P.; Gawron, W.; Stepien, D.; Benyahia, D.; Kowalewski, A.; Michalczewski, K.; Rogalski, A. Demonstration of Mid-Wave Type-II Superlattice InAs/GaSb Single Pixel Barrier Detector with GaAs Immersion Lens. IEEE Electron Device Lett. 2016, 37, 64–66. [Google Scholar] [CrossRef]




| Structure | p-i-n | p-Bp_bulk-i-n | p-Bp_SL-i-n |
|---|---|---|---|
| Absorber | |||
| GaAs IF thickness (ML/Å) | 0.5/1.5 | 0.5/1.4 | 0.5/1.4 |
| InAs layer thickness (ML/Å) | 10.0/30.3 | 9.9/30 | 10.2/31 |
| InSb IF thickness (ML/Å) | 1.5/4.8 | 1.5/5.0 | 1.5/5.0 |
| GaSb layer thickness (ML/Å) | 10.1/30.7 | 9.8/30 | 9.9/30.1 |
| (Δa/a)⊥ (ppm) | −920 | −280 | −280 |
| electron barrier | |||
| type | − | bulk AlSb | AlSb/GaSb SL |
| AlSb layer thickness (ML/Å) | − | −/500 | 4.4/13.6 |
| GaSb layer thickness (ML/Å) | − | − | 7.6/23.1 |
| (Δa/a)⊥ (ppm) | − | 11,800 | 4950 |
| Photodetector | ΔT1 | Ea1 (meV) | ΔT2 | Ea2 (meV) | ΔT3 | Ea3 (meV) |
|---|---|---|---|---|---|---|
| p-i-n | >244 K | 111 | 100–244 K | 2.5 | <100 K | 1.4 |
| p-Bp_bulk-i-n | >240 K | 220 | 112–240 K | 2.6 | <112 K | 9.3 |
| p-Bp_SL-i-n | >260 K | 132 | 104–260 K | 9.2 | <104 K | 6.8 |
| Photodiode | U (V) | Si_approx._1 (A2/Hz) | Si_approx._2 (A2/Hz) | Si_exp (A2/Hz) | D* approx._1 (Jones) | D* approx._2 (Jones) | D*exp (Jones) |
|---|---|---|---|---|---|---|---|
| p-i-n | 0 | 3.45 × 10−24 | 3.45 × 10−24 | 3.35 × 10−24 | 1.61 × 1010 | 1.61 × 1010 | 6.16 × 109 |
| −0.9 | 6.55 × 10−22 | 3.89 × 10−18 | 1.45 × 10−19 | 1.63 × 109 | 2.11 × 107 | 1.1 × 108 | |
| p-Bp_bulk-i-n | 0 | 9.8 × 10−26 | 1.11 × 10−25 | 3.59 × 10−26 | 1.43 × 108 | 1.35 × 108 | 2.4 × 108 |
| −1 | 1.37 × 10−24 | 1.63 × 10−23 | 4.97 × 10−20 | 2.44 × 108 | 7.05 × 107 | 1.3 × 106 | |
| p-Bp_SL-i-n | 0 | 4.87 × 10−25 | 4.88 × 10−25 | 7.28 × 10−25 | 1.52 × 108 | 1.52 × 108 | 1.25 × 108 |
| −1.12 | 3.27 × 10−22 | 2.27 × 10−18 | 9.34 × 10−20 | 1.76 × 109 | 2.12 × 107 | 1.04 × 108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czuba, K.; Ciura, Ł.; Sankowska, I.; Papis-Polakowska, E.; Jasik, A. The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes. Sensors 2021, 21, 7005. https://doi.org/10.3390/s21217005
Czuba K, Ciura Ł, Sankowska I, Papis-Polakowska E, Jasik A. The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes. Sensors. 2021; 21(21):7005. https://doi.org/10.3390/s21217005
Chicago/Turabian StyleCzuba, Krzysztof, Łukasz Ciura, Iwona Sankowska, Ewa Papis-Polakowska, and Agata Jasik. 2021. "The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes" Sensors 21, no. 21: 7005. https://doi.org/10.3390/s21217005
APA StyleCzuba, K., Ciura, Ł., Sankowska, I., Papis-Polakowska, E., & Jasik, A. (2021). The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes. Sensors, 21(21), 7005. https://doi.org/10.3390/s21217005






