A Flow Sensor-Based Suction-Index Control Strategy for Rotary Left Ventricular Assist Devices
Abstract
1. Introduction
2. Methods
2.1. Modeling of the Biventricular Cardiovascular System
2.2. The Rotary LVAD Model
2.3. SIMPF Control Strategy
2.4. Comparison with the Other Control Strategies
2.5. Simulation Description and Data Analysis
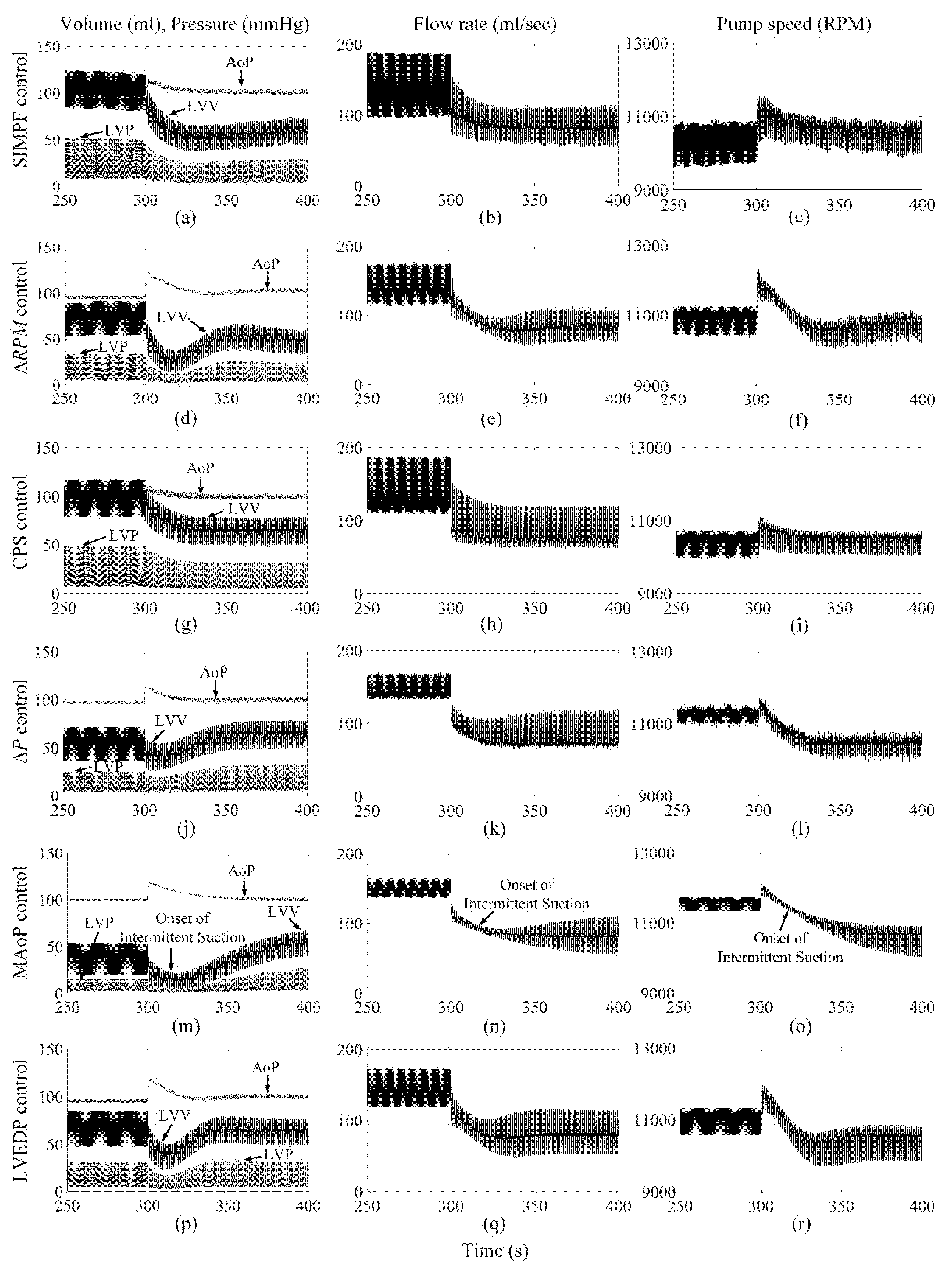
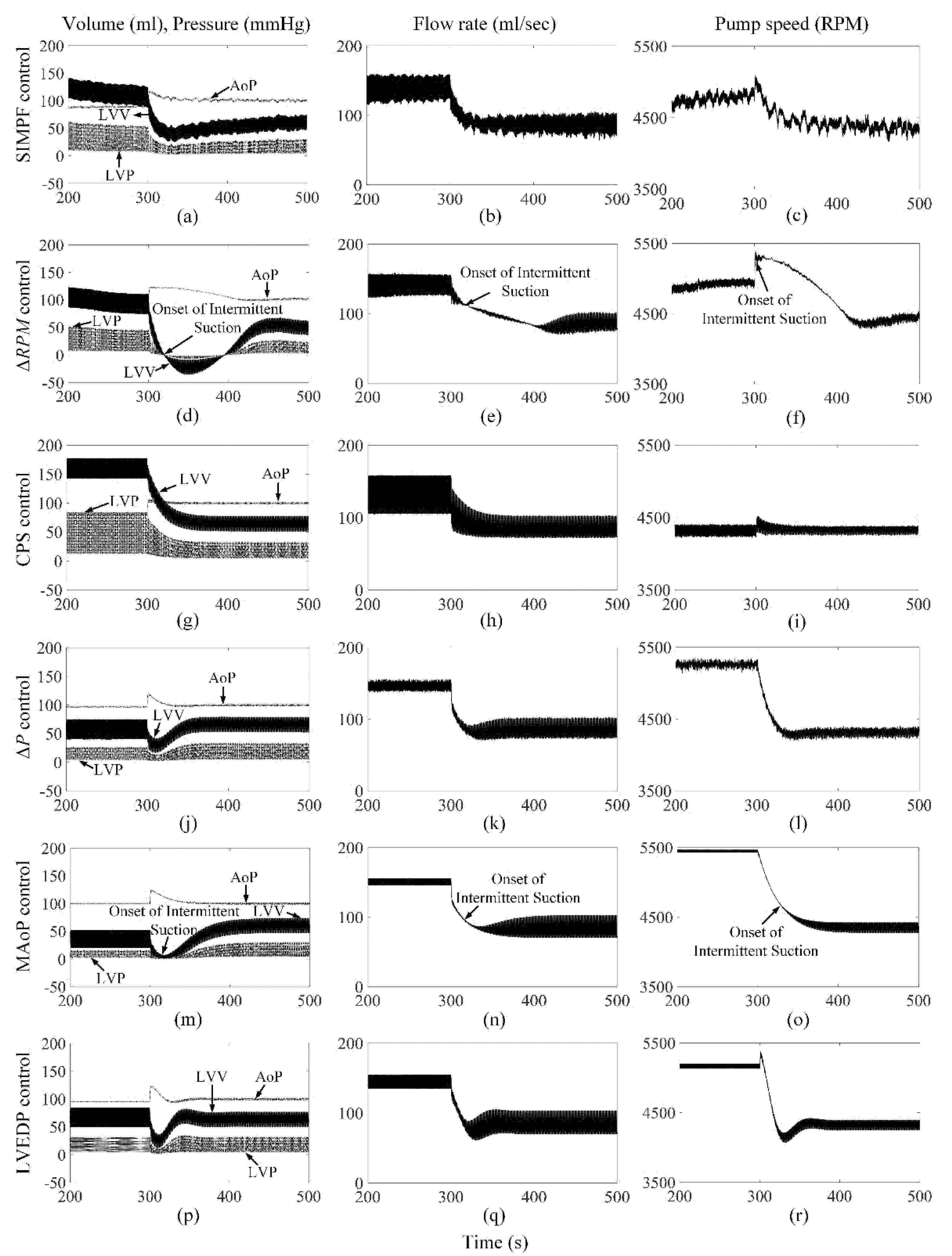
3. Results
3.1. The Proposed SIMPF Control Algorithm
3.2. ΔRPM Control Algorithm
3.3. CPS Control Algorithm
3.4. ΔP Control Algorithm
3.5. MAoP Control Algorithm
3.6. LVEDP Control Algorithm
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Metra, M.; Teerlink, J.R. Heart Failure. Lancet 2017, 390, 1981–1995. [Google Scholar] [CrossRef]
- Mancini, D.; Lietz, K. Selection of cardiac transplantation candidates in 2010. Circulation 2010, 122, 173–183. [Google Scholar] [CrossRef]
- Simaan, M.A.; Ferreira, A.; Chen, S.; Antaki, J.F.; Galati, D.G. A dynamical state space representation and performance analysis of a feedback-controlled rotary left ventricular assist device. IEEE Trans. Control Syst. Technol. 2009, 17, 15–28. [Google Scholar] [CrossRef]
- Slaughter, M.S.; Rogers, J.G.; Milano, C.A.; Russell, S.D.; Conte, J.V.; Feldman, D.; Sun, B.; Tatooles, A.J.; Delgado, R.M., 3rd; Long, J.W. Advanced heart failure treated with continuous-flow left ventricular assist device. N. Engl. J. Med. 2009, 361, 2241–2251. [Google Scholar] [CrossRef]
- Felix, S.E.A.; de Jonge, N.; Caliskan, K.; Birim, O.; Damman, K.; Kuijpers, M.; Tops, L.F.; Palmen, M.; Ramjankhan, F.Z. The role of long-term mechanical circulatory support in patients with advanced heart failure. Neth. Heart J. 2020, 28, 115–121. [Google Scholar] [CrossRef]
- Carpenter, B.A.; Gonzalez, C.J.; Jessen, S.L.; Moore, E.J.; Thrapp, A.N.; Weeks, B.R.; Clubb, F.J., Jr. A brief review of ventricular assist devices and a recommended protocol for pathology evaluations. Cardiovasc. Pathol. 2013, 22, 408–415. [Google Scholar] [CrossRef]
- Kirklin, J.K.; Pagani, F.D.; Kormos, R.L.; Stevenson, L.W.; Blume, E.D.; Myers, S.L.; Miller, M.A.; Baldwin, J.T.; Young, J.B.; Naftel, D.C. Eighth annual INTERMACS report: Special focus on framing the impact of adverse events. J. Heart Lung Transplant. 2017, 36, 1080–1086. [Google Scholar] [CrossRef]
- Gross, C.; Shima, H.; Schlöglhofer, T.; Dimitrov, K.; Maw, M.; Riebandt, J.; Wiedemann, D.; Zimpfer, D.; Moscato, F. Continuous LVAD monitoring reveals high suction rates in clinically stable outpatients. Artif. Organs 2020, 44, E251–E262. [Google Scholar] [CrossRef] [PubMed]
- Fukamachi, K.; Shiose, A.; Massiello, A.; Horvath, D.J.; Golding, L.A.R.; Lee, S.; Starling, R.C. Preload sensitivity in cardiac assist devices. Ann. Thorac. Surg. 2013, 95, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Giridharan, G.A.; Koenig, S.C.; Slaughter, M.S. Do axial-flow LVADs unload better than centrifugal-flow LVADs? ASAIO J. 2014, 60, 137–139. [Google Scholar] [CrossRef] [PubMed]
- Vollkron, M.; Voitl, P.; Ta, J.; Wieselthaler, G.; Shima, H. Suction events during left ventricular support and ventricular arrhythmias. J. Heart Lung Transplant. 2007, 26, 819–825. [Google Scholar] [CrossRef] [PubMed]
- Vollkron, M.; Schima, H.; Huber, L.; Benkowski, R.; Morello, G.; Wieselthaler, G. Development of a suction detection system for axial blood pumps. Artif. Organs 2004, 28, 709–716. [Google Scholar] [CrossRef]
- Karantonis, D.M.; Lovell, N.H.; Ayre, P.J.; Mason, D.G.; Cloherty, S.L. Identification and classification of physiologically significant pumping states in an implantable rotary blood pump. Artif. Organs 2006, 30, 671–679. [Google Scholar] [CrossRef] [PubMed]
- Karantonis, D.M.; Cloherty, S.L.; Lovell, N.; Mason, D.G.; Salamonsen, R.F.; Ayre, P. Noninvasive detection of suction in an implantable rotary blood pump using neural networks. Int. J. Comput. Intell. Appl. 2008, 7, 237–247. [Google Scholar] [CrossRef]
- Wang, Y.; Simaan, M.A. A suction detection system for rotary blood pumps based on the Lagrangian support vector machine algorithm. IEEE J. Biomed. Health Inform. 2013, 17, 654–663. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Katertsidis, N.S.; Karvounis, E.C.; Tsipouras, M.G.; Rigas, G.; Goletsis, Y.; Zielinski, K.; Fresiello, L.; Di Molfetta, A.; Ferrari, G.; et al. Modeling and simulation of speed selection on left ventricular assist devices. Comput. Biol. Med. 2014, 51, 128–139. [Google Scholar] [CrossRef]
- Gaddum, N.R.; Stevens, M.; Lim, E.; Fraser, J.; Lovell, N.; Mason, D.; Timms, D.; Salamonsen, R. Starling–Like Flow Control of a Left Ventricular Assist Device: In Vitro Validation. Artif. Organs 2014, 38, E46–E56. [Google Scholar] [CrossRef]
- Rüschen, D.; Prochazka, F.; Amacher, R.; Bergmann, L.; Leonhardt, S.; Walter, M. Minimizing left ventricular stroke work with iterative learning flow profile control of rotary blood pumps. Biomed. Signal Process. Control 2017, 31, 444–451. [Google Scholar] [CrossRef]
- Ochsner, G.; Wilhelm, M.J.; Amacher, R.; Petrou, A.; Cesarovic, N.; Staufert, S.; Röhrnbauer, B.; Maisano, F.; Hierold, C.; Meboldt, M.; et al. In vivo evaluation of physiologic control algorithms for left ventricular assist devices based on left ventricular volume or pressure. ASAIO J. 2017, 63, 568–577. [Google Scholar] [CrossRef]
- Gregory, S.D.; Stevens, M.C.; Pauls, J.P.; Schummy, E.; Diab, S.; Thomson, B.; Anderson, B.; Tansley, G.; Salamonsen, R.; Fraser, J.F.; et al. In vivo evaluation of active and passive physiological control systems for rotary left and right ventricular assist devices. Artif. Organs 2016, 40, 894–903. [Google Scholar] [CrossRef]
- Pauls, J.P.; Stevens, M.C.; Schummy, E.; Tansley, G.; Fraser, J.F.; Timms, D.; Gregory, S.D. In vitro comparison of active and passive physiological control systems for biventricular assist devices. Ann. Biomed. Eng. 2016, 44, 1370–1380. [Google Scholar] [CrossRef] [PubMed]
- Bakouri, M. Physiological control law for rotary blood pumps with full-state feedback method. Appl. Sci. 2019, 9, 4593. [Google Scholar] [CrossRef]
- Arndt, A.; Nüsser, P.; Graichen, K.; Müller, J.; Lampe, B. Physiological control of a rotary blood pump with selectable therapeutic options: Control of pulsatility gradient. Artif. Organs 2008, 32, 761–771. [Google Scholar] [CrossRef] [PubMed]
- AlOmari, A.H.; Savkin, A.V.; Karantonis, D.M.; Lim, E.; Lovell, N.H. Non-invasive estimation of pulsatile flow and differential pressure in an implantable rotary blood pump for heart failure patients. Physiol. Meas. 2009, 30, 371–386. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.; Boston, J.R.; Antaki, J.F. A control system for rotary blood pumps based on suction detection. IEEE Trans. Biomed. Eng. 2009, 56, 656–665. [Google Scholar] [CrossRef]
- Wang, Y.; Koenig, S.C.; Wu, Z.J.; Slaughter, M.S.; Giridharan, G.A. Sensorless Physiologic Control, Suction prevention, and Flow Balancing Algorithm for Rotary Biventricular Assist Devices. IEEE Trans. Control Syst. Technol. 2019, 27, 717–729. [Google Scholar] [CrossRef]
- Meki, M.; Wang, Y.; Sethu, P.; Ghazal, M.; El-Baz, A.; Giridharan, G. A sensorless rotational speed-based control system for continuous flow left ventricular assist devices. IEEE Trans. Biomed. Eng. 2019, 67, 1050–1060. [Google Scholar] [CrossRef]
- Liang, L.; Meki, M.; Wang, W.; Sethu, P.; El-Baz, A.; Giridharan, G.A.; Wang, Y. A suction index based control system for rotary blood pumps. Biomed. Signal Process. Control 2020, 62, 102057. [Google Scholar] [CrossRef]
- Guruprasad, G.A.; Skliar, M. Physiological control of blood pumps using intrinsic pump parameters: A computer simulation study. Artif. Organs 2006, 30, 301–307. [Google Scholar]
- Wu, Y.; Allaire, P.E.; Tao, G.; Olsen, D. Modeling, estimation, and control of human circulatory system with a left ventricular assist device. IEEE Trans. Control Syst. Technol. 2007, 15, 754–767. [Google Scholar] [CrossRef]
- Bullister, E.; Reich, S.; Sluetz, J. Physiologic control algorithms for rotary blood pumps using pressure sensor input. Artif. Organs 2002, 26, 931–938. [Google Scholar] [CrossRef] [PubMed]
- Demirozu, Z.T.; Arat, N.; Kucukaksu, D.S. Fine-tuning management of the Heart Assist 5 left ventricular assist device with two- and three-dimensional echocardiography. Cardiovasc. J. Afr. 2016, 27, 208–212. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ising, M.; Warren, S.; Sobieski, M.A.; Slaughter, M.S.; Koenig, S.C.; Giridharan, G.A. Flow modulation algorithms for continuous flow left ventricular assist devices to increase vascular pulsatility: A computer simulation study. Cardiovasc. Eng. Technol. 2011, 2, 90–100. [Google Scholar] [CrossRef]
- Soucy, K.G.; Koenig, S.C.; Sobieski, M.A.; Slaughter, M.S.; Giridharan, G.A. Fault detection in rotary blood pumps using motor speed response. ASAIO J. 2013, 59, 410–419. [Google Scholar] [CrossRef]
- Choi, S.; Boston, J.R.; Thomas, D.; Antaki, J.F. Modeling and identification of an axial flow blood pump. In Proceedings of the 1997 American Control Conference (ACC), Albuquerque, NM, USA, 6 June 1997; pp. 3714–3715. [Google Scholar]
- Pillay, P.; Krishnan, R. Modeling, simulation and analysis of permanent-magnet motor drives, part II: The brushless DC motor drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar] [CrossRef]
- Petrou, A.; Kuster, D.; Lee, J.; Meboldt, M.; Daners, M.S. Comparison of flow estimators for rotary blood pumps: An in vitro and in vivo study. Ann. Biomed. Eng. 2018, 46, 2123–2134. [Google Scholar] [CrossRef]
- Giridharan, G.A.; Skliar, M.; Olsen, D.B.; Pantalos, G.M. Modeling and control of a brushless DC axial flow ventricular assist device. ASAIO J. 2002, 48, 272–289. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Academic Press: New York, NY, USA, 1970; pp. 277–281. [Google Scholar]
- Picard, J. Efficiency of the extended Kalman filter for nonlinear systems with small noise. SIAM J. Appl. Math. 1991, 51, 843–885. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Orfanidis, S.J. Introduction to Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1996; pp. 427–462. [Google Scholar]
- Sen, A.; Larson, J.S.; Kashani, K.B.; Libricz, S.L.; Patel, B.M.; Guru, P.K.; Alwardt, C.M.; Pajaro, O.; Farmer, J.C. Mechanical circulatory assist devices: A primer for critical care and emergency physicians. Crit. Care 2016, 20, 1–20. [Google Scholar] [CrossRef]




| CO (L/min) | AoP (mmHg) | Min LVP (mmHg) | LVV (mL) | Mean PS (RPM) | Suction | |
|---|---|---|---|---|---|---|
| Healthy heart without LVAD support | ||||||
| Rest | 5.0 | 122/80 | 2.7 | 43/106 | N/A | No |
| Exercise | 8.6 | 121/74 | 2.8 | 42/114 | N/A | No |
| HF without LVAD support | ||||||
| Rest | 3.8 | 97/63 | 15.5 | 181/229 | N/A | No |
| Exercise | 6.8 | 95/58 | 15.4 | 178/234 | N/A | No |
| HF with AFP support at rest | ||||||
| SIMPF control 1 | 4.9 | 102/97 | 4.7 | 54/82 | 10,365 | No |
| SIMPF control 2 | 5.0 | 103/98 | 4.4 | 49/77 | 10,441 | No |
| ΔRPM control | 5.1 | 104/101 | 3.3 | 35/62 | 10,717 | No |
| CPS control | 5.0 | 103/97 | 4.4 | 49/78 | 10,448 | No |
| ΔP control | 5.0 | 103/97 | 4.4 | 50/78 | 10,447 | No |
| MAoP control | 5.0 | 103/99 | 4.1 | 46/74 | 10,506 | No |
| LVEDP control | 5.0 | 103/98 | 4.4 | 49/77 | 10,449 | No |
| HF with AFP support at exercise | ||||||
| SIMPF control 1 | 8.1 | 94/89 | 6.7 | 75/106 | 10,505 | No |
| SIMPF control 2 | 8.2 | 95/91 | 6.1 | 68/98 | 10,653 | No |
| ΔRPM control | 8.5 | 97/94 | 4.8 | 51/80 | 11,000 | No |
| CPS control | 8.1 | 94/88 | 7.0 | 79/109 | 10,450 | No |
| ΔP control | 8.7 | 99/96 | 3.5 | 36/64 | 11,276 | No |
| MAoP control | 9.0 | 101/99 | 2.2 | 20/47 | 11,590 | No |
| LVEDP control | 8.5 | 98/94 | 4.5 | 48/77 | 11,037 | No |
| HF with AFP support during 8-fold increase in PVR at rest | ||||||
| SIMPF control 1 | 4.3 | 90/85 | 1.2 | 46/68 | 9712 | No |
| SIMPF control 2 | 4.3 | 90/86 | 1.1 | 42/64 | 9800 | No |
| ΔRPM control | 4.4 | 90/87 | 0.8 | 37/58 | 9900 | IS |
| CPS control | 4.6 | 94/92 | 0.5 | 14/29 | 10,448 | IS |
| ΔP control | 4.6 | 93/91 | 0.6 | 17/34 | 10,355 | IS |
| MAoP control | 5.0 | 100/100 | −1.8 | −2/−1 | 11,065 | CS |
| LVEDP control | 4.2 | 89/84 | 2.3 | 54/77 | 9547 | No |
| HF with AFP support during 8-fold increase in PVR at exercise | ||||||
| SIMPF control 1 | 7.1 | 83/78 | 2.7 | 65/90 | 9867 | No |
| SIMPF control 2 | 7.2 | 84/79 | 2.3 | 58/83 | 10,013 | No |
| ΔRPM control | 7.3 | 85/81 | 1.4 | 51/75 | 10,176 | No |
| CPS control | 7.5 | 86/83 | 2.2 | 38/60 | 10,450 | No |
| ΔP control | 8.1 | 92/90 | 0.5 | 13/26 | 11,149 | IS |
| MAoP control | 8.9 | 100/100 | −5.1 | −13/−7 | 11,950 | CS |
| LVEDP control | 7.3 | 84/80 | 1.7 | 53/77 | 10,125 | No |
| CO (L/min) | AoP (mmHg) | Min LVP (mmHg) | LVV (mL) | Mean PS (RPM) | Suction | |
|---|---|---|---|---|---|---|
| Healthy heart without LVAD support | ||||||
| Rest | 5.0 | 122/80 | 2.7 | 43/106 | N/A | No |
| Exercise | 8.6 | 121/74 | 2.8 | 42/114 | N/A | No |
| HF without LVAD support | ||||||
| Rest | 3.8 | 97/63 | 15.5 | 181/229 | N/A | No |
| Exercise | 6.8 | 95/58 | 15.4 | 178/234 | N/A | No |
| HF with DP2 support at rest | ||||||
| SIMPF control 1 | 5.0 | 102/98 | 4.2 | 50/76 | 4337 | No |
| SIMPF control 2 | 5.0 | 103/100 | 3.0 | 38/63 | 4419 | No |
| ΔRPM control | 5.1 | 104/101 | 3.2 | 35/60 | 4385 | No |
| CPS control | 5.0 | 102/98 | 4.5 | 51/77 | 4336 | No |
| ΔP control | 5.0 | 101/98 | 4.6 | 53/78 | 4326 | No |
| MAoP control | 5.0 | 102/99 | 4.2 | 47/74 | 4363 | No |
| LVEDP control | 5.0 | 102/98 | 4.5 | 51/77 | 4339 | No |
| HF with DP2 support at exercise | ||||||
| SIMPF control 1 | 8.0 | 92/89 | 7.4 | 85/112 | 4856 | No |
| SIMPF control 2 | 8.3 | 94/92 | 5.8 | 66/93 | 5023 | No |
| ΔRPM control | 8.1 | 92/90 | 6.9 | 78/105 | 4957 | No |
| CPS control | 7.3 | 84/80 | 12.0 | 142/169 | 4337 | No |
| ΔP control | 8.7 | 98/96 | 3.8 | 40/67 | 5268 | No |
| MAoP control | 9.0 | 101/100 | 2.3 | 21/47 | 5453 | No |
| LVEDP control | 8.5 | 96/94 | 4.6 | 50/77 | 5173 | No |
| HF with DP2 support during 8-fold increase in PVR at rest | ||||||
| SIMPF control 1 | 4.3 | 89/86 | 1.0 | 41/62 | 4048 | No |
| SIMPF control 2 | 4.4 | 91/88 | 0.5 | 32/51 | 4104 | IS |
| ΔRPM control | 4.4 | 90/87 | −0.4 | 36/56 | 4067 | IS |
| CPS control | 4.7 | 95/93 | 0.3 | 11/24 | 4336 | CS |
| ΔP control | 4.6 | 93/91 | 0.6 | 18/34 | 4243 | IS |
| MAoP control | 5.0 | 100/100 | −1.8 | −3/−1 | 4566 | CS |
| LVEDP control | 4.2 | 88/84 | 2.4 | 56/77 | 3911 | No |
| HF with DP2 support during 8-fold increase in PVR at exercise | ||||||
| SIMPF control 1 | 7.1 | 81/78 | 3.0 | 70/92 | 4462 | No |
| SIMPF control 2 | 7.3 | 83/81 | 2.0 | 54/76 | 4616 | No |
| ΔRPM control | 6.9 | 79/76 | 1.5 | 82/105 | 4340 | No |
| CPS control | 6.9 | 79/76 | 5.9 | 83/106 | 4337 | No |
| ΔP control | 8.1 | 91/90 | 0.5 | 15/28 | 5101 | IS |
| MAoP control | 8.9 | 100/100 | −5.1 | −13/−8 | 5572 | CS |
| LVEDP control | 7.3 | 83/81 | 1.5 | 55/77 | 4604 | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Qin, K.; El-Baz, A.S.; Roussel, T.J.; Sethu, P.; Giridharan, G.A.; Wang, Y. A Flow Sensor-Based Suction-Index Control Strategy for Rotary Left Ventricular Assist Devices. Sensors 2021, 21, 6890. https://doi.org/10.3390/s21206890
Liang L, Qin K, El-Baz AS, Roussel TJ, Sethu P, Giridharan GA, Wang Y. A Flow Sensor-Based Suction-Index Control Strategy for Rotary Left Ventricular Assist Devices. Sensors. 2021; 21(20):6890. https://doi.org/10.3390/s21206890
Chicago/Turabian StyleLiang, Lixue, Kairong Qin, Ayman S. El-Baz, Thomas J. Roussel, Palaniappan Sethu, Guruprasad A. Giridharan, and Yu Wang. 2021. "A Flow Sensor-Based Suction-Index Control Strategy for Rotary Left Ventricular Assist Devices" Sensors 21, no. 20: 6890. https://doi.org/10.3390/s21206890
APA StyleLiang, L., Qin, K., El-Baz, A. S., Roussel, T. J., Sethu, P., Giridharan, G. A., & Wang, Y. (2021). A Flow Sensor-Based Suction-Index Control Strategy for Rotary Left Ventricular Assist Devices. Sensors, 21(20), 6890. https://doi.org/10.3390/s21206890








