Secure Outsourcing of Matrix Determinant Computation under the Malicious Cloud
Abstract
:1. Introduction
- We propose a secure outsourcing algorithm for the matrix determinant computation under the malicious cloud model, which can not only ensure the confidentiality of matrix, but also detect the forged results returned from the malicious cloud. We use the permutation, mix-row/mix-column, and split operations in our algorithm to protect privacy, which achieves the currently known lowest computation cost.
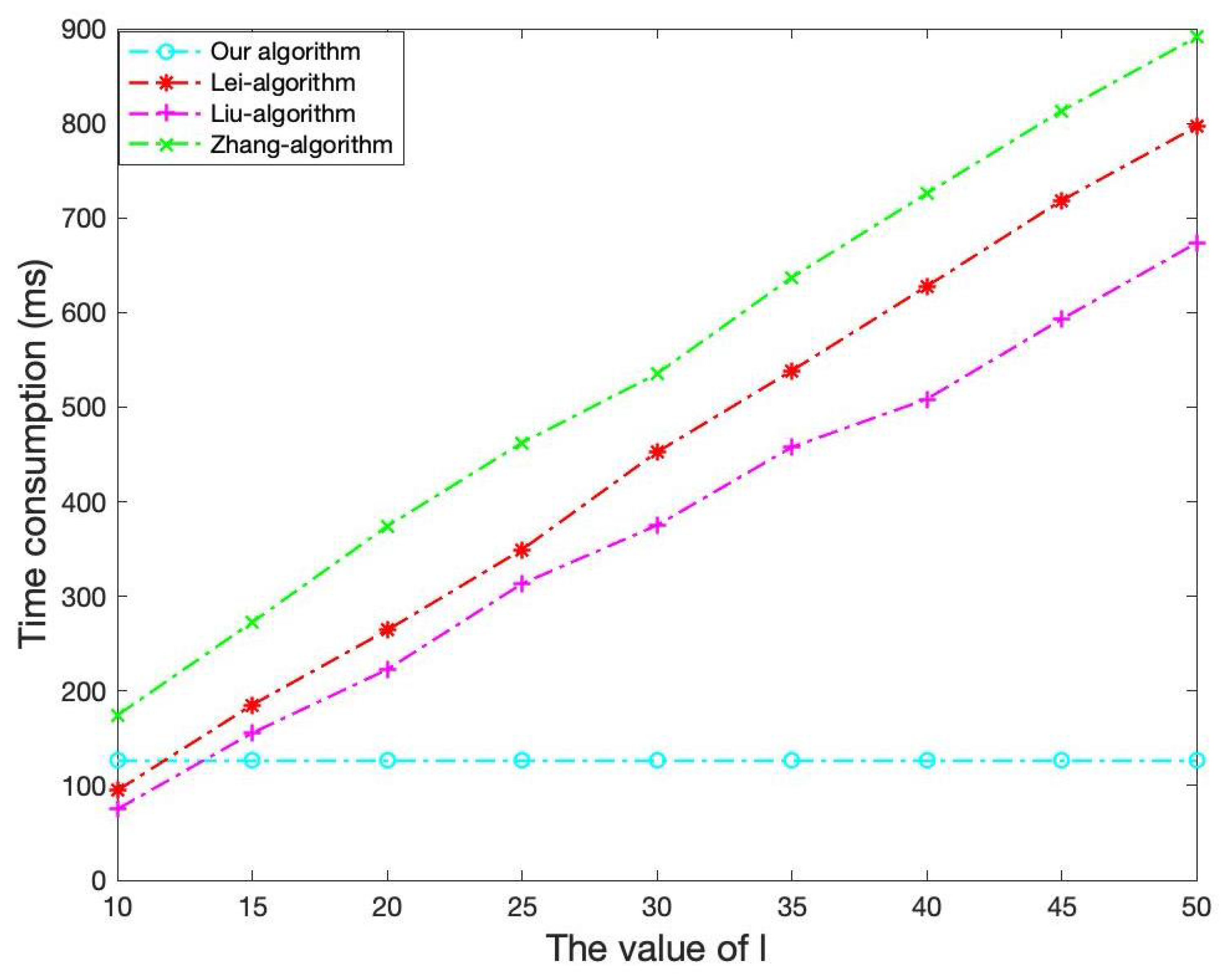
- We propose a one-round verification method in the proposed algorithm, which achieves a high cheating detectability. The malicious forged results can only escape our local verification with the probability of , given a matrix of dimensions. In all the previous algorithms, the detectability of malicious forged results depends on the rounds of verification, and to achieve a high cheating detectability, multiple rounds of verification are required, which also brings high computational burden to the client. In the previous three algorithms [4,5,6], the succeeding probability of malicious forged results is , where l is the number of verification rounds and recommended to be greater than 20.
- We conduct theoretical proofs of the correctness, efficiency, privacy protection, and cheating detectability for the proposed algorithm. Experimental results also demonstrate the superior efficiency of the proposed algorithm.
2. Related Work and Comparative Analysis
3. Preliminary
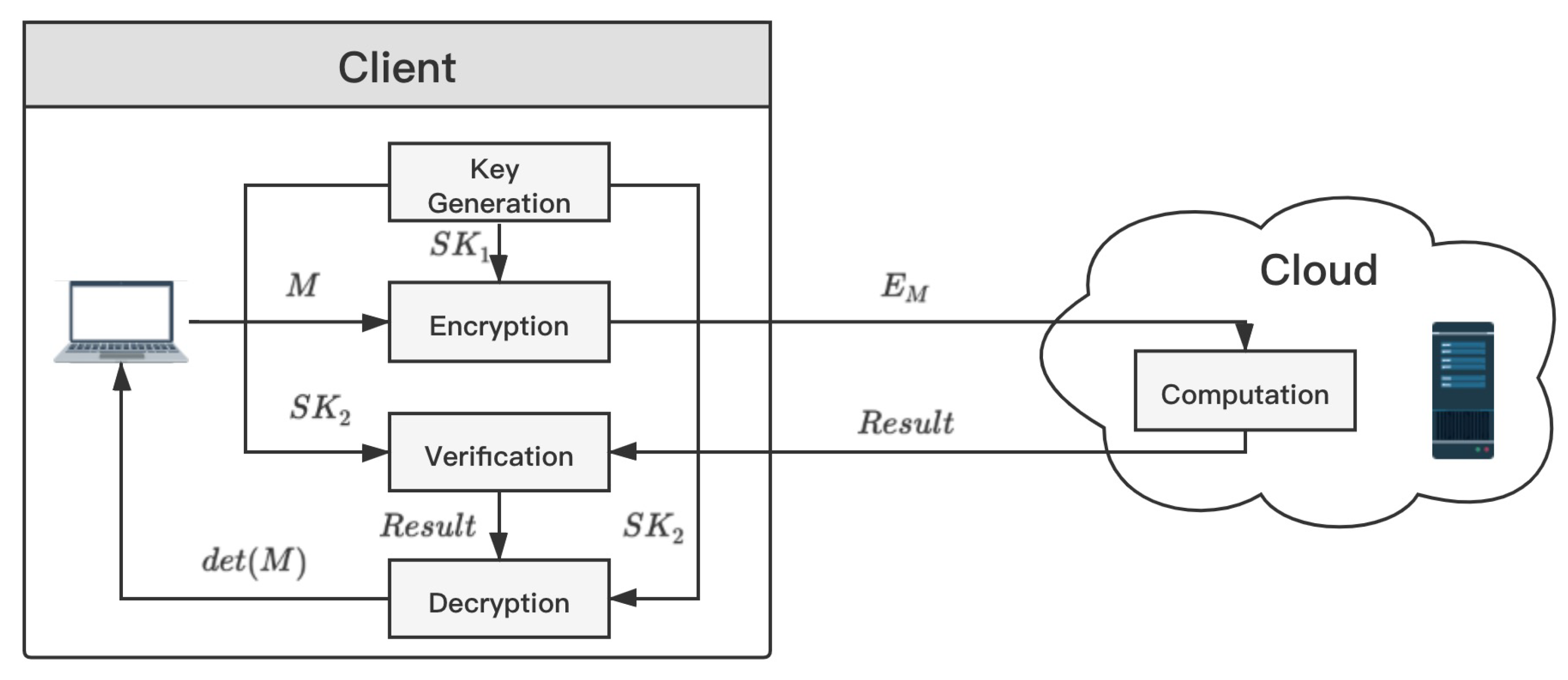
3.1. System Model
- KeyGen() : is a security parameter related to key generation. The generated key is used to encrypt the input data, and is used to verify and decrypt the returned results. Both and should be kept privately by the client C.
- Encrypt(x, ) : x is the input data. The client uses to encrypt the input x and gets encrypted data . is sent to the server S for computing.
- Compute(f, ) : f is a function given by the client. The server computes using the given function f and encrypted data .
- Verify(, ) : The client verifies the results returned from the cloud. If the is valid, the output of this function is Ture. Otherwise, the output is ⊥.
- Decrypt(, ) : The client uses the secret key to decrypt and obtains the result y.
3.2. Definitions of Correctness, Efficiency, and Security
4. Secure Outsourcing of Matrix Determinant
4.1. Key Generation
- The client needs to input a key space . Eight diagonal matrices are generated by selecting random nonzero values from . Then, the client picks 8 random parameters (lines 2 and 3 of Algorithm 1).
- The client computes by lines 4–6 of Algorithm 1. It is easy to see that in is the determinant of .
- The client computes by lines 7–14 of Algorithm 1.
| Algorithm 1 Procedure of Secret Key Generation |
|
4.2. Encryption
- While keeping the other rows, the client randomly splits the ith and jth rows of to get four matrices . (lines 2–3 of Algorithm 2).
- The client computes by lines 4–7 of Algorithm 2.
| Algorithm 2 Procedure of Encryption |
|
4.3. Computations of Server
- After receiving the matrices, the cloud computes the LU decomposition for , , , and to get , , , where is the LU decomposition function (lines 2–5 of Algorithm 3).
- The cloud computes determinants of and obtains . (lines 6–9 of Algorithm 3).
- The cloud returns to the client.
| Algorithm 3 Procedure of Computation |
|
4.4. Verification
- The client initializes the flag to true.
- The verifications in lines 6–17 verify all the diagonal elements in at least once. If any verification is invalid, the function returns ⊥.
- If all the verifications are valid, the function returns true.
| Algorithm 4 Procedure of Verification |
|
4.5. Decryption
- The client computes the result (Algorithm 5) .
| Algorithm 5 Procedure of Decryption |
|
5. Correctness, Security, and Computational Complexity Analysis
5.1. Correctness
5.2. Computational Complexity
5.3. Security
5.3.1. Privacy against Passive Attacks
5.3.2. Security against Active Attacks
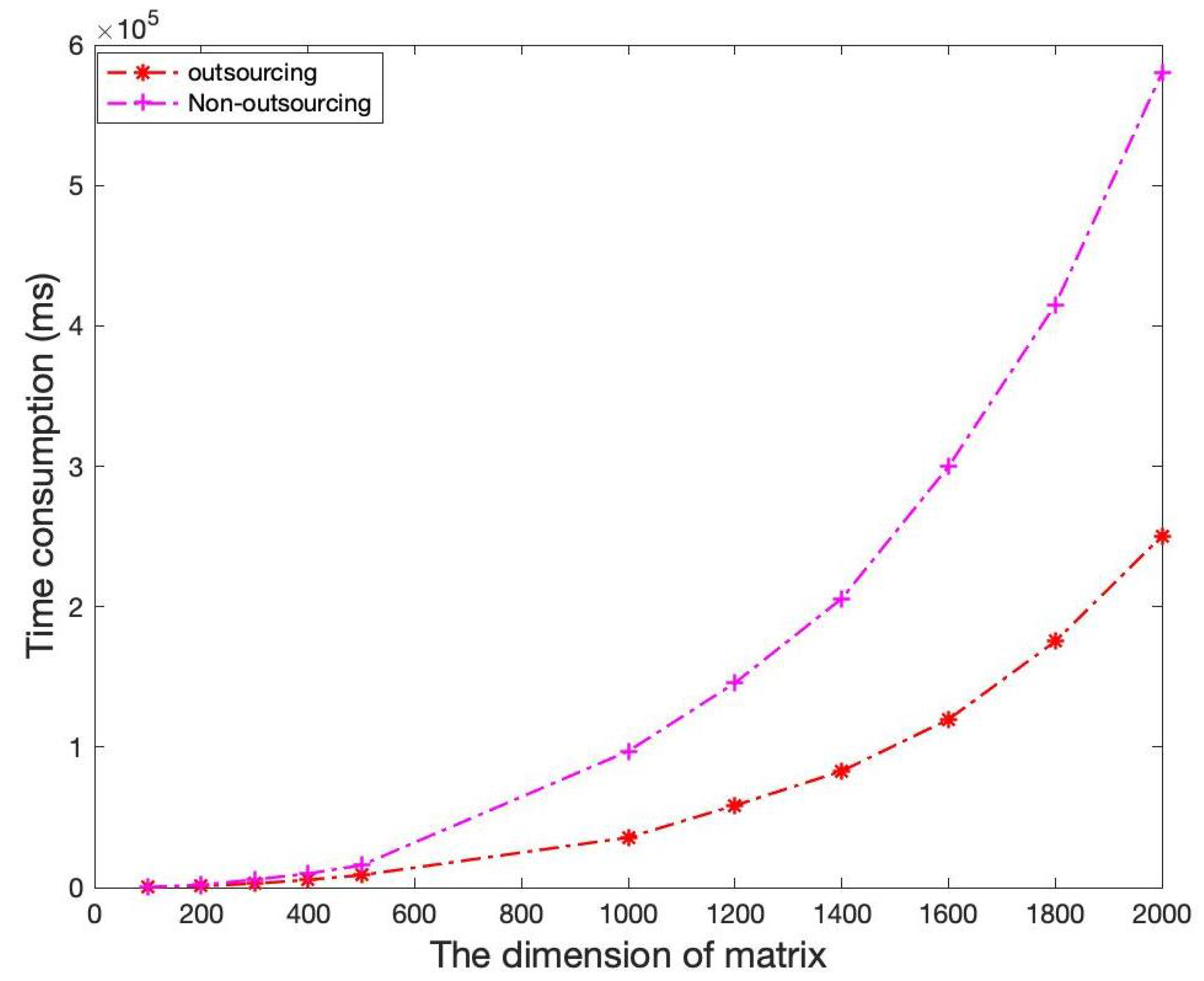
6. Performance Evaluation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brunette, G.; Mogull, R. Security guidance for critical areas of focus in cloud computing v2.1. Cloud Secur. Alliance 2017, 1–76. Available online: http://www.cloudsecurityalliance.org/csaguide.pdf (accessed on 4 September 2021).
- Bolton, T.; Dargahi, T.; Belguith, S.; Al-Rakhami, M.S.; Sodhro, A.H. On the security and privacy challenges of virtual assistants. Sensors 2021, 21, 2312. [Google Scholar] [CrossRef] [PubMed]
- Goldreich, O.; Micali, S.; Wigderson, A. How to play any mental game, or a completeness theorem for protocols with honest majority. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali; ACM: New York, NY, USA, 2019; pp. 307–328. [Google Scholar]
- Zhang, S.; Tian, C.; Zhang, H.; Yu, J.; Li, F. Practical and Secure Outsourcing Algorithms of Matrix Operations Based on a Novel Matrix Encryption Method. IEEE Access 2019, 7, 53823–53838. [Google Scholar] [CrossRef]
- Lei, X.; Liao, X.; Huang, T.; Li, H. Cloud computing service: The caseof large matrix determinant computation. IEEE Trans. Serv. Comput. 2014, 8, 688–700. [Google Scholar] [CrossRef]
- Liu, J.; Bi, J.; Li, M. Secure outsourcing of large matrix determinant computation. Front. Comput. Sci. 2020, 14, 1–12. [Google Scholar] [CrossRef]
- Nykvist, C.; Larsson, M.; Sodhro, A.H.; Gurtov, A. A lightweight portable intrusion detection communication system for auditing applications. Int. J. Commun. Syst. 2020, 33, e4327. [Google Scholar] [CrossRef]
- Kayes, A.; Kalaria, R.; Sarker, I.H.; Islam, M.; Watters, P.A.; Ng, A.; Hammoudeh, M.; Badsha, S.; Kumara, I. A survey of context-aware access control mechanisms for cloud and fog networks: Taxonomy and open research issues. Sensors 2020, 20, 2464. [Google Scholar] [CrossRef]
- Brakerski, Z. Fully homomorphic encryptionwithout modulus switching from classical GapSVP. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2012; pp. 868–886. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast fully homomorphic encryption over the torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar] [CrossRef]
- Shen, T.; Wang, F.; Chen, K.; Wang, K.; Li, B. Efficient leveled (multi) identity-based fully homomorphic encryption schemes. IEEE Access 2019, 7, 79299–79310. [Google Scholar] [CrossRef]
- Da Silva, D.W.; de Araujo, C.P.; Chow, E.; Barillas, B.S. A new approach towards fully homomorphic encryption over geometric algebra. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 0241–0249. [Google Scholar]
- Li, J.; Yu, Q.; Zhang, Y.; Shen, J. Key-policy attribute-based encryption against continual auxiliary input leakage. Inf. Sci. 2019, 470, 175–188. [Google Scholar] [CrossRef]
- Waters, B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 53–70. [Google Scholar]
- Attrapadung, N. Unbounded dynamic predicate compositions in attribute-based encryption. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2019; pp. 34–67. [Google Scholar]
- Fu, A.; Li, S.; Yu, S.; Zhang, Y.; Sun, Y. Privacy-preserving composite modular exponentiation outsourcing with optimal checkability in single untrusted cloud server. J. Netw. Comput. Appl. 2018, 118, 102–112. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, R.; Xue, R. Secure outsourcing algorithms for composite modular exponentiation based on single untrusted cloud. Comput. J. 2020, 63, 1271. [Google Scholar] [CrossRef]
- Zhou, Q.; Tian, C.; Zhang, H.; Yu, J.; Li, F. How to securely outsource the extended euclidean algorithm for large-scale polynomials over finite fields. Inf. Sci. 2020, 512, 641–660. [Google Scholar] [CrossRef]
- Ren, Y.; Ding, N.; Wang, T.; Lu, H.; Gu, D. New algorithms for verifiable outsourcing of bilinear pairings. Sci. China Inf. Sci. 2016, 59, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; He, D.; Huang, X.; Xie, X.; Choo, K.K.R. Blockchain-based system for secure outsourcing of bilinear pairings. Inf. Sci. 2020, 527, 590–601. [Google Scholar] [CrossRef]
- Tong, L.; Yu, J.; Zhang, H. Secure Outsourcing Algorithm for Bilinear Pairings without Pre-Computation. In Proceedings of the 2019 IEEE Conference on Dependable and Secure Computing (DSC), Hangzhou, China, 18–20 November 2019; pp. 1–7. [Google Scholar]
- Song, M.; Sang, Y.; Zeng, Y.; Luo, S. Blockchain-Based Secure Outsourcing of Polynomial Multiplication and Its Application in Fully Homomorphic Encryption. Secur. Commun. Netw. 2021, 2021, 9962575. [Google Scholar]
- Zhang, Y.; Blanton, M. Efficient secure and verifiable outsourcing of matrix multiplications. In International Conference on Information Security; Springer: Berlin/Heidelberg, Germany, 2014; pp. 158–178. [Google Scholar]
- Kumar, M.; Mishra, V.; Shukla, A.; Singh, M.; Vardhan, M. A novel publicly delegable secure outsourcing algorithm for large-scale matrix multiplication. J. Intell. Fuzzy Syst. 2020, 38, 6445–6455. [Google Scholar] [CrossRef]
- Wang, S.; Huang, H. Secure outsourced computation of multiple matrix multiplication based on fully homomorphic encryption. KSII Trans. Internet Inf. Syst. (TIIS) 2019, 13, 5616–5630. [Google Scholar]
- Wu, Y.; Liao, Y.; Liang, Y.; Liu, Y. Secure and Efficient Protocol for Outsourcing Large-Scale Matrix Multiplication to the Cloud. IEEE Access 2020, 8, 227556–227565. [Google Scholar] [CrossRef]
- Duan, J.; Zhou, J.; Li, Y. Secure and verifiable outsourcing of nonnegative matrix factorization (NMF). In Proceedings of the 4th ACM Workshop on Information Hiding and Multimedia Security, Vigo, Spain, 20–22 June 2016; pp. 63–68. [Google Scholar]
- Liu, Z.; Li, B.; Han, Q. Secure and verifiable outsourcing protocol for non-negative matrix factorisation. Int. J. High Perform. Comput. Netw. 2018, 11, 14–23. [Google Scholar] [CrossRef]
- Fu, A.; Chen, Z.; Mu, Y.; Susilo, W.; Sun, Y.; Wu, J. Cloud-based outsourcing for enabling privacy-preserving large-scale non-negative matrix factorization. IEEE Trans. Serv. Comput. 2019. [Google Scholar] [CrossRef]
- Duan, J.; Zhou, J.; Li, Y. Secure and verifiable outsourcing of large-scale nonnegative matrix factorization (NMF). IEEE Trans. Serv. Comput. 2019. [Google Scholar] [CrossRef]
- Hu, C.; Alhothaily, A.; Alrawais, A.; Cheng, X.; Sturtivant, C.; Liu, H. A secure and verifiable outsourcing scheme for matrix inverse computation. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Pan, S.; Wang, Q.; Zheng, F.; Dong, J. Secure and efficient outsourcing of large-scale matrix inverse computation. In International Conference on Wireless Algorithms, Systems, and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 374–386. [Google Scholar]
- Chen, Z.; Fu, A.; Xiao, K.; Su, M.; Yu, Y.; Wang, Y. Secure and verifiable outsourcing of large-scale matrix inversion without precondition in cloud computing. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Pramkaew, C.; Ngamsuriyaroj, S. Lightweight scheme of secure outsourcing SVD of a large matrix on cloud. J. Inf. Secur. Appl. 2018, 41, 92–102. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Chen, R.; Peng, W. SHOSVD: Secure Outsourcing of High-Order Singular Value Decomposition. In Australasian Conference on Information Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2020; pp. 309–329. [Google Scholar]
- Kim, D.; Son, Y.; Kim, D.; Kim, A.; Hong, S.; Cheon, J.H. Privacy-preserving approximate GWAS computation based on homomorphic encryption. BMC Med. Genom. 2020, 13, 77. [Google Scholar] [CrossRef] [PubMed]
- Zong, H.; Huang, H.; Wang, S. Secure Outsourced Computation of Matrix Determinant Based on Fully Homomorphic Encryption. IEEE Access 2021, 9, 22651–22661. [Google Scholar] [CrossRef]
- Freivalds, R. Probabilistic Machines Can Use Less Running Time. In Proceedings of the IFIP Congress, Toronto, ON, Canada, 8–12 August 1977; Volume 839, p. 842. [Google Scholar]
- Chen, Y.; Nguyen, P.Q. Faster algorithms for approximate common divisors: Breaking fully-homomorphic-encryption challenges over the integers. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2012; pp. 502–519. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]

| Algorithm | Local Multiplications | Probability of Privacy Leakage | Probability of Cheating Success |
|---|---|---|---|
| Our algorithm | |||
| Lei’s algorithm [5] | |||
| Liu’s algorithm [6] | |||
| Zhang’s algorithm [4] |
| Symbol | Implication |
|---|---|
| A vector | |
| A full rank matrix | |
| The determinant of matrix | |
| Choose an element from set randomly | |
| Security parameter | |
| The probability that attacker A obtains the secret input x using data | |
| The probability that the client C detects the forged results using data | |
| The element in the ith row and jth column of matrix | |
| / | The ith row of matrix |
| / | The jth column of matrix |
| The transpose of | |
| The inner product of vector and vector | |
| The Low triangle and Up triangle decomposition of matrix |
| Function | Total | ||||
|---|---|---|---|---|---|
| Our algorithm | 1 | ||||
| Lei’s algorithm [5] | n | ||||
| Liu’s algorithm [6] | n | ||||
| Zhang’s algorithm [4] |
| Function | Total | ||||
|---|---|---|---|---|---|
| Our algorithm | 1 | ||||
| Lei’s algorithm [5] | 0 | 0 | |||
| Liu’s algorithm [6] | 0 | 0 | |||
| Zhang’s algorithm [4] | 0 |
| Function | |||||
|---|---|---|---|---|---|
| Our algorithm | |||||
| Lei’s algorithm [5] | |||||
| Liu’s algorithm [6] | |||||
| Zhang’s algorithm [4] |
| Attack | Our Algorithm | Liu’s Algorithm [6] | Lei’s Algorithm [5] | Zhang’s Algorithm [4] |
|---|---|---|---|---|
| Privacy Leakage | ||||
| Result cheating |
| Notations | Implication |
|---|---|
| The time consumption of nonoutsourcing scheme. | |
| The time consumption of cloud. | |
| The time consumption of client in key generation and encryption. | |
| The time consumption of client in decryption and verification. | |
| The time consumption of client. | |
| Acceleration ratio of client. |
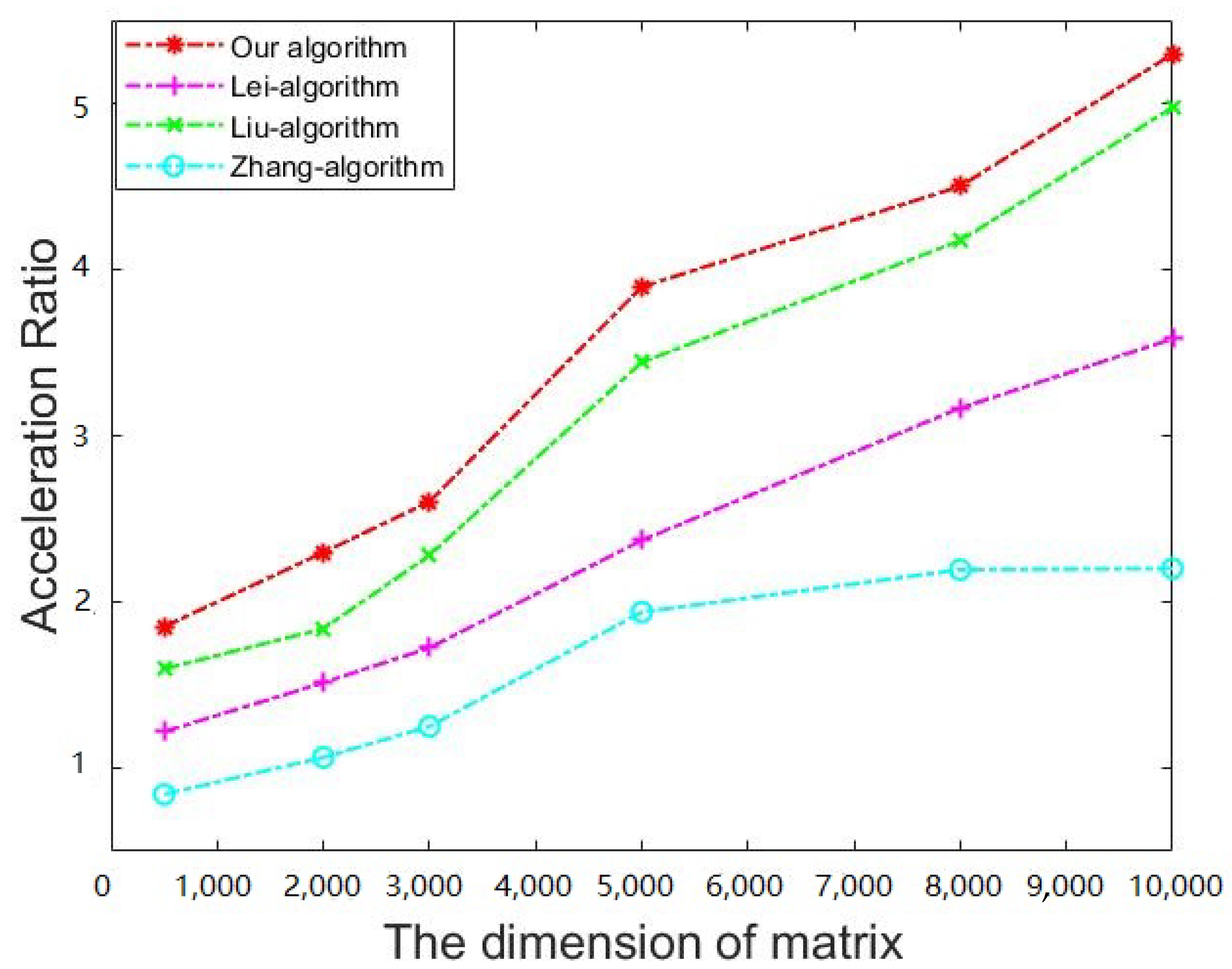
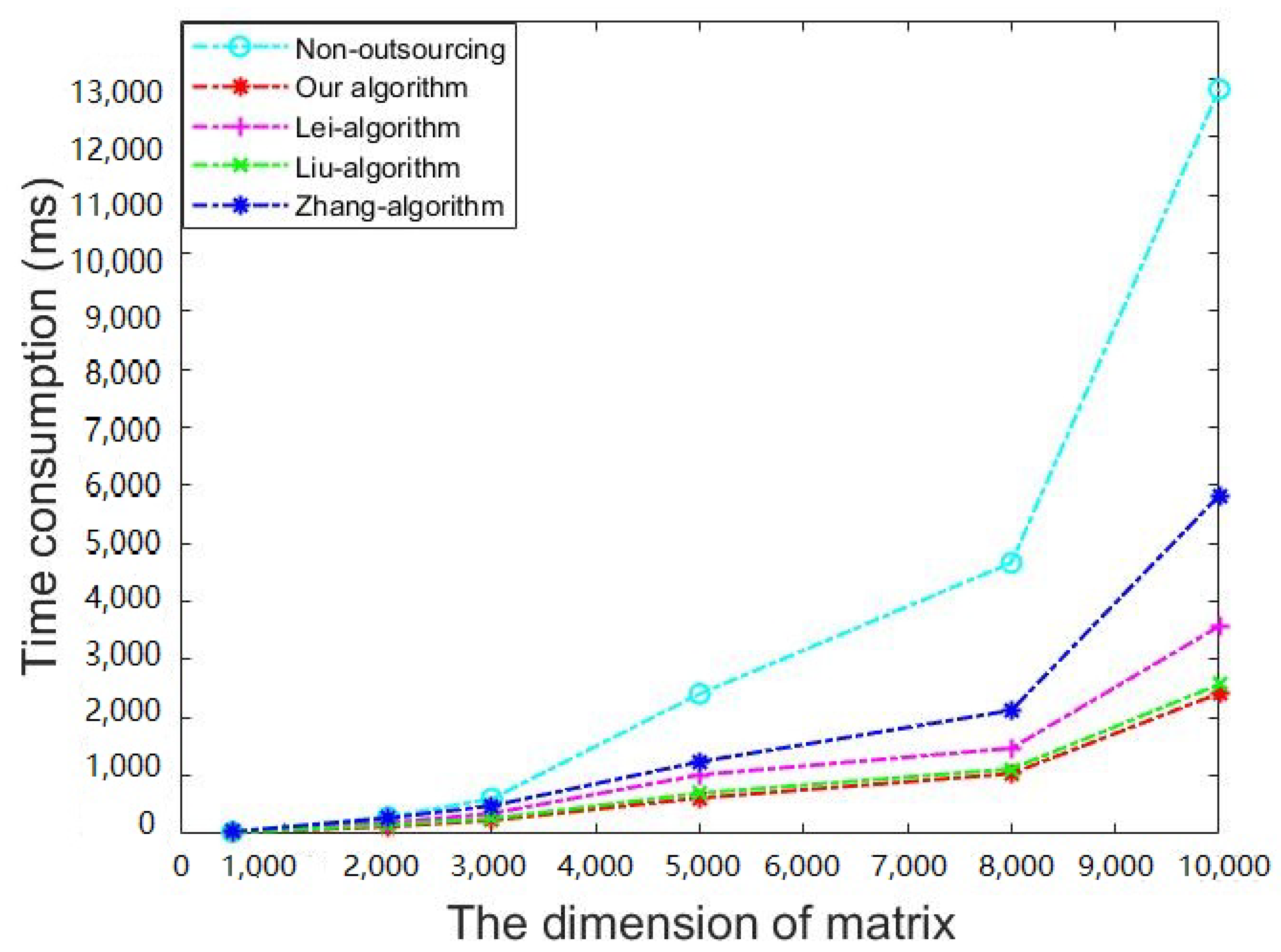
| Algorithm | Dimension | ||||||
|---|---|---|---|---|---|---|---|
| Our algorithm | 500 | 32.829 | 14.188 | 3.547 | 17.735 | 49.264 | 1.851 |
| 2000 | 290.013 | 94.517 | 31.670 | 126.187 | 352.725 | 2.298 | |
| 3000 | 606.768 | 191.122 | 41.954 | 233.078 | 903.288 | 2.603 | |
| 5000 | 2410.926 | 470.294 | 148.515 | 618.809 | 2982.729 | 3.896 | |
| 8000 | 4666.675 | 808.776 | 228.117 | 1036.893 | 6163.738 | 4.501 | |
| 10,000 | 12,818.648 | 1960.510 | 459.867 | 2420.337 | 15,895.125 | 5.296 | |
| Lei’s algorithm [5] | 500 | 32.829 | 1.747 | 25.184 | 26.931 | 45.775 | 1.219 |
| 2000 | 290.013 | 5.528 | 186.026 | 191.554 | 348.904 | 1.514 | |
| 3000 | 606.768 | 10.951 | 341.002 | 351.953 | 894.031 | 1.724 | |
| 5000 | 2410.926 | 42.309 | 974.528 | 1016.837 | 2767.491 | 2.371 | |
| 8000 | 4666.675 | 274.662 | 1198.869 | 1473.532 | 5495.207 | 3.167 | |
| 10,000 | 12,818.648 | 796.518 | 2779.116 | 3575.634 | 14,175.942 | 3.585 | |
| Liu’s algorithm [6] | 500 | 32.829 | 0.793 | 19.764 | 20.557 | 38.379 | 1.597 |
| 2000 | 290.013 | 4.923 | 152.771 | 157.694 | 311.684 | 1.839 | |
| 3000 | 606.768 | 7.595 | 258.414 | 266.009 | 894.031 | 2.281 | |
| 5000 | 2410.926 | 30.519 | 669.924 | 701.443 | 2531.673 | 3.442 | |
| 8000 | 4666.675 | 132.731 | 985.303 | 1118.034 | 4951.749 | 4.174 | |
| 10,000 | 12,818.648 | 551.634 | 2024.461 | 2576.095 | 13,667.593 | 4.976 | |
| Zhang’s algorithm [4] | 500 | 32.829 | 18.475 | 20.498 | 38.973 | 37.517 | 0.842 |
| 2000 | 290.013 | 104.772 | 167.538 | 272.310 | 324.941 | 1.065 | |
| 3000 | 606.768 | 207.462 | 277.737 | 485.199 | 875.963 | 1.251 | |
| 5000 | 2410.926 | 522.743 | 720.335 | 1243.078 | 2539.492 | 1.939 | |
| 8000 | 4666.675 | 983.769 | 1142.779 | 2126.548 | 5027.820 | 2.194 | |
| 10,000 | 12,818.648 | 2647.539 | 3176.957 | 5824.496 | 12,741.742 | 2.201 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Sang, Y. Secure Outsourcing of Matrix Determinant Computation under the Malicious Cloud. Sensors 2021, 21, 6821. https://doi.org/10.3390/s21206821
Song M, Sang Y. Secure Outsourcing of Matrix Determinant Computation under the Malicious Cloud. Sensors. 2021; 21(20):6821. https://doi.org/10.3390/s21206821
Chicago/Turabian StyleSong, Mingyang, and Yingpeng Sang. 2021. "Secure Outsourcing of Matrix Determinant Computation under the Malicious Cloud" Sensors 21, no. 20: 6821. https://doi.org/10.3390/s21206821
APA StyleSong, M., & Sang, Y. (2021). Secure Outsourcing of Matrix Determinant Computation under the Malicious Cloud. Sensors, 21(20), 6821. https://doi.org/10.3390/s21206821






