Dynamics and Control of a Magnetic Transducer Array Using Multi-Physics Models and Artificial Neural Networks
Abstract
:1. Introduction
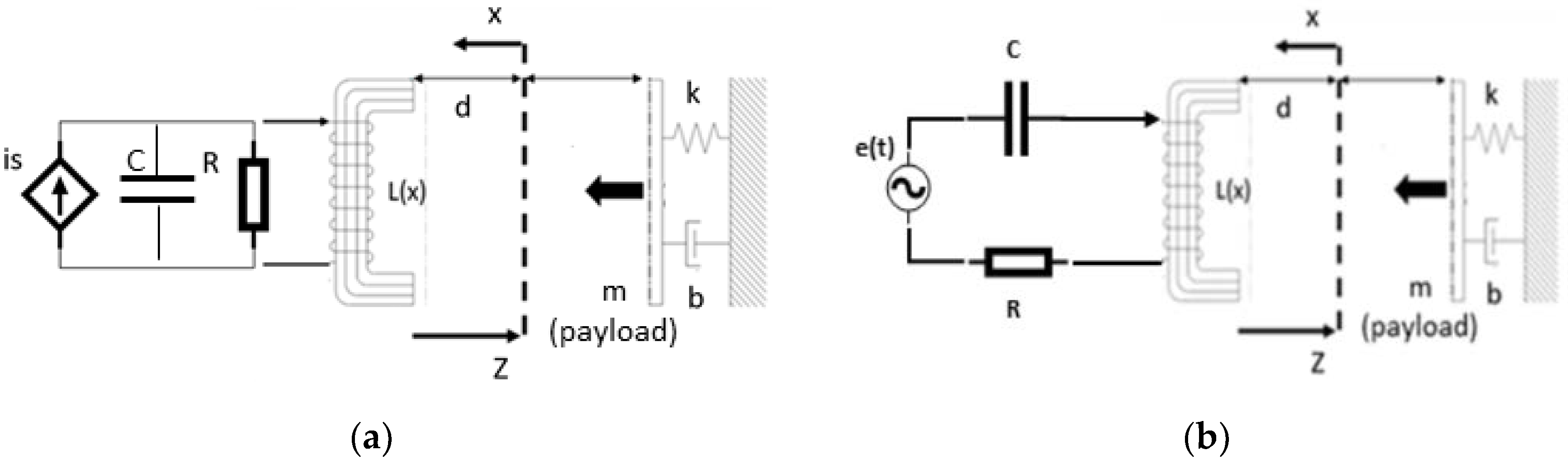
2. The Electromechanical Oscillator
2.1. Lagrangian Formulation of the System
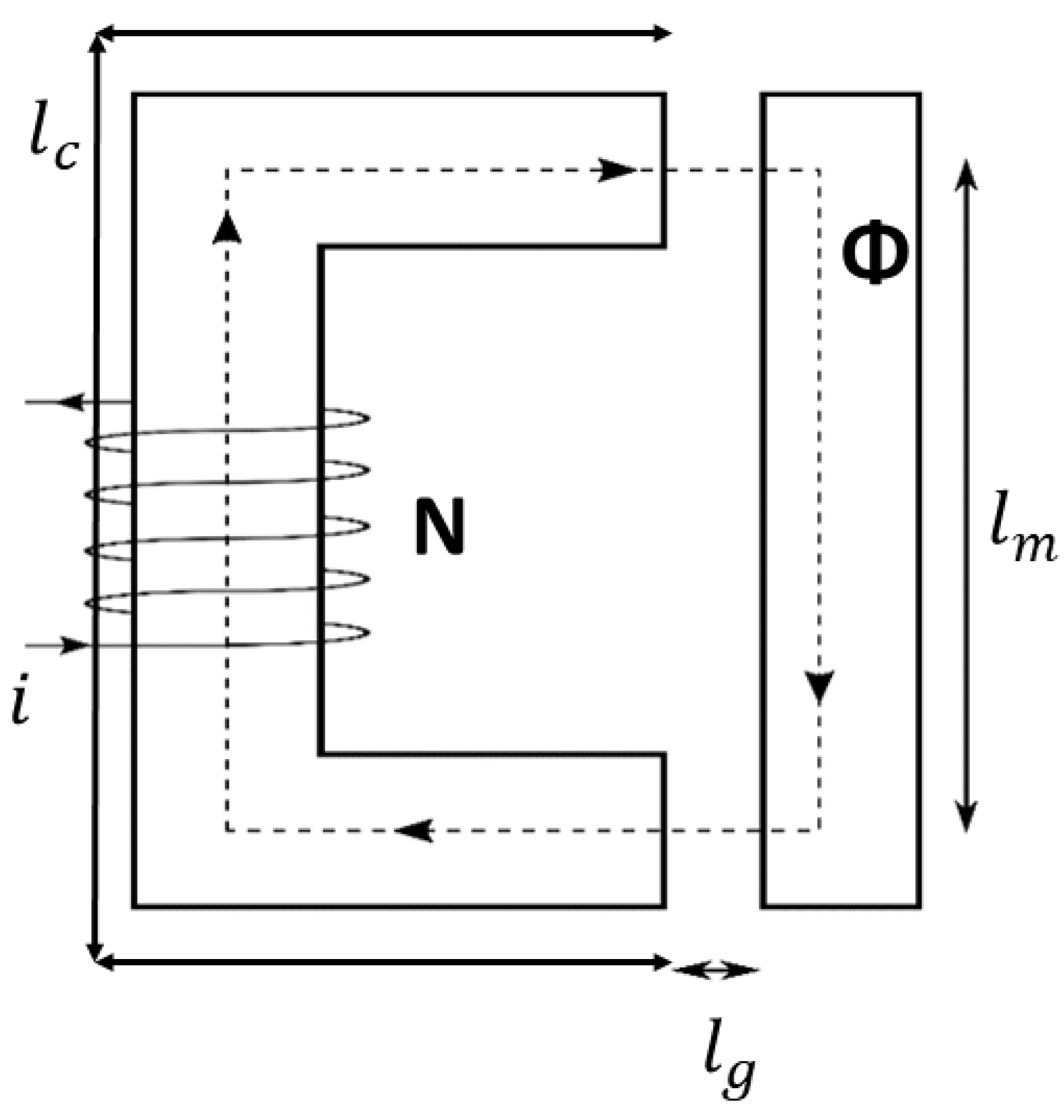
2.2. Electromagnetic Subsystem
2.3. Electromechanical System Simulation
- Matlab Simulink Simscape;
- Matlab Simulink;
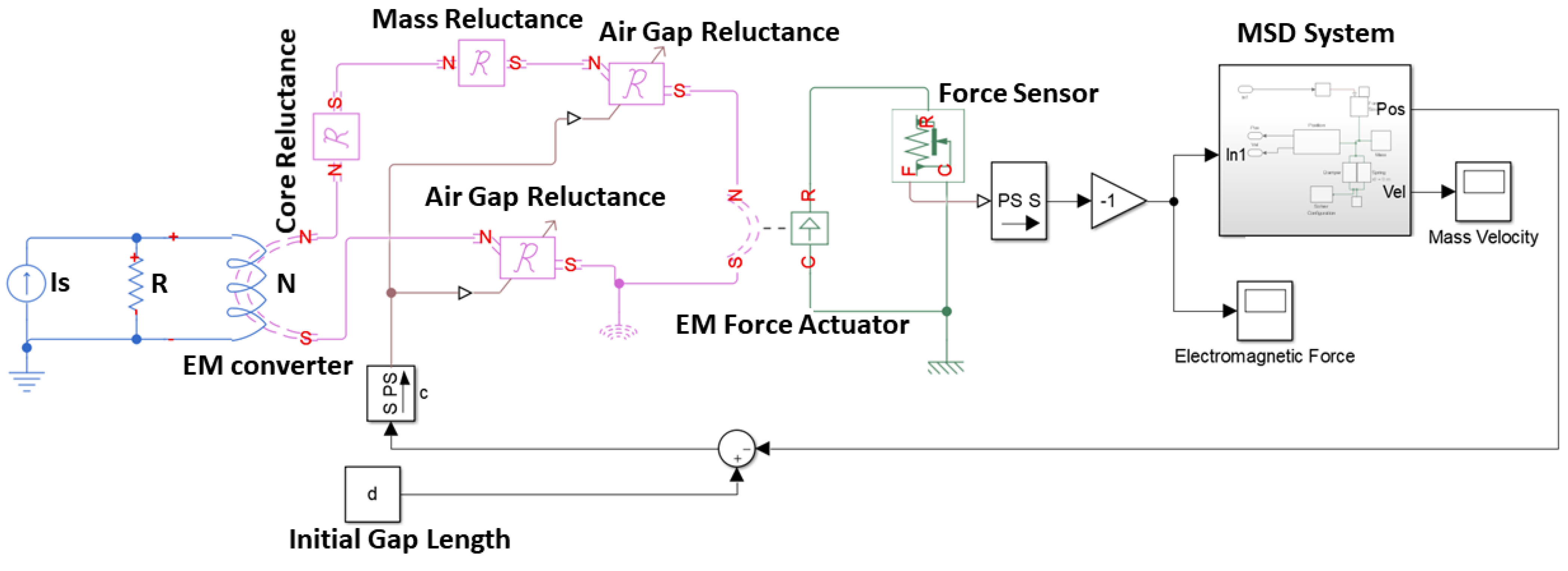
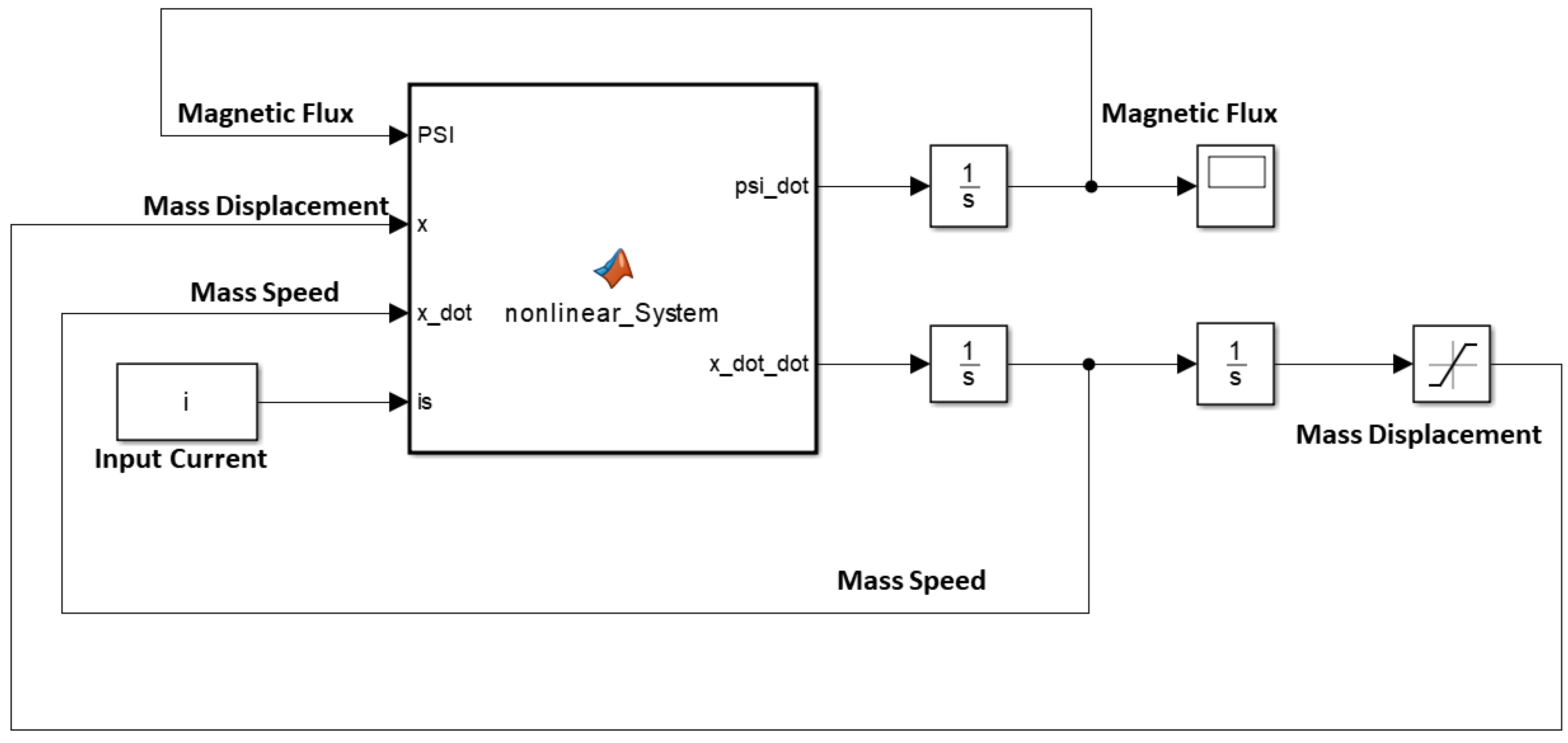
2.3.1. Simscape Implementation
2.3.2. Simulink Implementation
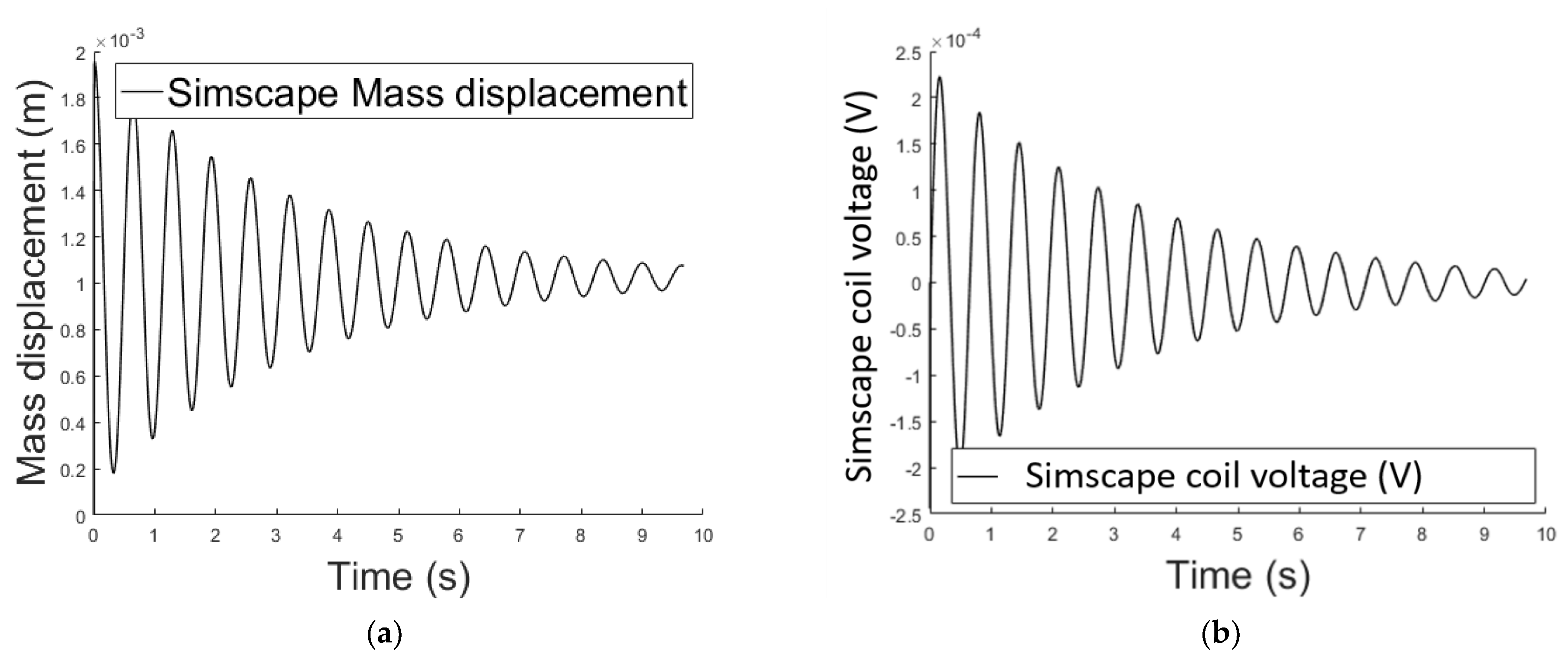
2.3.3. Methods Comparison
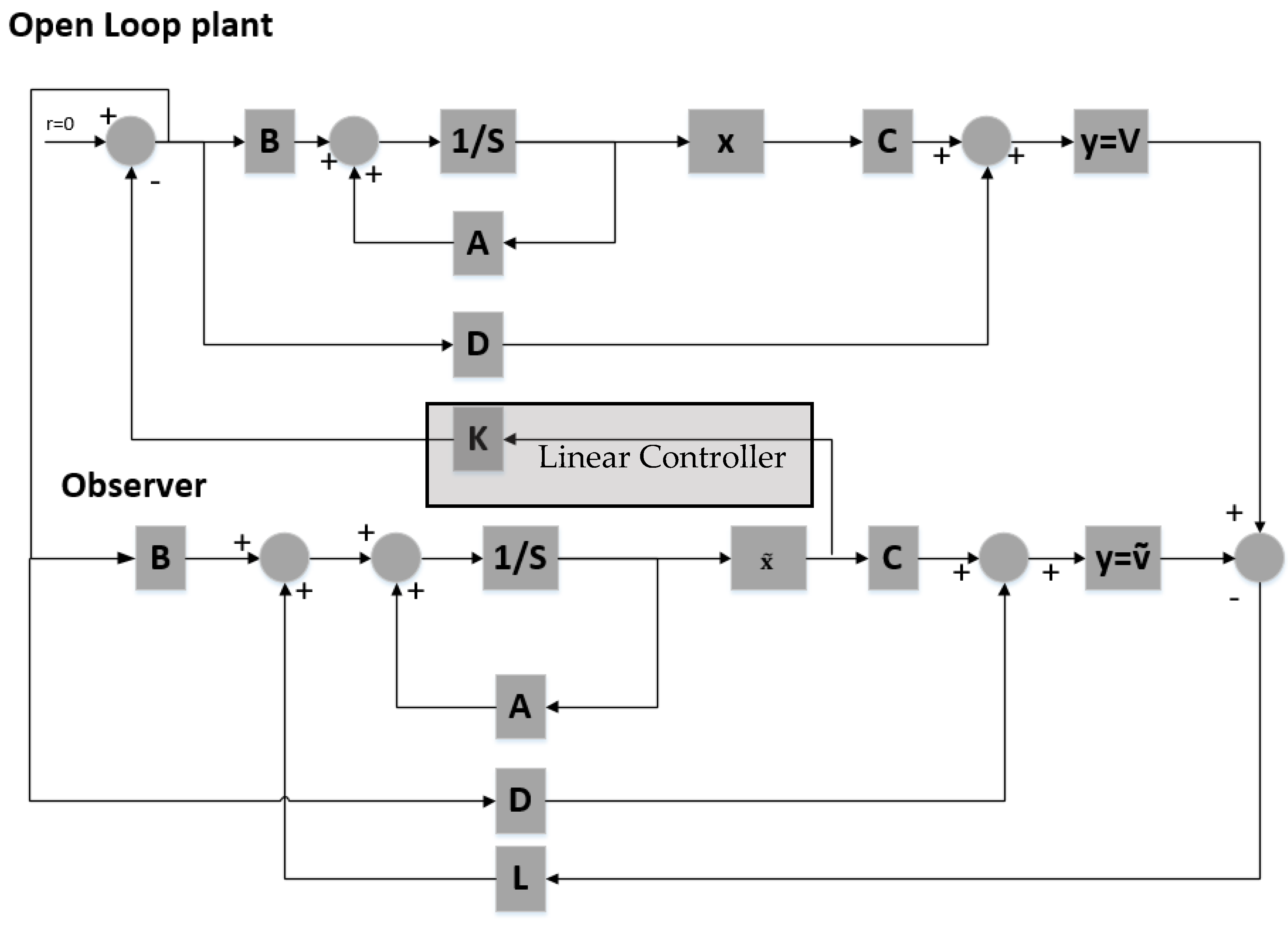
3. State-Space Problem Formulation
4. System Controllability and Observability
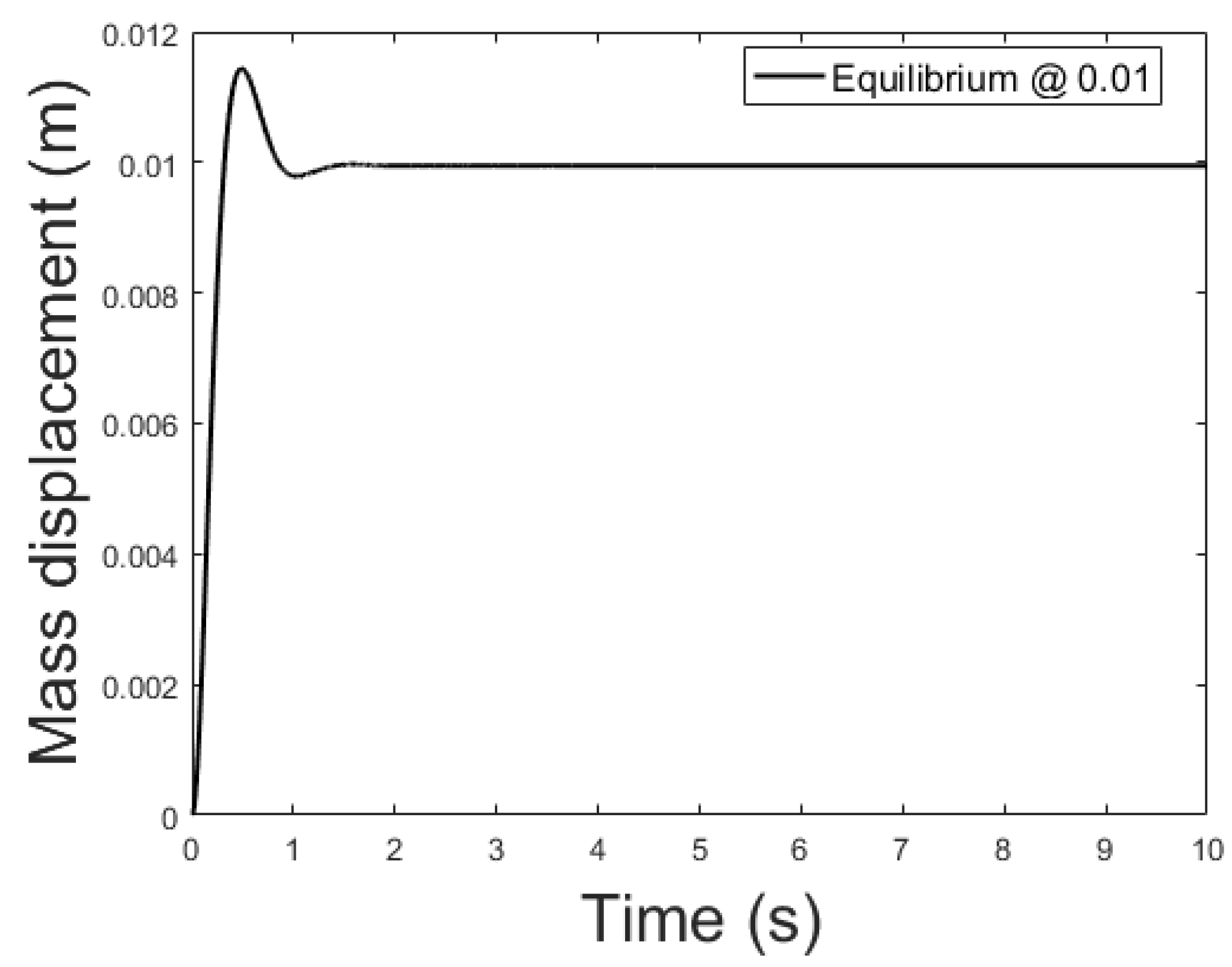
4.1. Linear Controller Design Using Pole Placement
- overshot
- settling time
- , and
- , and
- , and
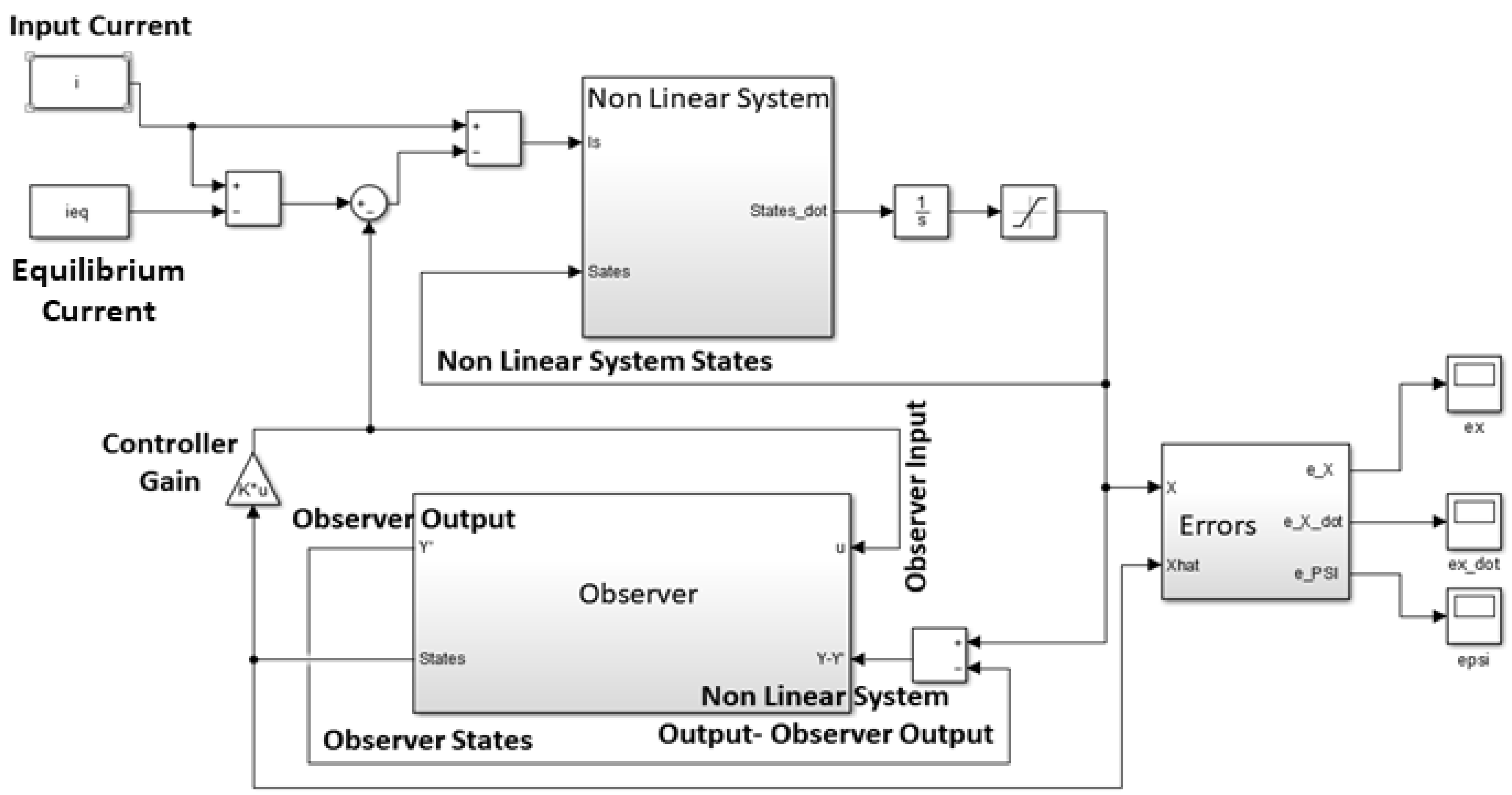
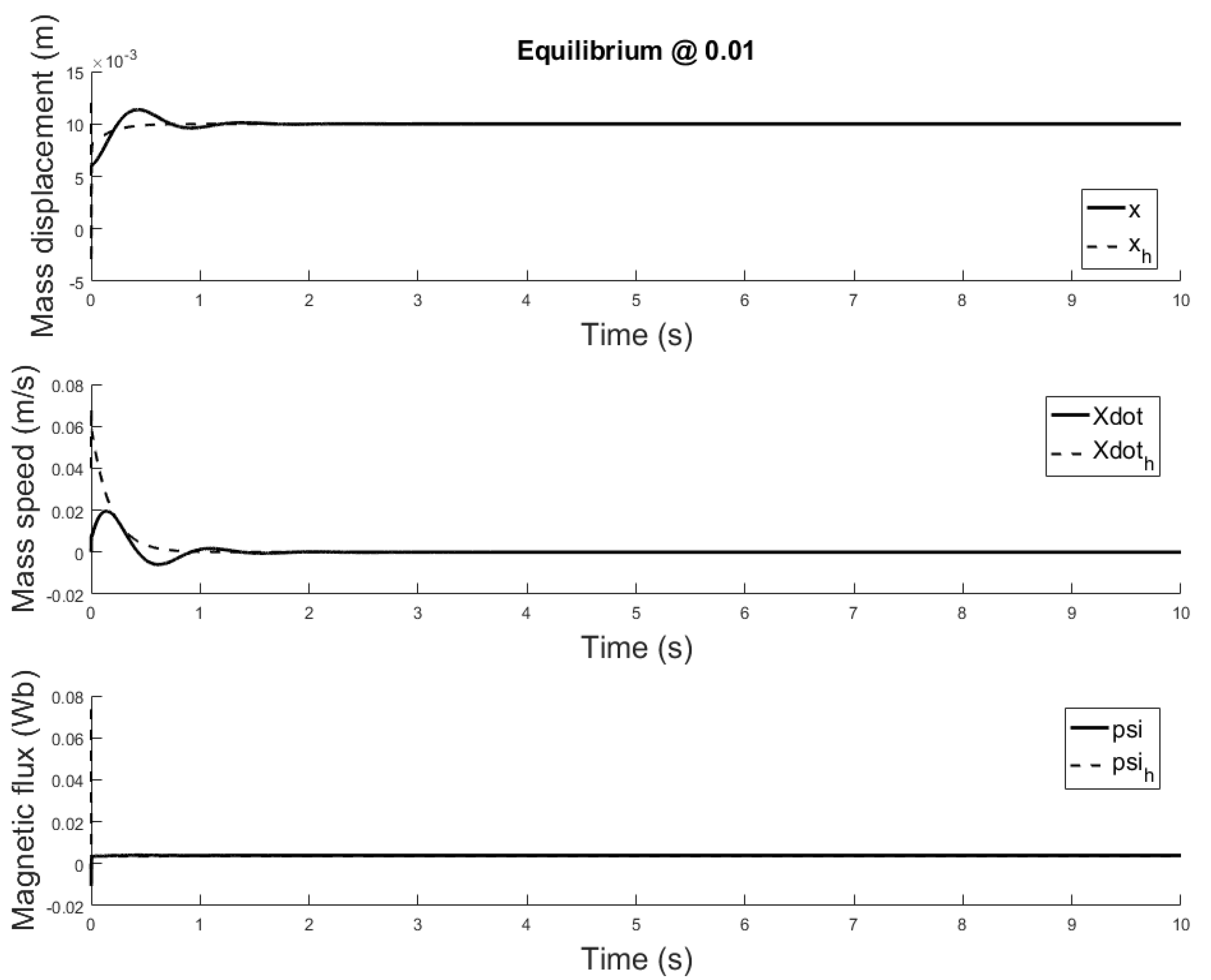
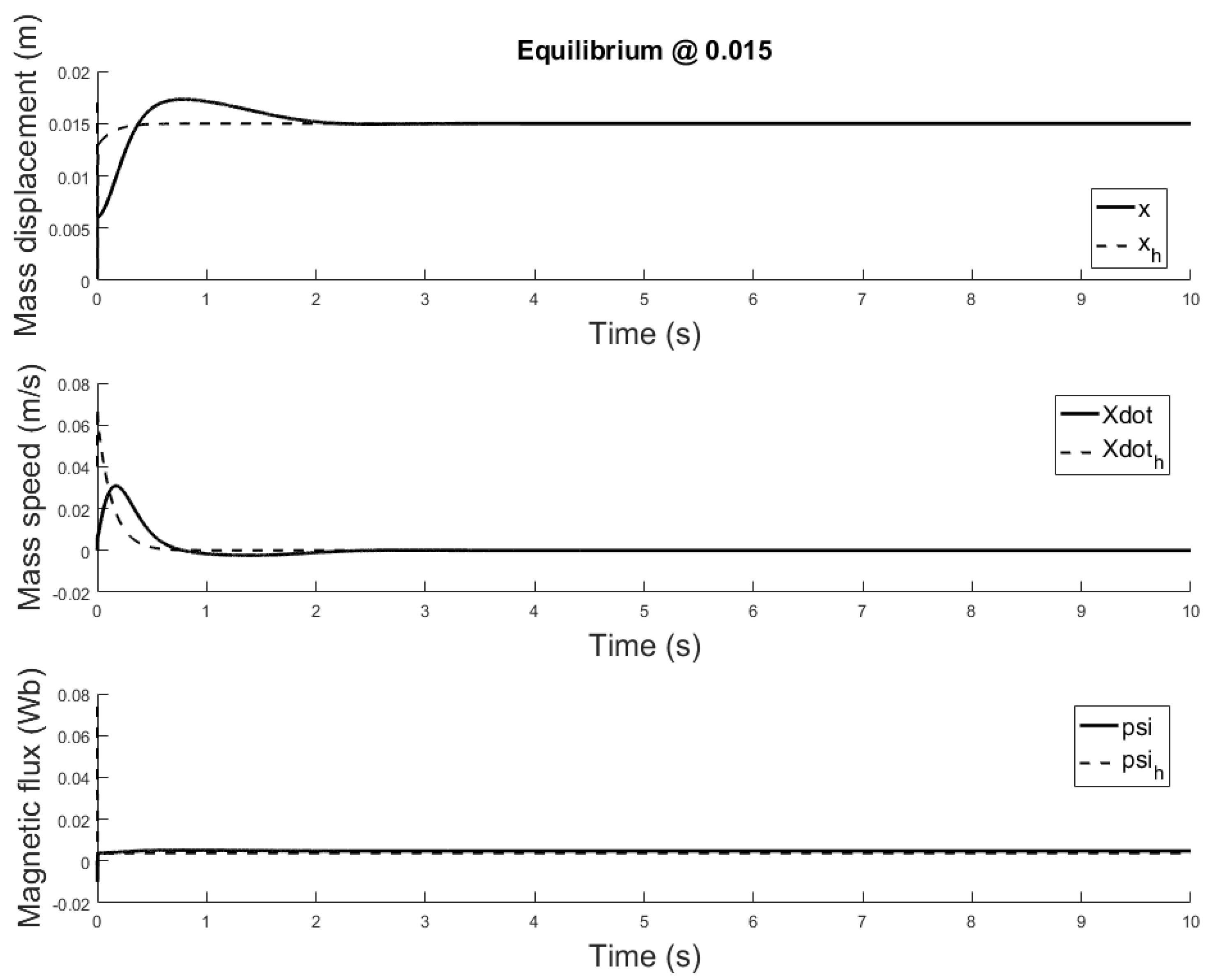
4.2. Observer Design
- m, m
- m/s, m/s
- ,
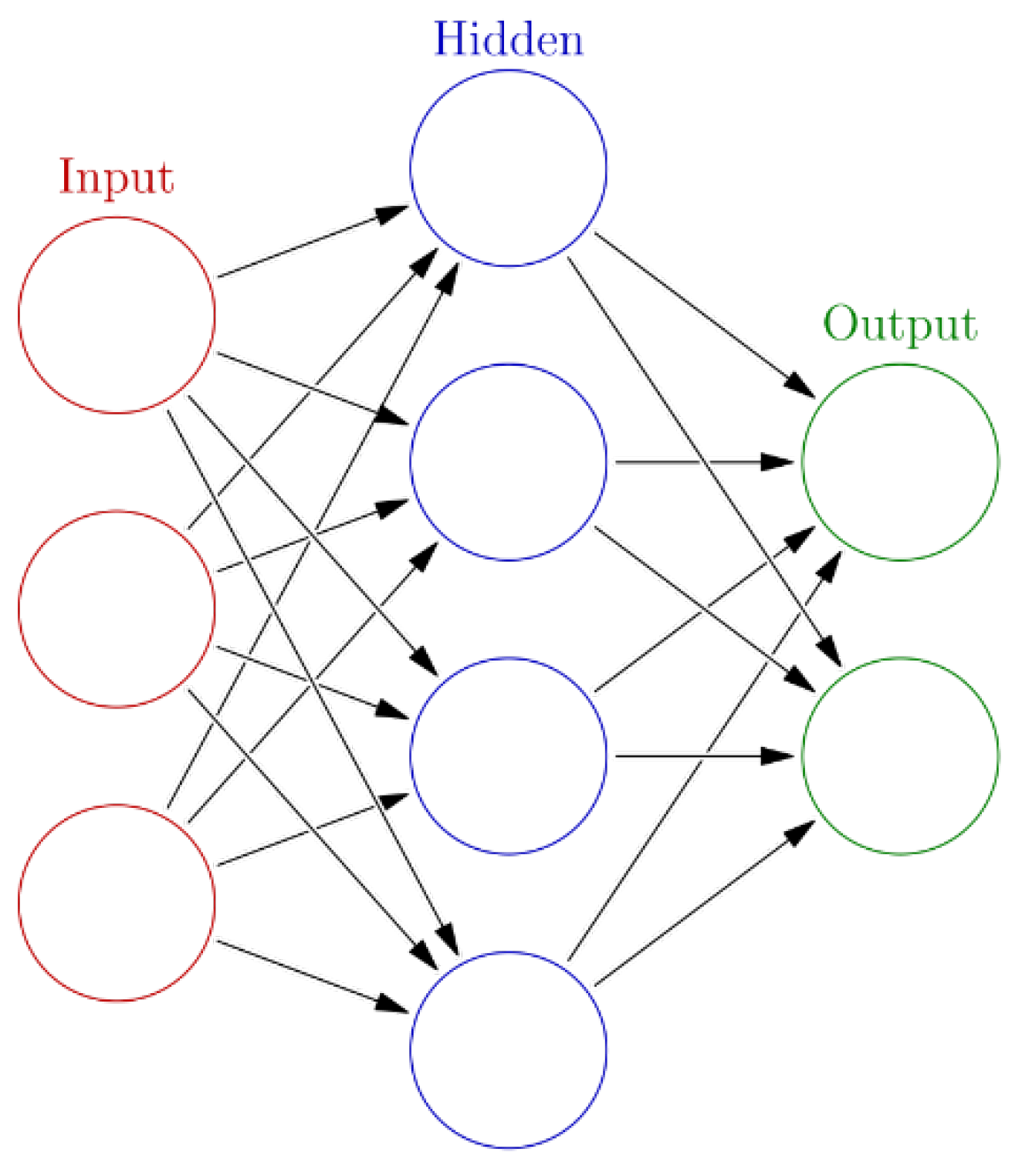
5. Artificial Neural Network (ANN) Representation of the System
- the input layer, where there is no real processing done, is essentially a “fan-out” layer where the input vector is distributed to the hidden layer;
- the hidden layer, being the computational core of the ANN;
- the output layer, which combines all the “votes” of the hidden layer.
- the logistic sigmoid function (Figure 6), commonly abbreviated as logsig,
- the hyperbolic tangent function (Figure 6), commonly abbreviated as tansig,
5.1. ANN System Configuration
- Collect data
- Create the network
- Configure the network
- Initialize the weights and biases
- Train the network
- Validate the network
- Use the network
5.1.1. Generation of ANN Data
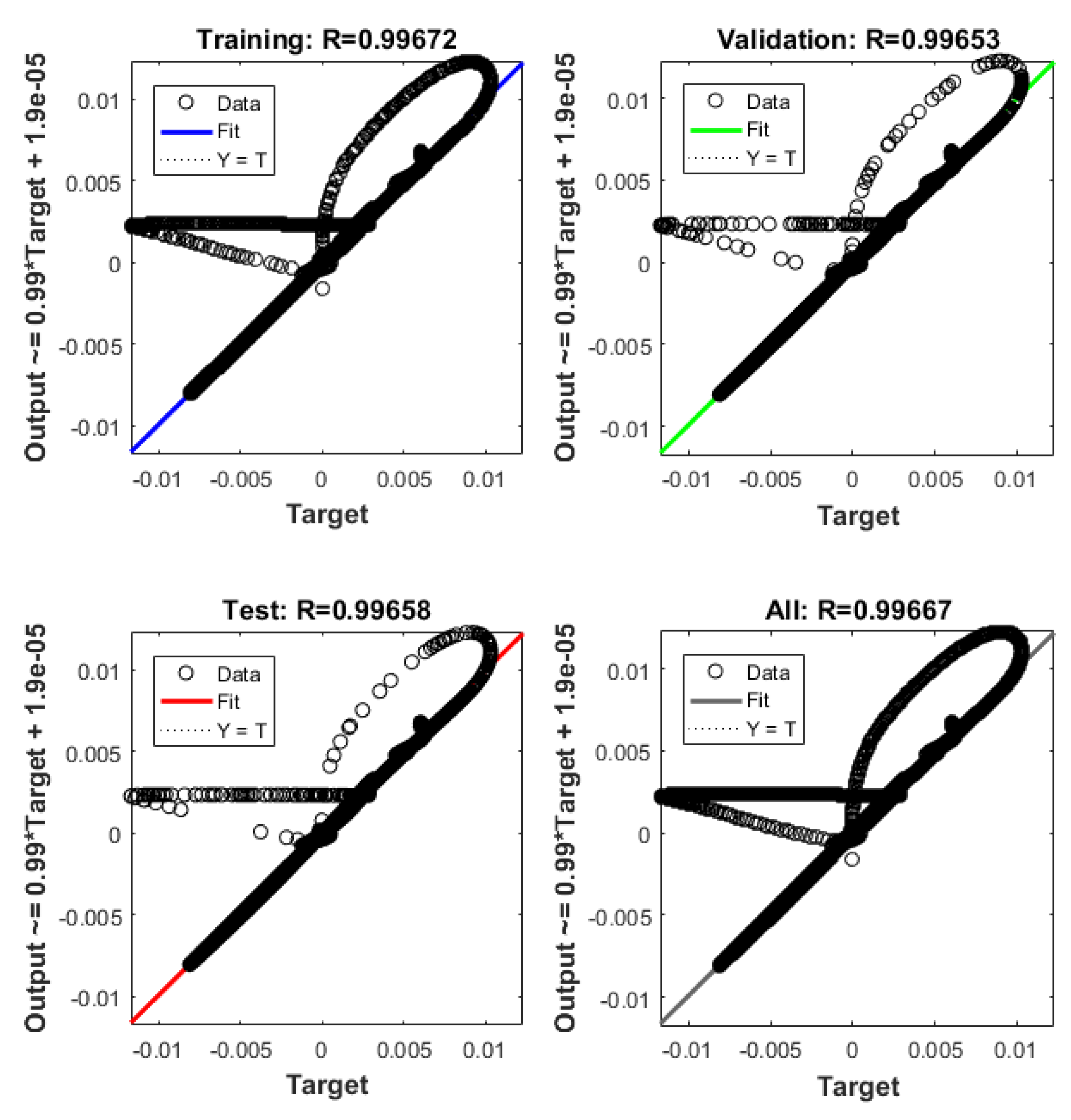
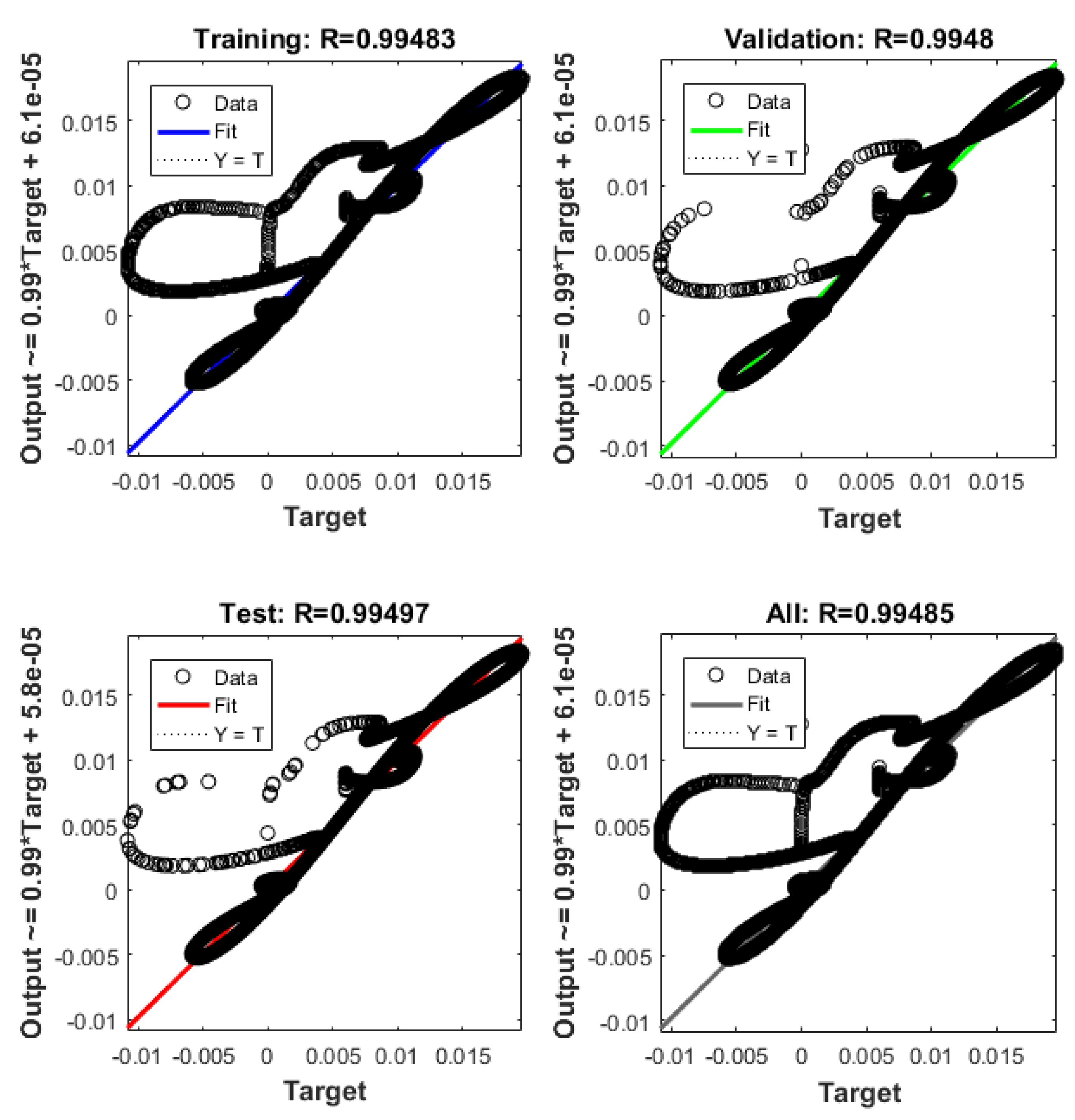
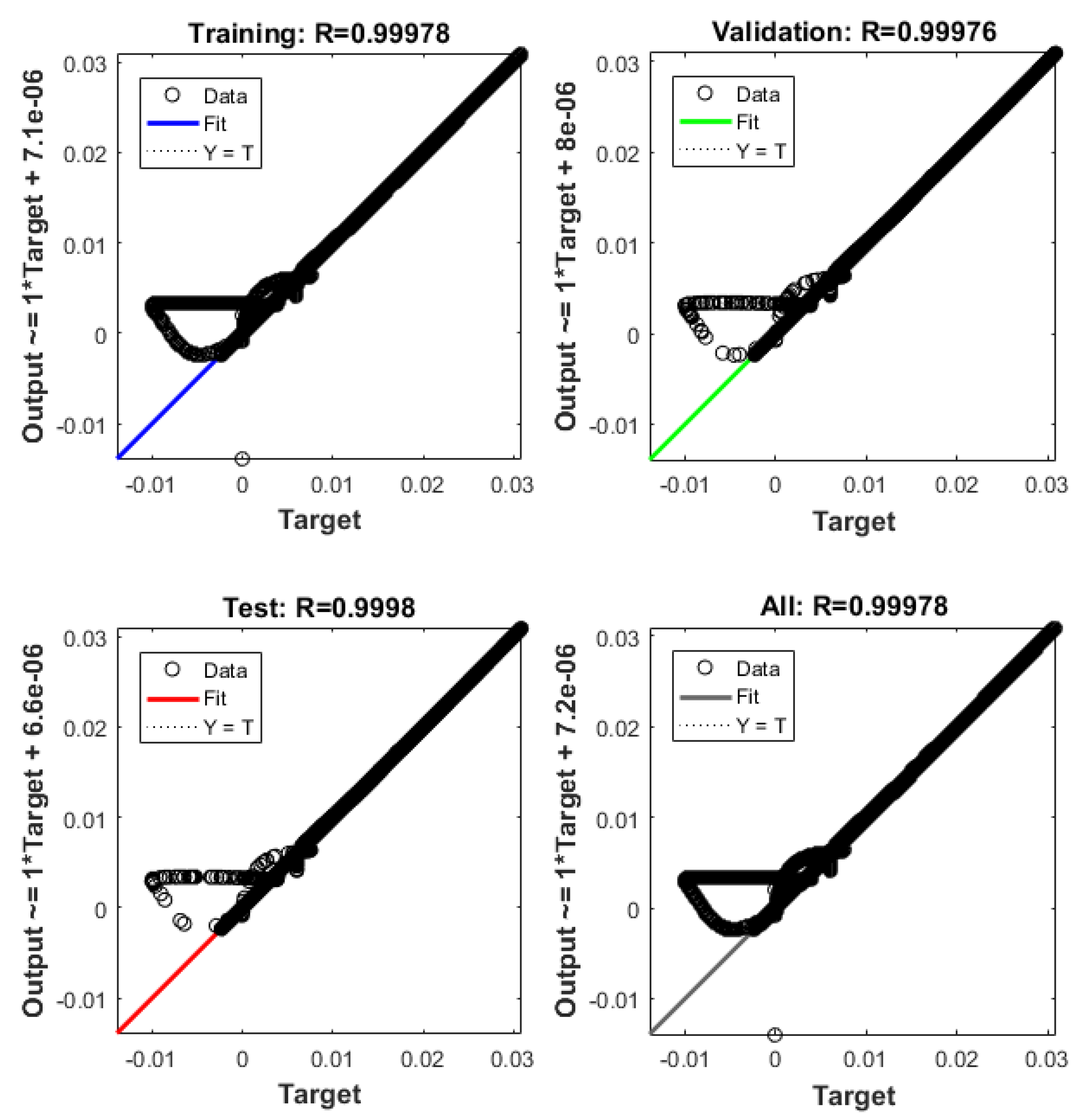
5.1.2. ANN Implementation and Training
- training, 70% of the data;
- validation, 15% of the data;
- and the remaining 15% for testing.
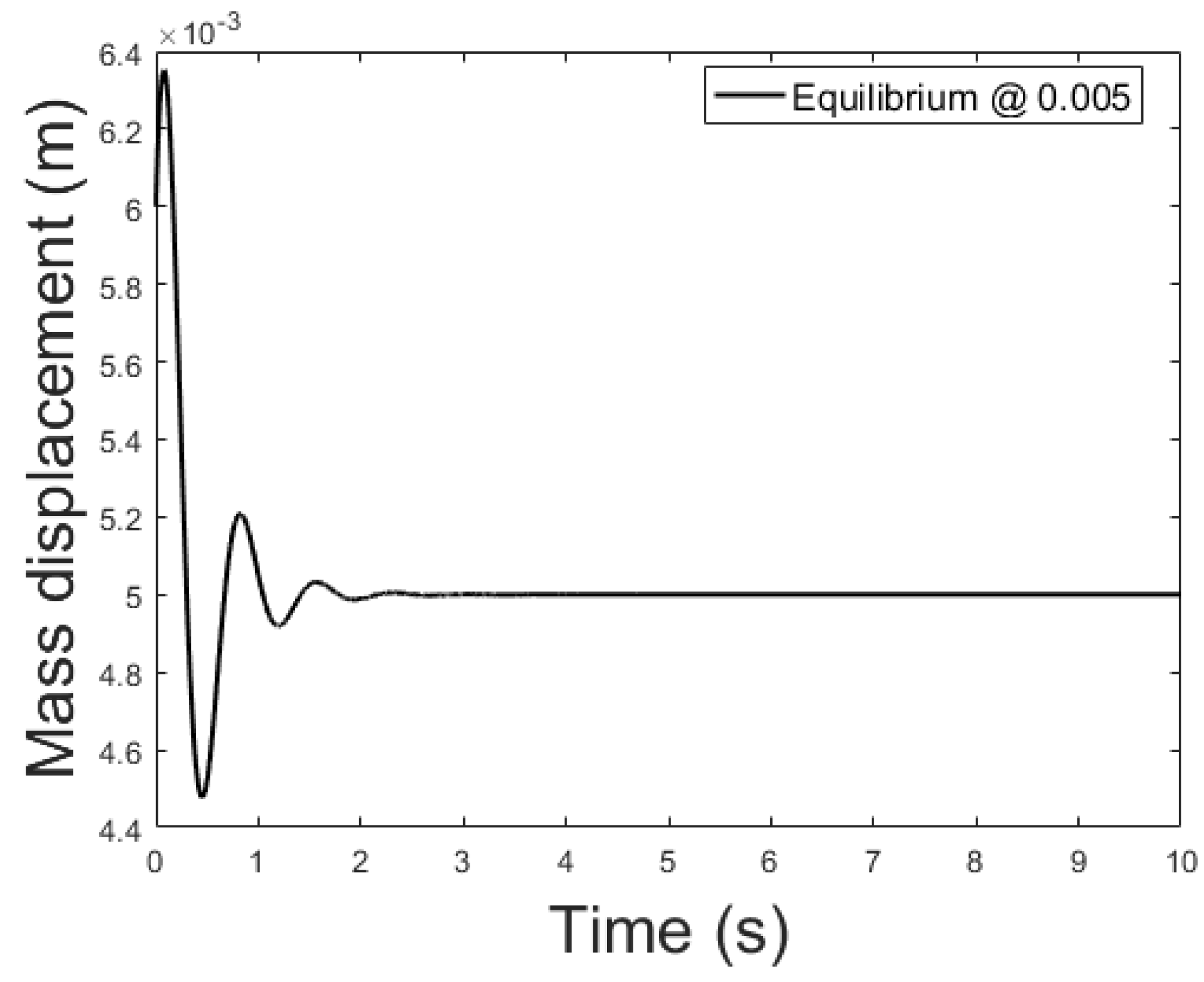
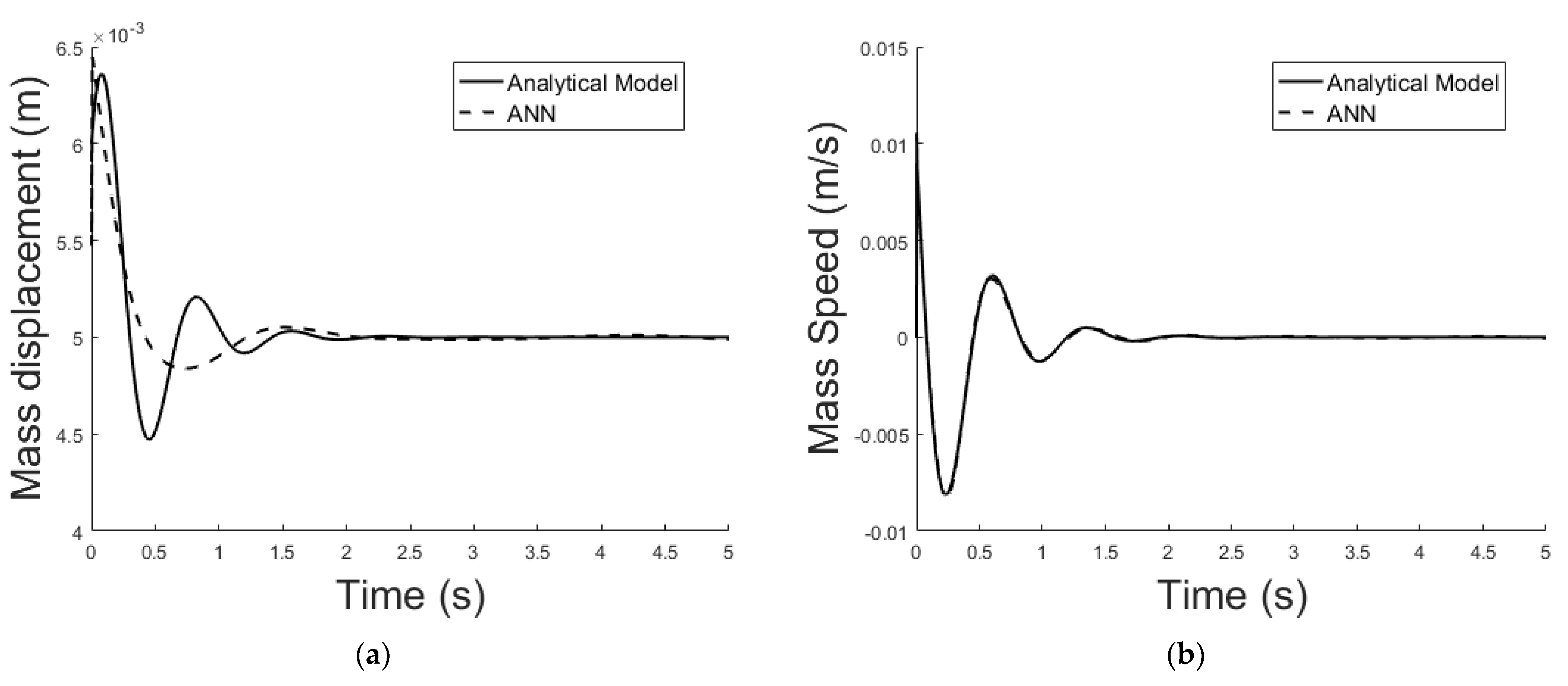
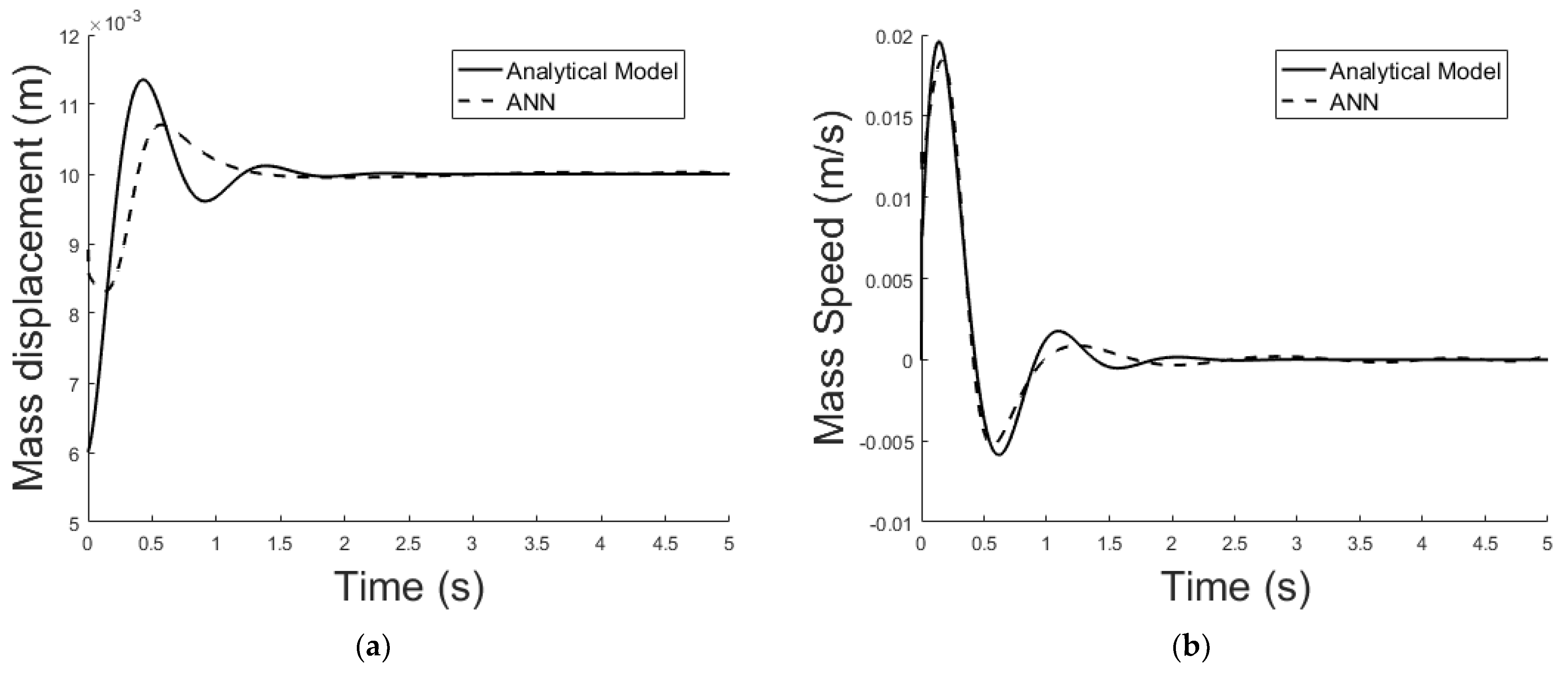
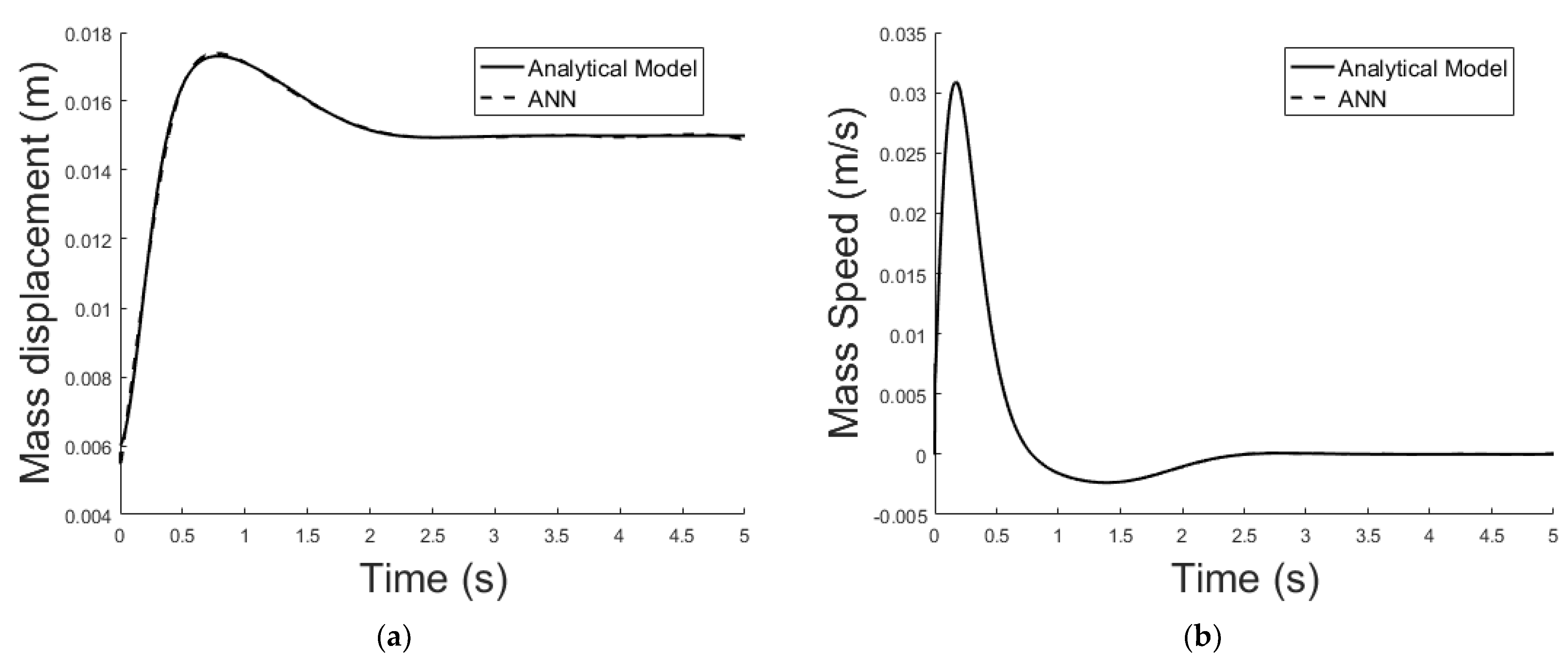
5.2. ANN Simulation of the Non-Linear System-Linear Controller-Observer
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| System matrix | |
| Cross section (m2) | |
| Core cross section (m2) | |
| Closed loop system matrix | |
| Gap cross section (m2) | |
| Mass cross section (m2) | |
| Input matrix | |
| Magnetic flux density (Wb) | |
| Damping constant (Ns/m) | |
| ANN scalar bias | |
| Output matrix | |
| Capacitance (F) | |
| Feedforward matrix | |
| Initial gap length (m) | |
| Energy (J) | |
| LSM error | |
| Observer error | |
| Observer error variation over time | |
| Electromagnetic force (N) | |
| Force (N) | |
| Function | |
| Activation function | |
| Conductance (Ω−1) | |
| Function | |
| Current amplitude (A) | |
| Current (A) | |
| Inductance current (A) | |
| Equilibrium point current (A) | |
| Source current (A) | |
| Source current at equilibrium (A) | |
| Kinetic energy (J) | |
| Constant | |
| Constant | |
| Electrical kinetic energy (J) | |
| Gain matrix | |
| Mechanical kinetic energy (J) | |
| Spring constant (N/m) | |
| Inductance (H) | |
| Lagrangian quantity | |
| Observer gain matrix | |
| Core length (m) | |
| Gap length (m) | |
| Mass length (m) | |
| Controllability matrix | |
| Mass (Kg) | |
| Number of turns | |
| Observability matrix | |
| Dissipation term (J) | |
| Poles | |
| Independent variables | |
| Resistance (Ω) | |
| Magnetic reluctance (H−1) | |
| Core magnetic reluctance (H−1) | |
| Gap magnetic reluctance (H−1) | |
| Mass magnetic reluctance (H−1) | |
| Constant | |
| Potential energy (J) | |
| Electrical potential energy (J) | |
| Mechanical potential energy (J) | |
| Taylor expansion function | |
| Stelling time (s) | |
| Input control vector | |
| Voltage (V) | |
| Inductor voltage (V) | |
| ANN weight matrix between hidden and hidden layer | |
| Displacement (m) | |
| State variable vector | |
| Estimated state variable vector | |
| ANN input vector | |
| Equilibrium point displacement (m) | |
| Equilibrium point speed (m/s) | |
| Observer equilibrium point displacement (m) | |
| Observer equilibrium point speed (m/s) | |
| Output vector | |
| Estimated output vector | |
| ANN output | |
| Neutral position of electromagnetic system | |
| Current deviation from equilibrium point (A) | |
| Displacement deviation from equilibrium point (m) | |
| Speed deviation from equilibrium point (m/s) | |
| Acceleration deviation from equilibrium point (m2/s) | |
| Magnetic flux deviation from equilibrium point (Wb) | |
| Voltage deviation from equilibrium point (V) | |
| Damping ratio | |
| Eigenvalue | |
| Core relative material permeability | |
| Mass relative material permeability | |
| Air permeability (H/m) | |
| Inductance constant | |
| Inductance constant | |
| Inductance constant | |
| Magnetic flux (Wb) | |
| Magnetic flux at equilibrium (Wb) | |
| Observer equilibrium point magnetic flux (Wb) | |
| Natural frequency |
References
- Davino, D.; Loschiavo, V.P. Numerical Simulation of Magnetic Materials. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Schroedter, R.; Csencsics, E.; Schitter, G. Towards the Analogy of Electrostatic and Electromagnetic Transducers. IFAC-PapersOnLine 2020, 53, 8941–8946. [Google Scholar] [CrossRef]
- Ozbay, H. Introduction to Feedback Control Theory, 1st ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Nebyloz, A. Aerospace Sensors; Momentum Press: New York, NY, USA, 2012. [Google Scholar]
- Erjavec, J.; Thompson, R. Automotive Technology: A Systems Approach, 6th ed.; Delmar Cengage Learning: Clifton Park, NY, USA, 2014. [Google Scholar]
- Vera Lucia Da Silveira Nantes Button. Principles of Measurement and Transduction of Biomedical Variables; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Xiros, N.I. Feedback Linearization Systems with Modulated States for Harnessing Water Wave Power. Synthesis Lectures on Ocean Systems Engineering; Morgan & Claypool Publishers: San Rafael, CA, USA, 2020. [Google Scholar]
- Regtien, P.; Dertien, E. Inductive and Magnetic Sensors. In Sensors for Mechatronics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Farmakopoulos, M.G.; Loghis, E.; Nikolakopoulos, P.G.; Xiros, N.I.; Papadopoulos, C. Modeling and Control of the Electrical Actuation System of a Magnetic Hydrodynamic Bearing. In Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition IMECE2014, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Bullo, F.; Cortes, J.; Martinez, S. Distributed Control of Robotic Networks: A Mathematical Approach to Motion Co-Ordination Algorithms; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Tan, Z.; Yang, P.; Nehorai, A. An optimal and distributed demand response strategy with electric vehicles in the smartgrid. IEEE Trans. Smart Grid 2014, 5, 861–869. [Google Scholar] [CrossRef]
- Ogren, P.; Fiorelli, E.; Leonard, N.E. Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment. IEEE Trans. Autom. Control. 2004, 49, 1292–1302. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Yu, W.; Kochurov, N.; Hao, Q.; Hu, F. A Multi-Agent-Based Intelligent Sensor and Actuator Network Design for Smart House and Home Automation. J. Sens. Actuator Netw. 2013, 2, 557–588. [Google Scholar] [CrossRef]
- Xiros, N.I.; Loghis, E.K. Dynamic Modeling and Identification of a Surface Marine Vehicle for Autonomous Swarm Applications. In Proceedings of the ASME 2012 International Mechanical Engineering Congress & Exposition IMECE2012, Houston, TX, USA, 9–15 November 2012. [Google Scholar]
- Xiros, N.I.; Loghis, E. System Identification Using Neural Nets for Dynamic Modeling of a Surface Marine Vehicle. In Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition IMECE2014, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Xiros, N.I.; Loghis, E. A Dynamic Interaction Simulator for Studying Macroscopic Swarm Self-organization of Autonomous Surface Watercraft. In Proceedings of the Twenty-Sixth International Offshore and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Hu, W.; Liu, L.; Feng, G. Consensus of linear multi-agent systems by distributed event-triggered strategy. IEEE Trans. Cybern. 2016, 46, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, M.Z.Q.; Su, H.; Li, C. Consensus networks with switching topology and time-delays over finite fields. Automatica 2016, 68, 39–43. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of multi-agent systems with general linear and Lipschitz nonlinear dynamics using distributed adaptive protocols. IEEE Trans. Autom. Control. 2013, 58, 1786–1791. [Google Scholar] [CrossRef] [Green Version]
- Meng, M.; Liu, L.; Feng, G. Adaptive output regulation of heterogeneous multiagent systems under Markovian switching topologies. IEEE Trans. Cybern. 2018, 48, 2962–2971. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control. 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multiagent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.; Xiros, N.I. Robust Asymptotic and Finite-time Tracking for Second-order Nonlinear Multi-agent Autonomous Systems, International. J. Control. Autom. Syst. 2019, 17, 3069–3078. [Google Scholar] [CrossRef]
- Xiros, N.I. Feedback Linearization of Dynamical Systems with Modulated States for Harnessing Water Wave Power. Synth. Lect. Ocean. Syst. Eng. 2020, 1, 1–75. [Google Scholar] [CrossRef]
- Xiros, N.I. Nonlinear Dynamic Analysis for Control of Electromechanical Systems with Coupled Oscillators. J. Mechatron. 2015, 3, 126–141. [Google Scholar] [CrossRef]
- Panofsky, W.K.H.; Phillips, M. Classical Electricity and Magnetism; Addison-Wesley Pub. Co.: Reading, MA, USA; New Delhi, Indian, 1962. [Google Scholar]
- MATLAB; 9.7.0.1190202 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2018.
- Cairano, S.D.; Bemporad, A.; Kolmanovsky, I.V.; Hrovat, D. Model predictive control of magnetically actuated mass spring dampers for automotive applications. Int. J. Control. 2007, 80, 1701–1716. [Google Scholar] [CrossRef]
- Galushkin, A.I. Neural Network Theory; Springer: New York, NY, USA, 2007. [Google Scholar]









| Partial Derivative | Analytical | Numerical |
|---|---|---|
| −124.01 | −124.86 | |
| −389.97 | −390.76 | |
| −910.103 | −910.45 |
| States | Input | Output |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsakyridis, G.; Xiros, N.I. Dynamics and Control of a Magnetic Transducer Array Using Multi-Physics Models and Artificial Neural Networks. Sensors 2021, 21, 6788. https://doi.org/10.3390/s21206788
Tsakyridis G, Xiros NI. Dynamics and Control of a Magnetic Transducer Array Using Multi-Physics Models and Artificial Neural Networks. Sensors. 2021; 21(20):6788. https://doi.org/10.3390/s21206788
Chicago/Turabian StyleTsakyridis, Georgios, and Nikolaos I. Xiros. 2021. "Dynamics and Control of a Magnetic Transducer Array Using Multi-Physics Models and Artificial Neural Networks" Sensors 21, no. 20: 6788. https://doi.org/10.3390/s21206788
APA StyleTsakyridis, G., & Xiros, N. I. (2021). Dynamics and Control of a Magnetic Transducer Array Using Multi-Physics Models and Artificial Neural Networks. Sensors, 21(20), 6788. https://doi.org/10.3390/s21206788







