Adaptive Strategy to Change Firing Phases of Collided Nodes in Extended-Desync TDMA-Based MANETs
Abstract
1. Introduction
- We deal with the potential and critical problem that Ext-Desync-based schemes have when operated in MANETs, which has been overlooked in other studies. The problem definition in detail and its effect on the networking performances are illustrated in Section 3.1.
- We derive an analytical model to evaluate the problem mathematically. Then, we also derive an optimal criterion for the probability that a collided node will change its firing phase in the following next period after it acknowledges the collision.
- With the criterion, a method for a collided node to determine whether it changes its firing phase or not in a distributed manner is proposed.
- The performances of the proposed method are compared with existing Ext-Desync-based TDMA schemes and CSMA/CA.
2. Background
2.1. Desync-TDMA
2.2. Ext-Desync
3. Extended-Desync TDMA with Optimal Criterion to Change the Firing Phase
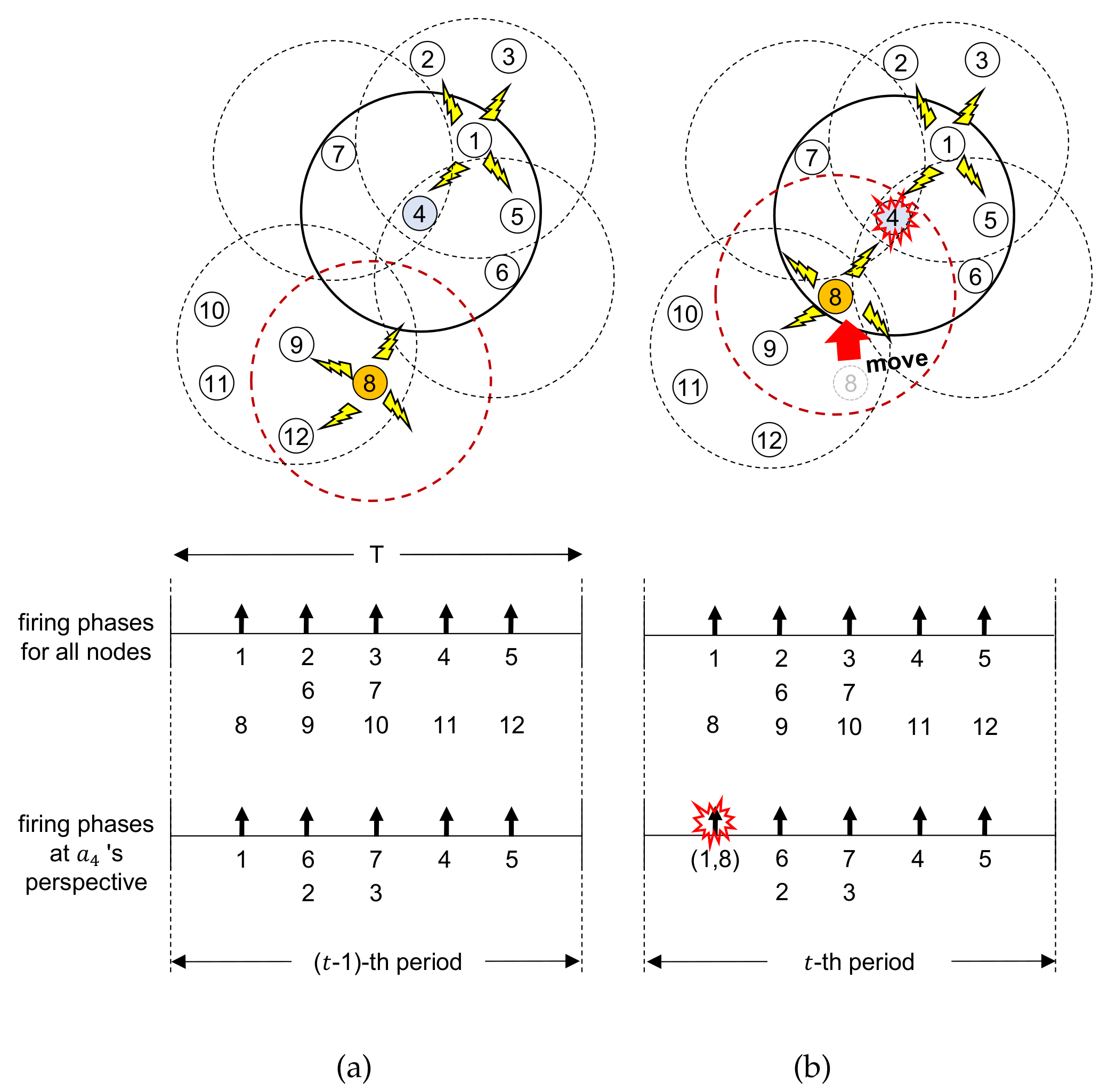
3.1. Problem Definition
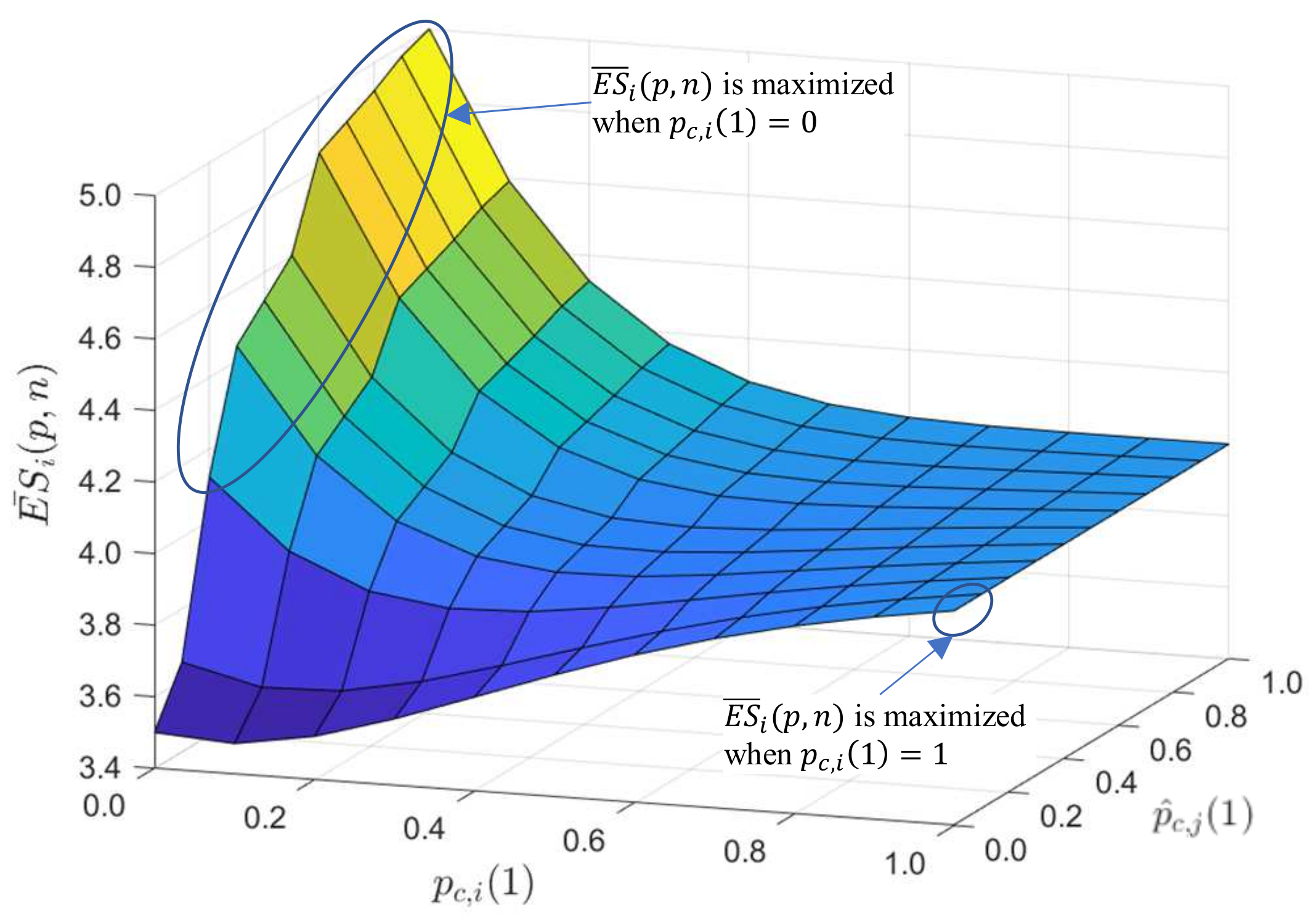
3.2. Criterion of Firing Phase Change to Maximize Slot Utilization
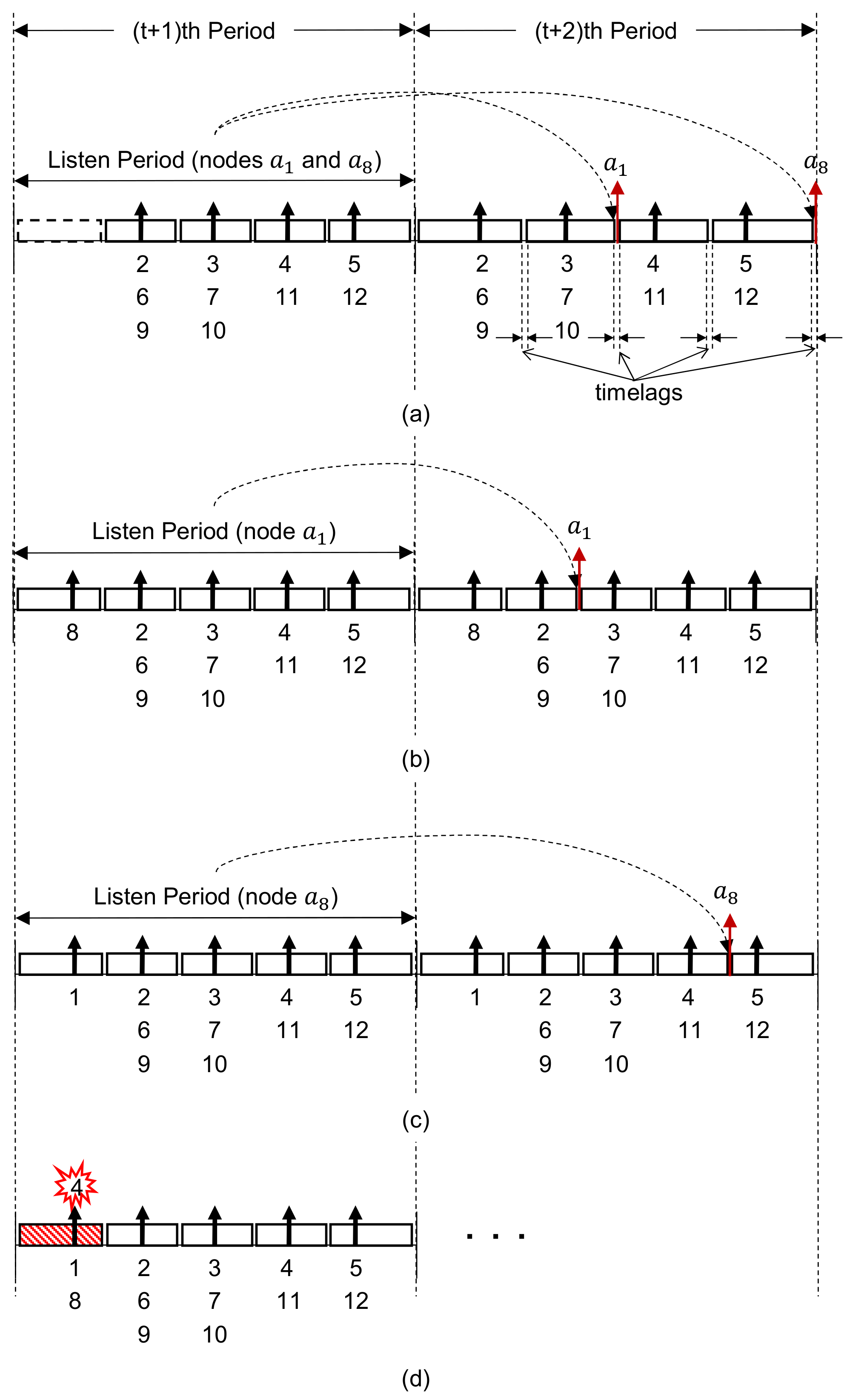
3.3. Ext-Desync TDMA with Optimal Criterion of Firing Phase Change
| Algorithm 1: Proposed Ext-Desync TDMA Procedure with Optimal Criterion of Firing Phase Change. |
 |
| Algorithm 2: Determination of Firing Phase Change with Optimal Criterion. |
 |
4. Numerical Results
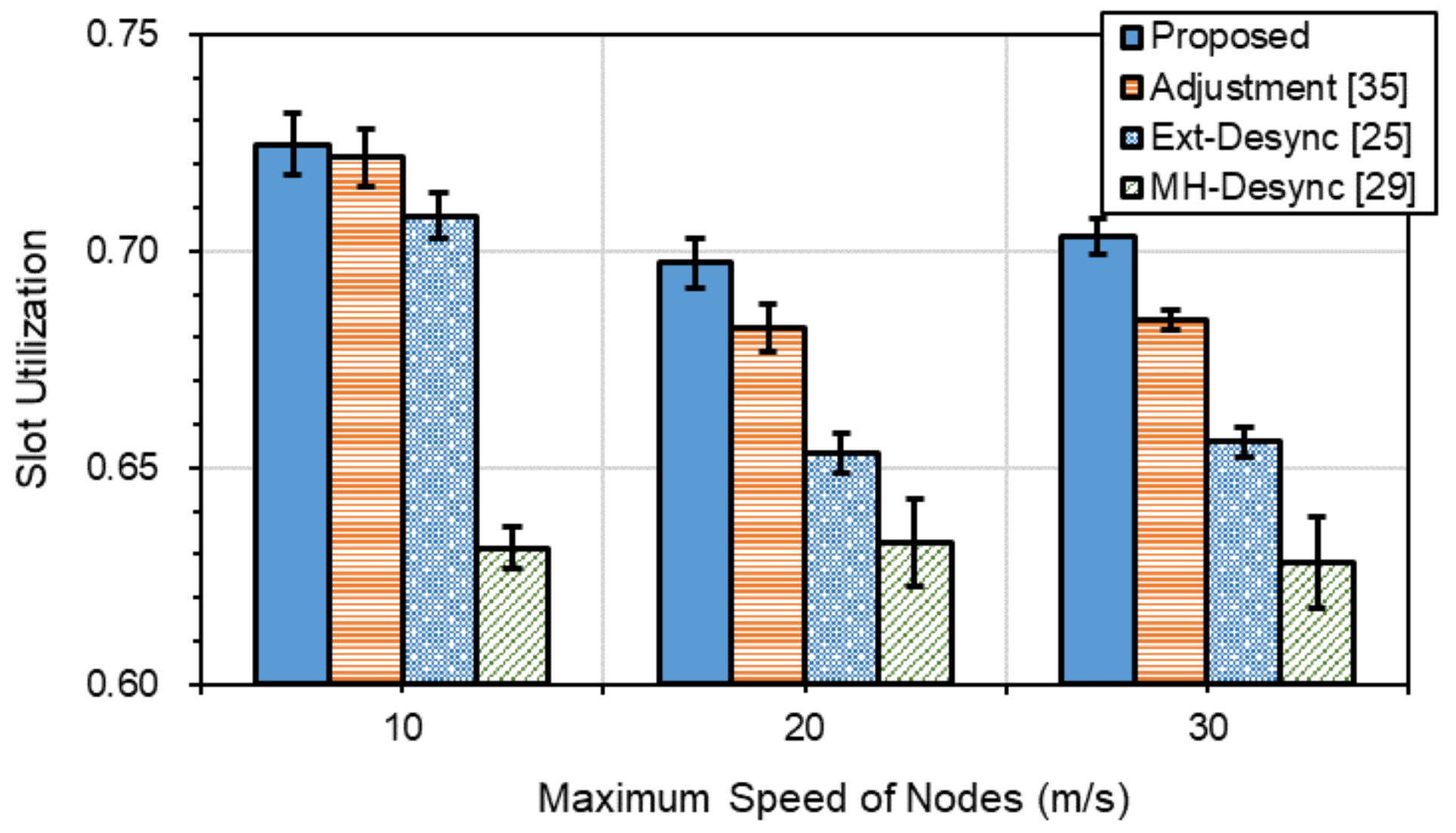
4.1. Collision Resolution Performances
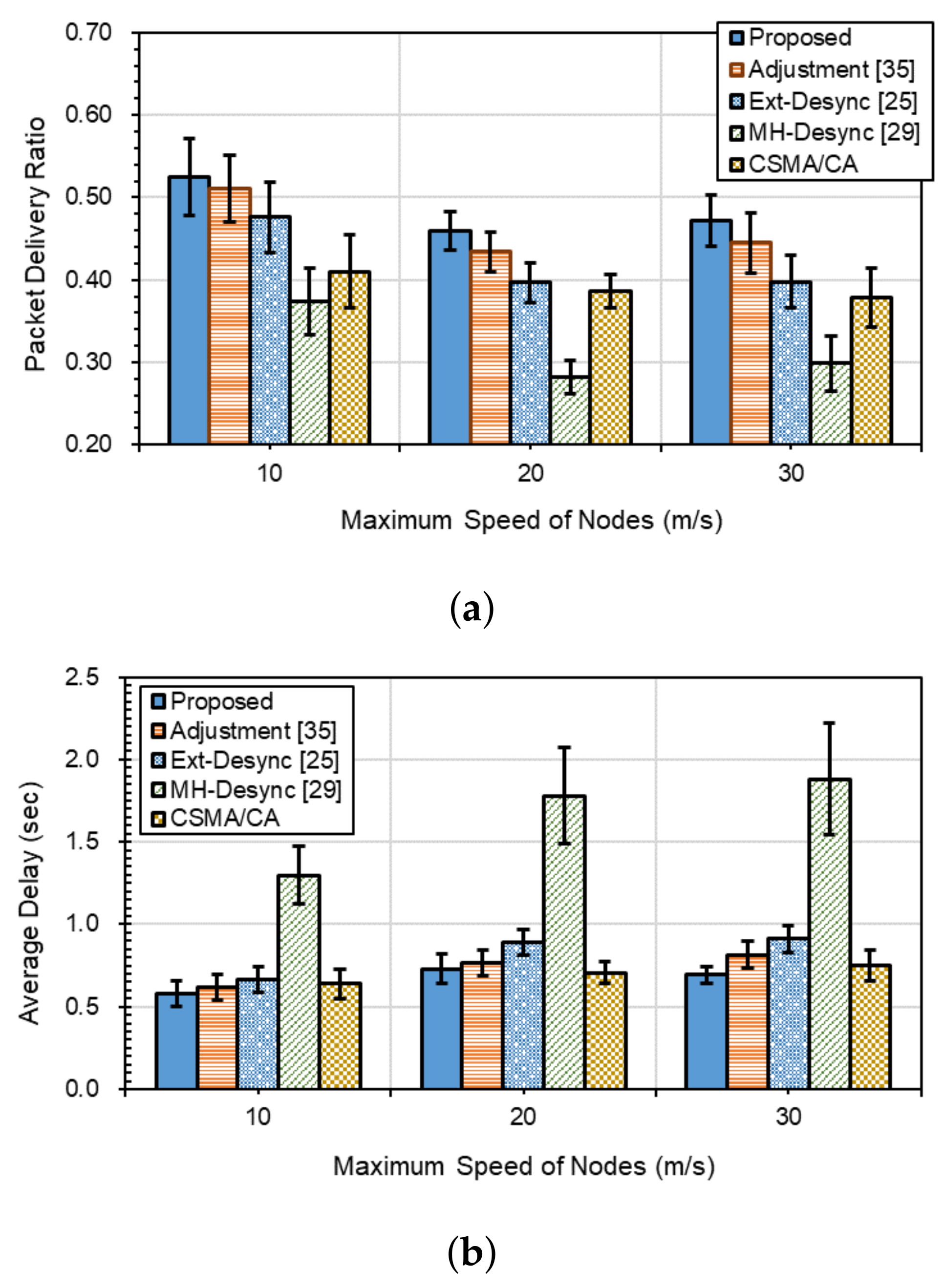
4.2. Packet Delivery Performances
5. Related Work and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| Abbreviation | Meaning |
| BS | Base Station |
| CSMA/CA | Carrier Sense Multiple Access with Congestion Avoidance |
| Desync-TDMA | Desynchronization-based TDMA |
| E2ED | End-to-End Delay |
| Ext-Desync | Extended Desync-TDMA |
| MAC | Medium Access Control |
| MANET | Mobile Ad-hoc Network |
| MH-Desync | Multi-hop Desync-TDMA |
| NOMA | Non-Orthogonal Multiple Access |
| PDR | Packet Delivery Ratio |
| QoS | Quality of Service |
| RTS/CTS | Request To Send/Clear To Send |
| TDMA | Time Division Multiple Access |
| WSN | Wireless Sensor Network |
References
- Zhang, F.; Yang, G. A Stable Backup Routing Protocol for Wireless Ad Hoc Networks. Sensors 2020, 20, 6743. [Google Scholar] [CrossRef] [PubMed]
- Kaszuba-Chęcińska, A.; Chęciński, R.; Gajewski, P.; Łopatka, J. Cognitive Radio MANET Waveform Design and Evaluation. Sensors 2021, 21, 1052. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.K.; Basavaraju, T.; Puttamadappa, C. Ad Hoc Mobile Wireless Networks: Principles, Protocols, and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Sobrinho, J.L.; De Haan, R.; Brazio, J.M. Why RTS-CTS is not your ideal wireless LAN multiple access protocol. In Proceedings of the IEEE Wireless Communications and Networking Conference 2005, New Orleans, LA, USA, 13–17 March 2005. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, X.; Xie, L.; Qin, K. A Dynamic TDMA Scheduling Strategy for MANETs Based on Service Priority. Sensors 2020, 20, 7218. [Google Scholar] [CrossRef] [PubMed]
- Hasan, K.F.; Wang, C.; Feng, Y.; Tian, Y.C. Time synchronization in vehicular ad-hoc networks: A survey on theory and practice. Veh. Commun. 2018, 14, 39–51. [Google Scholar] [CrossRef]
- Jain, M.; Sharma, N.; Gupta, A.; Rawal, D.; Garg, P. Performance Analysis of NOMA Assisted Mobile Ad Hoc Networks for Sustainable Future Radio Access. IEEE Trans. Sustain. Comput. 2021, 6, 347–357. [Google Scholar] [CrossRef]
- Zhang, Z.; Long, K.; Wang, J.; Dressler, F. On Swarm Intelligence Inspired Self-Organized Networking: Its Bionic Mechanisms, Designing Principles and Optimization Approaches. IEEE Commun. Surv. Tutor. 2014, 16, 513–537. [Google Scholar] [CrossRef]
- Jung, J.; Choi, H.; Lee, J. Survey of Bio-Inspired Resource Allocation Algorithms and MAC Protocol Design Based on a Bio-Inspired Algorithm for Mobile Ad Hoc Networks. IEEE Commun. Mag. 2018, 56, 119–127. [Google Scholar] [CrossRef]
- Degesys, J.; Rose, I.; Patel, A.; Nagpal, R. DESYNC: Self-organizing desynchronization and TDMA on wireless sensor networks. In Proceedings of the 2007 6th International Symposium on Information Processing in Sensor Network, Cambridge, MA, USA, 25–27 April 2007. [Google Scholar] [CrossRef]
- Patel, A.; Degesys, J.; Nagpal, R. Desynchronization: The theory of self-organizing algorithms for round-robin scheduling. In Proceedings of the First International Conference on Self-Adaptive and Self-Organizing Systems (SASO 2007), Cambridge, MA, USA, 9–11 July 2007. [Google Scholar] [CrossRef]
- Hinterhofer, T.; Schwefel, H.P.; Tomic, S. RD2: Resilient dynamic desynchronization for TDMA over Lossy Networks. In Proceedings of the 2012 IEEE 31st Symposium on Reliable Distributed Systems, Irvine, CA, USA, 8–11 October 2012. [Google Scholar] [CrossRef]
- Choochaisri, S.; Apicharttrisorn, K.; Korprasertthaworn, K.; Taechalertpaisarn, P.; Intanagonwiwat, C. Desynchronization with an artificial force field for wireless networks. ACM SIGCOMM Comput. Commun. Rev. 2012, 42, 7–15. [Google Scholar] [CrossRef]
- Lien, C.; Chang, S.; Chang, C.; Lee, D. Anchored desynchronization. In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012. [Google Scholar] [CrossRef]
- Taniguchi, Y. Desynchronization-based weighted scheduling adaptive to traffic load for wireless networks. In Proceedings of the 2014 International Conference on Computer, Communications, and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014. [Google Scholar] [CrossRef]
- Gao, H.; Wang, Y. On phase response function based decentralized phase desynchronization. IEEE Trans. Signal Process. 2017, 65, 5564–5577. [Google Scholar] [CrossRef]
- Ceriotti, M.; Murphy, A.L. Reins-MAC: Firefly Inspired Communication Scheduling for Reliable Low-Power Wireless. In Proceedings of the 2018 IEEE 12th International Conference on Self-Adaptive and Self-Organizing Systems (SASO), Trento, Italy, 3–7 September 2018; pp. 140–149. [Google Scholar] [CrossRef]
- Kim, K.; Roh, B.; Shin, S. Firing Offset Adjustment of Bio-Inspired DESYNC-TDMA to Improve Slot Utilization Performances in Wireless Sensor Networks. KSII Trans. Internet Inf. Syst. 2017, 11, 1492–1509. [Google Scholar] [CrossRef]
- Yu, U.; Choi, H.; Lee, J. Kuramoto-Desync: Distributed and Fair Resource Allocation in a Wireless Network. IEEE Access 2019, 7, 104769–104776. [Google Scholar] [CrossRef]
- Hyun, S.; Kim, G.; Yang, D. PD-DESYNC: Practical and Deterministic Desynchronization in Wireless Sensor Networks. KSII Trans. Internet Inf. Syst. 2019, 13, 3880–3899. [Google Scholar] [CrossRef]
- Alshudukhi, J.S.; Al-Mekhlafi, Z.G.; Alshammari, M.T.; Mohammed, B.A. Desynchronization Traveling Wave Pulse-Coupled-Oscillator Algorithm Using a Self-Organizing Scheme for Energy-Efficient Wireless Sensor Networks. IEEE Access 2020, 8, 196223–196234. [Google Scholar] [CrossRef]
- Ron, D.; Lee, J.R. Fair and Distributed Resource Allocation in Wireless Networks Using Frogs’ Calling Behavior Algorithm. IEEE Access 2019, 7, 87313–87322. [Google Scholar] [CrossRef]
- Al-Mekhlafi, Z.G.; Hanapi, Z.M.; Shamsan Saleh, A.M. Firefly-Inspired Time Synchronization Mechanism for Self-Organizing Energy-Efficient Wireless Sensor Networks: A Survey. IEEE Access 2019, 7, 115229–115248. [Google Scholar] [CrossRef]
- Butt, M.M.; Dey, I.; Dzaferagic, M.; Murphy, M.; Kaminski, N.; Marchetti, N. Agent-Based Modeling for Distributed Decision Support in an IoT Network. IEEE Internet Things J. 2020, 7, 6919–6931. [Google Scholar] [CrossRef]
- Mühlberger, C.; Kolla, R. Extended Desynchronization for Multi-Hop Topologies. Technical Report. 2009. Available online: https://www.informatik.uni-wuerzburg.de/fileadmin/10030500/user_upload/staff/muehlberger/Extended_Desynchronization_for_Multi-Hop_Topologies__TR_460_.pdf (accessed on 23 September 2021).
- Pagliari, R.; Hong, Y.; Scaglione, A. Bio-inspired algorithms for decentralized round-robin and proportional fair scheduling. IEEE J. Sel. Areas Commun. 2010, 28, 564–575. [Google Scholar] [CrossRef]
- Zheng, C.; Huang, S.; Wei, J.; Dong, Q. MD-MAC: A Distributed TDMA Protocol Based on Desynchronization for Multi-Hop Topologies. Sensors 2019, 19, 5102. [Google Scholar] [CrossRef]
- Ferrari, L.; Scaglione, A.; Gentz, R.; Hong, Y.P. Convergence results on pulse coupled oscillator protocols in locally connected networks. IEEE/ACM Trans. Netw. 2016, 25, 1004–1019. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, H.; Lee, J. A bioinspired fair resource-allocation algorithm for TDMA-based distributed sensor networks for IoT. Int. J. Distrib. Sens. Netw. 2016, 12, 7296359. [Google Scholar] [CrossRef]
- Yu, U.; Jung, J.; Kong, E.; Choi, H.; Lee, J. Weighted-DESYNC and its application to end-to-end throughput fairness in wireless multihop network. Mob. Inf. Syst. 2017, 2017, 2504604. [Google Scholar] [CrossRef]
- Gentz, R.; Scaglione, A.; Ferrari, L.; Hong, Y. PulseSS: A pulse-coupled synchronization and scheduling protocol for clustered wireless sensor networks. IEEE Internet Things J. 2016, 3, 1222–1234. [Google Scholar] [CrossRef]
- Kim, K.; Lee, C.; Roh, B.H.; Roh, B.S.; Han, M. Routing Metric based on Slot Length of AODV on Multihop DESYNC-TDMA. EAI Endorsed Trans. Mob. Commun. Appl. 2017, 3. [Google Scholar] [CrossRef]
- Roh, B.S.; Han, M.; Hoh, M.; Park, H.; Kim, K.; Roh, B.H. Distributed Call Admission Control for DESYNC-TDMA in Mobile Ad Hoc Networks. EAI Endorsed Trans. Mob. Commun. Appl. 2017, 3. [Google Scholar] [CrossRef][Green Version]
- Jung, J.Y.; Lee, J.R. Distributed Fair Resource Allocation Algorithm in Wireless Multihop Network Systems. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Lee, C.; Lee, G.; Roh, B. Adjustment of firing phase changing probability in extended-Desync TDMA. In Proceedings of the 2018 Wireless Telecommunications Symposium (WTS), Phoenix, AZ, USA, 17–20 April 2018. [Google Scholar] [CrossRef]
- Degesys, J.; Nagpal, R. Towards desynchronization of multi-hop topologies. In Proceedings of the 2008 Second IEEE International Conference on Self-Adaptive and Self-Organizing Systems, Venezia, Italy, 20–24 October 2008. [Google Scholar] [CrossRef]
- Mühlberger, C. Analyzing a self-organizing multi-hop protocol: Ease of simulations and need for real-world tests. In Proceedings of the 2013 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 1–5 July 2013. [Google Scholar] [CrossRef]
- Riverbed. Riverbed Modeler: The Fastest Discrete Event-Simulator for Network Modeling. Available online: https://www.riverbed.com/sg/products/npm/riverbed-modeler.html (accessed on 23 September 2021).




| Variable | Description |
|---|---|
| T | The cyclic period of Desync- and Ext-Desync-based schemes |
| N | The number of nodes in tne network |
| The firing phase of node i in t-th T cycle | |
| The firing phase of other node just before | |
| The firing phase of other node just after | |
| The start time of the node i in t-th period | |
| The end time of the node i in t-th period | |
| constant indicating how is calculated from the average of and | |
| The list of firing phase information of h-hop neighbors managed by node i in the t-th period | |
| Identifier of j-th h-hop neighbor node of node i in t-th period | |
| The relative firing phase with node i of j-th h-hop neighbor node in t-th period | |
| The number of h-hop neighbor node of node i in t-th period | |
| The firing phase of node | |
| G | The length of the timelag of Ext-Desync-based schemes |
| Variable | Description |
|---|---|
| Node that acknowledged the collision of its firing message in the 0-th period | |
| Number of one-hop neighbors of in the n-th period () | |
| Number of hidden nodes that cause the collision to ’s firing message in the n-th period () | |
| Nodes of hidden to in the n-th period () | |
| Probability that changes its firing phase in the n-th period () | |
| Probability that does not change its firing phase until the n-th period ( () | |
| Expected slot size for when it changes its firing phase before n-th period () | |
| Expected slot size for when it does not change its firing phase until the n-th period () | |
| Probability estimated by that a node , caused the collision of ’s firing message in the n-th period, will change its firing phase in the n-th period, where () | |
| Amount of slot size available to up to the n-th period() | |
| Amount of slot size that fails to transmit data due to the collision up to the n-th period () | |
| Amount of slot size that succeeds to transmit data up to the n-th period, () |
| Features | Proposals | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Degesys et al. [10,11] | Hinterhofer et al. [12] | Choochaisri et al. [13] | Lien et al. [14] | Taniguchiet al. [15] | Gao et al. [16] | Ceriotti et al. [17] | Kim, Shin et al. [18] | Yu, Choi et al. [19] | Hyun et al. [20] | Alshudukhi et al. [21] | Ron et al. [22] | Muhlberger et al. [25] | Pagliari et al. [26] | Zheng et al. [27] | Ferrari et al. [28] | Kim, Choi et al. [29] | Yu, Jung et al. [30] | Gentz et al. [31] | Jung et al. [34] | Lee et al. [35] | This work | |
| MH support | X | X | X | X | X | X | X | X | X | X | X | X | O | O | O | O | O | O | O | O | O | O |
| HTP resolution in MH comm. | X | X | X | X | X | X | X | X | X | X | X | X | O | X | O | X | O | O | O | O | O | O |
| nodes’ mobility support | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | O | O |
| robustness on firing message collision | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | O | O |
| consideration of PL degradation in resolving collisions | X | O | X | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | O |
| consideration of SU degradation in resolving collisions | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | O |
| requirement on global time synchronization | X | X | X | X | X | X | X | X | X | X | X | O | X | X | O | X | O | O | X | O | X | X |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-W.; Lee, G.-M.; Roh, B.-H. Adaptive Strategy to Change Firing Phases of Collided Nodes in Extended-Desync TDMA-Based MANETs. Sensors 2021, 21, 6776. https://doi.org/10.3390/s21206776
Lee C-W, Lee G-M, Roh B-H. Adaptive Strategy to Change Firing Phases of Collided Nodes in Extended-Desync TDMA-Based MANETs. Sensors. 2021; 21(20):6776. https://doi.org/10.3390/s21206776
Chicago/Turabian StyleLee, Cheol-Woong, Gyu-Min Lee, and Byeong-Hee Roh. 2021. "Adaptive Strategy to Change Firing Phases of Collided Nodes in Extended-Desync TDMA-Based MANETs" Sensors 21, no. 20: 6776. https://doi.org/10.3390/s21206776
APA StyleLee, C.-W., Lee, G.-M., & Roh, B.-H. (2021). Adaptive Strategy to Change Firing Phases of Collided Nodes in Extended-Desync TDMA-Based MANETs. Sensors, 21(20), 6776. https://doi.org/10.3390/s21206776







